1. Introduction
During acquisition and transmission, the quality of digital images inevitably degrades owing to corruption caused by various reasons. Therefore, the ability to recover a clean image from a noisy one is of great importance, and image denoising is a fundamental step applied in all image processing pipelines. In the computer vision field, image denoising has been a research hotspot since the 1990s. After decades of research, many denoising algorithms had achieved good results through approaches such as non-local self-similarity in natural images [
1,
2,
3], low rankness-based models [
4,
5], sparse representation-based models [
3,
6,
7], and fuzzy (or neuro-fuzzy)-based models [
8,
9]. Nevertheless, researchers are still aiming to further improve the performance of image denoising algorithms.
Existing denoising algorithms can be roughly divided into internal algorithms and external algorithms [
10]. Internal algorithms utilize the noisy image itself, while the external algorithms exploit clean, natural images related to the noisy image. Internal image denoising algorithms include filter algorithms, low rankness-based models, and sparse representation-based algorithms. Representative examples of filter algorithms are the non-local means (NLM) algorithm and the block-matching and 3D filtering (BM3D) algorithm. The NLM algorithm [
1], proposed by Baudea et al. in 2005, exploited non-local self-similarity in natural images. It first finds similar patches and obtains their weighted average to achieve the denoised patches. Although it exhibits excellent performance, the NLM algorithm is limited by its inability to identify truly similar patches in a noisy environment. BM3D [
2], a benchmark denoising algorithm, starts with the block-matching of each reference block, and obtains 3D arrays by grouping similar blocks together. The authors used a two-step algorithm to denoise an image. First, they denoised the input image simply and obtained a basic estimate; next, they achieved an improved denoising effect through collaborative filtering of the basic estimate. Among low rankness-based methods, nuclear norm minimization (NNM) and weighted nuclear norm minimization (WNNM) are two well-known algorithms. The NNM algorithm [
4] was proposed by Ji et al. for video denoising. In their work, the problem of removing noise was transformed into a low-rank matrix completion problem, which can be well solved by singular value decomposition. However, the authors equalized each singular value to ensure the convexity of the objective function, which severely restricts its capability and flexibility when dealing with denoising problems. Based on the NMM algorithm and proposed in [
5], the WNNM algorithm takes advantage of the non-local self-similarity of the image for denoising. Among sparse representation-based algorithms, the K-singular value decomposition (K-SVD) algorithm, the learned simultaneous sparse coding (LSSC) algorithm, and the non-locally centralized sparse representation (NCSR) algorithm are three noteworthy algorithms. K-SVD [
6] is a classic dictionary learning algorithm, which utilizes the sparsity and redundancy of over-complete learning dictionaries to produce high-quality denoising images. LSSC [
3] exploits the combination of the self-similarity of image patches and sparse coding to further boost denoising performance. The NCSR [
7] algorithm was proposed by Dong et al. and utilizes non-local self-similarity and sparse representation of images. It introduces the concept of sparse coding noise with the goal of suppressing the sparse coding noise to denoise an image. In general, most of these traditional denoising methods use custom-made image priority and multiple, manually selected parameters, providing ample room for improvement.
In recent years, deep learning-based methods have become a popular research direction in the field of image denoising. These methods can be categorized as external methods whose denoising performance is superior to internal methods. The main idea is to collect a large number of noise-clean image pairs, and then train the deep neural network denoiser using end-to-end learning. These methods have significant advantages in accumulating knowledge from big datasets; thus, they can achieve superior denoising performance. In 2017, Zhang et al. proposed Deep CNN (DnCNN) [
11], which exploited the residual learning strategy to remove noise. They introduced the batch normalization technique as it not only reduced the training time, but also boosted the denoising effect quantitatively and qualitatively. However, it is only effective when the noise level is within a pre-set range. Hence, Zhang et al. proposed FFDNet in [
12]. FFDNet showed considerable improvement in flexibility and robustness using a single network. Specifically, it was formulated as
, where
x is the expected output,
y is the input noise observation, and
M is a noise level map. In the DnCNN model
, the parameters
change with the noise level. As for the FFDNet model,
M is modeled as the input and the hyper-parameters have no relationship to the noise level. Therefore, it could handle different noise levels in a flexible manner using a single network. The consensus neural network (CsNet) was proposed by Choi et al. [
13], and combines multiple relatively weak image denoisers to produce a satisfactory result. CsNet exhibits superior performance in three aspects: solving the noise level mismatch, incorporating denoisers for different image classes, and uniting different denoiser types. In summary, these supervised denoising networks are exceedingly effective when supplied with plenty of noise-clean image pairs for training, but collecting clean images of the ground truth in many real-world scenarios is very difficult. Moreover, if the image priors are significantly different from the image to be denoised, the supervised denoising networks tend to produce hallucination-like effects when handling an unseen noisy image, because the previously learned image statistics cannot handle the untouched image content and noise level well. These networks have strong data dependence [
14], leading to a lack of flexibility.
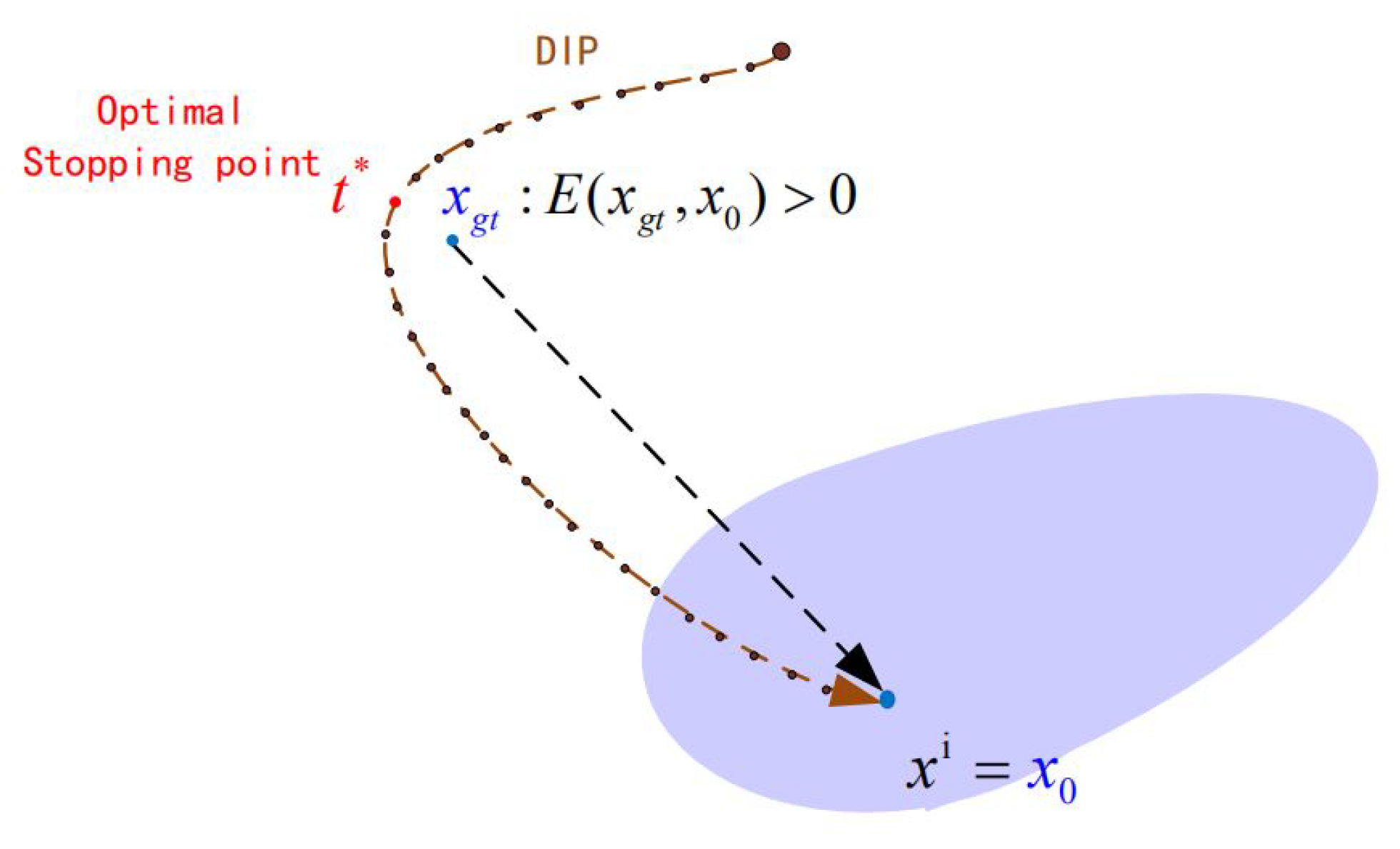
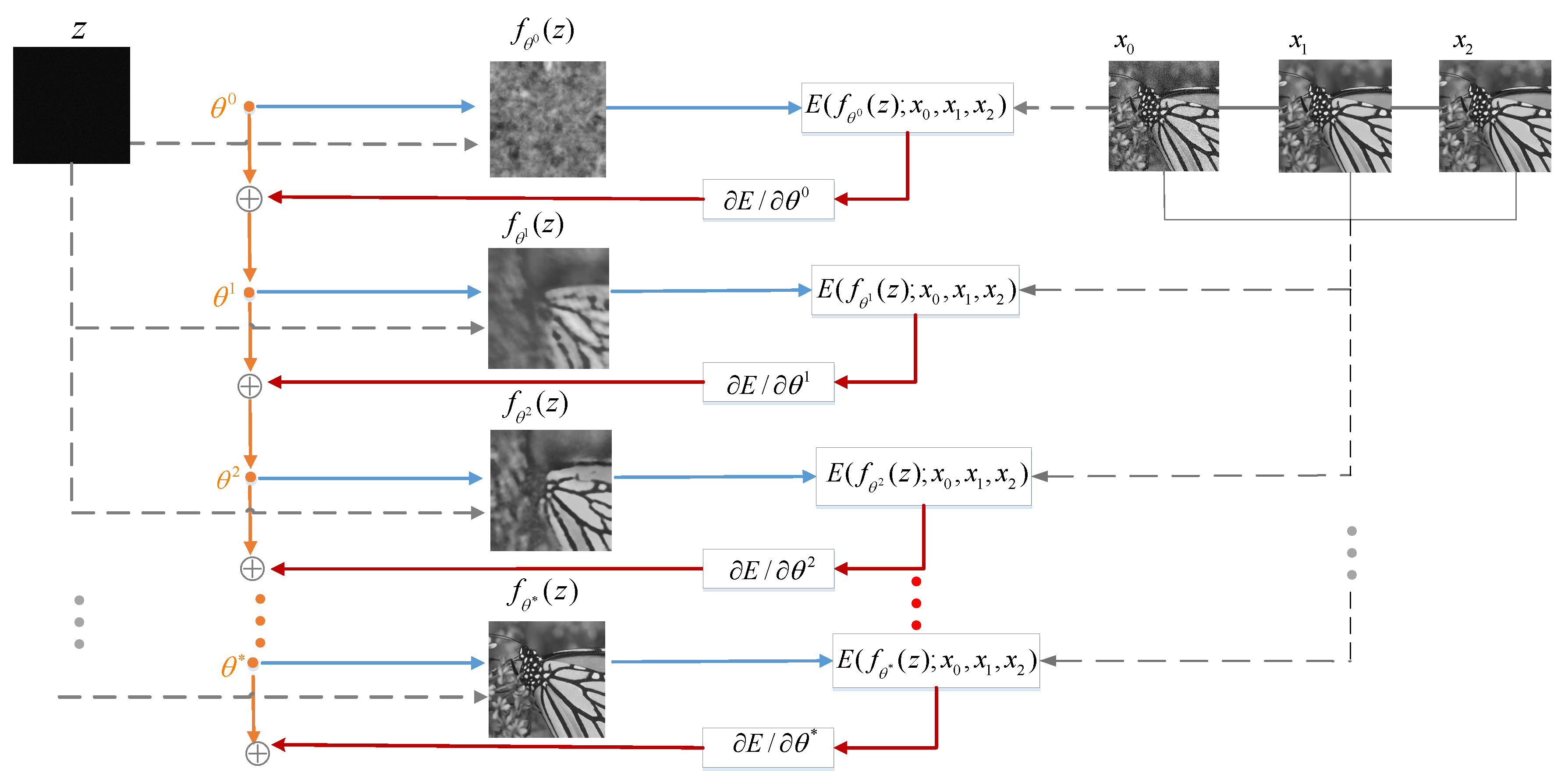
To overcome the aforementioned limitations, researchers have focused on training unsupervised denoising networks without training images. Recently, research on generative networks using the deep image prior (DIP) framework [
15] demonstrated that even if only the input image itself is used in training, deep convolutional neural networks (CNNs) can still provide superior performance on various inverse problems. No prior training is required, and random noise is used as the network input to generate denoised images. It can be widely used in image noise reduction, super-resolution, and other image restoration problems. Because the hyper-parameters of DIP are determined based on the specific noisy image, it may, in some cases, achieve better denoising results than the supervised denoising models. As shown in
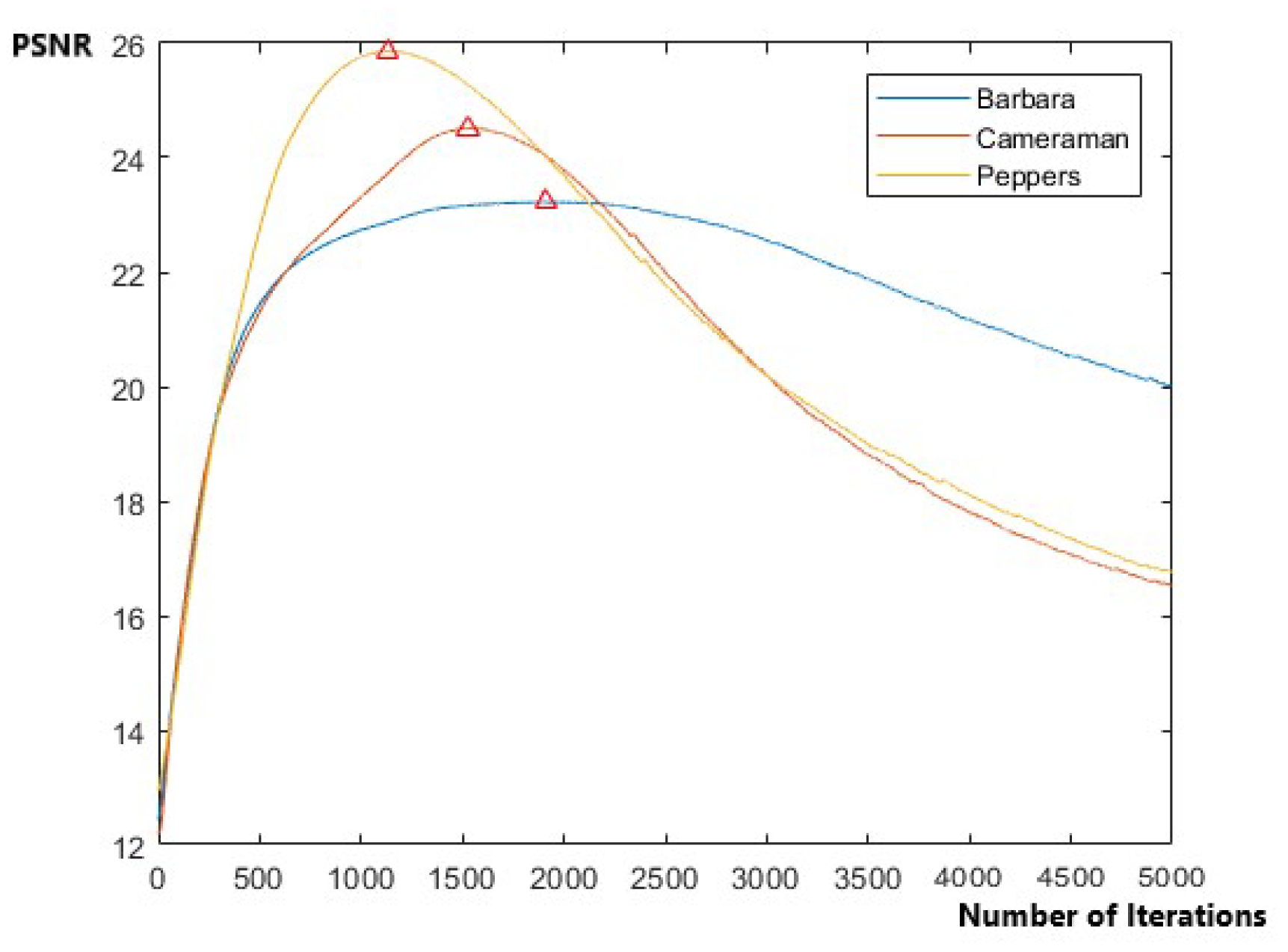
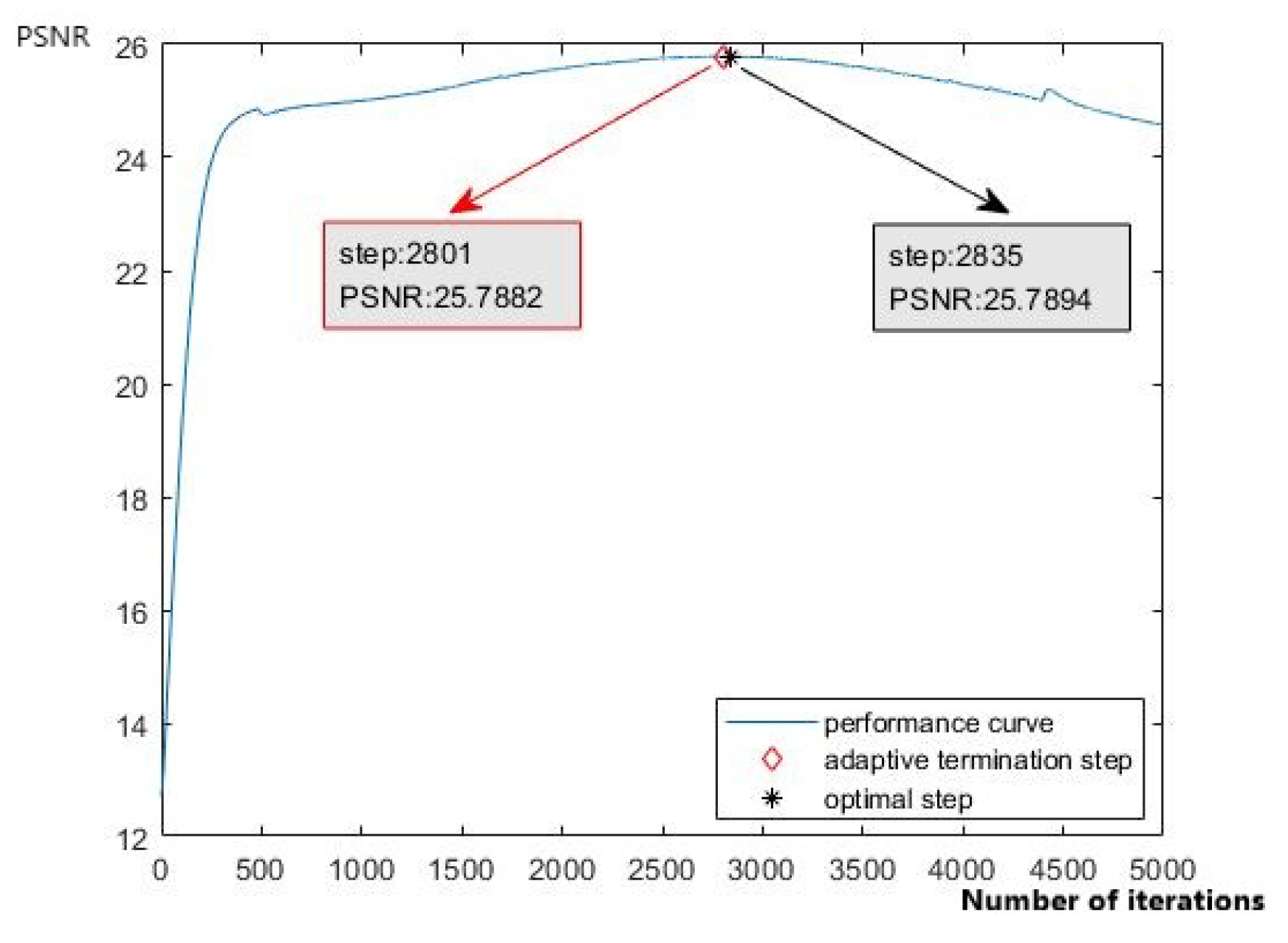
Figure 1, although the general denoising performance of DIP is inferior to that of DnCNN, we can still find some local details, such as the magnified part of the images, that DIP can preserve more accurately as compared with DnCNN. The reason is that the prior knowledge captured by DnCNN cannot handle the subtle information that DIP can. DIP performs the inference by stopping the training early. However, in the original DIP model, the early stopping point is set as a fixed number of iterations using experimental data, so the result is not always optimal. Furthermore, the noisy image is used as the target image that provides poor guidance and leads to slow convergence of the generative network. Thus, the denoising performance of DIP is much lower than that of deep learning in some cases, and it still leaves room for improvement. In view of the limitations of the existing DIP method, we propose a novel deep generative network with multiple target images and an adaptive termination condition, which not only retains the flexibility of the original DIP model, but also improves denoising performance. Specifically, instead of the noisy image, we use two target images of higher quality to participate in the formation of the loss functions. In addition, we adopt a noise level estimation (NLE) method to automatically terminate the iterative process to resolve the early stopping problem, prevent over-fitting, and ensure an optimal output image.
The remainder of the paper is organized as follows:
Section 2 introduces a literature review of related work. In
Section 3, we describe the proposed approach in detail.
Section 4 discusses our experimental results and analysis. We discuss our current work and future work in
Section 5. Finally, we conclude this paper in
Section 6.
5. Discussions
It is well known that Gaussian noise is widely used in image denoising, thus our generative network can fully manage such noise. However, real-world noise, such as Poisson noise, Gaussian–Poisson noise, and salt and pepper noise, is usually non-Gaussian. Poisson noise and Gaussian–Poisson noise are so-called signal-related noise. In an image, their noise levels are variable while the noise level of Gaussian noise is fixed. To handle these cases, we can exploit the average noise level [
32] rather than the fixed noise level in our method. To handle salt and pepper noise, we must utilize the corresponding denoising algorithms to obtain preliminary images and use the noise ratio as a condition. That is, the criterion for over-fitting is no longer the noise level, but the noise ratio. Therefore, under the framework of our method, as long as the preliminary denoising images and the iteration termination conditions are modified accordingly, the salt and pepper noise or other types of noise can also be handled well.
In this work, we adopt the mixed loss function, in which the three terms have the same weight, and achieved satisfactory results. Here, we adopt the noisy image to utilize its internal information, but its guiding ability is interfered with by different noise levels to varying degrees. Theoretically, when the noise level is relatively low, the noise image contains more useful information, so it can occupy more weight; when the noise level is relatively high, the noise image is seriously disturbed, and it contains less useful information, so it will occupy less weight. In future work, we consider assigning different weights to the terms to further improve the denoising performance of our generated network.
Further, we exploit the MSE loss function that uses the L2 norm to characterize the distance between the generative image and the noisy image, and preliminary denoising images, respectively. Although the MSE loss function can easily reach local minimums and is sensitive to errors, it still has some defects. For example, it could over-penalize larger errors and may not capture complex characteristics in some cases; meanwhile, the mean absolute error (MAE) loss function that uses the L1 norm to describe the distance may allow our network to obtain better results. Thus, we are considering exploring a mixed loss function with more norms in future work.
It should be noted that although the proposed method obtains the optimal result through online training, it requires a large number of gradient updates, resulting in long inference times. Thus, its execution efficiency is relatively low. In the future, we will consider adopting transfer learning [
33] to first find a suitable general initial parameter to improve performance for a faster denoising process.