TAPP: DNN Training for Task Allocation through Pipeline Parallelism Based on Distributed Deep Reinforcement Learning
Abstract
:1. Introduction
- Task partition is based on the feedforward neural network. The DNN model is grouped by layers. For a DNN model, the task partition network can divide each layer into corresponding groups. For each layer, the partition network generates the probability value of each packet and divides it into the packet with the highest probability.
- Attention mechanism is introduced to task allocation. According to the grouping result of the task partition network, the task allocation network allocates corresponding computing nodes for each grouping. Before the task allocation network is processed, the information of each group needs to be integrated. Similar to the task partitioning network, the allocation network also transforms the grouping results into word vectors. The allocation network considers the operation name, parameter metric, and the next packet information of all layers in the whole packet. In this paper, the average of the relevant information of the containing layer in the group is taken as the word vector of the group.
- Strategy gradient joint training is carried out. The prediction network uses the policy gradient to train the task partition and allocation network. The purpose of the network is to get the task allocation scheme which can minimize the total training time of a single training batch. The DNN model is trained in the total time of a batch under the condition of the task allocation scheme, including a forward calculation, a backward propagation, and a parameter update. In order to avoid running time measurement variance, we allocate a scheme to each predicted task. Then the DNN model is run on the actual computing node according to the scheme, the running time of the DNN model is measured several times to calculate the average value, the reward function of the current scheme is calculated, the parameters of the prediction network model are updated backwards, and the task allocation scheme with the shortest actual running time is obtained through several iterations.
2. Related Works
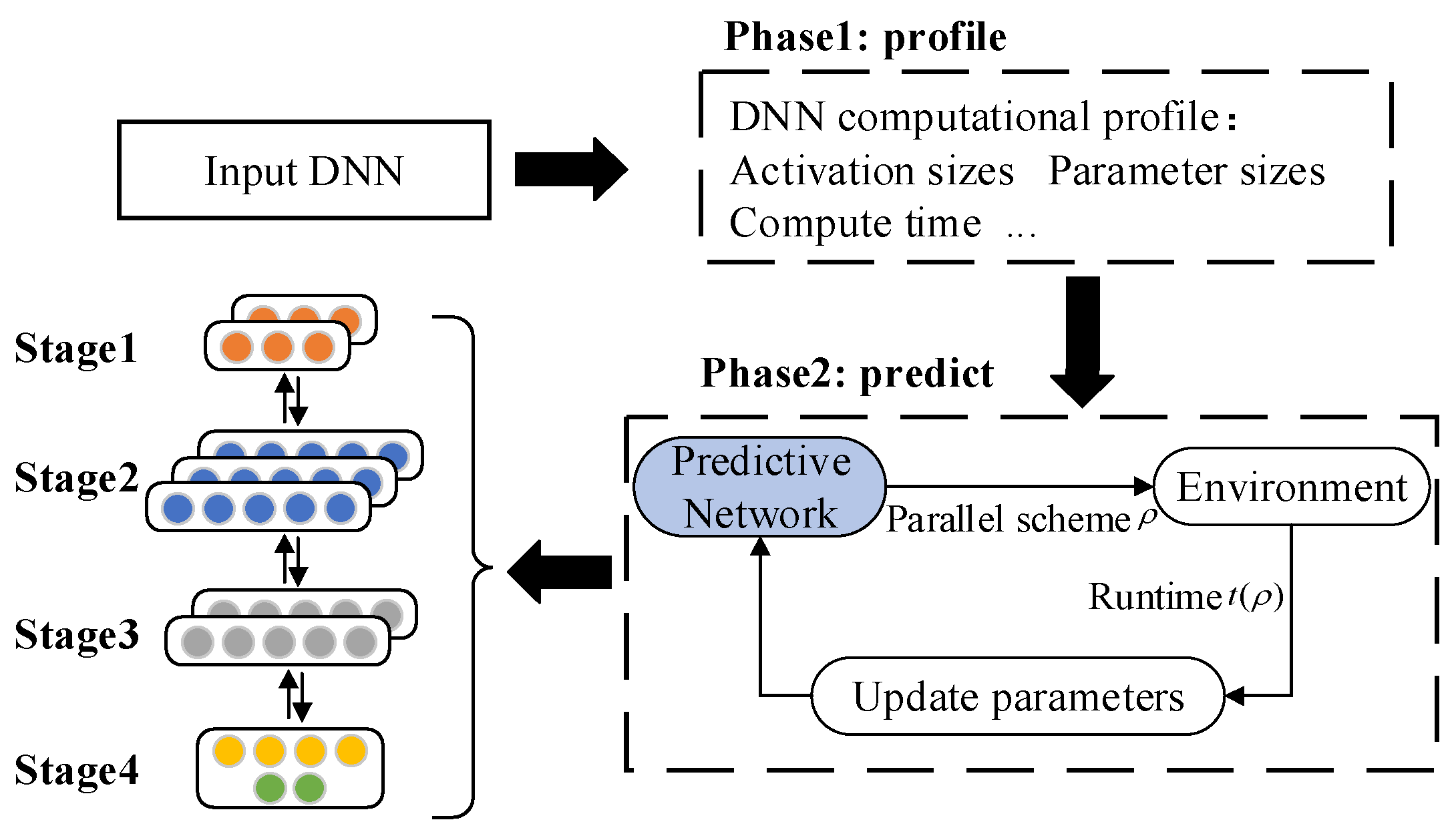
3. Overall Framework
- (1)
- Analyze the operating status of the target model and build a model parameter text library. Then analyze the short-term operating status of the model to be trained and record detailed model information, including the total number of layers of the model, the name of each layer, calculation time, calculation amount, parameter amount, and activation value, and build a text library of the model parameters to be trained.
- (2)
- Construct a task allocation prediction network, according to the parameter information of the model to be trained. Then use the predictive network to generate a pipelined parallel training task allocation plan, , for the DNN model to be trained. According to the allocation plan, , several batches of training are performed in the experimental environment, sampling to obtain the average training time of a single batch , calculating the reward function, and updating the parameters in the prediction network backwards. After that, the prediction network is trained several times until it generates a task allocation plan with the smallest running time . If the model is deployed to heterogeneous computing nodes by the plan, a pipelined parallel training allocation plan for the target network to be trained will be obtained.
4. Task Allocation Prediction Network
4.1. Task Partition Based on Feedforward Neural Network
- (1)
- Operation name: In the DNN model, each layer corresponds to a different operation, such as convolution operation, pooling operation, and fully connected operation. Since the operation names are all character types, they are converted to word vectors. The experiment encodes the operation name of each layer and builds a dictionary library, which will be constantly updated during the training process. In the experiment, the width of the code is set to 16 bits and five commonly used operation names are selected: Convolution, Relu, Pooling, Fully-Connected, and Padding. For the remaining operation names, use Unknown instead.
- (2)
- Parameter metric: The parameter metric of each layer of the model includes the number of parameters, the amount of calculation, and the size of the generated activation value. The required parameter quantity of each layer is calculated according to the model structure definition for which the unit is expressed in MB, the required calculation quantity according to the parameter quantity of each layer and the corresponding calculation operation is estimated for which the unit is expressed in GFLOPS, and the size of the generated activation value of each layer according to the parameter quantity of each layer and the corresponding calculation operation is estimated for which the unit is expressed in MB. Each metric is allocated 4 bits of coding width, that is, the total coding width of the parameter metric is 12 bits.
- (3)
- Associated next layer: The DNN model is composed of several layers. The output of each layer is used as the input of other layers. In this paper, the DNN model is numbered layer by layer. The numbering starts from 1. The number is used to indicate the next layer associated with the current layer. Because the number of the next layer associated with each layer in the model is different, the number of experiments is set to 2, and each number is assigned a 2-bit code width. If there is no information in the next layer, we will fill it with −0.1.
4.2. Task Allocation Based on Attention Mechanism
- (1)
- Operation name: The word vectors of the operation names in the group are averaged to get the operation name information of the current group.
- (2)
- Parameter metric: The parameter metric information of all layers in the group is averaged to get this part of information.
- (3)
- The next set of information: One-hot encoding is used to indicate the dependency between groups. If a DNN layer in the current group is connected to the layer in the ith group, this article will set the ith bit of the current group to 1, otherwise it will be set to 0.
4.3. Joint Training of Policy Gradient
| Algorithm 1 Task allocation in pipeline parallel training based on deep reinforcement learning |
| Input: DNN model, G; heterogeneous computing node set, D; number of iterations, n. Output: Task allocation plan, . |
| 1: Initialize , |
| 2: for step = 0 to n do |
| 3: for layer in G |
| 4: Assign layer to group |
| 5: for group in G |
| 6: Assign group to device |
| 7: Assign DNN to devices, D, according to parallelism scheme, |
| 8: Sample runtime, |
| 9: Update parameters , |
| 10: end for |
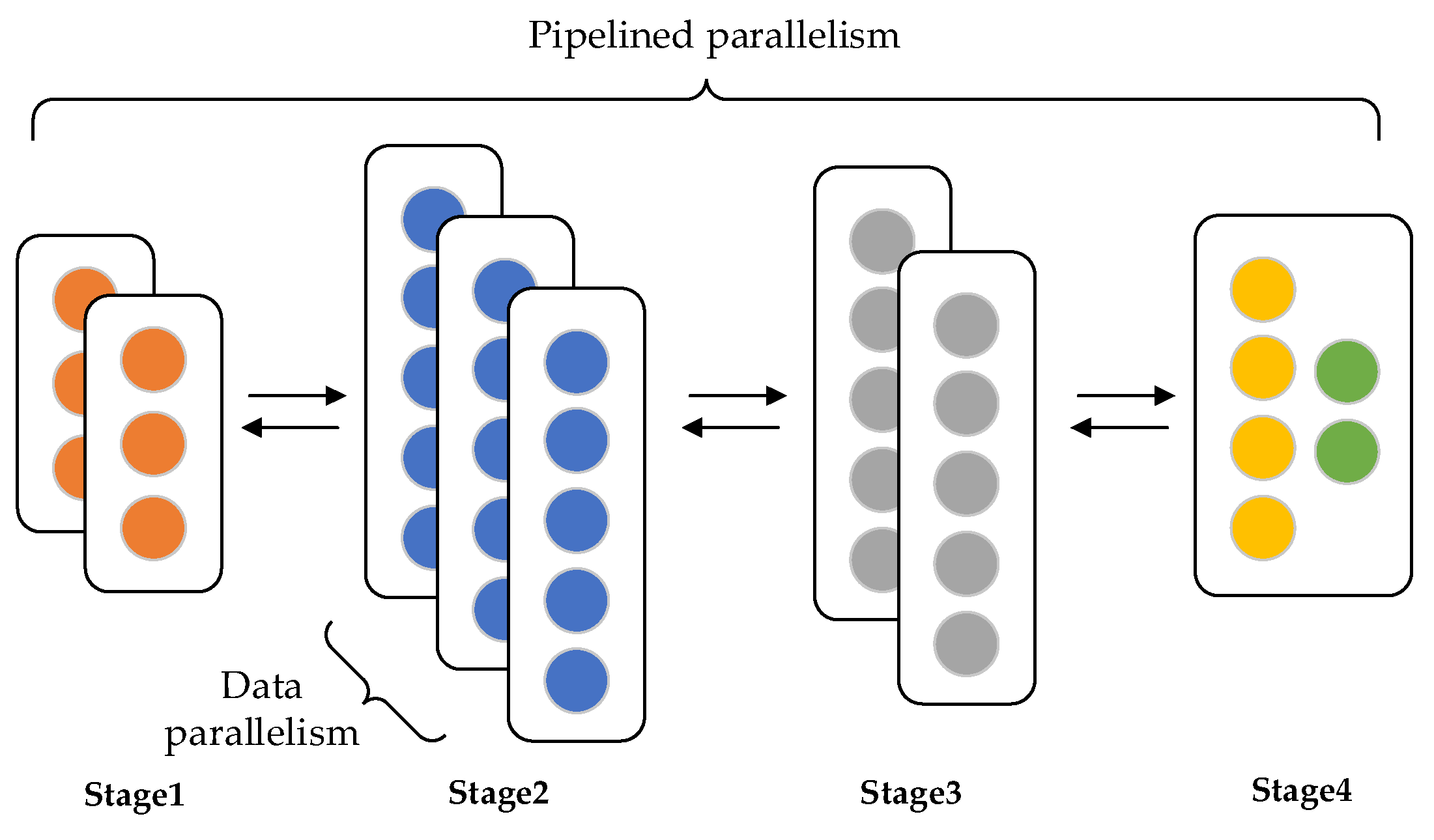
4.4. Pipeline Parallel Training of Task Allocation
5. Performance Evaluation
5.1. Experiment Setup
5.1.1. Data Set
5.1.2. Benchmark
5.1.3. Metric
- (1)
- Single-step training time
- (2)
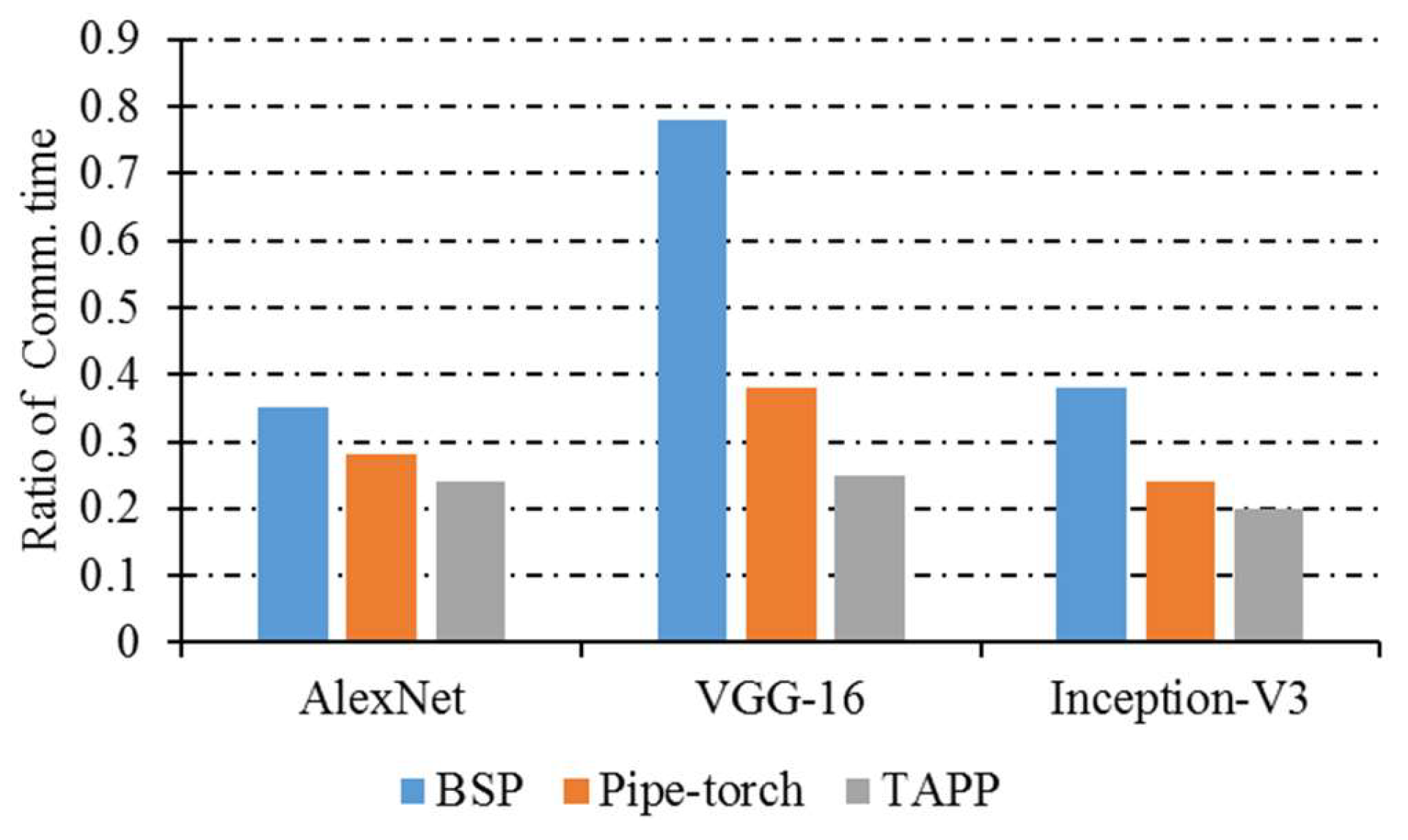
- Proportion of communication time
- (3)
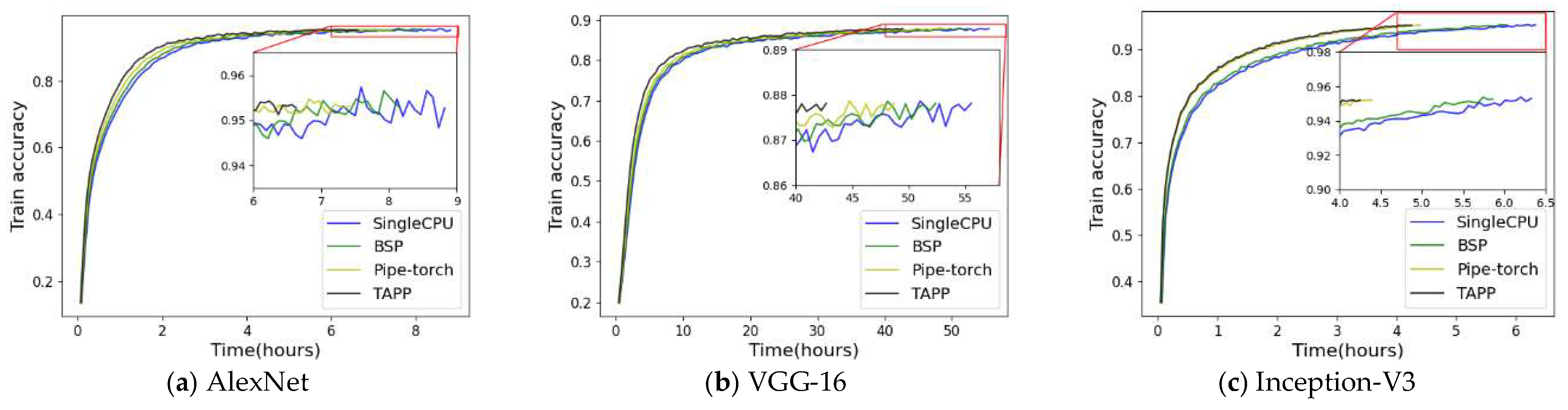
- Training accuracy
5.2. Experimental Results and Analysis
5.2.1. Pipeline Parallel Training
- (1)
- Single-step training time
- (2)
- Proportion of communication time
- (3)
- Training accuracy
5.2.2. TAPP Algorithm Evaluation
- (1)
- Experiment with different computing power
- (2)
- Experiment with different batch sizes
5.2.3. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Bakkali, S.; Ming, Z.; Coustaty, M.; Rusinol, M. Cross-Modal Deep Networks for Document Image Classification. In Proceedings of the IEEE International Conference on Image Processing, Abu Dhabi, United Arab Emirates, 25–28 October 2020; pp. 2556–2560. [Google Scholar]
- Xie, X.; Zhou, Y.; Kung, S.Y. Exploring Highly Efficient Compact Neural Networks for Image Classification. In Proceedings of the IEEE International Conference on Image Processing, Abu Dhabi, United Arab Emirates, 25–28 October 2020; pp. 2930–2934. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to Sequence Learning with Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 3104–3112. [Google Scholar]
- Huang, Z.; Ng, T.; Liu, L.; Mason, H.; Zhuang, X.; Liu, D. SNDCNN: Self-Normalizing Deep CNNs with Scaled Exponential Linear Units for Speech Recognition. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Barcelona, Spain, 4–8 May 2020; pp. 6854–6858. [Google Scholar]
- Ali, A.; Chowdhury, S.A.; Afify, M.; EI-Hajj, W.; Hajj, H.M.; Abbas, M.; Hussein, A.; Ghneim, N.; Abushariah, M.; Alqudah, A. Connecting Arabs: Bridging the gap in dialectal speech recognition. Commun. ACM 2020, 64, 124–129. [Google Scholar] [CrossRef]
- Kim, J.; El-Khamy, M.; Lee, J. Residual LSTM: Design of a Deep Recurrent Architecture for Distant Speech Recognition. In Proceedings of the Annual Conference of the International Speech Communication Association, Stockholm, Sweden, 20–24 August 2017; pp. 1591–1595. [Google Scholar]
- Arivazhagan, N.; Cherry, C.; Te, I.; Macherey, W.; Baljekar, P.; Foster, G.F. Re-Translation Strategies for Long Form, Simultaneous, Spoken Language Translation. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Barcelona, Spain, 4–8 May 2020; pp. 7919–7923. [Google Scholar]
- Huang, Y.; Cheng, Y.; Bapna, A.; Firat, O.; Chen, D.; Chen, M.X.; Lee, H.; Ngiam, J.; Le, Q.V.; Wu, Y.; et al. GPipe: Efficient Training of Giant Neural Networks using Pipeline Parallelism. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 103–112. [Google Scholar]
- Real, E.; Aggarwal, A.; Huang, Y.; Le, Q.V. Regularized Evolution for Image Classifier Architecture Search. In Proceedings of the Association for the Advancement of Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; pp. 4780–4789. [Google Scholar]
- Wang, M.; Huang, C.; Li, J. Supporting Very Large Models using Automatic Dataflow Graph Partitioning. In Proceedings of the European Conference on Computer Systems, Dresden, Germany, 25–28 March 2019; pp. 1–26. [Google Scholar]
- Jin, T.; Hong, S. Split-CNN: Splitting Window-based Operations in Convolutional Neural Networks for Memory System Optimization. In Proceedings of the Conference on Architectural Support for Programming Languages and Operating Systems, Providence, RI, USA, 13–17 April 2019; pp. 835–847. [Google Scholar]
- Park, J.H.; Yun, G.; Chang, M.Y.; Nguyen, N.T.; Lee, S.; Choi, J.; Noh, S.H.; Choi, Y. HetPipe: Enabling Large DNN Training on (whimpy) Heterogeneous GPU Clusters through Integration of Pipelined Model Parallelism and Data Parallelism. In Proceedings of the USENIX Annual Technical Conference, Virtual, 15–17 July 2020; pp. 307–321. [Google Scholar]
- Brown, T.B.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language Models are Few-Shot Learners. In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 6–12 December 2020. [Google Scholar]
- Li, Y.; Yu, M.; Li, S.; Avestimehr, S.; Kim, N.S.; Schwing, A.G. Pipe-SGD: A Decentralized Pipelined SGD Framework for Distributed Deep Net Training. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 8056–8067. [Google Scholar]
- Li, Y.; Zeng, Z.; Li, J.; Yan, B.; Zhao, Y.; Zhang, J. Distributed Model Training Based on Data Parallelism in Edge Computing-Enabled Elastic Optical Networks. IEEE Commun. Lett. 2021, 25, 1241–1244. [Google Scholar] [CrossRef]
- Dean, J.; Corrado, G.; Monga, R.; Chen, K.; Devin, M.; Le, Q.V.; Mao, M.Z.; Ranzato, M.; Senior, A.W.; Tucker, P.A.; et al. Large Scale Distributed Deep Networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1223–1231. [Google Scholar]
- Du, J.; Zhu, X.; Shen, M.; Du, Y.; Lu, Y.; Xiao, N.; Liao, X. Model Parallelism Optimization for Distributed Inference Via Decoupled CNN Structure. IEEE Trans. Parallel Distrib. Syst. 2021, 32, 1665–1676. [Google Scholar]
- Zinkevich, M.; Weimer, M.; Smola, A.J.; Li, L. Parallelized Stochastic Gradient Descent. In Proceedings of the Advances in Neural Information Processing Aystems, Vancouver, BC, Canada, 6–9 December 2010; pp. 2595–2603. [Google Scholar]
- Zhang, S.; Choromanska, A.E.; LeCun, Y. Deep Learning with Elastic Averaging SGD. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 685–693. [Google Scholar]
- Agarwal, A.; Duchi, J.C. Distributed Delayed Stochastic Optimization. In Proceedings of the 51st IEEE Conference on Decision and Control, Maui, HI, USA, December 10–13 2012; pp. 5451–5452. [Google Scholar]
- Harlap, A.; Narayanan, D.; Phanishayee, A.; Seshadri, V.; Devanur, N.R.; Ganger, G.R.; Gibbons, P.B.; Zaharia, M. PipeDream: Generalized Pipeline Parallelism for DNN Training. In Proceedings of the 27th ACM Symposium on Operating Systems Principles, Huntsville, ON, Canada, 27–30 October 2019; pp. 1–15. [Google Scholar]
- Isard, M.; Prabhakaran, V.; Currey, J.; Wieder, U.; Talwar, K.; Goldberg, A.V. Quincy: Fair Scheduling for Distributed Computing Clusters. In Proceedings of the ACM SIGOPS 22nd Symposium on Operating Systems Principles, Big Sky, MT, USA, 11–14 October 2009; pp. 261–276. [Google Scholar]
- Gog, I.; Schwarzkopf, M.; Gleave, A.; Watson, R.N.M.; Hand, S. Firmament: Fast, Centralized Cluster Scheduling at Scale. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016; pp. 99–115. [Google Scholar]
- Jia, Z.; Lin, S.; Qi, C.R.; Aiken, A. Exploring Hidden Dimensions in Parallelizing Convolutional Neural Networks. In Proceedings of the 35th International Conference on Machine Learning, Stockholmsmässan, Stockholm, Sweden, 10–15 July 2018; pp. 2279–2288. [Google Scholar]
- Jia, Z.; Zaharia, M.; Aiken, A. Beyond Data and Model Parallelism for Deep Neural Networks. In Proceedings of the Machine Learning and Systems, Stanford, CA, USA, 31 March–2 April 2019. [Google Scholar]
- Zhan, J.; Zhang, J. Pipe-torch: Pipeline-Based Distributed Deep Learning in a GPU Cluster with Heterogeneous Networking. In Proceedings of the Seventh International Conference on Advanced Cloud and Big Data, Suzhou, China, 21–22 September 2019; pp. 55–60. [Google Scholar]
- Fan, S.; Rong, Y.; Meng, C.; Cao, Z.; Wang, S.; Zheng, Z.; Wu, C.; Long, G.; Yang, J.; Xia, L.; et al. DAPPLE: A Pipelined Data Parallel Approach for Training Large Models. In Proceedings of the 26th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, Virtual, 27 February 27–3 March 3 2021; pp. 431–445. [Google Scholar]
- Mirhoseini, A.; Pham, H.; Le, Q.V.; Steiner, B.; Larsen, R.; Zhou, Y.; Kumar, N.; Norouzi, M.; Bengio, S.; Dean, J. Device Placement Optimization with Reinforcement Learning. In Proceedings of the 34th International Conference on Machine Learning, Sydney, NSW, Australia, 6–11 August 2017; pp. 2430–2439. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Liu, W.; Peng, L.; Cao, J.; Fu, X.; Liu, Y.; Pan, Z.; Yang, J. Ensemble Bootstrapped Deep Deterministic Policy Gradient for Vision-Based Robotic Grasping. IEEE Access 2021, 9, 19916–19925. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. In Handbook of Systemic Autoimmune Diseases; Elsevier: Amsterdam, The Netherlands, 2009; Volume 1. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015; pp. 1–14. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Tieleman, T.; Hinton, G. Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude. COURSERA Neural Netw. Mach. Learn. 2012, 4, 26–31. [Google Scholar]



| SingleCPU | Pipe-Torch | BSP | TAPP | Speedup (BSP/TAPP) | |
|---|---|---|---|---|---|
| AlexNet | 0.811 | 0.675 | 0.803 | 0.602 | 1.33× |
| VGG-16 | 1.972 | 1.634 | 1.865 | 1.432 | 1.30× |
| Inception-V3 | 0.985 | 0.632 | 0.914 | 0.614 | 1.49× |
| AlexNet | VGG-16 | Inception-V3 | |
|---|---|---|---|
| SingleCPU | 0.5 | 1.6 | 0.8 |
| SingleGPU | 0.3 | 0.6 | 0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, Y.; Tu, Z.; Xi, F.; Wang, Q.; Xu, S. TAPP: DNN Training for Task Allocation through Pipeline Parallelism Based on Distributed Deep Reinforcement Learning. Appl. Sci. 2021, 11, 4785. https://doi.org/10.3390/app11114785
Mao Y, Tu Z, Xi F, Wang Q, Xu S. TAPP: DNN Training for Task Allocation through Pipeline Parallelism Based on Distributed Deep Reinforcement Learning. Applied Sciences. 2021; 11(11):4785. https://doi.org/10.3390/app11114785
Chicago/Turabian StyleMao, Yingchi, Zijian Tu, Fagang Xi, Qingyong Wang, and Shufang Xu. 2021. "TAPP: DNN Training for Task Allocation through Pipeline Parallelism Based on Distributed Deep Reinforcement Learning" Applied Sciences 11, no. 11: 4785. https://doi.org/10.3390/app11114785
APA StyleMao, Y., Tu, Z., Xi, F., Wang, Q., & Xu, S. (2021). TAPP: DNN Training for Task Allocation through Pipeline Parallelism Based on Distributed Deep Reinforcement Learning. Applied Sciences, 11(11), 4785. https://doi.org/10.3390/app11114785






