Random-Forest Machine Learning Approach for High-Speed Railway Track Slab Deformation Identification Using Track-Side Vibration Monitoring
Abstract
:Featured Application
Abstract
1. Introduction
- Deformation detection methods for operating HSRs can rarely meet the following requirements simultaneously: the method should not interrupt the normal operation of trains or directly contact track slabs and should obtain track deformation information in the track occupancy condition and in real-time;
- HSR field monitoring signals contain massive noise and redundant information, and the commonly used EMD methods cannot effectively obtain vibration signal characteristics because of modal confusion, negative frequency, and endpoint effect problem;
- The train grouping, operating speed, load of high-speed trains, and decay process of wheel-track vibration signals have considerable effect on the vibration signals, resulting in complex track-side vibration signals and thus numerous features or attributes of data.
- The track-side real-time monitoring method based on fiber optic sensing technology is capable of obtaining track-side vibration signals in real time without interrupting normal train operation and in track occupancy conditions, compensating for the shortcomings of existing track slab detection methods;
- The LMD method for feature extraction of complex track-side vibration signal overcomes the problems of modal confusion, negative frequency and endpoint effect problem caused by EMD method commonly used in track structure feature extraction;
- The advantages of the random-forest model, such as fewer parameters, high classification accuracy and robustness to noise, enable simple identification of complex track-side vibration signals containing a great deal of attributes.
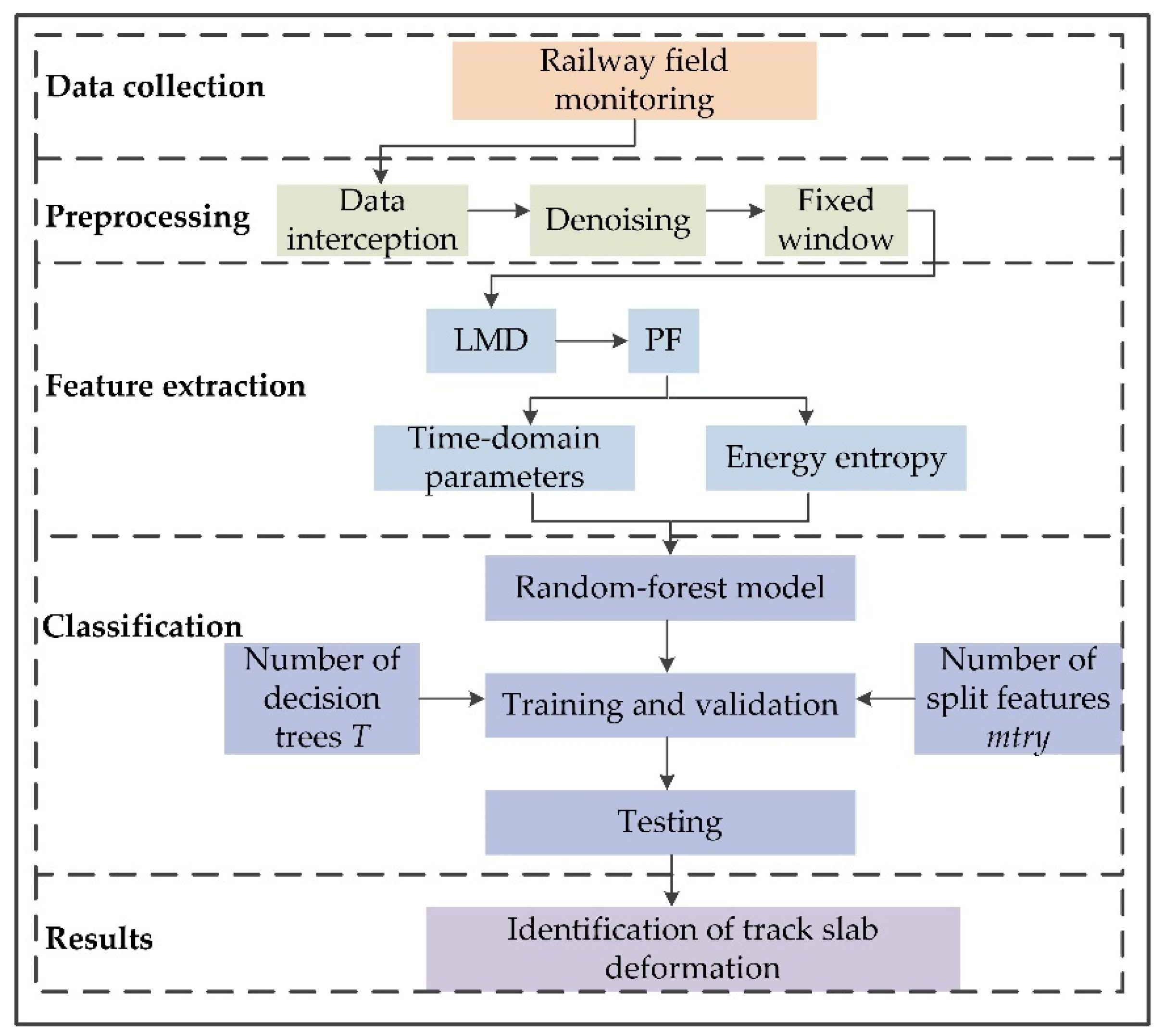
2. Track-Side Real-Time Monitoring for Track Slab Deformation
3. Preprocessing of Monitoring Data
4. Time-Domain and Time-Frequency-Domain Feature Extraction Based on the LMD Method
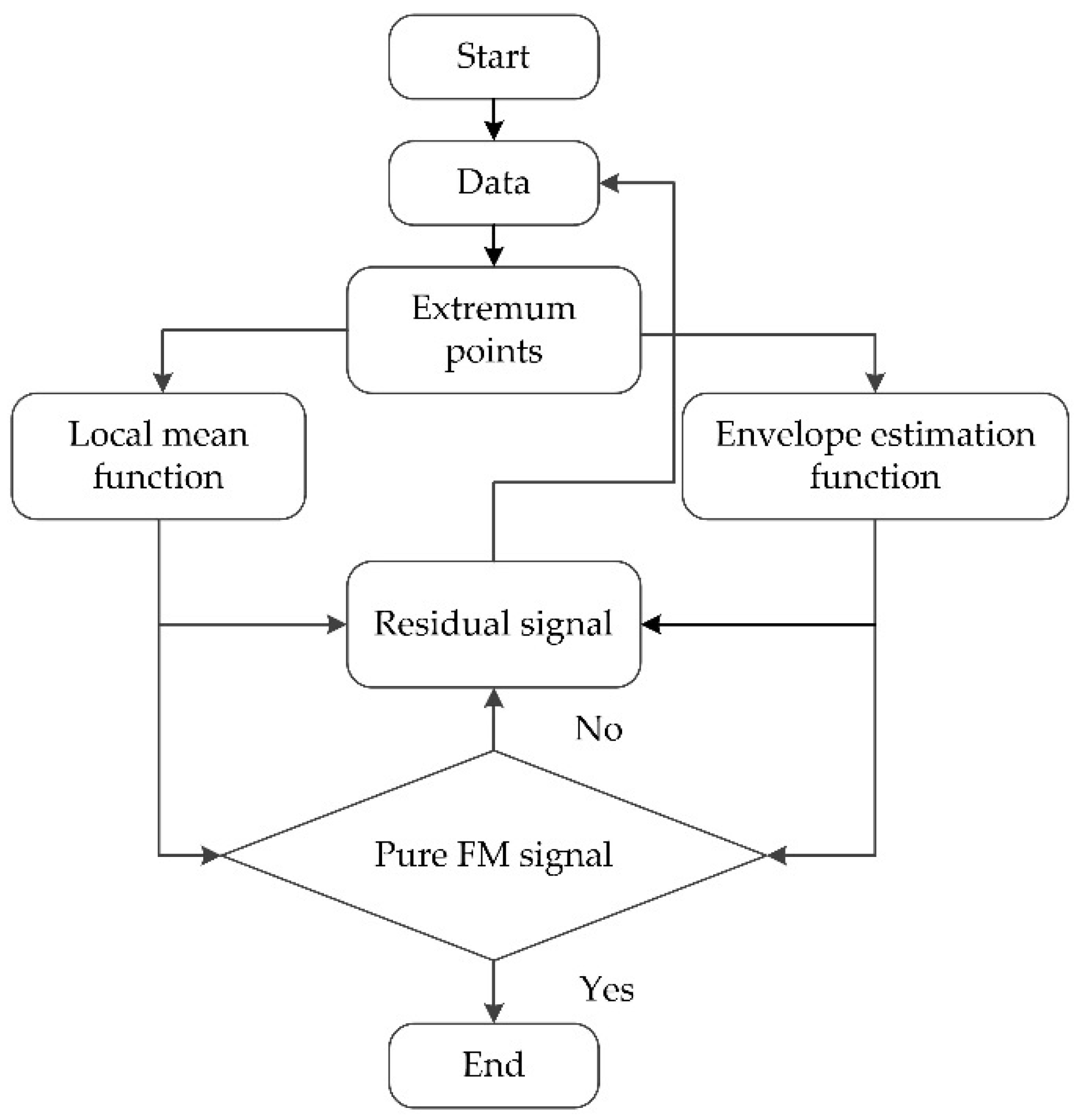
4.1. LMD Method
- All local extremum points Ni of the original signal x(t) are calculated and the average mi of all adjacent local extremum points Ni and Ni+1 is derived:
- 2.
- The local amplitude ai is obtained from the adjacent local extrema Ni and Ni+1:
- 3.
- By separating the local mean function m11(t) from the original signal x(t), Equation (3) can be obtained:
- 4.
- By dividing h11(t) with the envelope estimation function a11(t) to demodulate h11(t), Equation (4) can be obtained:
- The envelope signal a1(t) is obtained by multiplying all the envelope estimation functions obtained in the iterative process.
- 2.
- The first PF of the original signal is obtained by multiplying the envelope signal a1(t) with the pure frequency modulation signal s1n(t):
- 3.
- PF1(t) is separated from the original signal x(t) to obtain a residual signal u(t), and the residual signal u(t) is repeated as the original signal for k iterations until uk(t) is a monotonic function.
4.2. Selection of Characteristic PFs Based on Pearson Correlation Coefficient
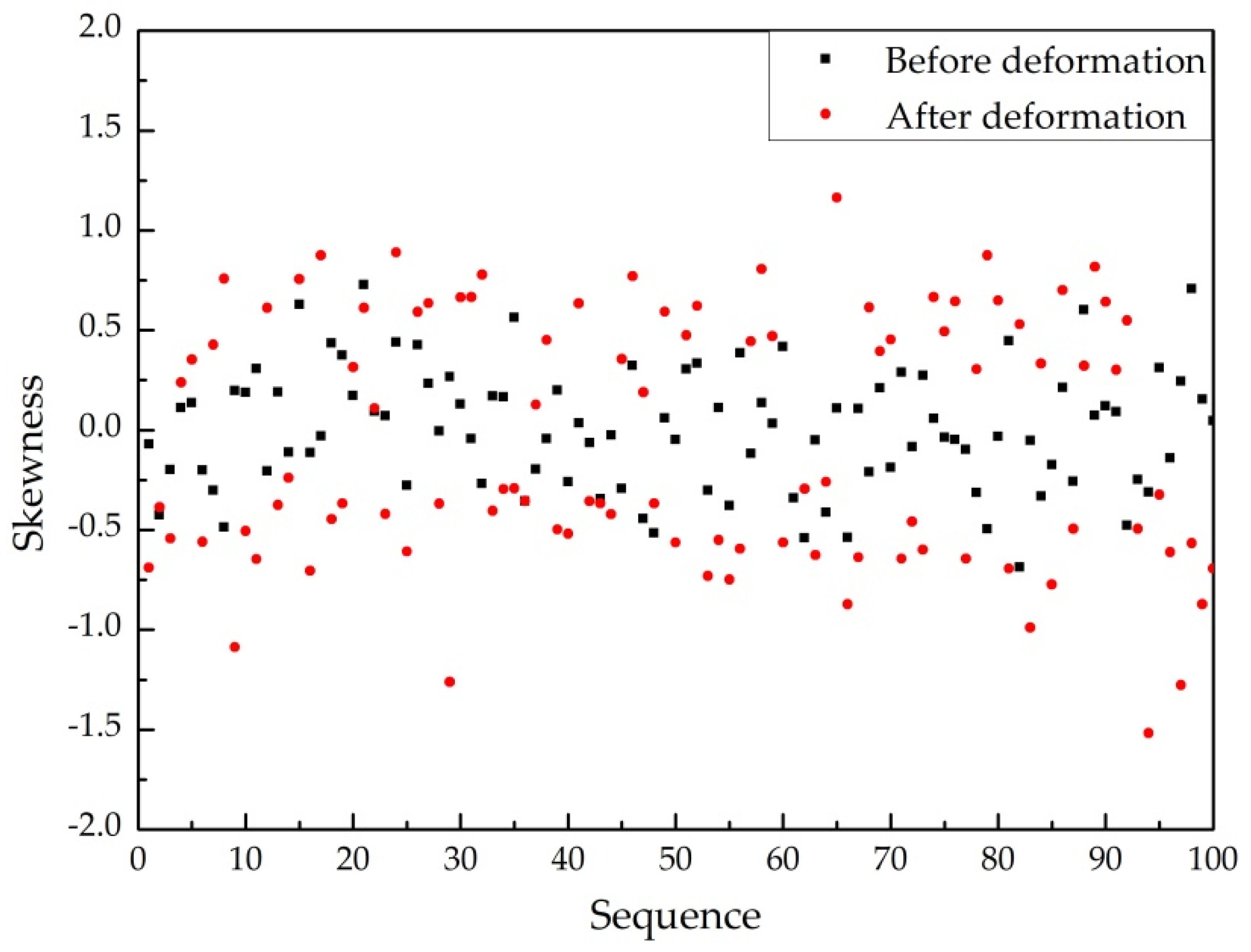
4.3. Time-Domain Feature Extraction
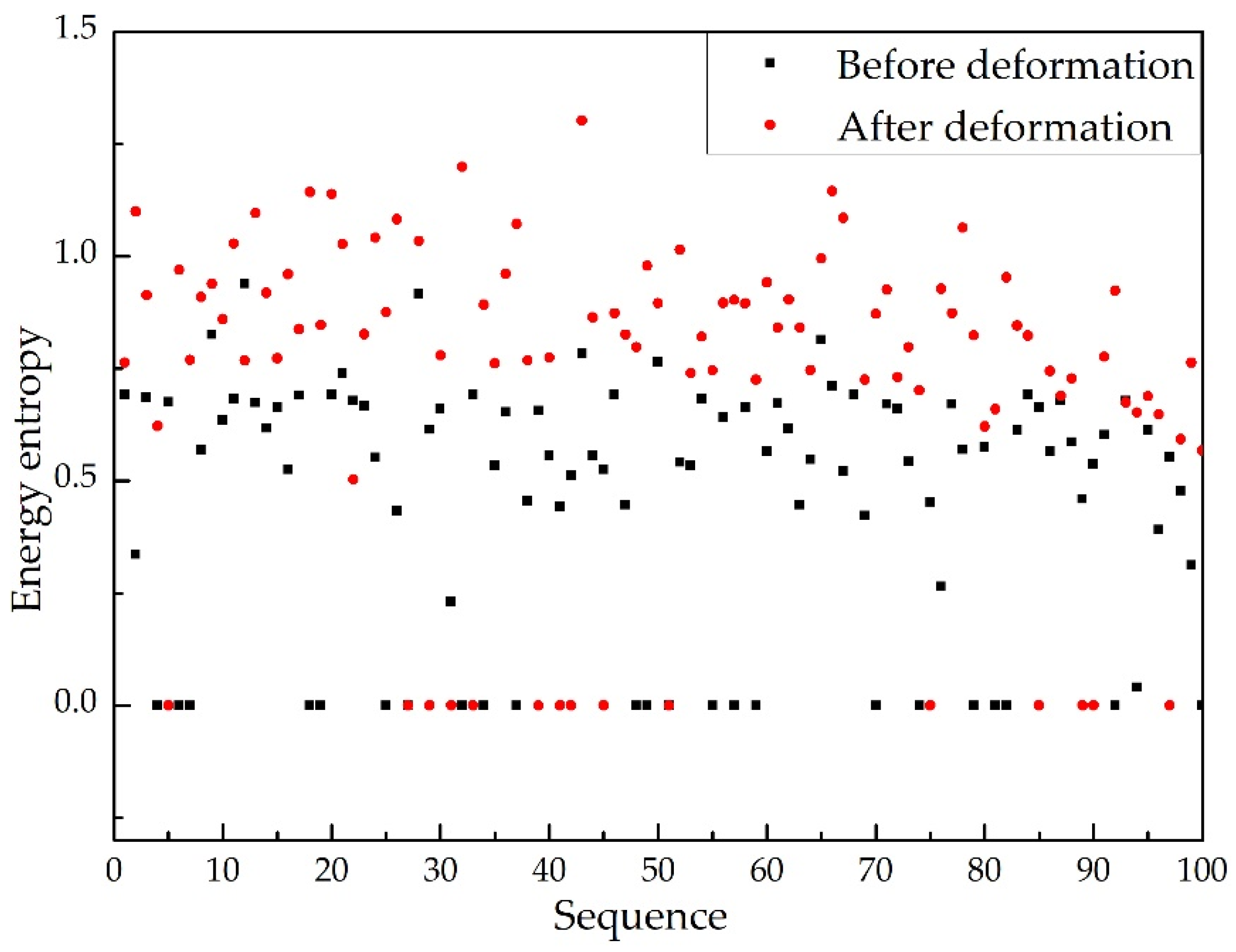
4.4. Time-Frequency-Domain Feature Extraction
- Calculate the energy of the qth characteristic PF:
- 2.
- Calculate the total energy of these r efficient characteristic PFs:
- 3.
- Calculate the energy entropy of characteristic PFs:
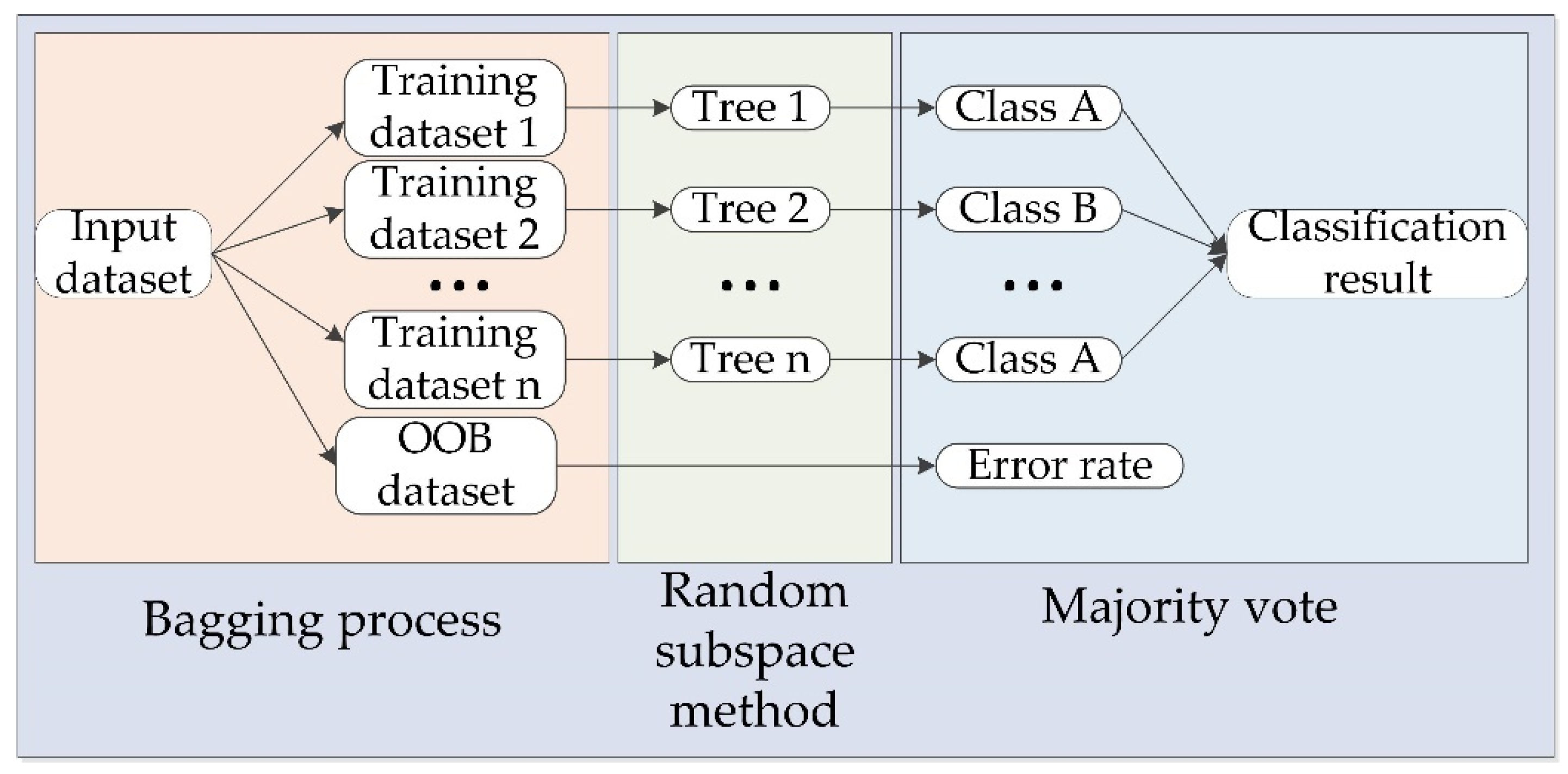
5. Establishment of Random-Forest Model
6. Results and Discussion
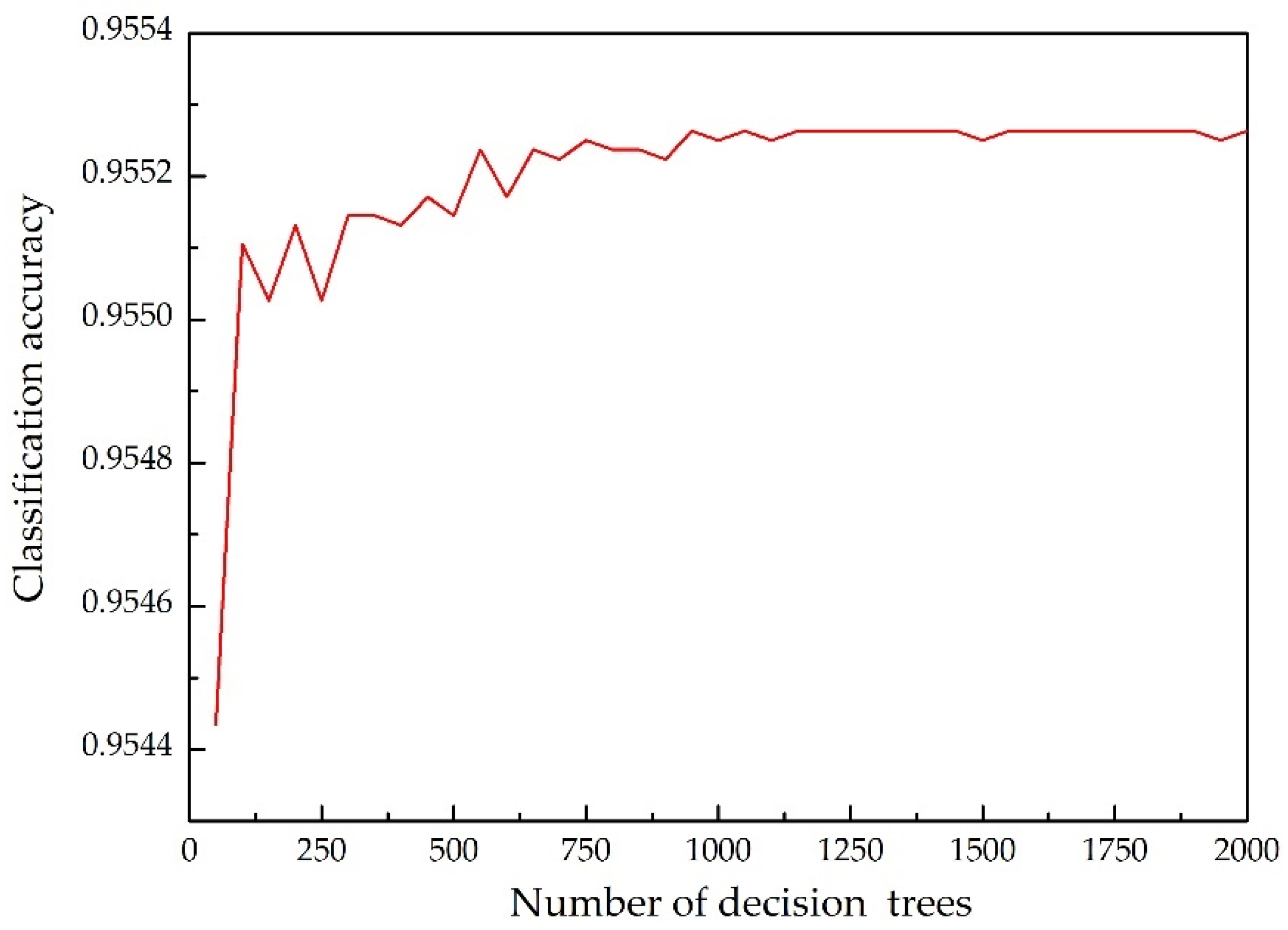
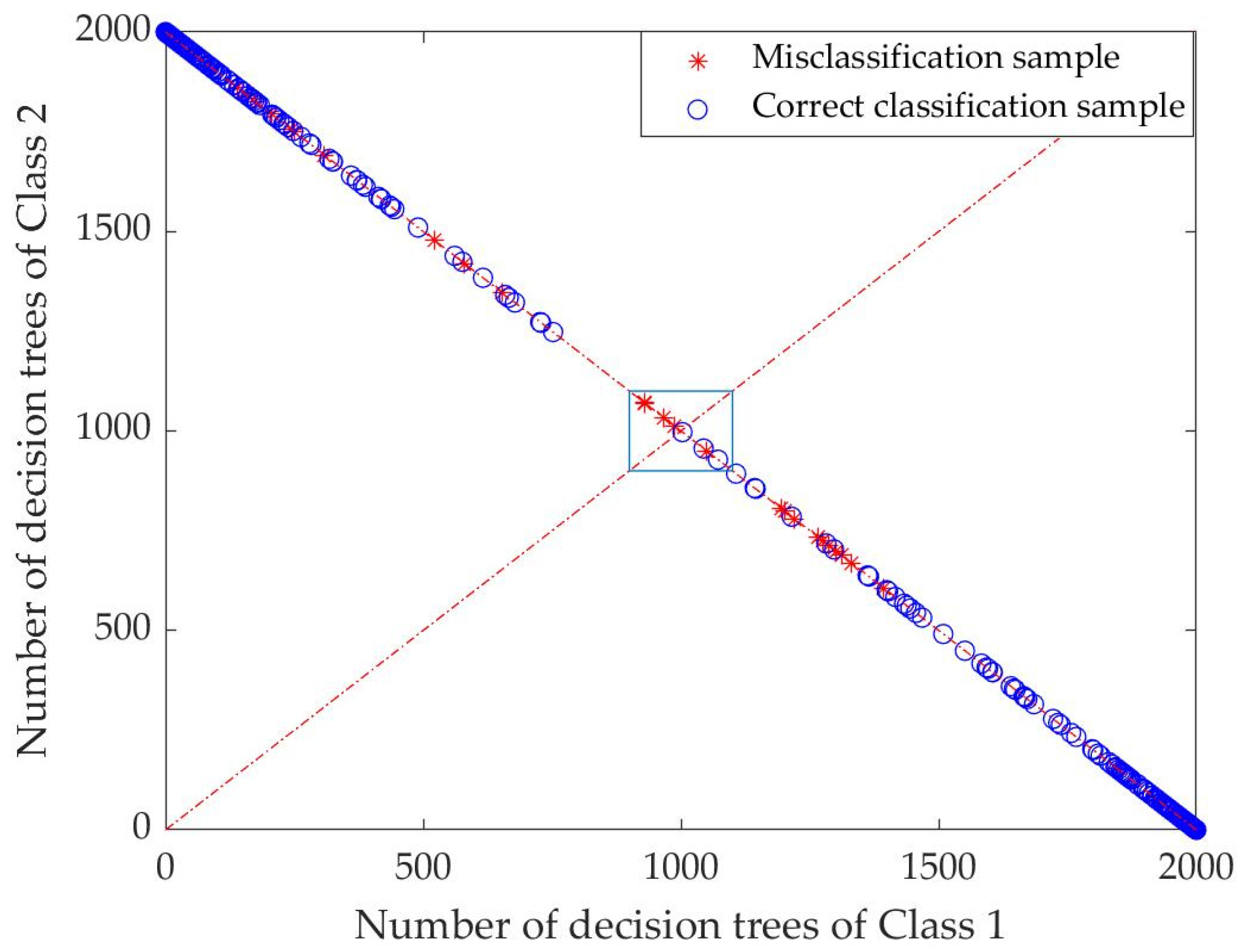
6.1. Random-Forest Model Results
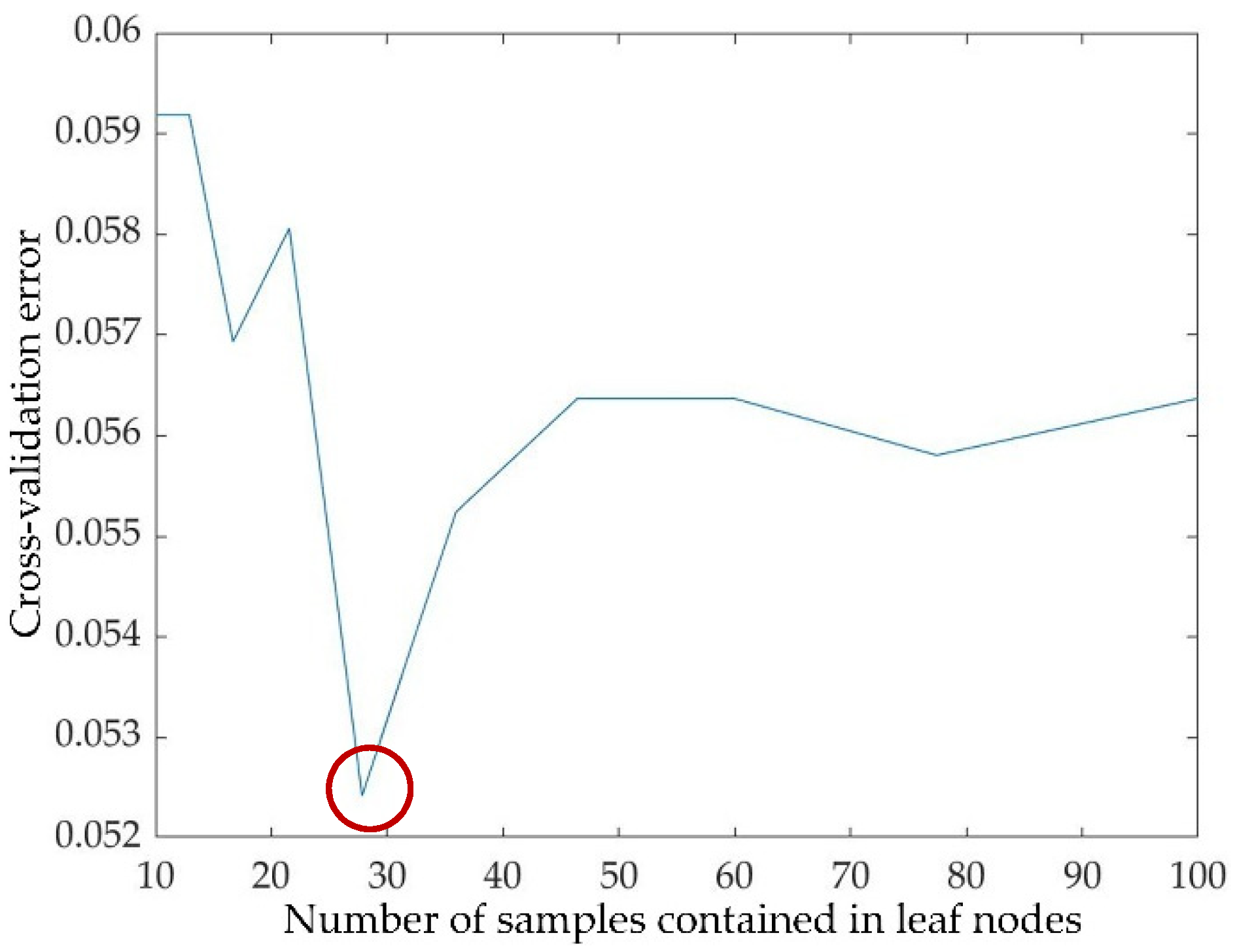
6.2. Decision-Tree Model Results
7. Conclusions
- A track-side vibration monitoring method based on fiber optic vibration sensing technology can effectively capture vibration signals that contain the information of train vibration, track slab deformation, noise, and environmental vibration.
- The preprocessing methods of data interception, denoising, and data segmentation can effectively eliminate the effects of environmental vibration, noise, and time differences on the recognition effects. In addition, the time-domain and time-frequency-domain feature extraction methods based on LMD effectively extract the crucial information for detecting the deformation of track slabs.
- The proposed intelligent recognition algorithm based on random-forest model can accurately identify the deformation of track slabs. The verification test results showed that the recognition accuracy reached 96.09%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Gao, L.; An, B.; Xin, T.; Wang, J.; Wang, P. Measurement, analysis, and model updating based on the modal parameters of high-speed railway ballastless track. Measurement 2020, 161, 107891. [Google Scholar] [CrossRef]
- Statistical Bulletin 2020 of China Railway. Available online: http://baijiahao.baidu.com/s?id=1691683529166535242 (accessed on 18 March 2021).
- Wang, P.; Xu, H.; Chen, R. Effect of cement asphalt mortar debonding on dynamic properties of CRTS II slab ballastless track. Adv. Mater. Sci. Eng. 2014, 2014, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.W.; Liu, X.Z.; He, Y.L. Identification of temperature-induced deformation for HSR Slab track using track geometry measurement data. Sensors 2019, 19, 5446. [Google Scholar] [CrossRef] [Green Version]
- Yang, M.H. Temperature warping deformation and modification of longitudinal slab-type ballastless track structure on bridge. China Railw. 2012, 04, 78–81. [Google Scholar]
- Li, Y.; Chen, J.J.; Wang, J.X.; Shi, X.F.; Chen, L. Analysis of damage of joints in CRTS II slab track under temperature and vehicle loads. KSCE J. C. Eng. 2020, 24, 1209–1218. [Google Scholar] [CrossRef]
- Gao, L.; Liu, Y.; Zhong, Y.L.; You, M.X.; Xin, T. Influence of damage of wide and narrow joints on mechanical performance of CRTS II slab-type ballastless track CWR. Railw. Eng. 2016, 5, 58–63. [Google Scholar]
- Xu, Y.D.; Yan, D.B.; Zhu, W.J.; Zhou, Y. Study on the mechanical performance and interface damage of CRTS II slab track with debonding repairment. Constr. Build. Mater. 2020, 257, 119600. [Google Scholar] [CrossRef]
- Shi, H.; Yu, Z.J.; Shi, H.M.; Zhu, L.Q. Recognition algorithm for the disengagement of cement asphalt mortar based on dynamic responses of vehicles. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 233, 270–282. [Google Scholar] [CrossRef]
- Yu, C.Y.; Xiang, J.; Mao, J.H.; Gong, K.; He, S.Y. Influence of slab arch imperfection of double-block ballastless track system on vibration response of high-speed train. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 109. [Google Scholar] [CrossRef]
- Ma, Z.R.; Gao, L.; Zhong, Y.L.; Ma, S.; An, B.L. Arching detection method of slab track in high-speed railway based on track geometry data. Appl. Sci. 2020, 10, 6799. [Google Scholar] [CrossRef]
- Cai, X.P.; Luo, B.C.; Zhong, Y.L.; Zhang, Y.R.; Hou, B.W. Arching mechanism of the slab joints in CRTS II slab track under high temperature conditions. Eng. Fail. Anal. 2019, 98, 95–108. [Google Scholar] [CrossRef]
- Zhao, L.; Zhou, L.Y.; Zhang, G.C.; Wei, T.Y.; Mahunon, A.D.; Jiang, L.Q.; Zhang, Y.Y. Experimental study of the temperature distribution in CRTS II ballastless tracks on a high-speed railway bridge. Appl. Sci. 2020, 10, 1980. [Google Scholar] [CrossRef] [Green Version]
- Zhu, S.Y.; Cai, C.B. Interface damage and its effect on vibrations of slab track under temperature and vehicle dynamic loads. Int.J. Nonlin. Mech. 2014, 58, 222–232. [Google Scholar] [CrossRef]
- Singh, M.; Singh, S.; Jaiswa, J.; Hernpshall, J. Autonomous rail track inspection using vision based system. In Proceedings of the IEEE International Conference on Computational Intelligence for Homeland Security & Personal Safety, Alexandria, VA, USA, 16–17 October 2006. [Google Scholar]
- Resendiz, E.; Hart, J.M.; Ahuja, N. Automated Visual Inspection of Railroad Tracks. IEEE T. Intell. Transp. 2013, 14, 751–760. [Google Scholar] [CrossRef] [Green Version]
- Yin, F. Research on detection method of gap caused by camber of CRTS II track slab. Railw. Eng. 2018, 58, 117–120. [Google Scholar]
- Ke, Y.T.; Cheng, C.C.; Lin, Y.C.; Ni, Y.Q.; Hsu, K.T.; Wai, T.T. Preliminary study on assessing delaminated cracks in cement asphalt mortar layer of high-speed rail track using traditional and normalized impact–echo methods. Sensors 2020, 20, 3022. [Google Scholar] [CrossRef]
- Xu, J.M.; Wang, P.; An, B.Y.; Ma, X.C.; Chen, R. Damage detection of ballastless railway tracks by the impact-echo method. Proc. Inst. Civ. Eng. Transp. 2018, 171, 106–114. [Google Scholar] [CrossRef]
- Pierre, A.B. Performance Evaluation of Impact Echo Method for Detection of Cavity Underneath a Concrete Slab Track Using Finite Element Method. Master’s Thesis, Pai Chai University, Daejeon, Korea, June 2019. [Google Scholar]
- Yang, Y.; Zhao, W.G. Curvelet transform-based identification of void diseases in ballastless track by ground penetrating radar. Struct. Control Health Monit. 2019, 26, e2322. [Google Scholar] [CrossRef]
- Liao, H.J.; Zhu, Q.N.; Jiu, Y.W.; Xie, Y.Y.; Sun, J.Y. Detection of ballastless track diseases in high-speed railway based on ground penetrating radar. J. Southwest Jiaotong Univ. 2016, 51, 8–13. [Google Scholar]
- Zhang, J.X.; Huang, W.Z.; Zhang, W.T.; Li, F.; Du, Y.L. Train-induced vibration monitoring of track slab under long-term temperature load using fiber-optic accelerometers. Sensors 2021, 21, 787. [Google Scholar] [CrossRef]
- Hussaini, S.K.K.; Indraratna, B.; Vinod, J.S. Application of optical-fiber Bragg grating sensors in monitoring the rail track deformations. Geotech. Test. J. 2015, 38, 387–396. [Google Scholar] [CrossRef] [Green Version]
- Chapeleau, X.; Sedran, T.; Cottineau, L.M.; Cailliau, J.; Taillade, F.; Gueguen, I.; Henault, J.M. Study of ballastless track structure monitoring by distributed optical fiber sensors on a real-scale mockup in laboratory. Eng. Struct. 2013, 56, 1751–1757. [Google Scholar] [CrossRef]
- Milne, D.; Masoudi, A.; Ferro, E.; Waston, G.; Louis, L.P. An analysis of railway track behaviour based on distributed optical fibre acoustic sensing. Mech. Syst. Signal Pr. 2020, 142, 106769. [Google Scholar] [CrossRef]
- Wang, Z.C.; Zhao, Z.G.; Chai, X.S.; Jin, M.; Feng, Y.J.; Ling, L.P.; Liu, Y.F. Research on monitoring technology of track slab upwarp based on distributed optical fiber sensing. Railw. Eng. 2020, 60, 42–45. [Google Scholar]
- Gao, W.H. Study on Analytical Method of Track Geometrical Irregularities for High-Speed Railway. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2020. [Google Scholar]
- Duan, Z.Q.; Meng, E.L.; Wang, L.M.; Li, H. Fault diagnosis for wind turbine transmission systems via demodulation analysis based on EEMD and energy separation. Noise. Vib. Control 2018, 38, 161–166. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.L.C.; Shih, H.H.; Zheng, Q.N.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. P Math. Phy. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- He, Y.F. Research on the Rail Defect Detection and Identification of the Urban Rail Transit. Master’s Thesis, Beijing Jiaotong Unviersity, Beijing, China, 2016. [Google Scholar]
- Ning, J. Study on the Time-Frequency Analysis by EMD and Cohen’s Kernel and Application in Track. Ph.D. Thesis, Southwest Jiaotong University, Sichuan, China, 2011. [Google Scholar]
- Chen, X.M. Time-Frequency Analysis and Prediction Study on Track Irregularities. Ph.D. Thesis, Institute of Railway Science, Beijing, China, 2006. [Google Scholar]
- Chen, T.T.; Zhao, W.G.; Li, R.Z.; Yang, Y.; Tian, X.S. Study on identification of CA mortar layer void based on convolution neural network. Railw. Stand. Des. 2021, 65, 1–8. [Google Scholar]
- Smith, J.S. The local mean decomposition and its application to EEG perception data. J. R. Soc. Interface 2005, 2, 443–454. [Google Scholar] [CrossRef]
- Gu, Z.Q.; Lin, Y.D. Fault diagnosis of rolling bearing based on improved LMD and comprehensive characteristic index. J. Hefei Univ. Tech. Nat. Sci. 2021, 44, 145–150. [Google Scholar]
- Zhang, Y.L.; Zhang, P.J.; Fang, Y.H.; Dong, X.Y. Research on signal feature extraction method of LMD-KICA rolling bearing. Mach. Des. Manuf. 2021, 02, 15–18. [Google Scholar]
- Li, X.; Ma, J.; Wang, X.D.; Wu, J.D.; Li, Z.R. An improved local mean decomposition method based on improved composite interpolation envelope and its application in bearing fault feature extraction. ISA Trans. 2020, 97, 365–383. [Google Scholar] [CrossRef]
- Kocbek, S.; Gabrys, B. Automated machine learning techniques in prognostics of railway track defects. In Proceedings of the International Conference on Data Mining Workshops (ICDMW), Beijing, China, 8–11 November 2019. [Google Scholar]
- Li, D.; Wang, Y.; Yan, W.J.; Ren, W.X. Acoustic emission wave classification for rail crack monitoring based on synchrosqueezed wavelet transform and multi-branch convolutional neural network. Struct. Health Monit. 2020, 2, 147592172092279. [Google Scholar] [CrossRef]
- Zhan, Y.; Dai, X.X.; Yang, E.H.; Wang, K.C.P. Convolutional neural network for detecting railway fastener defects using a developed 3D laser system. Int. J. Rail Transp. 2020, 1–21. [Google Scholar] [CrossRef]
- Yao, D.C.; Sun, Q.; Yang, J.W.; Liu, H.C.; Zhang, J. Railway fastener fault diagnosis based on generative adversarial network and residual network model. Shock. Vib. 2020, 2020, 8823050. [Google Scholar] [CrossRef]
- Cui, H.; Li, J.; Hu, Q.W.; Mao, Q.Z. Real-time inspection system for ballast railway fasteners based on point cloud deep learning. IEEE Access 2020, 8, 61604–61614. [Google Scholar] [CrossRef]
- Wei, X.K.; Yang, Z.M.; Liu, Y.X.; Wei, D.H.; Jia, L.M.; Li, Y.J. Railway track fastener defect detection based on image processing and deep learning techniques: A comparative study. Eng. Appl. Artif. Intel. 2019, 80, 66–81. [Google Scholar] [CrossRef]
- Ferreno, D.; Sainz-Aja, J.A.; Carrascal, I.A.; Guartas, M.; Pombo, J.; Casado, J.A.; Diego, S. Prediction of mechanical properties of rail pads under in-service conditions through machine learning algorithms. Adv. Eng. Softw. 2021, 151, 102927. [Google Scholar] [CrossRef]
- Zhuang, Z.; Zhang, G.H.; Dong, W.; Sun, X.Y.; Wang, C.J. Intelligent fault detection of high-speed railway turnout based on hybrid deep learning. In Proceedings of the 31st Australasian Joint Conference on Artificial Intelligence, Wellington, New Zealand, 11–14 December 2018. [Google Scholar]
- Li, W.J.; Shen, Z.H.; Li, P.G. Crack detection of track plate based on YOLO. In Proceedings of the 12th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 14–15 December 2019. [Google Scholar]
- Wang, W.; Hu, W.; Wang, W.; Xu, X.; Wang, M.; Shi, Y.; Qiu, S.; Tutumluer, E. Automated crack severity level detection and classification for ballastless track slab using deep convolutional neural network. Autom. Constr. 2021, 124, 103484. [Google Scholar] [CrossRef]
- Hu, Q.; Xu, W.; Gao, F.; Zhu, H.P. Damage identification of CA mortar layer of CRTS Ⅰ slab track based on BP neural network. J. Civ. Eng. Manag. 2018, 35, 90–96. [Google Scholar]
- Guo, G.R.; Cui, X.H.; Du, B.W. Monitoring technology for deformation of key sections of CRTS Ⅱ slab ballastless track foundation. China Railw. 2019, 11, 60–66. [Google Scholar]
- Zhou, Z.H. Machine Learning, 1st ed; Tsinghua University Press: Beijing, China, 2016; pp. 101–102. [Google Scholar]
- Zhang, L.H.; Ni, Y.Q.; Lai, S.; Wang, S.G. A novel machine learning technique for online health monitoring of high-speed trains. In Proceedings of the 2nd International Workshop on Structural Health Monitoring for Railway System, Qingdao, China, 17–19 October 2018. [Google Scholar]
- Chen, X.Y. Research and Application of Intrusion Detection Technology Based on Features Analysis and Support Vector Machines. Master’s Thesis, Beijing University of Posts and Telecommunications, Beijing, China, 2015. [Google Scholar]
- Meng, D.M. Study on the Structural Damage Identification Based on the Free Response Signal and Neural Network. Master’s Thesis, Qingdao Technological University, Qingdao, China, 2012. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Jiang, D.S.; Zhang, W.T.; Li, F. All-metal optical fiber accelerometer with low transverse sensitivity for seismic monitoring. IEEE Sens. J. 2013, 13, 4556–4560. [Google Scholar] [CrossRef]
- Cheng, J.S.; Zhang, K.; Yang, Y.; Yu, D.J. Comparison between the methods of local mean decomposition and empirical mode decomposition. J. Vib. Shock 2009, 28, 13–17. [Google Scholar]
- Buda, A.; Jarynowski, A. Life Time of Correlations and its Applications; Wydawnictwo Niezalezne: Wroclaw, Poland, 2010; pp. 5–21. [Google Scholar]
- Wang, Y.M. Study on the Structural Damage Identification Based on the Response and PSO-SVM. Master’s Thesis, Qingdao University of Technology, Qingdao, China, 2019. [Google Scholar]
- Yuan, C.Q.; Zhao, D.; Yu, Y.H. Identifying the damage degree of structure based on empirical mode decomposition and parameters in time domain amplitude. Nondestruct. Test. 2008, 30, 84–86. [Google Scholar]
- Wu, S.S. Research on Void Detection Method of CRTS Ⅱ Slab Track Based on Transient Impulse Response. Master’s Thesis, Shijiazhuang Tiedao University, Shijiazhuang, China, 2018. [Google Scholar]
- Zhou, T.L. Research on Structural Damage Identification Method Based on CEEMD. Master’s Thesis, Changsha University of Technology, Changsha, China, 2016. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Koga, S.S.; Zhou, X.L.; Dickson, D.W. Machine learning-based decision tree classifier for the diagnosis of progressive supranuclear palsy and corticobasal degeneration. Neuropathol. Appl. Neurobiol. 2021, 00, 1–11. [Google Scholar]


| Name | Expression | Description |
|---|---|---|
| Peak-to-Peak | The difference between the maximum and minimum values. | |
| Variance | The average of the sum of squares of the difference between the data and the mean value. | |
| Root mean square | Indicates the magnitude of the energy of the vibration signal. | |
| Shape factor | Refers to a value that is affected by the shape of waveforms. | |
| Crest factor | Detects the existence of shocks. | |
| Skewness | Measures the skewness of the data distribution |
| Category | Symbol | Name |
|---|---|---|
| variables | x | Vibration signal |
| t | Time | |
| N | Local extremum point | |
| i | Local extremum point variable | |
| m | Average of local extremum point | |
| a | Local amplitude | |
| h | Intermediate process variable | |
| s | Pure frequency modulation signal | |
| PF | Product function | |
| nn | Pure frequency modulation signal iteration count variable | |
| kk | Monotonic signal iteration count variable | |
| u | Residual signal | |
| q | Number of characteristic product function variable | |
| j | Length of characteristic product function variable | |
| E | Total energy | |
| p | Normalized energy | |
| H | Energy entropy | |
| parameters | n | Pure frequency modulation signal iteration count |
| k | Monotonic signal iteration count | |
| r | Number of characteristic product function | |
| l | Length of characteristic product function |
| Category | mtry = 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Class 1 | 98.18 | 96.63 | 96.58 | 97.83 | 97.50 | 96.58 | 97.28 |
| Class 2 | 91.51 | 92.89 | 95.59 | 93.75 | 91.46 | 90.69 | 91.87 |
| Average | 94.85 | 94.76 | 96.09 | 95.79 | 94.48 | 93.64 | 94.58 |
| Category | Original Decision-Tree | Optimized Decision-Tree | Pruned Decision-Tree |
|---|---|---|---|
| Class 1 | 93.65 | 94.96 | 94.05 |
| Class 2 | 89.32 | 91.15 | 90.96 |
| Average | 91.49 | 93.06 | 92.51 |
| Error | 6.76 | 5.23 | 6.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, G.; Cui, X.; Du, B. Random-Forest Machine Learning Approach for High-Speed Railway Track Slab Deformation Identification Using Track-Side Vibration Monitoring. Appl. Sci. 2021, 11, 4756. https://doi.org/10.3390/app11114756
Guo G, Cui X, Du B. Random-Forest Machine Learning Approach for High-Speed Railway Track Slab Deformation Identification Using Track-Side Vibration Monitoring. Applied Sciences. 2021; 11(11):4756. https://doi.org/10.3390/app11114756
Chicago/Turabian StyleGuo, Gaoran, Xuhao Cui, and Bowen Du. 2021. "Random-Forest Machine Learning Approach for High-Speed Railway Track Slab Deformation Identification Using Track-Side Vibration Monitoring" Applied Sciences 11, no. 11: 4756. https://doi.org/10.3390/app11114756
APA StyleGuo, G., Cui, X., & Du, B. (2021). Random-Forest Machine Learning Approach for High-Speed Railway Track Slab Deformation Identification Using Track-Side Vibration Monitoring. Applied Sciences, 11(11), 4756. https://doi.org/10.3390/app11114756






