Characterization of Shear Strain on PDMS: Numerical and Experimental Approaches
Abstract
1. Introduction
2. Numerical Constitutive Models
3. Materials and Methods
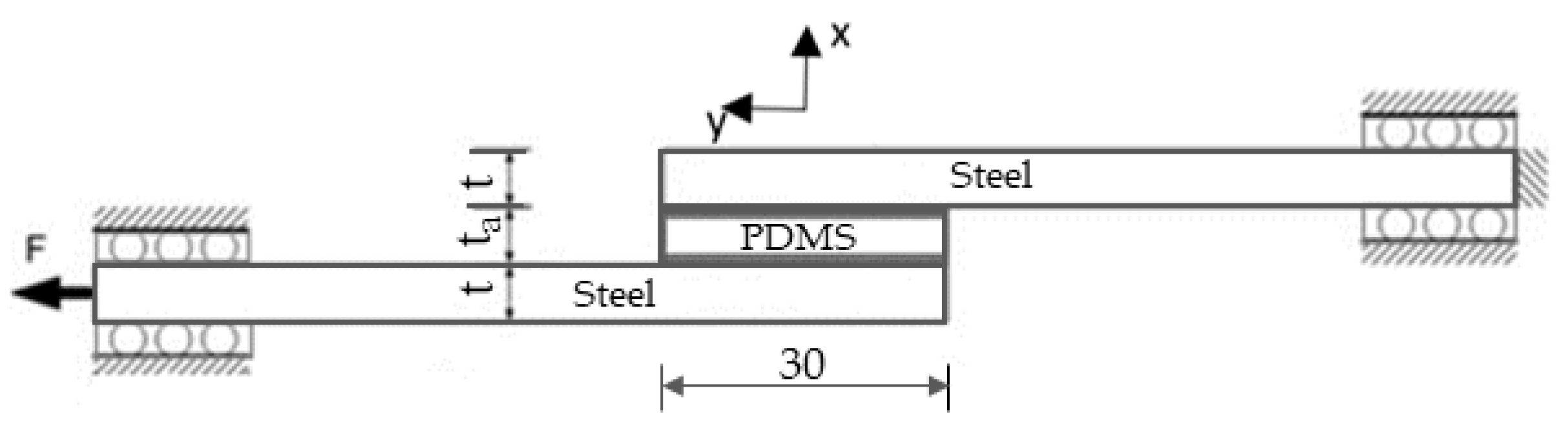
3.1. Experimental Tests
3.1.1. Tensile Testing
3.1.2. Shear Testing
3.2. Numerical Simulation
4. Results and Discussion
4.1. Experimental
4.2. Numerical
4.3. Comparison
5. Conclusions
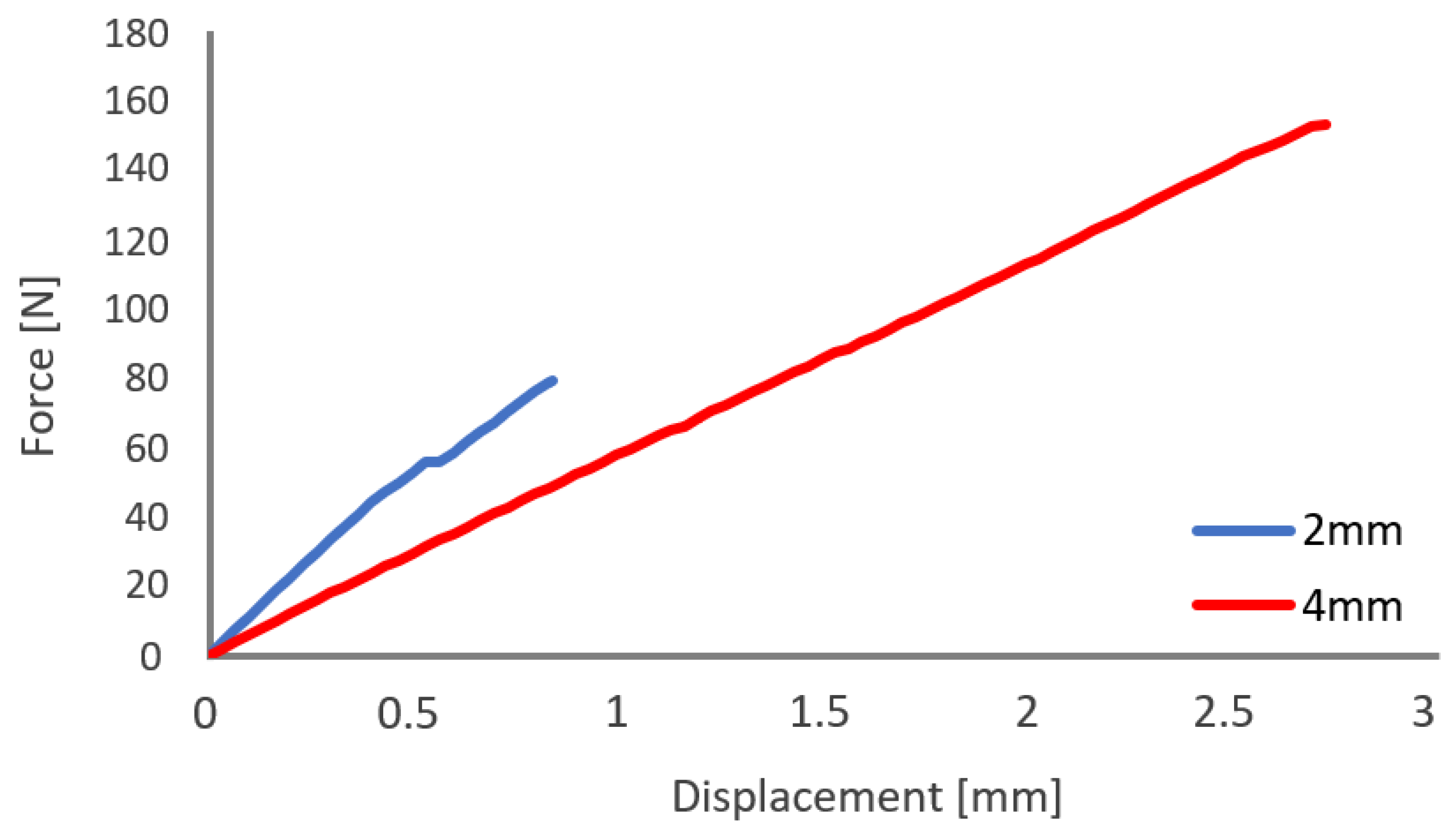
- From experimental tests, the hyperelastic behavior of PDMS was verified using a simple shear test. The DIC tests showed that the most significant shear strain occurred in the centre of the PDMS plate. These experimental tests also verified that the PDMS rupture occurred at the bonding interface between the steel and PDMS plates. The rupture happened for different PDMS thicknesses. For 4 mm of PDMS, the specimen broke up at a 154 N of shear force. The specimen with 2 mm of PDMS suffered rupture at a shear force of 80 N. For an equal value of shear force, a higher value of displacement happened for the higher PDMS thickness.
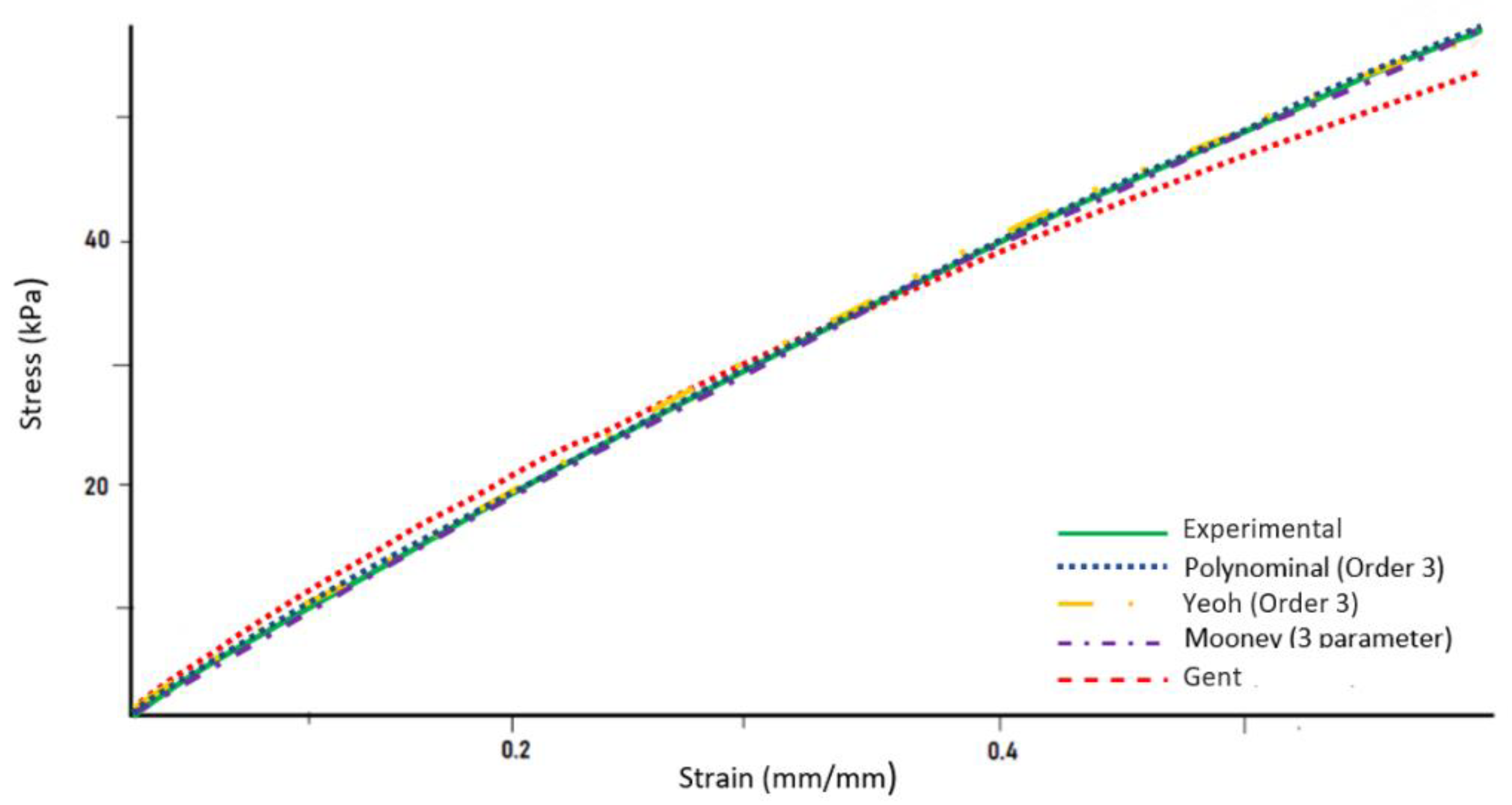
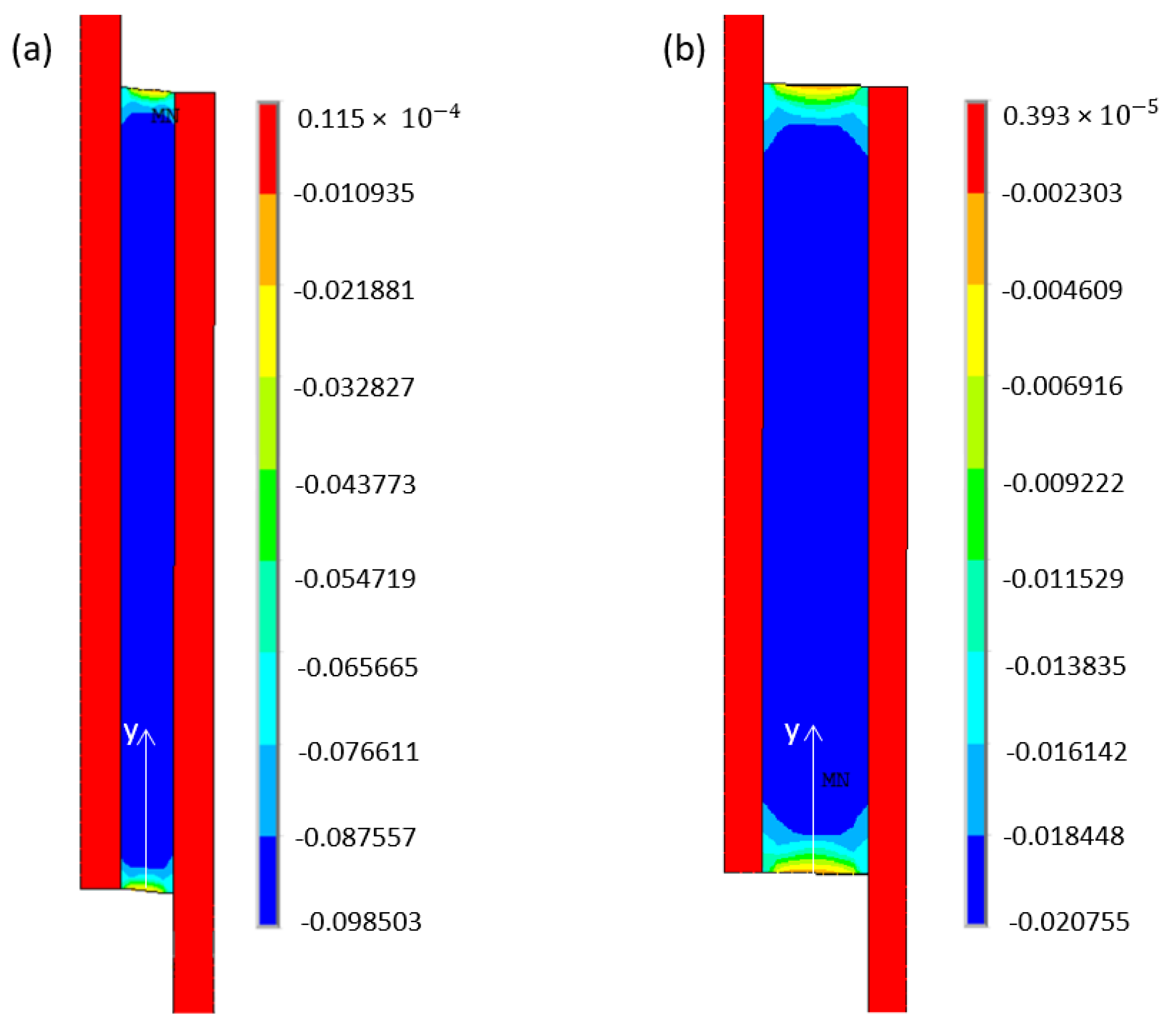
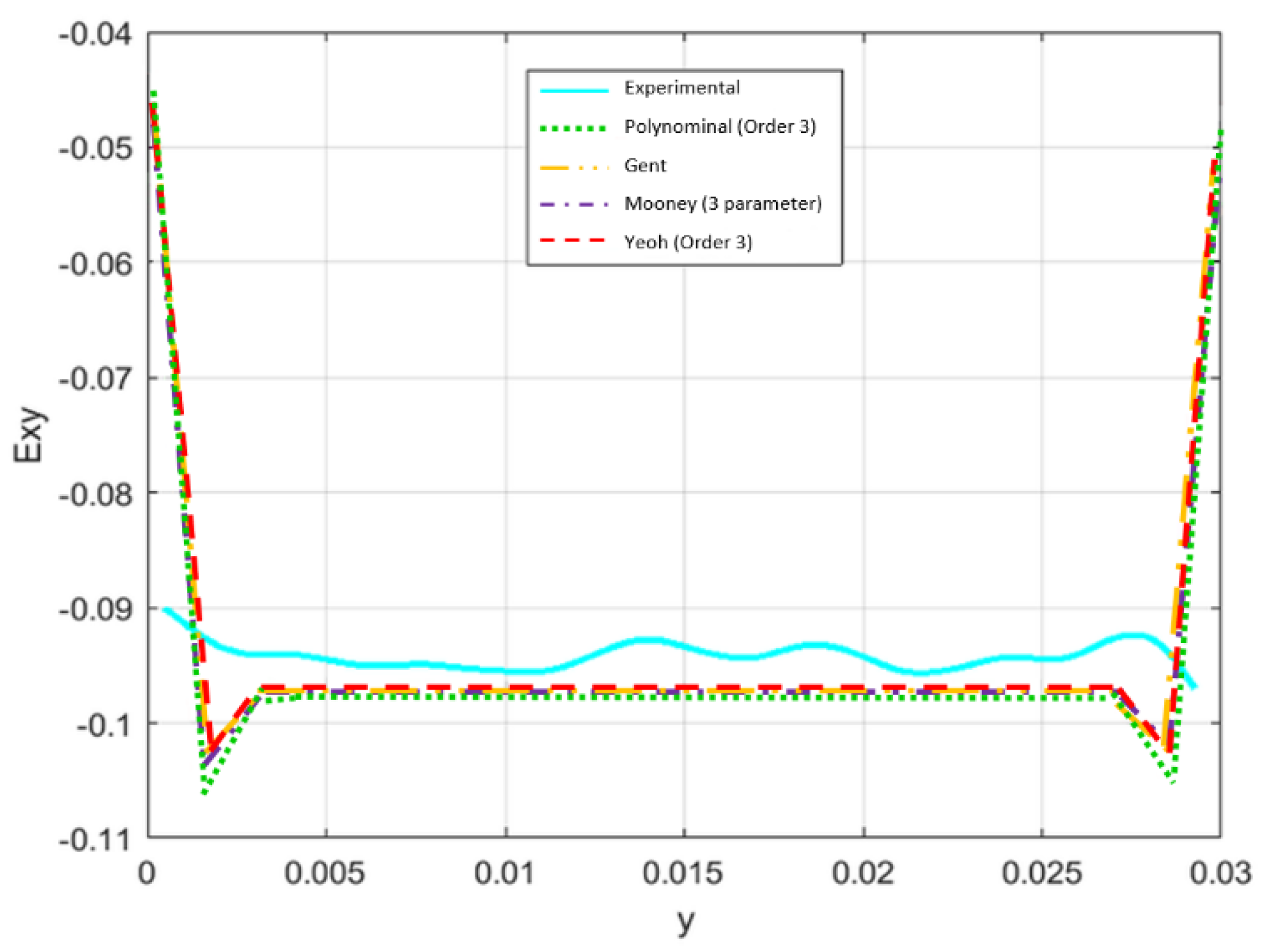
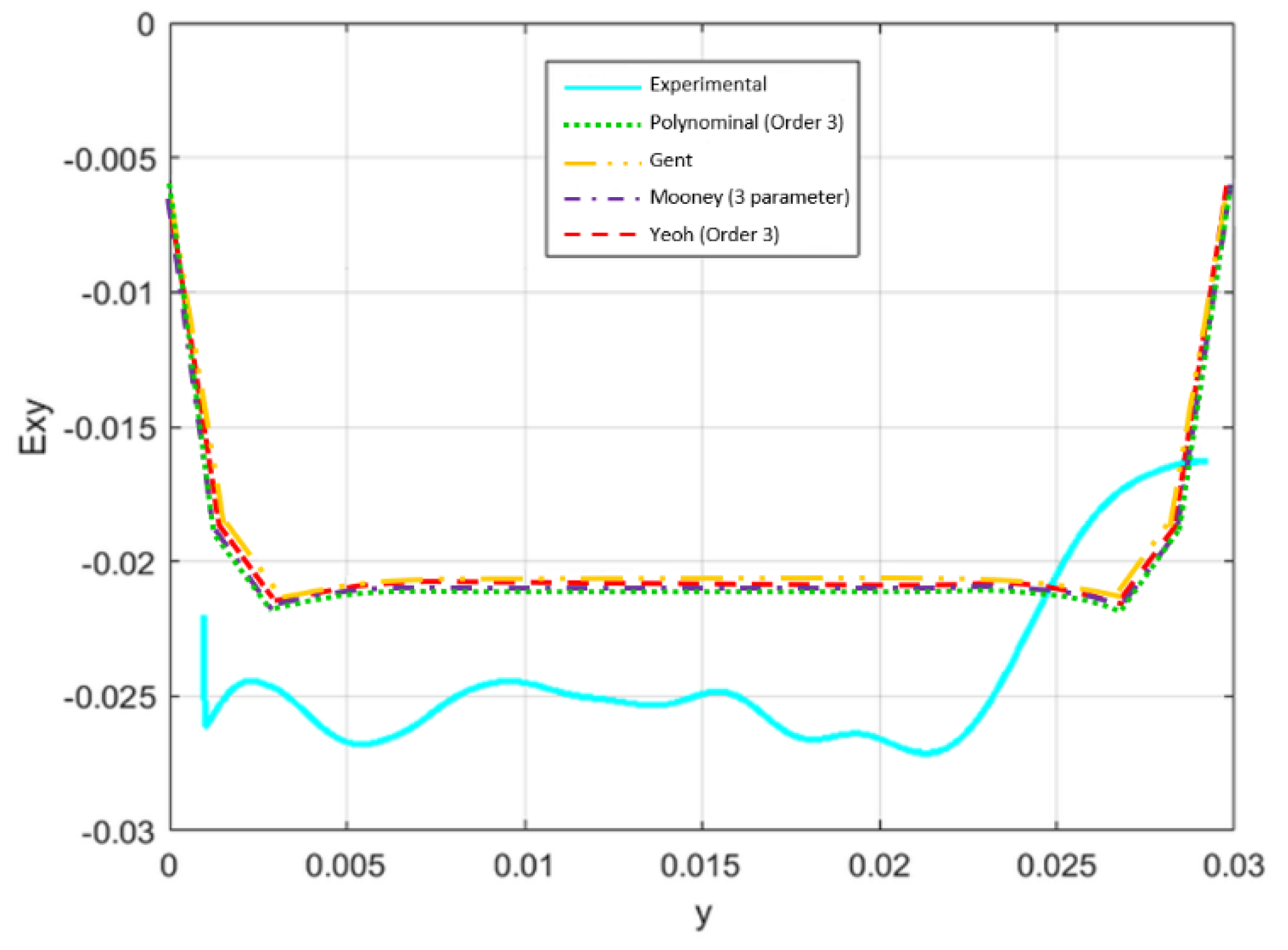
- The numerical simulations were done using four hyperelastic constitutive models (Mooney–Rivlin, Yeoh, Gent and polynomial). All the hyperelastic constitutive models presented similar results despite some critical differences. The main reason to obtain similar results in shear stress was due to the appliance of low displacement values and the constitutive models, for this displacement level, have identical behavior. The values that show a greater difference in shear strain occurred for the Mooney–Rivlin constitutive model when compared with the other constitutive models (see Table 2). The numerical model with 2 mm of PDMS results in higher values of shear strain than with 4 mm. So, for low displacement levels it is possible to use any of the hyperelastic constitutive to simulate the shear test.
- Qualitatively, in the central region of the specimen, the numerical and experimental results have similar behavior, and the values of shear strain are close. Nevertheless, the maximum relative error between the numerical and experimental results is very different for the two thickness values. It is possible to conclude that, for higher values of displacement and thicknesses, the numerical simulation results move further away from experimental values.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Martin, S.; Bhushan, B. Transparent, wear-resistant, superhydrophobic and superoleophobic poly(dimethylsiloxane) (PDMS) surfaces. J. Coll. Int. Sci. 2017, 488, 118–126. [Google Scholar] [CrossRef] [PubMed]
- Hassler, C.; Boretius, T.; Stieglitz, T. Polymers for neural implants. J. Polym. Sci. Part B Polym. Phys. 2011, 49, 18–33. [Google Scholar] [CrossRef]
- Roh, C.; Lee, J.; Kang, C. Physical Properties of PDMS (Polydimethylsiloxane) Microfluidic Devices on Fluid Behaviors: Various Diameters and Shapes of Periodically-Embedded Microstructures. Materials 2016, 9, 836. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.H.; Lau, K.T.; Shepherd, R.; Wu, Y.; Wallace, G.; Diamond, D. Performance characteristics of a polypyrrole modified polydimethylsiloxane (PDMS) membrane based microfluidic pump. Sens. Actuators A Phys. 2008, 148, 239–244. [Google Scholar] [CrossRef]
- Lin, Y.H.; Kang, S.W.; Wu, T.Y. Fabrication of polydimethylsiloxane (PDMS) pulsating heat pipe. Appl. Therm. Eng. 2009, 29, 573–580. [Google Scholar] [CrossRef]
- Casanova-Moreno, J.; To, J.; Tony Yang, C.W.; Turner, R.F.; Bizzotto, D.; Cheung, K.C. Fabricating devices with improved adhesion between PDMS and gold-patterned glass. Sens. Actuators B Chem. 2017, 246, 904–909. [Google Scholar] [CrossRef]
- Jewkes, R.; Burton, H.; Espino, D. Towards Additive Manufacture of Functional, Spline-Based Morphometric Models of Healthy and Diseased Coronary Arteries: In Vitro Proof-of-Concept Using a Porcine Template. J. Funct. Biomater. 2018, 9, 15. [Google Scholar] [CrossRef]
- Teixeira, A.; Hernández-Rodríguez, J.; Wu, L.; Oliveira, K.; Kant, K.; Piairo, P.; Diéguez, L.; Abalde-Cela, S. Microfluidics-Driven Fabrication of a Low Cost and Ultrasensitive SERS-Based Paper Biosensor. Appl. Sci. 2019, 9, 1387. [Google Scholar] [CrossRef]
- Farfán-Cabrera, L.I.; Pascual-Francisco, J.B.; Gallardo-Hernández, E.A.; Susarrey-Huerta, O. Application of digital image correlation technique to evaluate creep degradation of sealing elastomers due to exposure to fluids. Polym. Test. 2018, 65, 134–141. [Google Scholar] [CrossRef]
- Bashirzadeh, Y.; Qian, S.; Maruthamuthu, V. Non-intrusive measurement of wall shear stress in flow channels. Sens. Actuators A. Phys. 2018, 271, 118–123. [Google Scholar] [CrossRef]
- Rodrigues, R.O.; Pinho, D.; Bento, D.; Lima, R.; Ribeiro, J. Wall expansion assessment of an intracranial aneurysm model by a 3D Digital Image Correlation System. Measurement 2016, 88, 262–270. [Google Scholar] [CrossRef]
- Huang, Y.M.; Tsai, N.C.; Lai, J.Y. Development of tactile sensors for simultaneous, detection of normal and shear stresses. Sens. Actuators A Phys. 2010, 159, 189–195. [Google Scholar] [CrossRef]
- Unver, O.; Uneri, A.; Aydemir, A.; Sitti, M. Geckobot: A Gecko Inspired Climbing Robot Using Elastomer Adhesives. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation (2006 ICRA), Orlando, FL, USA, 15–19 May 2006. [Google Scholar]
- Xu, F.; Li, X.; Shi, Y.; Li, L.; Wang, W.; He, L.; Liu, R. Recent Developments for Flexible Pressure Sensors: A Review. Micromachines 2018, 9, 580. [Google Scholar] [CrossRef] [PubMed]
- Fallahi, H.; Zhang, J.; Phan, H.-P.; Nguyen, N.-T. Flexible Microfluidics: Fundamentals, Recent Developments, and Applications. Micromachines 2019, 10, 830. [Google Scholar] [CrossRef]
- Banea, M.; Silva, L. The effect of temperature on the mechanical properties of adhesives for the automotive industry. Proc. Inst. Mech. Eng. Part L J. Mat. Des. Applic. 2010, 224, 51–62. [Google Scholar] [CrossRef]
- Moreira, D.; Nunes, L. Comparison of simple and pure shear for an incompressible isotropic hyperelastic material under large deformation. Polym. Test. 2013, 32, 240–248. [Google Scholar] [CrossRef]
- Nunes, L.S. Shear modulus estimation of the polymer polydimethylsiloxane (PDMS) using digital image correlation. Mater. Des. 2010, 31, 583–588. [Google Scholar] [CrossRef]
- Nunes, L.S. Mechanical characterization of hyperelastic polydimethylsiloxane by simple shear test. Mater. Sci. Eng. A 2011, 528, 1799–1804. [Google Scholar] [CrossRef]
- Post, D.; Han, B.; Ifju, P. High Sensitivity Moiré: Experimental Analysis for Mechanics and Materials; Springer: Berlin/Heidelberg, Germany, 1997; ISBN 978-1-4612-4334-2. [Google Scholar]
- Wang, Y.; Gao, X.; Xie, X.; Wu, S.; Liu, Y.; Yang, L. Simultaneous dual directional strain measurement using spatial phase-shift digital shearography. Opt. Las. Eng. 2016, 87, 197–203. [Google Scholar] [CrossRef]
- Ribeiro, J.; Fernandes, C.S.; Lima, R. Numerical Simulation of Hyperelastic Behaviour in Aneurysm Models. In Lecture Notes Computational Vision and Biomechanics; Springer: Cham, Switzerland, 2017; pp. 937–944. [Google Scholar] [CrossRef]
- Xue, L.; Pham, J.T.; Iturri, J.; Del Campo, A. Stick-Slip Friction of PDMS Surfaces for Bioinspired Adhesives. Langmuir 2016, 32, 2428–2435. [Google Scholar] [CrossRef]
- Besson, J.; Cailetaud, G.; Chaboche, J.; Forest, S.; Blétry, M. Non-Linear Mechanics of Materials; Springer: London, UK, 2010. [Google Scholar] [CrossRef]
- Ribeiro, J.; Lopes, H.; Martins, P. A hybrid method to characterize the mechanical behaviour of biological hyperelastic tissues. Comp. Meth. Biomech. Biomed. Eng. Imag. Vis. 2017, 5, 157–164. [Google Scholar] [CrossRef]
- Holzapfel, G. Nonlinear Solid Mechanics: A Continuum Approach for Engineering; John Wiley & Sons Ltd.: New York, NY, USA, 2000; ISBN 978-0-471-82319-3. [Google Scholar]
- Wriggers, P. Nonlinear Finite Element Methods; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 978-3-540-71000-4. [Google Scholar]
- Yeoh, O.H. Some forms of the strain energy function for rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Bhowmick, A.K. Rubber Products Manufacturing Technology; CRC Press: New York, NY, USA, 1994; ISBN 9780824791124. [Google Scholar]
- Guo, Z.; Sluys, J. Application of a new constitutive model for the description of rubber-like materials under monotonic loading. Int. J. Solid Struct. 2006, 43, 2799–2819. [Google Scholar] [CrossRef]
- Proulx, T. Mechanics of Biological Systems and Materials. In Proceedings of the Annual Conference on Experimental and Applied Mechanics, Uncasville, CT, USA, 13–16 June 2011; Springer Science & Business Media: New York, NY, USA, 2011. [Google Scholar]
- Laksari, K.; Shafieian, M.; Darvish, K. Constitutive model for brain tissue under finite compression. J. Biomech. 2012, 45, 642–646. [Google Scholar] [CrossRef]
- Hartmann, S.; Neff, P. Polyconvexity of generalized polynomial-type hyperelastic strain energy functions for near-incompressibility. Int. J. Solid Struct. 2003, 40, 2767–2791. [Google Scholar] [CrossRef]
- Ritto, T.G.; Nunes, L.S. Bayesian model selection of hyperelastic models for simple and pure shear at large deformations. Comput. Struct. 2015, 156, 101–109. [Google Scholar] [CrossRef]
- ASTM D412-0:2011. Standard Test Methods for Vulcanized Rubber and Thermoplastic Elastomers—Tension; ASTM International: West Conshohocken, PA, USA, 2016. [Google Scholar]
- Krahmer, D.M.; Polvorosa, R.; Lacalle, L.N.; Alonso-Pinillos, U.; Abate, G.; Riu, F. Alternatives for Specimen Manufacturing in Tensile Testing of Steel Plates. Exp. Tech. 2016, 40, 1555–1565. [Google Scholar] [CrossRef]
- Silva, C.M.A.; Rosa, P.A.R.; Martins, P.A.F. Innovative Testing Machines and Methodologies for the Mechanical Characterization of Materials. Exp. Tech. 2016, 40, 569–581. [Google Scholar] [CrossRef]
- Dixit, U.S.; Joshi, S.N.; Davim, J.P. Incorporation of material behavior in modeling of metal forming and machining processes: A review. Mater. Des. 2011, 32, 3655–3670. [Google Scholar] [CrossRef]
- Aurrekoetxea, M.; Lacalle, L.N.; Llanos, I. Machining Stresses and Initial Geometry on Bulk Residual Stresses Characterization by On-Machine Layer Removal. Materials 2020, 13, 1445. [Google Scholar] [CrossRef]
- López, M.; Rubio, M.; Sadek, S.H.; Veja, E.J. A simple emulsification technique for the production of micro-sized flexible powder of polydimethylsiloxane (PDMS). Pow. Tecnh. 2020, 306, 610–616. [Google Scholar] [CrossRef]
- Zhang, J.; Sweedy, A.; Gitzhofer, F.; Baroud, G. A novel method for repeatedly generating speckle patterns used in digital image correlation. Opt. Las. Eng. 2018, 100, 259–266. [Google Scholar] [CrossRef]
- Cardoso, C.; Fernandes, C.; Lima, R.; Ribeiro, J. Biomechanical analysis of PDMS channels using different hyperelastic numerical constitutive models. Mech. Res. Commun. 2018, 90, 26–33. [Google Scholar] [CrossRef]
- Ribeiro, J.; Lopes, H.; Martins, P.; César, M.B. Mechanical analysis of PDMS material using biaxial test. AIMS Mater. Sci. 2019, 6, 97–110. [Google Scholar] [CrossRef]







| Numerical Simulation | Displacement [mm] |
|---|---|
| 1 | 0.5 |
| 2 | 0.2 |
| Constitutive Model | Average | Minimum | Maximum | |
|---|---|---|---|---|
| Mooney-Rivlin 3 parameter | −0.09684 | −0.04678 | −0.10238 | PDMS Thickness 2 mm |
| Yeoh 3rd Order | −0.09680 | −0.04722 | −0.10237 | |
| Polynomial 3rd Order | −0.09680 | −0.04362 | −0.10514 | |
| Gent | −0.09680 | −0.04709 | −0.10240 | |
| Mooney-Rivlin 3 parameter | −0.02056 | −0.00585 | −0.02128 | PDMS Thickness 4 mm |
| Yeoh 3rd Order | −0.02060 | −0.00585 | −0.02128 | |
| Polynomial 3rd Order | −.02060 | −0.00585 | −0.02128 | |
| Gent | −0.02060 | −0.00585 | −0.02128 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Souza, A.; Marques, E.; Balsa, C.; Ribeiro, J. Characterization of Shear Strain on PDMS: Numerical and Experimental Approaches. Appl. Sci. 2020, 10, 3322. https://doi.org/10.3390/app10093322
Souza A, Marques E, Balsa C, Ribeiro J. Characterization of Shear Strain on PDMS: Numerical and Experimental Approaches. Applied Sciences. 2020; 10(9):3322. https://doi.org/10.3390/app10093322
Chicago/Turabian StyleSouza, Andrews, Eduardo Marques, Carlos Balsa, and João Ribeiro. 2020. "Characterization of Shear Strain on PDMS: Numerical and Experimental Approaches" Applied Sciences 10, no. 9: 3322. https://doi.org/10.3390/app10093322
APA StyleSouza, A., Marques, E., Balsa, C., & Ribeiro, J. (2020). Characterization of Shear Strain on PDMS: Numerical and Experimental Approaches. Applied Sciences, 10(9), 3322. https://doi.org/10.3390/app10093322






