Influence of Frequency and Distance on Acoustic Emission Velocity Propagating in Various Dielectrics

Abstract

The results obtained for the measurements of acoustic emission (AE) signal parameters emitted in three dielectric liquids are presented in this paper. In particular, the velocity of AE wave was calculated based on the time of arrival of the AE signal. A frequency modulated signal was generated by a piezoelectric transducer and measured at various distances by a hydrophone. The changes in velocity values at particular distances and for different frequencies were investigated. The analyses include the determination of the dependency of the velocity values from the distance between the communicating devices. A nonlinear regression model was calculated, and the differences between AE velocities propagating in the considered dielectrics were determined. Similarly, the influence of modulation frequency on the AE velocity was determined using nonlinear regression. Based on the calculation data, it can clearly be stated that the velocity of AE wave depends significantly on the frequency and distance at which it is registered. These two factors may have an important influence on the localization of partial discharges (PD) occurring in these types of dielectric liquids.

1. Introduction

Acoustic emission (AE) is one of the noninvasive methods used for the detection and localization of partial discharges (PD), occurring in the insulation systems of power transformers [1,2,3]. PD may pose a serious risk to the proper functioning of this type of equipment. In the field of high-voltage power transformer diagnostics, there are various other existing methods to calculate their technical condition estimation, e.g., optical spectrophotometry [4,5,6], or UHV [7,8,9] methods. The advantage of non-invasive PD detection methods is their resistance to electromagnetic interference, which makes them appropriate for application under on-line operation [10,11,12].

Apart from the detection of the PD occurrence, its localization inside the device is crucial [11,13]. Knowing the speed of the waveform of AE is the key parameter in the application of methods for locating incomplete discharges. The location of the PD source is calculated by assuming the known AE velocity value and coordinates of the measuring sensor. Regarding the AE velocity, within literature, various values are defined, e.g., the speed of 1417 m/s is assumed in [13], 1431 m/s in [14] or 1400 m/s in [15,16]. Both within literature and in the IEEE standard C57.127-2007 [17], the impact from temperature and moisture content is mentioned.

The speed of AE wave has an important impact on the localization result, as shown in [18], where authors measured AE velocity changes at various distances while propagating in concrete. Therefore, in this study, experiments have been carried out to determine the AE wave velocity in the chosen propagation centers. At the present time, new electro- and thermo-insulating materials are being developed. Aside from mineral oils, this also includes natural and synthetic esters [19,20,21].

PD emit AE waves in a wide-frequency spectrum. Therefore, the effect of modulation frequencies was studied in this paper. In practice, the surveyors do not know where the AE source is located, thus, they place the sensors at various locations. For that reason, the AE velocity at different distances between the source and receiver was determined. Transformers are usually large in size, but the distance from the isolation system to the sensor can be up to several meters long. As the AE wave undergoes significant attenuation, especially in the HF range, it is impossible to record pressure changes over long distances. The distances considered in this study were chosen experimentally, as part of basic works [22]. In real transformers, the AE wave will undergo additional phenomena such as damping, refraction, reflections, etc. In this work, we did not analyze the barriers to propagation as the primary objective was to determine the AE velocity in barrier-free centers.

The main contribution of the here presented research study lies in the determination of the influence of distance and modulation frequency of the AE wave on its velocity, in various dielectric liquids. The results of preliminary works were obtained for natural ester and are presented in [22]. In this article, comparative analyses for the velocity measurements of AE waves propagating in three types of dielectrics are presented. In particular, mineral oil type TRAFO EN [23], natural ester type eN1204 [24], and synthetic ester type 7131 [25] are considered.

2. Materials and Methods

The measurements were conducted in a laboratory. The system was modelled to test the parameters of the acoustic wave propagating in a typical propagation medium such as mineral oil or ester, which are used in the insulation systems of power transformers. A piezoelectric transducer (disc type PRYY+0354, material type PIC255 [26]) was applied as the AE source and a spherical hydrophone type 8105 [27] was used as the AE receiver. Standard AE measuring apparatus was used for signal registration. The signals propagated in a plastic tank of the following dimensions: 187 mm wide, 147 mm high and 1000 mm long. The tank was filled with the considered dielectric liquids, details of their physical properties are given in Table 1. A detailed description of the measuring setup and parameters of the applied transducers is given in previously published work [22]. A scheme diagram of the experimental setup is depicted in Figure 1.

Table 1. Properties of the considered dielectric liquids [23,24,25].

Property	Density at 20 °C (g/cm3)	Viscosity at 40 °C (mm2/s)	Water content	Breakdown Voltage (kV)
Test method	ISO 3675	ISO 3104	IEC 60814	IEC 60156/ASTM D877/IEC 60296
Natural ester	0.92	37	50 (mg/kg)	≥ 30
Synthetic ester	0.97	29	50 (mg/kg)	≥ 75
Mineral oil	0.87	9.9	50 (m/m)	≥ 69

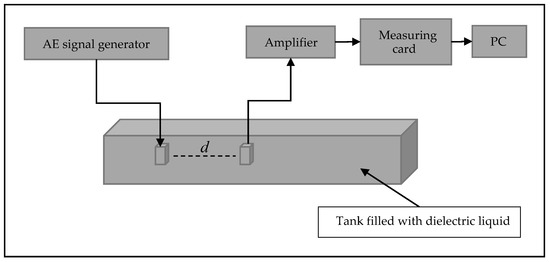
Figure 1. Scheme diagram of the experimental setup.

The measuring procedure involved 2 tasks: (1) investigation of frequency modulated AE signals, in particular, values up to 400 Hz were considered. AE waves up to 400 kHz were generated and recorded, but values above 400 Hz were not detectable, and so were therefore not included in this paper. The frequency range presented was a result of hardware limitations, and (2) an investigation of the influence of distance between the transducers in the range from 2.5 cm to 82.5 cm. Within the first task, the frequency modulated AE signal was emitted at a constant location, in a series of 32 samples for each of the regarded frequency values. Within the second task, the AE signal was registered with a sampling frequency of 250 MHz at various distances to the source. The AE velocity was calculated as quotient of the distance between the measuring devices and the time of arrival t_a values. An exemplary AE waveform generated at frequency f = 150 Hz is depicted in Figure 2. An exemplary AE waveform measured by a hydrophone at distance d = 82.5 cm and frequency f = 150 Hz is depicted in Figure 3. In Figure 3, the vertical line shows the value of t_a.

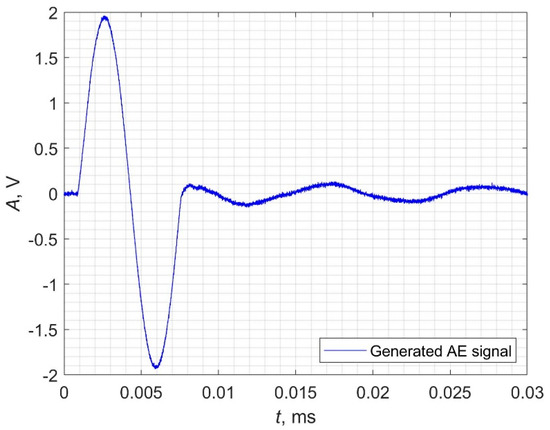
Figure 2. Exemplary acoustic emission (AE) waveform generated at frequency f = 150 Hz.

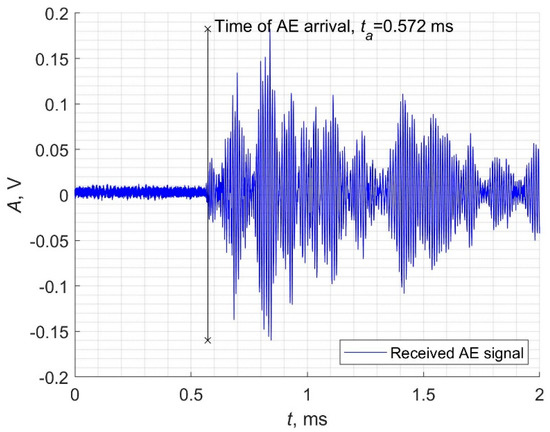
Figure 3. Exemplary AE waveform measured by hydrophone at distance d = 82.5 cm and frequency f = 150 Hz.

3. Results Analysis and Discussion

In Figure 4, detailed results depicting the median velocity values calculated for AE waveform generated in synthetic ester at various frequencies and measured at various distances, are presented in the form of heat maps. The values should be read as on a chessboard—each value represents a particular row and column, as described on the axes. The shade of grey corresponds to the AE velocity. Darker fields indicate higher values and lighter fields indicate lower values. The observation of colors allows for the consideration of the dynamics of speed changes, depending on the parameter f or d. It should be noted that in the diagrams, the values are not presented in a linear way for the frequency. Linear increments are used only for distances. Corresponding results gathered for the natural ester and mineral oil are depicted in Figure 5 and Figure 6, respectively.

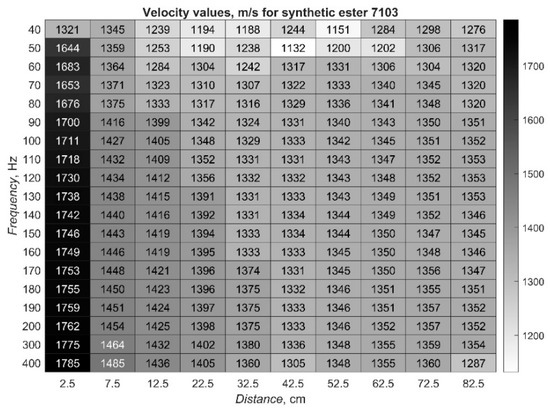
Figure 4. Detailed results depicting velocity values calculated for AE waveform generated in synthetic ester at various frequencies and measured at various distances.

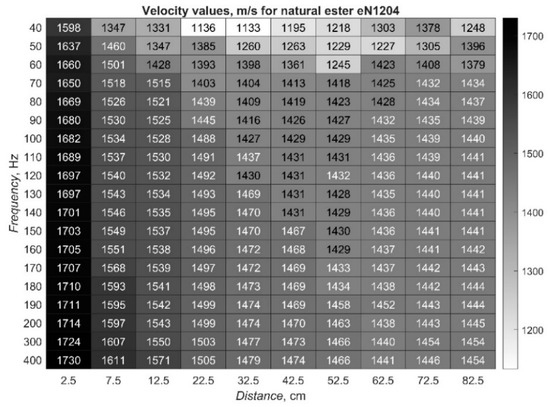
Figure 5. Detailed results depicting velocity values calculated for AE waveform generated in natural ester at various frequencies and measured at various distances.

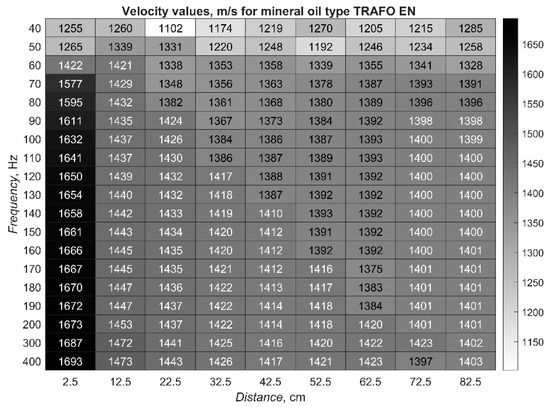
Figure 6. Detailed results depicting velocity values calculated for AE waveform generated in mineral oil at various frequencies and measured at various distances.

From the values depicted in Figure 4, Figure 5 and Figure 6, it can clearly be seen that the velocity of the AE wave strongly depends on the location it is measured, and that the values differ significantly in the differing liquids. They are more stable, despite modulation frequency, only in the synthetic ester (see Figure 4), while they change more dynamically in the natural ester (see Figure 5) and in the mineral oil (see Figure 6).

From Figure 4, Figure 5 and Figure 6, it can also be seen that the highest velocities registered were for the greatest frequencies and the smallest distances between the AE source and sensor location. The values reached 1785 m/s for the synthetic ester, 1730 m/s for the natural ester and 1693 m/s for mineral oil. Contrary to this, the lowest values were registered at the smallest modulation frequencies, but at various distances between the emitter and receiver. In these cases, the AE wave propagated at 1132 m/s in synthetic ester, 1133 m/s in natural ester, and 1102 m/s in mineral oil.

In Figure 7, corresponding results depicting the velocity values in function of generation frequencies are presented. In Figure 8, detailed results depicting the median velocity values calculated for the AE waveform generated in the considered dielectrics, in function of distance between the emitter and receiver, are shown.

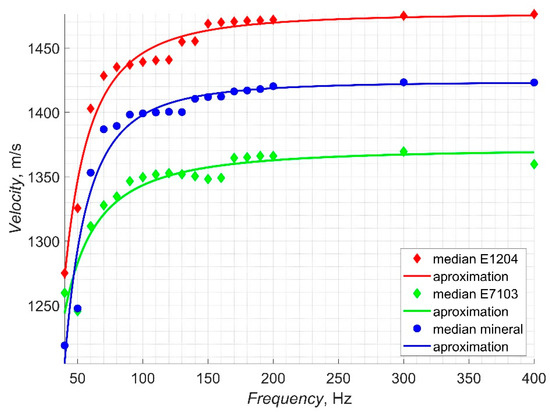
Figure 7. Detailed results depicting the median velocity values calculated for AE waveform generated in the considered dielectrics, in function of generation frequencies.

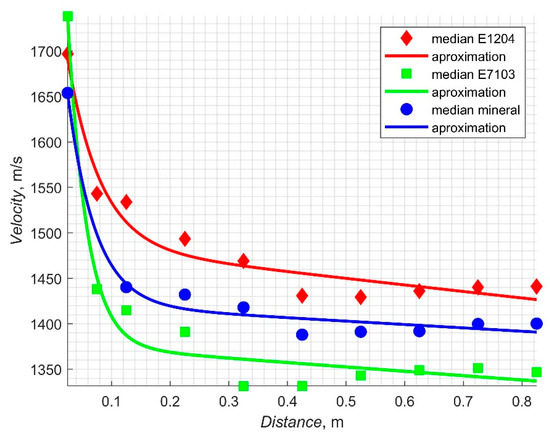
Figure 8. Detailed results depicting the median velocity values calculated for AE waveform generated in the considered dielectrics, in function of distance between the emitter and receiver.

In order to determine the trend for the relationships shown in Figure 7 and Figure 8, appropriate models of the regression functions were selected. The regression process was performed in the MATLAB programming environment with the use of the cftool tool, which allows for the selection of any set of regression functions. Dependency (1), depicts the regression model F₁(f) applied for the approximation of the impact from generation frequencies f on the velocity values. This is used as a power function. Dependency (2), depicts the corresponding regression model F₂(d) applied for the distance d impact determination. This model is a sum of two exponential functions. The resulted approximation curves are depicted in Figure 7 and Figure 8. The regression coefficients a₁-a₃ and b₁-b₄ were calculated with 95% confidence bounds for both models.

$$F_1\left(f\right)=a_1{f}^{a_2}+a_3$$

(1)

$$F_2\left(d\right)=b_1{e}^{b_{2}d}+b_3{e}^{b_{4}d}$$

(2)

In Table 2, the F₁(f) regression model coefficients a₁-a₃, calculated for the median velocities of AE signals propagating in the considered dielectric liquids regarding the dependency from frequency and the goodness parameters: SSE, Rsquare, Adjrsquare, RMSE are summarized. In Table 3, the corresponding values calculated for the second regression model F₂(d) coefficients b₁-b₄ are summarized.

Table 2. Regression coefficients for F₁(f) and goodness parameters calculated for the median velocities of AE signals propagating in the considered dielectric liquids.

Property	Natural Ester	Synthetic Ester	Mineral Oil
Coeff. a1	−424,600	−53,840	−1,182,000
Coeff. a2	−2.069	−1.638	−2.329
Coeff. a3	1477	1372	1424
SSE	1565	2251	3324
Rsquare	0.968	0.892	0.942
Adjrsquare	0.965	0.879	0.935
RMSE	9.89	11.86	14.41

Table 3. Regression coefficients for F₂(d) and goodness parameters calculated for the median velocities of AE signals propagating in the considered dielectric liquids.

Property	Natural Ester	Synthetic Ester	Mineral Oil
Coeff. b1	323.4	778.3	−398.4
Coeff. b2	−17.86	−30.69	−21.47
Coeff. b3	1487	1377	1422
Coeff. b4	−0.05	−0.03557	−0.02653
SSE	2615	3244	915
Rsquare	0.958	0.976	0.983
Adjrsquare	0.937	0.964	0.974
RMSE	20.87	23.25	13.53

As mentioned in previous section, the results obtained refer to the median values calculated over 32 samples for each distance and modulation frequency. In order to determine a specific numerical value, the median over all considered frequencies (see Figure 7) and distances (see Figure 8) was analyzed. Based on these charts, the differences are clearly recognizable. Another significant issue that may be noticed is the rapid increase in AE speed up to 100 Hz, which was confirmed by the power function applied for the regression analysis F₁(f), and a rapid decrease in these values at the smallest distances between the applied sensors, which was confirmed by the exponential function F₂(d).

Both regression analyses were performed achieving high goodness parameters (see Table 2 and Table 3), e.g., Rsquare values exceeding 0.89 for all liquids. The value of the coefficient a₃ is closely related to the stabilized velocity value, regarding the dependency from modulation frequency. It can therefore be stated that the stable AE velocity equals to 1372 m/s in the synthetic ester, 1424 m/s in the mineral oil, and 1477 m/s in the natural ester.

In the case of dependency from the distance between the source and receiver, the AE velocity may be determined from the value of coefficient b_3, which differs slightly, with amounts of 1377 m/s in the synthetic ester, 1422 m/s in the mineral oil, and 1487 m/s in the natural ester.

It must also be stated that the measured AE speed values do not correlate directly with the densities of the dielectric liquids (see Table 1).

From the mathematical dependencies F₁(f) and F₂(d), it can be predicted that a further increase in modulation frequency or distance between the sensors will not significantly influence the AE velocity, as both models indicate stabilized tail values. Nevertheless, it may be beneficial to consider obtaining further measurements, including higher distances, frequencies and temperature influences on the velocities of AE waves in the considered liquids.