Simplifying the Verification of Simulation Models through Petri Net to FlexSim Mapping
Abstract
1. Introduction
2. Literature Review
3. Petri Nets
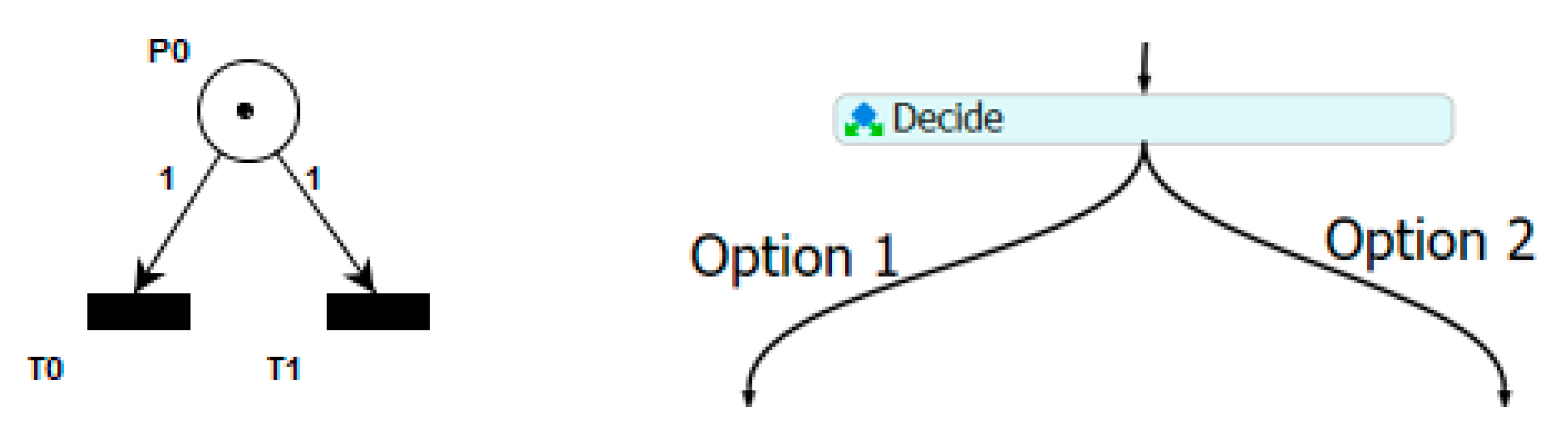
3.1. Basic Definition
- P = {P1, P2, P3, ....., Pnp} is a finite set of places;
- T = {T1, T2, T3, ....., Tne} is a finite set of transitions;
- A = {A1, A2, A3, ....., Ana} is a finite set of arcs that connect places to transitions and vice versa;
- W: Ai → {1, 2, 3, ....} ∀ Ai is the weight associated with each arc;
- M0: Pi → {1, 2, 3, ....} ∀ Pi is the initial number of entities in each place (initial marking).
3.2. Timed Petri Nets
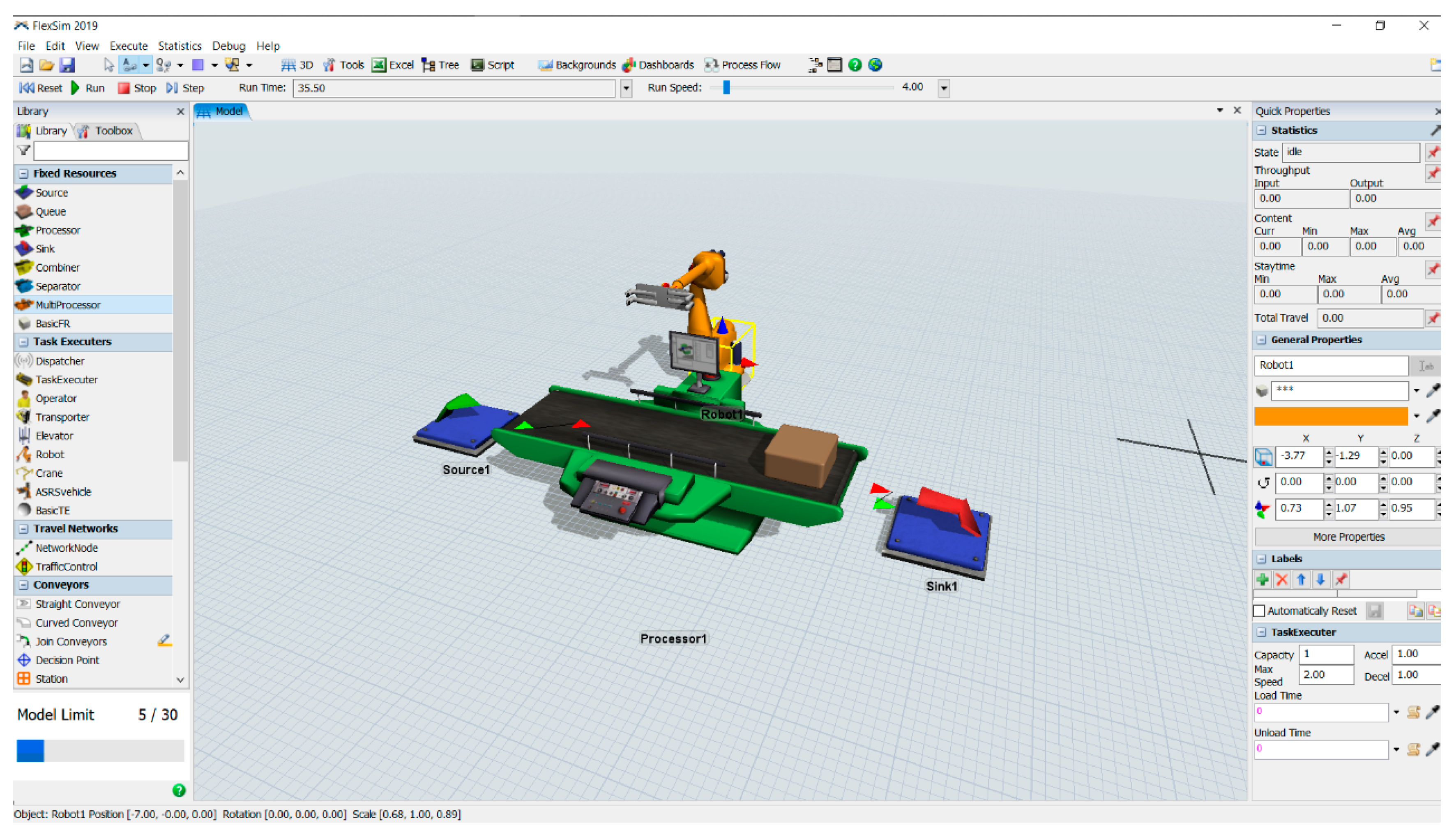
4. FlexSim
5. Mapping Petri Nets to a FlexSim Model
5.1. Sequential Execution
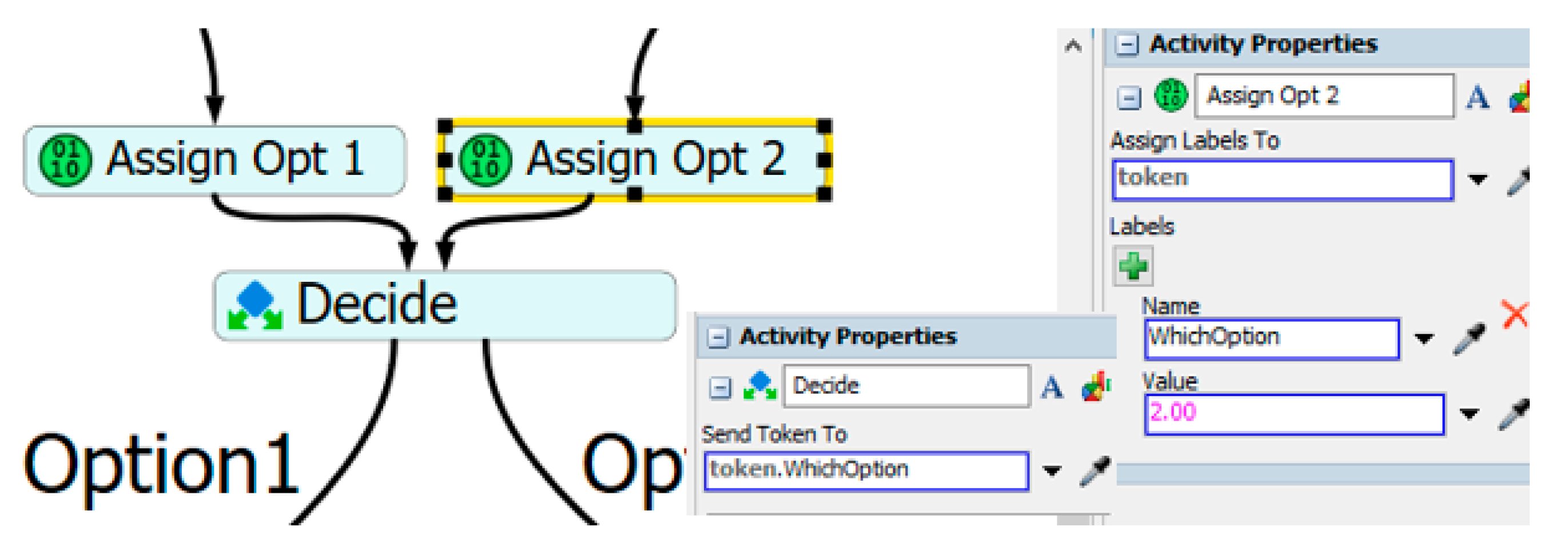
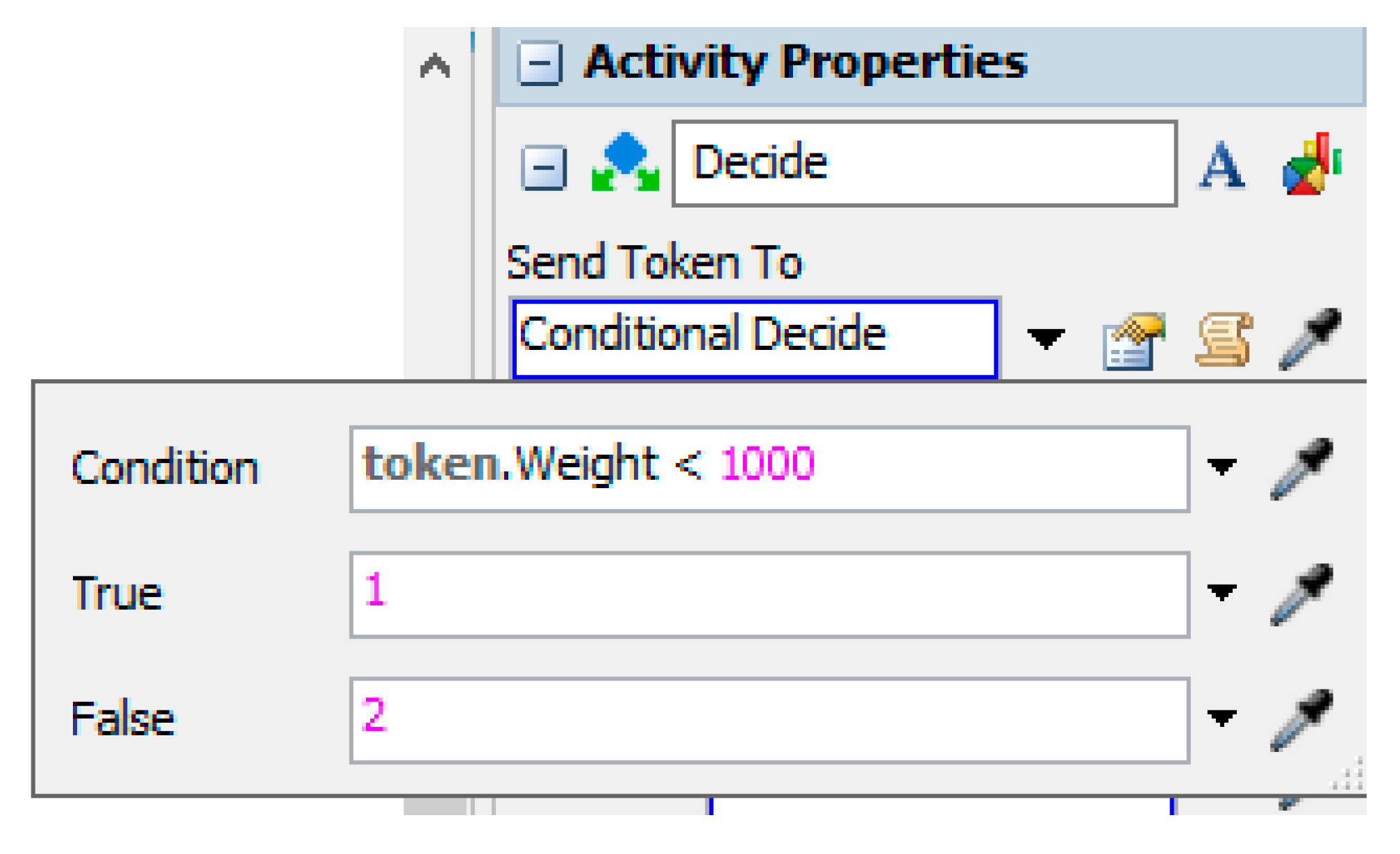
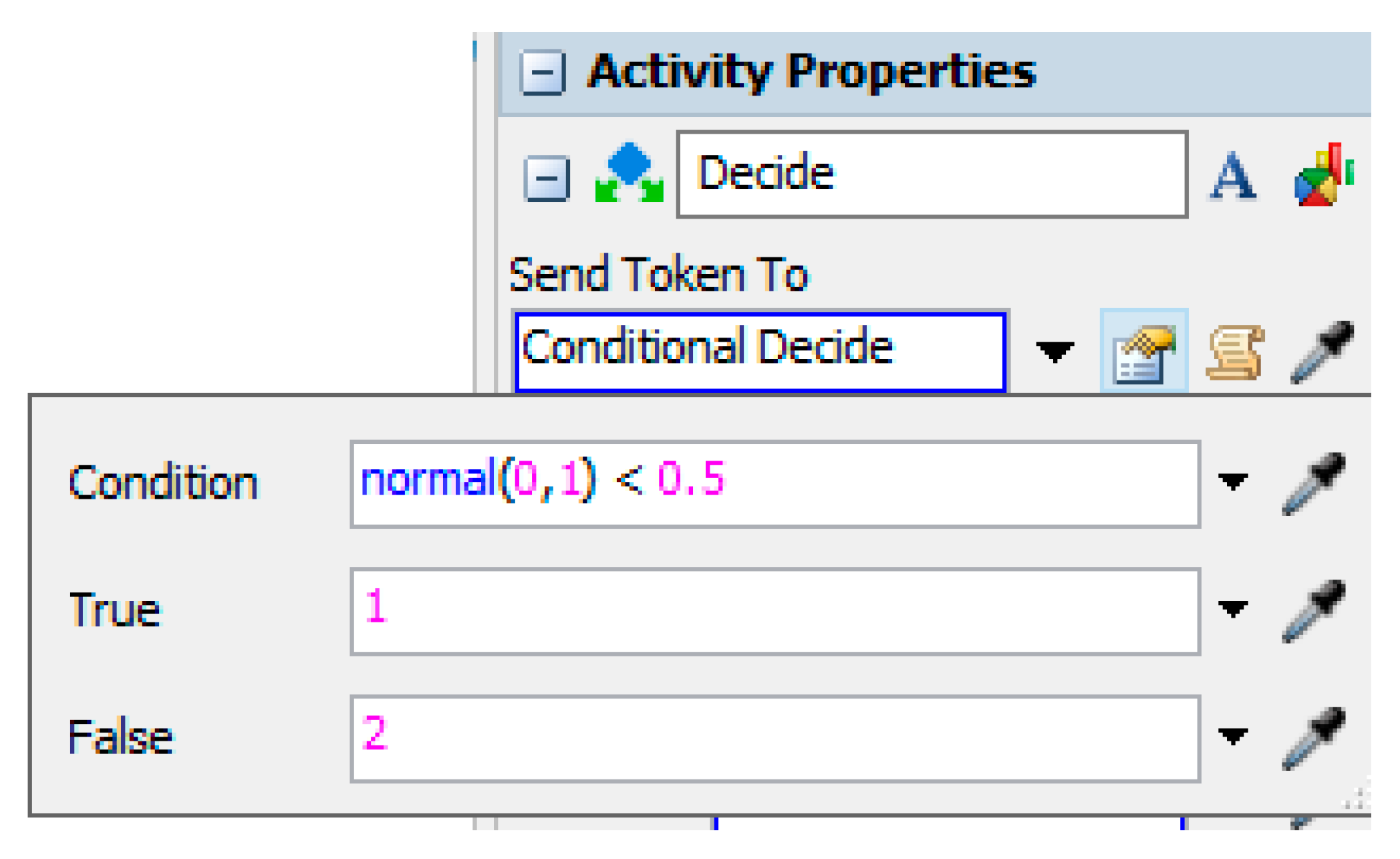
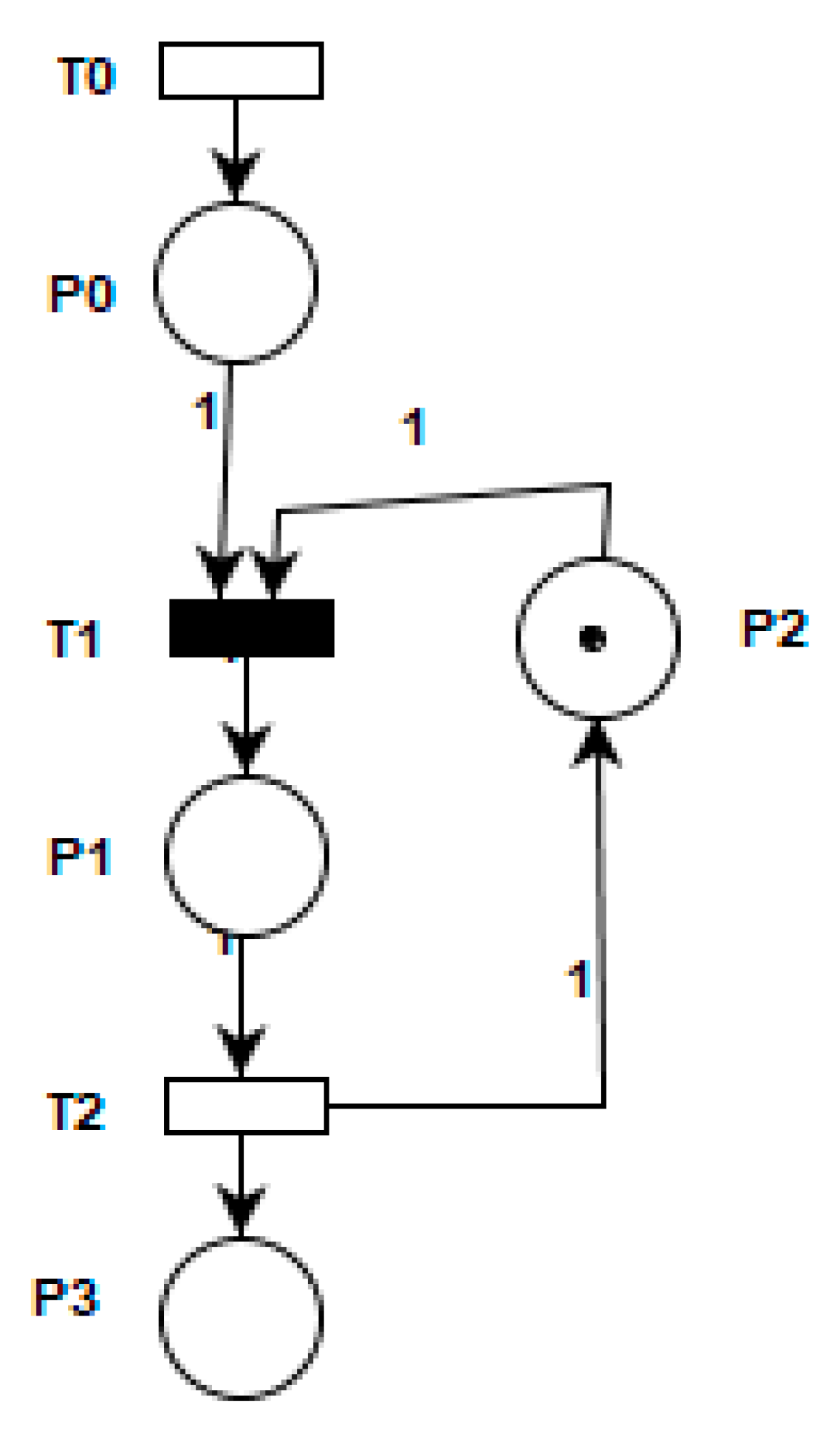
5.2. Conflict
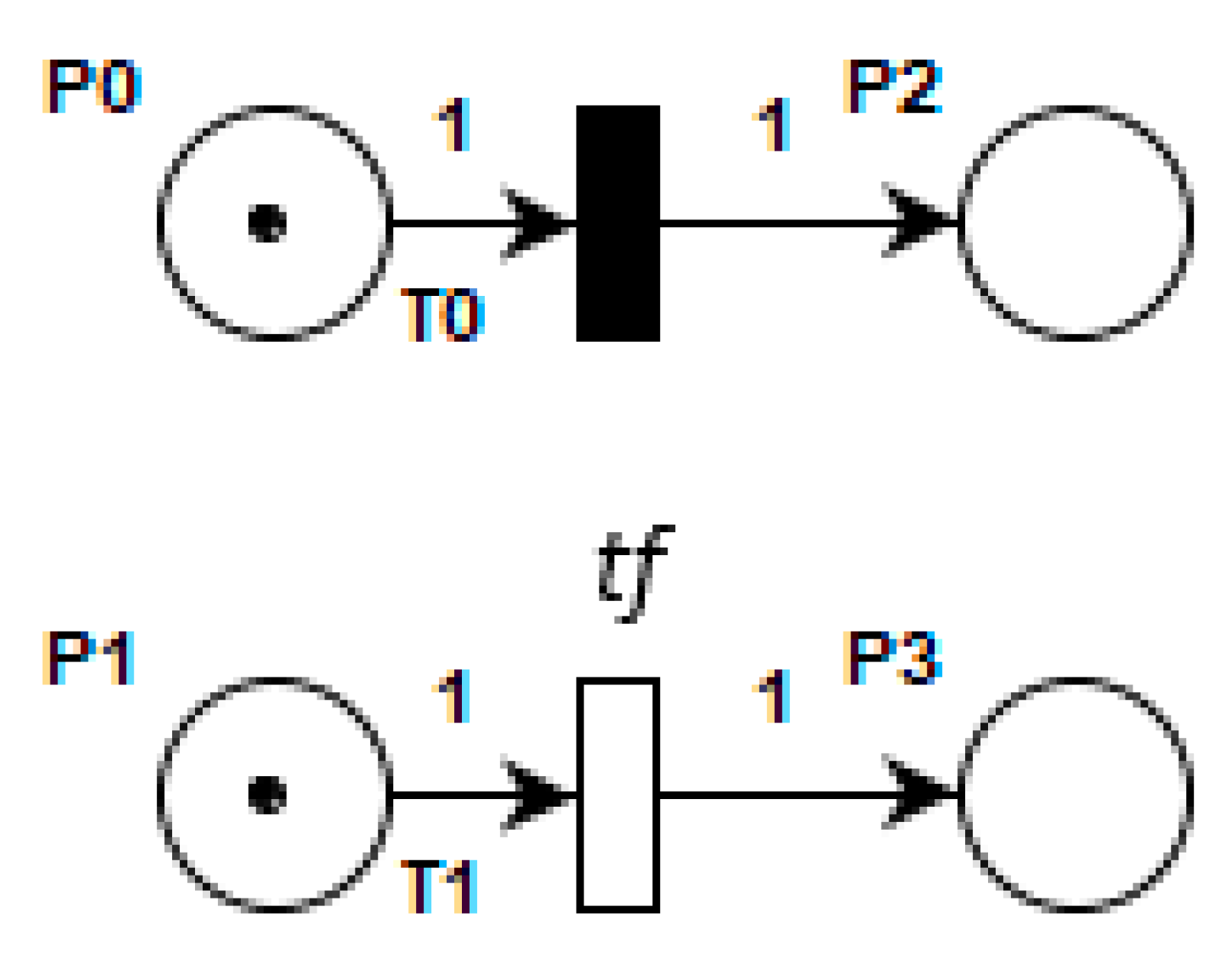
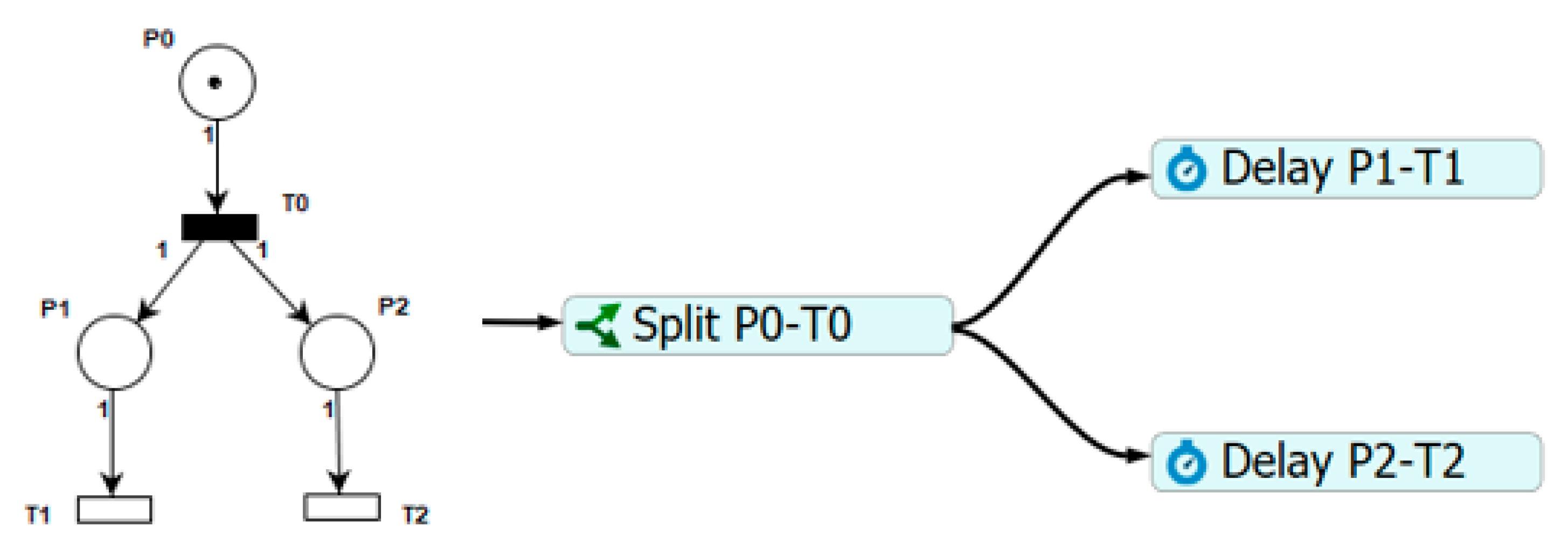
5.3. Concurrency with Temporal Entities
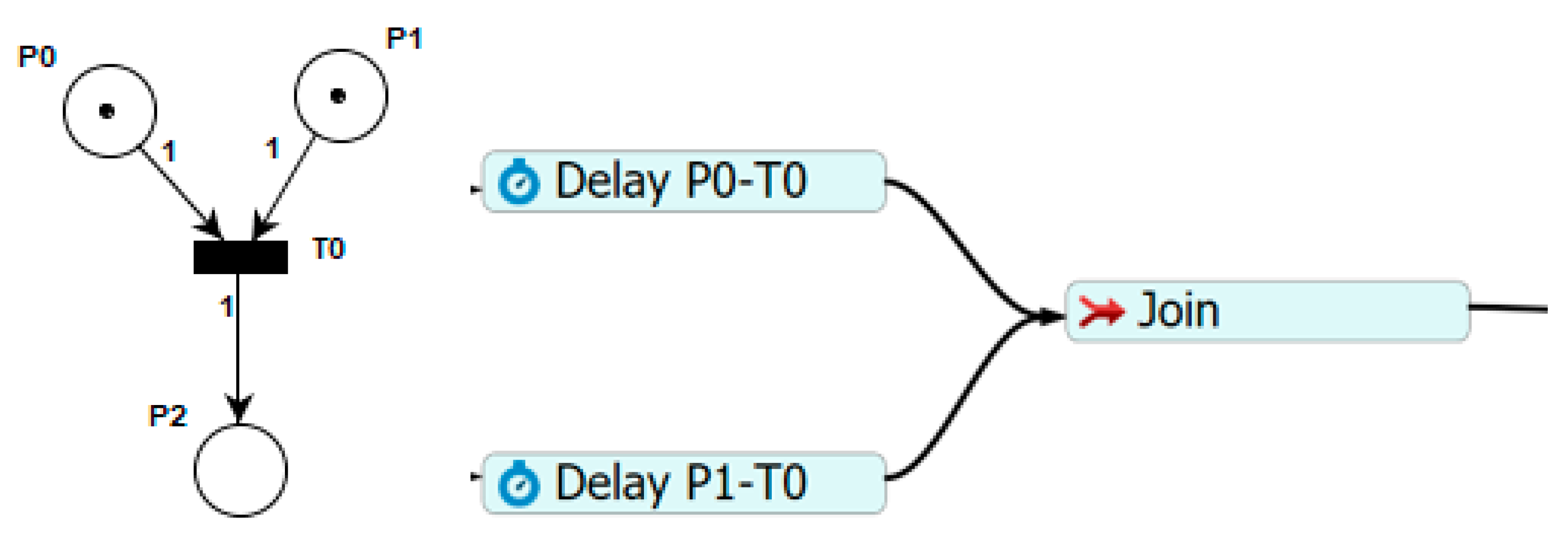
5.4. Synchronization with Temporal Entities
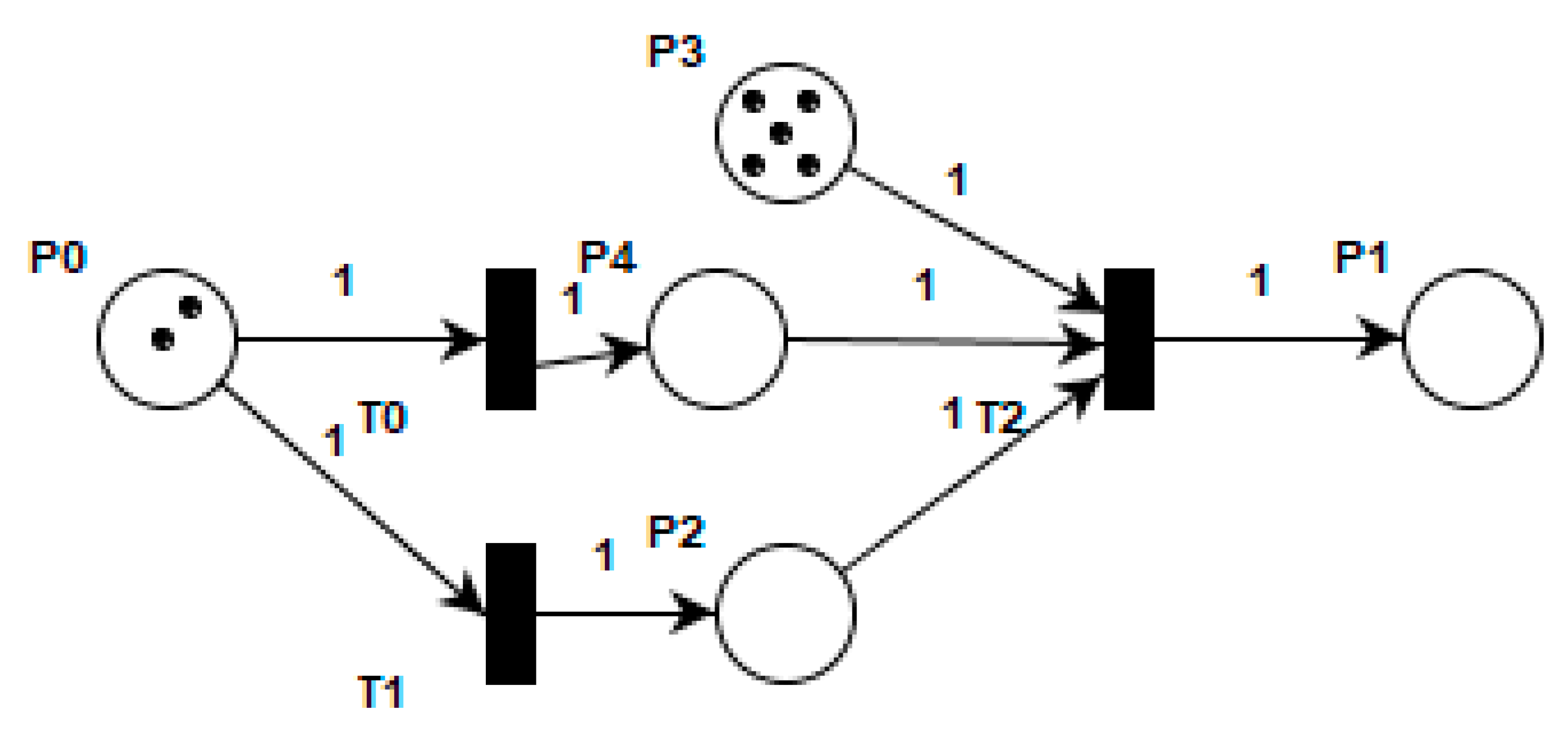
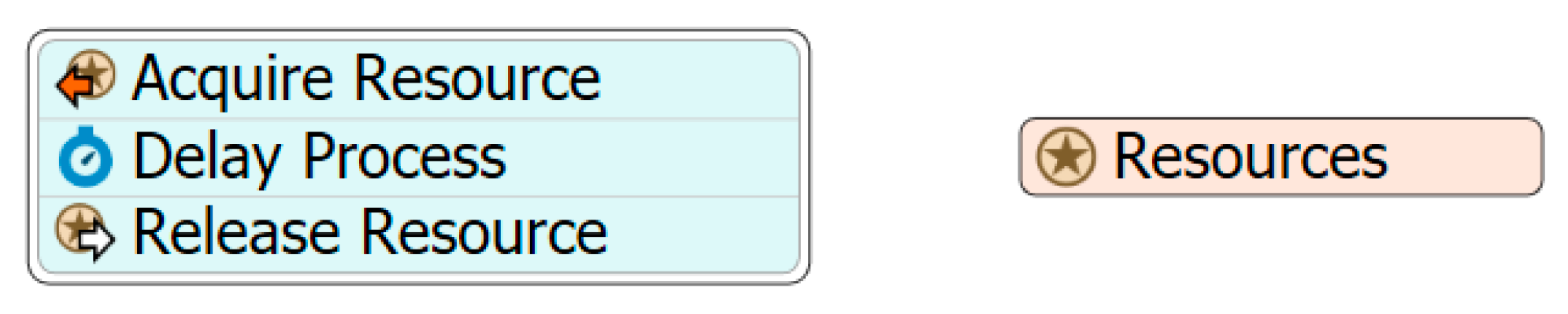
5.5. Concurrency and Synchronization with Resources
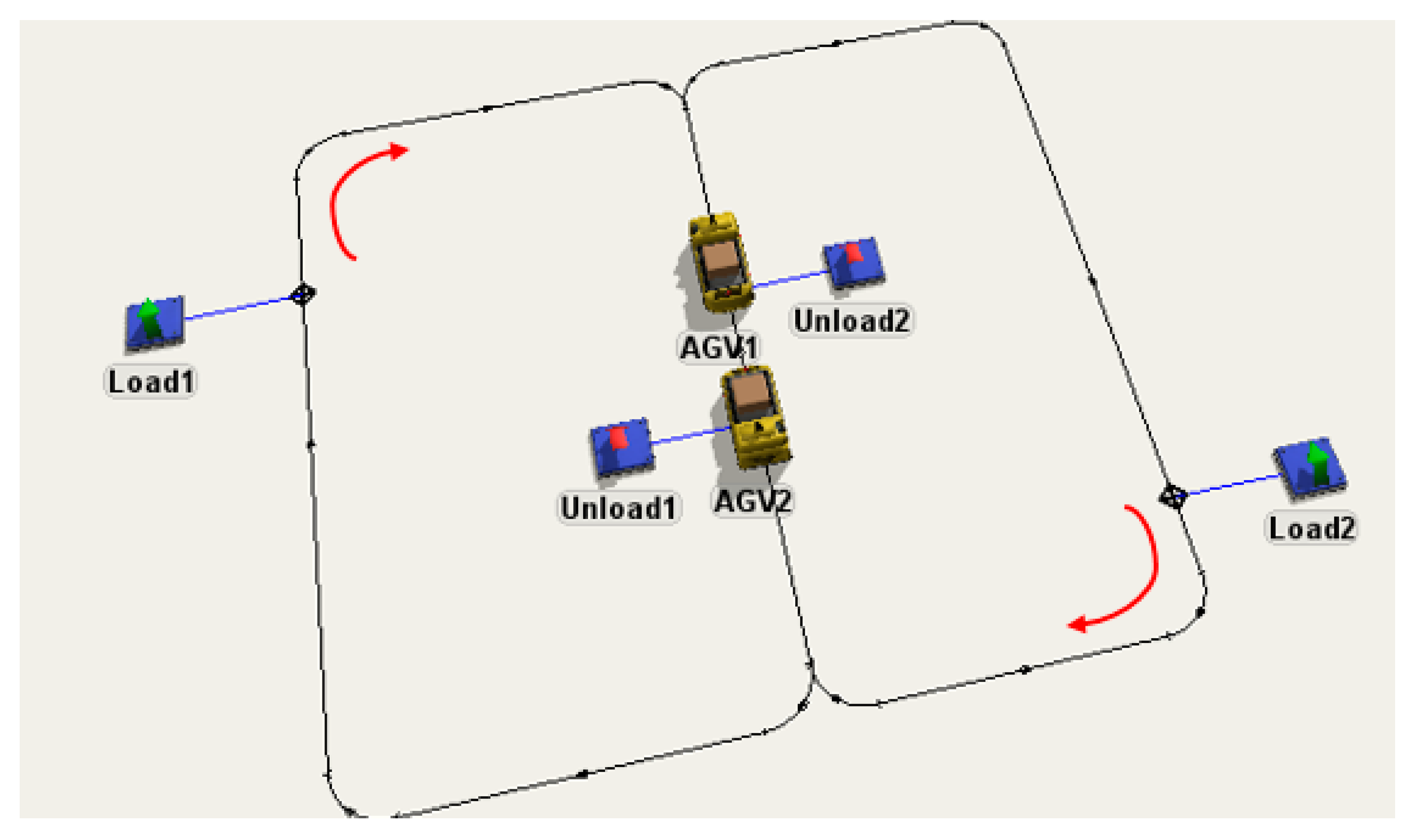
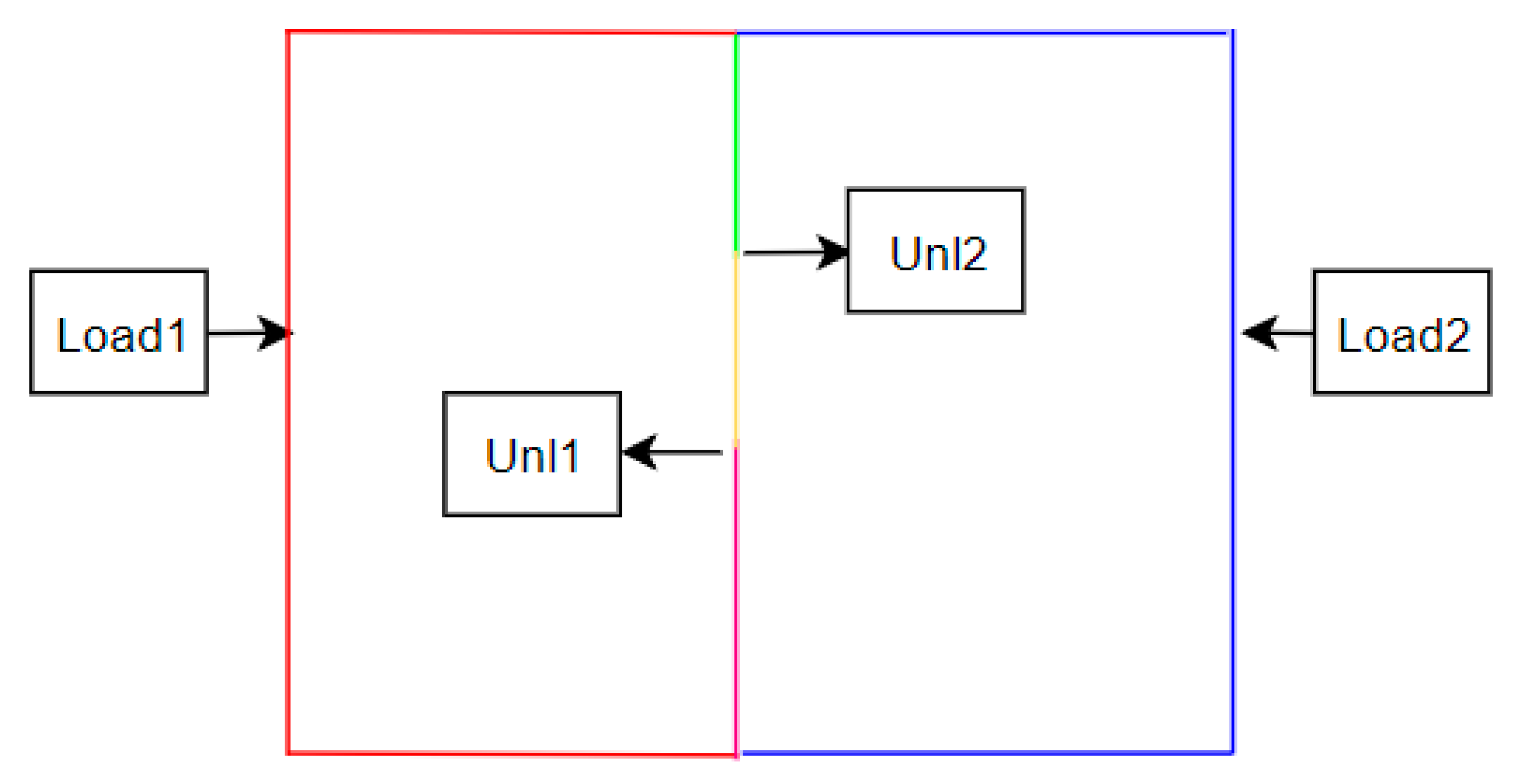
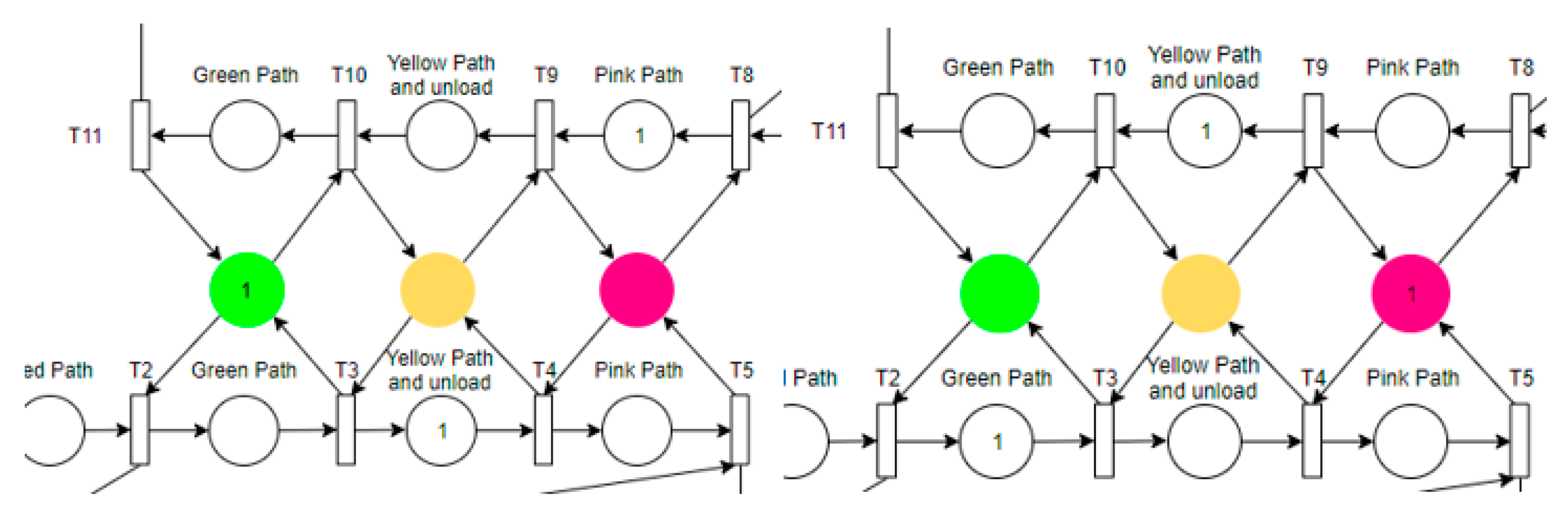
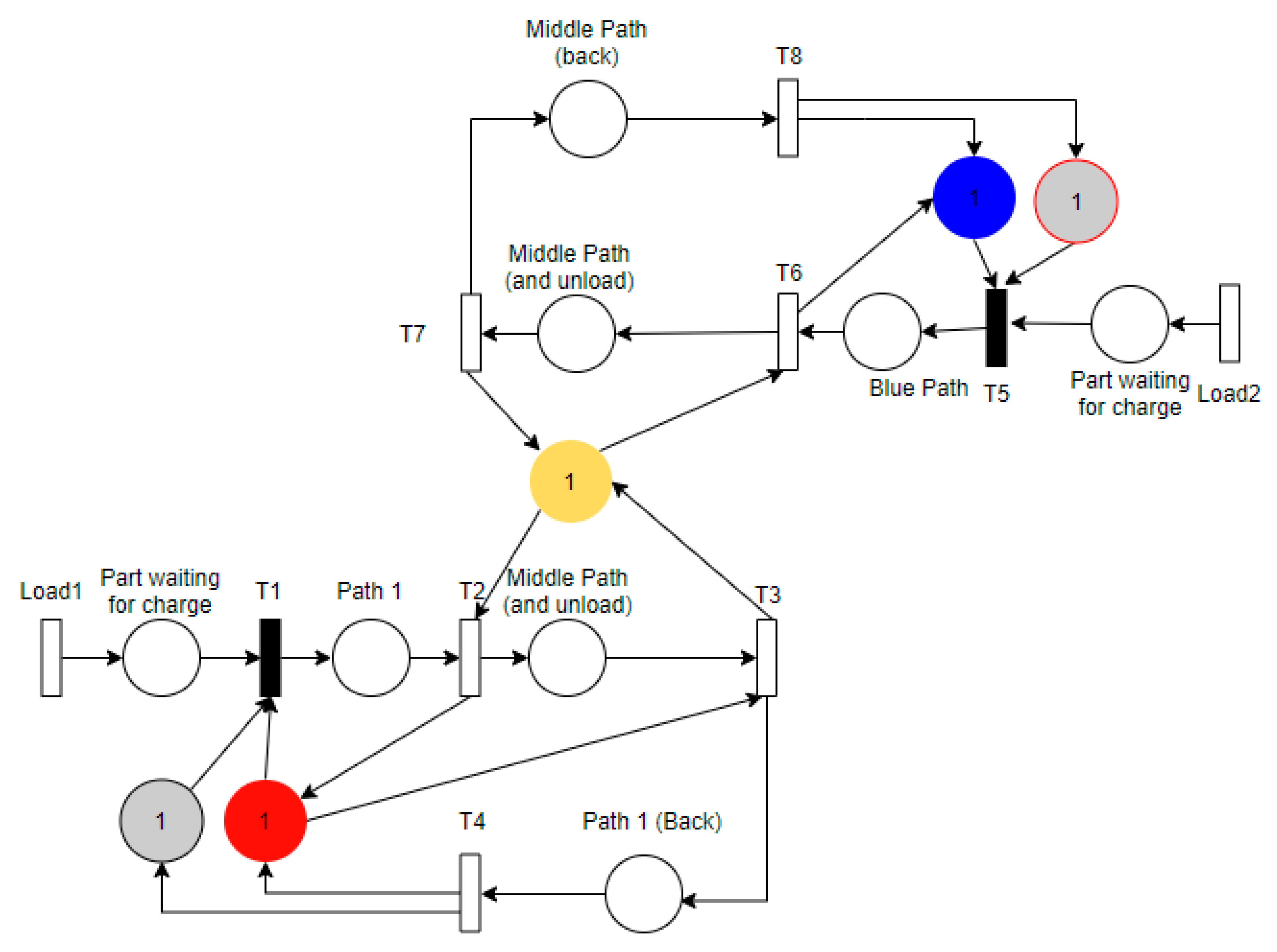
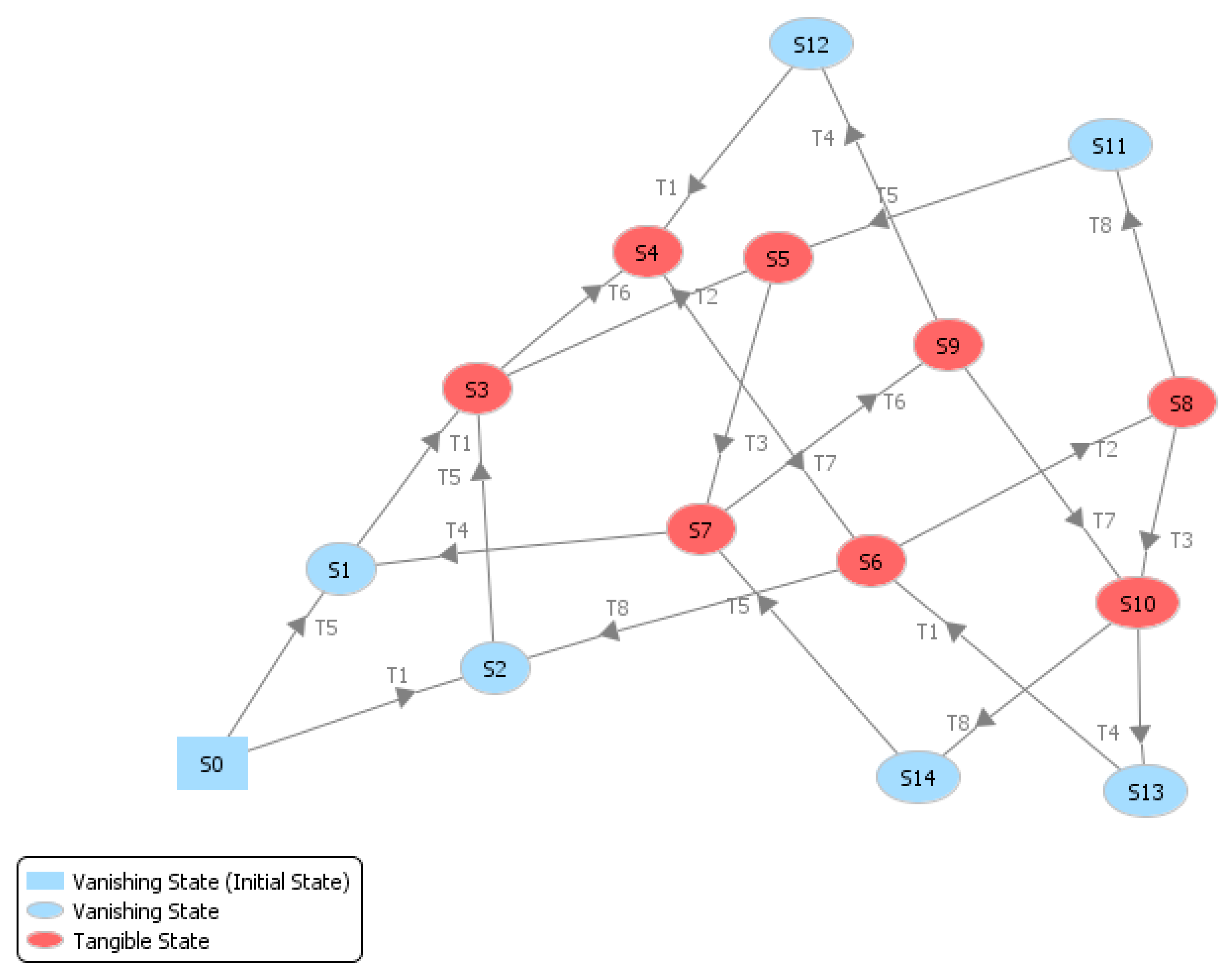
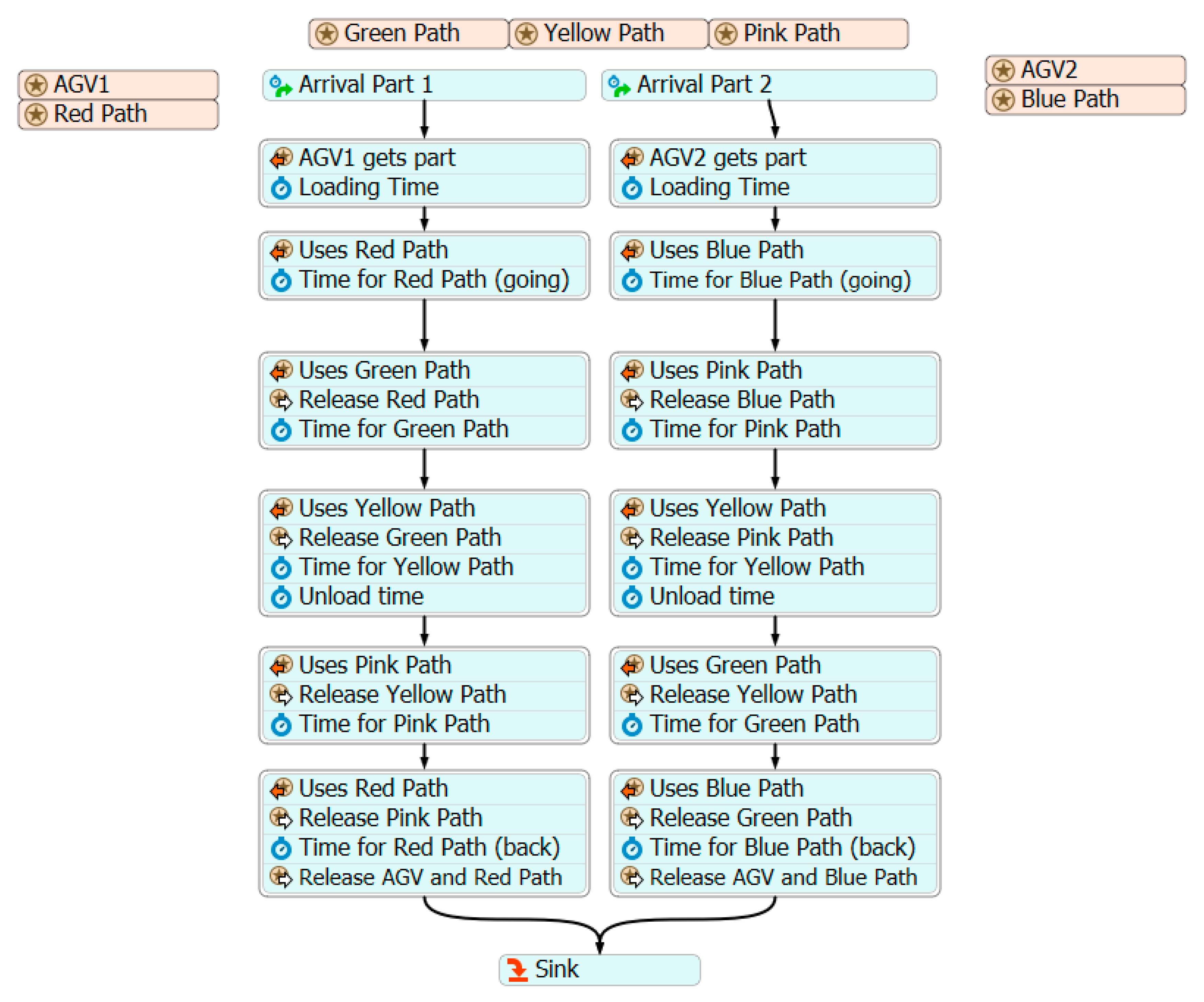
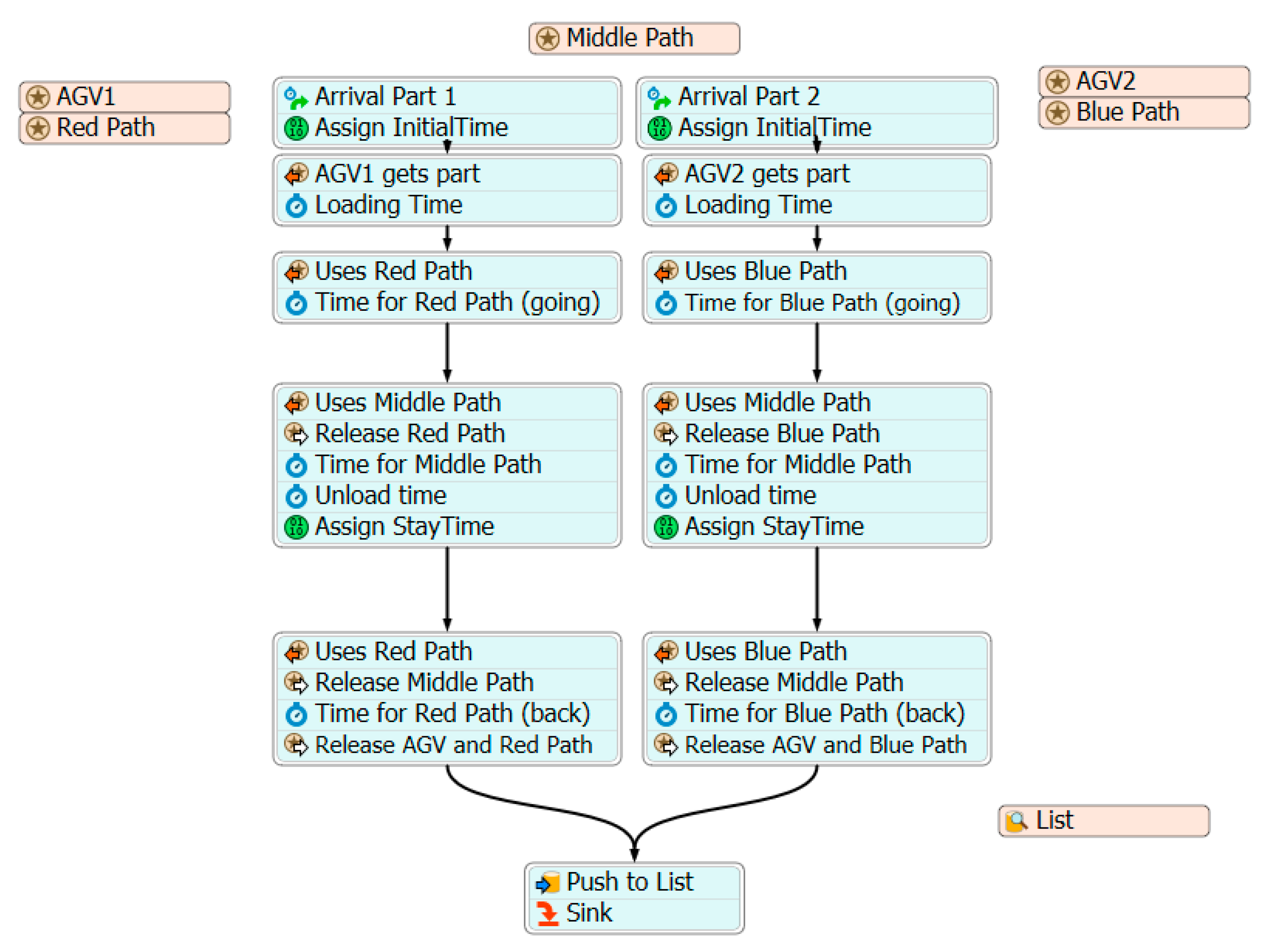
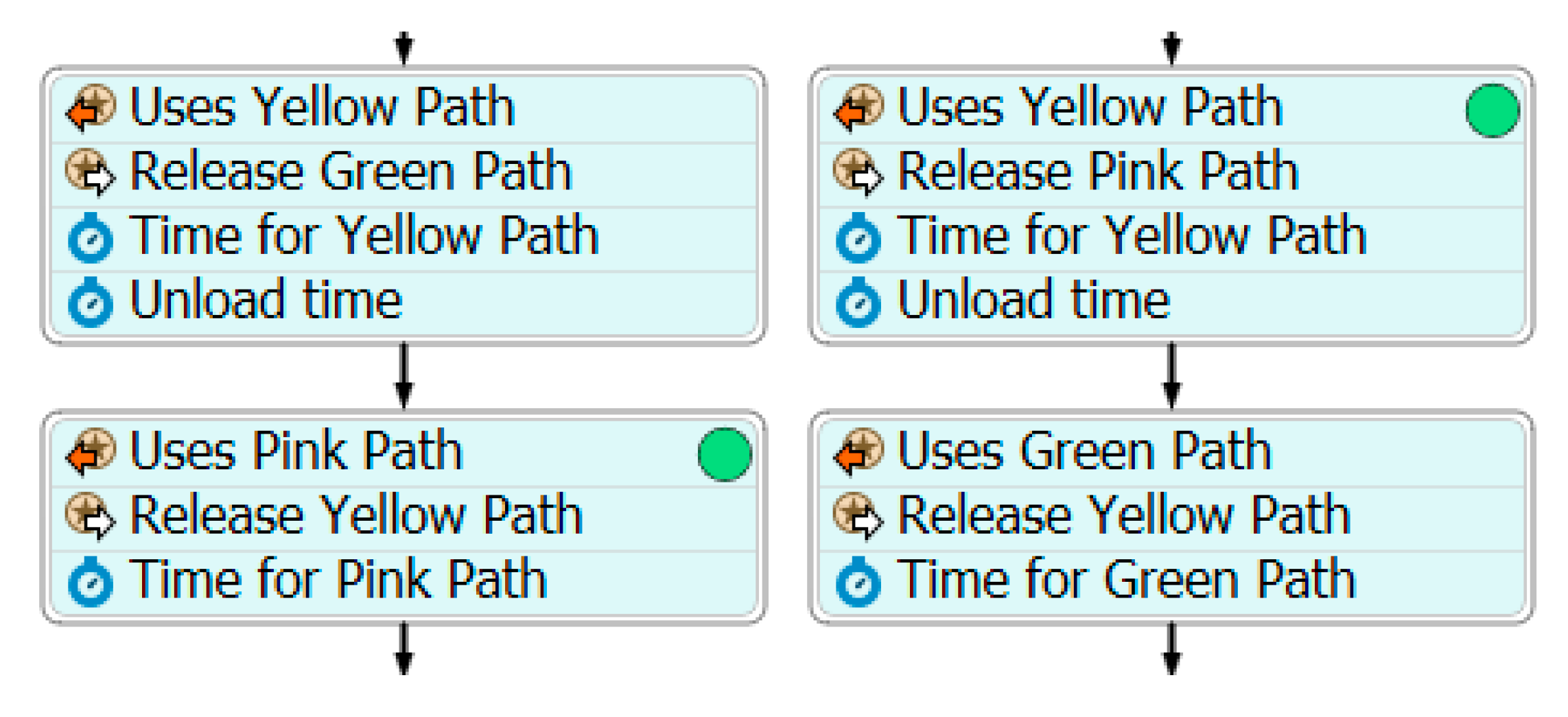
6. Example: Bridge Crossing Deadlock
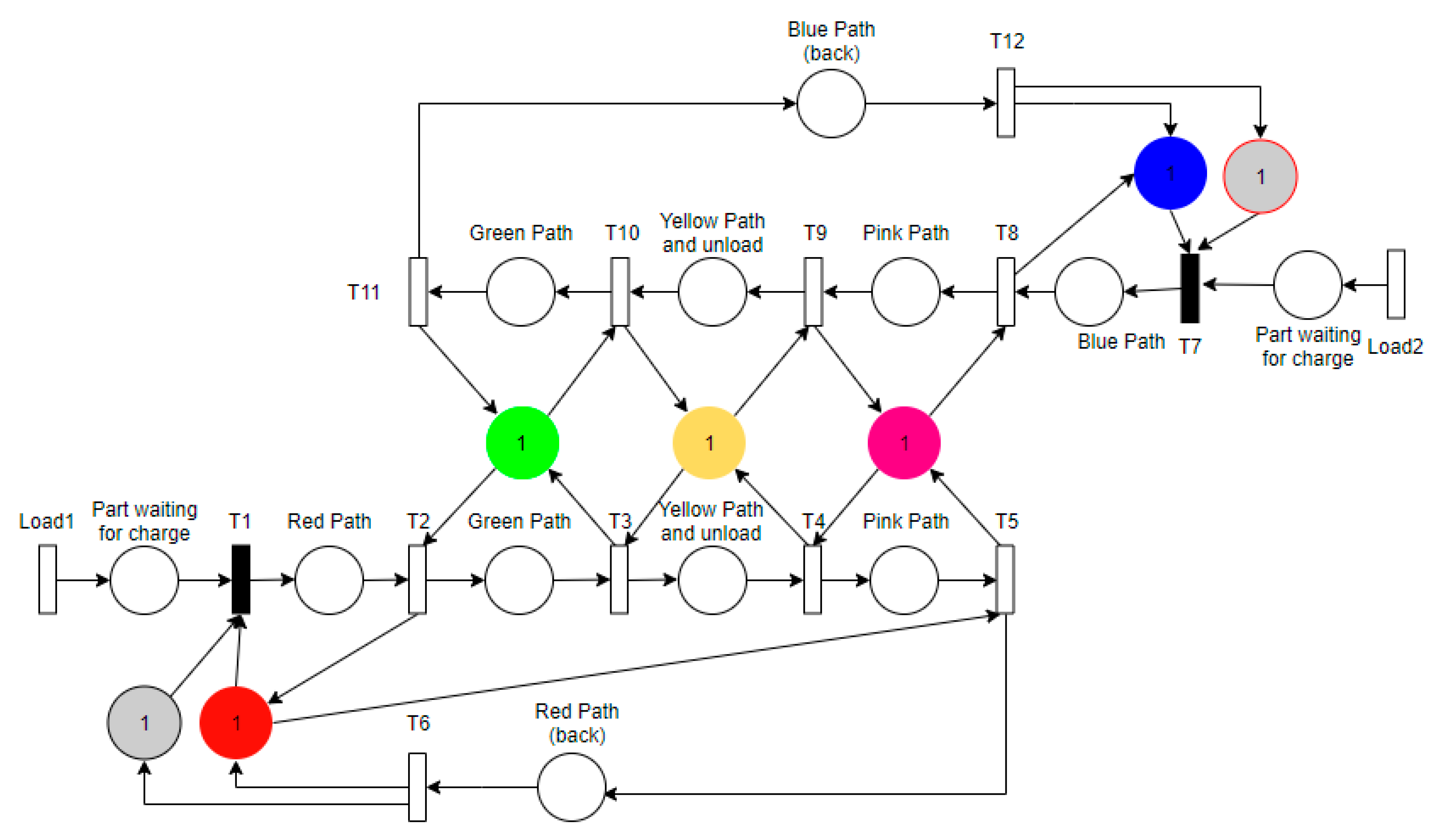
6.1. Petri Net Model
Alternative 1: Avoiding Deadlock
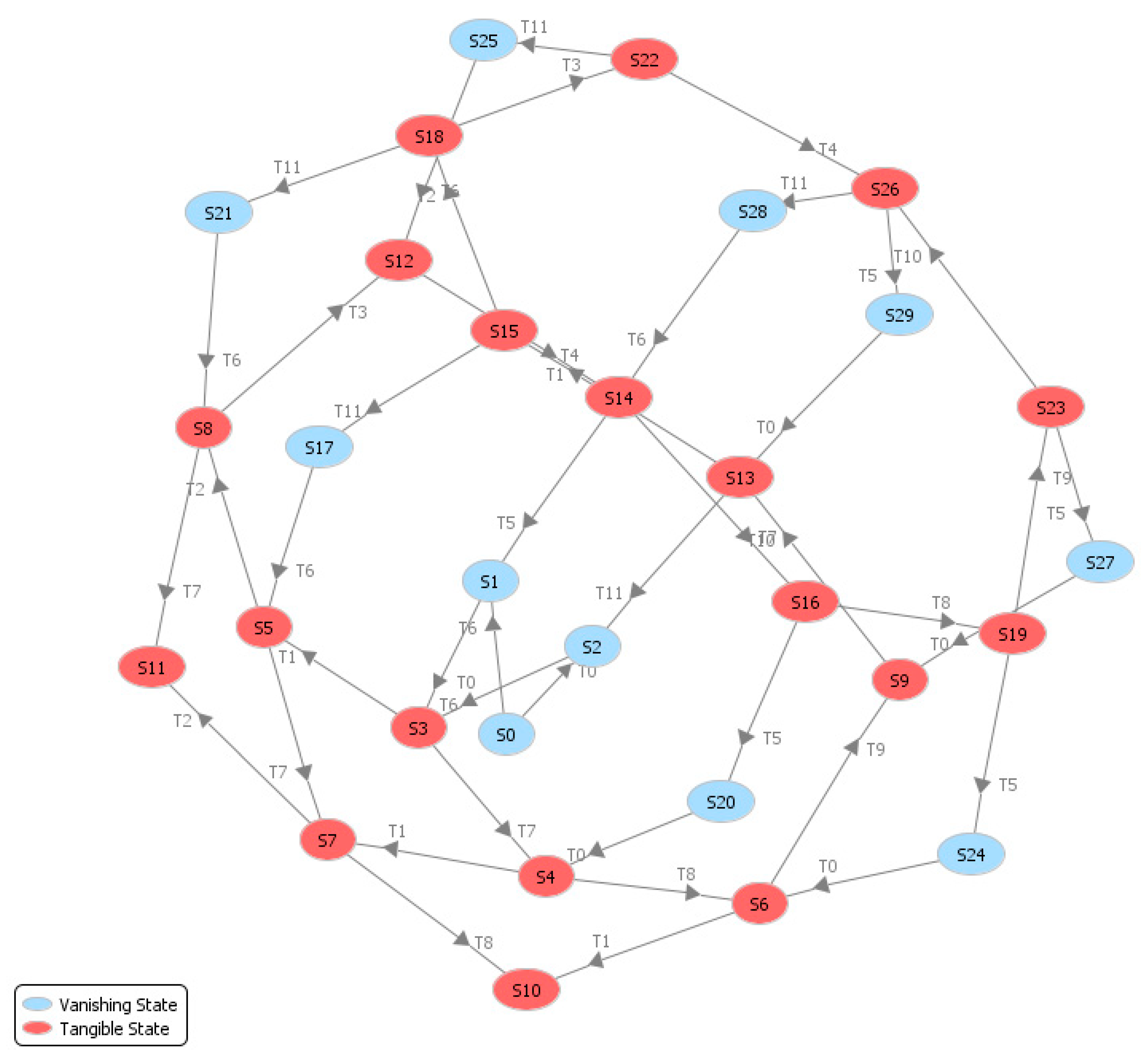
6.2. FlexSim Process Simulation Flow
7. Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Doldi, L. SDL Illustrated-Visually Design Executable Models; MSO Systems: Old Main, PA, USA, 2001. [Google Scholar]
- ITU-T. Specification and Description Language–Overview of SDL-2010; ITU-T: Geneva, Switzerland, 2011. [Google Scholar]
- Guasch, A.; Figueras, J.; Casanovas, J. Conceptual modeling using Petri Nets. In Formal Languages Forcomputer Simulation: Transdisciplinary Models and Applications; IGI Global: Hershey, PA, USA, 2013. [Google Scholar]
- Cabasino, M.P.; Giua, A.; Seatzu, C. Introduction to petri nets. Lect. Notes Control Inf. Sci. 2013, 433, 191–211. [Google Scholar] [CrossRef]
- Van der Aalst, W.M.P. Timed Coloured Petri Nets and Their Application to Logistics. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 1992. [Google Scholar] [CrossRef]
- Zeigler, B.P.; Praehofer, H.; Kim, T.G. Theory of Modeling and Simulation Handbook of Simulator-BASED Training Creating Computer Simulation Systems: An Introduction to the High Level Architecture; Academic Press: Oxford, UK, 2000. [Google Scholar] [CrossRef]
- Vangheluwe, H.L.M. DEVS as a common denominator for multi-formalism hybrid systemsmodelling. CACSD. In Proceedings of the IEEE International Symposium on Computer-Aided Control System Design (Cat. No.00TH8537), Anchorage, AK, USA, 25–27 September 2000. [Google Scholar]
- Fonseca i Casas, P. Transforming classic Discrete Event System Specification models to Specification and Description Language. Simulation 2015, 91, 249–264. [Google Scholar] [CrossRef]
- Boukelkoul, S.; Redjimi, M. Mapping between Petri nets and DEVS models. In Proceedings of the 2013 3rd International Conference on Information Technology and e-Services (ICITeS), Sousse, Tunisia, 24–26 March 2013; pp. 1–6. [Google Scholar] [CrossRef]
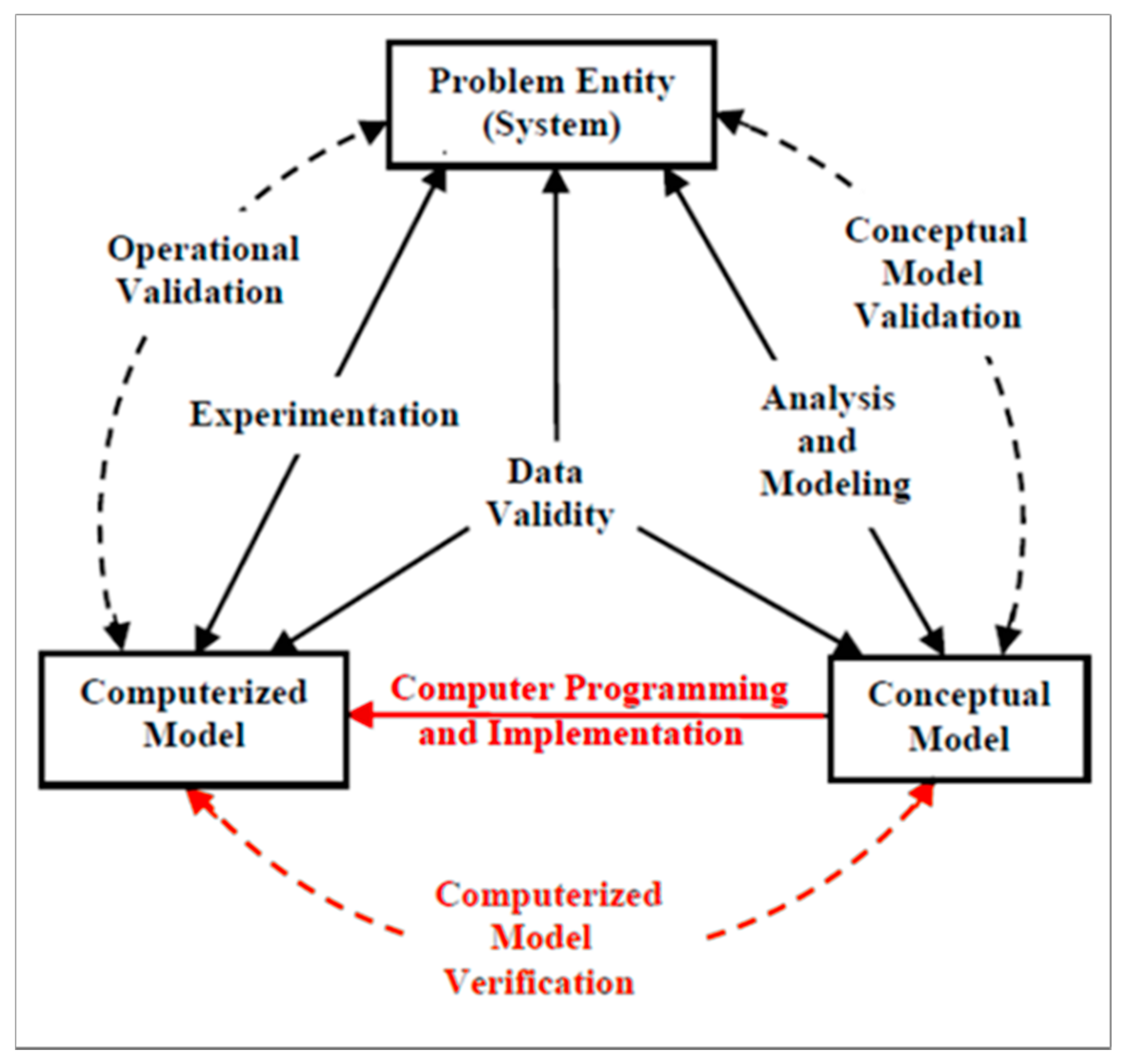
- Sargent, R. Verification and validation of simulation models. In Proceedings of the 2009 Winter Simulation Conference (WSC); Rossetti, M.D., Hill, R.R., Johansson, B., Dunkin, A., Ingalls, R.G., Eds.; WSC: Austin, TX, USA, 2009; p. 66. [Google Scholar] [CrossRef][Green Version]
- Van Bruggen, A.; Nikolic, I.; Kwakkel, J. Modeling with stakeholders for transformative change. Sustainability 2019, 11, 825. [Google Scholar] [CrossRef]
- Brailsford, S.C.; Bolt, T.; Connell, C.; Klein, J.H.; Patel, B. Stakeholder engagement in health care simulation. Proc.-Winter Simul. Conf. 2009, 1840–1849. [Google Scholar] [CrossRef]
- Proudlove, N.C.; Bisogno, S.; Onggo, B.S.S.; Calabrese, A.; Levialdi Ghiron, N. Towards fully-facilitated discrete event simulation modelling: Addressing the model coding stage. Eur. J. Oper. Res. 2017, 263, 583–595. [Google Scholar] [CrossRef]
- Onggo, B.S.S.; Proudlove, N.C.; D’Ambrogio, S.A.; Calabrese, A.; Bisogno, S.; Levialdi Ghiron, N. A BPMN extension to support discrete-event simulation for healthcare applications: An explicit representation of queues, attributes and data-driven decision points. J. Oper. Res. Soc. 2018, 69, 788–802. [Google Scholar] [CrossRef]
- Aagesen, G.; Krogstie, J. BPMN 2.0 for Modeling Business Processes. In Handbook on Business Process Management 1; Springer: Berlin/Heidelberg, Germany, 2015; pp. 219–250. [Google Scholar] [CrossRef]
- Leiva, J.; Fonseca i Casas, P.; Ocana, J. Modeling anesthesia and pavilion surgical units in a Chilean hospital with Specification and Description Language. Simulation 2013, 89, 1020–1035. [Google Scholar] [CrossRef]
- Fonseca i Casas, P. SDL distributed simulator. In 2008 Winter Simulation Conference; Winter Simulation Conference: Miami, FL, USA, 2008. [Google Scholar] [CrossRef]
- PragmaDev SARL. PragmaDev Studio. Available online: http://www.pragmadev.com/product/index.html (accessed on 15 February 2020).
- Wainer, G.A. Modeling and simulation of complex systems with cell-DEVS. In Proceedings of the 2004 Winter Simulation Conference, Washington, DC, USA, 5–8 December 2004; Ingalls, R.G., Rossett, M.D., Smith, J.S., Peters, B.A., Eds.; Winter Simulation Conference: Washington, DC, USA, 2004. [Google Scholar]
- López, J.; Santana-Alonso, A.; Medina, M.D.C. Formal verification for task description languages. A petri net approach. Sensors (Switzerland) 2019, 19, 4965. [Google Scholar] [CrossRef]
- Kucera, E.; Haffner, O.; Leskovsky, R. PN2ARDUINO—A new petri net software tool for control of discrete-event and hybrid systems using arduino microcontrollers. Proc. 2019 Fed. Conf. Comput. Sci. Inf. Syst. FedCSIS 2019, 18, 915–919. [Google Scholar] [CrossRef]
- Peleg, M.; Rubin, D.; Altman, R.B. Using Petri Net tools to study properties and dynamics of biological systems. J. Am. Med. Inform. Assoc. 2005, 12, 181–199. [Google Scholar] [CrossRef]
- Liang, X.; Zhang, S.; Liu, Y.; Ma, Y. Information Propagation Formalized Representation of Micro-blog Network Based on Petri Nets. Sci. Rep. 2020, 10, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Balogh, Z.; Kuchárik, M. Predicting student grades based on their usage of LMS moodle using Petri nets. Appl. Sci. 2019, 9, 4211. [Google Scholar] [CrossRef]
- Su, Z.; Qiu, M. Airport surface modelling and simulation based on timed coloured petri net. Promet-Traffic -Traffico. 2019, 31, 479–490. [Google Scholar] [CrossRef]
- Tolba, C.; Lefebvre, D.; Thomas, P.; El Moudni, A. Continuous and timed Petri nets for the macroscopic and microscopic traffic flow modelling. Simul. Model. Pract. Theory 2005, 13, 407–436. [Google Scholar] [CrossRef]
- An, Y.; Wu, N.; Zhao, X.; Li, X.; Chen, P. Hierarchical Colored Petri nets for modeling and analysis of transit signal priority control systems. Appl. Sci. 2018, 8, 141. [Google Scholar] [CrossRef]
- Meghzili, S.; Chaoui, A.; Strecker, M.; Kerkouche, E. An Approach for the Transformation and Verification of BPMN Models to Colored Petri Nets Models. Int. J. Softw. Innov. 2020, 8, 17–49. [Google Scholar] [CrossRef]
- Gulati, U.; Vatanawood, W. Transforming Flowchart into Coloured Petri Nets. In Proceedings of the 2019 3rd International Conference on Software and e-Business; ACM: New York, NY, USA, 2019; pp. 75–80. [Google Scholar] [CrossRef]
- Mutarraf, U.; Barkaoui, K.; Li, Z.; Wu, N.; Qu, T. Transformation of Business Process Model and Notation models onto Petri nets and their analysis. Adv. Mech. Eng. 2018, 10, 1–21. [Google Scholar] [CrossRef]
- Haustermann, M. Petri Nets Tool Database. Available online: https://www.informatik.uni-hamburg.de/TGI/PetriNets/tools/db.html (accessed on 15 February 2020).
- Abohamad, W.; Ramy, A.; Arisha, A. A Hybrid Process-Mining Approach for Simulation Modeling. In Proceedings of the 2017 Winter Simulation Conference; Winter Simulation Conference: Las Vegas, NV, USA, 2017. [Google Scholar] [CrossRef]
- Bergmann, S.; Strassburger, S. Challenges for the Automatic Generation of Simulation Models for Production Systems. In Proceedings of the 2010 Summer Computer Simulation Conference, Ottawa, ON, Canada, 11–14 July 2010; SCSC: Ottawa, ON, Canada, 2010; pp. 545–549. [Google Scholar]
- Santillán Martínez, G.; Sierla, S.A.; Karhela, T.A.; Lappalainen, J.; Vyatkin, V. Automatic Generation of a High-Fidelity Dynamic Thermal-Hydraulic Process Simulation Model From a 3D Plant Model. IEEE Access. 2018, 6, 45217–45232. [Google Scholar] [CrossRef]
- Dias, L.M.S.; Vieira, A.A.C.; Oliveira, G.A.B.P.J.A. Discrete Simulation Software Ranking—A Top List of the Worldwide Most Popular and Used Tools. Proc. 2016 Winter Simul. Conf. 2016, 53, 1689–1699. [Google Scholar] [CrossRef]
- Huang, B.; Tang, H. Study of Workshop Production System Based on Petri Nets and Flexsim. In Proceedings of the 22nd International Conference on Industrial Engineering and Engineering Management 2015; Qi, E., Shen, J., Dou, R., Eds.; Atlantis Press: Paris, France, 2016; pp. 833–844. [Google Scholar] [CrossRef]
- Xu, S.Z. A Petri Net-Based Hybrid Heuristic Scheduling Algorithm for Flexible Manufacturing System. Int. J. Simul. Model. 2019, 18, 325–334. [Google Scholar] [CrossRef]
- Altiok, T.; Melamed, B. Simulation Modeling and Analysis with ARENA; Elsevier: Piscataway, NJ, USA, 2007. [Google Scholar]
- Figueras, J.I.J.; Guasch, A.I.P.; Fonseca, P.I.C.; Casanovas-Garcia, J. Teaching system modelling and simulation through Petri Nets and Arena. In Proceedings of the Winter Simulation Conference, Savanah, GA, USA, 7–10 December 2014; pp. 3662–3673. [Google Scholar] [CrossRef]
- Wang, J. Petri Nets for Dynamic Event-Driven System Modeling. In Handbook of Dynamic System Modeling; Fishwick, P.A., Ed.; Chapman & Hall: Gainesville, FL, USA, 2007; pp. 17–24. [Google Scholar] [CrossRef]
- Dingle, N.; Knottenbelt, W.; Suto, T. PIPE2: a tool for the performance evaluation of generalised stochastic Petri Nets. ACM SIGMETRICS Perform. Eval. Rev. 2009, 36, 34. [Google Scholar] [CrossRef]
- Bonet, P.; Lladó, C. PIPE v2. 5: A Petri net tool for performance modelling. In Proceedings of the 23rd Latin American Conference on Informatics (CLEI 2007), Osijek, Croatia, 9–12 October 2007; Faculty of Law, Josip Juraj Strossmayer University in Osijek: Osijek, Croatia, 2007; Volume 12. [Google Scholar]
- FlexSim Software Products Inc. FlexSim Problem Solved. Available online: https://www.flexsim.com/ (accessed on 15 February 2020).
- Law, A.M.; Kelton, W. Simulation Modeling and Analysis; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- OPC Foundation. Unified Architecture. Available online: https://opcfoundation.org/about/opc-technologies/opc-ua/ (accessed on 15 February 2020).
- Pels, H.J.; Goossenaerts, J. A Conceptual Modeling Technique for Discrete Event Simulation of Operational Processes. In Advances in Production Management Systems; Springer: Boston, MA, USA, 2007; pp. 305–312. [Google Scholar] [CrossRef]
- Sargent, R.G. Verification and validation of simulation models. J. Simul. 2013, 7, 12–24. [Google Scholar] [CrossRef]
- Chew, J.; Sullivan, C. Verification, validation, and accreditation in the life cycle of models and simulations. In 2000 Winter Simulation Conference Proceedings; Winter Simulation Conference: San Diego, CA, USA, 2000; pp. 813–818. [Google Scholar]
- Balci, O. Golden rules of verification, validation, testing, and certification of modeling and simulation applications. SCS M S Mag. 2010, 4, 1–7. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fonseca i Casas, P.; Lijia Hu, D.; Guasch i Petit, A.; Figueras i Jové, J. Simplifying the Verification of Simulation Models through Petri Net to FlexSim Mapping. Appl. Sci. 2020, 10, 1395. https://doi.org/10.3390/app10041395
Fonseca i Casas P, Lijia Hu D, Guasch i Petit A, Figueras i Jové J. Simplifying the Verification of Simulation Models through Petri Net to FlexSim Mapping. Applied Sciences. 2020; 10(4):1395. https://doi.org/10.3390/app10041395
Chicago/Turabian StyleFonseca i Casas, Pau, Daniel Lijia Hu, Antoni Guasch i Petit, and Jaume Figueras i Jové. 2020. "Simplifying the Verification of Simulation Models through Petri Net to FlexSim Mapping" Applied Sciences 10, no. 4: 1395. https://doi.org/10.3390/app10041395
APA StyleFonseca i Casas, P., Lijia Hu, D., Guasch i Petit, A., & Figueras i Jové, J. (2020). Simplifying the Verification of Simulation Models through Petri Net to FlexSim Mapping. Applied Sciences, 10(4), 1395. https://doi.org/10.3390/app10041395




