FEM Based Preliminary Design Optimization in Case of Large Power Transformers
Abstract
1. Introduction
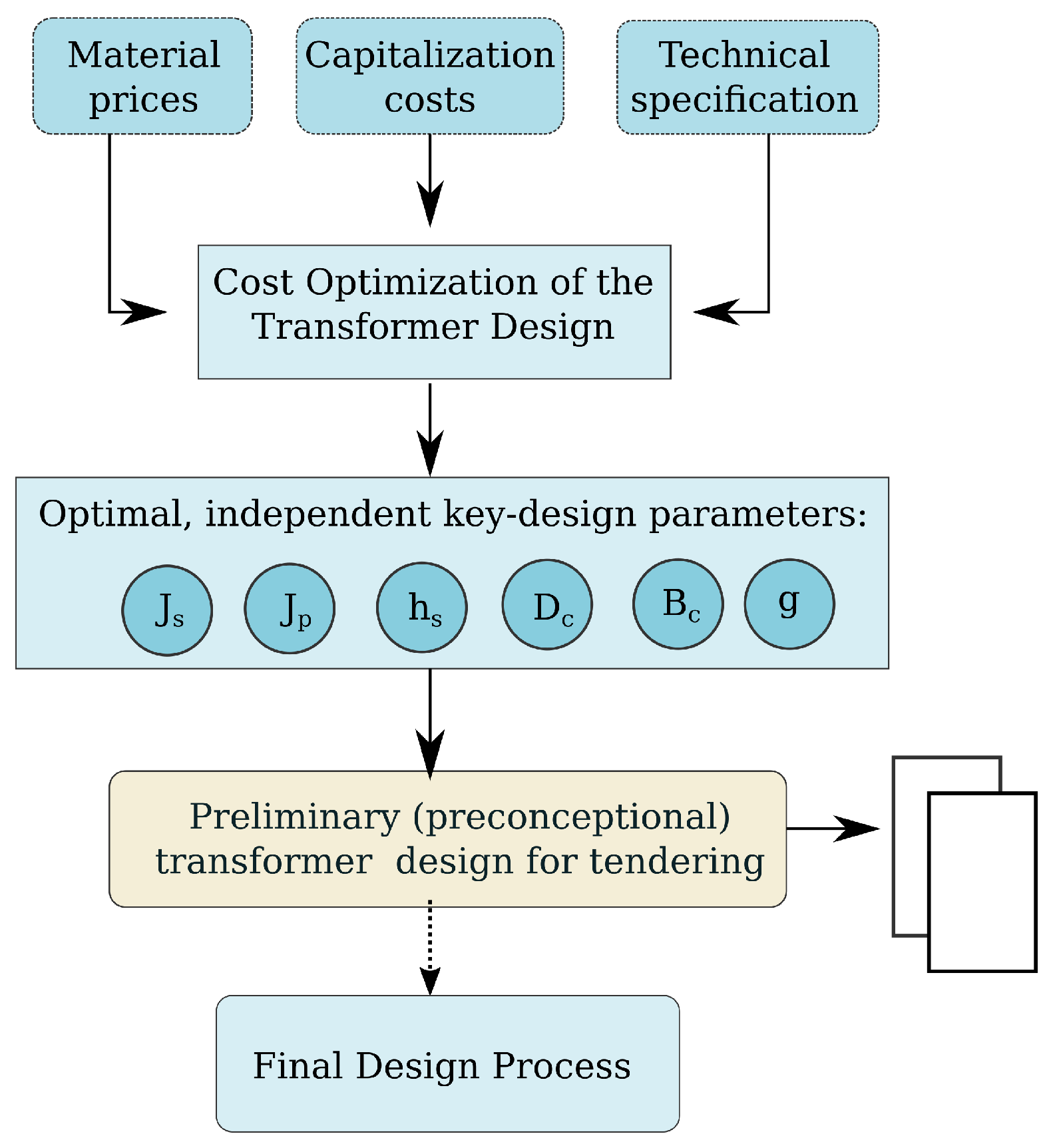
2. Proposed Methodology
2.1. Transformer Model for the Optimization
| Algorithm 1 Transformer Model Evaluator |
| function Evaluator(p) ▹ p means the independent design parameters, which generated by NSGA-II within the given search space
|
2.2. Objective Function—Total Cost of Ownership
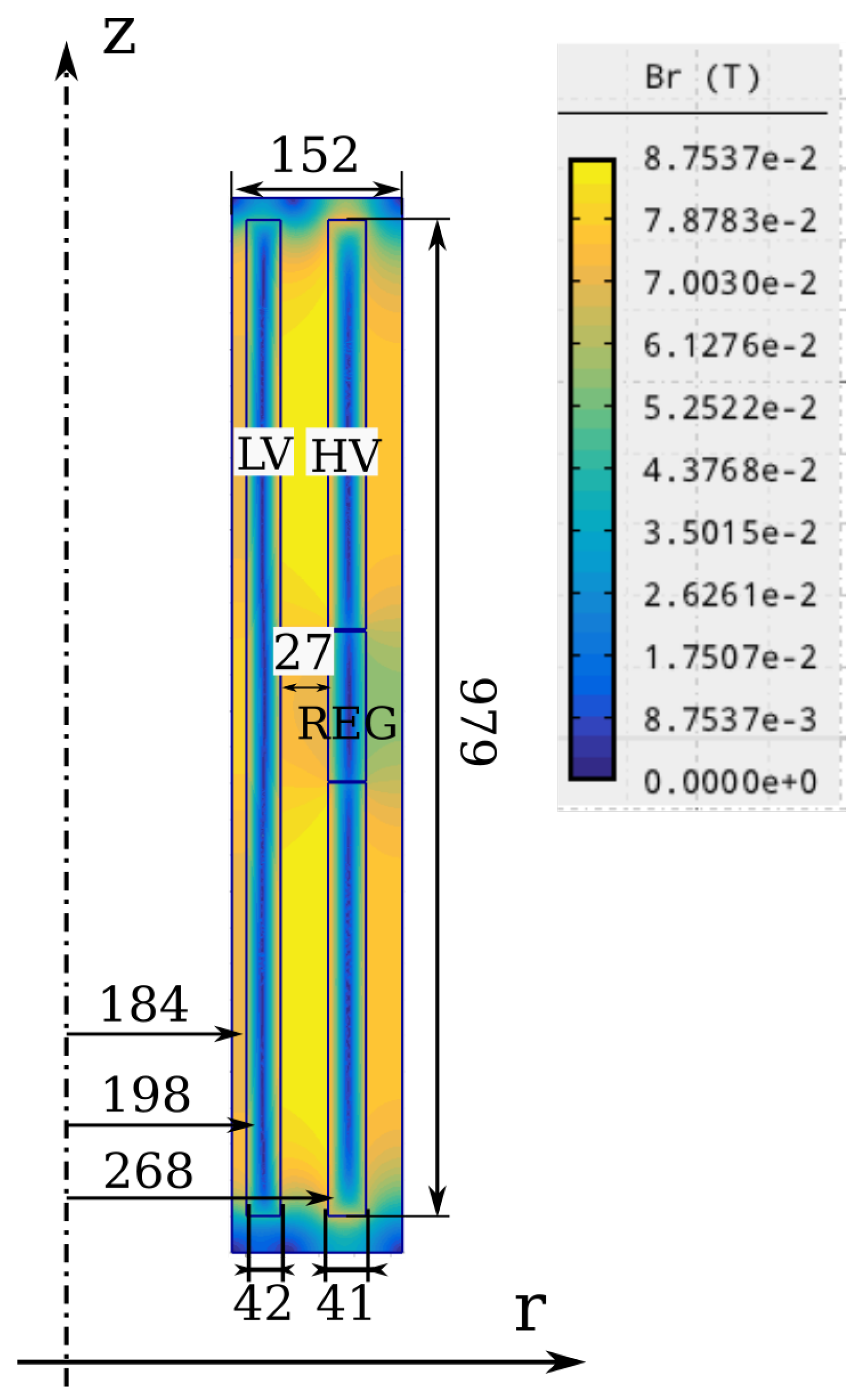
2.3. FEM Model
2.4. Ārtap
2.5. NSGA-II
| Algorithm 2 NSGA II |
|
2.6. Analytical Calculations
2.7. Power Criteria in Working Window
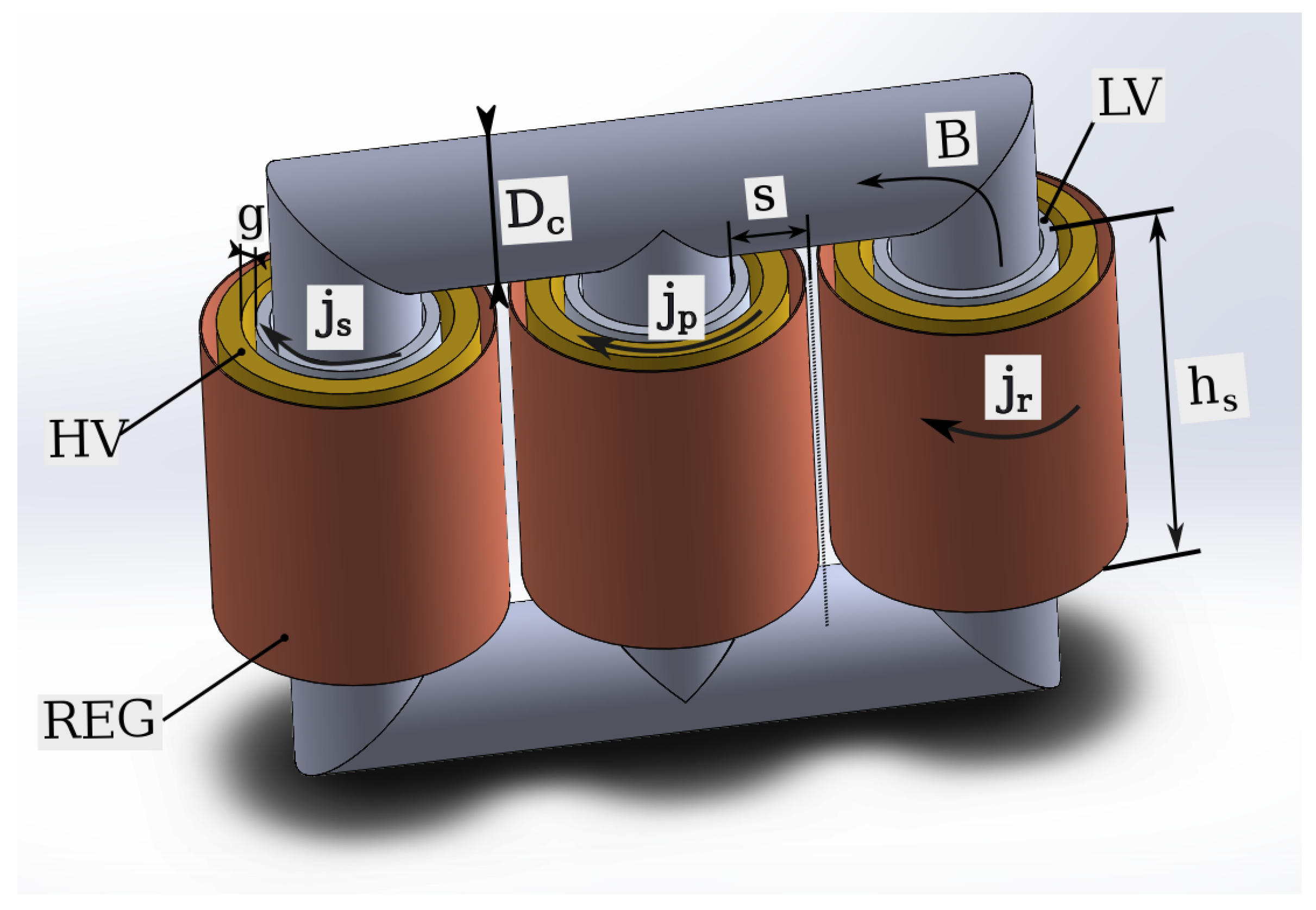
2.8. Regulating Winding Dimensions
Turn Voltage
2.9. Core Mass and No-Load Loss Calculation
2.10. Geometric Programming
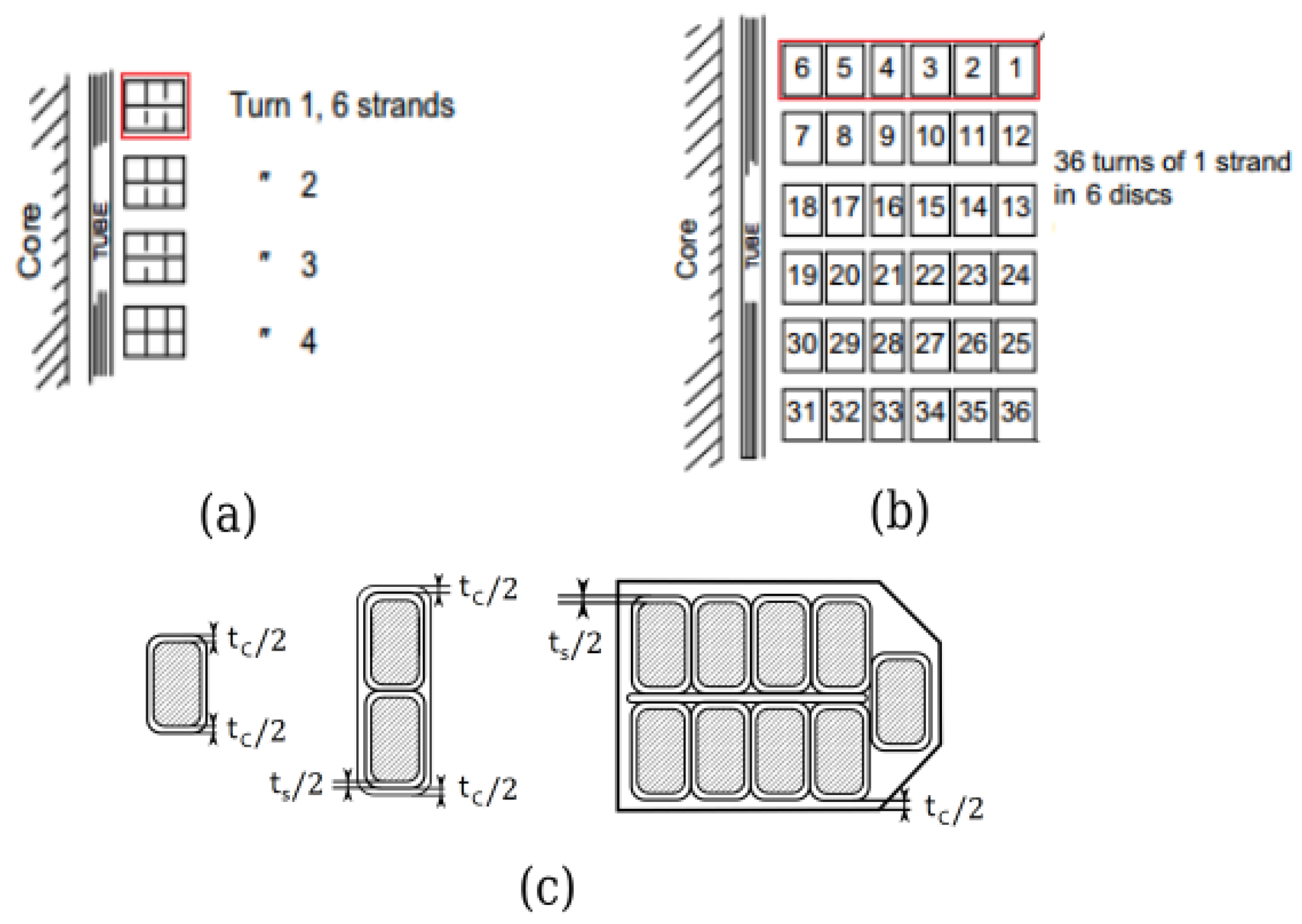
2.11. GP Based Embedded Winding Model
2.11.1. Eddy Losses in the Windings
2.11.2. Geometry
3. Results and Discussion
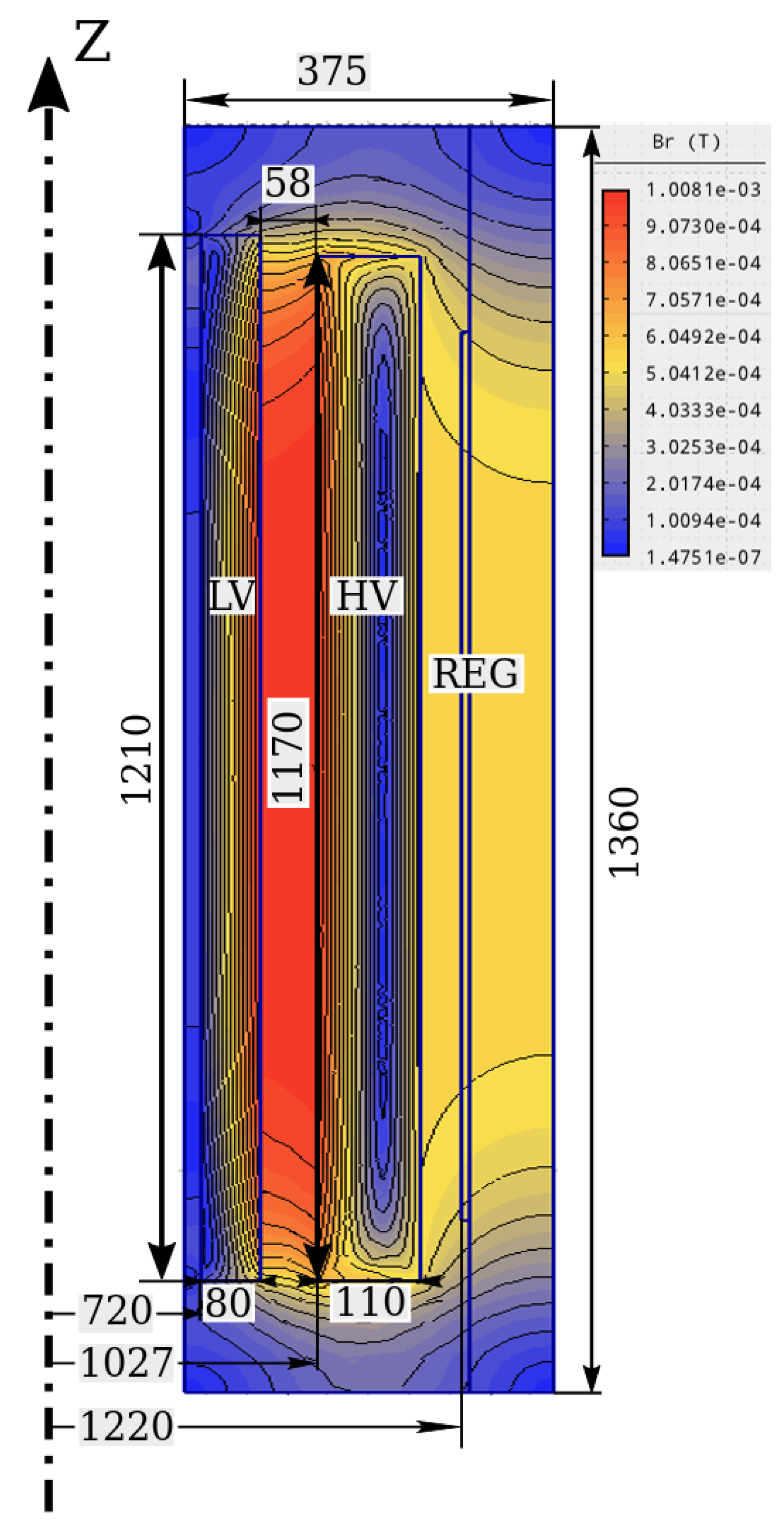
3.1. Validation of the Transformer Model
- mm is the core diameter,
- T is the flux density,
- mm is the height of the low voltage winding,
- mm is the main gap distance is,
- is the current density in the LV winding,
- is the current density in the HV winding,
- is the current density in the REG.
3.2. Input Parameters of the Test Transformer
3.3. Discussion of the Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ryan, H.M. High Voltage Engineering and Testing; Institution of Engineering and Technology: London, UK, 2013. [Google Scholar]
- Georgilakis, P.S. Spotlight on Modern Transformer Design; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]
- Kulkarni, S.V.; Khaparde, S. Transformer Engineering: Design and Practice; CRC Press: Boca Raton, FL, USA, 2004; Volume 25. [Google Scholar]
- IEEE Guide for Loss Evaluation of Distribution and Power Transformers and Reactors; IEEE: Piscataway, NJ, USA, 2017. [CrossRef]
- Topalis, F.V.; Targosz, R.; Irrek, W.; Rialhe, A.; Baginski, A. Strategies for development and diffusion of energy efficient distribution transformers in Europe. In Proceedings of the 13th Biennial IEEE Conference on Electromagnetic Field Computation IEEE CEFC, Athens, Greece, 11–15 May 2008. [Google Scholar]
- Orosz, T.; Sőrés, P.; Raisz, D.; Tamus, Á.Z. Analysis of the green power transition on optimal power transformer designs. Period. Polytech. Electr. Eng. Comput. Sci. 2015, 59, 125–131. [Google Scholar] [CrossRef]
- Orosz, T.; Poór, P.; Pánek, D.; Karban, P. Power Transformer Design Optimization for Carbon Footprint. In Proceedings of the IEEE 11th International Conference 2019 Electric Power Quality and Supply Reliability (PQ) together with 2019 Symposium of Electrical Engineering and Mechatronics (SEEM), Kärdla, Estonia, 12–15 June 2019. [Google Scholar]
- Orlova, S.; Rassõlkin, A.; Kallaste, A.; Vaimann, T.; Belahcen, A. Lifecycle analysis of different motors from the standpoint of environmental impact. Latv. J. Phys. Tech. Sci. 2016, 53, 37–46. [Google Scholar] [CrossRef]
- Del Vecchio, R.M.; Poulin, B.; Feghali, P.T.; Shah, D.M.; Ahuja, R. Transformer Design Principles: With Applications to Core-Form Power Transformers; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Orosz, T. Evolution and modern approaches of the power transformer cost optimization methods. Period. Polytech. Electr. Eng. Comput. Sci. 2019, 63, 37–50. [Google Scholar] [CrossRef]
- Khatri, A.; Rahi, O. Optimal design of transformer: A compressive bibliographical survey. Int. J. Sci. Eng. Technol. 2012, 1, 159–167. [Google Scholar]
- Amoiralis, E.I.; Tsili, M.A.; Georgilakis, P.S. The state of the art in engineering methods for transformer design and optimization: A survey. J. Optoelectron. Adv. Mater. 2008, 10, 1149. [Google Scholar]
- Ong, Y.S.; Nair, P.B.; Lum, K.Y. Max-min surrogate-assisted evolutionary algorithm for robust design. IEEE Trans. Evol. Comput. 2006, 10, 392–404. [Google Scholar]
- Orosz, T.; Borbély, B.; Tamus, Z.Á. Performance comparison of multi design method and meta-heuristic methods for optimal preliminary design of core-form power transformers. Period. Polytech. Electr. Eng. Comput. Sci. 2017, 61, 69–76. [Google Scholar] [CrossRef]
- Amoiralis, E.I.; Tsili, M.A.; Georgilakis, P.S.; Kladas, A.G.; Souflaris, A.T. A parallel mixed integer programming-finite element method technique for global design optimization of power transformers. IEEE Trans. Magn. 2008, 44, 1022–1025. [Google Scholar] [CrossRef]
- Amoiralis, E.I.; Georgilakis, P.S.; Tsili, M.A.; Kladas, A.G.; Souflaris, A.T. Complete Software Package for Transformer Design Optimization and Economic Evaluation Analysis. Mater. Sci. Forum 2010, 1058, 535. [Google Scholar] [CrossRef]
- Georgilakis, P. Recursive genetic algorithm-finite element method technique for the solution of transformer manufacturing cost minimisation problem. IET Electr. Power Appl. 2009, 3, 514–519. [Google Scholar] [CrossRef]
- Omorogiuwa Eseosa, O. A review of intelligent based optimization techniques in power transformer design. Appl. Res. J. 2015, 1, 79–88. [Google Scholar]
- Mohammed, M.S.; Vural, R.A. NSGA-II+FEM Based Loss Optimization of Three Phase Transformer. IEEE Trans. Ind. Electron. 2018. [Google Scholar] [CrossRef]
- Andersen, O.W. Transformer Leakage Flux Program Based on the Finite Element Method. IEEE Trans. Power Appar. Syst. 1973, PAS-92, 682–689. [Google Scholar] [CrossRef]
- Tóth, B. Multi-field dual-mixed variational principles using non-symmetric stress field in linear elastodynamics. J. Elast. 2016, 122, 113–130. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Orosz, T.; Nagy, T.; Tamus, Z.Á. A Generalized Geometric Programming Sub-problem of Transformer Design Optimization. In Technological Innovation for Smart Systems; Camarinha-Matos, L.M., Parreira-Rocha, M., Ramezani, J., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 373–381. [Google Scholar]
- Pánek, D.; Orosz, T.; Karban, P. Artap: Robust Design Optimization Framework for Engineering Applications. In Proceedings of the 2019 Third International Conference on Intelligent Computing in Data Sciences (ICDS), Marrakesh, Morocco, 28–30 October 2019; pp. 1–6. [Google Scholar]
- Del Vecchio, R.M.; Poulin, B.; Feeney, M.E.F.; Feghali, P.T.; Shah, D.M.; Ahuja, R.; Shah, D.M. Transformer Design Principles: With Applications to Core-Form Power Transformers; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Jabr, R.A. Application of geometric programming to transformer design. IEEE Trans. Magn. 2005, 41, 4261–4269. [Google Scholar] [CrossRef]
- Orosz, T.; Sleisz, A.; Tamus, Z.A. Metaheuristic Optimization Preliminary Design Process of Core-Form Autotransformers. IEEE Trans. Magn. 2016, 52, 1–10. [Google Scholar] [CrossRef]
- Charalambous, C.A.; Milidonis, A.; Lazari, A.; Nikolaidis, A.I. Loss evaluation and total ownership cost of power transformers—Part I: A comprehensive method. IEEE Trans. Power Deliv. 2013, 28, 1872–1880. [Google Scholar] [CrossRef]
- OpenMDAO.org | An Open-Source Framework for Efficient Multidisciplinary Optimization. Available online: https://openmdao.org/ (accessed on 14 February 2020).
- Platypus—Multiobjective Optimization in Python—Platypus Documentation. Available online: https://platypus.readthedocs.io/en/latest/ (accessed on 14 February 2020).
- Pánek, D.; Orosz, T.; Karban, P.; Doležel, I. Comparison of Simplified Techniques for Solving Selected Coupled Electroheat Problems. COMPEL—Int. J. Comput. Math. Electr. Electron. Eng. 2020. [Google Scholar] [CrossRef]
- Pánek, D.; Orosz, T.; Kropík, P.; Karban, P.; Doležel, I. Reduced-Order Model Based Temperature Control of Induction Brazing Process. In Proceedings of the 2019 Electric Power Quality and Supply Reliability (PQ), Hiiumaa, Estonia, 12–15 June 2019. [Google Scholar]
- Kaska, J.; Doležel, I.; Pechánek, R.; Orosz, T.; Karban, P.; Pánek, D. Optimization of Reluctance Motor. In Proceedings of the 22nd International Conference on the Computation of Electromagnetic Fields (COMPUMAG 2019), Paris, France, 15–19 July 2019. [Google Scholar]
- Karban, P.; Mach, F.; Kůs, P.; Pánek, D.; Doležel, I. Numerical solution of coupled problems using code Agros2D. Computing 2013, 95, 381–408. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Kennedy, J. Particle swarm optimization. In Encyclopedia of Machine Learning; Springer: Berlin, Germany, 2010; pp. 760–766. [Google Scholar]
- Hanne, T. A multiobjective evolutionary algorithm for approximating the efficient set. Eur. J. Oper. Res. 2007, 176, 1723–1734. [Google Scholar] [CrossRef]
- Martinez-Cantin, R. Bayesopt: A bayesian optimization library for nonlinear optimization, experimental design and bandits. J. Mach. Learn. Res. 2014, 15, 3735–3739. [Google Scholar]
- Johnson, S.G. The NLopt Nonlinear-Optimization Package. 2014. Available online: https://nlopt.readthedocs.io/en/latest/ (accessed on 14 February 2020).
- Jones, E.; Oliphant, T.; Peterson, P. {SciPy}: Open Source Scientific Tools for {Python}. 2014. Available online: https:/www.scipy.org (accessed on 14 February 2020).
- Biscani, F.; Izzo, D.; Yam, C.H. A global optimisation toolbox for massively parallel engineering optimisation. arXiv 2010, arXiv:1004.3824. [Google Scholar]
- Padhye, N.; Deb, K. Multi-objective optimisation and multi-criteria decision making in SLS using evolutionary approaches. Rapid Prototyp. J. 2011, 17, 458–478. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Lamont, G.B.; Van Veldhuizen, D.A. Evolutionary Algorithms for Solving Multi-Ojective Problems; Springer: Berlin, Germany, 2007; Volume 5. [Google Scholar]
- Karsai, K.; Kerényi, D.; Kiss, L. Large Power Transformers; Elsevier Science Pub. Co. Inc.: New York, NY, USA, 1987. [Google Scholar]
- AK-Steel. TRAN-COR® H Grain Oriented Electrical Steels; AK-Steel: Middletown, OH, USA, 2013. [Google Scholar]
- Orosz, T.; Sleisz, Á.; Vajda, I. Core-form transformer design optimization with branch and bound search and geometric programming. In Proceedings of the 2014 IEEE 55th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 14 October 2014; pp. 17–21. [Google Scholar]
- Duffin, R.J.; Peterson, E.L.; Zener, C. Geometric Programming: Theory and Application; Wiley: New York, NY, USA, 1967. [Google Scholar]
- Boyd, S.; Kim, S.J.; Vandenberghe, L.; Hassibi, A. A tutorial on geometric programming. Optim. Eng. 2007, 8, 67–127. [Google Scholar] [CrossRef]
- International Standard Commission. IEC Temperature Rise; IEC Std 60076-2; International Standard Commission: Geneva, Switzerland, 2006. [Google Scholar]


| Quantity | Dimension | Variable |
|---|---|---|
| Independent variables | ||
| Core diameter | mm | |
| Flux density in the core | T | B |
| Main insulation distance | mm | g |
| Current density in the secondary coil | A/mm | |
| Current density in the primary coil | A/mm | |
| Current density in the regulating coil | A/mm | |
| Height of the secondary winding | mm | |
| Dependent parameters (Analytical) | ||
| Width of the working window | mm | s |
| Core mass | t | |
| Radial thickness of secondary winding | mm | |
| Mean radius of secondary winding | mm | |
| Radial thickness of primary winding | mm | |
| Mean radius of primary winding | mm | |
| Radial thickness of regulating winding | mm | |
| Mean radius of regulating winding | mm | |
| No Load Loss | kW | |
| Dependent parameters (FEM) | ||
| Short circuit impedance | % | |
| Maximum of radial flux density in LV | T | |
| Maximum of radial flux density in HV | T | |
| Maximum of axial flux density in LV | T | |
| Maximum of axial flux density in HV | T | |
| Dependent parameters (GP sub-problem) | ||
| Number of turns in a winding | # | n |
| Number of conductors in a turn | # | |
| Number of axial turns | # | |
| Number of radial turns | # | |
| Copper area in one turn | mm | |
| Copper volume in the winding | mm | |
| Copper mass in the winding | kg | |
| Optimal conductor height | mm | |
| Optimal conductor width | mm | |
| Dependent parameters (Complex) | ||
| Load Loss | kW | |
| Total Cost of Ownership | € | |
| LV | HV | ||||
|---|---|---|---|---|---|
| Reference | Model | Reference | Model | ||
| Line voltage | kV | 22 | 35 | ||
| Connection | kV | D | Y | ||
| Phase Voltage | kV | 22 | 20.23 | ||
| Number of turns | # | 708 | 650 | ||
| Phase current | A | 95.5 | 104 | ||
| Turn area | mm | 31.623 | 56.0 | ||
| Conductor height | mm | 11.6 | 6.6 | 11.4 | 8.1 |
| Conductor width | mm | 2.7 | 2.7 | 3 | 2.7 |
| Mean diameter | mm | 437 | 436 | 578 | 572 |
| Winding width | mm | 42.9 | 42.8 | 40.7 | 41.1 |
| Copper mass | kg | 813 | 824 | 1071 | 1082 |
| Loss | kW | 19.150 | 19.23 | 25.948 | 23.979 |
| Parameter | Dimension | Value | |
|---|---|---|---|
| Nominal power | MVA | 31.5 | |
| Frequency | Hz | 50 | |
| Connection group | Dyn1 | ||
| Number of phases | # | 3 | |
| Short circuit impedance | % | 14.5 | |
| Main gap | mm | 37 | |
| Sum of the end insulation | mm | 150 | |
| Phase distance | mm | 37 | |
| Core-Inner winding distance | mm | 20 | |
| Core | Number of legs | # | 3 |
| Flux density limit in columns | T | 1.7 | |
| Filling Factor | % | 90 | |
| Material Type | M1H | ||
| Material Price | €/kg | 3.5 | |
| Low Voltage Winding | Line Voltage | kV | 33 |
| Phase Voltage | kV | 19.05 | |
| BIL | kV | 125 | |
| AC | kV | 50 | |
| Copper filling factor | % | 60 | |
| Material and manufacturing price | €/kg | 10 | |
| High Voltage Winding | Line Voltage | kV | 120 |
| Phase Voltage | kV | 69.36 | |
| BIL | kV | 550 | |
| AC | kV | 230 | |
| Copper filling factor | % | 60 | |
| Material and manufacturing price | €/kg | 8.5 | |
| Regulating Winding | Regulating range | % | |
| Insulation | Fully insulated | ||
| Regulated winding | High voltage | ||
| Filling factor | % | 65 | |
| Parameter | Dimension | Lower Bound | Upper Bound |
|---|---|---|---|
| mm | 400 | 700 | |
| B | T | 1.4 | 1.7 |
| g | mm | 37 | 70 |
| A/mm | 1.5 | 3.0 | |
| A/mm | 1.5 | 3.0 | |
| A/mm | 1.5 | 3.5 | |
| mm | 1200 | 2000 |
| Design Parameters | Dimension | Metaheuristic | NSGA2+GP |
|---|---|---|---|
| Core data | |||
| core diameter | mm | 570 | 600 |
| flux density | T | 1.64 | 1.58 |
| core mass | t | 16.65 | 21.05 |
| turn voltage | V | 83.6 | 89.3 |
| main gap | mm | 37 | 58 |
| Low voltage winding | |||
| inner diameter | mm | 610 | 720 |
| winding height | mm | 1003 | 1210 |
| winding width | mm | 89 | 80 |
| turn number | # | 228 | 214 |
| current density | A/mm | 2.35 | 2.02 |
| h* | mm | - | 3.6 |
| w* | mm | - | 2.5 |
| High voltage winding | |||
| inner diameter | mm | 861 | 1027 |
| winding height | mm | 973 | 1170 |
| winding width | mm | 107 | 110 |
| turn number | 1579 | 1478 | |
| h* | mm | - | 8.1 |
| w* | mm | - | 2.7 |
| current density | A/mm | 2.01 | 1.53 |
| Regulating winding | |||
| inner diameter | mm | 1149 | 1220 |
| winding height | mm | 853 | 1025 |
| winding width | mm | 10 | 10 |
| current density | A/mm | 2.7 | 2.71 |
| load loss | kW | 114.9 | 88.3 |
| core loss | kW | 13.2 | 17.82 |
| TOC | € | 447,627 | 448,597 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orosz, T.; Pánek, D.; Karban, P. FEM Based Preliminary Design Optimization in Case of Large Power Transformers. Appl. Sci. 2020, 10, 1361. https://doi.org/10.3390/app10041361
Orosz T, Pánek D, Karban P. FEM Based Preliminary Design Optimization in Case of Large Power Transformers. Applied Sciences. 2020; 10(4):1361. https://doi.org/10.3390/app10041361
Chicago/Turabian StyleOrosz, Tamás, David Pánek, and Pavel Karban. 2020. "FEM Based Preliminary Design Optimization in Case of Large Power Transformers" Applied Sciences 10, no. 4: 1361. https://doi.org/10.3390/app10041361
APA StyleOrosz, T., Pánek, D., & Karban, P. (2020). FEM Based Preliminary Design Optimization in Case of Large Power Transformers. Applied Sciences, 10(4), 1361. https://doi.org/10.3390/app10041361






