Abstract
Variable impedance control has been required to perform a variety of interactive tasks in contact with environments. In some cases, the time-varying stiffness matrix of the impedance model can be used to achieve high performance for uneven contact tasks. In the paper, two sufficient conditions are proposed to ensure the input-to-state stability (ISS) irrespective of time-varying stiffness. Furthermore, the update rule of the stiffness is also suggested in such a way that the asymptotic stability is guaranteed under certain region conditions. Even when the update rule is not applied, the ISS is at least assured. In other words, the error is always bounded only if the external force/torque is bounded. In detail, two sufficient conditions offer the lower bound of stiffness and the upper bound of its time derivative. Simulation results show that the ISS of variable impedance control is achieved if the proposed sufficient conditions are satisfied. Also, we can confirm the asymptotic behavior in the simulation when the stiffness is updated according to the given rule.
1. Introduction
External forces and torques appear in contact with environments or with humans. Dealing with external forces and torques is important in achieving a stable and safe cooperating task with wide robotic applications. Impedance control is one of the methods of handling expected or unexpected external forces and torques [1]. When the impedance control is applied to the robot, it behaves like a linear second-order system, such as a mass-spring-damper model that can be very intuitive to predict how the system works. Furthermore, Colgate and Hogan [2] proposed an interaction controller to adjust the force contacting with environments. In the paper, necessary and sufficient conditions are proposed to ensure the stability of the coupled linear impedance model under a single interaction port for passive environments. Recent research on robotic manipulation and cooperation has focused on the fact that the robotic manipulator brings accurate and fast results, as well as safe collaborations with the human. Calinon et al. [3] proposed a learning by demonstration approach for a robotic manipulator operating in the unstructured environment while interacting with a human operator.
As a common method, impedance control uses constant parameters, but the method might bring performance limitations in conducting cooperative works between robot and human or between robot and objects having uneven surfaces and various elasticities. As part of that, impedance control using time-varying parameters, called variable impedance control, was proposed; for example, Ikeura and Inooka [4] analyzed the characteristics of impedance parameters of the human arm itself in order to execute the human-robot cooperative tasks. The impedance of the human arm was approximated using the variable impedance model that the resultant motions were planned and implemented. Also, Ficuciello et al. [5] suggested the modulation scheme of Cartesian impedance parameters for redundant manipulators in order to improve the control performance during the physical interaction between humans and robots. The aforementioned methods dealt with how to make appropriate varying profiles of impedance parameters, ultimately, for achieving the desired interaction task motion and its planning. Ferraguti et al. [6] proposed the variable impedance control with an update rule on the stiffness parameter. The proposed method guarantees that the system is passive with any variable stiffness matrix, but the specific method to design the remaining impedance parameters was not suggested. Kronander and Billard [7] proposed the concept of state-independent stability for the variable impedance control, and it broadens the possibility to design update rules on the stiffness and damping matrices. Nevertheless, choosing the desired inertia parameter correctly was a remaining issue. As a matter of fact, impedance control is closely related to joint torques applied externally, but the aforementioned references did not deal with the external joint torques for designing the update rule on the stiffness and damping matrices.
This paper aims at finding the sufficient conditions of variable impedance control for guaranteeing the input-to-state stability (ISS) as well as deriving the stiffness update rule from the asymptotic stability of the closed-loop control system. The ISS in [8] can be interpreted in two viewpoints: one is that the system behavior should remain bounded if its inputs are bounded, and the other is that the system states should tend to equilibrium if the inputs tend to zero. These concepts can be usefully applied to the variable impedance control because the impedance control operates in both motion spaces such as the constrained motion space and free (or unconstrained) motion space. For example, if the robotic manipulator is in the free motion without any contacts, then the variable impedance control acts like the conventional position control without any variations of impedance parameters. On the contrary, if the robotic manipulator is in contact with the environment or human, then the variable impedance control can change its stiffness parameters using the mechanical power generated by externally applied torques and time derivative of the inertia matrix. This paper focuses on finding the sufficient conditions of variable impedance control to assure the ISS despite the impedance parameter variations. In addition, the update rule of stiffness is derived from the asymptotic stability with some region condition.
The paper is organized as follows. Section 2 introduces the variable impedance control in the joint space. Section 3 suggests the main results of the paper, such as the ISS proof of variable impedance control, the derivation of update rule, and the guidelines to choose the stiffness and damping matrices. Section 4 shows the simulation results to confirm the effectiveness of the proposed stiffness update rule, including the aforementioned sufficient conditions. Finally, Section 5 draws the conclusions and future works.
2. Variable Impedance Control in Joint Space
Impedance control is usually derived and described in the task (or operational) space. However, this paper deals with it in the joint space because the task space dynamics can be easily obtained from the joint space dynamics only if we know the kinematic structure of the robotic manipulator. Consider the well-known dynamics of the robotic manipulator in [9]:
where is a symmetric and positive definite inertia (or mass) matrix, the Coriolis and centrifugal matrix, the gravity force/torque vector, and the Jacobian matrix obtained from the kinematic structure of robotic manipulator, the joint position, velocity and acceleration, respectively, the joint force/torque, the externally applied force/torque, n the dimension of joint space, m the dimension of task space, and finally, the friction and unknown disturbances were ignored in the dynamics in order to avoid the difficulties of theoretical derivation, although the frictions affect the control performance badly, especially, in case of the impedance control. Also, it is obvious in [10] that the inertia matrix is uniformly bounded and the following property always holds:
where is an identity matrix, and denote the minimum and maximum eigenvalues of matrix (•), respectively.
The impedance control makes the closed-loop control system act like a sort of linear mass-spring-damper system, and it is referred to as the generalized dynamic impedance in case of robotic manipulators in [9]. For simplicity, the stiffness parameter is chosen as a time-varying one. Now, let us assume that the generalized dynamic impedance is given as follow:
where denotes constant positive definite damping matrix and implies time-varying positive definite stiffness matrix. In order to implement the given generalized dynamic impedance, the inverse dynamics control method in [9] is designed as the following form:
where denotes a control input to be applied to the robotic manipulator described by Equation (1), here , and is an auxiliary control input to be designed from the generalized dynamic impedance of Equation (3) and it has the following form:
where represent the desired joint position, velocity and acceleration, respectively. If Equation (5) is applied to term of Equation (4), then we have the variable impedance control in the joint space as follow:
It is noted that the externally applied force/torque term disappears in the control algorithm as shown in Equation (6), in other words, Equation (6) does not require any explicit force/torque measurement feedback. As a result, when the control input of Equation (6) is applied to the robotic manipulator of Equation (1), we can obtain the generalized dynamic impedance of Equation (3) as the behavior of closed-loop control system. From now on, we will use Equation (3) as variable impedance model in the next sections.
3. ISS of Variable Impedance Model
Figure 1 illustrates a block diagram of the variable impedance control scheme for robotic manipulators. To begin with, we prove the ISS of the variable impedance model (closed-loop control system) of Equation (3) that is obtained by applying the impedance control of Equation (6) to the robotic manipulator of Equation (1). While proving the ISS, two sufficient conditions are derived from the stability criterion. For notational convenience, external joint torque vector that is distributed from the externally applied force/torque is newly introduced as follow:
where denotes n-dimensional external joint torque. Let us define a state vector using the position and velocity errors as follows:
where is -dimensional state vector, and:
in which and express n-dimensional position and velocity error, respectively. Now, the variable impedance model (VIM) can be simply expressed either by using the definitions of errors:
or by using the state vector notations:
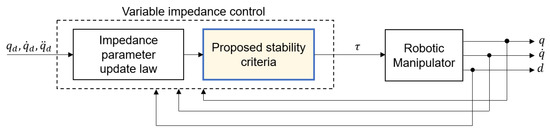
Figure 1.
Variable impedance control scheme; denote the joint position, velocity and the externally applied joint force/torque, respectively, and the desired joint position, velocity and acceleration, respectively, and the control input.
To help understanding the concept of ISS, it is shortly explained. For given system
it is assumed that the function is piecewise continuous in t and locally Lipschitz in x and d, and furthermore, it is assumed that external joint torque is also piecewise continuous in t and bounded function for all . Then the existence and uniqueness of the solution of first-order nonlinear differential equation of Equation (11) are guaranteed. Additionally, it is noted that is called a class K function if it is strictly increasing with , and as a class function if it belongs to the class K and as . Now, the well-known theorem regarding the ISS in [8,11] is introduced in the following.
Theorem 1
(ISS Theorem, [8]). Let be a continuously differentiable function such that except the equilibrium . Here, if and only if there exist a class function and a class K function such that the following inequality is satisfied:
then the system (11) is input-to-state stable(ISS).
The proof is omitted because we can easily find it from many references including [8]. On the other hand, suppose that there exists a function such that the following holds for all x and d:
with class functions and , then the system is ISS as well. In other words, if the size of the state vector is lower-bounded as a class function , then the time derivative of the Lyapunov function is negative definite for all state vectors.
3.1. ISS Proof
By using aforementioned notations and theorem, new theorem regarding the sufficient conditions for the variable impedance model (VIM) to be ISS is suggested as follow:
Theorem 2.
(Sufficient Conditions of VIM to be ISS) Assume that the variable impedance model of Equation (10) is piecewise continuous in t and locally Lipschitz in x and d, and also assume that the joint torque d is piecewise continuous in t and bounded function for all . If the following conditions hold:
where is the lower bound of matrix • and α is an arbitrary constant chosen within , then the VIM is ISS.
Proof.
(Step 1. Setting Lyapunov function candidate) Let us take Lyapunov function candidate using kinetic plus potential energies with scaling factor as follow:
where . Since and , the Lyapunov function candidate must be positive definite for all x and K.
(Step 2. Derivative of Lyapunov function candidate) Let us take time derivative of the Lyapunov function candidate as follow:
Now, if the VIM of Equation (10) is applied to above equation, then we have:
Let us rearrange above equation as follow:
If the inequality of is applied to above equation, then we can get
Once again, let us rearrange above equation as follow:
Using the completion of squares for last two terms as follows:
where , then above Equation (19) is rearranged as following from:
Since first two terms of the right-hand side of Equation (21) should be negative semi-definite, the sufficient conditions can be chosen as follows,
where is the lower bound of matrix •. If the Equation (22) is satisfied, Equation (21) can be expressed as following simplified form:
where belongs to a class and a class K function. Therefore, we can conclude that the VIM (closed-loop control system) of Equation (10) is ISS under two conditions of Equations (12) and (13). □
In the above Theorem 2, the sufficient conditions for the variable impedance control to stabilize the closed-loop control system have been suggested as Equations (12) and (13). In the Equation (12), the upper bound of variation of stiffness matrix was proposed, in particular, it should be smaller than the scalar multiple of the current stiffness. Thus we can say that the variation of stiffness matrix has its upper bound by the function of the current stiffness matrix. Also, Equation (13) shows that the matrix lower bound of a sum of stiffness and damping matrices should be larger than the variation of the inertia matrix. Here, has the following property,
where is a Coriolis and centrifugal matrix, and refer [12] for more information. Skew-symmetric property of is well-known in the robotics and plays a core role in proving the stability. Above Equation (24) can be easily derived like this:
Since the Coriolis and centrifugal matrix is bounded by the joint velocity of a robotic manipulator with some scalar, i.e., , we can conclude that the sum of stiffness and damping matrices should be larger than some scalar multiplication of joint velocity. For practical use, the above conclusion can be interpreted that as the joint velocity becomes fast, so the stiffness matrix should be larger and vice versa.
3.2. Update Rule of Stiffness Matrix
The variable impedance control was designed to improve the control performance by handling the disturbance such as the external joint torque. However, it was difficult to define the desired performance of the variable impedance control. Dubey et al. [13] proposed the strategy that chooses the impedance parameters by using force and velocity. He et al. [14] suggested the neural network method to solve the interaction problem. Tsumugiwa et al. [15] proposed the selection strategy of the impedance parameters using a passivity index and an extreme value of force applied by the human operator.
In this section, the stiffness update rule is proposed. For this purpose, we assume a situation that the manipulator interacts with an environment that has an uneven surface and various stiffnesses. For example, consider the scene of a disaster: several interactive tasks such as handling the tools and cutting the objects would be required. Even in this situation, the robotic manipulator should achieve a target position by updating its stiffness property, in fact, it is designed to be adjusted according to the external joint torque, i.e., d, in the following Theorem.
Theorem 3.
Assume that Theorem 2 holds. If the following update rule:
is utilized for the variable stiffness adjustment, then the closed-loop control system is either asymptotically stable or ISS, where is some positive constant.
Proof.
First, consider the condition of , since of Equation (19) is a scalar function, we can get
By using above property, we have the following inequality from Equation (19),
Let us define the positive definite matrices and ,
By subtracting the above equation from the below, we have:
Since we can choose with and , we assume that . Now, we can define the update rule as follow,
Furthermore, the time derivative of Lyapunov function holds:
Thus we can conclude the closed loop control system is asymptotically stable under the condition of . Second, in case of , the ISS can be easily proved from the previous Theorem 2. □
From the stiffness update rule of Equation (26), we can know that the time derivative of the inertia matrix of the robotic manipulator should influence the variation of the joint stiffness matrix and its size. In addition, since the time derivative of manipulator inertia is closely related to the Coriolis and centrifugal matrix, the stiffness update is also affected by the size of the Coriolis and centrifugal matrix related to the joint velocity. Also, the outer product of the joint external torque and the joint velocity error influences the stiffness matrix update. For example, if the joint velocity error of the manipulator and an external joint torque have the same signs, then the all the elements of the outer product of for and will have positive signs in the matrix. It results in a hard motion of the manipulator by increasing the joint stiffness matrix. On the other hand, if they have the opposite signs, then the element of outer product of will have negative, and it brings the soft motion of the manipulator by decreasing the joint stiffness matrix.
For implementing the stiffness matrix update of Equation (26), the information of external joint torque is required, as an alternative, the momentum observer [16] can be used to estimate the external joint torque using the momentum dynamics. Since the variable impedance control of Equation (6) does not require any force/torque sensor attached to the end-effector of the manipulator, the momentum observer would be a good alternative.
One of the leading roles of the proposed sufficient conditions in Theorem 2 and the subsequent update rule in Theorem 3 is to consider the external forces for stability analysis, and it brings the difference from the reference [7]. The external force is a necessary factor in determining the stability of the closed-loop control system since the variable impedance control is used in interactive situations with the environment and its update rules/profiles also work when external forces are detected. Theorem 1 in [7] demonstrated the stability of the control system under the assumption of a free (unconstrained) motion situation. It means that the update profiles for the stiffness and damping matrices cannot guarantee stability when the external forces affect the motion of the robotic manipulator. On the other hand, the proposed sufficient conditions and the update rule promise the ISS of the closed-loop control system even when the external forces are applied to the control system, and further, the asymptotic stability can be proven in the case of free motion ().
3.3. Selection Guideline for Stiffness and Damping Matrices
In this section the selection guidelines of stiffness and damping matrices are suggested from the sufficient conditions in Theorem 2. The variable impedance control should be considered in two aspects such as the constrained motion with contact and the free motion without any contacts as follows:
(Case 1, when to denote the free motion) Assume that any external forces and torques are not exerted to robotic manipulator, then the impedance parameters such as stiffness and damping are set up as the constants. Since and in Equation (19), we have
where and . Now we can find the condition to guarantee as follow:
From Equation (34), we have
where is the lower bound of matrix •. To calculate the time derivative of inertia matrix, Equation (24) could be used. On the other hand, as presented in [17], since the upper bound of time derivative of inertia matrix has following properties:
the condition of Equation (35) can be simplified to:
Above inequality provides some insight to us in selecting the stiffness and damping matrix, for example, the faster robotic motion is required, the bigger stiffness and damping are required to guarantee the stability.
(Case 2, when to denote the constrained motion with contacts) In the case of nonzero external joint torques yielded from the interaction between the robotic manipulator and the environment or human operator, the time-varying stiffness can be used to guarantee the stability only if the sufficient conditions of Equations (12) and (13) in the Theorem 2 are satisfied. In detail, Equation (26) is used to update the stiffness according to the variations of external joint torques yielded from environmental changes. As we can see in the Equation (26), smaller makes the stiffness update be faster.
4. Simulation
In order to illustrate the characteristics of the proposed sufficient conditions for the ISS, a two-link manipulator was simulated by using the MATLAB 2017a. In the simulation, the update rule of satisfying both Equations (12) and (13) was used in order to accomplish the ISS. From the Equation (24), it is noted that can be upper bounded by the joint velocity with some proportional constant , i.e.,, and and D are the design parameters. Now, assume within and , then the minimum of can be chosen as follows:
The design procedures for simulation are suggested as follows:
- Select the initial stiffness matrix and the damping matrix D, respectively. Equation (13) or Equation (37) should be considered.
- Obtain from .
In the simulation, we set the initial gains,
Furthermore, the mass and length of each link are set by 1 kg and 0.5 m, respectively. Figure 2 shows the snapshots of the simulation result according to the time progress. The manipulator starts to move toward a given target position , and then the target position was changed into another position of at the instant of 1 s. The simulator does not require any trajectory generation method because the proposed method was based on the set-point regulation. To show the effect of time-varying stiffness matrix according to the proposed update rule, the x-axis external force was applied to the end-effector with 50 N amplitude. It was applied to the end-effector backward and forward directions alternatively with a 0.25 s duration. The simulation was conducted for 2 s.
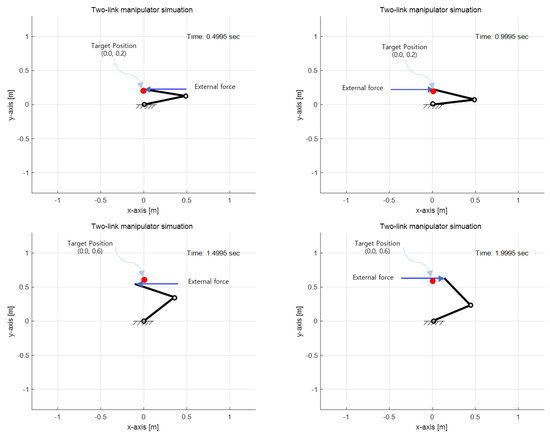
Figure 2.
Snapshots of simulation result according to time progress, where the robotic manipulator used in the simulation has two links. The external force is applied to the x-axis direction forward and backward, alternatively, with 0.25 s duration. Also, was set at a target position from the beginning, and then the target position was changed into at the instant of 1 s.
Figure 3 shows the data plots during the simulation suggested in Figure 2. The behavior of the robotic manipulator was evaluated in the viewpoint of the Lyapunov function and the sufficient conditions suggested in Equations (12) and (13) as main contributions. The Lyapunov function composed of total energy could not go to zero (equilibrium) as observed in Figure 3a when the external force was applied. In Figure 3a, we should notice that the Lyapunov function value was changed suddenly at the instant of 1 s because the target was then exchanged from to . However, we could confirm that its time derivative remains negative as shown in Figure 3b, in spite of abrupt target change. Also, the proposed sufficient conditions were satisfied all the time as shown in Figure 3c,d. Also, x-directional 50 N force was applied to the end-effector of the robotic manipulator as shown in Figure 3e. These external joint torques suggested in Figure 3f were obtained from the external force by using Equation (7). As a result, the joint position and velocity errors remain as shown in Figure 3g,h. In other words, we could know that the system error states remain inside the energy boundary caused by the external joint torques. Further, we could know that the closed-loop control system is maintained to be ISS, even if the stiffness matrix varies. The next section deals with six-degrees-of-freedom (6-DoFs) robotic manipulator as a further example.
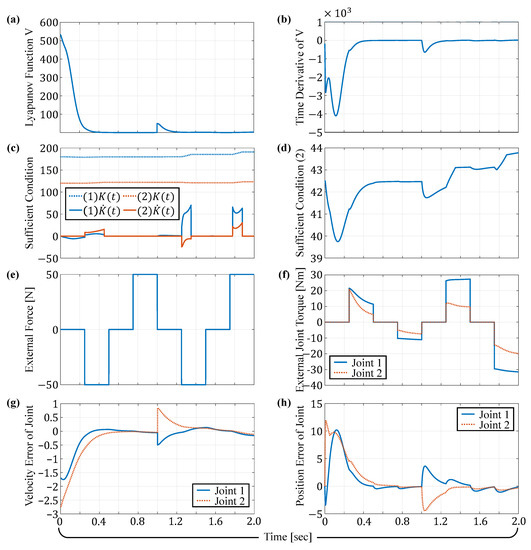
Figure 3.
Simulation data while performing the simulation suggested in Figure 2; (a) Lyapunov function value of Equation (14) with , where it was designed using kinetic plus potential energies. (b) Time derivative of Lyapunov function of Equation (21), where we could confirm whether the closed-loop control system is being stable. (c) and were expressed with the proposed update rule Equation (26). We could confirm that the first sufficient condition of Equation (12) was satisfied. (d) Second sufficient condition, that is, of Equation (13), where we could confirm that Equation (13) was satisfied even though the impedance parameters of and (its time derivative ) were changed according to the joint configuration. (e) External force N applied to the x-axis, alternatively backward and forward with 0.25 s intervals. (f) External joint torques obtained by Equation (7). (g) Velocity error of the each joint. (h) Position error of each joint.
Extension to 6-DoFs Manipulator
The planar two-link manipulator simulation is extended to the 6-DoFs spatial manipulator in this section. For the consistency, we keep the same design procedures as introduced in the previous section, for example, and . Thus, the lower bound of linear combination of and D becomes equal to Equation (38). The initial gains are chosen for simplicity as follows;
where is an identity matrix. The simulation was conducted using the Gazebo in the ROS (Robot Operating System) environment. The Neuromeka Indy5 was selected for the simulation model, because Indy5 is a commonly used 6-DoFs manipulator like UR5, KUKA-series. A ball-shaped load model was attached to the end-effector of the manipulator to generate the external force. The mass of the load model was assumed to be 5 kg for simulation conditions similar to the two-link manipulator. Also, the force/torque sensor was attached to obtain the force data generated from the ball-shaped load.
Figure 4 shows snapshots regarding the simulation progress. For simplicity, all the desired joint angles are set to be the same values in response to the target posture changes. The initial posture was upright with , for , the first target was given by at the instant of 5 s, the second target by at the instant of 10 s, and finally, the target was changed into the initial upright at the instant of 15 s. Figure 5 shows the data plots during the simulation suggested in Figure 4. The behavior of the robotic manipulator was evaluated in the viewpoint of the Lyapunov function and the sufficient conditions suggested in Equations (12) and (13) as main contributions. The data plots were represented similarly to those of the previous two-link manipulator simulation. The Lyapunov function composed of total energy could not go to zero (equilibrium) as observed in Figure 5a when the external force was applied. Also, it is noted that the Lyapunov function value was abruptly increased at the instants of target changes. The time derivative of the Lyapunov function shown in Figure 5b was used to validate the stability of the closed-loop control system. The update rule for the stiffness matrix of Equation (26) was applied as the manner suggested in Theorem 3. If the joint velocity error exceeds the preset limit , the update rule was activated. It could be confirmed by comparing the joint velocity error of Figure 5f and the stiffness matrix profiles of Figure 5c. It was evident that the error states of the control system remain stable (bounded) even though the stiffness matrix is time-varying. In other words, the closed-loop control system was maintained to be ISS, even when the stiffness matrix was changed.
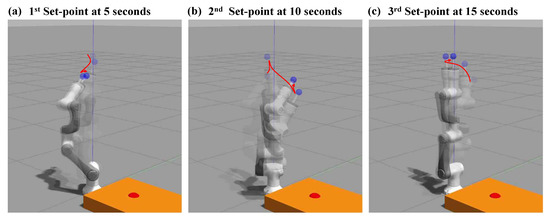
Figure 4.
Snapshots of simulation result according to time progress, where the robotic manipulator used in the simulation is Neuromeka Indy5 having 6-DoFs. The ball-shaped load model denoted by a blue color provides the external force to the manipulator. The initial posture was upright, and, first target was given by for all joints at the instant of 5 s, and then the target was changed into at the instant of 10 s, and finally, the target was recovered to the initial upright posture at the instant of 15 s.

Figure 5.
Simulation data while performing the simulation suggested in Figure 4; (a) Lyapunov function value of Equation (14) with , where it was designed using kinetic plus potential energies. (b) Time derivative of Lyapunov function of Equation (21), where we could confirm whether the closed-loop control system is being stable. (c) and were expressed using the proposed update rule Equation (26). (d) Second sufficient condition, that is, of Equation (13), where we could confirm that Equation (13) was satisfied even though the impedance parameters of and (its time derivative ) were changed according to the joint configuration. (e) External joint torques obtained using Equation (7). (f) Velocity error of the each joint. (g) Position error of each joint.
5. Conclusions
The sufficient conditions for the ISS and the stiffness update rule were proposed in the paper. In summary, the time derivative of the stiffness matrix was upper-bounded by the size of the stiffness matrix itself and lower-bounded by the size of the time derivative of the inertia matrix, respectively. The sufficient conditions of Equations (12) and (13) could guarantee the ISS of the variable impedance control even when the external force exists. Besides, the variable impedance control expressed by the Equation (6) does not require measuring the external force, although the stiffness update rule requires the use of joint torque sensor. As an alternative, the momentum observer [16] and external force observer [18] to estimate the external joint torques will be necessary.
The limitations of the proposed method are summarized as follows. The update rule for the damping matrix was not proposed. Modifying the Lyapunov function to suggest the damping update rule will be necessary for the whole system. An improved update rule for the stiffness and damping is our next goal. The selection of the impedance parameters such as stiffness and damping is still complicated because of the Equation (13) consists of the time derivative of the inertia matrix. Simplifying the sufficient conditions for the ISS will be one of our challenging works. Also, consideration of the model uncertainty of the dynamic parameters will be our future work. Further, experimental verification will be necessary for the near future.
Author Contributions
J.P. is a PhD student of Hanyang University and Y.C. is a Professor of Hanyang University. For this research article with two authors, conceptualization, J.P.; methodology, J.P.; software, J.P.; validation, J.P.; formal analysis, J.P.; investigation, J.P.; writing—original draft preparation, J.P.; writing—review and editing, Y.C.; visualization, J.P.; supervision, Y.C.; project administration, Y.C.; funding acquisition, Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Convergence Technology Development Program for Bionic Arm through the National Research Foundation of Korea funded by the Ministry of Science, ICT & Future Planning (NRF-2015M3C1B2052811), in part by the Technology Innovation Program (or Industrial Strategic Technology Development Program) (20001856, Development of robotic work control technology capable of grasping and manipulating various objects in everyday life environment based on multimodal recognition and using tools) funded By the Ministry of Trade, Industry & Energy(MOTIE, Korea), Republic of Korea.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hogan, N. Impedance control—An approach to manipulation. J. Dyn. Syst. Meas. Contr. 1985, 107, 8–16. [Google Scholar] [CrossRef]
- Colgate, J.E.; Hogan, N. Robust control of dynamically interacting systems. Int. J. Control 1988, 48, 65–88. [Google Scholar] [CrossRef]
- Calinon, S.; Sardellitti, I.; Caldwell, D.G. Learning-based control strategy for safe human-robot interaction exploiting task and robot redundancies. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 249–254. [Google Scholar]
- Ikeura, R.; Inooka, H. Variable impedance control of a robot for cooperation with a human. In Proceedings of the 1995 IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995; pp. 3097–3102. [Google Scholar]
- Ficuciello, F.; Villani, L.; Siciliano, B. Variable impedance control of redundant manipulators for intuitive human-robot physical interaction. IEEE Trans. Rob. 2015, 31, 850–863. [Google Scholar] [CrossRef]
- Ferraguti, F.; Secchi, C.; Fantuzzi, C. A tank-based approach to impedance control with variable stiffness. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 4948–4953. [Google Scholar]
- Kronander, K.; Billard, A. Stability Considerations for Variable Impedance Control. IEEE Trans. Rob. 2016, 32, 1298–1305. [Google Scholar] [CrossRef]
- Sontag, E.D.; Wang, Y. On characterizations of the input-to-state stability property. Syst. Control Lett. 1995, 24, 351–359. [Google Scholar] [CrossRef]
- de Wit, C.C.; Siciliano, B.; Bastin, G. Theory of Robot Control; Springer Science &lBusiness Media: London, UK, 2012. [Google Scholar]
- Ghorbel, F.; Srinivasan, B.; Spong, M.W. On the positive definiteness and uniform boundedness of the inertia matrix of robot manipulators. In Proceedings of the 32nd IEEE Conference on Decision and Control, San Antonio, TX, USA, 15–17 December 1993; pp. 1103–1108. [Google Scholar]
- Choi, Y.; Chung, W.K.; Suh, I.H. Performance and H∞ optimality of PID trajectory tracking controller for Lagrangian systems. IEEE Trans. Robot. Autom. 2001, 17, 857–869. [Google Scholar] [CrossRef]
- Choi, Y.; Chung, W.K. PID Trajectory Tracking Control for Mechanical Systems; Springer Science & Business Media: New York, NY, USA, 2004; Volume 298. [Google Scholar]
- Dubey, R.V.; Chan, T.F.; Everett, S.E. Variable damping impedance control of a bilateral telerobotic system. IEEE Control Syst. 1997, 17, 37–45. [Google Scholar]
- He, W.; Dong, Y.; Sun, C. Adaptive Neural Impedance Control of a Robotic Manipulator With Input Saturation. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 334–344. [Google Scholar] [CrossRef]
- Tsumugiwa, T.; Yokogawa, R.; Hara, K. Variable impedance control with regard to working process for man-machine cooperation-work system. In Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems, Maui, HI, USA, 29 October–3 November 2001; Volume 3, pp. 1564–1569. [Google Scholar]
- Garofalo, G.; Mansfeld, N.; Jankowski, J.; Ott, C. Sliding Mode Momentum Observers for Estimation of External Torques and Joint Acceleration. In Proceedings of the 2019 IEEE International Conference on Robotics and Automation, Montreal, QC, Canada, 20–24 May 2019; pp. 6117–6123. [Google Scholar]
- Mulero-MartÍnez, J.I. Uniform Bounds of the Coriolis/Centripetal Matrix of Serial Robot Manipulators. IEEE Trans. Robot 2007, 23, 1083–1089. [Google Scholar] [CrossRef]
- Ishihara, M.; Ito, K.; Inuzuka, K. Force sensorless power assist control using operation force observer for nursing lift. In Proceedings of the 2015 IEEE International Conference on Mechatronics (ICM), Nagoya, Japan, 6–8 March 2015; pp. 216–221. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).