Regressed Terrain Traversability Cost for Autonomous Navigation Based on Image Textures
Abstract
1. Introduction
1.1. Background
1.2. Related Works on Unsupervised Learning Approaches to Traversability Prediction
1.3. Objective and Approach
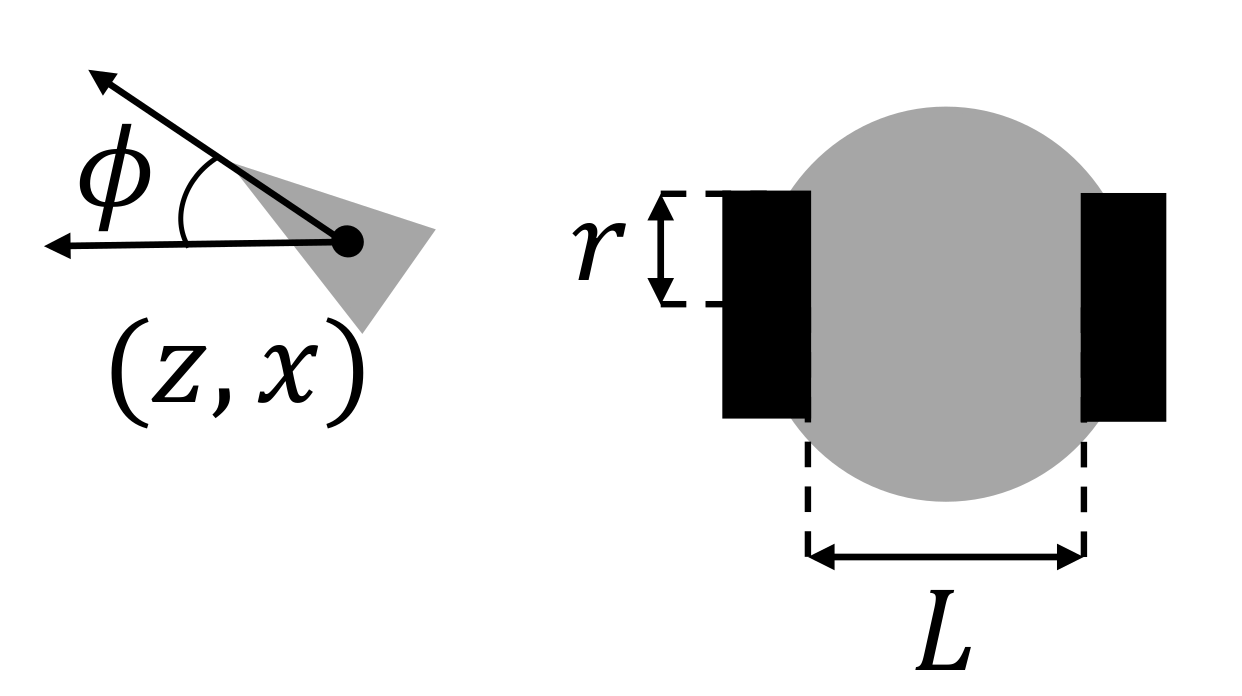
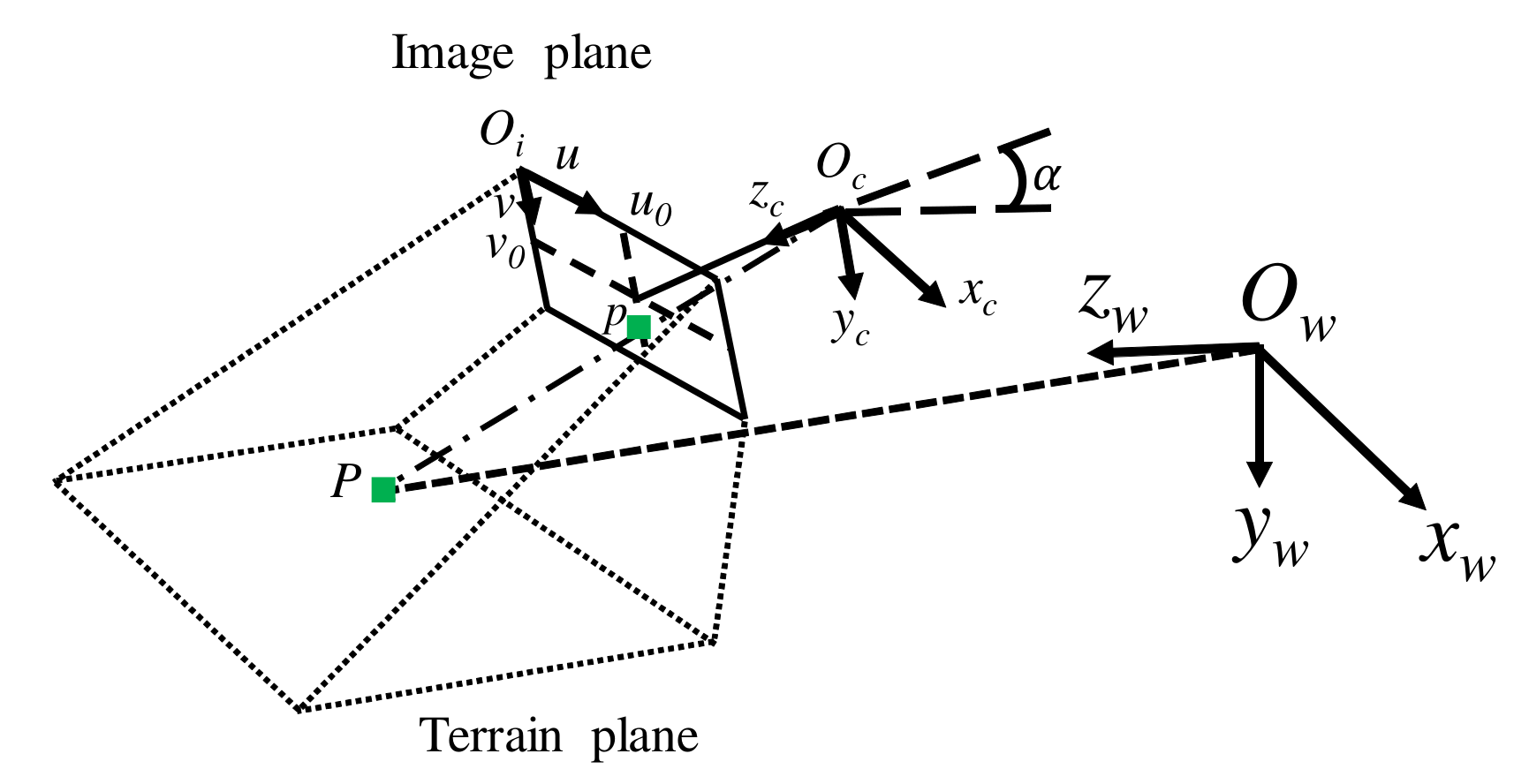
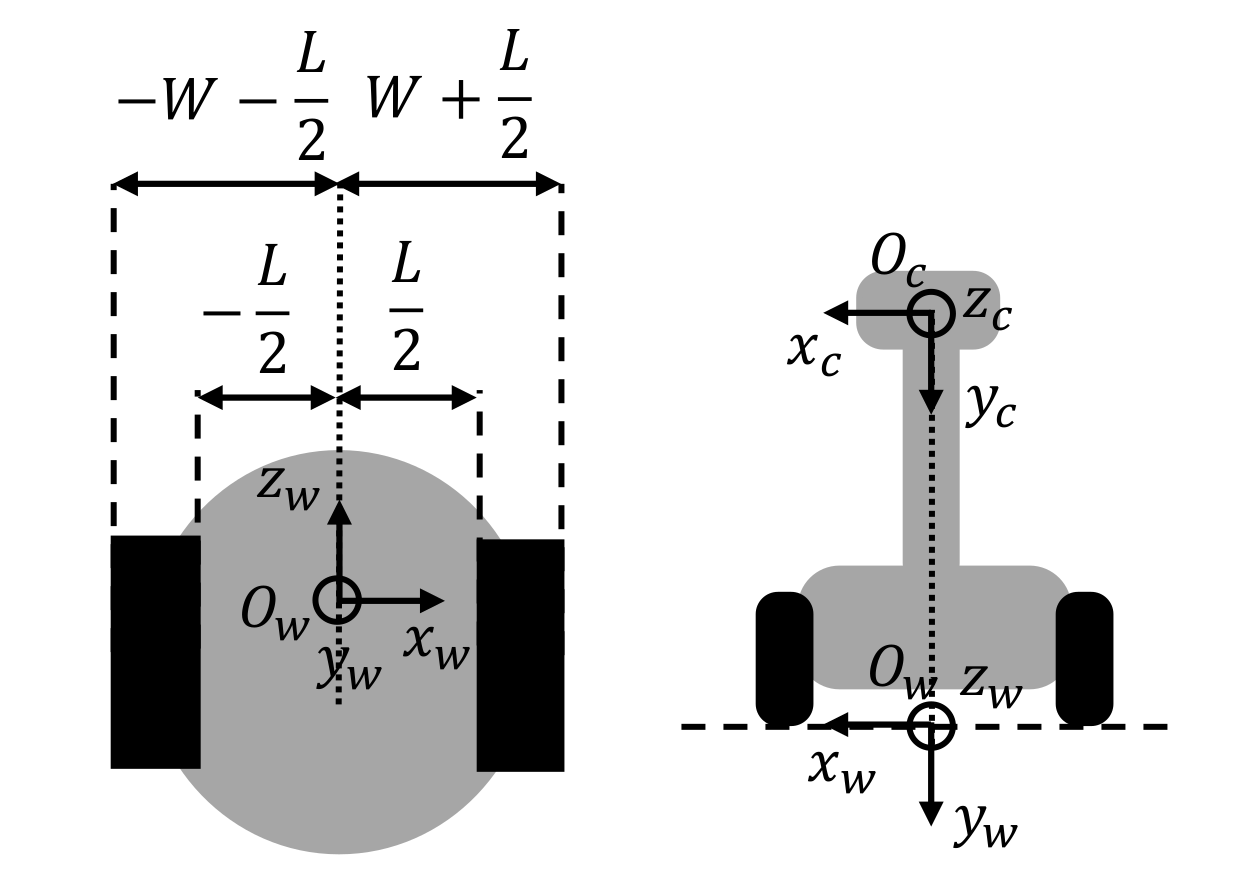
2. Problem Definition
3. Traversability Cost Prediction
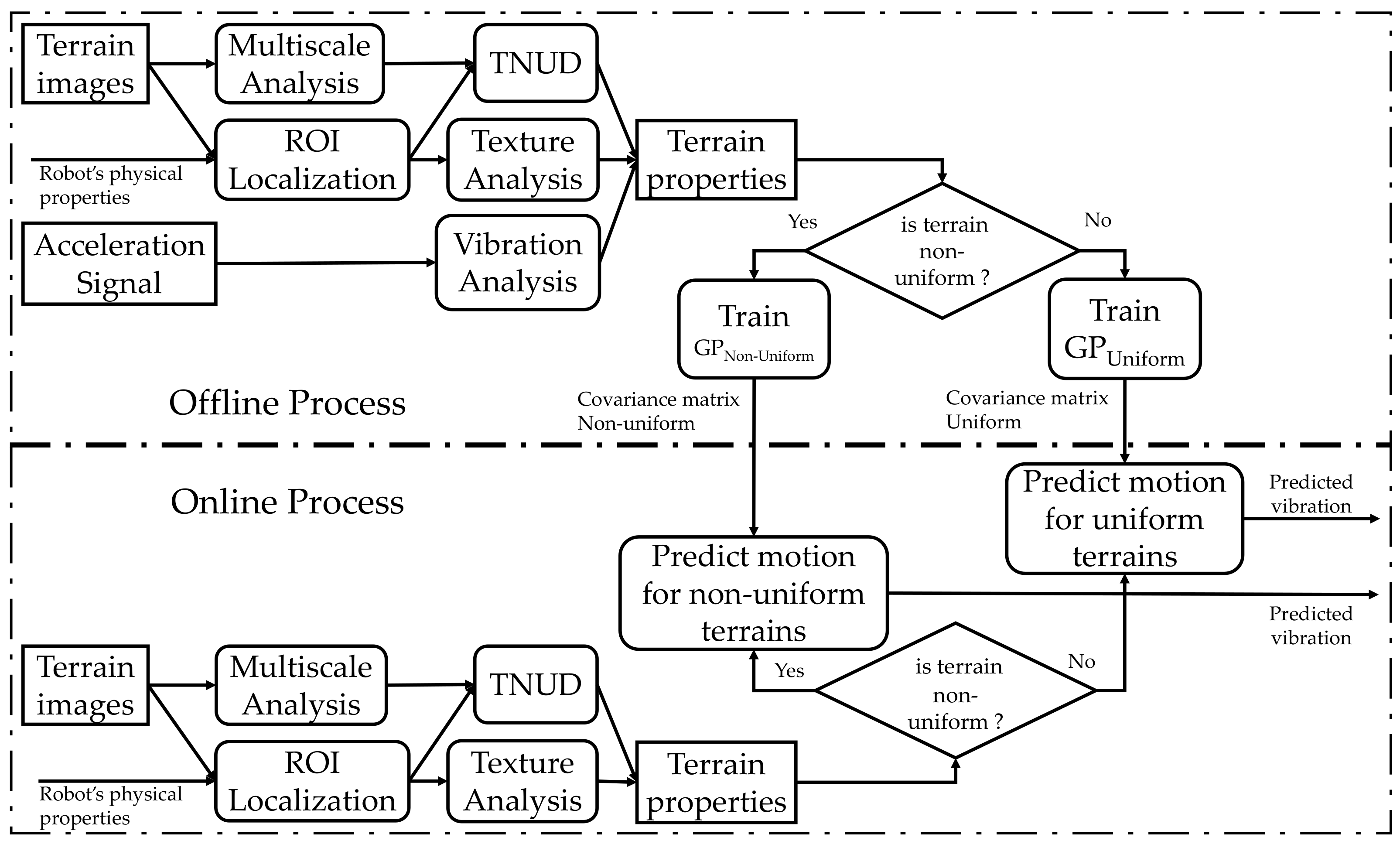
3.1. Algorithm Architecture–Overview
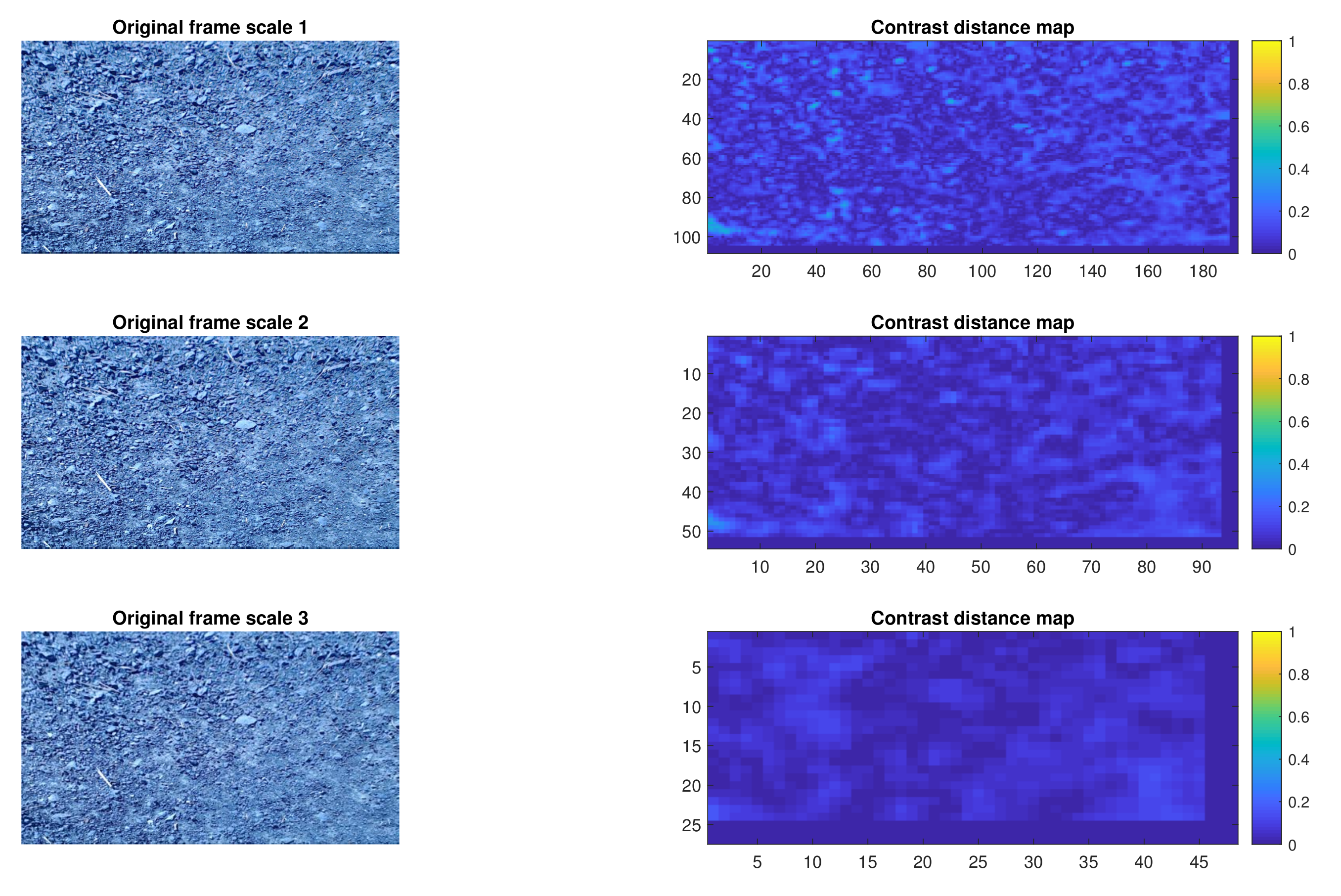
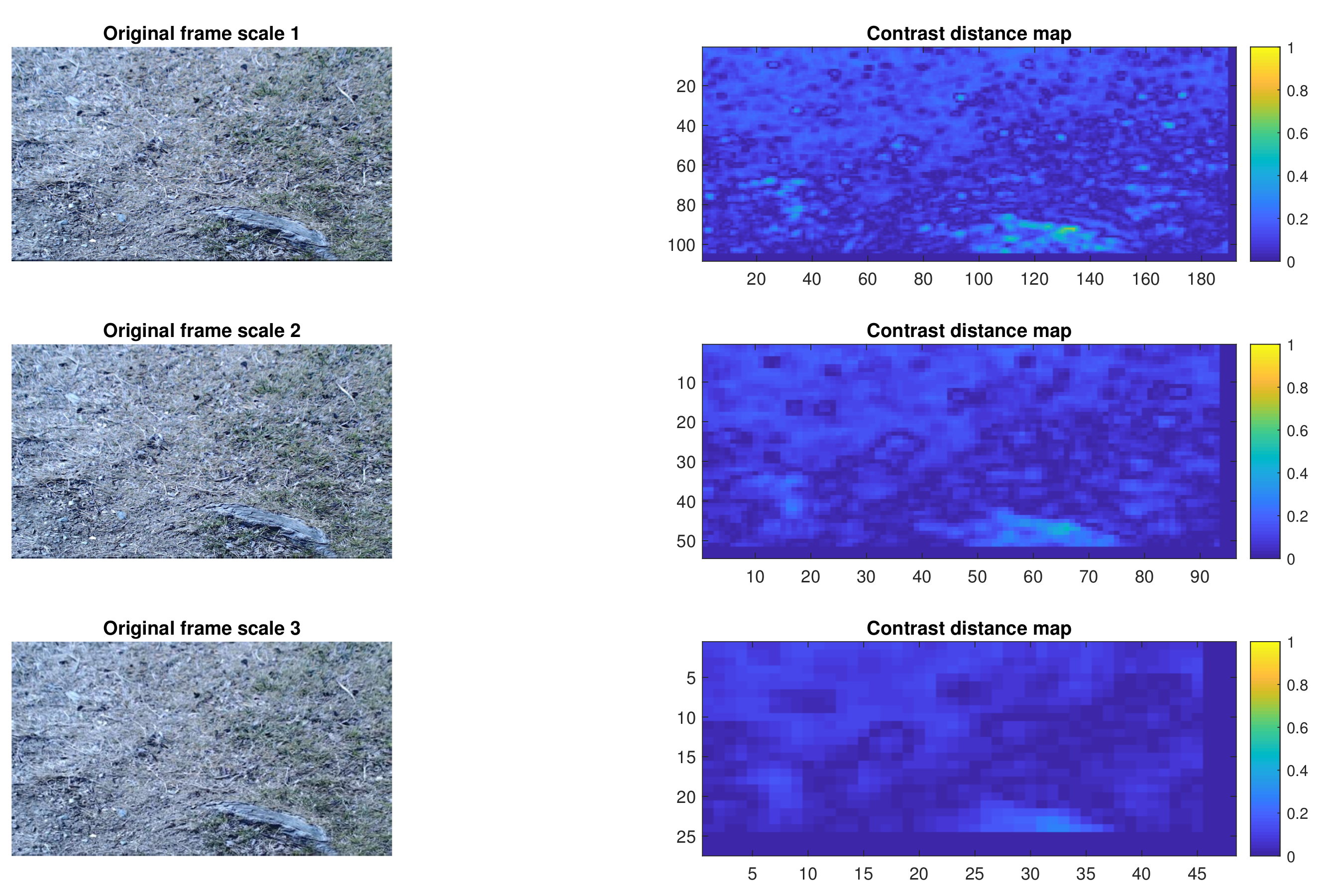
3.2. Terrain Non Uniformity Detection-Region Extraction
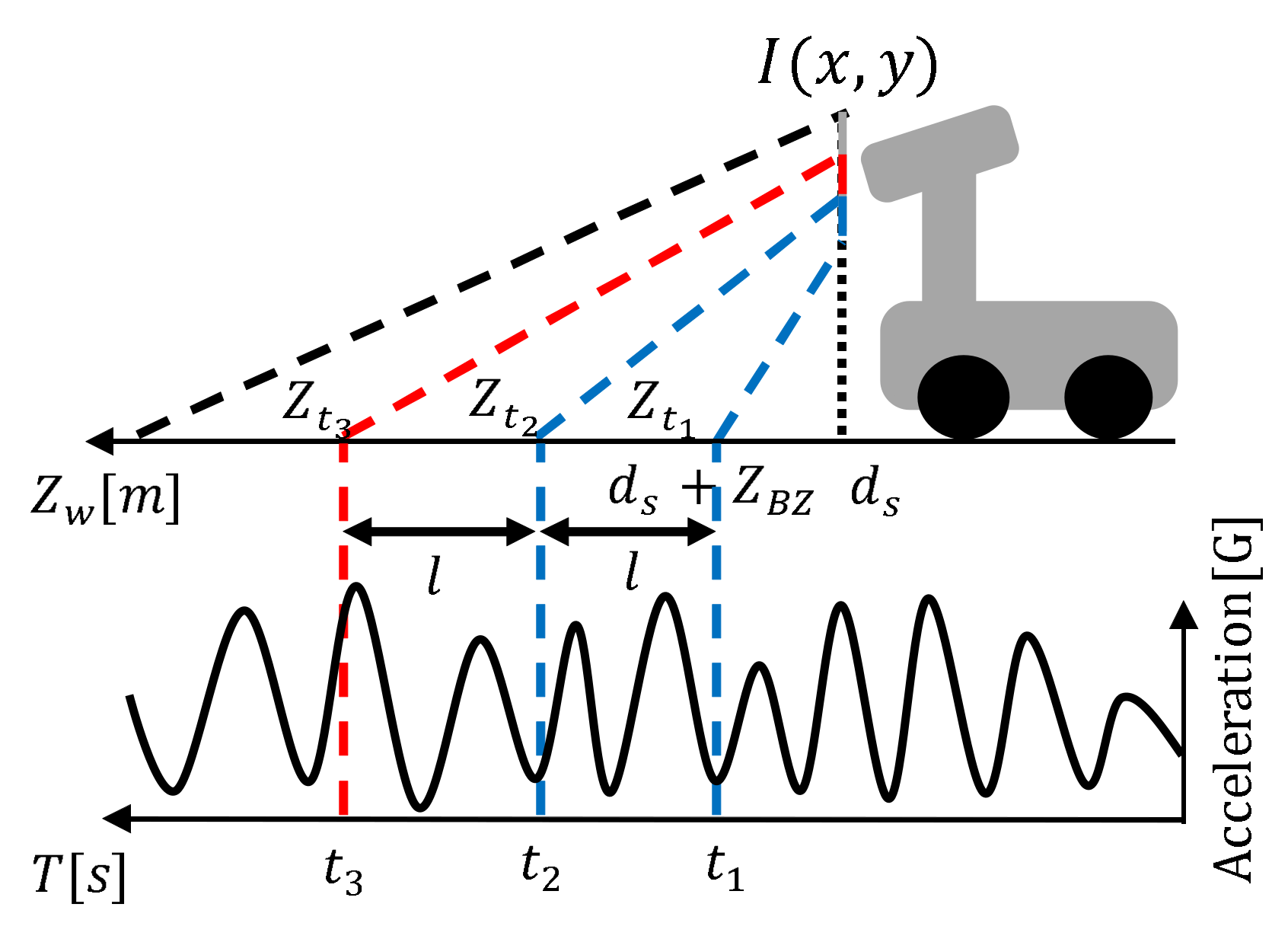
3.3. Texture and Vibration Features Extraction/Association
3.4. Traversability Cost Regression using Gaussian Process (GP)
4. Experiment and Results
4.1. Experimental Settings
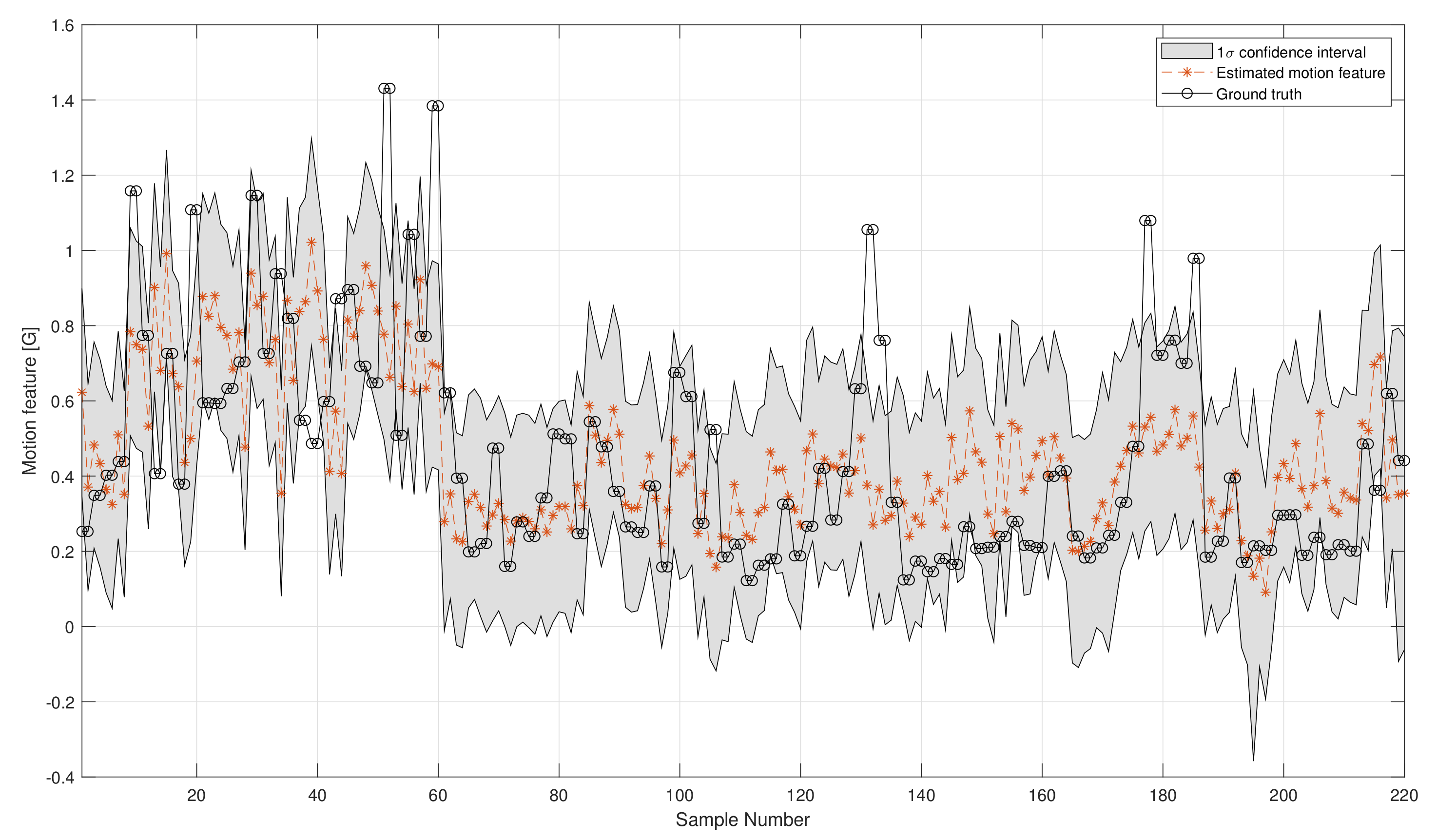
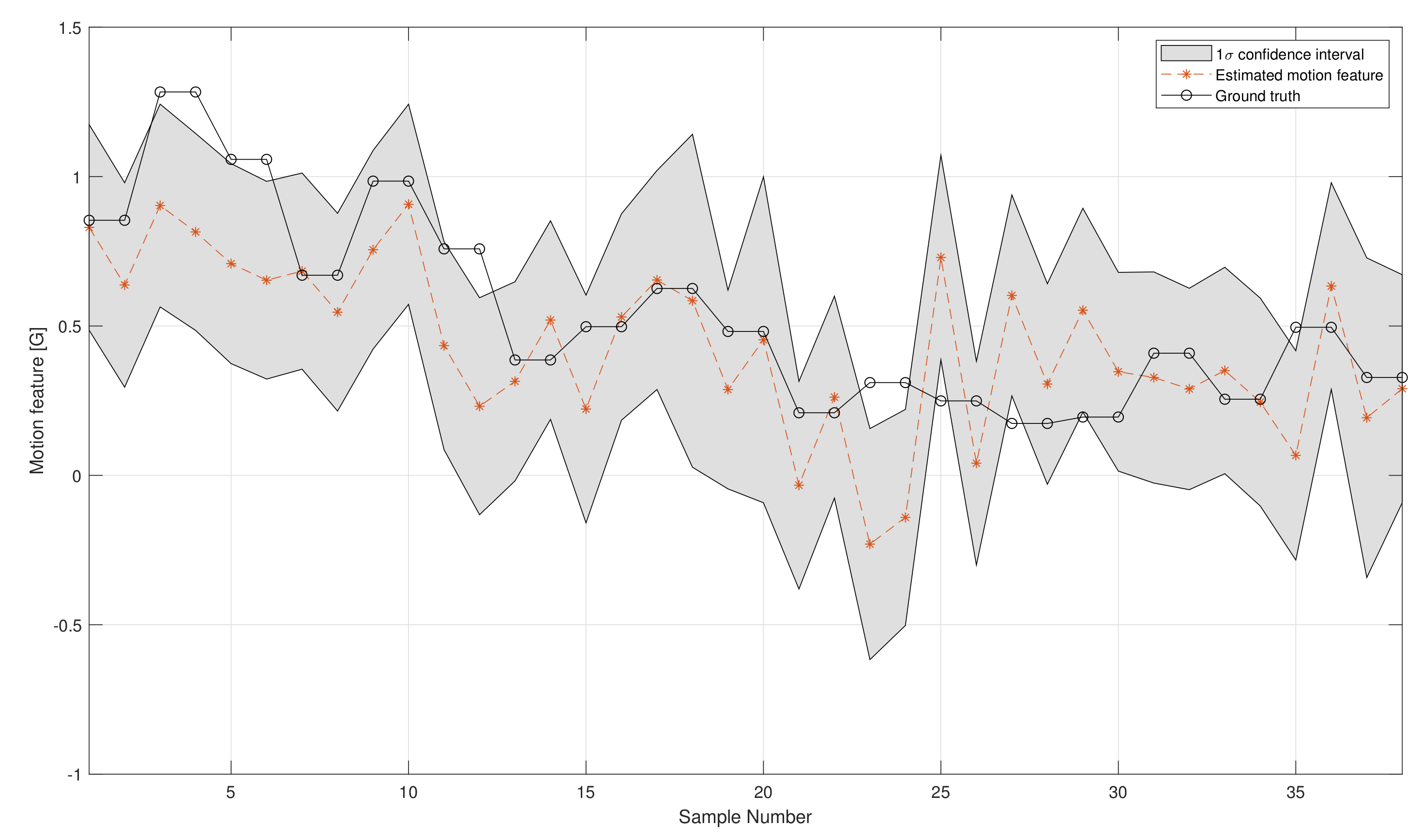
4.2. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sancho-Pradel, D.; Gao, Y. A survey on terrain assessment techniques for autonomous operation of planetary robots. J. Br. Interplanet. Soc. 2010, 63, 206–217. [Google Scholar]
- Savkin, A.V.; Huang, H. Proactive Deployment of Aerial Drones for Coverage over Very Uneven Terrains: A Version of the 3D Art Gallery Problem. Sensors 2019, 19, 1438. [Google Scholar] [CrossRef] [PubMed]
- Nagatani, K. Recent Trends and Issues of Volcanic Disaster Response with Mobile Robots. J. Robot. Mechatron. 2014, 26, 436–441. [Google Scholar] [CrossRef]
- Zhou, F.; Arvidson, R.E.; Bennett, K.; Trease, B.; Lindemann, R.; Bellutta, P.; Iagnemma, K.; Senatore, C. Simulations of Mars Rover Traverses. J. Field. Robot. 2014, 31, 141–160. [Google Scholar] [CrossRef]
- Mazhar, H.; Heyn, T.; Pazouki, A.; Melanz, D.; Seidl, A.; Bartholomew, A.; Tasora, A.; Negrut, D. CHRONO: A parallel multi-physics library for rigid-body, flexible-body, and fluid dynamics. Mech. Sci. 2013, 4, 49–64. [Google Scholar] [CrossRef]
- Cunningham, C.; Ono, M.; Nesnas, I.; Yen, J.; Whittaker, W.L. Locally-adaptive slip prediction for planetary rovers using Gaussian processes. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5487–5494. [Google Scholar]
- Hong, T.; Chang, T.; Rasmussen, C.; Shneier, M. Road detection and tracking for autonomous mobile robots. In Proceedings of the SPIE Aeroscience Conference 2002, Orlando, FL, USA, 1–5 April 2002. [Google Scholar]
- Manduchi, R.; Castano, A.; Talukder, A.; Matthies, L. Obstacle detection and terrain classification for autonomous off-road navigation. Auton. Robot. 2003, 18, 81–102. [Google Scholar] [CrossRef]
- Suger, B.; Steder, B.; Burgard, W. Traversability analysis for mobile robots in outdoor environments: A semi-supervised learning approach based on 3D-lidar data. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 3941–3946. [Google Scholar]
- Stavens, D.; Thrun, S. A self-supervised terrain roughness estimator for off-road autonomous driving. In Proceedings of the UAI’06, the Twenty-Second Conference on Uncertainty in Artificial Intelligence, Cambridge, MA, USA, 13–16 July 2006; pp. 469–476. [Google Scholar]
- Ho, K. A Near-to-Far Non-Parametric Learning Approach for Estimating Traversability in Deformable Terrain. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 2827–2833. [Google Scholar]
- Krebs, A.; Pradalier, C.; Siegwart, R. Adaptive rover behavior based on online empirical evaluation: Rover-terrain interaction and near-to-far learning. J. Field. Robot. 2010, 27, 158–180. [Google Scholar] [CrossRef]
- Castelnovi, M.; Arkin, R.; Collins, T. Reactive speed control system based on terrain roughness detection. In Proceedings of the International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 891–896. [Google Scholar]
- Papadakis, P. Terrain traversability analysis methods for unmanned ground vehicles: A survey. Eng. Appl. Artif. Intel. 2013, 26, 1373–1385. [Google Scholar] [CrossRef]
- Chilian, A.; Hirschmuller, H. Stereo camera based navigation of mobile robots on rough terrain. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 4571–4576. [Google Scholar]
- Hadsell, R.; Sermanet, P.; Ben, J.; Erkan, A.; Scoffier, M.; Kavukcuoglu, K.; Muller, U.; LeCun, Y. Learning long-range vision for autonomous off-road driving. J. Field Robot. 2009, 26, 120–144. [Google Scholar] [CrossRef]
- Labayrade, R.; Gruyer, D.; Royere, C.; Perrollaz, M.; Aubert, D. Obstacle Detection Based on Fusion Between Stereovision and 2D Laser Scanner. Mob. Robot. Percept. Navig. 2007. [Google Scholar] [CrossRef]
- Lalonde, J.-F.; Vandapel, N.; Huber, D.F.; Hebert, M. Natural terrain classification using three-dimensional ladar data for ground robot mobility. J. Field. Robot. 2006, 23, 839–861. [Google Scholar] [CrossRef]
- Bellutta, P.; Manduchi, R.; Matthies, L.; Owens, K.; Rankin, A. Terrain perception for DEMO III. In Proceedings of the IEEE Intelligent Vehicles Symposium 2000 (Cat. No.00TH8511), Dearborn, MI, USA, 5 October 2000; pp. 326–331. [Google Scholar]
- Brooks, C.A.; Iagnemma, K.D. Self-Supervised Classification for Planetary Rover Terrain Sensing. In Proceedings of the 2007 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2007; pp. 1–9. [Google Scholar]
- Brooks, C.; Iagnemma, K.; Dubowsky, S. Vibration-based Terrain Analysis for Mobile Robots. In Proceedings of the IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 3415–3420. [Google Scholar]
- Otsu, K.; Ono, M.; Fuchs, T.J.; Baldwin, I.; Kubota, T. Autonomous Terrain Classification With Co- and Self-Training Approach. IEEE Robot. Autom. Lett. 2016, 1, 814–819. [Google Scholar] [CrossRef]
- Ho, K.; Peynot, T.; Sukkarieh, S. Nonparametric Traversability Estimation in Partially Occluded and Deformable Terrain. J. Field Robot. 2016, 33, 1131–1158. [Google Scholar] [CrossRef]
- Bekhti, M.A.; Kobayashi, Y. Prediction of Vibrations as a Measure of Terrain Traversability in Outdoor Structured and Natural Environments. In Proceedings of the PSIVT 2015 Image and Video Technology, Auckland, New Zealand, 23–27 November 2015; pp. 282–294. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning (Adaptive Computation and Machine Learning); MIT Press: Cambridge, UK, 2006. [Google Scholar]
- Howard, A.; Turmon, M.; Matthies, L.; Tang, B.; Angelova, A.; Mjolsness, E. Towards learned traversability for robot navigation: From underfoot to the far field. Field Robot. 2006, 23, 1005–1017. [Google Scholar] [CrossRef]
- Chavez-Garcia, R.O.; Guzzi, J.; Gambardella, L.M.; Giusti, A. Learning Ground Traversability From Simulations. IEEE RA-L 2018, 3, 1695–1702. [Google Scholar] [CrossRef]
- Metka, B.; Franzius, M.; Bauer-Wersing, U. Outdoor Self-Localization of a Mobile Robot Using Slow Feature Analysis. In Proceedings of the ICONIP 2013 International Conference on Neural Information Processing, Daegu, Korea, 3–7 November 2013; pp. 249–256. [Google Scholar]
- Ordonez, C.; Collins, E.G. Rut Detection for Mobile Robots. In Proceedings of the SSST 2008 40th Southeastern Symposium on System Theory, New Orleans, LA, USA, 16–18 March 2008; pp. 334–337. [Google Scholar]
- Collier, J.; Ramirez-Serrano, A. Environment Classification for Indoor/Outdoor Robotic Mapping. In Proceedings of the CRV 2009 Canadian Conference on Computer and Robot Vision, Kelowna, BC, Canada, 25–27 May 2009; pp. 276–283. [Google Scholar]
- Chandler, D.M.; Vu, C.T. Main subject detection via adaptive feature refinement. J. Electron. Imaging 2011, 20, 013011. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Costa, A.F.; Humpire-Mamani, G.; Traina, A.J.M. An efficient algorithm for fractal analysis of textures. In Proceedings of the 25th SIBGRAPI Conference on Graphics, Patterns and Images, Ouro Preto, Brazil, 22–25 August 2012; pp. 39–46. [Google Scholar]
- Liao, P.; Chen, T.; Chung, P. A fast algorithm for multilevel thresholding. J. Inf. Sci. Eng. 2001, 17, 713–727. [Google Scholar]
- Bekhti, M.A.; Kobayashi, Y.; Matsumura, K. Terrain traversability analysis using multi-sensor data correlation by a mobile robot. In Proceedings of the 2014 IEEE/SICE International Symposium on System Integration, Tokyo, Japan, 13–15 December 2014; pp. 615–620. [Google Scholar]
- Matsumura, K.; Bekhti, M.A.; Kobayashi, Y. Prediction of motion over traversable obstacles for autonomous mobile robot based on 3D reconstruction and running information. In Proceedings of the ICAM 2015 International Conference on Advanced Mechatronics, Tokyo, Japan, 5–8 December 2015. [Google Scholar]





| Mean | Standard Deviation | SNR |
|---|---|---|
| 1.0346 | 0.0101 | 102.6474 |
| 1.0339 | 0.0102 | 101.5350 |
| 1.0250 | 0.0096 | 106.7354 |
| 1.0335 | 0.0099 | 104.2580 |
| Application of TNUD | Uniform terrains | 0.2373 |
|---|---|---|
| Non-uniform terrains | 0.268 | |
| Non-application of TNUD | - | 0.3567 |
| Application of TNUD | Uniform terrains | 0.4640 |
|---|---|---|
| Non-uniform terrains | 0.4419 | |
| Non-application of TNUD | - | 0.6048 |
| Process | Computation Time |
|---|---|
| Multiscale analysis–contrast distance scale 1 | 880 ms |
| Multiscale analysis–contrast distance scale 2 | 200 ms |
| Multiscale analysis–contrast distance scale 3 | 47 ms |
| Multiscale analysis–fusion (refined contrast distance map) | 2.2 ms |
| Texture extraction | 67 ms |
| Motion feature | 47 μs |
| Prediction for non-uniform terrains | 100 ms |
| Predictor for uniform terrains | 22 ms |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bekhti, M.A.; Kobayashi, Y. Regressed Terrain Traversability Cost for Autonomous Navigation Based on Image Textures. Appl. Sci. 2020, 10, 1195. https://doi.org/10.3390/app10041195
Bekhti MA, Kobayashi Y. Regressed Terrain Traversability Cost for Autonomous Navigation Based on Image Textures. Applied Sciences. 2020; 10(4):1195. https://doi.org/10.3390/app10041195
Chicago/Turabian StyleBekhti, Mohammed Abdessamad, and Yuichi Kobayashi. 2020. "Regressed Terrain Traversability Cost for Autonomous Navigation Based on Image Textures" Applied Sciences 10, no. 4: 1195. https://doi.org/10.3390/app10041195
APA StyleBekhti, M. A., & Kobayashi, Y. (2020). Regressed Terrain Traversability Cost for Autonomous Navigation Based on Image Textures. Applied Sciences, 10(4), 1195. https://doi.org/10.3390/app10041195





