Abstract
In the triangular meshes obtained in additive repair, it is a challenge to find one single hole-filling method to close all holes and make the filling patches assort with surrounding meshes well with low time complexity, which is mainly caused by the shape complexity and size difference of the various holes, especially in the fields of intelligent manufacturing, 3D measurement, and reverse engineering. Therefore, it is reasonable to adopt different algorithms to fill different types of holes. In this research, a fast hole-filling method for triangular mesh is proposed based on the hole size. First, a group of basic concepts is defined to make them uniform throughout the whole text, followed by the descriptions of hole detection and boundary cleaning. Second, three different algorithms are developed to fill the small-sized, middle-sized, and large-sized holes classified by hole size respectively, which can fill all the detected holes in a fast and proper manner. Finally, two experiments are carried out to verify the efficiency, robustness, and ability to recover the shape of our method. Compared to two state-of-the-art hole-filling methods in the first experiment, the quantitative evaluation results demonstrate that our proposed method is much faster than them with the ability to guarantee the regularity of most filling triangles. The second experiment proves that our method can produce satisfactory filling results by making the filling patches be compatible with surrounding meshes well.
1. Introduction
With the rapid development of three-dimensional (3D) printing and 3D scanning technologies, additive manufacturing repair, as a typical cost-saving, digital, and intelligent manufacturing method, has been widely used to extend the damaged parts’ lifespan in the fields of mechanical manufacturing, emergency rescuing, biomedical engineering, etc. [1]. However, the traditional manual repair is typically time-consuming and labor intensive, and also generates inconsistent quality [2]. Effective and automatic repair for defective parts is of significant importance. A typical repair process consists of three stages: 3D surface reconstruction, digital geometry processing, and 3D printing repair. With the aid of computer vision and digital image processing technologies, the 3D optical scanning devices can be used to capture the surface model of the damaged parts in form of 3D point cloud. By comparing the nominal and scanning models, the missing area contained in the worn part can be identified and positioned. The nominal model actually refers to the initial CAD model which represents its original geometric shape. Due to the self-contained limitations of 3D scanning devices and the occlusion between the physical object and the used scanner, the measured 3D point cloud is usually incomplete, which may result in several holes after the point cloud triangulation. Besides, some triangular mesh processing algorithms may also cause a small number of holes in their outputs, such as defect repair. The existence of holes in mesh decreases the performance of the downstream mesh processing algorithms, e.g., mesh alignment, Boolean operation, which may introduce some illness problems or result in processing failure. On the other hand, incomplete triangular meshes may lead to poor visualization effects.
Although many hole-filling techniques have been proposed in the last two decades [3,4], most of them are originally designed to handle one or fewer types of holes. For example, to repair the mesh holes generated by the Poisson surface reconstruction algorithm towards 3D printing, Sheng et al. proposed an iterative postprocessing algorithm for partial differential equation (PDE) patch generation based on biharmonic-like four-order PDEs [5]. However, this method seems to be complicated and time-consuming. Due to the variety of hole size, it is still a challenge to adopt one single algorithm to fill all holes quickly while ensuring the filling patches to assort with the surrounding meshes well, especially in additive manufacturing repair. In the case of small-sized holes, the missing shapes are usually small and will not affect the completeness of the whole mesh. Instead of using one complex algorithm to close the small-sized holes, a fast and simple hole-filling method is desirable. As for middle-sized holes, they usually account for a large proportion of the total number of holes occurring in one mesh. To make the resulting mesh as close to the original mesh as possible, the missing regions must not only be filled but also ensure the shapes of the filling patches are compatible with surrounding meshes well. Hence, efficiency and the ability to shape recovery for the missing regions are two important factors that need to be considered. Regarding large-sized holes, the size of the hole boundary vertices is greater than that of middle-sized holes. The hole-filling processing may be heavily time-consuming if a traditional technique is applied, such as the minimum area triangulation [6], so how to close large-sized holes fastly has become a hot research topic in additive repair.
The goal of this work is to provide a fast hole-filling method for triangular mesh based on hole size, especially towards the additive manufacturing repair. The developed method is efficient, robust, and has the ability to recover the geometric shapes of the missing regions when closing holes. Our method can be used in the fields of 3D geometry measurement, geometry modeling, intelligent manufacturing as well as additive repair, etc. The developed approach consists of two main stages: preprocessing and hole-filling. In the first stage, a group of basic concepts is defined, followed by hole detection and boundary cleaning. In the second stage, three different hole-filling algorithms are discussed in detail, which are then used to fill three types of holes classified according to hole size.
The main contributions of this work are given as follows:
- 1
- A robust and efficient hole-filling method is proposed. In most cases, each hole occurring in one mesh can be automatically assigned a proper hole-filling algorithm based on hole size, which can not only produce satisfactory hole-filling results but also achieve a good balance between the efficiency and filling quality.
- 2
- A fast and shape-recovery hole-filling algorithm for large-sized holes is developed. It can not only directly close large-sized holes without any further refinement and fairing steps, but also ensure that the filling patches are compatible with surrounding meshes well.
The rest of this paper is organized as follows: Section 2 briefly discusses the related work. The overview of our method is presented in Section 3. Section 4 shows the preliminaries. The fast hole-filling method is discussed in Section 5. Experimental results and discussion are given in Section 6, followed by the conclusion in Section 7.
2. Related Work
2.1. Additive Manufacturing Repair
In recent years, a great improvement in 3D scanning techniques contributes to the 3D point cloud-based surface reconstruction. However, due to the occlusion between the scanner and the object, as well as the low reflectance of the object surface, the measured point cloud usually includes many holes which would weaken the ability of post-processing and visual effects of triangular mesh [3]. Besides, the Boolean difference for triangular mesh has been widely used to extract repair volume in additive repair. However, in most cases, the input meshes are required to be complete, i.e., without any holes. Gao et al. [7] presented current barriers, findings, and future trends significantly about additive manufacturing in engineering. Ngo et al. [8] also carried out a comprehensive review of the main 3D printing methods, materials and their development in additive repair. Wilso et al. [9] utilized a Boolean difference to yield a parameterized geometric representation of the repair volume and then applied the laser direct deposition to repair defective turbine blades. Feng et al. [10] developed a repair volume extraction method that integrates surface reconstruction and repair volume extraction in additive repair. Ding et al. [11] proposed an automatic multi-direction slicing algorithm to deal with components with a large number of holes by additive manufacturing. Li et al. [12] proposed a systematic framework to aid the reverse engineering-based additive repair process of worn parts, in which they utilized a Boolean operation to yield a parameterized geometric representation of the repair volume of two mesh models. Um et al. [13] applied a STEP-based numerical control (STEP0NC)-based process planning method in additive manufacturing for automating the derivation of the repair section. Feng et al. [14] proposed a method to predict and reconstruct an expected profile of the edge shape in adaptive machining. Zheng et al. [15] developed a hybrid method to repair damaged parts by using additive manufacturing techniques, which integrates coordinate measuring machine data collection, defective model regeneration, and decision marking for process selection for the repair. It can be seen that most of the existing methods focus on 3D measurement of damaged parts, repair volume extraction, machining process planning, and repair material development, etc. Therefore, it is necessary to develop an efficient and fast hole-filling algorithm to reduce the gap between the 3D geometry processing and additive manufacturing repair.
2.2. Hole-Filling
According to the work from Ju et al. [16], the hole-filling methods based on a triangular mesh can be classified into two groups: surface-based methods and volume-based methods. In most cases, the former operates directly on the given mesh and follows the same stages: hole detection, initial filling and refinement [4]. The latter converts the input mesh into a signed distance function over a volumetric grid to fill holes and then extracts a completed mesh from a zero-level set of the distance function [17]. Liepa et al. [6] described an approach to fill holes in unstructured triangular meshes by interpolating the shape and density of the surrounding mesh by taking into account the area and angle of triangles. Zhao et al. [18] proposed an advancing front hole-filling technique which generates an initial closure of the detected holes and then modified them by estimating the appropriate normal vectors, finally repositioned the 3D coordinates of each new vertex through the resolution of Poisson equations. In recent work, Wang et al. [19] devised a novel multi-scale geometry detail recovery algorithm for 3D surfaces based on Empirical Mode Decomposition (EMD). In the case of complex holes, they are first partitioned into sub-holes by feature curves extended from the existing parts, and then typical hole-filling methods can be performed on these sub-holes [20,21]. In cases of complex holes, Enkhbayar et al. [22] created a set of contour curves by shortening the flow of the boundary edges of the holes and then applied the Delaunay triangulation. There are some other non-polygonal methods which apply implicit functions to complete mesh surface, such as Radial Basis Functions (RBFs) [23], Moving Least Squares (MLS) [24], and Bezier surface [25]. To recover the missing geometry details [19], texture synthesis-based methods [26,27], exampled-based methods [28,29], context-based methods [17,30] have also been reported to fill holes while preserving features. For volume-based methods, Devis et al. [31] applied a diffusion process to fill holes, while Ju et al. [32] constructed an inside\outside volume using an octree grid and reconstructed a surface by contouring. Nooruddin et al. [33] applied a voxel-based method to simplify and repair mesh models by adopting open and close morphological operators. Guo et al. [34] introduced an oriented voxel global diffusion method to fill holes in complex surfaces. Centin et al. [35] employed a Poisson reconstruction step to generate an implicit function for completing the missing parts. Argudo et al. [36] presented an adaptive, multigrid algorithm for mesh completion in general and complex cases by using the Bi-Harmonic fields. The main advantage of volume-based methods is its robustness in resolving geometric errors, and the drawback is the loss of geometric detail. For more works, please refer to these two survey papers [3,4]. Based on the above analysis, fast hole-filling, especially for different sizes of holes, is still a challenge.
3. Overview
In this paper, a fast hole-filling method for triangular mesh based on hole size is proposed. The pipeline of our method is illustrated in Figure 1. The detected holes are classified into three categories based on the size of hole boundary vertices: small (), middle (), and large-sized holes (). For each type of holes, three different algorithms are used to fill them.
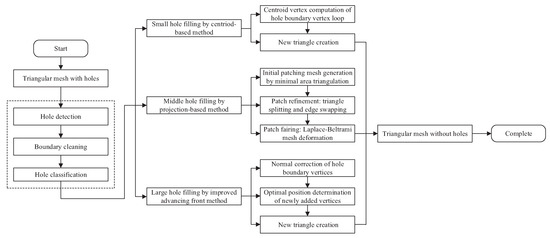
Figure 1.
The pipeline of our method.
First, a set of basic concepts are defined to make them uniform throughout the whole text. After that, the main steps of hole detection based on the check of boundary edges are briefly described. Next, a preprocessing step called boundary cleaning is applied to remove tooth faces for making the hole boundary cleaner.
Second, three different algorithms are developed to fill the small-sized, middle-sized, and large-sized holes respectively. In the case of small-sized holes, a centroid-based method is utilized to iteratively create new triangles by directly connecting each pair of two continuous hole boundary vertices and the centroid vertex of the hole loop. Regarding middle-sized holes, an initial filling patch is first generated by using the minimum area triangulation, then followed by patch refinement and patch fairing. The former is used to maintain a Delaunay-like triangulation by iterative triangle splitting and edge swapping, and the latter to make the filling patch assort with the surrounding mesh well via a Laplace-Beltrami mesh deformation technique. For large-sized holes, an improved advancing front method is used to close holes fastly without any further refinement and fairing steps, while ensuring the patching mesh to be compatible with the surrounding mesh well.
Third, two experiments are carried out to verify the efficiency, robustness, and shape-recovery ability of our method. Compared to the two state-of-the-art hole-filling methods in the first experiment, the quantitative evaluation results show that our technique is much faster and can guarantee most of the filling triangles are regular. The second experiment proves that our method can not only produce satisfactory filling results but also make the filling patches compatible with surrounding meshes well.
4. Preliminaries
4.1. Basic Concepts
As shown in Figure 2a, a triangular mesh is composed of a set of vertices and triangles, in which a boundary edge is an edge that only has one adjacent triangle, and a boundary vertex is a vertex that is adjacent to a boundary edge. In addition, all triangles and vertices who share one common vertex are called 1-ring triangles and 1-ring vertices respectively. In order to make the notations appeared in this paper uniform, a group of symbols are defined: is a vertex, is an edge from to , is a triangle with vertices (, , ) in counterclockwise order and its normal is , is a halfedge from to , and is the normal at vertex . In this work, a halfedge data structure of triangular mesh is adopted for quick query, as shown in Figure 2b, in which two triangles , share a common edge , so we call them as the adjacent triangles of . Since the startpoint of the edge is the same as the endpoint of , is regared as the next edge of . Similarly, its previous edge is the edge . Furthermore, two vectors and are defined as the halfedges of . This data structure enables us to efficiently and rapidly access its topological elements for one selected vertex or edge. Assuming that all mesh models used in this paper are manifold, and especially there are no islands inside the detected holes.
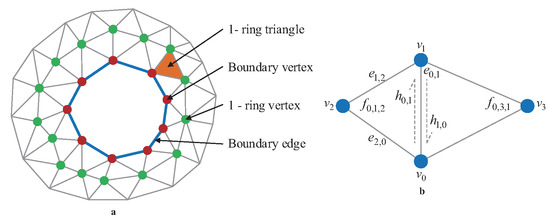
Figure 2.
Preliminaries. (a) Triangular mesh with a hole. (b) Halfedge data structure.
4.2. Hole Detection
The first step of hole-filling is to identify all the holes in one given incomplete model. A hole is usually a closed loop of boundary edges (see Figure 2a). As mentioned in Section 3, the holes are partitioned into three categories to make our hole-filling method faster and more robust when handling holes with different sizes. The specific process of hole identification is conducted as follows: given a seed boundary edge, its next boundary edge can be easily checked depending on the halfedge data structure. Then we proceed to identify the next boundary edge of the just detected next boundary edge. By repeating the same way, all boundary edges can be automatically detected by checking the number of their 1-ring triangles until a closed loop is reached.
4.3. Boundary Cleaning
In most cases, the boundary of one hole suffers from a few tooth faces, each of which contains at least two boundary edges, as shown in Figure 3a. The purpose of applying boundary cleaning is to remove these tooth faces that will introduce illness in the subsequent hole-filling procedures especially regarding the advancing front hole-filling algorithm [18], and to make the boundary curve of the hole smoother. The main steps of the cleaning process are as follows: first, the 2-ring adjacent faces of the hole boundary detected by using the previously described method are searched. Second, it will be removed if one face has been checked as a tooth one by iterating over the collected faces, as shown in Figure 3a,b. Next, the vertex-face topology of the remaining faces within the 2-ring range needs to be updated. Finally, in the same way, other new tooth faces can be removed and our method terminates without any new tooth faces being detected. After the boundary cleaning, the boundary curves of all identified holes become cleaner and smoother, as shown in Figure 3c.
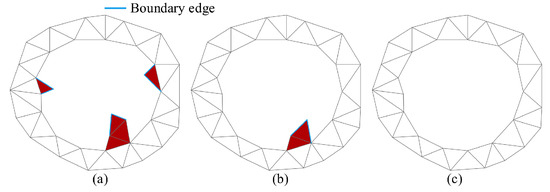
Figure 3.
Hole boundary cleaning. (a) Initially detected tooth faces in red color. (b) New tooth faces caused by the deletion of (a). (c) The final hole after boundary cleaning.
5. Hole Filling Based on Hole Size
5.1. Small-Sized Hole Filling by Centriod-Based Method
In the case of small-sized holes, since the number of hole boundary vertices is small and their boundary shapes are not complicated, the missing regions will not heavily affect the completeness of the whole mesh. Besides, fastly closing the small-sized holes can also make the filling patches assort with surrounding meshes well wherever they appear in flat or high curvature regions. Therefore, a fast and simple technique may be very reasonable for handling this type of holes instead of applying advanced hole-filling algorithms. In our work, a simple and fast algorithm named centroid-based method is utilized to fill small-sized holes, and the pseudocode is in the Algorithm 1. The hole-filling process is as follows: as shown in Figure 4a, there exists a closed loop including six boundary vertices , and the hole can be identified by using the method described in Section 4.2. Depending on these hole boundary vertices, their centroid vertex can be calculated, as shown in Figure 4b. For each pair of two continuous boundary vertices, they will be connected with to create a new triangle in counterclockwise order with oriented normal (see Figure 4c). By looping the rest of boundary vertices in the same way, the other five new triangles can be created. Therefore, the hole shown in Figure 4a is finally closed by inserting six newly created triangles.
| Algorithm 1 Small-sized hole filling |
Input: () Output:
|
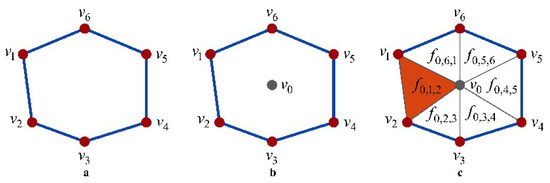
Figure 4.
Small-sized hole filling by centriod-based method. (a) Original hole. (b) The computed centroid vertex in gray color. (c) Newly created triangles.
5.2. Middle-Sized Hole Filling by Projection-Based Method
Since the majority of the holes occurring in one incomplete triangular mesh are middle-sized ones, the missing regions not only need to be fully closed but also should assort with surrounding meshes well after filling. Considering these facts, we hope to get a balance between the efficiency and the ability to shape recovery in the process of hole-filling. Therefore, the minimum area triangulation [6] and Laplace-Beltrami techniques are combined to achieve the initial filling and the deformation on the patching mesh respectively in this paper, specifically including three stages: initial triangulation, patch refinement, and patch fairing. The corresponding pseudocode is in the Algorithm 2.
| Algorithm 2 Middle-sized hole filling |
Input:() Output:
|
Initial triangulation The key idea of the minimum area triangulation is to create every single triangle by directly connecting three ones among all the hole boundary vertices. As shown in Figure 5, there is a hole with six boundary vertices (), and it is obvious that six filling schemes are available after looping all the boundary vertices. For each scheme, the total area of all filling triangles needs to be computed, and then these areas will be compared to find the smallest one. We assume that the scheme shown in Figure 5e has the smallest area, so the patching mesh of this scheme is finally chosen as the initial filling patch by using the minimum area triangulation. It can be seen that the filling efficiency of the minimum area triangulation is closely related to the size of the hole boundary vertices. This is the main reason why the minimum area triangulation is not suitable for filling large-sized holes.
where denotes the final filling patch, and denotes the area of a patch or triangle.
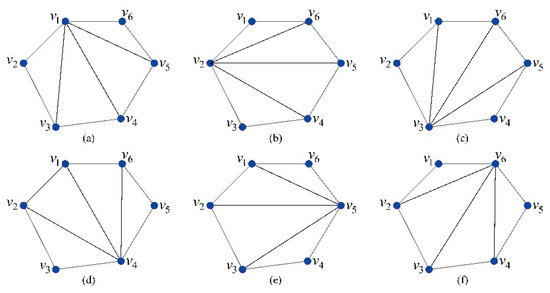
Figure 5.
Minimum are triangulation. (a–f) Six different filling schemes.
Patch refinement Since the shapes of the newly created triangles by the minimum area triangulation are relatively large and incompatible with the surrounding mesh, a refinement step is necessary to make them assort with the density of all the vertices of the filling patch well, specifically including two stages: triangle splitting and edge swapping.
- 1
- Triangle splitting. Triangle splitting is to partition the big triangle into three sub-triangles. As shown in Figure 6, bule dots and red lines represent the hole boundary vertices and edges respectively. Faces are the initial filling triangles. First, all interior edges of the patching mesh, i.e., (), are collected as an edge set S for later edge swapping. For each hole boundary vertex , a scale factor is defined as the average length of the edges that connect to except for the hole boundary edges. Then, in case of each initial filling triangle , its centroid vertex and the corresponding scale factor can be calculated. If and , triangle is replaced with three smaller ones , , and . In the same way, the splitting operation terminates until no new triangles created. After completing the splitting operation, all newly created interior edges, such as , etc, are also added to the edge set S.
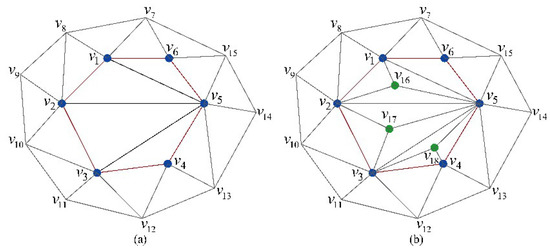 Figure 6. Triangle splitting. (a) Before splitting, (b) After splitting.
Figure 6. Triangle splitting. (a) Before splitting, (b) After splitting. - 2
- Edge swapping. To maintain a Delaunay-like triangulation, edge swapping is necessary after the triangle splitting. The swapping process is: for the two triangles adjacent to one edge, each of the two-mutual vertices of these triangles is checked. Then, the edge needs to be swapped if the vertex lies outside of the circum-sphere of its opposing triangle. As shown in Figure 7b, since lies inside the circumcircle of the triangle adjacent to the edge , both and are swapped. After edge swapping, the triangles and become more regular.
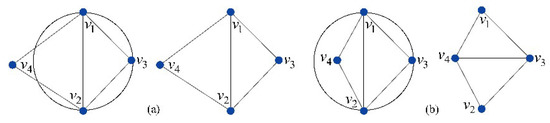 Figure 7. Edge swapping. (a) Don’t need edge swapping, (b) Need edge swapping.
Figure 7. Edge swapping. (a) Don’t need edge swapping, (b) Need edge swapping.
Patch fairing To improve the regularity of the patching triangles and make the filling patch assort with the surrounding mesh well, the 3D coordinates of the refined patching vertices should be faired by using a proper mesh deformation method. In this work, the Dirichlet energy function [37] defined in Equation (2) is selected to achieve the desired shape of the refined patch by minimizing .
Note that a 1D version of Equation (2) will be discussed for making the following contents clearer. We hope to find a function that minimizes the energy function within the domain , and assume that actually is the minimizer of .
Let be any function that satisfies and . Further we consider as a function of the scalar parameter , then this function has a minimum at . Next, the left-hand side of Equation (3) can be expanded and the derivative of with respect to is defined in Equation (4). For convenience, we will further write as u and as f.
Consequently, the right-hand side of Equation (4) has to vanish when . After integrating by parts and exploiting by multiple times, Equation (4) can be transformed into Equation (5).
Equation (5) implies that the minimizer of is a function whose fourth derivative is always zero within the domain . Insteading of solving for the f whose fourth derivative with respect to x is zero, it can be seen that the Bi-Laplacian of f is also zero, i.e., . Therefore, the condition is equivalent to Equation (6).
where is often called the Bi-Laplacian or the Laplace-Beltrami operator, i.e., the Laplacian of the Laplacian.
Until now, it is obvious that the minimization problem for the 1D case actually is to solve for the Bi-Laplacian. Therefore, the same mechanism can be applied to the minimization of Equation (2), but it requires using more boundary constraints. Finally, the continuous formulation can be transferred to discrete triangle meshes by replacing the continuous coordinate with the vertex coordinate , and then a deformed mesh can be produced by using the Laplace-Beltrami operator. Figure 8 shows an example of how to deform a refined patch. First, both the 1-ring adjacent vertices of the hole and the refined vertices are utilized to fit a deformed surface, then the refined vertices are projected onto this surface based on the constraints (1-ring adjacent and hole boundary vertices) so that the 3D coordinates of all refined vertices are updated. Finally, all refined vertices are relocated on the deformed surface, which makes the refined patch assort with the surrounding mesh well.
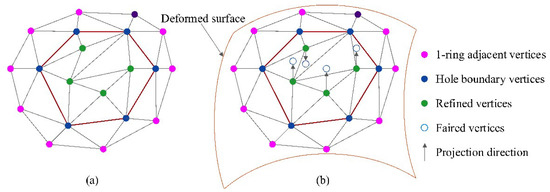
Figure 8.
Patch fairing. (a) Refined hole-filling patch, (b) Faired hole-filling patch.
5.3. Large-Sized Hole Filling by Improved Advancing Front Method
Although the minimum area triangulation has been regarded as a popular hole-filling method, it is not always effective especially for large-sized holes since it is both time-intensive and memory-intensive. In addition, the sizes of the newly created triangles commonly tend to be big and incompatible with the surrounding mesh. Besides that, the traditional advancing front method [18] can not fully guarantee that the missing region of a divergent hole can be smoothly closed, as shown in Figure 9a. To address these problems, an improved advancing front method is presented to fill large-sized holes, especially for divergent cases. Of course, our algorithm also works well on convergent holes illustrated in Figure 9b. The pseudocode of this algorithm is in the Algorithm 3.
| Algorithm 3 Large-sized hole filling |
Input: () Output:
|
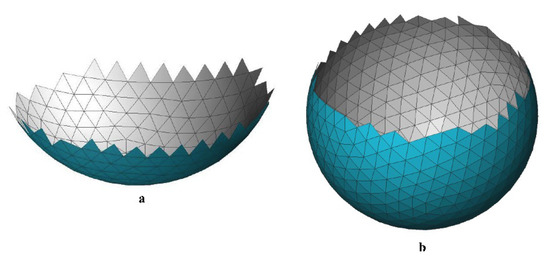
Figure 9.
Two typical large-sized holes. (a) Divergent hole. (b) Convergent hole.
Basic principle Given a hole loop, the angle between two adjacent boundary edges at each vertex should be first calculated. Then, starting from the vertex with the smallest angle , new triangles can be created on the plane determined by with three rules illustrated in Figure 10. If , () can be directly connected to form a new triangle. If , a new vertex needs to added on the bisector with the average edge length of and . For the last case, two new vertices need to inserted on the trisector also with the average edge length of and . This is the basic principle of the traditional advancing front hole-filling method.
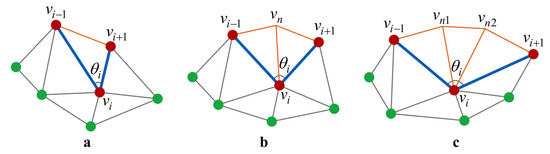
Figure 10.
Three rules for adding new triangles. (a) . (b) . (c) .
According to the basic principle, the quality of the final filling patch, as well as the hole-filling speed, heavily depend on the proper determination of the 3D coordinates and the directions for the newly added vertices. In this paper, by taking both the adjacent vertices and local curvature of the hole boundary vertices into account, the 3D coordinates and directions of the newly added vertices can be appropriately determined. Our algorithm consists of two stages: vertex normal correction and optimal position determination.
Vertex normal correction To make the newly created triangles tend to the center of the hole as fast as possible, that is, reducing the hole-filling times, the normal of each hole boundary vertex needs to be corrected. Especially for most of the divergent holes, the missing regions are unable to be closed by directly utilizing the traditional advancing front method. In addition, based on the corrected vertex normals, the convergent holes can also be closed quickly.
After loading a triangle mesh such as in STL format, the vertex normals are usually known, and these built-in normals are sufficient for most mesh processing algorithms. However, the original normal of a vertex is simply determined by weighting the average of the normals of its 1-ring adjacent faces, which does not reflect the curve of the hole boundary. Therefore, in this work, other hole boundary vertices are taken into account. As shown in Figure 11, assuming that there are n continuous boundary vertices () on the left-hand side of , n edge vectors by directly connected with one by one can be produced. In the same way, another n edge vectors can also be obtained on its right-hand side of . After obtaining these two edge vector sets, another two edge vectors and (see Figure 11b) can be calculated by using the formula below. Here, we set , in which is the size of the hole boundary vertices.
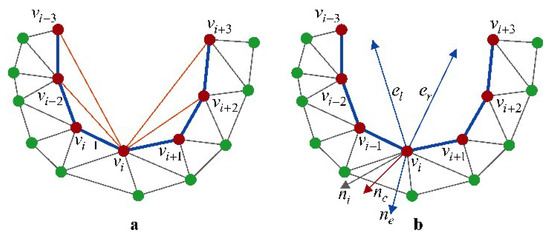
Figure 11.
Vertex normal correction. (a) Adjacent edge vectors in orange color. (b) The corrected vertex normal .
Depending on and , their cross product at vertex can be easily determined as , as shown in Figure 11b. Until now, a new vector reflecting the topology of the hole boundary has been obtained. In order to make the origianl normal of tend to smoothly, two weights () are assigned to and respectively. As a result, the corrected normal can be easily determined by the formula: , where .
Optimal position determination In order to make the newly added triangles become more regular and the filling patch assorts with the surrounding mesh well in terms of geometric shape and vertex valence, the optimal 3D coordinates of new vertices should be determined. As shown in Figure 12, the vertex with angle () is chosen as an example to illustrate the determination process in 3D space domain. Specifically, the local curvature and corrected normal of a vertex are combined to define a new weight function for determining the optimal vertex .
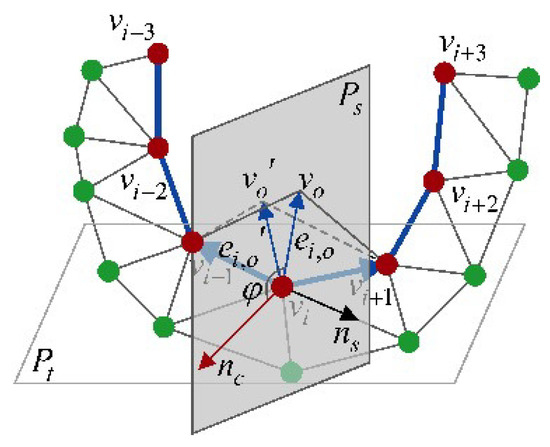
Figure 12.
Optimal position determination.
First, the curvature of the vertex is computed. Due to the good linear characteristics of the Taubin curvature [38] in time and space, we choose it to directly calculate the vertex curvature of and . As mentioned above, the neighboring vertices of should be considered, therefore, the Taubin curvature of is determined by averaging the Taubin curvature of and instead of direct calculation via the formula below:
where T inside is the unit projection vector of the optimal inserted edge on the tangent plane of .
Then, in order to obtain the optimal vertex , an initial insertion edge should be first calculated. As shown in Figure 10a, should locate on the bisector of the angle , and its length can be determined by simply averaging the length of and via the formula below.
where .
Once completing the calculation of and , both of them are combined to define a weight function
where .
To avoid degenerated triangles when creating new filling triangles, the optimal edge is restricted on the plane whose normal is . Then, can be defined in polar coordinate form where is the angle between and .
Next, is calculated by minimizing the just defined weight function . To simplify this calculation process, we set . In addition, in most cases, due to , can be calculated by using this formula . Once the angle is obtained, the optimal insertion edge vector can be determined by the formula where is a rotation matrix determined by rotating around the plane normal in counterclockwise.
Depending on , the optimal position of the newly added vertex in 3D space domain can be easily computed by this formula . Therefore, two new triangles and are created. In the case of , the optimal vertex can be determined in the same way.
6. Experimental Results and Discussion
To verify the efficiency, robustness, and the ability to shape recovery of the proposed approach in this paper, two experiments were carried out. In the first experiment, two state-of-the-art hole-filling methods were quantitatively compared to demonstrate the efficiency and shape-recovery ability of our method, especially for large-sized holes. In the second experiment, four example models were used to further show the advantages of our method. All the developed algorithms were implemented in C++ by using Visual Studio 2013 and tested on a PC equipped with CPU 3.60 GHz and 8 GB of RAM on Windows 10.
6.1. Quantitative Evaluation
Figure 13 shows the hole-filling results on two mechanical models. The results shown in Figure 13c–e are obtained by the algorithms of Liepa [6], Polymender [32], and our method respectively. Table 1 gives the statistics of the quantitative evaluation results. Figure 13c demonstrates that Liepa’s algorithm has the ability to close the holes of the tube and sphere models, but it fails to recover the geometry shapes of the missing regions. The reason is that the Liepa’s algorithm is usually taken as an initial filling technique to roughly close the holes in a simple way. Regarding the Polymender, it falls into the category of voxel-based methods, so the whole models have been modified when performing the hole-filling operation. From the results shown in Figure 13d, it is obvious that the produced results are not satisfactory since many non-hole regions have also been modified. Besides, a large number of degenerated triangles are contained in the resulting models. In contrast, the results obtained by our method (as illustrated in Figure 13e) not only can make the shapes of the filling patches assort with their surrounding meshes but also can ensure that most of the newly added triangles and vertices are both highly regular. Although all three algorithms can produce completed models, the results obtained by our method are obviously better than others. From the view of model shape, out method has the ability to make the filling patch assort with the surrounding mesh well.

Figure 13.
Hole filling results on tube and sphere models. (a) The incomplete models. (b) The results after hole boundary clean. (c) The results of Liepa’s method. (d) The results of Polymender’s method. (e) The results of our method.

Table 1.
Statistics of the quantitative evaluation results.
Before analysing Table 1, Figure 14 and Figure 15, two notations are defined: triangle quality factor and vertex valence . Given a triangle, the ratio of its shortest edge to the radius of its circumscribed circle is denoted as the triangle quality factor . If a triangle is closer to be a regular one, the closer is to 1.73. In this work, the triangles whose is greater than 1.39 will be regarded as high-quality ones, and then their percentage in the total number of the filling triangles will be computed. For one vertex, the number of its one-ring adjacent triangles is defined as its vertex valence . As one highly regular triangular mesh, the of most vertices is six. From Table 1, it can be observed that the hole-filling times for closing the sphere model by our method is almost one-fifth of that of Liepa’s method (19 VS 102.73 ), and one-eighth of that of Polymender’s method (19 VS 158 ). The main reason for the efficient performance of our method is the refined vertex normals can enable the newly added vertices to close the hole in a very fast and proper way. Besides, both the regularity of the inserted triangles and vertex value are guaranteed during the closing stage without needing any further postprocessing steps, which can efficiently reduce the filling times. These results indicate that our method is very fast especially for handling large-sized holes. On the other hand, the evaluation results show that the quality level of the filling patches obtained by our method is almost twice as high as that by the other two methods, which can effectively demonstrate that our method can produce high-regularity filling patches, i.e., containing more regular triangles. Figure 14 shows the comparison results about vertex valence computation between ours and Liepa’s algorithm on the tube model. From the visualization view, it can be seen that most of the vertices inside the filling patch obtained by our method have the vertex valence to six (84%). However, the Liepa’s algorithm generates a few vertices with the vertex valence of three, which may cause degenerated triangle defects. Furthermore, Figure 15 shows that our method can ensure that the majority of the filling vertices have vertex valence of six (82.68%).
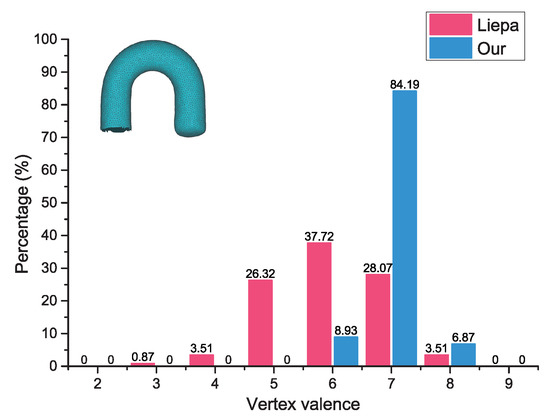
Figure 14.
Vertex valence statistics of the filling patch for the tube model.
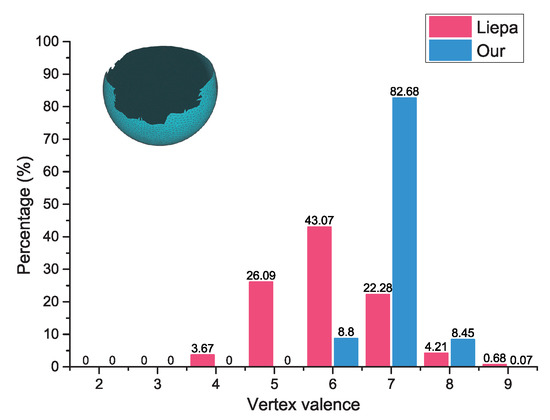
Figure 15.
Vertex valence statistics of the filling patch for the sphere model.
Based on the above evaluation results, it can be observed that our method is the most efficient compared with the other two existing methods, and can produce satisfactory filling results. Besides, our method can ensure the filling patches to be compatible with surrounding meshes well.
6.2. Other Examples
To further demonstrate the efficiency, robustness and shape-recovery ability of our method, four non-mechanical models were tested. For each model, it contains at least one of the three types of holes with different sizes, and then our algorithm is applied to fill them. Figure 16 shows a hole-filling gallery on these four models. Figure 16a illustrates the incomplete models, and it can be seen that most of them suffer from at least one or more types of holes, e.g., small-sized, middle-sized, and large-sized holes. In particular, the ones contained in the statue and head models are divergent holes. The cleaned meshes are shown in Figure 16b, and from the results, it can be observed that all the tooth faces occurring on the hole boundaries have been completely removed, which provides smooth inputs for the next processing step. The final filling results obtained by our method are illustrated in Figure 16c,d. From the viewpoint of visualization check, all the holes have been successfully closed by our method, besides, it can also ensure the filling patches to be compatible with surrounding meshes well. Table 2 gives the statistics of the hole-filling results obtained by our method on these four models. Regarding the head model, although it contains a large and divergent hole with a boundary vertex size of 160, our algorithm takes only 91.83 to close it. Unlike the Liepa’s algorithm, the closing and refining stages for a large hole are completed in a single step for our method, which can significantly reduce the hole filling times, especially for large ones. Compared with the Polymender’s algorithm, our method strictly limits the processing region to its adjacent area of one large hole, which can prevent the non-hole regions from being modified. From the ninth column of Table 2, it can be seen that the triangle quality evaluation results on all testing models are greater than 76%, which proves that the filling patch generated by our method is mainly composed of regular triangles. Furthermore, Figure 17, Figure 18, Figure 19 and Figure 20 present the statistics of the vertex valence computation results obtained by our method on these models. From these results, it can be seen that the vertex valence of the filling vertices obtained by our method only ranges from four to eight, and the vertices with vertex valence of six account for more than 71 % of the total number of the newly inserted vertices. These results demonstrate that our method can guarantee the majority of the newly added vertices to be high regular ones.

Figure 16.
Hole filling results on four example models. (a) The incomplete models. (b) The results after hole boundary clean. (c) The results of our method in one view. (d) The results of our method in another view.

Table 2.
Statistics of the hole-filling results on example models.
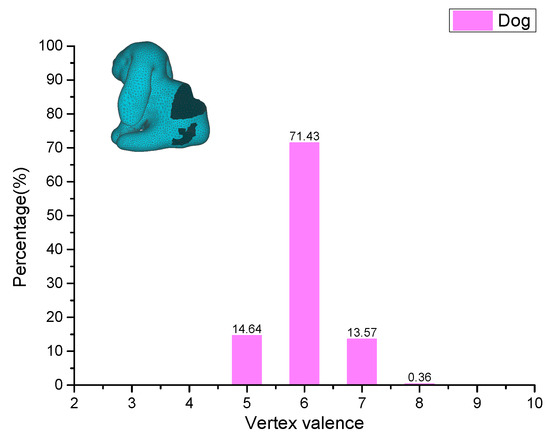
Figure 17.
Vertex valence statistics of the filling patch for the dog model.
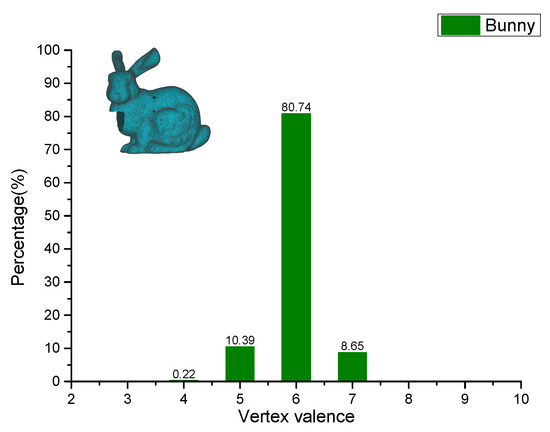
Figure 18.
Vertex valence statistics of the filling patch for the bunny model.
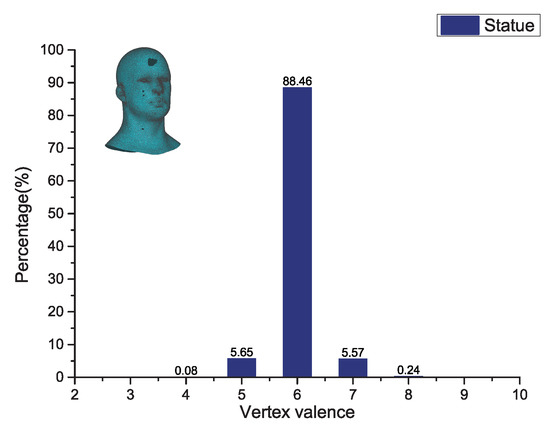
Figure 19.
Vertex valence statistics of the filling patch for the statue model.
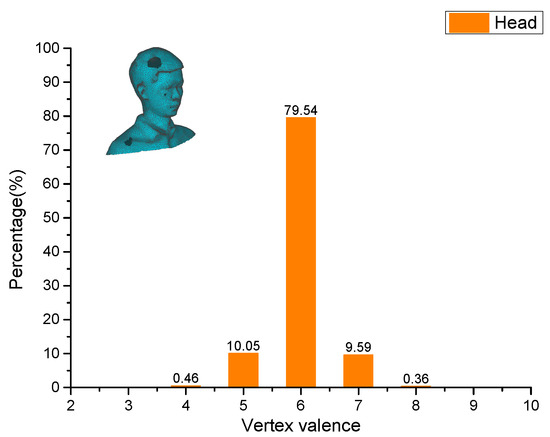
Figure 20.
Vertex valence statistics of the filling patch for the head model.
6.3. Advantages and Disadvantages
The proposed method provides a systematic solution to close the holes with different sizes in additive repair. In the case of small-sized holes, our hole-filling technique is very simple and enough robust, which ensures this technique to be smoothly applied in many practical applications. As for middle-sized holes, the presented algorithm achieves a good balance between the hole-filling efficiency and the ability to shape recovery. Regarding large-sized holes, our method can not only close the holes with very low time complexity but also ensure the filling patches to be compatible with surrounding meshes without any further refinement and fairing steps. Our approach can be used in the fields of geometry measurement, geometry modeling, intelligent manufacturing, and additive repair, etc.
Our method might not work well on some complex or special holes. To sum up, there are two main limitations. The first one is that it is difficult for our approach to handle holes with islands. Another limitation is that the filling patch may be a nonplanar surface if the shape curve of the hole is approximately planar by using our approach.
In future work, a novel algorithm will be developed to deal with nonplanar issues. In the case of the holes with islands, they will be first transformed into regular ones by removing the detected islands, and then be filled by our method presented in this work.
7. Conclusions
In this paper, a fast hole-filling method for triangular mesh based on hole size towards additive manufacturing repair is proposed. The detected holes are first classified into three categories: small-sized, middle-sized, and large-sized ones, and then filled by the centroid-based, projection-based, and improved advancing front methods respectively. In the end, two experiments are carried out to verify the efficiency, robustness, and the ability to shape recovery of our method.
First, three different algorithms are utilized to fill the small-sized, middle-sized, and large-sized holes respectively. In the case of small-sized holes, a simple and fast algorithm is used to iteratively create new triangles by directly connecting each pair of two continuous hole boundary vertices and the centroid vertex of the hole loop. As for middle-sized holes, to achieve a good balance between the efficiency and the ability to shape recovery of the hole-filling algorithm, the detected holes are first closed by an initial filling patch generated by using the minimum area triangulation algorithm. Then the patch refinement and fairing operations are applied to maintain a Delaunay-like triangulation and make the filling patches assort with surrounding meshes well via a Laplace-Beltrami mesh deformation technique. Regarding large-sized holes, an improved advancing front method is used to close holes fastly without any further refinement and fairing steps while ensuring the patching mesh to be compatible with the surrounding mesh well.
Second, two experiments specifically including the quantitative evaluation and other example testings are carried out to verify the effectiveness, robustness and shape-recovery ability of our hole-filling algorithm. Besides, the advantages and disadvantages of our approach, as well as the future work, are also given.
Our approach can also be used in the fields of 3D geometry measurement and geometry modeling, since the complete 3D model of one measured physical object is usually the input for its downstream geometry processing steps, such as mesh alignment, Boolean difference, etc.
Author Contributions
Conceptualization, C.F.; methodology, M.R.; software, G.Q.; validation, W.L.; formal analysis, C.F.; investigation, C.F.; resources, G.Q.; data curation, C.F.; writing—original draft preparation, C.F.; writing—review and editing, C.F. and Q.G.; visualization, S.L.; supervision, J.L.; project administration, J.L.; funding acquisition, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China grant number 51675404.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Matsumoto, M.; Yang, S.; Martinsen, K.; Kainuma, Y. Trends and research challenges in remanufacturing. Int. J. Precis. Eng. Manuf.-Green Technol. 2016, 3, 129–142. [Google Scholar] [CrossRef]
- Huang, H.; Zhou, L.; Chen, X.; Gong, Z. SMART Robotic System for 3D Profile Turbine Vane Airfoil Repair. Int. J. Adv. Manuf. Technol. 2003, 21, 275–283. [Google Scholar] [CrossRef]
- Guo, X.; Xiao, J.; Wang, Y. A survey on algorithms of hole filling in 3D surface reconstruction. Vis. Comput. 2018, 34, 93–103. [Google Scholar] [CrossRef]
- Pérez, E.; Salamanca, S.; Merchán, P.; Adán, A. A comparison of hole-filling methods in 3D. Int. J. Appl. Math. Comput. Sci. 2016, 26, 885–903. [Google Scholar] [CrossRef]
- Sheng, B.; Zhao, F.; Yin, X.; Zhang, C.; Wang, H.; Huang, P. A Lightweight Surface Reconstruction Method for Online 3D Scanning Point Cloud Data Oriented toward 3D Printing. Math. Probl. Eng. 2018, 2018, 1–16. [Google Scholar] [CrossRef]
- Liepa, P.; Kobbelt, L.; Schroeder, P.; Hoppe, H. Filling Holes in Meshes. In Eurographics Symposium on Geometry Processing; The Eurographics Association: Geneve Switzerland, 2003; pp. 200–205. [Google Scholar]
- Gao, W.; Zhang, Y.; Ramanujan, D.; Ramani, K.; Chen, Y.; Williams, C.B.; Wang, C.C.; Shin, Y.C.; Zhang, S.; Zavattieri, P.D. The status, challenges, and future of additive manufacturing in engineering. Comput.-Aided Des. 2015, 69, 65–89. [Google Scholar] [CrossRef]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Wilson, J.M.; Piya, C.; Shin, Y.C.; Zhao, F.; Ramani, K. Remanufacturing of turbine blades by laser direct deposition with its energy and environmental impact analysis. J. Clean. Prod. 2014, 80, 170–178. [Google Scholar] [CrossRef]
- Feng, C.; Liang, J.; Gong, C.; Pai, W.; Liu, S. Repair volume extraction method for damaged parts in remanufacturing repair. Int. J. Adv. Manuf. Technol. 2018, 98, 1523–1536. [Google Scholar] [CrossRef]
- Ding, D.; Pan, Z.; Cuiuri, D.; Li, H.; Larkin, N.; Van Duin, S. Automatic multi-direction slicing algorithms for wire based additive manufacturing. Robot. Comput.-Integr. Manuf. 2016, 37, 139–150. [Google Scholar] [CrossRef]
- Li, L.; Li, C.; Tang, Y.; Du, Y. An integrated approach of reverse engineering aided remanufacturing process for worn components. Robot. Comput.-Integr. Manuf. 2017, 48, 39–50. [Google Scholar] [CrossRef]
- Um, J.; Rauch, M.; Hascoët, J.Y.; Stroud, I. STEP-NC compliant process planning of additive manufacturing: Remanufacturing. Int. J. Adv. Manuf. Technol. 2017, 88, 1215–1230. [Google Scholar] [CrossRef]
- Feng, Y.; Ren, J.; Liang, Y. Prediction and reconstruction of edge shape in adaptive machining of precision forged blade. Int. J. Adv. Manuf. Technol. 2018, 96, 2355–2366. [Google Scholar] [CrossRef]
- Zheng, Y.; Qureshi, A.; Ahmad, R. Algorithm for remanufacturing of damaged parts with hybrid 3D printing and machining process. Manuf. Lett. 2018, 15, 38–41. [Google Scholar] [CrossRef]
- Ju, T. Fixing geometric errors on polygonal models: A survey. J. Comput. Sci. Technol. 2009, 24, 19–29. [Google Scholar] [CrossRef]
- Harary, G.; Tal, A.; Grinspun, E. Context-based coherent surface completion. ACM Trans. Graph. (TOG) 2014, 33, 5. [Google Scholar] [CrossRef]
- Wei, Z.; Gao, S.; Lin, H. A robust hole-filling algorithm for triangular mesh. Vis. Comput. 2007, 23, 987–997. [Google Scholar]
- Wang, X.; Hu, J.; Zhang, D.; Guo, L.; Qin, H.; Hao, A. Multi-scale geometry detail recovery on surfaces via empirical mode decomposition. Comput. Graph. 2018, 70, 118–127. [Google Scholar] [CrossRef]
- Ngo, H.T.M.; Lee, W.S. Feature-first hole filling strategy for 3D meshes. In International Conference on Computer Vision, Imaging and Computer Graphics; Springer: Berlin/Heidelberg, Germany, 2011; pp. 53–68. [Google Scholar]
- tae Jun, Y. A piecewise hole filling algorithm in reverse engineering. Comput.-Aided Des. 2005, 37, 263–270. [Google Scholar] [CrossRef]
- Altantsetseg, E.; Khorloo, O.; Matsuyama, K.; Konno, K. Complex hole-filling algorithm for 3D models. In Proceedings of the Computer Graphics International Conference, Yokohama, Japan, 27–30 June 2017; p. 10. [Google Scholar]
- Branch, J.; Prieto, F.; Boulanger, P. Automatic hole-filling of triangular meshes using local radial basis function. In Proceedings of the Third International Symposium on 3D Data Processing, Visualization, and Transmission (3DPVT’06), Chapel Hill, NC, USA, 14–16 June 2006; pp. 727–734. [Google Scholar]
- Wang, J.; Oliveira, M.M. Filling holes on locally smooth surfaces reconstructed from point clouds. Image Vis. Comput. 2007, 25, 103–113. [Google Scholar] [CrossRef]
- Li, Z.; Meek, D.S.; Walton, D.J. Polynomial blending in a mesh hole-filling application. Comput.-Aided Des. 2010, 42, 340–349. [Google Scholar] [CrossRef]
- Nguyen, M.X.; Yuan, X.; Chen, B. Geometry completion and detail generation by texture synthesis. Vis. Comput. 2005, 21, 669–678. [Google Scholar] [CrossRef]
- Breckon, T.P.; Fisher, R.B. Three-dimensional surface relief completion via nonparametric techniques. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 2249–2255. [Google Scholar] [CrossRef] [PubMed]
- Anguelov, D.; Srinivasan, P.; Koller, D.; Thrun, S.; Rodgers, J.; Davis, J. SCAPE: Shape completion and animation of people. ACM Trans. Graph. (TOG) 2005, 24, 408–416. [Google Scholar] [CrossRef]
- Sung, M.; Kim, V.G.; Angst, R.; Guibas, L. Data-driven structural priors for shape completion. ACM Trans. Graph. (TOG) 2015, 34, 175. [Google Scholar] [CrossRef]
- Sharf, A.; Alexa, M.; Cohen-Or, D. Context-based surface completion. ACM Trans. Graph. (TOG) 2004, 23, 878–887. [Google Scholar] [CrossRef]
- Davis, J.; Marschner, S.R.; Garr, M.; Levoy, M. Filling holes in complex surfaces using volumetric diffusion. In Proceedings of the First International Symposium on 3D Data Processing Visualization and Transmission, Padova, Italy, 19–21 June 2002; pp. 428–441. [Google Scholar]
- Ju, T. Robust repair of polygonal models. ACM Trans. Graph. (TOG) 2004, 23, 888–895. [Google Scholar] [CrossRef]
- Nooruddin, F.S.; Turk, G. Simplification and repair of polygonal models using volumetric techniques. IEEE Trans. Vis. Comput. Graph. 2003, 9, 191–205. [Google Scholar] [CrossRef]
- Guo, T.Q.; Li, J.J.; Weng, J.G.; Zhuang, Y.T. Filling holes in complex surfaces using oriented voxel diffusion. In Proceedings of the 2006 International Conference on Machine Learning and Cybernetics, Dalian, China, 13–16 August 2006; pp. 4370–4375. [Google Scholar]
- Centin, M.; Pezzotti, N.; Signoroni, A. Poisson-driven seamless completion of triangular meshes. Comput. Aided Geom. Des. 2015, 35, 42–55. [Google Scholar] [CrossRef]
- Argudo, O.; Brunet, P.; Chica, A.; Vinacua, À. Biharmonic fields and mesh completion. Graph. Models 2015, 82, 137–148. [Google Scholar] [CrossRef]
- Alexa, M.; Wardetzky, M. Discrete Laplacians on general polygonal meshes. ACM Trans. Graph. (TOG) 2011, 30, 102. [Google Scholar] [CrossRef]
- Taubin, G. Estimating the tensor of curvature of a surface from a polyhedral approximation. In Proceedings of the IEEE International Conference on Computer Vision, Cambridge, MA, USA, 20–23 June 1995; pp. 902–907. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).