Robust Geometries for Second-Harmonic-Generation in Microrings Exhibiting a 4-Bar Symmetry
Abstract
:Featured Application
Abstract
1. Introduction
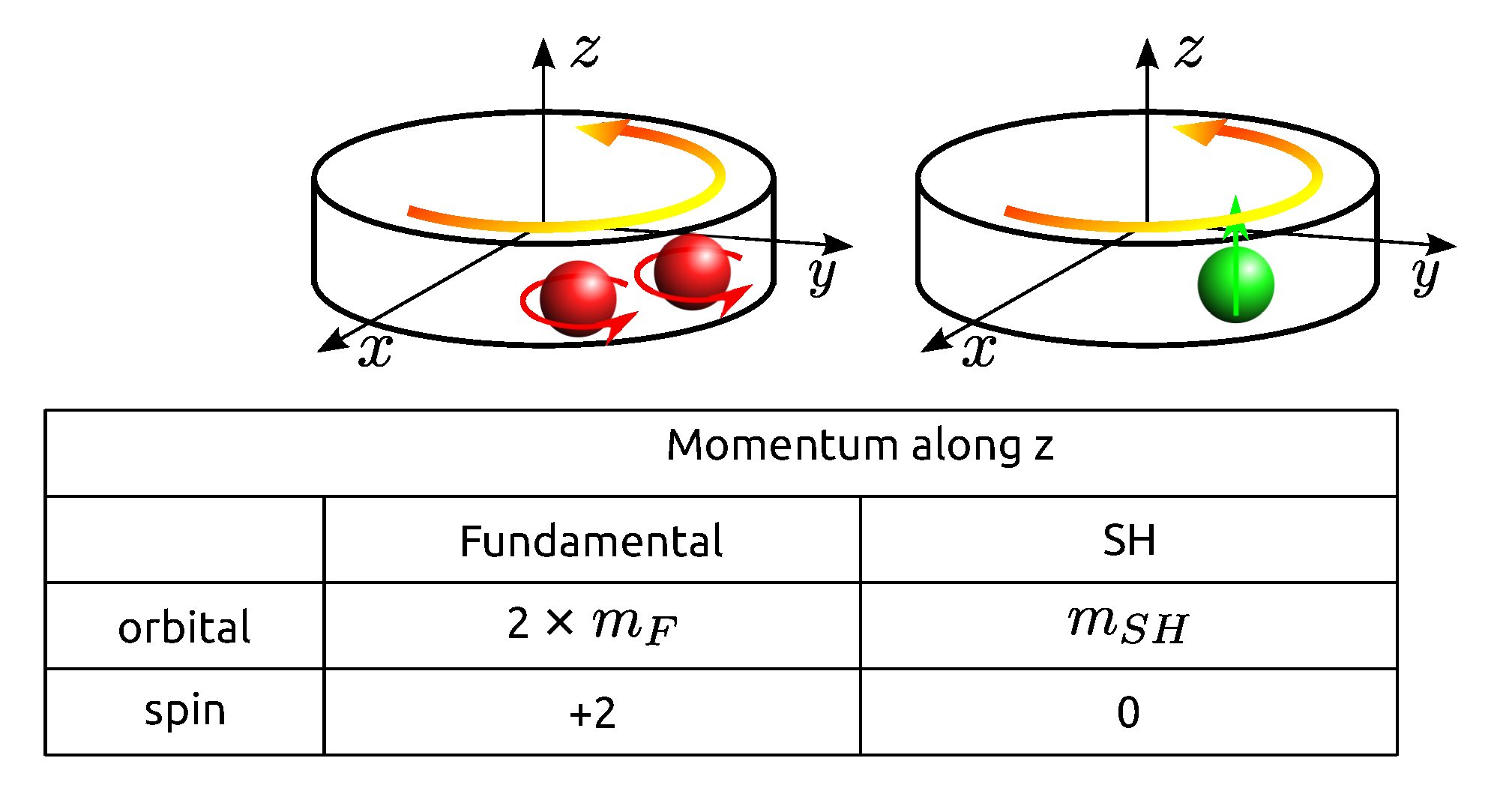
2. Conditions for SHG
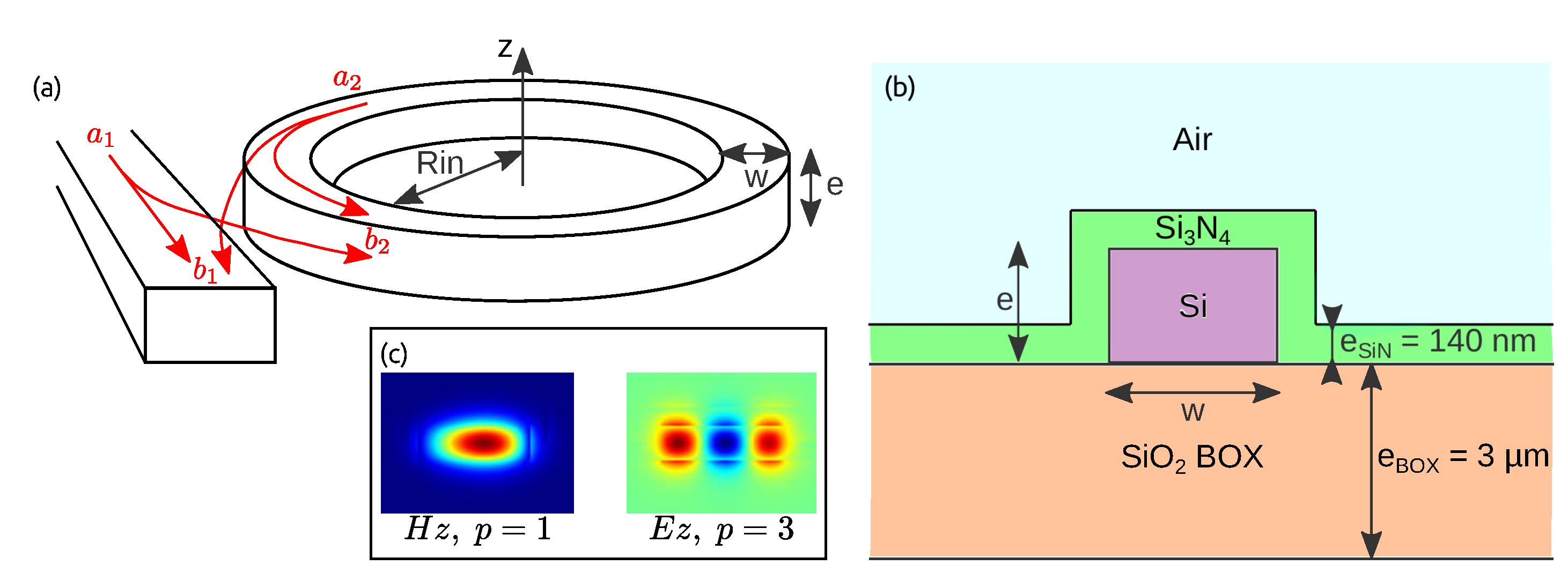
2.1. Method
2.2. Results
3. Conversion Efficiency
3.1. Method
3.2. Discussion
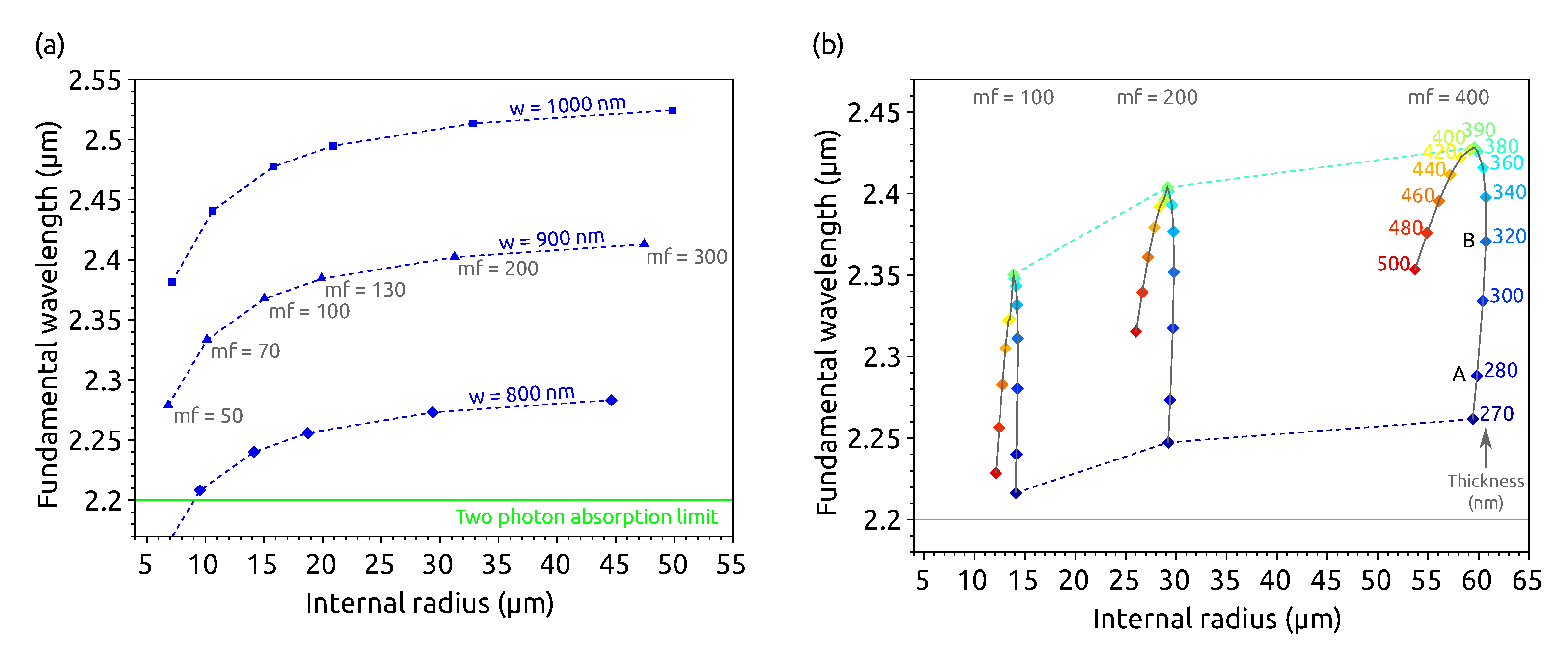
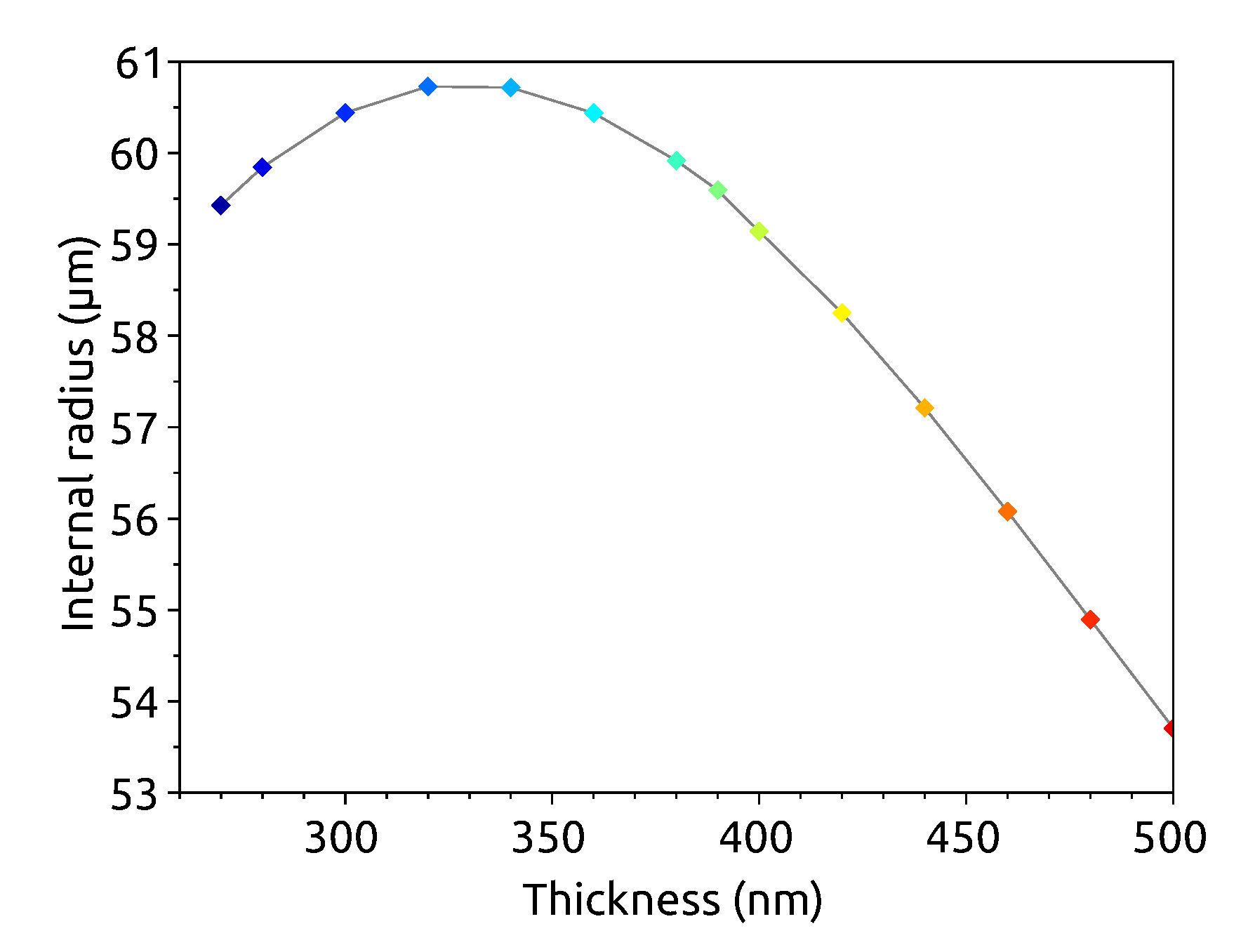
4. Robust Geometries against Fabrication Errors
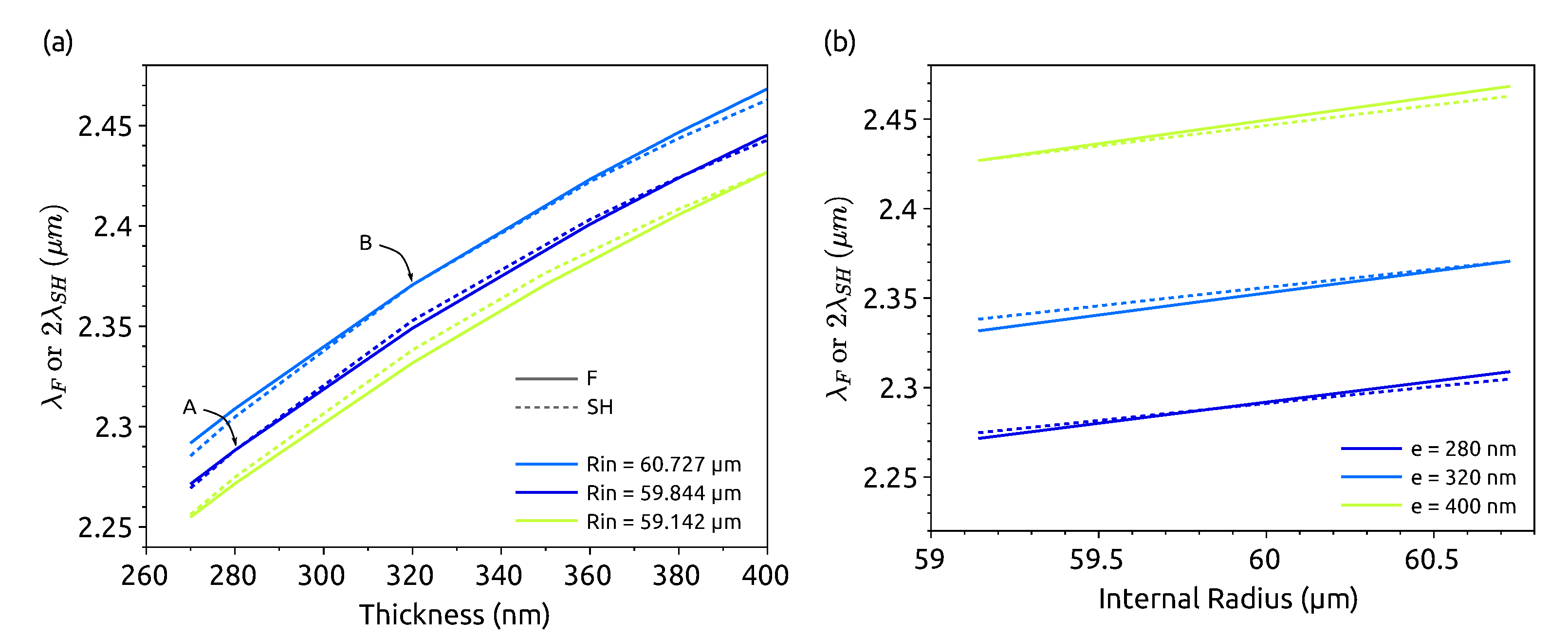
4.1. Analysis
4.2. General Observations
4.2.1. For Small Thicknesses, nm
4.2.2. For Thicknesses Larger than 320 nm
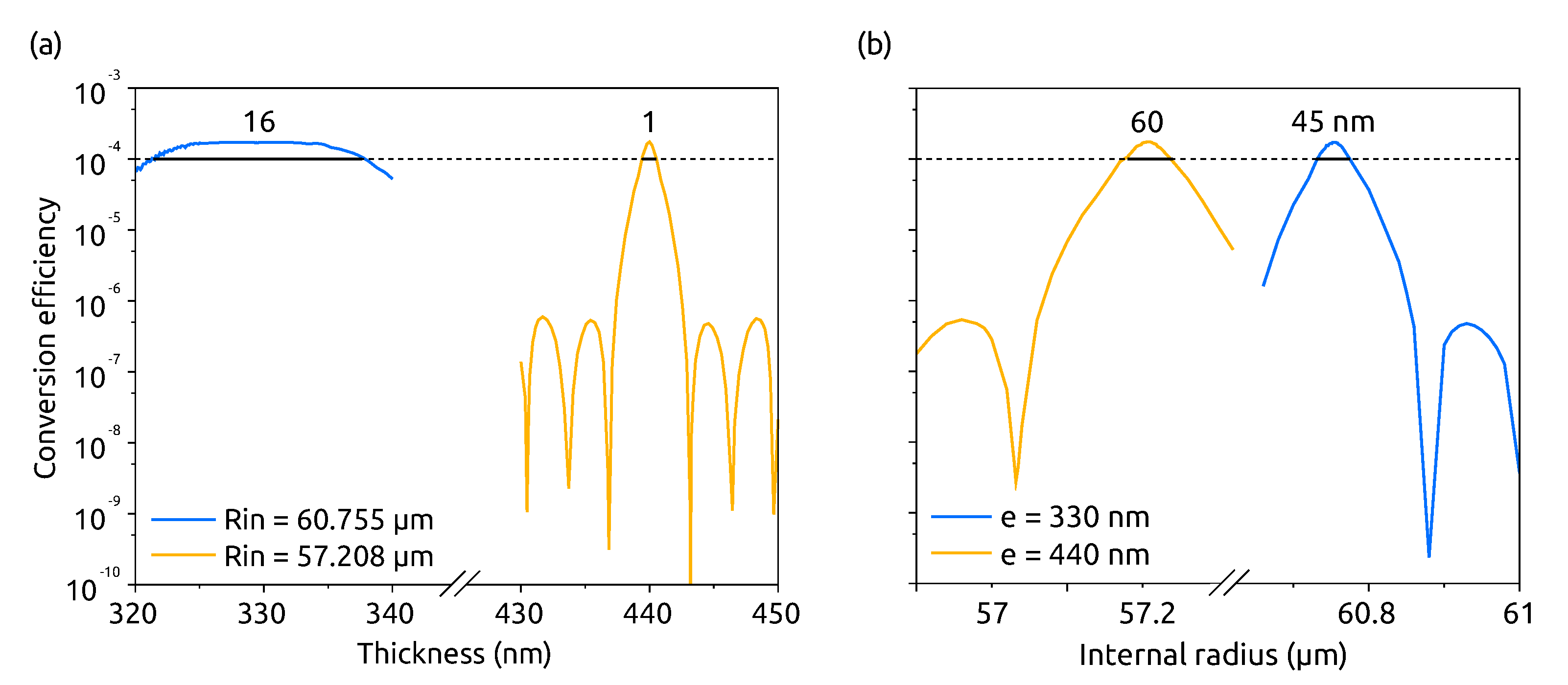
4.3. Application
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Refractive Indexes
- for Si
- for
- for
Appendix B. Phase Matching Condition
References
- Diddams, S.A.; Jones, D.J.; Ye, J.; Cundiff, S.T.; Hall, J.L.; Ranka, J.K.; Windeler, R.S.; Holzwarth, R.; Udem, T.; Hänsch, T.W. Direct Link between Microwave and Optical Frequencies with a 300 THz Femtosecond Laser Comb. Phys. Rev. Lett. 2000, 84, 5102–5105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Griffith, A.G.; Lau, R.K.; Cardenas, J.; Okawachi, Y.; Mohanty, A.; Fain, R.; Lee, Y.H.D.; Yu, M.; Phare, C.T.; Poitras, C.B.; et al. Silicon-chip mid-infrared frequency comb generation. Nat. Commun. 2015, 6, 6299. [Google Scholar] [CrossRef] [PubMed]
- Diddams, S.A.; Ma, L.S.; Ye, J.; Hall, J.L. Broadband optical frequency comb generation with a phase-modulated parametric oscillator. Opt. Lett. 1999, 24, 1747. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leo, F.; Hansson, T.; Ricciardi, I.; De Rosa, M.; Coen, S.; Wabnitz, S.; Erkintalo, M. Frequency-comb formation in doubly resonant second-harmonic generation. Phys. Rev. A 2016, 93. [Google Scholar] [CrossRef] [Green Version]
- Leo, F.; Hansson, T.; Ricciardi, I.; De Rosa, M.; Coen, S.; Wabnitz, S.; Erkintalo, M. Walk-Off-Induced Modulation Instability, Temporal Pattern Formation, and Frequency Comb Generation in Cavity-Enhanced Second-Harmonic Generation. Phys. Rev. Lett. 2016, 116. [Google Scholar] [CrossRef]
- Ricciardi, I.; Mosca, S.; Parisi, M.; Maddaloni, P.; Santamaria, L.; De Natale, P.; De Rosa, M. Frequency comb generation in quadratic nonlinear media. Phys. Rev. A 2015, 91. [Google Scholar] [CrossRef] [Green Version]
- Mosca, S.; Parisi, M.; Ricciardi, I.; Leo, F.; Hansson, T.; Erkintalo, M.; Maddaloni, P.; De Natale, P.; Wabnitz, S.; De Rosa, M. Modulation Instability Induced Frequency Comb Generation in a Continuously Pumped Optical Parametric Oscillator. Phys. Rev. Lett. 2018, 121. [Google Scholar] [CrossRef] [Green Version]
- Ilchenko, V.S.; Savchenkov, A.A.; Matsko, A.B.; Maleki, L. Nonlinear Optics and Crystalline Whispering Gallery Mode Cavities. Phys. Rev. Lett. 2004, 92. [Google Scholar] [CrossRef]
- Wang, C.; Burek, M.J.; Lin, Z.; Atikian, H.A.; Venkataraman, V.; Huang, I.C.; Stark, P.; Lončar, M. Integrated high quality factor lithium niobate microdisk resonators. Opt. Express 2014, 22, 30924. [Google Scholar] [CrossRef]
- Guo, X.; Zou, C.L.; Tang, H.X. Second-harmonic generation in aluminum nitride microrings with 2500%/W conversion efficiency. Optica 2016, 3, 1126. [Google Scholar] [CrossRef]
- Roland, I.; Gromovyi, M.; Zeng, Y.; El Kurdi, M.; Sauvage, S.; Brimont, C.; Guillet, T.; Gayral, B.; Semond, F.; Duboz, J.Y.; et al. Phase-matched second harmonic generation with on-chip GaN-on-Si microdisks. Sci. Rep. 2016, 6, 34191. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mariani, S.; Andronico, A.; Lemaître, A.; Favero, I.; Ducci, S.; Leo, G. Second-harmonic generation in AlGaAs microdisks in the telecom range. Opt. Lett. 2014, 39, 3062. [Google Scholar] [CrossRef] [PubMed]
- Kuo, P.S.; Bravo-Abad, J.; Solomon, G.S. Second-harmonic generation using -quasi-phasematching in a GaAs whispering-gallery-mode microcavity. Nat. Commun. 2014, 5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lake, D.P.; Mitchell, M.; Jayakumar, H.; dos Santos, L.F.; Curic, D.; Barclay, P.E. Efficient telecom to visible wavelength conversion in doubly resonant gallium phosphide microdisks. Appl. Phys. Lett. 2016, 108, 031109. [Google Scholar] [CrossRef]
- Vivien, L.; Pavesi, L. (Eds.) Handbook of Silicon Photonics; Series in Optics And Optoelectronics; OCLC: 914966931; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Borghi, M.; Castellan, C.; Signorini, S.; Trenti, A.; Pavesi, L. Nonlinear silicon photonics. J. Opt. 2017, 19, 093002. [Google Scholar] [CrossRef]
- Cazzanelli, M.; Bianco, F.; Borga, E.; Pucker, G.; Ghulinyan, M.; Degoli, E.; Luppi, E.; Véniard, V.; Ossicini, S.; Modotto, D.; et al. Second-harmonic generation in silicon waveguides strained by silicon nitride. Nat. Mater. 2011, 11, 148–154. [Google Scholar] [CrossRef]
- Castellan, C.; Trenti, A.; Vecchi, C.; Marchesini, A.; Mancinelli, M.; Ghulinyan, M.; Pucker, G.; Pavesi, L. On the origin of second harmonic generation in silicon waveguides with silicon nitride cladding. Sci. Rep. 2018. submitted. [Google Scholar] [CrossRef] [Green Version]
- Levy, J.S.; Foster, M.A.; Gaeta, A.L.; Lipson, M. Harmonic generation in silicon nitride ring resonators. Opt. Express 2011, 19, 11415. [Google Scholar] [CrossRef] [Green Version]
- Timurdogan, E.; Poulton, C.V.; Byrd, M.J.; Watts, M.R. Electric field-induced second-order nonlinear optical effects in silicon waveguides. Nat. Photonics 2017, 11, 200–206. [Google Scholar] [CrossRef] [Green Version]
- Franchi, R.; Castellan, C.; Ghulinyan, M.; Pavesi, L. Second-harmonic generation in periodically poled silicon waveguides with lateral pin junctions: Publisher’s note. Opt. Lett. 2020, 45, 3348. [Google Scholar] [CrossRef]
- Berciano, M.; Marcaud, G.; Damas, P.; Le Roux, X.; Crozat, P.; Alonso Ramos, C.; Pérez Galacho, D.; Benedikovic, D.; Marris-Morini, D.; Cassan, E.; et al. Fast linear electro-optic effect in a centrosymmetric semiconductor. Commun. Phys. 2018, 1, 64. [Google Scholar] [CrossRef]
- Kuo, P.S.; Solomon, G.S. On- and off-resonance second-harmonic generation in GaAs microdisks. Opt. Express 2011, 19, 16898–16918. [Google Scholar] [CrossRef] [PubMed]
- Snyder, A.W.; Love, J.D. Optical Waveguide Theory; Number 190 in Science Paperbacks; Chapman and Hall: London, UK; New York, NY, USA, 1983. [Google Scholar]
- Manganelli, C.L.; Pintus, P.; Bonati, C. Modeling of strain-induced Pockels effect in Silicon. Opt. Express 2015, 23, 28649–28666. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Olivares, I.; Parra, J.; Brimont, A.; Sanchis, P. Enhancing Pockels effect in strained silicon waveguides. Opt. Express 2019, 27, 26882–26892. [Google Scholar] [CrossRef]
- Lafforgue, C.; Berciano, M.; Deniel, L.; Marcaud, G.; Le Roux, X.; Alonso-Ramos, C.; Benedikovic, D.; Vakarin, V.; Ruiz-Caridad, A.; Crozat, P.; et al. Strain induced Pockels effect in silicon for electro-optic modulation. In Proceedings of the Silicon Photonics XV, International Society for Optics and Photonics, San Francisco, CA, USA, 3–6 February 2020; Volume 11285, p. 112850D. [Google Scholar]
- Dumeige, Y.; Féron, P. Whispering-gallery-mode analysis of phase-matched doubly resonant second-harmonic generation. Phys. Rev. A 2006, 74, 063804. [Google Scholar] [CrossRef] [Green Version]
- COMSOL AB, Stokholm Sweden. COMSOL Multiphysics v 5.3©. Available online: http://www.comsol.com (accessed on 15 September 2017).
- Bristow, A.D.; Rotenberg, N.; van Driel, H.M. Two-photon absorption and Kerr coefficients of silicon for 850–2200 nm. Appl. Phys. Lett. 2007, 90, 191104. [Google Scholar] [CrossRef]
- Yariv, A.; Yeh, P. Electromagnetic propagation in periodic stratified media II Birefringence, phase matching, and X-ray lasers. J. Opt. Soc. Am. 1977, 67, 438. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guillemé, P.; Vecchi, C.; Castellan, C.; Signorini, S.; Ghulinyan, M.; Bernard, M.; Parisi, M.; Pavesi, L. Robust Geometries for Second-Harmonic-Generation in Microrings Exhibiting a 4-Bar Symmetry. Appl. Sci. 2020, 10, 9047. https://doi.org/10.3390/app10249047
Guillemé P, Vecchi C, Castellan C, Signorini S, Ghulinyan M, Bernard M, Parisi M, Pavesi L. Robust Geometries for Second-Harmonic-Generation in Microrings Exhibiting a 4-Bar Symmetry. Applied Sciences. 2020; 10(24):9047. https://doi.org/10.3390/app10249047
Chicago/Turabian StyleGuillemé, Pierre, Chiara Vecchi, Claudio Castellan, Stefano Signorini, Mher Ghulinyan, Martino Bernard, Maria Parisi, and Lorenzo Pavesi. 2020. "Robust Geometries for Second-Harmonic-Generation in Microrings Exhibiting a 4-Bar Symmetry" Applied Sciences 10, no. 24: 9047. https://doi.org/10.3390/app10249047





