Analysis of the Influence of Terrain Orientation on the Design of PV Facilities with Single-Axis Trackers
Abstract
1. Introduction
2. Materials and Methods
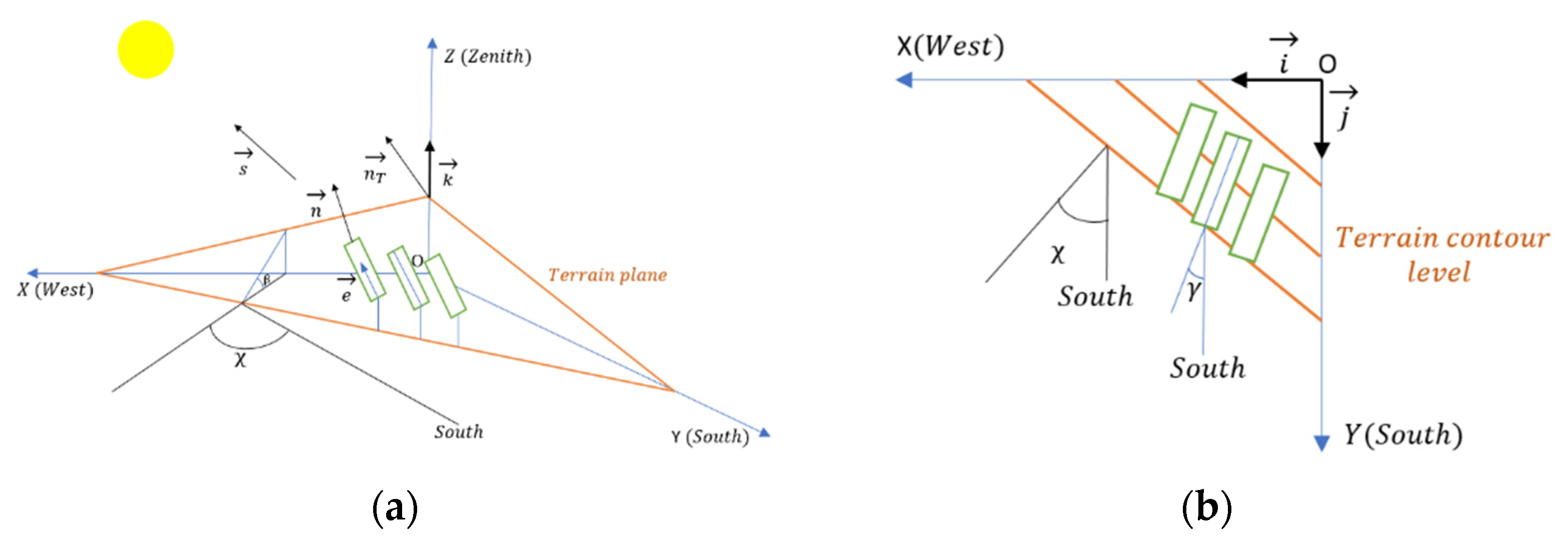
2.1. Astronomical Bases and Irradiance Model
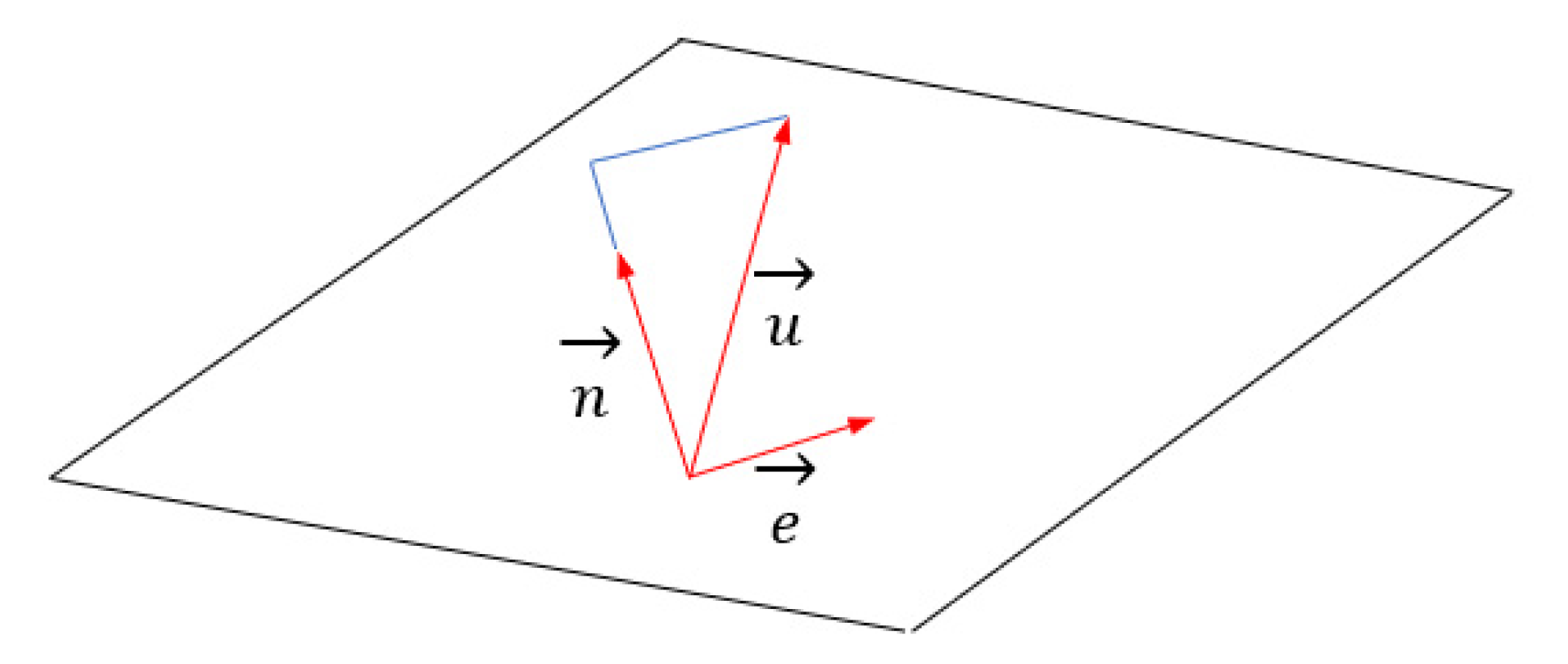
2.2. Optimisation of Collector Orientation
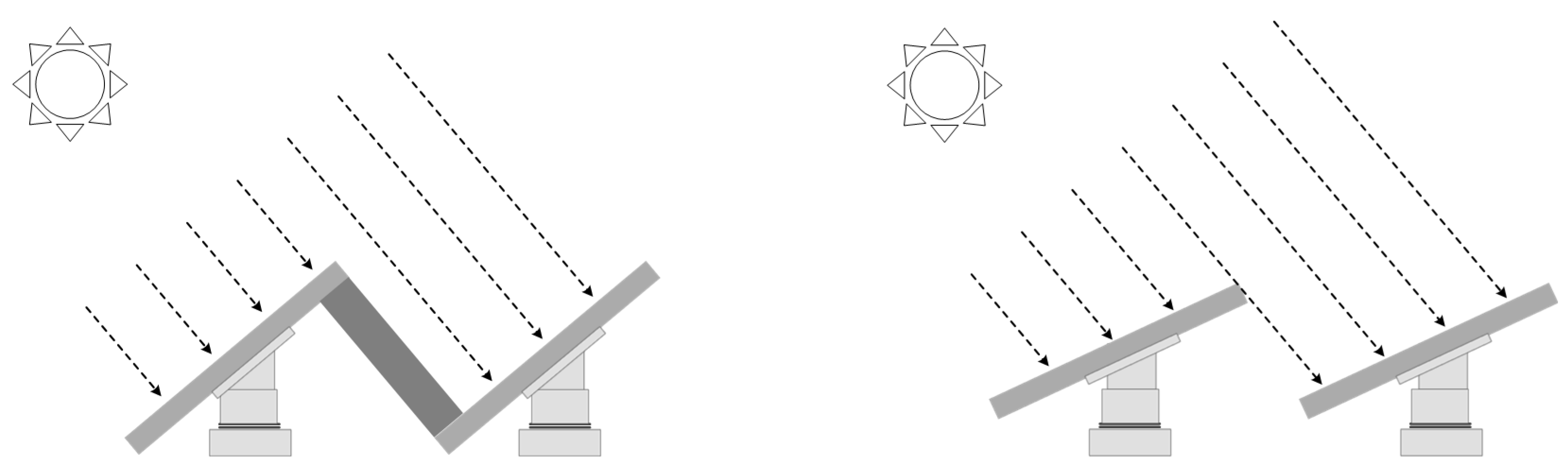
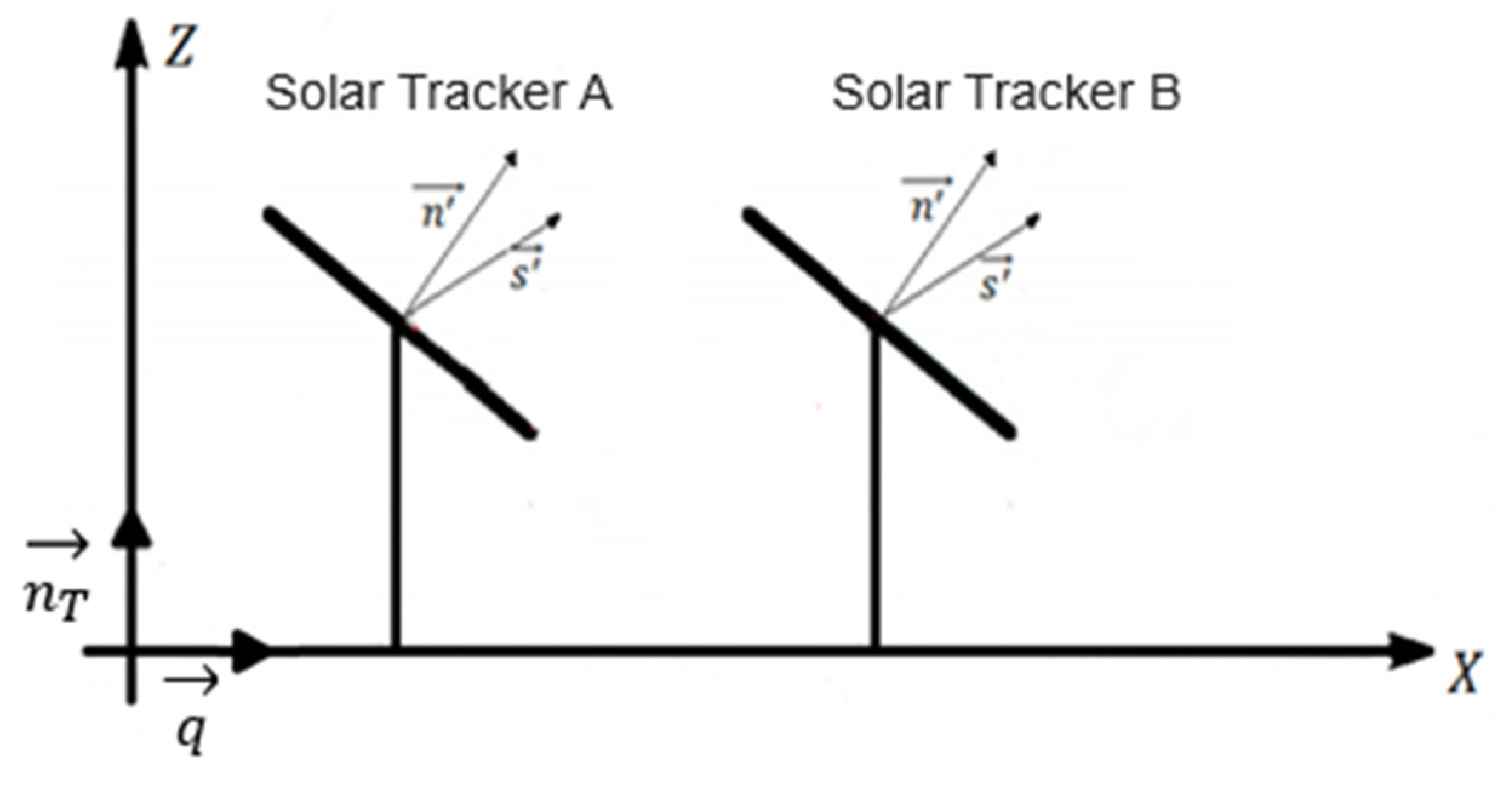
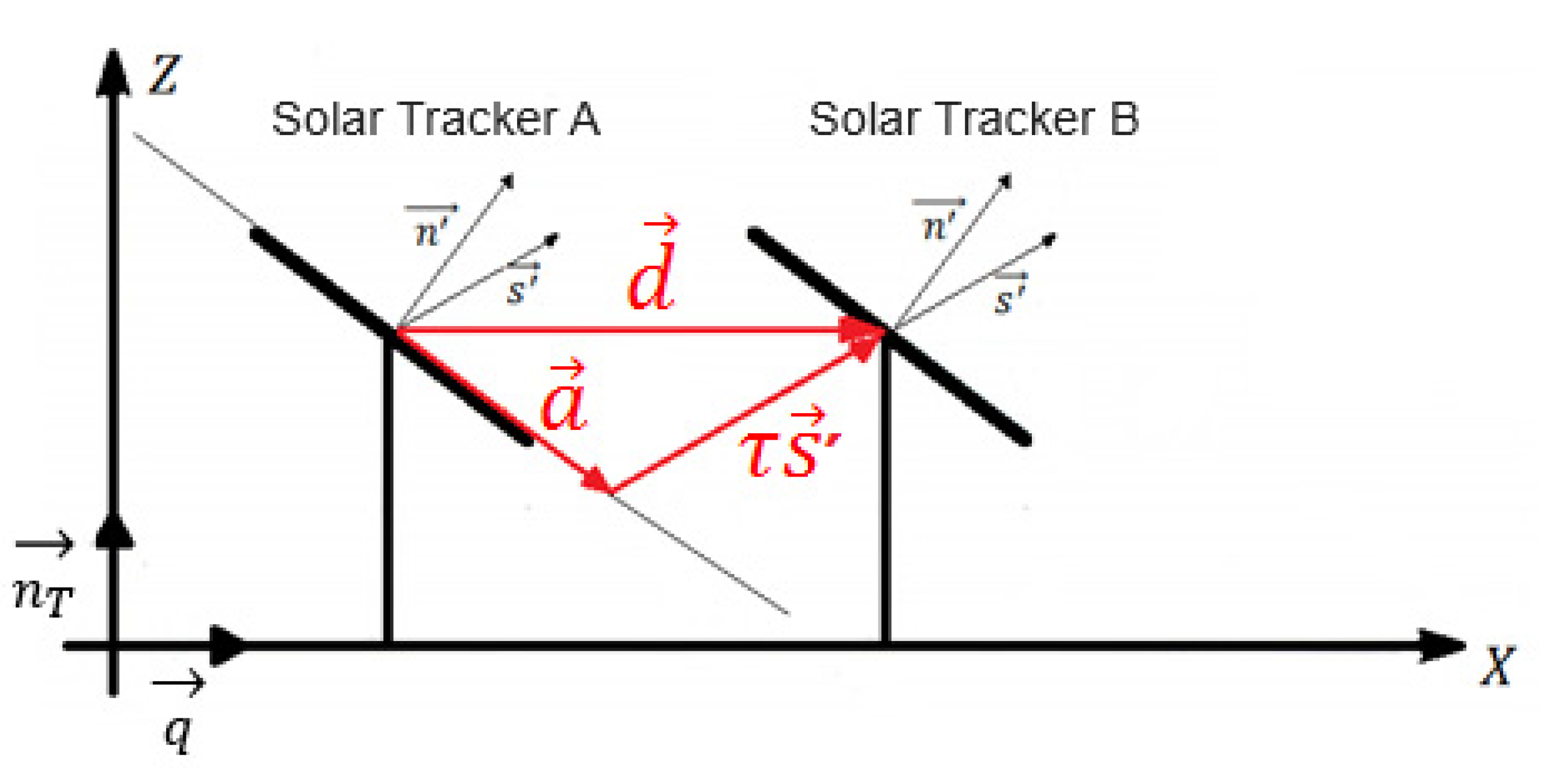
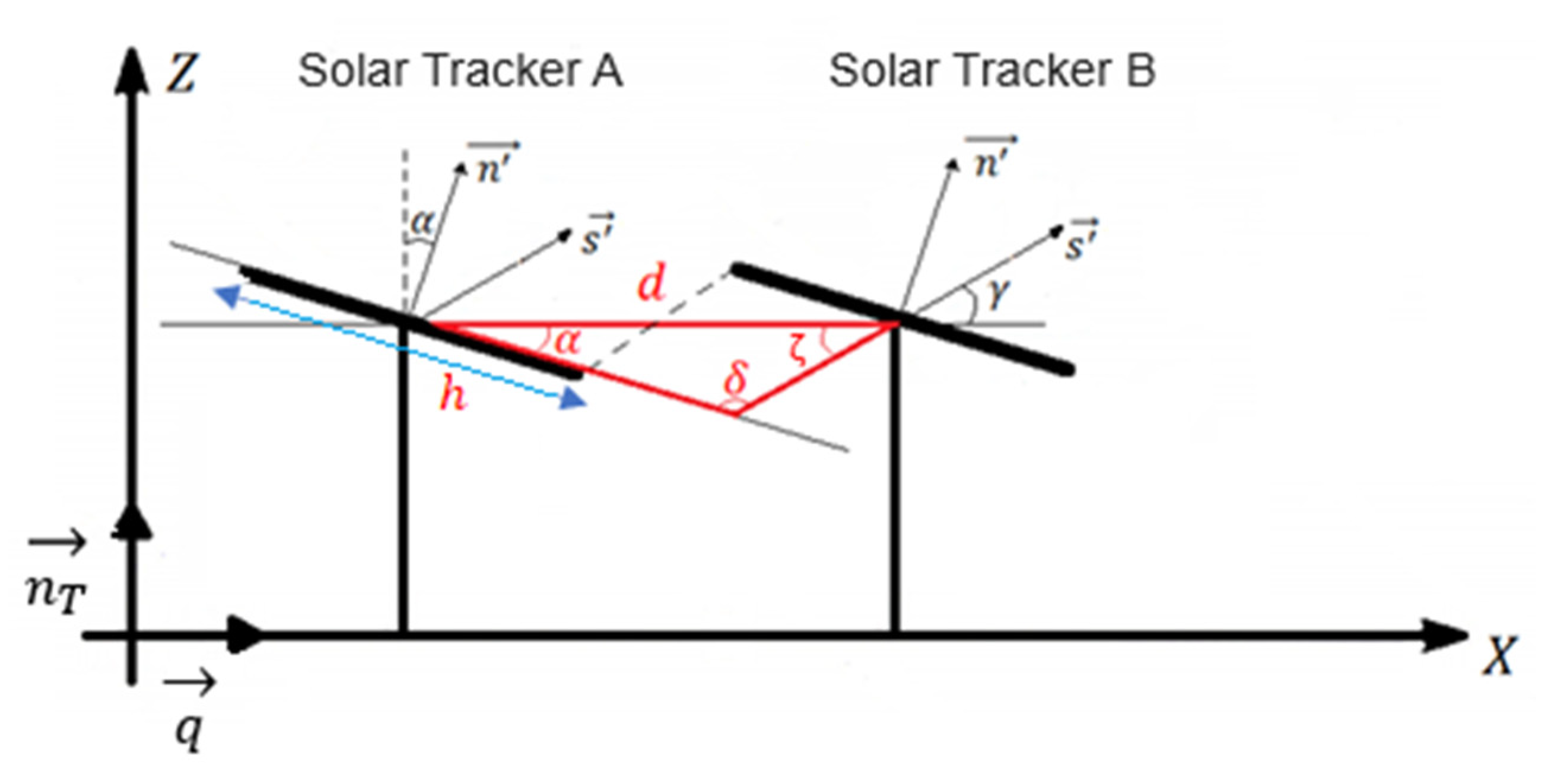
2.3. Backtracking
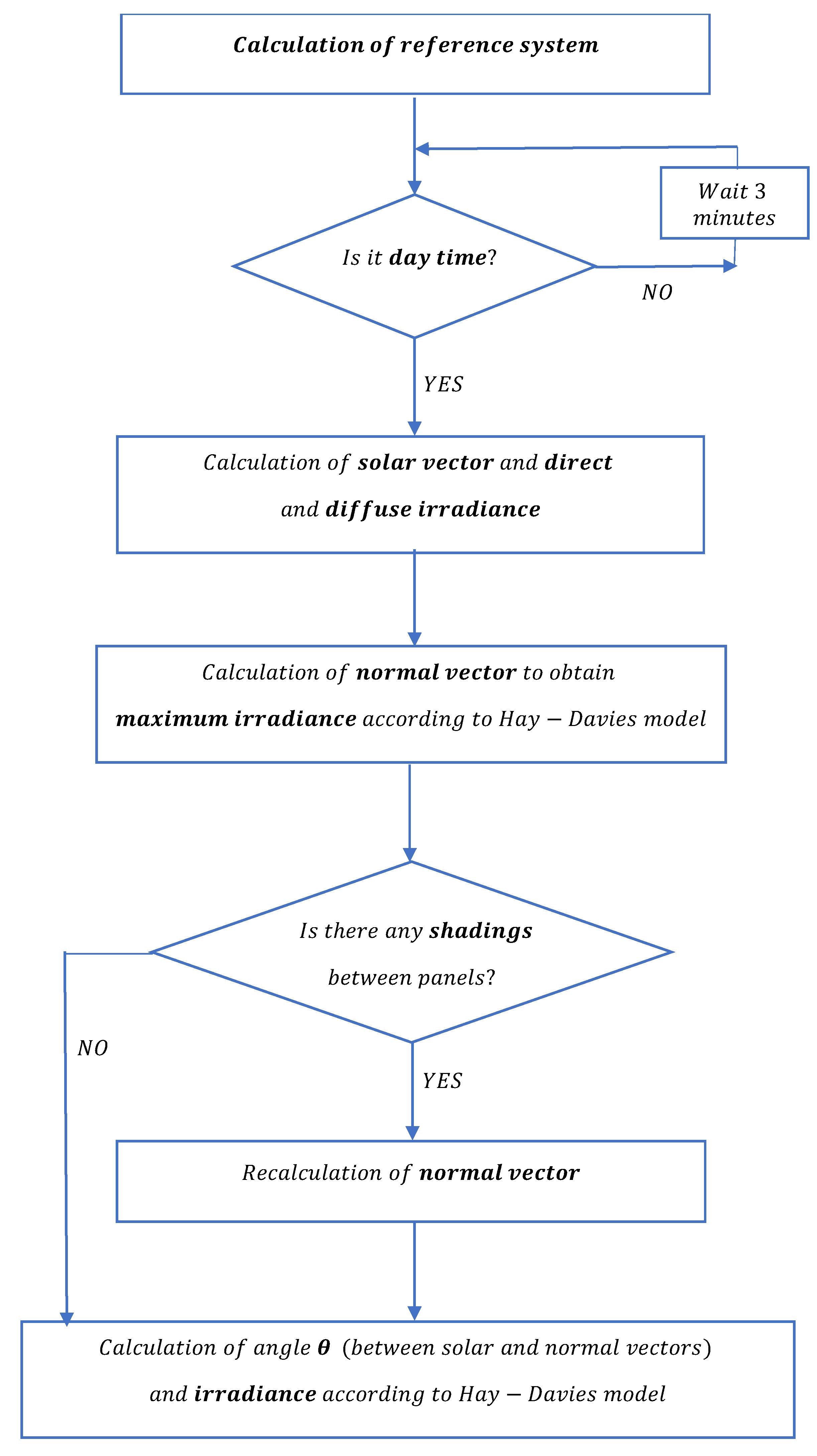
2.4. Software Applications for Analysis
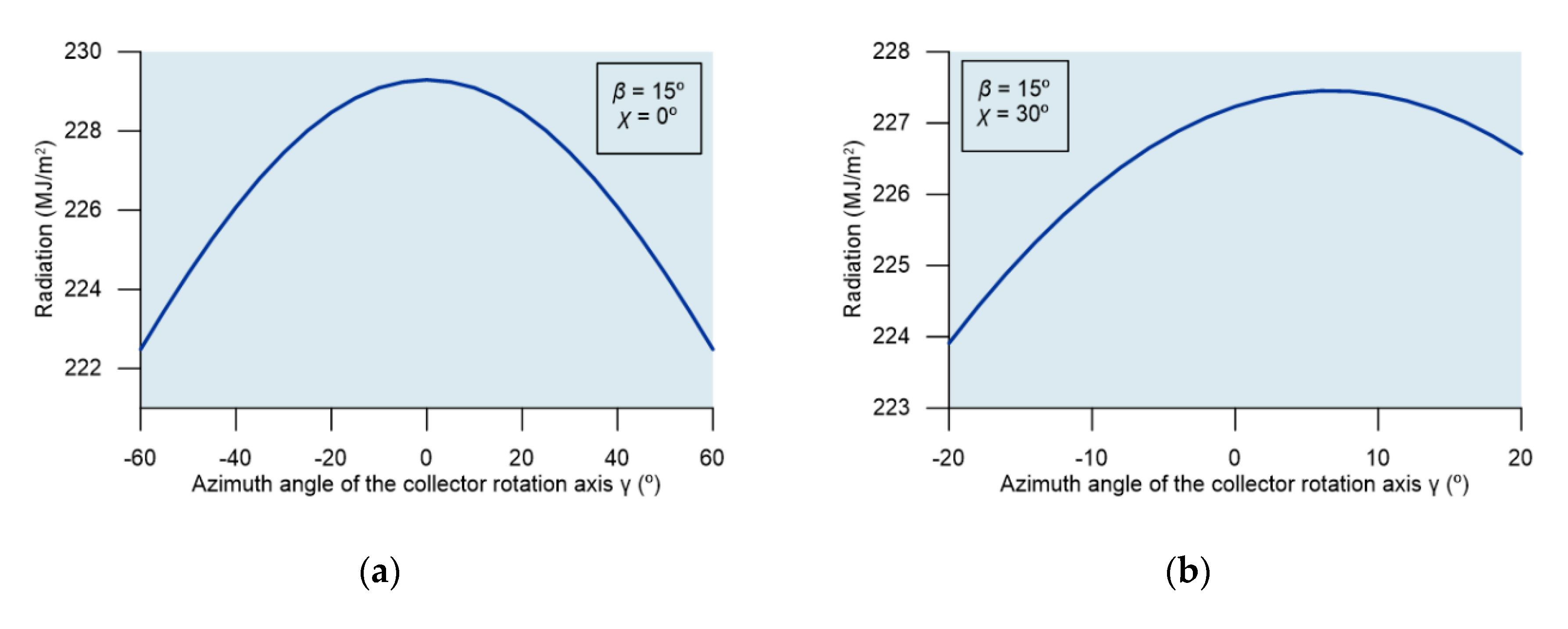
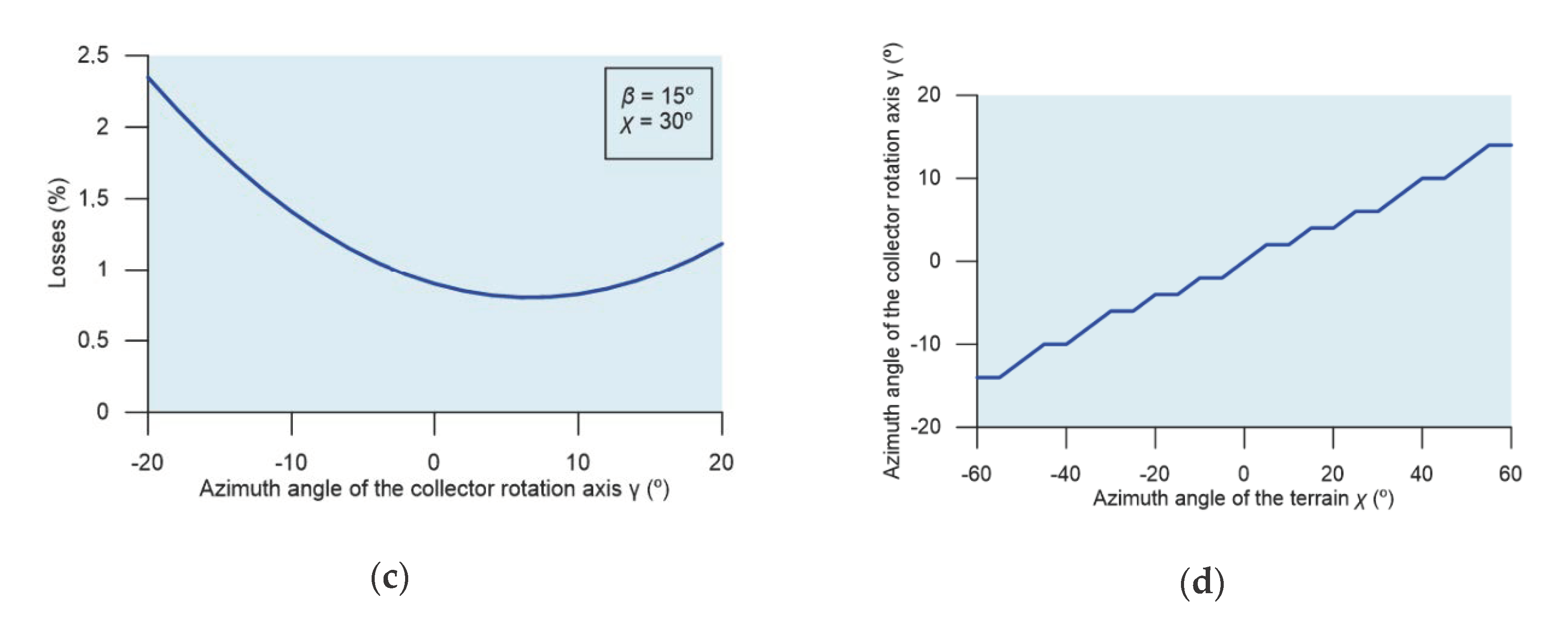
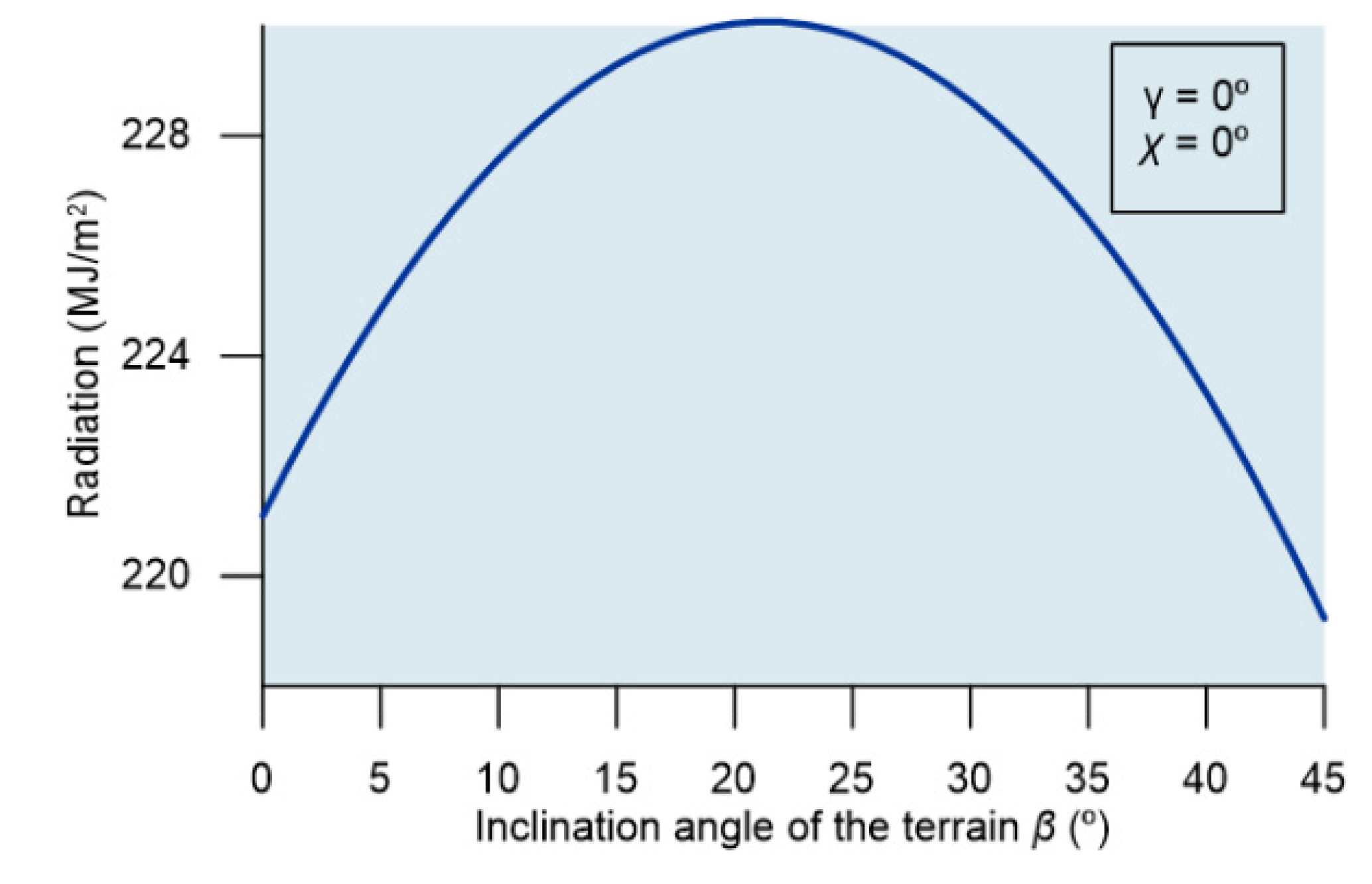
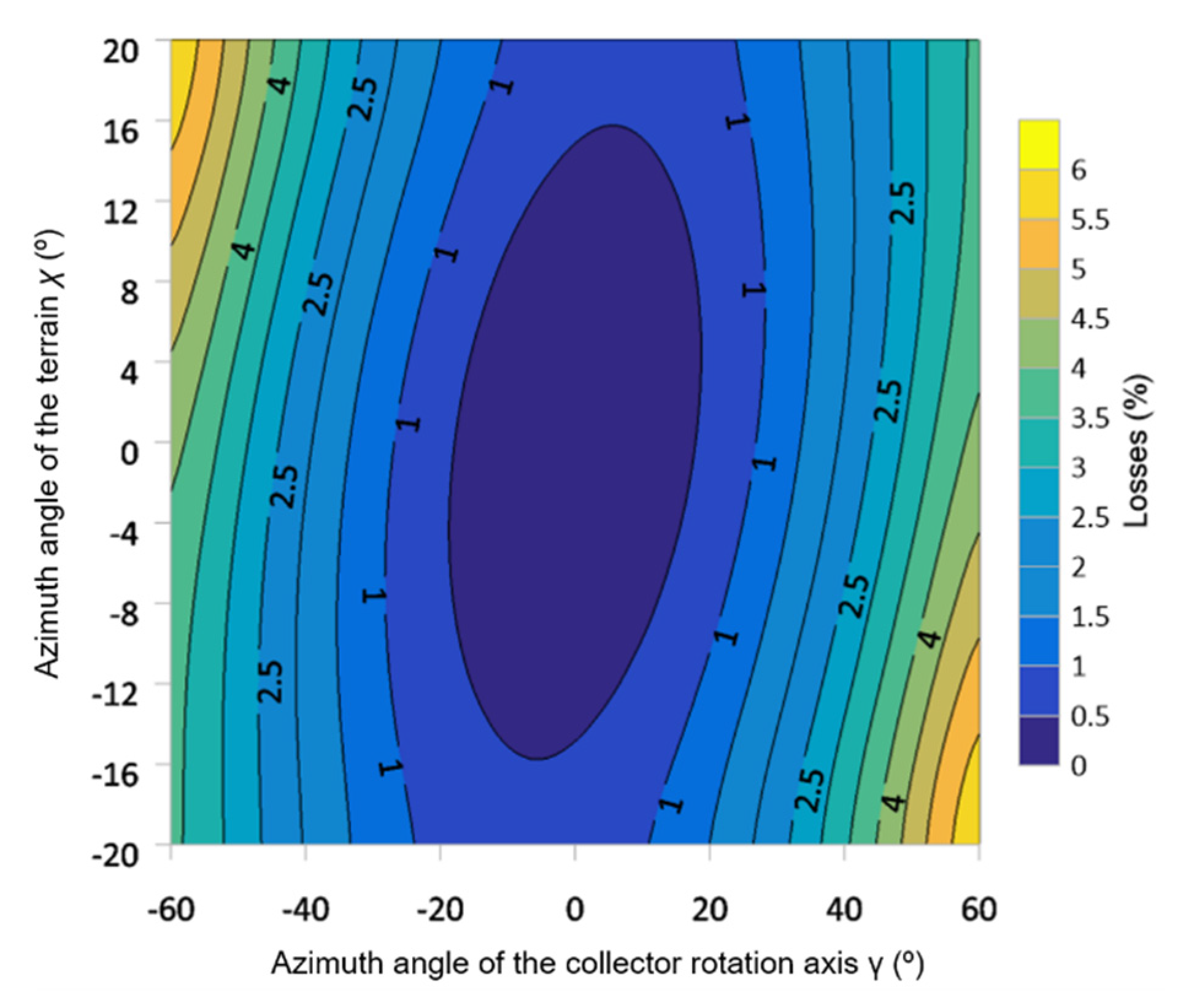
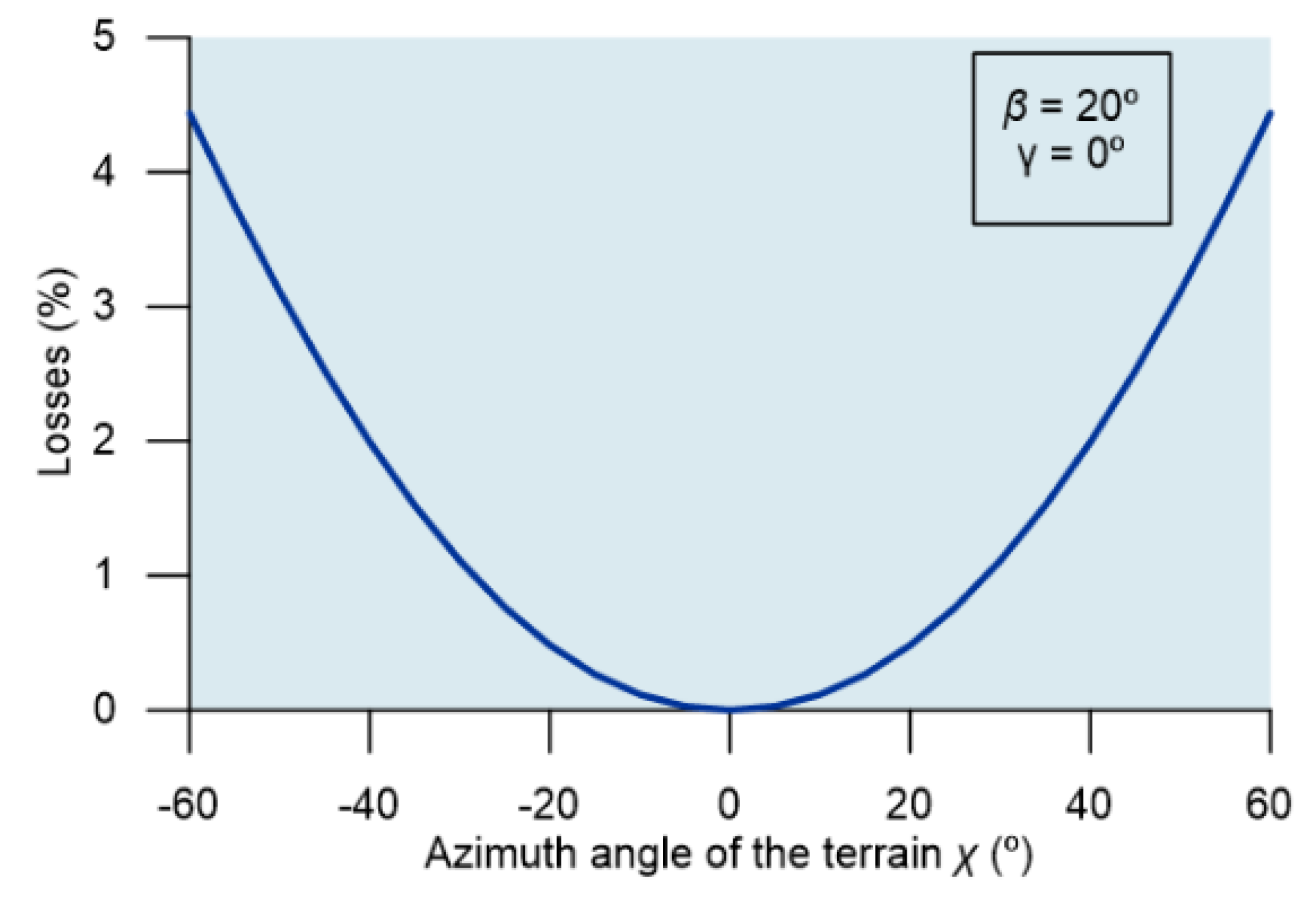
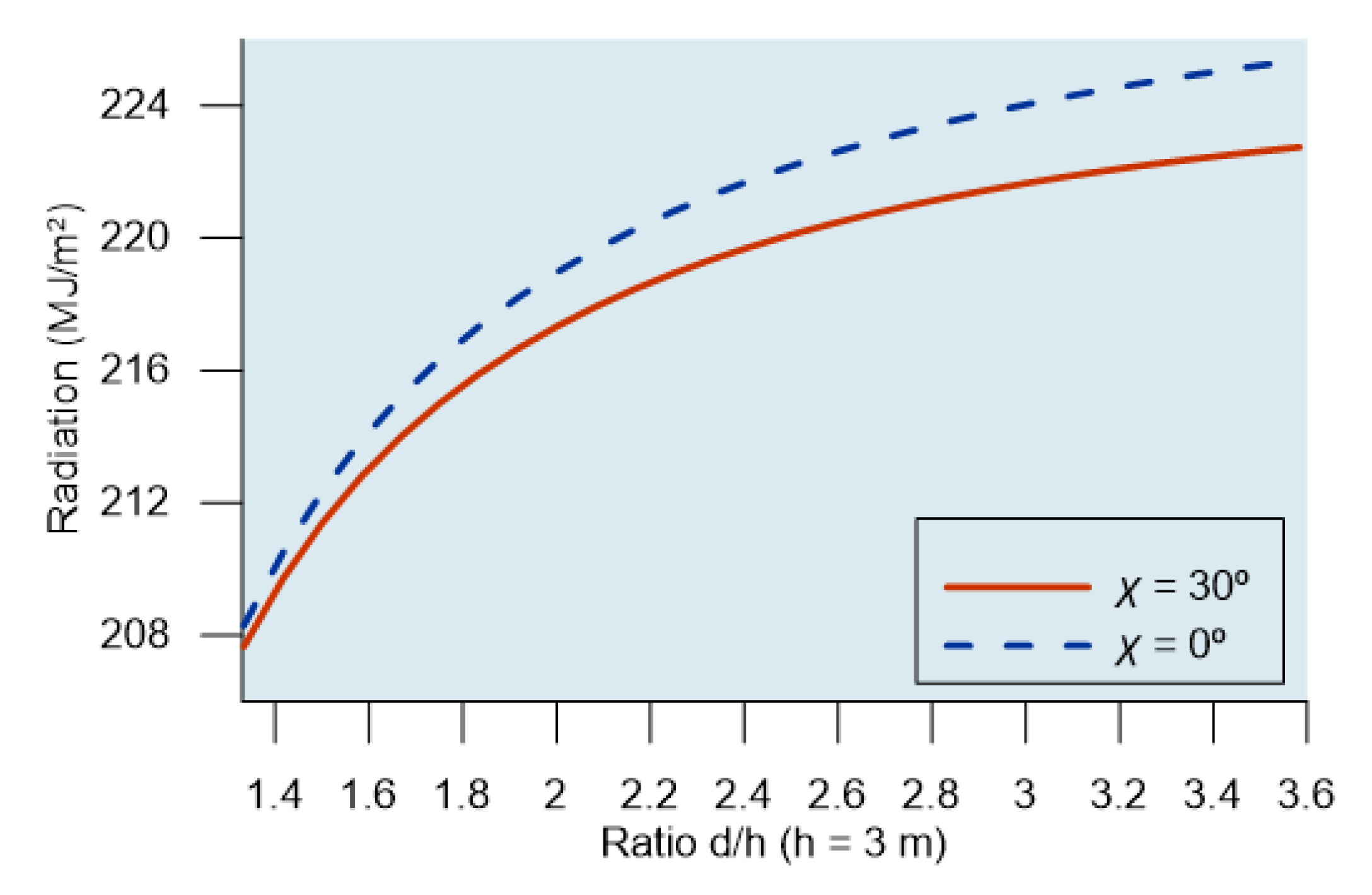
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| projection vector of the solar panel being studied for shading | |
| distance between the centers of two adjacent solar collectors | |
| unit vector contained in the collector rotation axis | |
| ground cover ratio | |
| collector width | |
| unit vectors associated with a local Cartesian system | |
| global solar irradiance on the tilted collector | |
| direct solar irradiance on the horizontal plane | |
| diffuse solar irradiance | |
| extraterrestrial irradiance | |
| normal vector to the surface | |
| optimal normal vector to the surface | |
| components of optimal normal vector to the surface | |
| normal terrain vector | |
| unit vector perpendicular to ground normal vector | |
| perpendicular vector to and | |
| solar vector | |
| components of solar vector | |
| optimal solar vector | |
| components of optimal solar vector | |
| irradiance gradient | |
| Greek Letters | |
| α | elevation angle of the collector |
| inclination angle of the terrain | |
| γ | azimuth angle of the collector rotation axis |
| solar declination | |
| inclination angle of the collector | |
| angle of incidence of sunbeams on the inclined plane | |
| solar zenith angle | |
| Lagrange multipliers | |
| albedo | |
| scalar multiplying solar vector to accomplish parallelogram rule | |
| latitude | |
| Lagrange function | |
| azimuth of the terrain | |
| Earth’s rotation speed | |
References
- Carballo, J.A.; Bonilla, J.; Roca, L.; Berenguel, M. New low-cost solar tracking system based on open source hardware for educational purposes. Sol. Energy 2018, 174, 826–836. [Google Scholar] [CrossRef]
- United Nations. The Sustainable Development Goals Report 2019; United Nations Publications (Department of Economic and Social Affairs): Herndon, VA, USA, 2019. [Google Scholar]
- Ribó-Pérez, D.; Van der Weijde, A.H.; Álvarez-Bel, C. Effects of self-generation in imperfectly competitive electricity markets: The case of Spain. Energy Policy 2019, 133, 110920. [Google Scholar] [CrossRef]
- International Renewable Energy Agency. Renewable Power Generation Costs in 2019; International Renewable Energy Agency: Abu Dhabi, UAE, 2020; ISBN 978-92-9260-244-4. [Google Scholar]
- Kavlak, G.; McNerney, J.; Trancik, J.E. Evaluating the causes of cost reduction in photovoltaic modules. Energy Policy 2018, 123, 700–710. [Google Scholar] [CrossRef]
- Hua, Z.; Ma, C.; Lian, J.; Pang, X.; Yang, W. Optimal capacity allocation of multiple solar trackers and storage capacity for utility-scale photovoltaic plants considering output characteristics and complementary demand. Appl. Energy 2019, 238, 721–733. [Google Scholar] [CrossRef]
- Hafez, A.Z.; Yousef, A.M.; Harag, N.M. Solar tracking systems: Technologies and trackers drive types—A review. Renew. Sustain. Energy Rev. 2018, 91, 754–782. [Google Scholar] [CrossRef]
- Nsengiyumva, W.; Chen, S.G.; Hu, L.; Chen, X. Recent advancements and challenges in Solar Tracking Systems (STS): A review. Renew. Sustain. Energy Rev. 2018, 81, 250–279. [Google Scholar] [CrossRef]
- Koussa, M.; Cheknane, A.; Hadji, S.; Haddadi, M.; Noureddine, S. Measured and modelled improvement in solar energy yield from flat plate photovoltaic systems utilizing different tracking systems and under a range of environmental conditions. Appl. Energy 2011, 88, 1756–1771. [Google Scholar] [CrossRef]
- Bahrami, A.; Okoye, C.O.; Atikol, U. The effect of latitude on the performance of different solar trackers in Europe and Africa. Appl. Energy 2016, 177, 896–906. [Google Scholar] [CrossRef]
- Abdallah, S.; Nijmeh, S. Two axes sun tracking system with PLC control. Energy Convers. Manag. 2004, 45, 1931–1939. [Google Scholar] [CrossRef]
- Braun, J.E.; Mitchell, J.C. Solar geometry for fixed and tracking surfaces. Sol. Energy 1983, 31, 439–444. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013; ISBN 9781118671603. [Google Scholar]
- Narvarte, L.; Lorenzo, E. Tracking and ground cover ratio. Prog. Photovolt. Res. Appl. 2008, 16, 703–714. [Google Scholar] [CrossRef]
- Parkin, R.E. Solar angles revisited using a general vector approach. Sol. Energy 2010, 84, 912–916. [Google Scholar] [CrossRef]
- Sproul, A.B. Derivation of the solar geometric relationships using vector analysis. Renew. Energy 2007, 32, 1187–1205. [Google Scholar] [CrossRef]
- Fan, X.; Deng, F.; Chen, J. Voltage band analysis for maximum power point tracking of stand-alone PV systems. Sol. Energy 2017, 144, 221–231. [Google Scholar] [CrossRef]
- Satpathy, P.R.; Sharma, R. Diffusion charge compensation strategy for power balancing in capacitor-less photovoltaic modules during partial shading. Appl. Energy 2019, 255. [Google Scholar] [CrossRef]
- Seyedmahmoudian, M.; Horan, B.; Soon, T.K.; Rahmani, R.; Than Oo, A.M.; Mekhilef, S.; Stojcevski, A. State of the art artificial intelligence-based MPPT techniques for mitigating partial shading effects on PV systems—A review. Renew. Sustain. Energy Rev. 2016, 64, 435–455. [Google Scholar] [CrossRef]
- Belhachat, F.; Larbes, C. Modeling, analysis and comparison of solar photovoltaic array configurations under partial shading conditions. Sol. Energy 2015, 120, 399–418. [Google Scholar] [CrossRef]
- Saint-Drenan, Y.M.; Barbier, T. Data-analysis and modelling of the effect of inter-row shading on the power production of photovoltaic plants. Sol. Energy 2019, 184, 127–147. [Google Scholar] [CrossRef]
- Perpiñán, O. Cost of energy and mutual shadows in a two-axis tracking PV system. Renew. Energy 2012, 43, 331–342. [Google Scholar] [CrossRef]
- Deline, C.; Dobos, A.; Janzou, S.; Meydbray, J.; Donovan, M. A simplified model of uniform shading in large photovoltaic arrays. Sol. Energy 2013, 96, 274–282. [Google Scholar] [CrossRef]
- Martínez-Moreno, F.; Muñoz, J.; Lorenzo, E. Experimental model to estimate shading losses on PV arrays. Sol. Energy Mater. Sol. Cells 2010, 94, 2298–2303. [Google Scholar] [CrossRef]
- Panico, D.; Garvison, P.; Wenger, H.; Shugar, D. Backtracking: A novel strategy for tracking PV systems. In Proceedings of the Conference Record of the Twenty-Second IEEE Photovoltaic Specialists Conference, Las Vegas, NV, USA, 7–11 October 1991; Volume 1, pp. 668–673. [Google Scholar] [CrossRef]
- Antonanzas, J.; Urraca, R.; Martinez-de-Pison, F.J.; Antonanzas, F. Optimal solar tracking strategy to increase irradiance in the plane of array under cloudy conditions: A study across Europe. Sol. Energy 2018, 163, 122–130. [Google Scholar] [CrossRef]
- Fernández-Ahumada, L.M.; Ramírez-Faz, J.; López-Luque, R.; Varo-Martínez, M.; Moreno-García, I.M.; Casares de la Torre, F. A novel backtracking approach for two-axis solar PV tracking plants. Renew. Energy 2020, 145, 1214–1221. [Google Scholar] [CrossRef]
- Kelly, N.A.; Gibson, T.L. Improved photovoltaic energy output for cloudy conditions with a solar tracking system. Sol. Energy 2009, 83, 2092–2102. [Google Scholar] [CrossRef]
- Quesada, G.; Guillon, L.; Rousse, D.R.; Mehrtash, M.; Dutil, Y.; Paradis, P.-L. Tracking strategy for photovoltaic solar systems in high latitudes. Energy Convers. Manag. 2015, 103, 147–156. [Google Scholar] [CrossRef]
- Fernández-Ahumada, L.M.; Casares, F.J.; Ramírez-Faz, J.; López-Luque, R. Mathematical study of the movement of solar tracking systems based on rational models. Sol. Energy 2017, 150, 20–29. [Google Scholar] [CrossRef]
- Hay, J.E. Calculating solar radiation for inclined surfaces: Practical approaches. Renew. Energy 1993, 3, 373–380. [Google Scholar] [CrossRef]
- Mousazadeh, H.; Keyhani, A.; Javadi, A.; Mobli, H.; Abrinia, K.; Sharifi, A. A review of principle and sun-tracking methods for maximizing solar systems output. Renew. Sustain. Energy Rev. 2009, 13, 1800–1818. [Google Scholar] [CrossRef]
- Muneer, T. Solar radiation model for Europe. Build. Serv. Eng. Res. Technol. 1990, 11, 153–163. [Google Scholar] [CrossRef]
- Perez, R.; Ineichen, P.; Seals, R.; Michalsky, J.; Stewart, R. Modeling daylight availability and irradiance components from direct and global irradiance. Sol. Energy 1990, 44, 271–289. [Google Scholar] [CrossRef]
- Diez-Mediavilla, M.; De Miguel, A.; Bilbao, J. Measurement and comparison of diffuse solar irradiance models on inclined surfaces in Valladolid (Spain). Energy Convers. Manag. 2005, 46, 2075–2092. [Google Scholar] [CrossRef]
- Loutzenhiser, P.G.; Manz, H.; Felsmann, C.; Strachan, P.A.; Frank, T.; Maxwell, G.M. Empirical validation of models to compute solar irradiance on inclined surfaces for building energy simulation. Sol. Energy 2007, 81, 254–267. [Google Scholar] [CrossRef]
- Mubarak, R.; Hofmann, M.; Riechelmann, S.; Seckmeyer, G. Comparison of modelled and measured tilted solar irradiance for photovoltaic applications. Energies 2017, 10, 1688. [Google Scholar] [CrossRef]
- Collares-Pereira, M.; Rabl, A. The average distribution of solar radiation-correlations between diffuse and hemispherical and between daily and hourly insolation values. Sol. Energy 1979. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez-Uceda, F.J.; Moreno-Garcia, I.M.; Jiménez-Martínez, J.M.; López-Luque, R.; Fernández-Ahumada, L.M. Analysis of the Influence of Terrain Orientation on the Design of PV Facilities with Single-Axis Trackers. Appl. Sci. 2020, 10, 8531. https://doi.org/10.3390/app10238531
Gómez-Uceda FJ, Moreno-Garcia IM, Jiménez-Martínez JM, López-Luque R, Fernández-Ahumada LM. Analysis of the Influence of Terrain Orientation on the Design of PV Facilities with Single-Axis Trackers. Applied Sciences. 2020; 10(23):8531. https://doi.org/10.3390/app10238531
Chicago/Turabian StyleGómez-Uceda, Francisco J., Isabel M. Moreno-Garcia, José M. Jiménez-Martínez, Rafael López-Luque, and Luis M. Fernández-Ahumada. 2020. "Analysis of the Influence of Terrain Orientation on the Design of PV Facilities with Single-Axis Trackers" Applied Sciences 10, no. 23: 8531. https://doi.org/10.3390/app10238531
APA StyleGómez-Uceda, F. J., Moreno-Garcia, I. M., Jiménez-Martínez, J. M., López-Luque, R., & Fernández-Ahumada, L. M. (2020). Analysis of the Influence of Terrain Orientation on the Design of PV Facilities with Single-Axis Trackers. Applied Sciences, 10(23), 8531. https://doi.org/10.3390/app10238531





