A Novel Method for Building Displacement Based on Multipopulation Genetic Algorithm
Abstract
1. Introduction
2. Related Work
2.1. Sequential Approaches
2.2. Optimal Approaches
2.2.1. Combinatorial Optimization Approaches
2.2.2. Functional Optimization Approaches
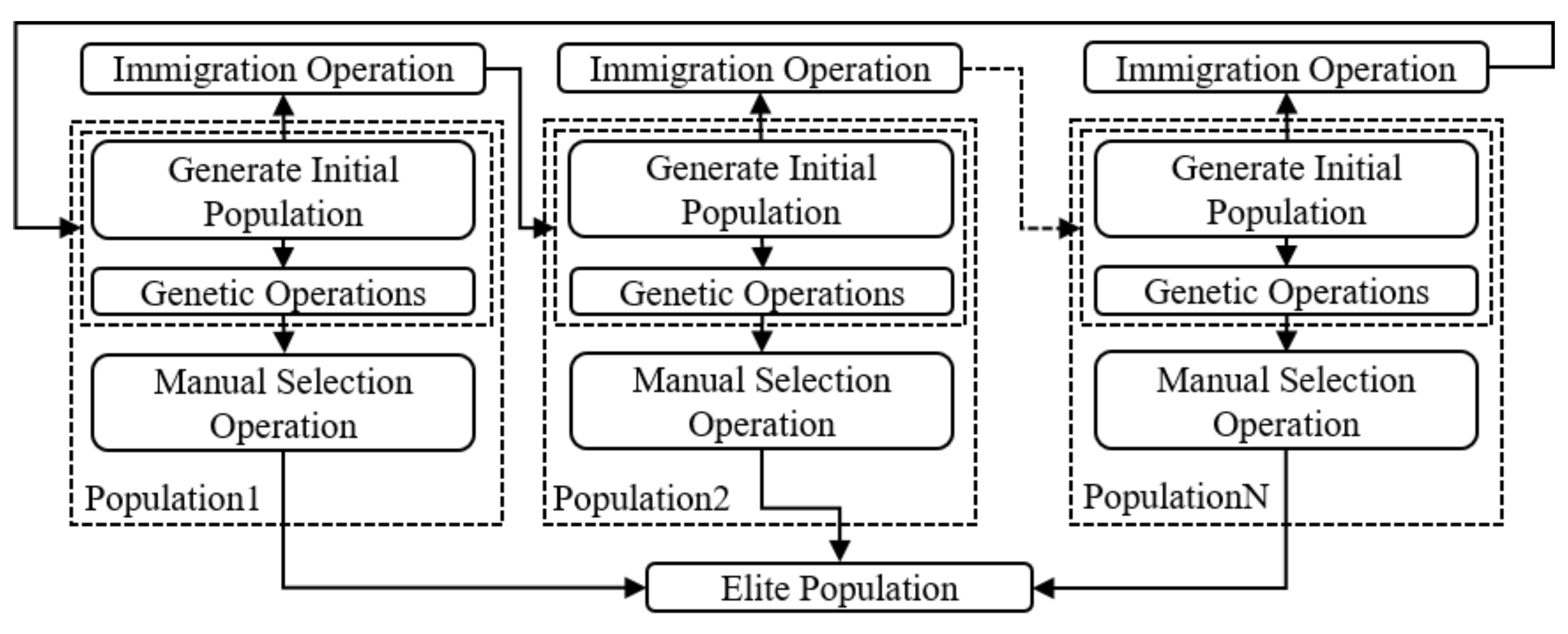
3. Introducing BDMPGA
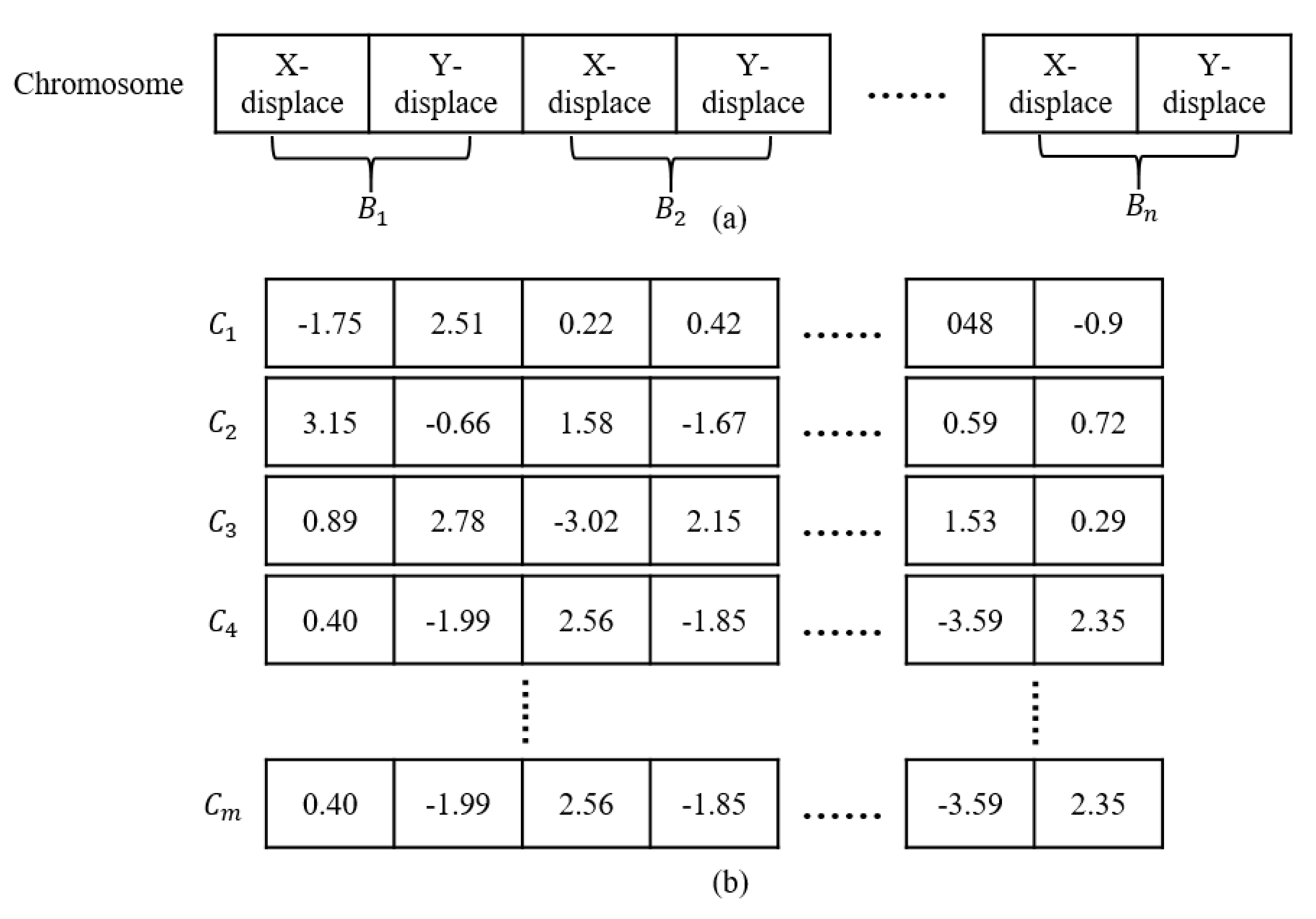
3.1. Chromosomal Encoding
3.2. Genetic Operations
3.3. Immigration Operation
3.4. Manual Selection Operation
- Initialize the elite population, which is used to preserve the best individual in each population during evolution. The number of individuals in the elite population is the number of populations.
- The individual with the highest fitness value in each population is selected and preserved in the elite population.
- Update the elite populations. If a subpopulation produces better individual, then the optimal individual is selected to update the corresponding individual in the elite population; otherwise, the elite population remains unchanged.
3.5. Objective Function and Fitness Function
- Number of conflicts between buildings. For two neighboring buildings and , is the minimum distance between buildings and . represents a spatial conflict between buildings and . If is less than then predefined distance threshold, then ; otherwise, . Thus, the number of conflicts between all buildings can be expressed as:
- Number of conflicts between buildings and roads. For building and road , is the minimum distance between building and road , and represents a spatial conflict between building and road . If is less than then predefined distance threshold, then ; otherwise, . Thus, the number of conflicts between buildings and roads can be expressed as:
- Total displacement distances of all the buildings. This measure is used to evaluate the positional accuracy after displacement. The displacement must be within a certain range of the positional accuracy, and the smaller the total displacement distances are, the better the positional accuracy is maintained. The total displacement distances of all the buildings are calculated by summing the displacement distances in the X and Y directions of all the buildings. The expression is as follows:
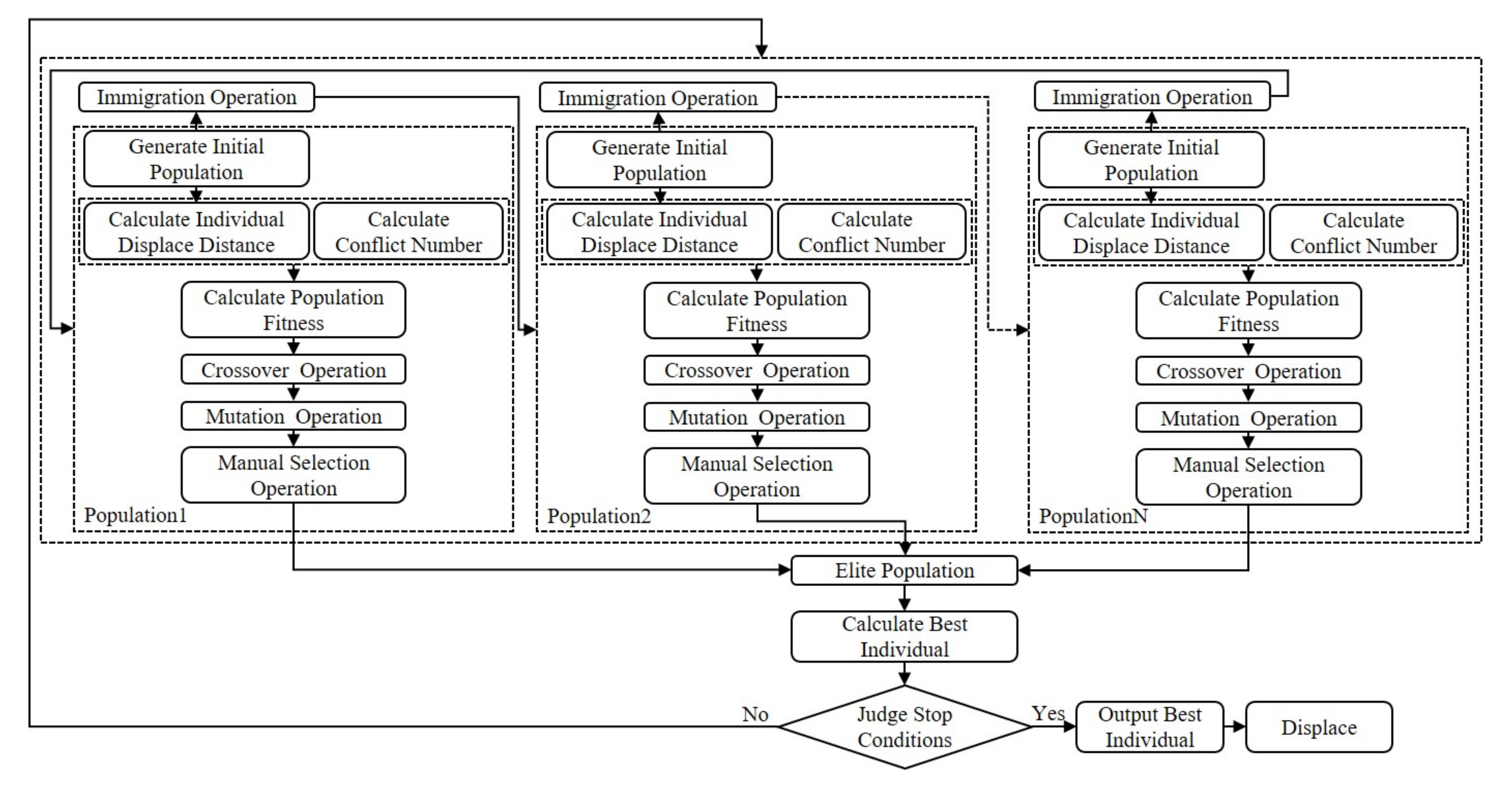
3.6. Algorithm Flowchart
- According to the given experimental data, the number of chromosomes in each population is determined. After that, populations are initialized by the real coding method.
- Detect spatial conflicts. The constraint Delaunay triangulation (CDT) is used to construct the skeleton line, and then the weighted width of the skeleton line is calculated. By comparing with the minimum distance threshold, the number of conflicts between buildings and between buildings and roads are calculated.
- Calculate the fitness value of each individual in each population.
- Perform crossover and mutation operations on each population to produce a new population.
- Perform immigration operations among the population. The optimal individual and the worst individual in each population were selected according to the fitness value. Then the optimal individual in the th population replaces the worst individual in the th population, so as to realize the information exchange between the two adjacent populations.
- Perform manual selection operation on each population. The optimal individual in each population is selected by using a manual selection operation and stored in the elite population to update the elite population.
- Judge termination condition. If the termination condition is satisfied, then the best individual in the elite population is obtained as the optimal displacement solution. If the termination condition is not satisfied, then the algorithm returns to step (2) to start the next iteration.
4. Experiments and Evaluations
4.1. Parameter Setting
4.2. Analysis and Evaluation of Experimental Results
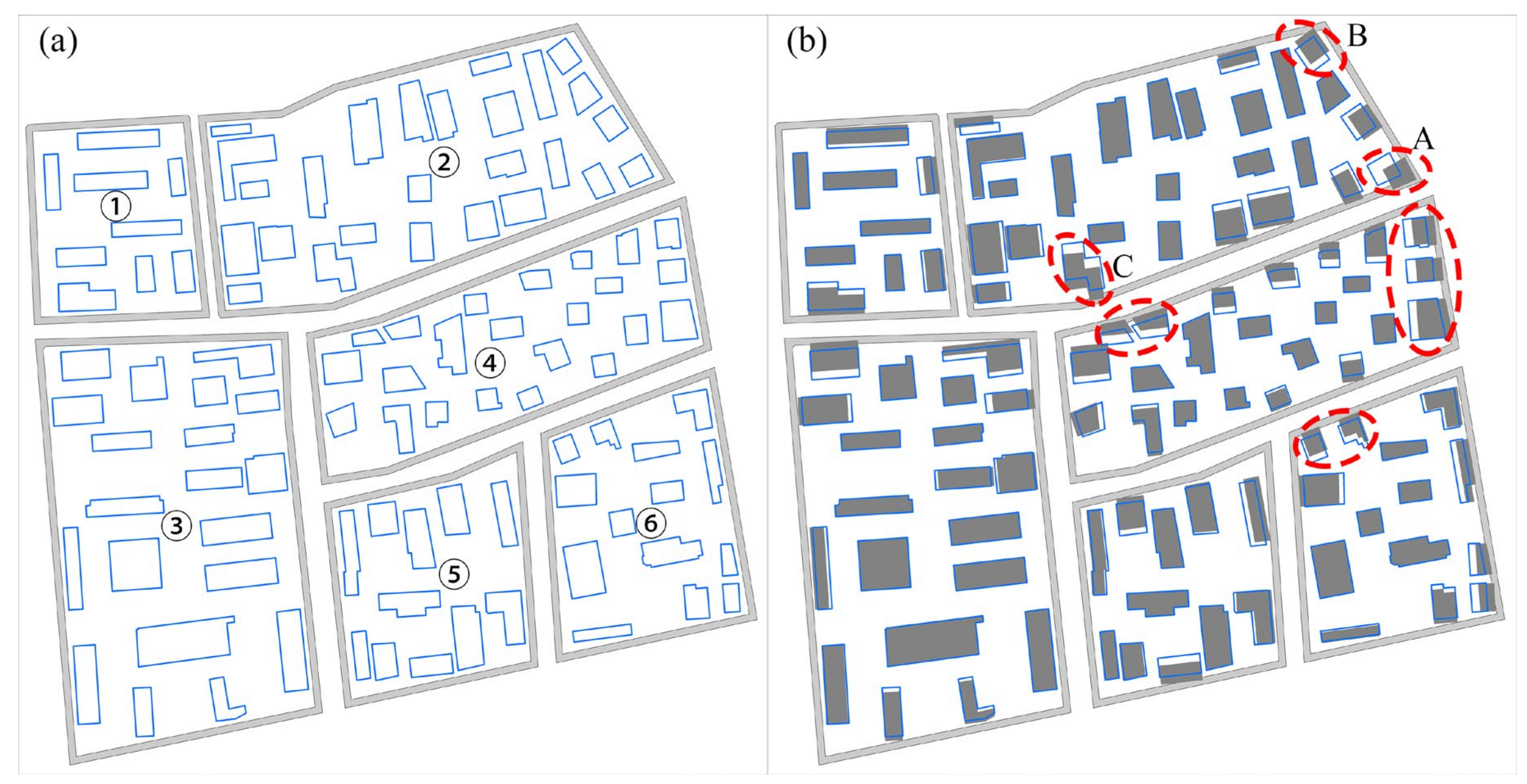
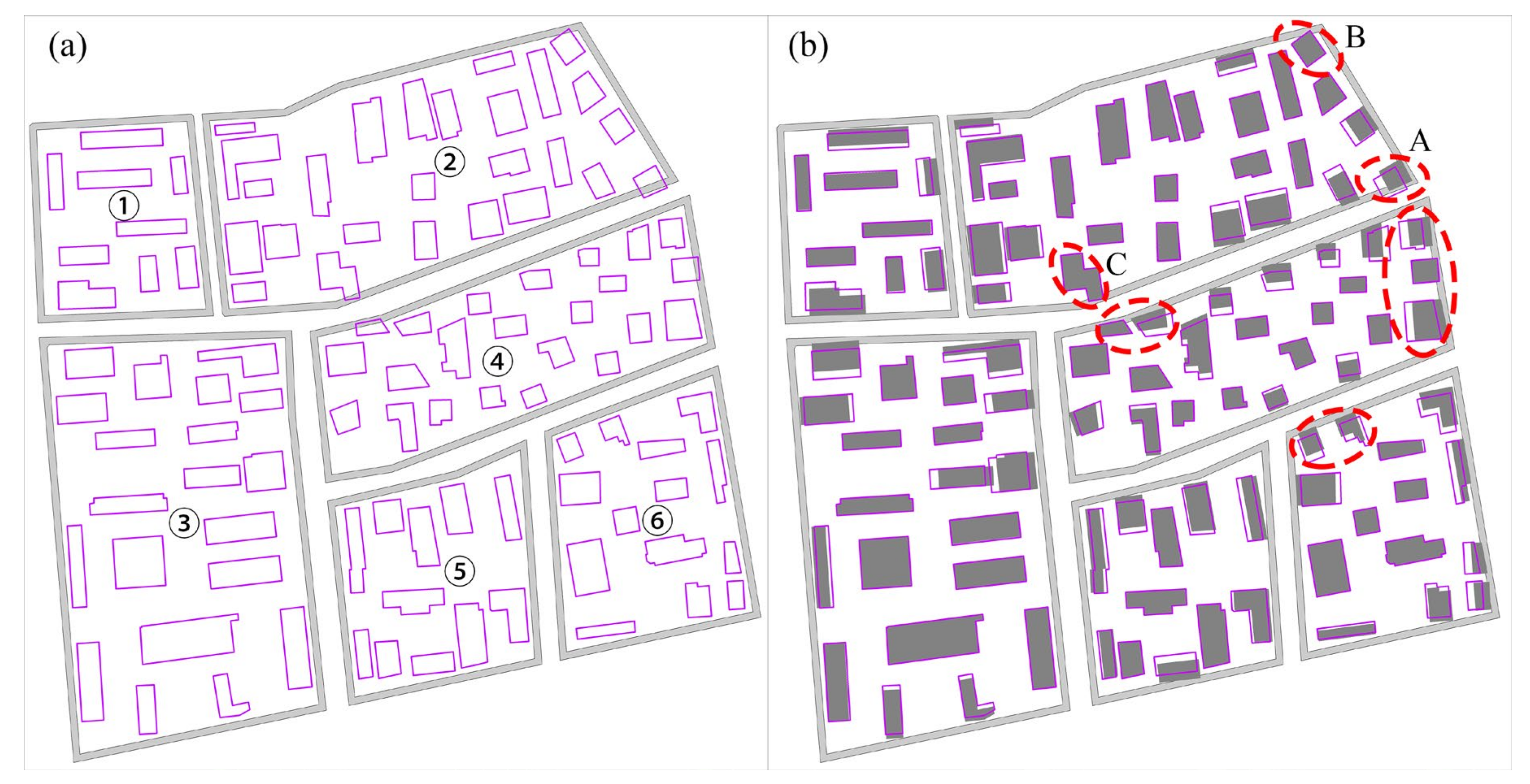
- Compared with the GA and the IGA, the proposed BDMPGA can generate more reasonable displacement results. For example, as shown in local area No.A in Table 5, when a building is located at an acute corner and is conflicted with multiple roads, the BDMPGA can better solve the conflict by moving a longer distance, and the displacement direction is the resultant direction of multiple conflicting roads. When a building is located at an obtuse corner and is conflicted with multiple roads, as shown in local area No.B in Table 5, the BDMPGA will make the building move a short distance to resolve the conflict. However, the GA cannot resolve multiple conflicts and even aggravate the conflicts. The IGA method only resolves some of the conflicts.
- The proposed BDMPGA has a better ability than the GA and IGA to maintain building positional accuracy. For example, as show in local area No.C in Table 5, the IGA tends to move long distances to resolve the conflict. However, the proposed BDMPGA only makes the conflict building move a shorter distance and satisfies the constraint condition of ensuring the positional accuracy of the building as much as possible while resolving the spatial conflicts. Table 6 shows the basic statistical information of the displacement distance for each method. As seen from the statistical information, the BDMPGA has a minimum displacement distance of 0.0 m, meaning that if a building does not conflict with surrounding objects, then it is not moved. The maximum displacement distance of the BDMPGA is 3.99 m, which meets the specified maximum displacement distance threshold (e.g., 0.5 mm). The total displacement distance of the BDMPGA is 133.19 m, less than 140.31 m of the GA and 149.71 m of the IGA, indicating that the positional accuracy of the BDMPGA is maintained well.
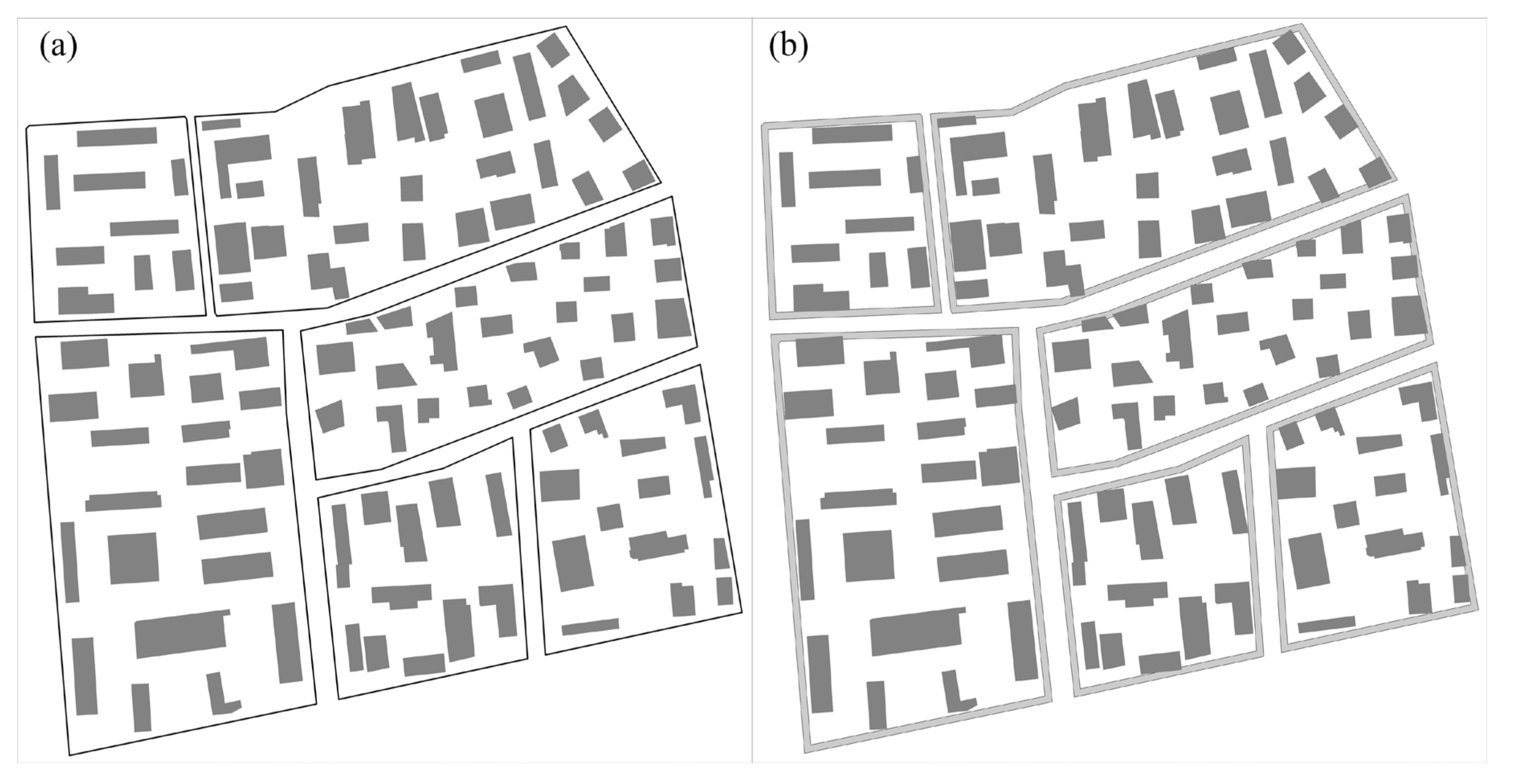
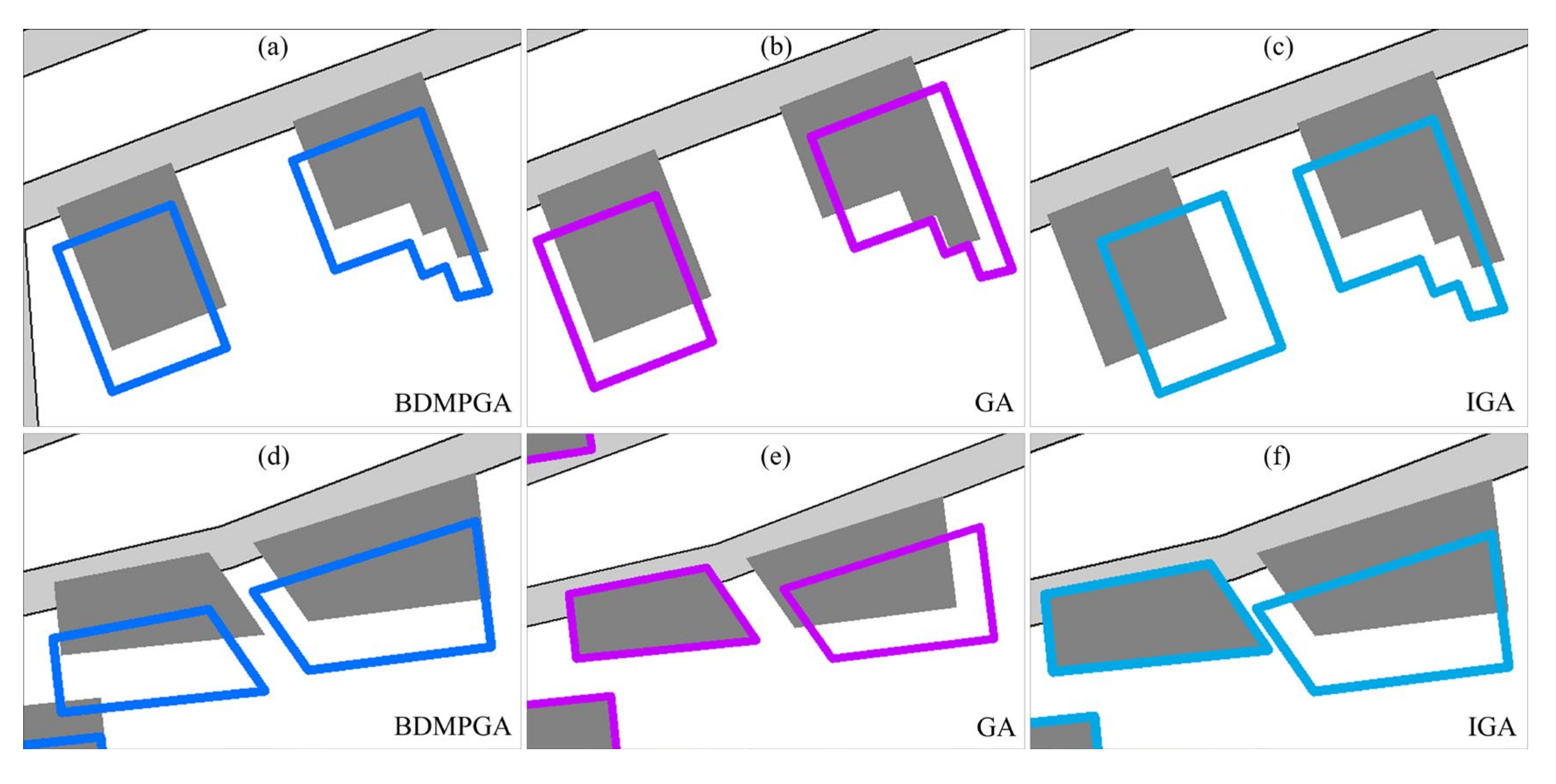
- Compared with the GA and IGA, the proposed BDMPGA can maintain the relative position between buildings during the displacement. For example, Figure 8a shows the displacement results of the BDMPGA, and the displacement results of the GA and the IGA are Figure 8b,c, respectively. By comparison, it can be seen that although both the GA and IGA can resolve spatial conflicts, the distance relations among buildings are changed after the displacement so that some buildings become closer (with the GA), while some become farther away (with the IGA). However, the proposed BDMPGA exhibits a good ability to avoid changing the relative position of the buildings because the conflicting buildings are all moving in the same direction and distance. Meanwhile, as shown in Figure 8d–f, two adjacent buildings are in conflict with the road, the GA and the IGA only move one building, and the conflict between the other buildings remains unresolved. At the same time, the GA increases the distance between buildings and the IGA produces a more serious secondary conflict. However, the proposed BDMPGA moves two buildings simultaneously and resolves all conflicts, which can keep the relative positions between buildings unchanged.
- Compared with the GA and IGA, the proposed BDMPGA can better maintain the linear arrangement and distribution pattern of buildings. For example, as shown in Figure 9, the comparative methods, including the GA and IGA, only move some buildings in the building group, which not only fails to solve all the spatial conflicts but also fails to maintain the arrangement and distribution pattern of the building group. However, the proposed BDMPGA has a better ability to overcome the shortcomings of the comparative methods because the BDMPGA takes the least preserving generation of the optimal individual as the termination condition, and the method will constantly optimize the shortest displacement distance after resolving spatial conflicts to ensure that the arrangement and distribution pattern of buildings do not change.
4.3. Limitations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, L.; Guo, Q.; Liu, Y.; Sun, Y.; Wei, Z. Contextual Building Selection Based on a Genetic Algorithm in Map Generalization. ISPRS Int. J. Geo Inf. 2017, 6, 271. [Google Scholar] [CrossRef]
- Ai, T.; Yin, H.; Shen, Y.; Yang, M.; Wang, L. A formal model of neighborhood representation and applications in urban building aggregation supported by Delaunay triangulation. PLoS ONE 2019, 14, e218877. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Ai, T.; Li, W.; Yang, M.; Feng, Y. A polygon aggregation method with global feature preservation using superpixel segmentation. Comput. Environ. Urban Syst. 2019, 75, 117–131. [Google Scholar] [CrossRef]
- Li, Z.; Choi, Y.H. Topographic Map Generalization: Association of Road Elimination with Thematic Attributes. Cartogr. J. 2002, 39, 153–166. [Google Scholar] [CrossRef]
- Regnauld, N. Contextual Building Typification in Automated Map Generalization. Algorithmica 2001, 30, 312–333. [Google Scholar] [CrossRef]
- Shen, Y.; Ai, T.; Li, J.; Wang, L.; Li, W. A tile-map-based method for the typification of artificial polygonal water areas considering the legibility. Comput. Geosci. 2020, 143, 104552. [Google Scholar] [CrossRef]
- Ai, T.A. Displacement of Building Cluster Based on Field Analysis. Acta Geodaetica Cartogr. Sin. 2004, 33, 89–94. [Google Scholar]
- Qi, Z.; Tinghua, A.; Xiang, Z. A Displacement Field Model to Resolve Multiple Spatial Conflicts. Acta Geodaetica Cartogr. Sin. 2013, 42, 615–620. [Google Scholar]
- Feng, Y.; Thiemann, F.; Sester, M. Learning Cartographic Building Generalization with Deep Convolutional Neural Networks. ISPRS Int. J. Geo Inf. 2019, 8, 258. [Google Scholar] [CrossRef]
- Yan, X.; Ai, T.; Yang, M.; Yin, H. A graph convolutional neural network for classification of building patterns using spatial vector data. ISPRS J. Photogramm. 2019, 150, 259–273. [Google Scholar] [CrossRef]
- Ware, J.M.; Jones, C.B.; Thomas, N. Automated map generalization with multiple operators: A simulated annealing approach. Int. J. Geogr. Inf. Sci. 2003, 17, 743–769. [Google Scholar] [CrossRef]
- Jones, C.B.; Mark Ware, J. Map generalization in the Web age. Int. J. Geogr. Inf. Sci. 2005, 19, 859–870. [Google Scholar] [CrossRef]
- Yu, L. Analysis of 30 Cases of MATLAB Intelligent Algorithm, 2rd ed.; Beijing University of Aeronautics and Astronautics Press: Beijing, China, 2011. [Google Scholar]
- Lu, F.; Deng, J.; Li, S.; Deng, H. A Hybrid of Differential Evolution and Genetic Algorithm for the Multiple Geographical Feature Label Placement Problem. ISPRS Int. J. Geo-Inf. 2019, 8, 237. [Google Scholar] [CrossRef]
- Chehreghan, A.; Ali Abbaspour, R. A geometric-based approach for road matching on multi-scale datasets using a genetic algorithm. Cartogr. Geogr. Inf. Sci. 2017, 45, 255–269. [Google Scholar] [CrossRef]
- Zhang, L.; Guilbert, E. A Genetic Algorithm for Tributary Selection with Consideration of Multiple Factors. Trans. GIS 2016, 21, 332–358. [Google Scholar] [CrossRef]
- Wilson, I.D.; Ware, J.M.; Ware, J.A. A Genetic Algorithm approach to cartographic map generalisation. Comput. Ind. 2003, 52, 291–304. [Google Scholar] [CrossRef]
- Ware, J.M.; Wilson, I.D.; Ware, J.A. A knowledge based genetic algorithm approach to automating cartographic generalisation. Knowl. Based Syst. 2003, 16, 295–303. [Google Scholar] [CrossRef]
- Lichtner, W. Computer-assisted processes of cartographic generalization in topographic maps. Geo-Processing 1979, 1, 183–199. [Google Scholar]
- Mackaness, W.A. An Algorithm for Conflict Identification and Feature Displacement in Automated Map Generalization. Cartogr. Geogr. Inf. Syst. 1994, 21, 219–232. [Google Scholar] [CrossRef]
- Ruas, A. A method for building displacement in automated map generalisation. Int. J. Geogr. Inf. Sci. 1998, 12, 789–803. [Google Scholar] [CrossRef]
- Fei, L. Solving graphic conflicts between streets and buildings in map compilation by simulating human cartographers. Geomat. Inf. Sci. Wuhan Univ. 2004, 29, 426–432. [Google Scholar]
- Basaraner, M. A zone-based iterative building displacement method through the collective use of Voronoi Tessellation, spatial analysis and multicriteria decision making. Boletim de Ciências Geodésicas 2011, 17, 161–187. [Google Scholar] [CrossRef]
- Ai, T.; Zhang, X.; Zhou, Q.; Yang, M. A vector field model to handle the displacement of multiple conflicts in building generalization. Int. J. Geogr. Inf. Sci. 2015, 29, 1310–1331. [Google Scholar] [CrossRef]
- Ware, J.M.; Jones, C.B. Conflict Reduction in Map Generalization Using Iterative Improvement. GeoInformatica 1998, 2, 383–407. [Google Scholar] [CrossRef]
- Ware, J.; Wilson, I.; Ware, J.; Jones, C. A tabu search approach to automated map generalization. In Proceedings of the ACM-GIS 2002, Tenth ACM International Symposium on Advances in Geographic Information Systems, McLean, VA, USA, 8–9 November 2002; pp. 101–106. [Google Scholar]
- Sun, Y.; Guo, Q.; Liu, Y.; Ma, X.; Weng, J. An Immune Genetic Algorithm to Buildings Displacement in Cartographic Generalization. Trans. GIS 2016, 20, 585–612. [Google Scholar] [CrossRef]
- Huang, H.; Guo, Q.; Sun, Y.; Liu, Y. Reducing Building Conflicts in Map Generalization with an Improved PSO Algorithm. ISPRS Int. J. Geo-Inf. 2017, 6, 127. [Google Scholar] [CrossRef]
- Harrie, L.; Sarjakoski, T. Simultaneous Graphic Generalization of Vector Data Sets. GeoInformatica 2002, 6, 233–261. [Google Scholar] [CrossRef]
- Harrie, L.E. The Constraint Method for Solving Spatial Conflicts in Cartographic Generalization. Cartogr. Geogr. Inf. Sci. 1999, 26, 55–69. [Google Scholar] [CrossRef]
- Harrie, L. Weight-Setting and Quality Assessment in Simultaneous Graphic Generalization. Cartogr. J. 2003, 40, 221–233. [Google Scholar] [CrossRef]
- Sester, M. Optimization approaches for generalization and data abstraction. Int. J. Geogr. Inf. Sci. 2005, 19, 871–897. [Google Scholar] [CrossRef]
- Højholt, P. Solving Space Conflicts in Map Generalization: Using a Finite Element Method. Cartogr. Geogr. Inf. Sci. 2000, 27, 65–74. [Google Scholar] [CrossRef]
- Burghardt, D.; Meier, S. Cartographic displacement using the snakes concept. In Semantic Modeling for the Acquisition of Topographic Information from Images and Maps; Birkhäuser: Basel, Switzerland, 1997; pp. 114–120. [Google Scholar]
- Wang, L.; Guo, Q.; Wei, Z.; Liu, Y. Spatial Conflict Resolution in a Multi-Agent Process by the Use of a Snake Model. IEEE Access 2017, 5, 24249–24261. [Google Scholar] [CrossRef]
- Bader, M. Energy Minimization Methods for Feature Displacement in Map Generalization. Ph.D. Thesis, University of Zurich, Zurich, Germany, 2001. [Google Scholar]
- Bader, M.; Barrault, M.; Weibel, R. Building displacement over a ductile truss. Int. J. Geogr. Inf. Sci. 2005, 19, 915–936. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, Q.; Sun, Y.; Ma, X. A Combined Approach to Cartographic Displacement for Buildings Based on Skeleton and Improved Elastic Beam Algorithm. PLoS ONE 2014, 9, e113953. [Google Scholar] [CrossRef] [PubMed]
- Michalewicz, Z.; Janikow, C.Z.; Krawczyk, J.B. A modified genetic algorithm for optimal control problems. Comput. Math. Appl. 1992, 23, 83–94. [Google Scholar] [CrossRef]
- Schaffer, J.D.; Caruana, R.; Eshelman, L.J.; Das, R. A study of control parameters affecting online performance of genetic algorithms for function optimization. In Proceedings of the Third International Conference on Genetic Algorithms; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1989; pp. 51–60. [Google Scholar]





| Method | Crossover Probability | Mutation Probability | Population Number | Maintained Generation Number |
|---|---|---|---|---|
| BDMPGA | [0.7, 0.9] | [0.001, 0.05] | 10 | 10 |
| GA | 0.8 | 0.008 | - | - |
| IGA | 0.8 | 0.008 | - | - |
| Block | Building Number | Initial | MaxGen | Population Number | Single Population Size | Final | Total Displacement Distances (m) | ||
|---|---|---|---|---|---|---|---|---|---|
| <B-B> Conflict Number | <B-R> Conflict Number | <B-B> Conflict Number | <B-R> Conflict Number | ||||||
| 1 | 9 | 0 | 4 | 222 | 10 | 16 | 0 | 0 | 7.53 |
| 2 | 26 | 1 | 15 | 478 | 10 | 64 | 0 | 0 | 35.33 |
| 3 | 20 | 1 | 9 | 347 | 10 | 40 | 0 | 0 | 17.55 |
| 4 | 23 | 0 | 13 | 431 | 10 | 52 | 0 | 0 | 40.36 |
| 5 | 11 | 2 | 8 | 198 | 10 | 40 | 0 | 0 | 11.51 |
| 6 | 14 | 0 | 11 | 239 | 10 | 44 | 0 | 0 | 20.92 |
| 103 | 4 | 60 | 1915 | 60 | 256 | 0 | 0 | 133.19 | |
| Block | Building Number | Initial | MaxGen | Population Size | Final | Total Displacement Distances (m) | ||
|---|---|---|---|---|---|---|---|---|
| <B-B> Conflict Number | <B-R> Conflict Number | <B-B> Conflict Number | <B-R> Conflict Number | |||||
| 1 | 9 | 0 | 4 | 135 | 16 | 0 | 0 | 12.08 |
| 2 | 26 | 1 | 15 | 390 | 64 | 0 | 3 | 29.88 |
| 3 | 20 | 1 | 9 | 300 | 40 | 0 | 0 | 24.95 |
| 4 | 23 | 0 | 13 | 345 | 52 | 0 | 2 | 35.57 |
| 5 | 11 | 2 | 8 | 165 | 40 | 0 | 0 | 13.42 |
| 6 | 14 | 0 | 11 | 210 | 44 | 0 | 0 | 24.39 |
| 103 | 4 | 60 | 1545 | 256 | 0 | 5 | 140.31 | |
| Block | Building Number | Initial | MaxGen | Population Size | Final | Total Displacement Distances (m) | ||
|---|---|---|---|---|---|---|---|---|
| <B-B> Conflict Number | <B-R> Conflict Number | <B-B> Conflict Number | <B-R> Conflict Number | |||||
| 1 | 9 | 0 | 4 | 135 | 16 | 0 | 0 | 14.24 |
| 2 | 26 | 1 | 15 | 390 | 64 | 0 | 1 | 43.20 |
| 3 | 20 | 1 | 9 | 300 | 40 | 0 | 0 | 23.04 |
| 4 | 23 | 0 | 13 | 345 | 52 | 1 | 3 | 29.70 |
| 5 | 11 | 2 | 8 | 165 | 40 | 0 | 1 | 13.30 |
| 6 | 14 | 0 | 11 | 210 | 44 | 0 | 0 | 26.24 |
| 103 | 4 | 60 | 1545 | 256 | 1 | 5 | 149.71 | |
| Local Area No | BDMPGA | GA | IGA |
|---|---|---|---|
| No.A | 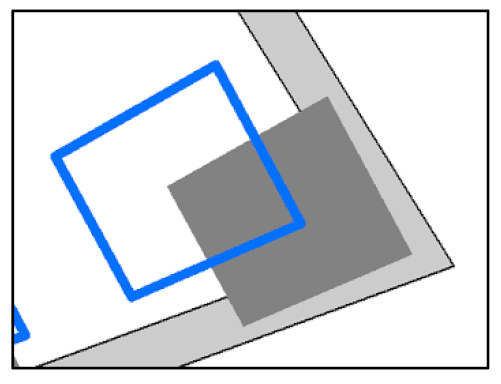 |  | 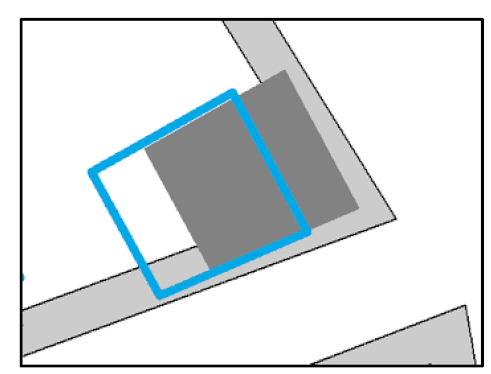 |
| No.B |  |  |  |
| No.C |  | 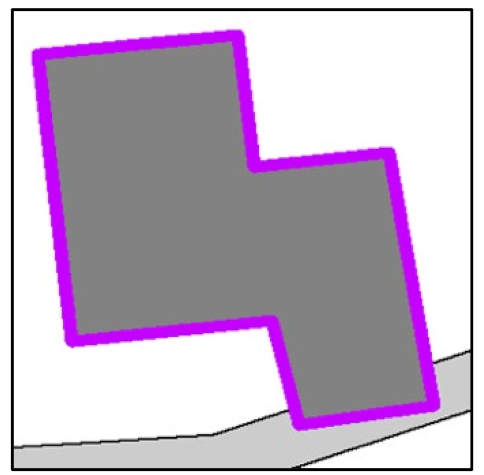 |  |
| Methods | Minimum (m) | Maximum (m) | Total (m) | Mean (m) | Std (m) |
|---|---|---|---|---|---|
| GA | 0.01 | 4.30 | 140.31 | 1.36 | 1.34 |
| IGA | 0.02 | 4.63 | 149.71 | 1.45 | 1.38 |
| BDMPGA | 0.00 | 3.99 | 133.19 | 1.29 | 1.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Ai, T.; Shen, Y.; Yang, W.; Wang, W. A Novel Method for Building Displacement Based on Multipopulation Genetic Algorithm. Appl. Sci. 2020, 10, 8441. https://doi.org/10.3390/app10238441
Li W, Ai T, Shen Y, Yang W, Wang W. A Novel Method for Building Displacement Based on Multipopulation Genetic Algorithm. Applied Sciences. 2020; 10(23):8441. https://doi.org/10.3390/app10238441
Chicago/Turabian StyleLi, Wende, Tinghua Ai, Yilang Shen, Wei Yang, and Weilin Wang. 2020. "A Novel Method for Building Displacement Based on Multipopulation Genetic Algorithm" Applied Sciences 10, no. 23: 8441. https://doi.org/10.3390/app10238441
APA StyleLi, W., Ai, T., Shen, Y., Yang, W., & Wang, W. (2020). A Novel Method for Building Displacement Based on Multipopulation Genetic Algorithm. Applied Sciences, 10(23), 8441. https://doi.org/10.3390/app10238441







