1. Introduction
Ultrasonic guided waves have played a major role in recent advances in non-destructive evaluation and structural health monitoring. The technology for long-range pipeline inspection using guided waves has already been commercialized [
1,
2,
3,
4,
5]. The industrial success of ultrasonic guided waves for non-destructive evaluation has prompted its adaptation to health monitoring of human long bones. The hollow pipe-like geometry of the appendicular bones in the human skeleton causes them to act like ultrasonic waveguides [
6,
7,
8]. The inherent sensitivity of ultrasonic guided waves to changes in the material and geometric properties of a waveguide suggest their strong potential to characterize bone fracture healing as well as cortical wall thinning due to developing osteoporosis [
9]. Ultrasonic guided waves can potentially supplement state-of-the-art radiological imaging techniques such as dual-energy X-ray absorptiometry (DEXA) and computed tomography (CT) scans, or possibly provide a portable, low-cost alternative.
Exploiting this potential necessitates a careful characterization of guided wave propagation in long bones. The hollow long bones are unlike regular uniform geometries such as plates and hollow cylinders [
10]. Long bones exhibit complexities in both material behavior (anisotropy and internal damping) and geometric features (lack of axisymmetry and variation along the length). For instance, the cross-section of a long bone is irregular in shape and changes along the long axis [
11]. This makes it difficult to identify the nature of the propagating modes in a cortical bone; hence, plate and shell approximations are often adopted.
We investigated the use of a shear transducer to generate guided waves in a long bone that may be less prone to leak into the soft tissue surrounding the bone. This idea was inspired by the practice of using torsional waves for long-distance pipe inspection because, unlike longitudinal wave modes, the shear-based torsional waves do not leak into the enclosed fluid. The objective was to assess whether a single omni-directional shear transducer can generate guided waves in a long bone that propagate long distances axially. As will be seen, the guided waves generated in a synthetic tibia are detected by a laser Doppler vibrometer, which only senses the displacement component normal to the surface at a point. It is curious that a shear transducer generates guided waves that have a significant displacement component normal to the surface. Thus, finite element simulations were conducted to understand these experimental results. The novelties of the research described herein are (i) the use of a unique shear transducer to actuate guided waves in a tibia, and (ii) analysis of wave propagation in a geometrically realistic model rather than a surrogate plate or pipe. In the remainder of this article,
Section 2 describes the experimental setup and numerical modeling, while
Section 3 presents the experimental and numerical results. Then,
Section 4 discusses the findings, and finally
Section 5 gives a brief summary and states the conclusions.
2. Methods
The experimental methods and test setup are described first, and then the basis for numerical studies is discussed.
2.1. Experimental Setup
The experimental setup consists of a RAM 5000 pulser-receiver system from Ritec (Warwick, RI, USA), an omni-directional transducer from Guidedwave (Bellefonte, PA, USA), a synthetic composite tibia from Sawbones (Seattle, WA, USA), an OFV-5000 Modular Vibrometer from Polytec GmbH, and a digital oscilloscope (Tektronix MSO 2014). The shear transducer was originally designed to detect acoustic emissions [
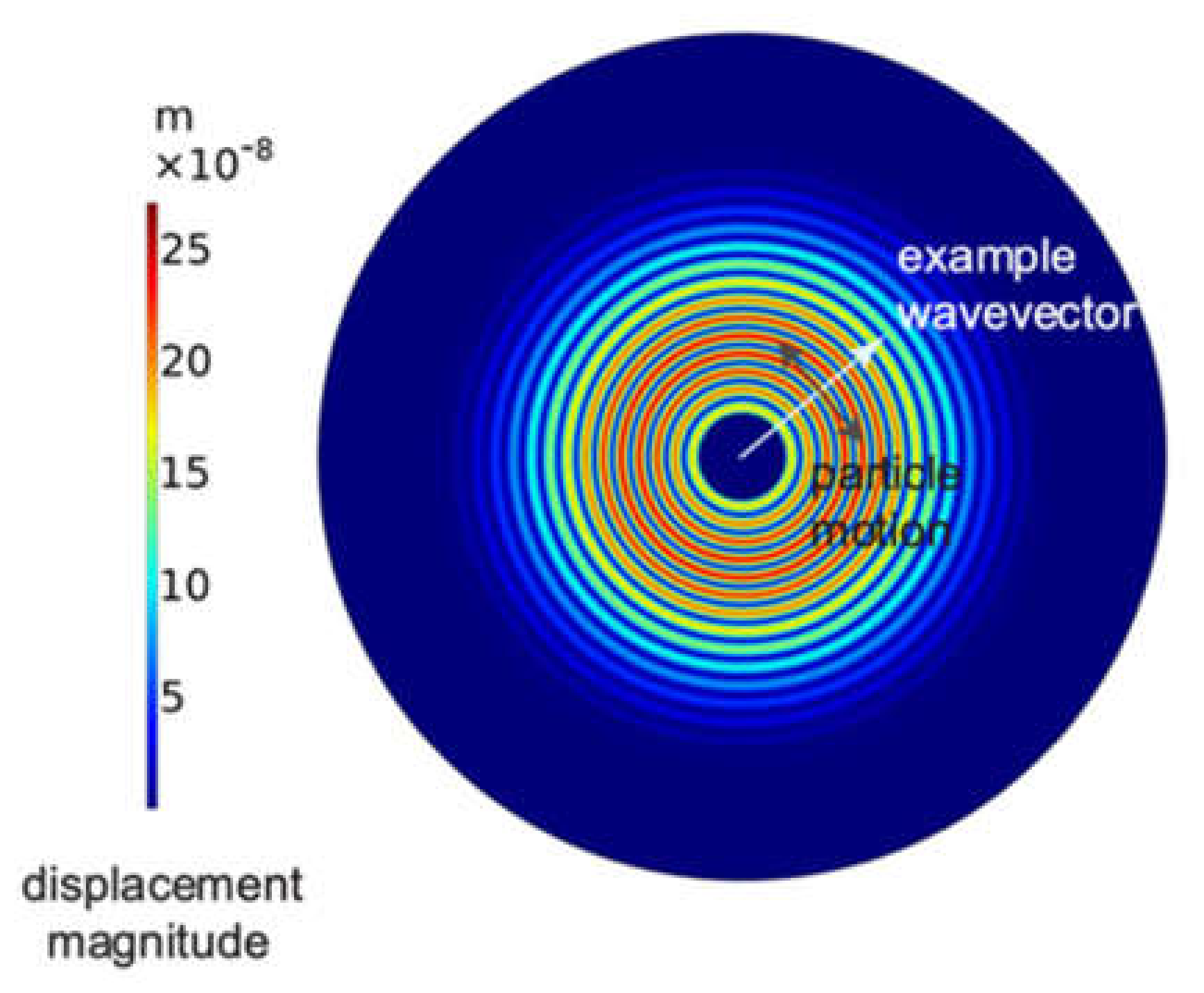
12] and has a central frequency close to 200 kHz, which, when coupled to a plate and used as an actuator in an active mode, excites shear-horizontal waves in all directions as a result of its piezoelectric shear ring element. The wave vector points outward in all directions from the center of the transducer, and the particle displacement is everywhere perpendicular to the wave vector. The result in an isotropic plate is circular-crested shear-horizontal waves that emanate from the transducer, as shown in
Figure 1. Since the transducer sends waves in all directions, or receives waves coming from any direction, it is known as omni-directional. The fundamental shear-horizontal mode (SH0) is non-dispersive, i.e., SH0 propagates with a velocity independent of the thickness of the waveguide and the excitation frequency. This is a significant advantage in waveguides having a variable wall thickness in the wave propagation direction.
For all these aforementioned reasons, omni-directional shear transducers [
13,
14] are being investigated for many industrial applications. However, the geometry of long bones is very different from uniform plates or pipes commonly encountered in industry. The cross-section’s lack of symmetry and the variation along the length results in propagating modes that are different from both SH0 waves in a plate, and the analogous torsional waves (i.e., T(0,1)) in a pipe. This is the first time this transducer has been used to generate guided waves in a long bone. The flat omni-directional shear transducer was coupled to the curved medial facet of the synthetic tibia using maple syrup as the couplant. Gaps exist between the transducer and the tibia due to the mismatching surfaces, but the setup works. We have found that maple syrup works very well as a couplant for shear transducers. Cortical bone is a lossy material; therefore, the relatively low frequency of 200 kHz was investigated in an attempt to minimize attenuation for propagation paths that cover a significant extent of the diaphysis [
15,
16].
The test sample, a synthetic left tibia, was made from a composite material whose mechanical properties mimic those of a cortical bone in a healthy adult [
17]. We did not have the full set of elastic properties for the synthetic bone material, but the supplier reports that the Young’s moduli in the longitudinal and transverse directions are 16 GPa and 10 GPa [
17], respectively. Some of the stiffness coefficients for the cortical bone-mimicking material, using the resonant ultrasound spectroscopy technique, are determined in [
18]. The transversely isotropic material properties used in our finite element analysis are listed in
Table 1 [
19,
20].
For detection, a 1D laser Doppler vibrometer (LDV) was used with the laser head oriented normal to the medial surface of the tibial diaphysis. Using the LDV, guided wave signals at multiple closely spaced locations were collected on the medial surface. Being a non-contact measurement, it was easy to scan along the long axis. The laser head was carefully oriented normal to the reflective tape, and maximum signal intensity was maintained. The experimental setup is shown in
Figure 2. The LDV decoder (VD-09-S) sensitivity to velocity is 40 mm/s per volt, from which displacements at frequencies up to 1 MHz can be computed. Since the composite material is not a good reflector of light, a thin strip of silver reflective tape was used. The tape is not retroreflective; therefore, only light normal to the surface is captured by the laser head.
The data collection commenced when a 10-cycle tone-burst excitation signal was sent to the transducer, which was driven at 288 volts peak to peak. The distance between the transducer housing and the location of the first detection point was 45 mm. Velocities normal to the surface were recorded by the LDV in 4 mm increments along the reflective tape, moving from the proximal end toward the distal end. Each received waveform was synchronously averaged 512 times. A 2D-FFT routine was used to process the collected time-history scans to generate the corresponding phase velocity dispersion curves and extract the propagating guided wave modes in terms of their phase velocities [
21,
22]. The matrix containing the spatial and temporal data was zero-padded in the spatial dimension to make the column and row dimensions comparable before transforming to the wavenumber-frequency domain. Wavenumbers are converted to phase velocity using
cp =
2πf/
k so that the results can be overlaid onto the dispersion curves.
2.2. Numerical Modeling
Two distinct finite element simulations using a commercial finite element package [
23] were conducted to help interpret the experimental results. These simulations were based on CT-scan data from the diaphysis of a human tibia and the mechanical properties representative of a human cortical bone given in
Table 1, while the experiments were conducted on synthetic bone. Due care must be taken when comparing experimental results from synthetic bone with finite element simulations from bone having different dimensions and properties. The first simulation determines the dispersion curves and associated wave structures for a selected cross-section of the tibial bone. This simulation provides information about the guided wave propagation characteristics for that specific cross-section. For the limited length of the sensing region along the long axis on the medial surface, the cross-sectional geometry is fairly constant. However, we must keep in mind that the tibia cross-section does change along the entire length [
11,
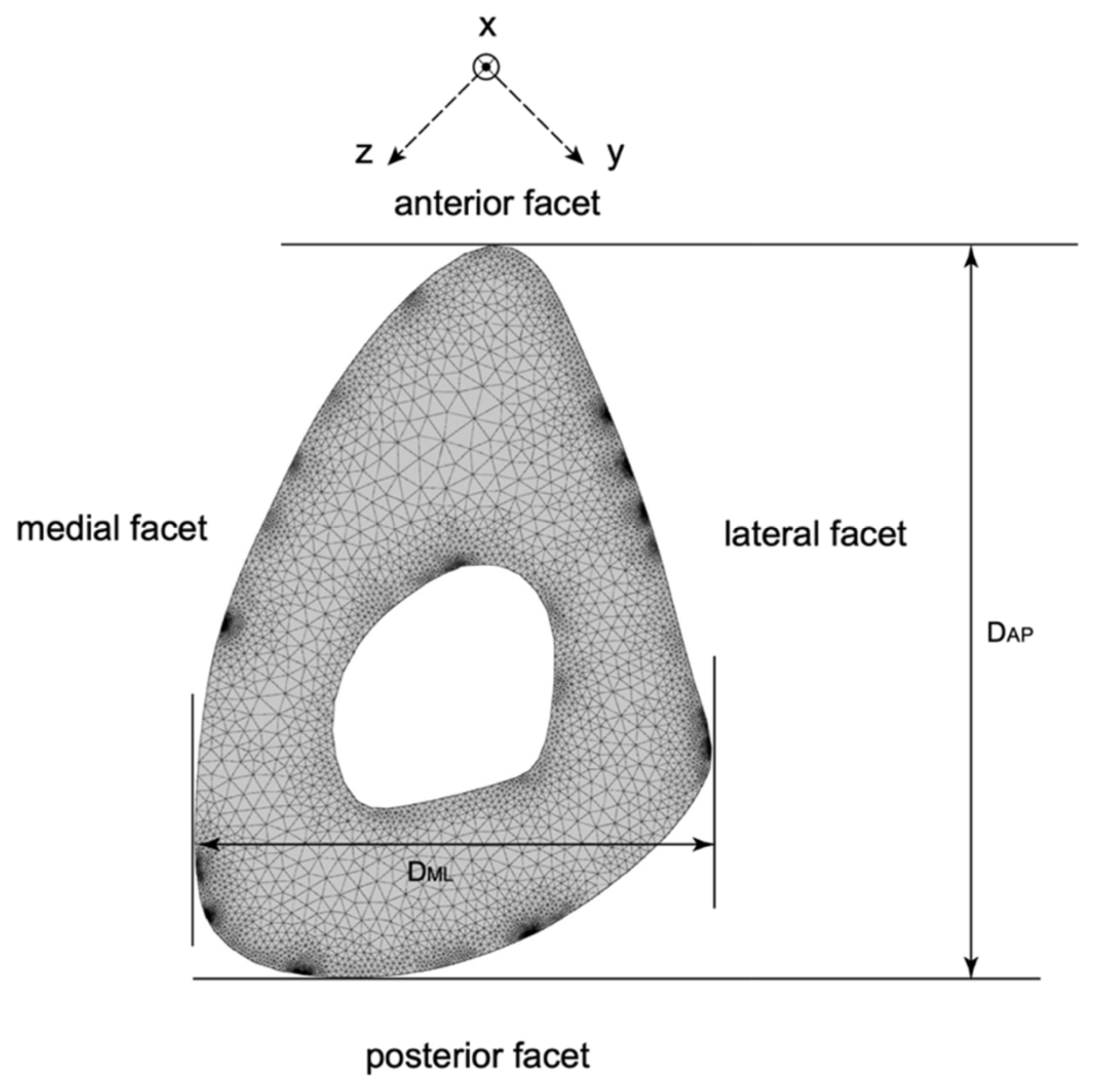
24]. Using the cross-section at the mid-span of the diaphysis where the reflective tape is located, a 2D semi-analytical finite element (SAFE) analysis was performed to extract the phase velocity dispersion curves for the cross-section at the mid-span of the human tibia shown in
Figure 3. The weak form PDE module in COMSOL Multiphysics was used to solve the quadratic eigenvalue problem [
25]. The dimensions of the cross-section geometry extracted from the human CT-scan are compared with those physically measured on the synthetic tibia in
Table 2.
The second simulation was a transient dynamics analysis based on the loading function provided by the omni-directional shear transducer. It provides a reference for, and understanding of, the experimental results. A cylindrical coordinate system was used for the transducer, and the displacement loading was applied as a 10-cycle tone-burst in the circumferential direction, thus mimicking a real omni-directional shear transducer. The transducer contact region was modeled as a circular footprint on the medial surface. The imperfect mating of transducer and synthetic bone was not modelled.
Material damping was included using the Rayleigh coefficients given in
Table 1. A time-marching solution for the diaphysis of the tibia was implemented. The maximum element size was 0.8 mm, and the time-step was 100 ns.
3. Results
3.1. Experimental Results
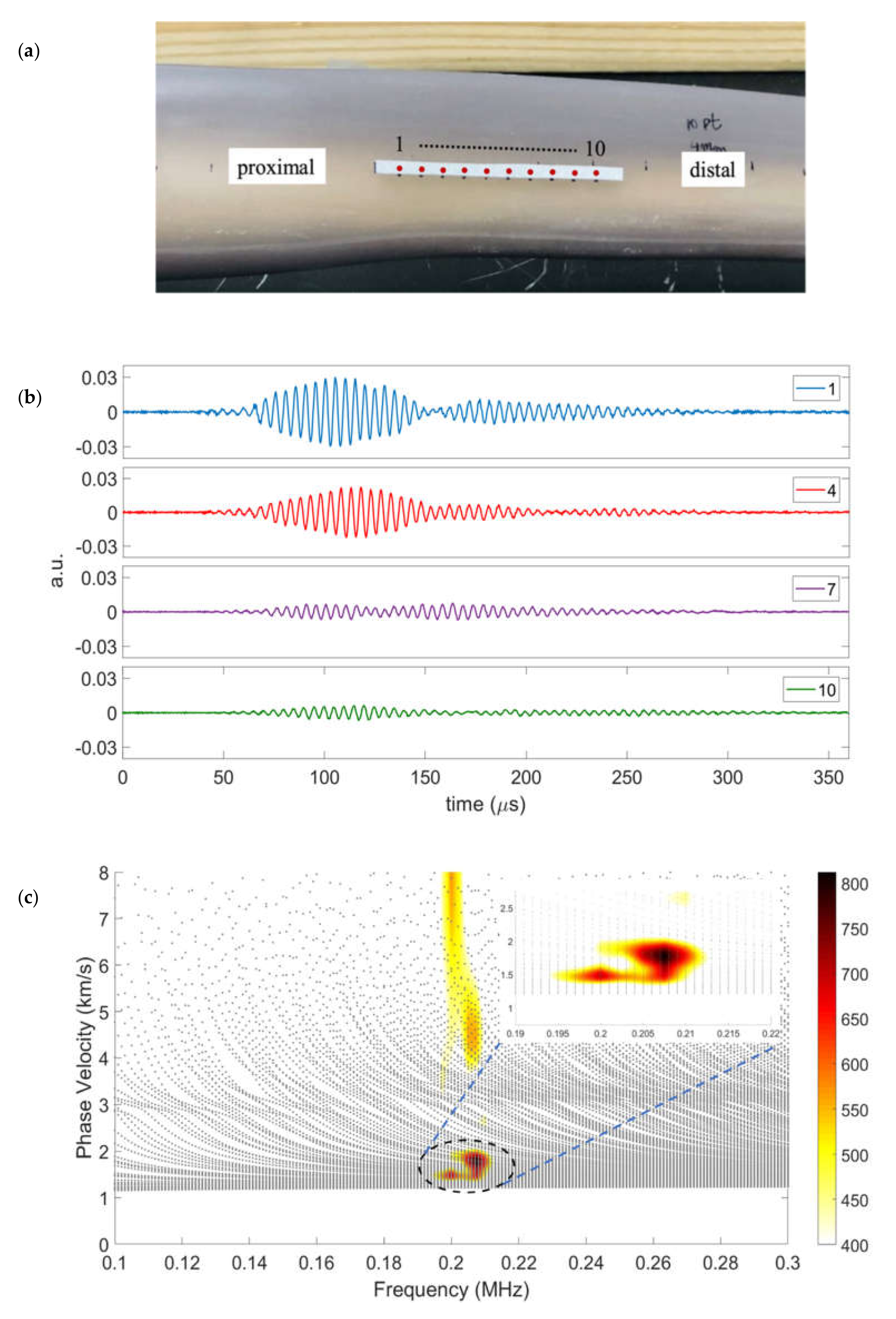
The time-history data obtained sequentially from each of the 10 sensing locations on the reflective tape (shown in
Figure 4a) were recorded. The two key features observed in the A-scans recorded at locations 1, 4, 7, and 10 (shown in
Figure 4b) are the multiple wave packets and substantial attenuation of the signal. Prior experience with guided waves in long bones agrees with these observations [
8,
26,
27]. A 2D-FFT was applied to the 10 time-series to extract the phase velocity spectrum, which was overlaid on the phase velocity dispersion curves for frequencies from 100 to 300 kHz obtained from the cross-section at the mid-span of a tibial diaphysis.
The highest-intensity phase velocities from the 2D-FFT are in the vicinity of 2 km/s, and are enclosed by an ellipse for emphasis in
Figure 4c, which is enlarged in the inset image. The propagating modes are nearly non-dispersive at the low phase velocities in this frequency range. The existence of non-dispersive propagating modes is not a surprise, but their generation by a shear transducer and reception via a normal LDV measurement is not intuitive. The next subsection will investigate the displacement components of the modes having these phase velocities to answer the question of why waves generated by an omni-directional shear transducer are detected by particle displacements normal to the surface.
3.2. Numerical Results
The transient dynamic finite element simulation confirms that the displacements in the wave field are measurable with an LDV. The displacement components related to those measured in the experiment are plotted in
Figure 5. The related contours of
are plotted on the cross-section in
Figure 6, where
and
are displacement components in the
and
directions shown in
Figure 3. The longitudinal displacement component
u is excluded from this analysis because the LDV used in the experiment did not sense it.
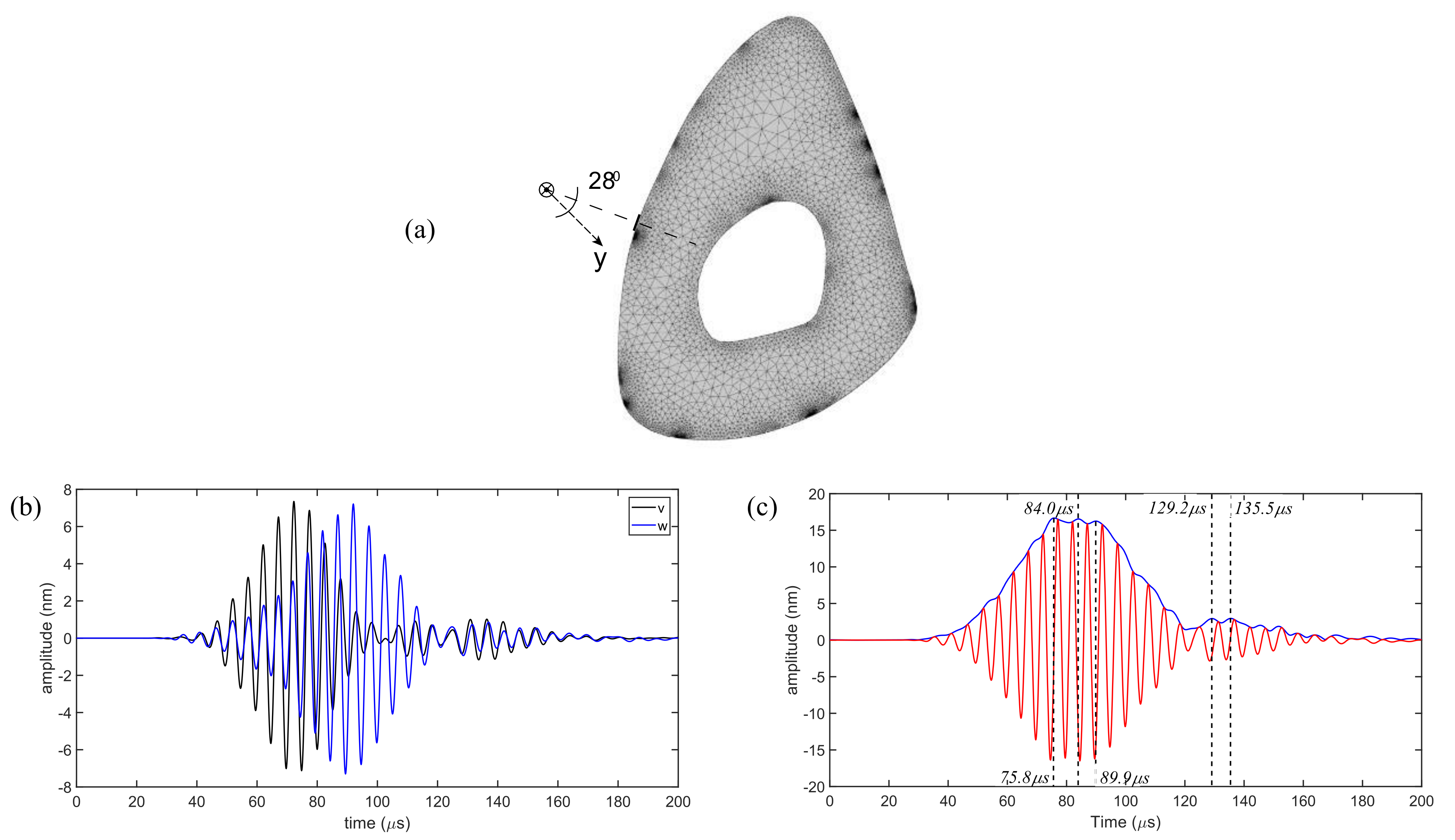
To calculate the displacement component normal to the surface as received by the laser head of the LDV, the normal direction to the laser reception points on the reflective tape was calculated. It was found that the normal to the reception point makes an angle of approximately
with respect to the y-axis (shown in
Figure 5a). The total displacement normal to the surface then becomes equal to
. The individual displacement components are shown in
Figure 5a, and the composite signal is shown in
Figure 5b; note the similarity between the simulated and experimental time histories shown earlier in
Figure 4b. Next, displacement magnitude profiles corresponding to the expression
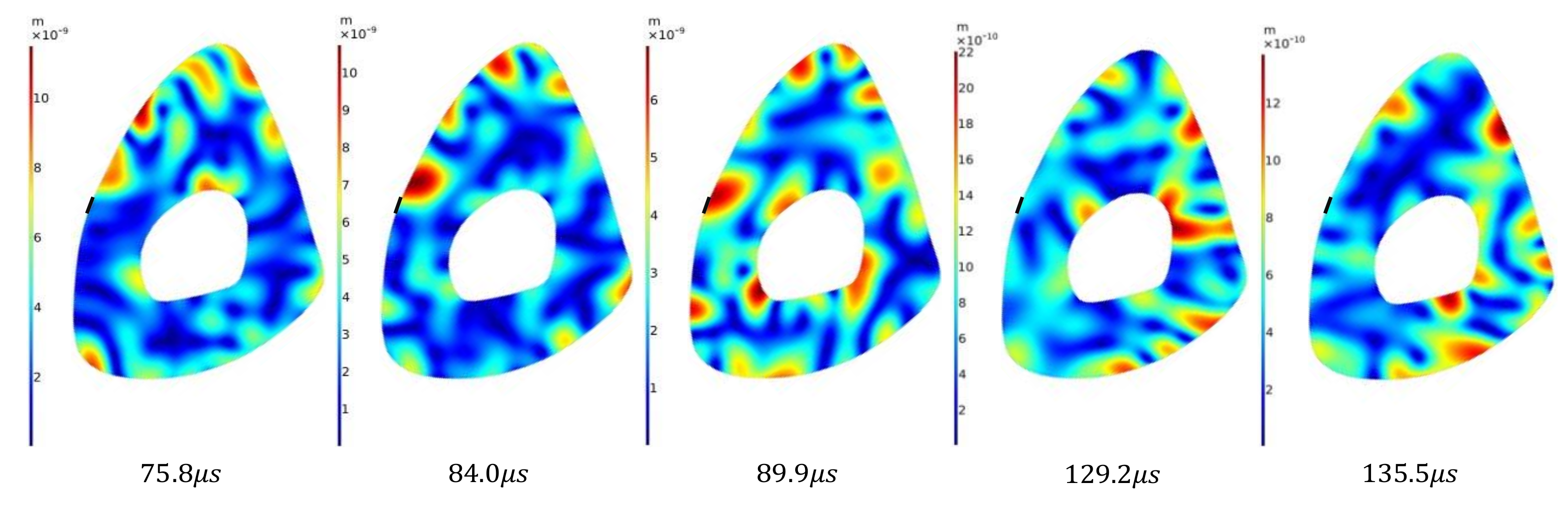
were extracted for the central cross-section of the diaphysis at multiple time instances corresponding to the peaks in the A-scan for the two wave packets in the composite signal.
The Hilbert transform was used to create an envelope and identify a number of displacement amplitude peaks (
Figure 5b). Our analysis identifies five peaks in total: three of them correspond to the first wave packet, and the remaining two belong to the second wave packet. The color bar values in
Figure 6 and
Figure 7 correspond to the expression
. To represent the relative location of the reflective tape on the medial surface, a black line segment is shown in
Figure 6 and
Figure 7. In the two cases corresponding to time values of
and
in
Figure 6, the displacement profiles have a localized region of significant intensity at the medial surface partially overlapping with the region where the reflective tape is present. Although the reflective tape is not exactly located at the center of the highest displacement intensity regions, this explains why the LDV is able to detect these waves. The last two displacement profiles for time values of
and
have small but non-zero displacement magnitude distribution on the medial surface. We do not attempt to assess whether these would be detectable.
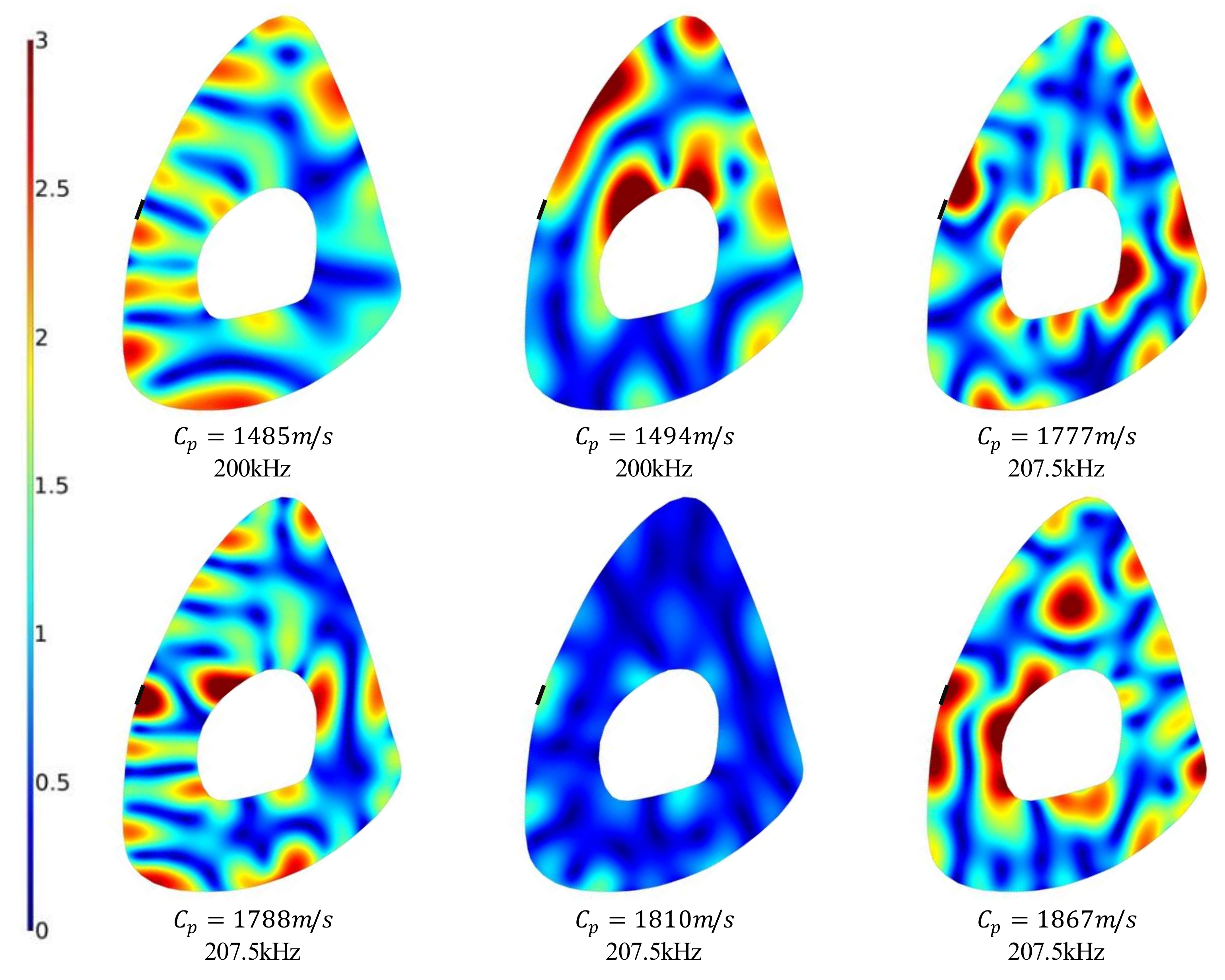
Additionally, wave structures were extracted from SAFE analysis corresponding to the eigenvalues within the propagating guided waves region highlighted in
Figure 4c. These wave structures are plotted in
Figure 7 for a number of eigenvalues and for the same combination of displacement components
. Nearly all the wave structures in
Figure 7 show localized high-intensity regions similar to the ones observed on the medial surface of two displacement profiles in
Figure 6. Specifically, the modes having frequency-phase velocity pairs (207.5 kHz, 1788 m/s), (207.5 kHz, 1810 m/s), and (207.5 kHz, 1867 m/s) all have a significant
component; therefore, a combination of these modes should be detectable when measuring the motion normal to the surface at the medial facet.
4. Discussion
The results presented in the previous section illustrate that the 200 kHz shear transducer actuated ultrasonic guided waves in a synthetic tibia that were received due to particle displacement normal to the medial surface at distances of 45–85 mm. While the transducer will generate omni-directional SH waves in a plate, the waves generated in the synthetic tibia bear no resemblance to torsional waves in a pipe. Even though the signal is attenuated over the propagation distance, it is measurable. The phase velocity spectrum computed from the received signals reveals that the propagating modes have phase velocities of ~1500–2000 m/s. The dispersion curves obtained for the tibial cross-section at the mid-diaphysis reveal that these modes are in the low phase velocity region and nearly non-dispersive. Thus, they can be expected to penetrate the lossy material relatively well. These wave modes, which are actuated by a shear transducer, are received by particle motion normal to the surface because the wave structures for the propagating modes consist partially of this displacement. The wave propagation simulation in the time domain confirms that the wave packet, which consists of multiple modes, has particle motion normal to the surface.
In the Results section, the wave structures for just five modes in the cluster were investigated. The displacement field for a mode is distributed over the entire cross-section, but not in a uniform way. Relatively large displacement values are localized. These fields suggest that if all the propagating modes were superposed together, the resulting displacement field might be more uniform. If this is the case, then the reception position would be more arbitrary, and the wave energy would interact with cracks located anywhere in the cross-section.
Deep-penetrating guided wave modes could be important for monitoring the fracture-healing process in long bones. Fractures can occur at many different locations, but non-invasive access points for transducers are somewhat limited. Therefore, the guided waves could be used to transport ultrasonic energy reasonably long distances in order for it to interact with the healing fracture. The wave–discontinuity interaction would be indicative of the state of the healing process.
Based on these findings, it is clear that penetrating guided wave propagation in long bones is complicated by the material properties and the geometry of the long bone waveguide. However, the fact that simulations conducted on the geometry of a human tibia and the properties of a human tibia showed good agreement with the results of an experiment conducted on a synthetic tibia suggests that at least some of the wave propagation characteristics for a population of human tibial bones are common. Future research is needed to quantify the guided wave characteristics in a diverse population of long bones.
The experiments presented herein used a laser Doppler vibrometer to conveniently scan along the synthetic bone. This would not be practical for a human subject, but a simple linear array of piezoelectric receivers should function in the same way, permitting percutaneous measurements at the medial facet. Finally, neither experiments nor simulations had soft tissue adjacent to the bone surfaces, as would be the case for in vivo measurements. Future research is needed to address whether wave energy leaks into the soft tissue. Preliminary experiments with this shear transducer give cause for optimism.
5. Conclusions
The research objective was to assess whether a single omni-directional shear transducer could generate guided waves in a long bone that propagate long distances axially. The experimental results showed that even with a flat transducer on a curved surface, the wave packets could be received 45–85 mm away in the mid-diaphysis region. Measurements outside the mid-diaphysis region were beyond the scope of the current research, but they would be an interesting subject for further investigation because the cross-sectional geometry changes substantially outside of the mid-diaphysis.