A Simple Scheme for Photonic Generation of Microwave Waveforms Using a Dual-drive Mach–Zehnder Modulator
Abstract
1. Introduction
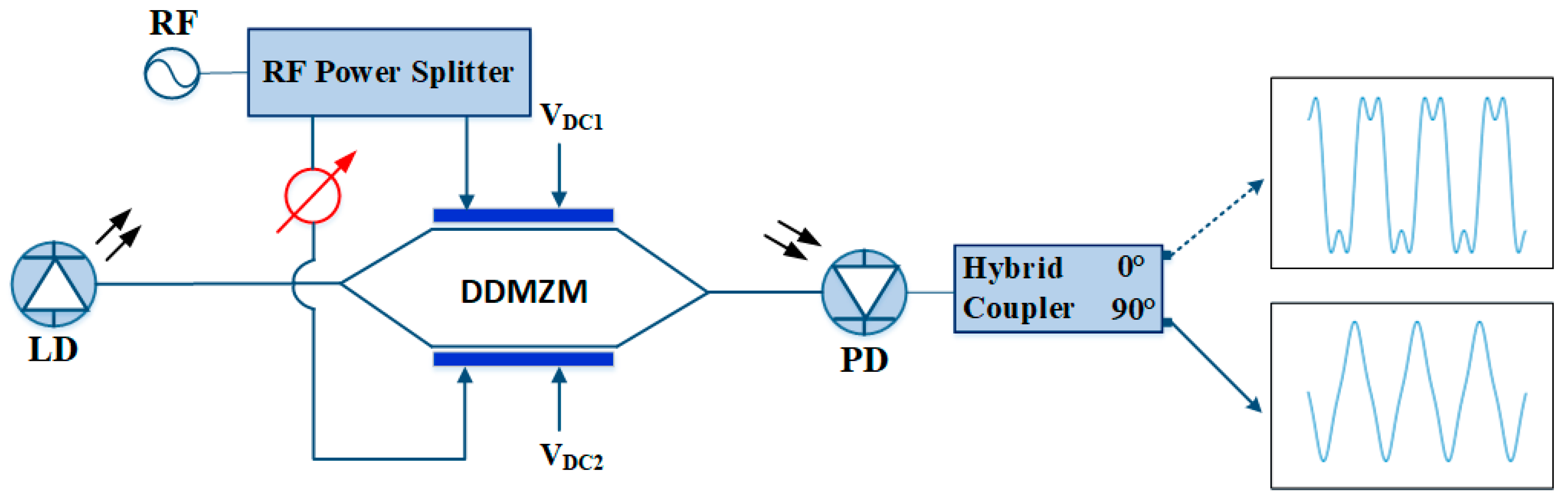
2. Operation Principle
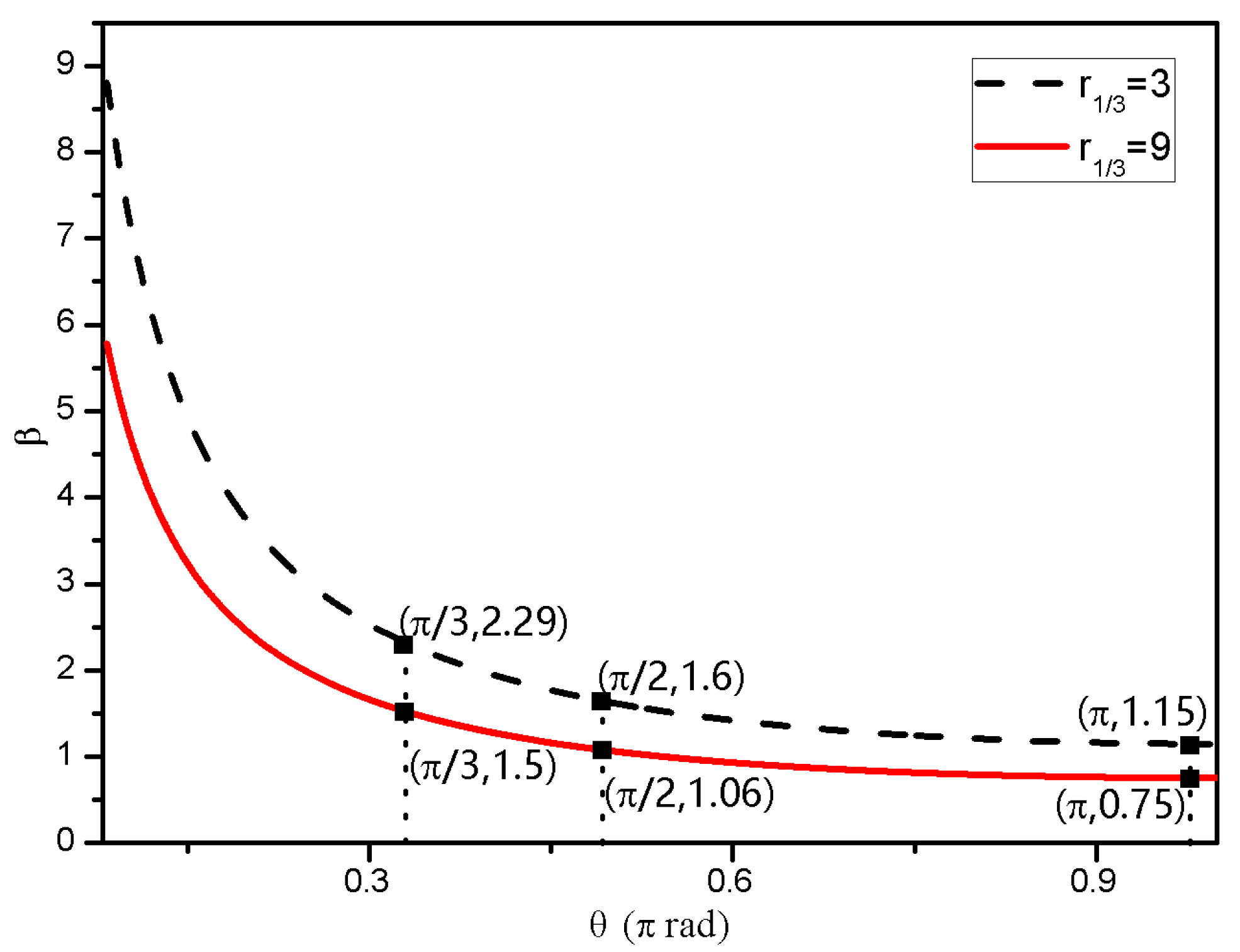
2.1. Square waveform
2.2. Triangular waveform
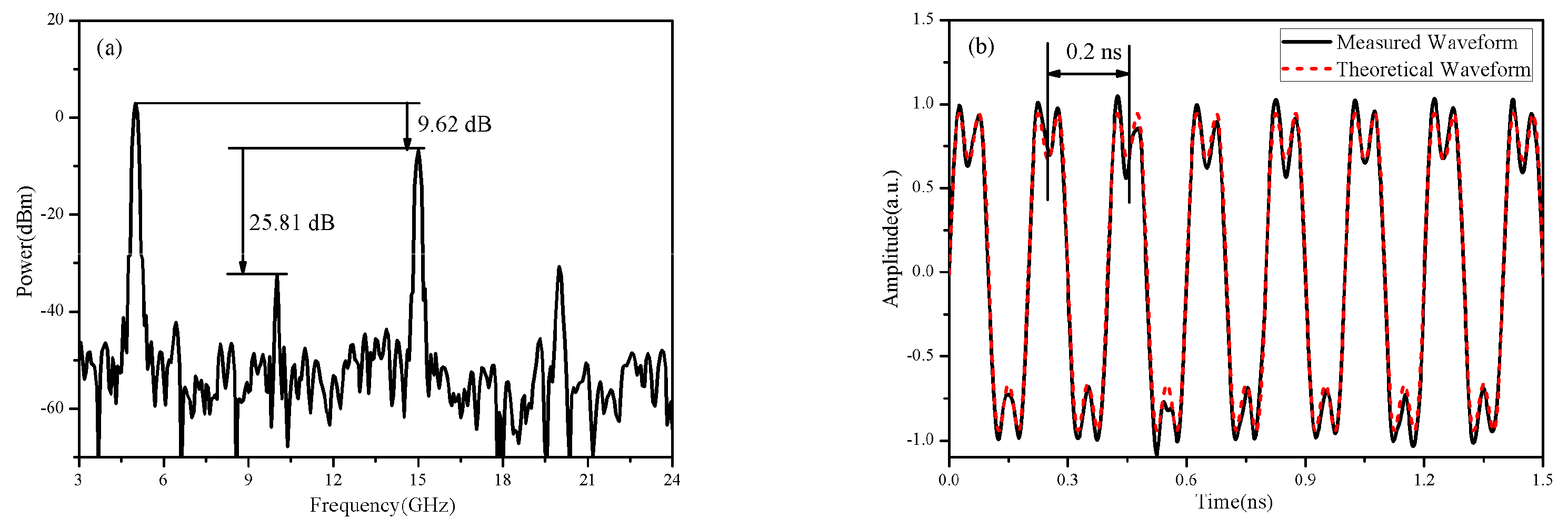
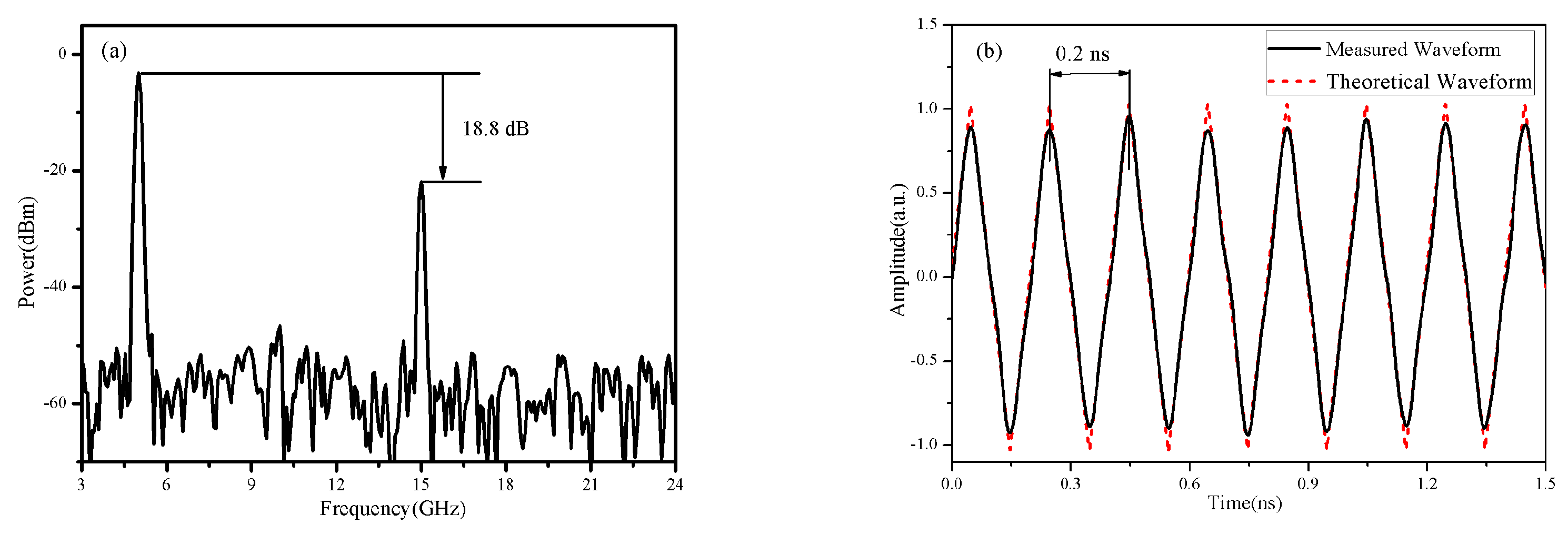
3. Experiment and Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Parmigiani, F.; Ibsen, M.; Petropoulos, P. Efficient All-Optical Wavelength-Conversion Scheme Based on a Saw-Tooth Pulse Shaper. IEEE Photonics Technol. Lett. 2009, 21, 1837–1839. [Google Scholar] [CrossRef]
- Jeongwoo, H.; Nguyen, C. A new ultra-wideband, ultra-short monocycle pulse generator with reduced ringing. IEEE Microw. Wirel. Compon. Lett. 2002, 12, 206–208. [Google Scholar] [CrossRef]
- Yuan, J.; Ning, T.; Li, J. Investigation on optical wavelength conversion based on SPM using triangular-shaped pulses. Opt. Int. J. Light Electron Opt. 2015, 127, 3049–3054. [Google Scholar] [CrossRef]
- Latkin, A.-I.; Boscolo, S.; Bhamber, R.-S. Doubling of optical signals using triangular pulses. J. Opt. Soc. Amer. B. 2009, 26, 1492–1496. [Google Scholar] [CrossRef]
- Won, Y.-S.; Kim, C.-H.; LEE, S.-G. Range resolution improvement of a 24 GHz ISM band pulse radar—A feasibility study. IEEE Sens. J. 2015, 15, 7142–7149. [Google Scholar] [CrossRef]
- Wang, X.-W.; Li, Y.-F.; Zhou, Y. Triangular-range-intensity profile spatial-correlation method for 3D super-resolution range-gated imaging. Appl. Opt. 2013, 52, 7399–7406. [Google Scholar]
- Zhou, P.; Zhang, F.; Guo, Q. A Modulator-Free Photonic Triangular Pulse Generator Based on Semiconductor Lasers. IEEE Photonics Technol. Lett. 2018, 30, 1317–1320. [Google Scholar] [CrossRef]
- He, Y.-T.; Jiang, Y.; Zi, Y.-J. Photonic microwave waveforms generation based on two cascaded single-drive Mach-Zehnder modulators. Opt. Express 2018, 26, 7829–7841. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Ning, T.; Li, J. Research on photonic generation of quadrupling triangular-shaped waveform using external modulation. Opt. Fiber Technol. 2018, 45, 352–358. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhang, L. Frequency-definable linearly chirped microwave waveform generation by a Fourier domain mode locking optoelectronic oscillator based on stimulated Brillouin scattering. Opt. Express 2020, 28, 13861–13870. [Google Scholar] [CrossRef]
- Song, C.; Qian, J.; Lei, M. A Chirp-Rate-Tunable Microwave Photonic Pulse Compression System for Multi-Octave Linearly Chirped Microwave Waveform. IEEE Photonics J. 2019, 11, 1–13. [Google Scholar] [CrossRef]
- Zhang, L.; Zeng, Z.; Zhang, Y. Photonics-assisted bandwidth-doubling dual-chirp microwave signal generation with freely-tunable central frequency. IEEE Photonics J. 2020, 12, 1–11. [Google Scholar] [CrossRef]
- Li, W.; Wang, W.; Sun, W. Generation of triangular waveforms based on a microwave photonic filter with negative coefficient. Opt. Express 2014, 22, 14993–15001. [Google Scholar] [CrossRef] [PubMed]
- Li, J. Photonic-assisted periodic triangular-shaped pulses generation with tunable repetition rate. IEEE Photon. Technol. Lett. 2013, 25, 952–954. [Google Scholar] [CrossRef]
- Sun, W.-H.; Li, W.; Wang, W.-T. Triangular Microwave Waveform Generation Based on Stimulated Brillouin Scattering. IEEE Photonics J. 2014, 6, 1–7. [Google Scholar] [CrossRef]
- Liu, X. Photonic generation of triangular-shaped microwave pulses using SBS-based optical carrier processing. J. Light W. Technol. 2014, 32, 3797–3802. [Google Scholar] [CrossRef]
- Zhai, W.-L.; Wen, A.-J. Photonic Generation and Transmission of Frequency-Doubled Triangular and Square Waveforms Based on Two Mach–Zehnder Modulators and a Sagnac Loop. J. Lightwave Technol. 2019, 37, 1937–1945. [Google Scholar] [CrossRef]
- Li, J. Photonic generation of triangular waveform signals by using dual-parallel Mach–Zehnder modulator. Opt. Lett. 2011, 36, 3828–3830. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Ge, X.; Pan, S.-L. Triangular pulse generation using a dual-parallel Mach–Zehnder modulator driven by a single-frequency radio frequency signal. Opt. Lett. 2013, 38, 4491–4493. [Google Scholar] [CrossRef]
- Sha, Z.; Xin, W. A simple photonic method to generate square and triangular microwave waveforms. Opt. Commun. 2018, 426, 654–657. [Google Scholar]
- Yuan, J.; Ning, T.; Li, J. Photonic Generation of Triangular-shaped Waveform Based on External Modulation. Sci. Rep. 2018, 8, 3369. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Li, J.; Zhao, J.; Ren, Z.; Gu, Y.; Zhao, M. A Simple Scheme for Photonic Generation of Microwave Waveforms Using a Dual-drive Mach–Zehnder Modulator. Appl. Sci. 2020, 10, 7914. https://doi.org/10.3390/app10217914
Hu J, Li J, Zhao J, Ren Z, Gu Y, Zhao M. A Simple Scheme for Photonic Generation of Microwave Waveforms Using a Dual-drive Mach–Zehnder Modulator. Applied Sciences. 2020; 10(21):7914. https://doi.org/10.3390/app10217914
Chicago/Turabian StyleHu, Jingjing, Jian Li, Jiayi Zhao, Zichen Ren, Yiying Gu, and Mingshan Zhao. 2020. "A Simple Scheme for Photonic Generation of Microwave Waveforms Using a Dual-drive Mach–Zehnder Modulator" Applied Sciences 10, no. 21: 7914. https://doi.org/10.3390/app10217914
APA StyleHu, J., Li, J., Zhao, J., Ren, Z., Gu, Y., & Zhao, M. (2020). A Simple Scheme for Photonic Generation of Microwave Waveforms Using a Dual-drive Mach–Zehnder Modulator. Applied Sciences, 10(21), 7914. https://doi.org/10.3390/app10217914





