Influence of Smart Spring Support Parameters on Vibration Characteristics of Three Support Shafting
Abstract
:1. Introduction
2. Vibration Reduction Test of Shafting with a Smart Spring
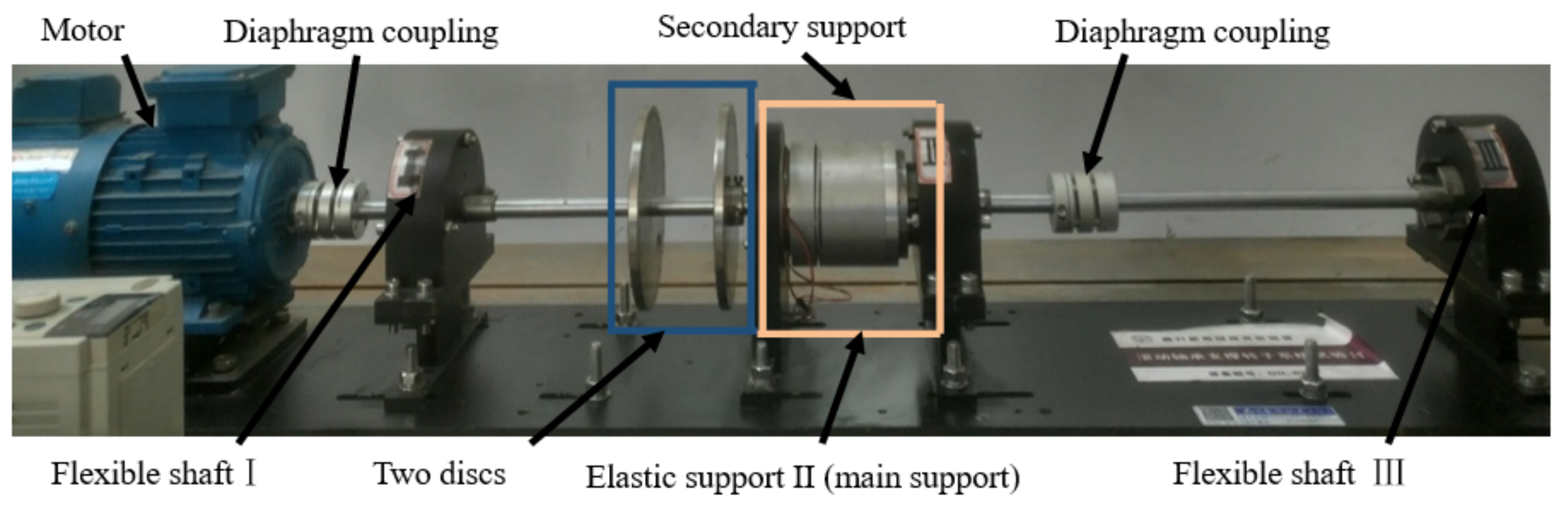
2.1. Design of Shafting Acceleration across a Critical Speed Test System
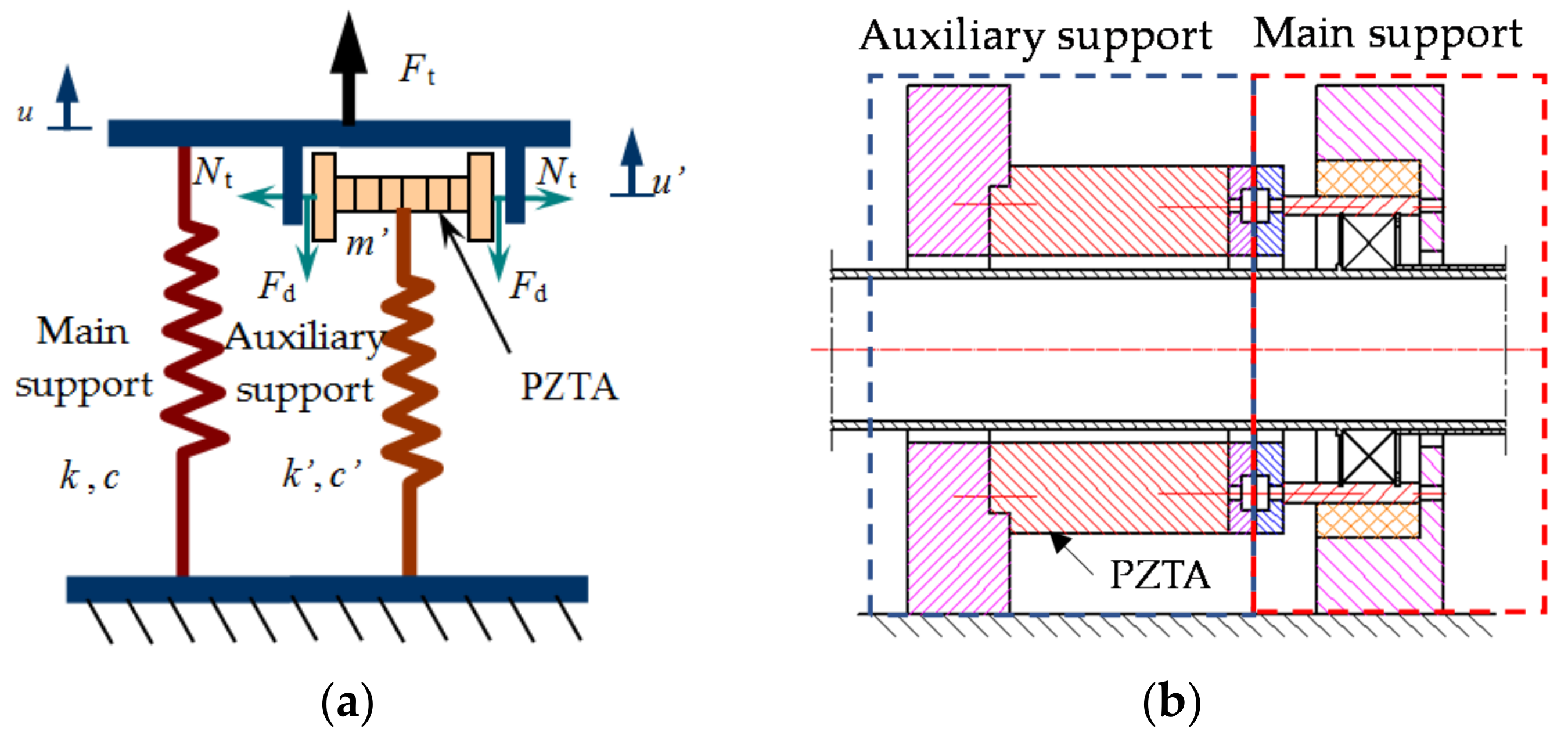
2.2. Analysis of Vibration Reduction Test Results of the Smart Spring
3. Establishment of the Dynamic Model of Three-Support Shafting
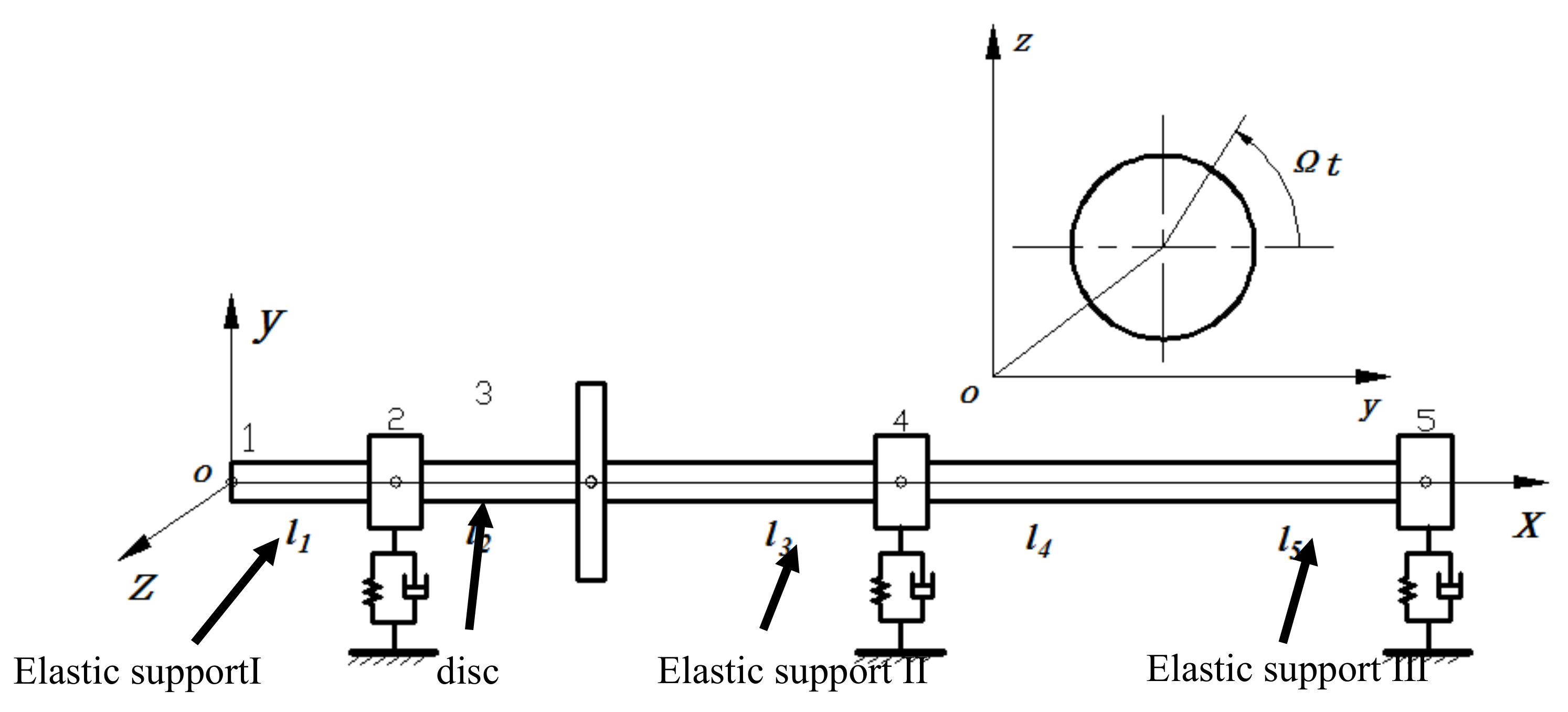
3.1. Dynamic Model Analysis of the Rotor Shaft System
3.2. Derivation of Motion Equation of the Three-Support Shafting
4. Analysis of the Influence of Support Parameters on the Steady-State Unbalance Response of Shafting
4.1. Solution of the Critical Speed of Three-Support Shafting
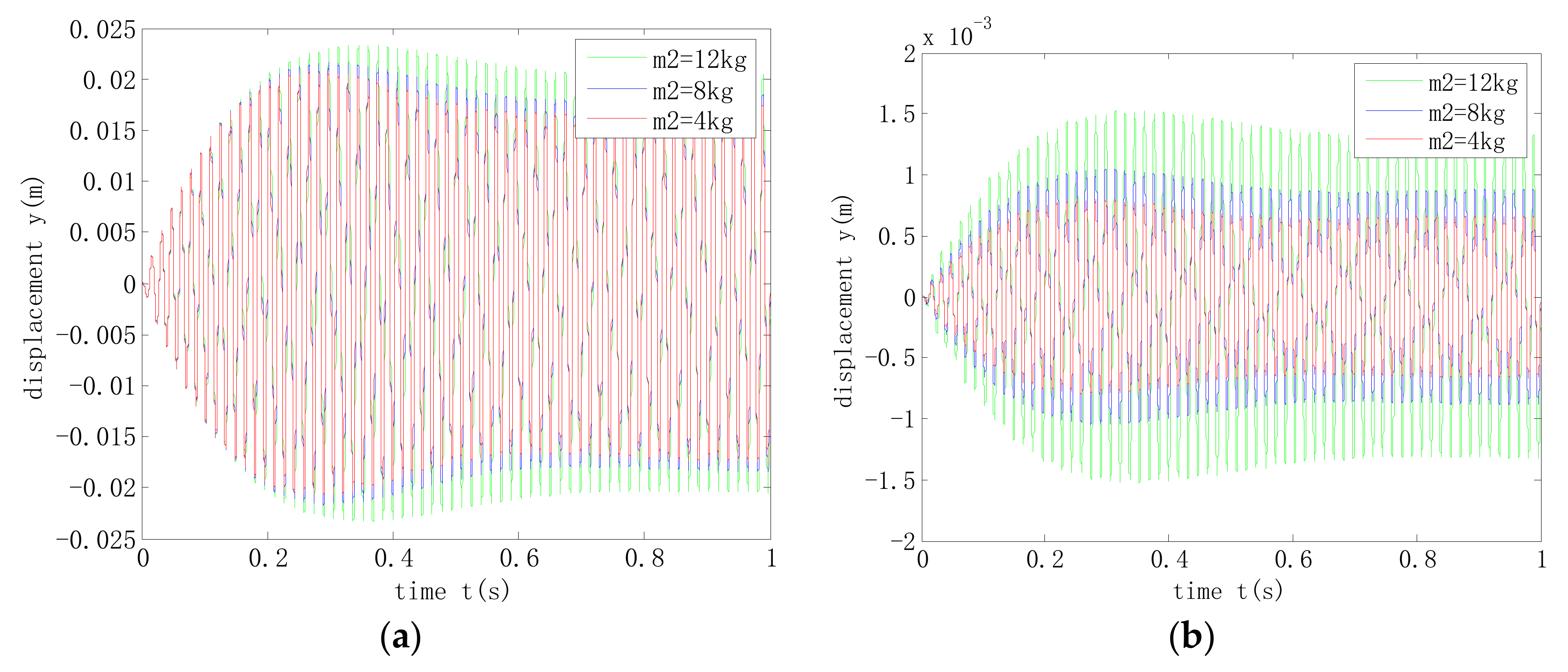
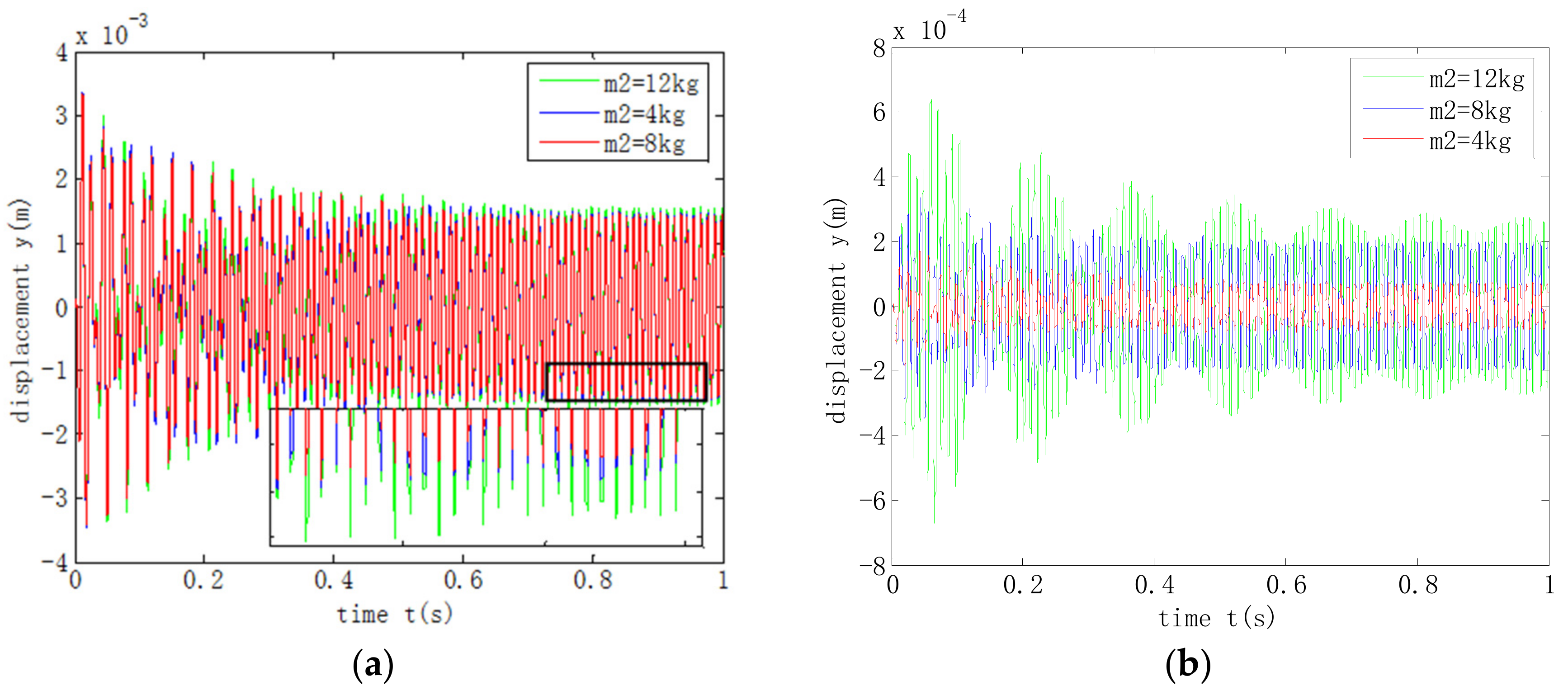
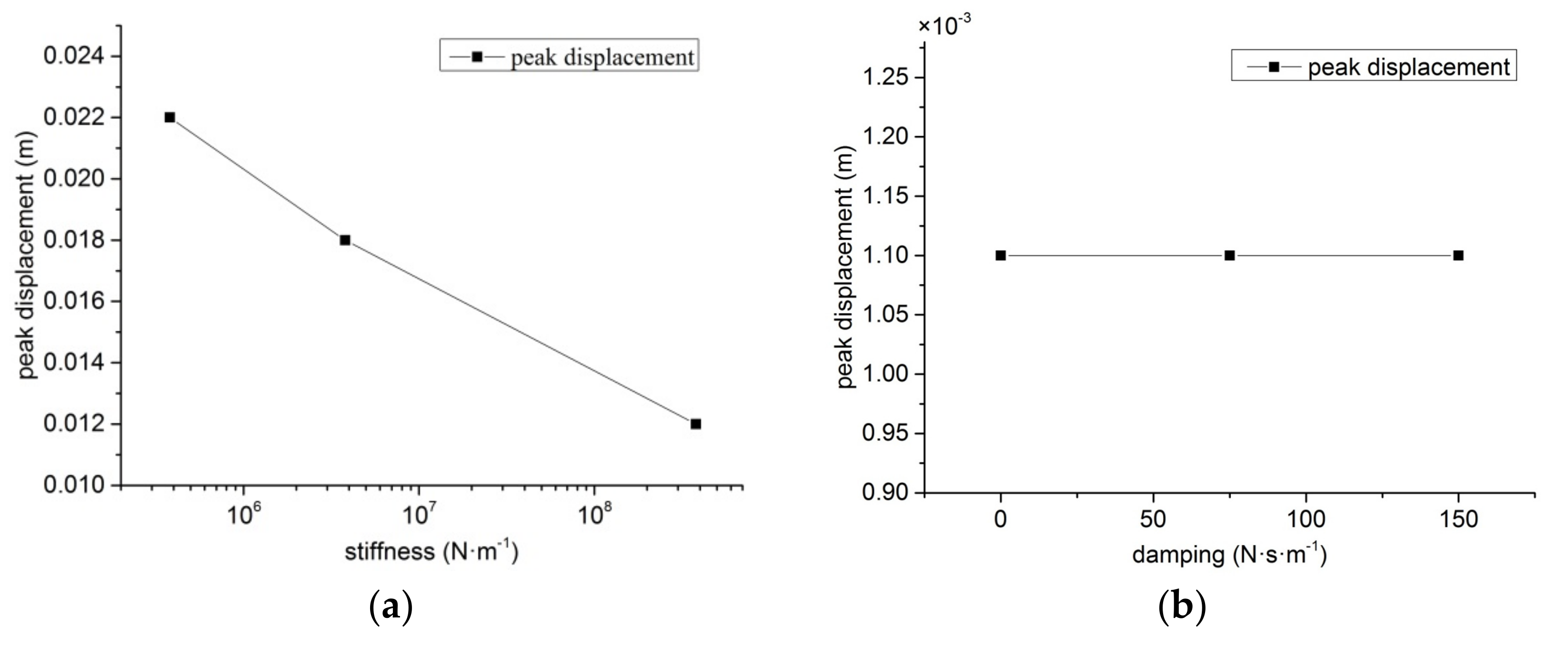
4.2. Analysis of the Influence of Support Parameters on Shafting Response
5. Conclusions
- (1)
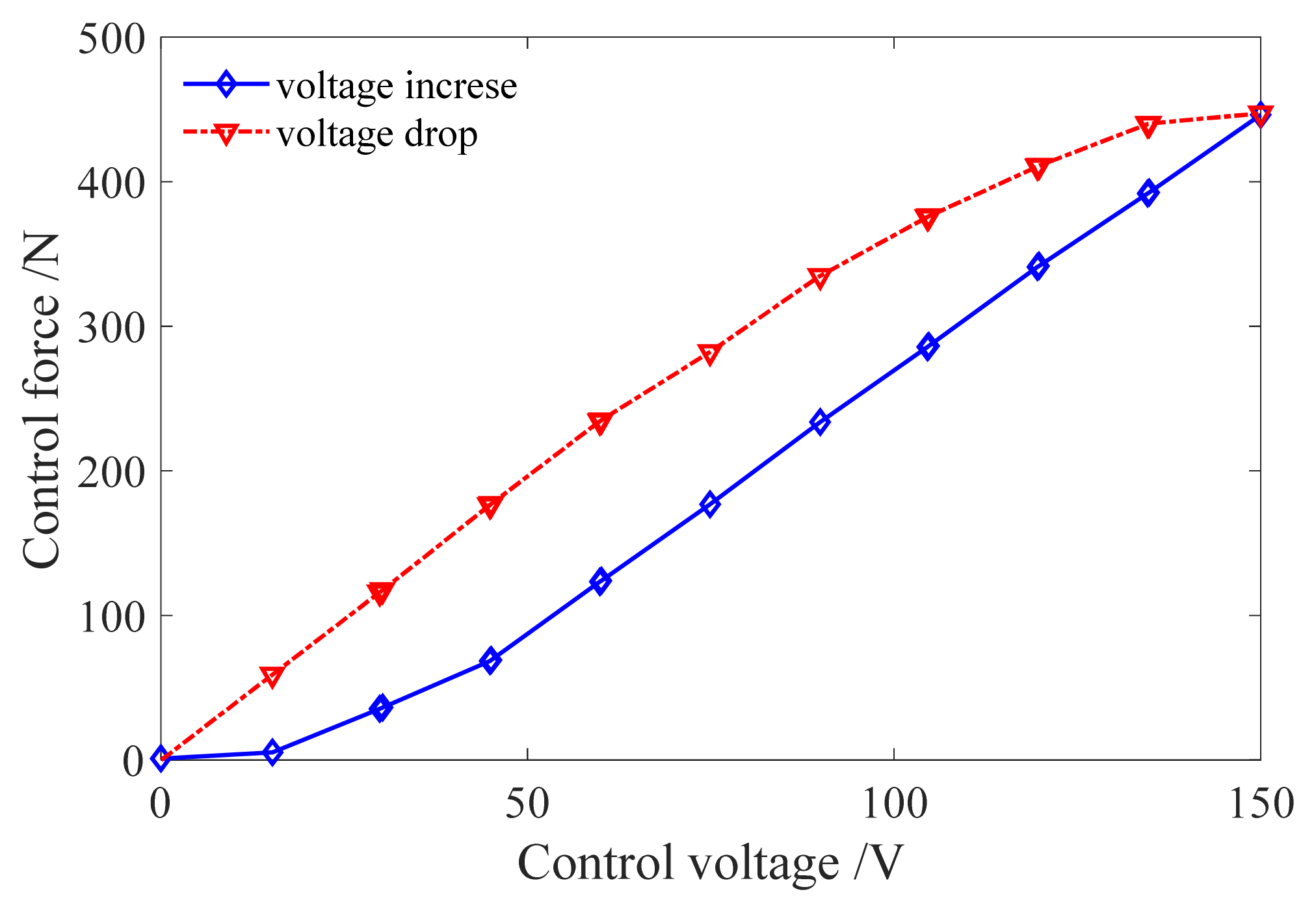
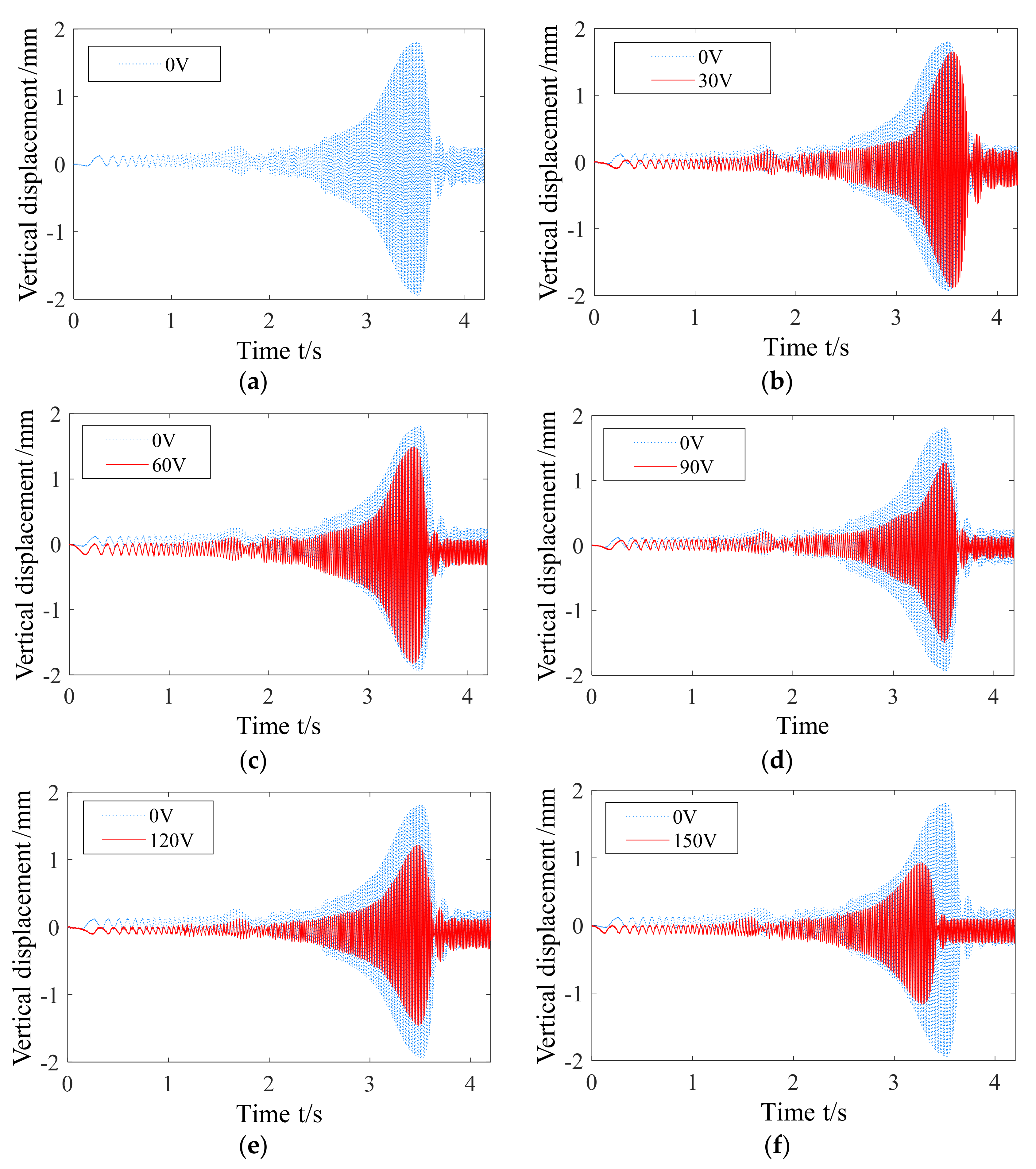
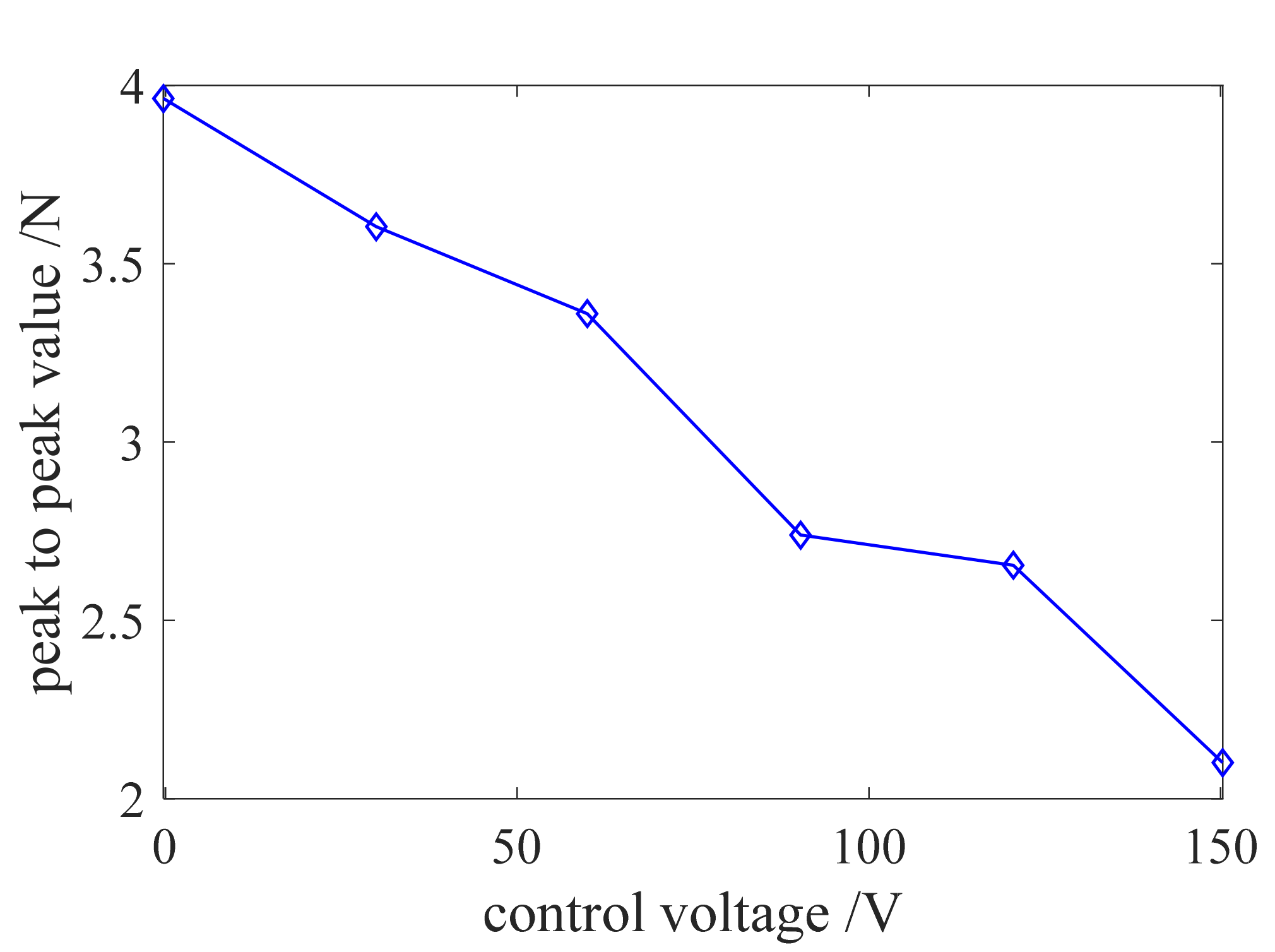
- On the basis of the smart spring test results, it was confirmed that when the maximum control voltage was 150 V, the maximum vibration reduction rate reached 44.2%, which verified that the smart spring support had a good control effect on the lateral bending vibration of the three-support shaft under the state of acceleration toward crossing critical speed.
- (2)
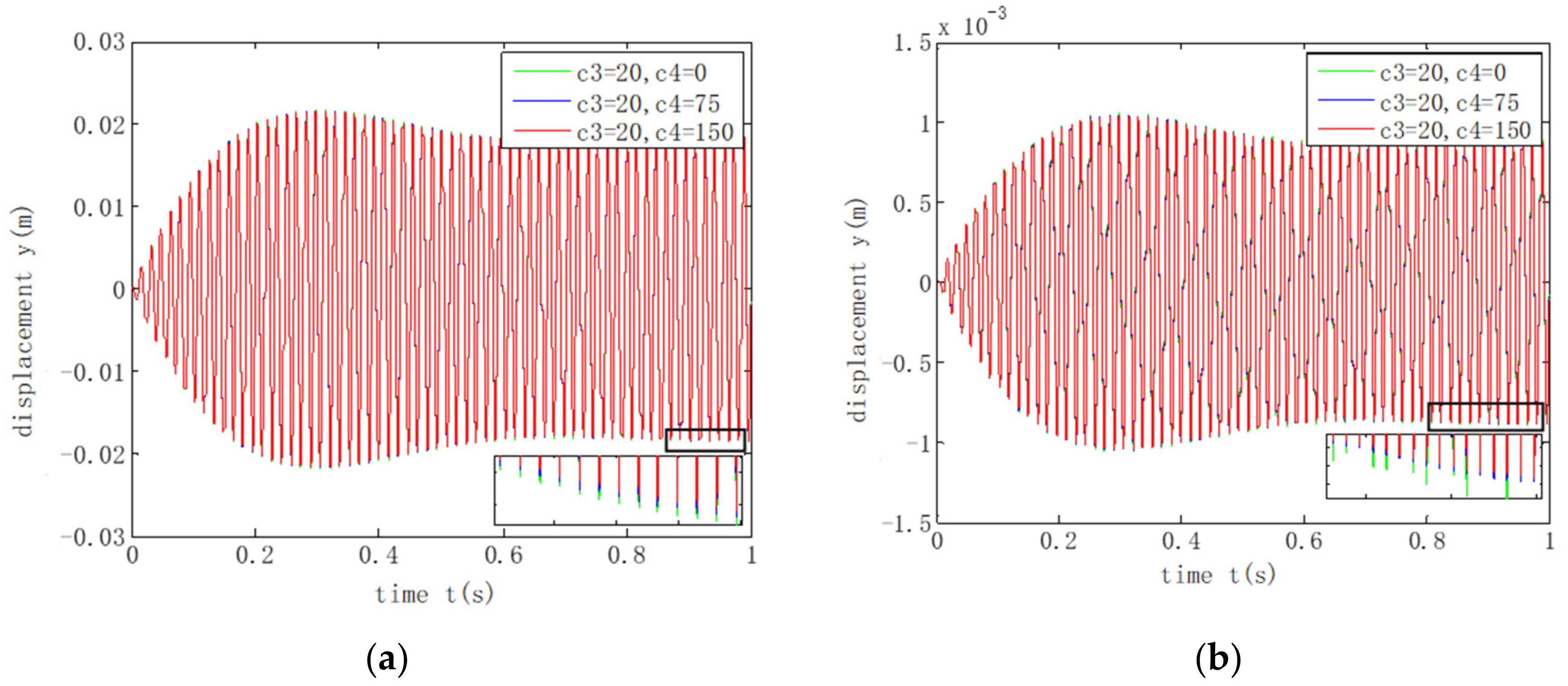
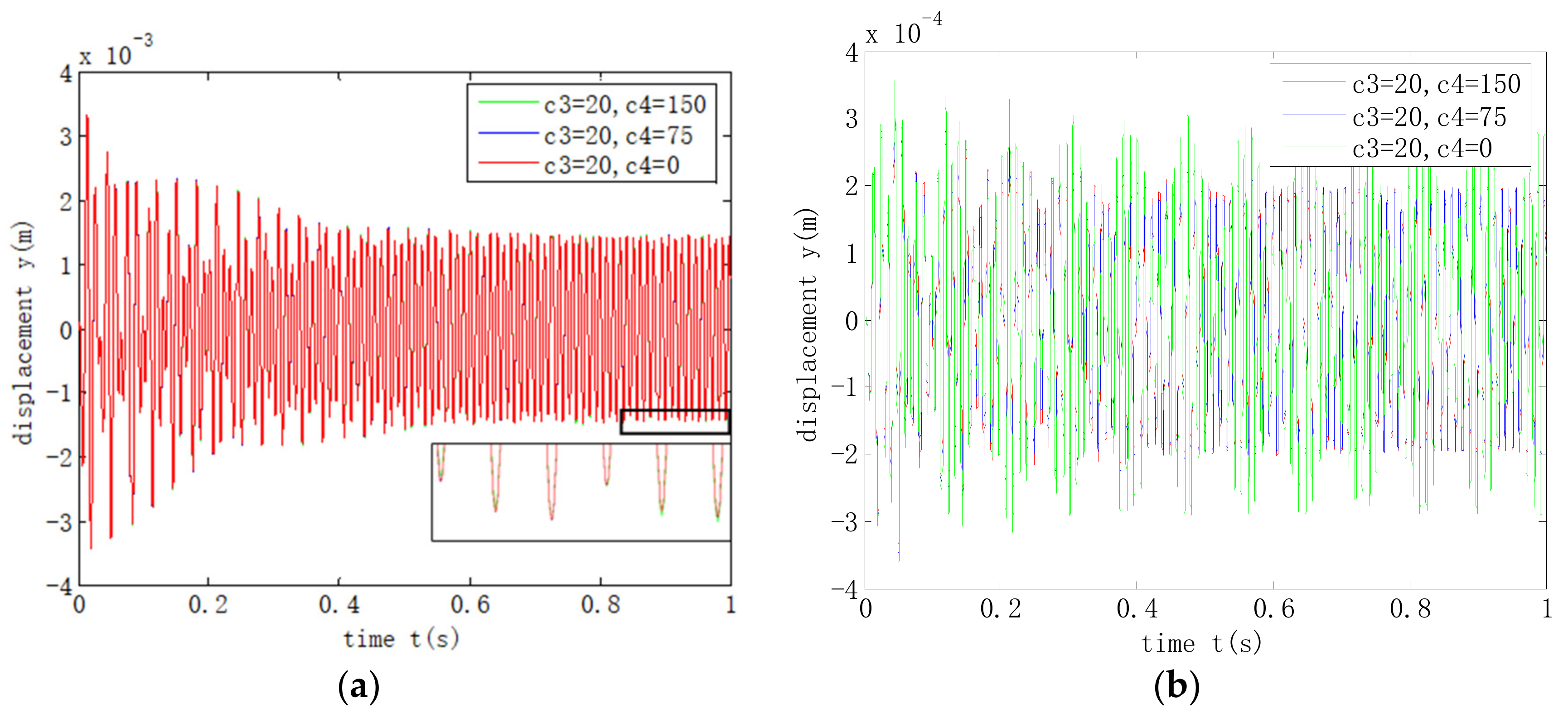
- During acceleration over the critical state of the shafting, the increase of the stiffness of the smart spring support could effectively reduce the amplitude of the three-support shafting. At this time, the change of damping at the smart spring support has no obvious effect on the vibration response of the system. In addition, the smaller the mass of the smart spring support, the smaller the vibration response of the system and the greater the impact on the support vibration.
Author Contributions
Funding
Conflicts of Interest
References
- Wenzhong, Q.; Jincai, S.; Yang, Q. Active control of vibration using a fuzzy control method. J. Sound Vib. 2004, 275, 917–930. [Google Scholar] [CrossRef]
- De, N. Research on Design Method of Smart Spring Damping System and Its Application in the Drive Shaft System. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2015. [Google Scholar]
- Nitzsche, F.; Feszty, D.; Grappasonni, C.; Coppotelli, G. Whirl-tower Open-loop Experiments and Simulations with an Adaptive Pitch Link Device for Helicopter Rotor Vibration. In Proceedings of the AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Boston, MA, USA, 8–11 April 2013; pp. 1–13. [Google Scholar]
- Afagh, F.; Nitzsche, F.; Morozova, N. Dynamic modelling and stability of hingeless helicopter blades with a smart spring. Aeronaut. J. 2004, 108, 369–377. [Google Scholar] [CrossRef]
- Coppotelli, G.; Marzocca, P.; Ulker, F.D.; Campbell, J.; Nitzsche, F. Experimental Investigation on Modal Signature of Smart Spring/Helicopter Blade System. J. Aircr. 2008, 45, 1373–1380. [Google Scholar] [CrossRef]
- Aldemir, A.C., Jr. Vibration attenuation in rotating machines using smart spring mechanism. Math. Probl. Eng. 2011, 1–14. [Google Scholar]
- Li, M..; Ma, L.L.; Wu, C.G.; Zhu, R.P. Study on the vibration active control of three-support shafting with smart spring while accelerating over the critical speed. Appl. Sci. 2020, 10, 6100. [Google Scholar] [CrossRef]
- Li, Q.-C.; Yu, Q.; Liu, W. Effect of supporting parameters on marine shaft vibration characteristics. Ship Sci. Technol. 2016, 38, 101–104. [Google Scholar]
- Li, H.-F.; Zhu, S.-J.; Liu, X.-W. Analysis of the effects of bearing stiffness on vibration transmission paths in ship propulsion shafting. Noise Vib. Control 2016, 36, 57–60. [Google Scholar]
- Li, X.; Zhu, H.; Yang, W.; Liu, L.; Yang, Z.R. Analysis of the influence of variable stiffness support on transverse vibration of ship shafting. China Ship. Repair. 2015, 28, 34–37. [Google Scholar]
- Van, T.N.; Dan, M.X. Analysis behavior of a rig shafting vibration set changes bearing parameters. Appl. Mech. Mater. 2013, 437, 98–101. [Google Scholar]
- Luo, J.-B.; Liu, Z.-H.; Shi, Y.; Xie, D.M.; Yu, X.G. The research on supporting stiffness of LP rotor of ultra-supercritical turbine. In Proceedings of the 2011 International Conference on Electrical and Control Engineering (ICECE), Yichang, China, 16–18 September 2011. [Google Scholar]
- Ma, J.; Dai, J.; Sun, B.-N.; Kou, X.-P.; Jing, J.-P. Supporting characteristics of bearings and their effects on dynamical behaviors of rotor system. Noise Vib. Control. 2011, 31, 22–26. [Google Scholar]
- Kumar, C.; Sarangi, S. Dynamic response of an unbalanced rigid rotor bearing system with a nonlinear hydrodynamic force. J. Comput. Nonlinear Dyn. 2018, 13, 090909-6. [Google Scholar] [CrossRef]
- Wang, B. Effect of bearing stiffness on ship shafting system vibration performance. J. Qiqihar Univ. 2009, 25, 55–60. [Google Scholar]
- Sun, B.-N.; Xie, F.; Jing, J.-P. Effects of bearings support characteristics on shaft stability. Noise Vib. Control 2012, 32, 137–140. [Google Scholar]
- Xu, J.-W.; Li, W.-B. Analysis on static and dynamic characteristics of electric spindle based on ANSYS. Mach. Des. Manuf. 2015, 09, 11–28. [Google Scholar]
- Su, C.-J.; Li, Z.; Xu, Y.-R. Analysis of vibration characteristics and response of the working ship propulsion shafting. Ship Ocean Eng. 2016, 45, 137–140. [Google Scholar]
- Zhang, X. Influence of equivalent supporting point location in stern bearing on shaft whirling vibration. Ship Ocean Eng. 2012, 41, 46–49. [Google Scholar]
- Jauhari, K. Vibration reduction of spindle-bearing system by design optimization. WSEAS Trans. Appl. Theor. Mech. 2018, 13, 85–91. [Google Scholar]
- Yücel, E.; Saruhan, H. Design optimization of rotor-bearing system considering critical speed using Taguchi method. Proc. Inst. Mech. Eng. Part E J. Process. Mech. Eng. 2016, 231, 138–146. [Google Scholar] [CrossRef]





| Parameter Name | Value/Unit | Parameter Name | Value/Unit |
|---|---|---|---|
| The density of the shaft ρ | 7850/(kg∙m−3) | Elastic modulus E | 2 × 1011/Pa |
| Shaft radius r | 7.5/mm | Disc radius R | 75/mm |
| Length of shaft l1 | 120/mm | Disc width b | 8/mm |
| Length of shaft l2 | 70/mm | Support stiffness kb | 1.7 × 105/(N∙m−1) |
| Length of shaft l3 | 80/mm | Support damping cb | 60/(N∙s∙m−1) |
| Length of shaft l4 | 270/mm | Unbalance magnitude e0 | 6.3 × 10−5/(kg∙m) |
| Length of shaft l3 | 420/mm | Auxiliary support stiffness ka | 6 × 105/(N∙m−1) |
| Parameter Name | Value/Unit |
|---|---|
| The density of the shaft (ρ) | 7850/(kg∙m−3) |
| Elastic modulus (E) | 2 × 1011/Pa |
| Disc radius (R) | 50/mm |
| Shaft radius (r) | 7/mm |
| Length of shaft (l1) | 198/mm |
| Length of shaft (l2) | 138/mm |
| Length of shaft (l3) | 322/mm |
| Length of shaft (l4) | 588/mm |
| Disc mass (m) | 1.05/kg |
| Support mass (mb1, mb2, mb3) | 8/kg |
| Stiffness of support I and III (kb1, kb3) | 2.89 × 108/(N∙m−1) |
| Stiffness of support II (kb2) | 3.8 × 106/(N∙m−1) |
| Support damping I and III (cb1, cb3) | 0 |
| Support damping II (cb2) | 75/(N∙s∙m−1) |
| Angular speed (Ω) | 400/(rad/s) |
| Eccentricity (e0) | 1/mm |
| Ω/Rad s−1 | First Positive Whirls ωF1/rad s−1 | Second Positive Whirls ωF2/rad s−1 | First Counter Whirls ωB1/rad s−1 | Second Counter Whirls ωB2/rad s−1 |
|---|---|---|---|---|
| 0 | 410.5 | 673.1 | −410.5 | −673.1 |
| 200 | 410.6 | 673.1 | −410.4 | −673.1 |
| 400 | 410.6 | 673.1 | −410.4 | −673.1 |
| 600 | 410.7 | 673.1 | −410.3 | −673.1 |
| 800 | 410.8 | 673.1 | −410.2 | −673.1 |
| Synchronous Positive Whirl | Synchronous Counter Whirl | ||
|---|---|---|---|
| ωFc/rad·s−1 | nFc/r·min−1 | ωBc/rad·s−1 | nBc/r·min−1 |
| 410.6 | 3923 | −410.4 | −3921 |
| 673.1 | 6431 | −673.1 | −6431 |
| Scheme | Stiffness/N m−1 | Damping/N s m−1 | Mass/kg |
|---|---|---|---|
| ① | 3.8e5 | 0 | 4 |
| ② | 3.8e6 | 75 | 8 |
| ③ | 3.8e8 | 150 | 12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.-m.; Ma, L.-l.; Wu, C.-g.; Li, Z.; Zhu, R.-p. Influence of Smart Spring Support Parameters on Vibration Characteristics of Three Support Shafting. Appl. Sci. 2020, 10, 7752. https://doi.org/10.3390/app10217752
Li M-m, Ma L-l, Wu C-g, Li Z, Zhu R-p. Influence of Smart Spring Support Parameters on Vibration Characteristics of Three Support Shafting. Applied Sciences. 2020; 10(21):7752. https://doi.org/10.3390/app10217752
Chicago/Turabian StyleLi, Miao-miao, Liang-liang Ma, Chuan-guo Wu, Zhuo Li, and Ru-peng Zhu. 2020. "Influence of Smart Spring Support Parameters on Vibration Characteristics of Three Support Shafting" Applied Sciences 10, no. 21: 7752. https://doi.org/10.3390/app10217752
APA StyleLi, M.-m., Ma, L.-l., Wu, C.-g., Li, Z., & Zhu, R.-p. (2020). Influence of Smart Spring Support Parameters on Vibration Characteristics of Three Support Shafting. Applied Sciences, 10(21), 7752. https://doi.org/10.3390/app10217752





