Theoretical Study on Prestress Loss in Cross-Tensioned Concrete Pavement with BFRP Tendons

Abstract

Cross-tensioned concrete pavement can reduce transverse joints and cracks and improve the durability of the pavement, and the decrease in slab thickness can be achieved without damaging the performance of the pavement. However, the corrosion of the steel can cause serious damage to the pavement structure, resulting in higher maintenance costs and shorter service life. Basalt fiber-reinforced polymer (BFRP) has been proven to be an effective alternative in both jointed plain concrete pavement (JPCP) and continuously reinforced concrete pavement (CRCP) due to its lightweight and corrosion-resistant properties. In this paper, a systematic theoretical method for determining the prestress loss of BFRP tendons in cross-tensioned concrete pavement was proposed, with the impact of the slab width and distribution angle of the prestressed tendon on the prestress loss being studied and compared to the results of traditional steel strands. Results showed that the proportion of the prestress loss due to anchorage deformation and prestress retraction in the prestressing stage rose with the increase in distribution angle and the decrease in slab width, while the prestress loss during the in-service stage was a constant value for both BFRP tendons and steel strands. The prestress loss of BFRP tendons was far lower than that of steel strands in both prestressing stage and in-service stage for a given slab width (3 m, 4.5 m, 9.0 m, 12.75 m) and distribution angle (20°, 25°, 30°, 35°, 40°, 45°), and the difference ranged from 6.4% to 16%, signifying the feasibility of BFRP tendons in cross-tensioned concrete pavement. Overall, the smaller the slab width, the greater the difference of the prestress loss between BFRP tendons and steel strands.

1. Introduction

Transverse joints in jointed plain concrete pavement (JPCP) can lead to several distresses, i.e., pumping, spalling, corner breaks, and even faulting, if they are not treated appropriately. Cross-tensioned concrete pavement has been proposed as an effective solution in enhancing the crack resistance of concrete pavement in order to improve the durability of concrete pavement and reduce the number of transverse joints.

Pre-compression stress can be produced in the concrete slab by imposing an external tensioning to the reinforcement tendon, counteracting the flexural and tensile stress caused by the traffic load and environmental factors; as a result, the crack resistance and durability of the concrete pavement can be significantly improved [1,2]. Merritt et al. [3,4] demonstrated the thickness and prestress requirements of prestressed concrete pavement by launching a precast prestressed concrete pavement pilot project near Georgetown, Texas. Currently, researchers [5,6,7,8,9,10] have carried out many studies on the design, construction, and structural analysis under vehicle load and thermal gradient of the prestressed concrete pavement given both theoretical and numerical methods, but without giving much consideration on the prestress loss, which is an important factor and cannot be neglected in the design of the cross-tensioned concrete pavement.

The concrete panel will continue to bear a high-level pre-compression stress with the overestimated prestress loss, resulting in excessive invert arch, which not only undermines the performance of the pavement structure but also causes the waste of materials [11]. On the contrary, if the estimated prestress loss is lower than the actual value, it will lead to insufficient pre-compression stress in the pavement slab, causing premature cracking of the slab and failure to achieve the desired effect of prestressed pavement [12]. Therefore, an accurate estimation of the prestress loss of prestressed tendons is necessary to ensure the performance and durability of the prestressed concrete pavement. Au and Si [13] proposed a new relaxation model for steel strands that was based on the equivalent creep coefficient to provide accurate time-dependent prestress loss of cable forces. Kim et al. [14] evaluated the friction coefficients between the strand and the duct with smart strands on the basis of a full-scale test specimen and two actual long-span girder bridges. Yang et al. [15] developed a refined method for the calculation of time-dependent prestress losses in prestressed concrete girders and verified the proposed method with numerical results. However, the existing studies on prestress loss are mainly for bridges and beams, and mostly involve steel strands.

Despite the decreased transverse cracks in cross-tensioned concrete pavement, the corrosion of the steel can still cause great damage to the performance and durability of the prestressed pavement structure, resulting in high maintenance costs [16,17]. Recently, new materials such as basalt fiber-reinforced polymer (BFRP), which is lightweight and corrosion-resistant [18], has been widely used as longitudinal reinforcement in continuously reinforced concrete pavement (CRCP), and has been proven to be a promising alternative to steel in CRCP given excellent bond relationship between the BFRP and the concrete [19,20]. Nonetheless, no study has been found in the literature regarding the application of the BFRP in cross-tensioned concrete pavement. Due to the difference in the relaxation mechanism of fiber-reinforced tendons and steel strands, the traditional method for calculating the prestress loss of steel strands cannot be directly used for calculating the prestress loss of BFRP tendons in cross-tensioned concrete pavements.

In this paper, a systematic theoretical method was proposed for calculating the prestress loss of BFRP tendons in cross-tensioned concrete pavement. The effect of the concrete slab width and distribution angle of the BFRP tendons on prestress loss was discussed using the proposed method. Given various slab width and distribution angles of the prestressed tendon, the prestress loss of BFRP tendons was then compared to that of the steel strands in order to demonstrate the feasibility of the BFRP tendon in cross-tensioned concrete pavement.

2. Theoretical Method for Determining Prestress Loss of BFRP Tendons

Generally, the prestress loss in cross-tensioned concrete pavements arise from five causes [21], namely, the loss caused by anchorage deformation and prestress retraction (σ_l1), the loss caused due to the friction between prestressed tendons and their surrounding casing pipes (σ_l2), the loss caused because of the elastic compression of concrete (σ_l3), the loss resulted from the relaxation of prestress tendons (σ_l4), and the loss arising from concrete shrinkage and concrete creep (σ_l5).

2.1. Prestress Loss Due to Anchorage Deformation and Prestress Retraction

After the BFRP tendons are stretched, relative displacement is produced due to the deformation of the anchor and the base plate as well as the retraction of the BFRP tendons, and as a result, the prestress loss caused by anchorage deformation and prestress retraction σ_l1 occurs around the anchorage area and can be calculated with Equation (1).

$${\sigma }_{l1}=\frac{a}{l}{E}_{\mathrm{f}\mathrm{p}}$$

(1)

where a is the length of the anchorage deformation and prestress retraction of BFRP tendons, l is the distance between the tension end and the anchor end, and E_fp is the elastic modulus of BFRP tendons.

2.2. Prestress Loss from the Friction between BFRP Tendons and the Surrounding Casing Pipe

BFRP tendons deflect under their own weight, resulting in friction between the prestressed BFRP tendons and the casing wall during tensioning. The friction is related to the length of the prestressed BFRP tendons, given the fact that the longer the length of the prestressed BFRP tendons, the higher the friction, and therefore the higher the prestress loss caused due to the friction, which can be obtained through Equation (2).

$${\sigma }_{l2}={\sigma }_{\mathrm{c}\mathrm{o}\mathrm{n}}\left(1-\frac{1}{e^{\kappa x+\mu \theta }}\right)$$

(2)

where σ_con is the tension control stress of the prestressed BFRP tendon, κ is the coefficient of the casing pipe, µ is the friction coefficient between the BFRP tendon and the casing wall, x is the distance between the calculation cross-section and the anchor end, and θ is the tangent angle between the calculation cross-section and the anchor end.

2.3. Prestress Loss Due to Elastic Compression of Concrete

Hypertension was adopted in cross-tensioned concrete pavements, and therefore the elastic compression loss arising from the batched tension process can be greatly reduced. As a result, the prestress loss caused by the elastic compression of concrete can be neglected in prestressed BFRP concrete pavements [22].

2.4. Prestress Loss from the Relaxation of Prestress Tendons

For BFRP tendons, plastic deformation appears with time under high stress or constant tensile stress. Therefore, the stress in BFRP tendons reduces with time, given the unchanged length of BFRP tendons, resulting in the relaxation of BFRP tendons. In addition, the deformation of BFRP tendons also increases with time if the stress of BFRP tendons keeps the same, which is the creep of BFRP tendons. For cross-tensioned concrete pavements, both the relaxation and the creep of BFRP tendons can give rise to the prestress loss [23,24], as shown in Equation (3).

$${\sigma }_{l4}=r{\sigma }_{\mathrm{c}\mathrm{o}\mathrm{n}}$$

(3)

where r is the relaxation loss rate. The prestress loss resulted from the relaxation of BFRP tendons can be calculated with Equation (4) on the basis of the relaxation mechanism of BFRP tendons.

$${\sigma }_{l4}={\sigma }_1+{\sigma }_2+{\sigma }_3$$

(4)

where σ₁ is the prestress loss arising from the creep of the BFRP tendon, and can be obtained with Equation (5); σ₂ is the prestress loss caused by fiber straightening, relating to the pultrusion process of the BFRP tendon, being around 0.01σ_con to 0.02σ_con; and σ₃ is the loss resulted from the relaxation of the prestressed fiber-reinforced polymer tendon itself and is related to the type of the fiber.

$${\sigma }_1=\frac{{\nu }_{\mathrm{r}}{\sigma }_{\mathrm{c}\mathrm{o}\mathrm{n}}{E}_{\mathrm{r}}}{E_{\mathrm{f}}}$$

(5)

where ν_r is the volume content of the resin in BFRP tendons, and E_r/E_f is the ratio of the elastic modulus of resin to the elastic modulus of filament of BFRP tendons.

2.5. Prestress Loss Due to Concrete Shrinkage and Creep

The concrete shrinkage refers to the volume change caused by concrete hardening and it has nothing to do with the load on the pavement structure, while the concrete creep refers to the phenomenon that the strain or deformation of the concrete structure increases with time when the structure is subjected to a long-term load. Both of the concrete shrinkage and concrete creep result in the increase in concrete deformation, which causes redistribution of stress in the reinforced concrete section, and therefore the prestress loss is produced. The calculation of the prestress loss caused due to concrete shrinkage and creep is defined in Equation (6) [25].

$${\sigma }_{l5}=\frac{55+300\frac{{\sigma }_{\mathrm{p}\mathrm{c}}}{f{\prime }_{\mathrm{c}\mathrm{u}}}}{1+15\rho }•\frac{E_{\mathrm{f}\mathrm{p}}}{E_{\mathrm{p}}}$$

(6)

where σ_pc is the normal compressive stress of the concrete at the resultant point of prestressed tendons; E_fp and E_p are the elastic modulus of the prestressed BFRP tendons and the steel strands, respectively; f′_cu is the compressive strength of the concrete; and ρ is the reinforcement ratio of BFRP tendons.

Given a specific physical project, material properties of the pre-stressed BFRP tendons and design parameters of the cross-tensioned pavement can be obtained, and therefore the corresponding pre-stress loss of BFRP tendons can be calculated with the proposed methods, as shown in Equations (1)–(6). With the accurate predicted pre-stress loss, an appropriate design of BFRP tendons can be achieved to avoid both excessive and insufficient pre-stress, which can result in invert arch and premature cracking in cross-tensioned concrete pavement, respectively.

3. Theoretical Analysis of Prestress Loss of BFRP Tendons

3.1. Input Parameters

The width of the cross-tensioned concrete pavement was assumed to be 3.0 m, 4.5 m, 9.0 m, and 12.75 m, with a thickness of 0.2 m. The elastic modulus of concrete was assumed to be 30 GPa. The diameter of the BFRP tendon was assumed to be 16 mm, and the corresponding nominal cross-sectional area was 201 mm². The ultimate tensile strength and elastic modulus were assumed to be 1300 MPa and 40 GPa, respectively, according to previous study [26].

A total of six distribution angles from 20° to 45° with an interval of 5° were selected for BFRP tendons. The tension control stress of the BFRP tendon was assumed to be 65% of the ultimate tensile strength, namely, 845 MPa in this case. In order to determine the spacing of the BFRP tendon at different distribution angles, the mean longitudinal compressive stress given the distribution angle and the spacing of 30° and 1000 mm was calculated by using Equation (7).

$${\sigma }_{\mathrm{p}\mathrm{y}}=\frac{2({\sigma }_{\mathrm{c}\mathrm{o}\mathrm{n}}-{\sigma }_l)\times A_{\mathrm{p}}\times \cos \alpha }{h\times l\times \tan \alpha }$$

(7)

where σ_py is the mean longitudinal compressive stress, σ_l is the total prestress loss, A_p is the nominal sectional area of the prestressed tendons, h is the thickness of the concrete slab, l is the longitudinal distance of the prestressed tendons, and α is the distribution angle of the prestressed tendons. Correspondingly, the mean longitudinal compressive stress of 2.55 MPa was obtained for BFRP tendons. On the basis of the mean longitudinal compressive stress, the spacing of BFRP tendons for each distribution angle (20°, 25°, 30°, 35°, 40°, and 45°) can be calculated, as summarized in

Table 1. The spacing of basalt fiber-reinforced polymer (BFRP) tendons at different distribution angles (mm).

Distribution Angle (°)	Spacing of BFRP Tendons (mm)
20	1720
25	1295
30	1000
35	779
40	608
45	471

, indicating that the greater the distribution angle of BFRP tendons, the less spacing there was between BFRP tendons.

3.2. Results and Discussions

On the basis of the appearance time, the prestress loss can be classified into two stages, i.e., prestressing stage and in-service stage, given that the losses in prestressing stage and in-service stage are instantaneous losses and time-dependent losses, respectively [27]. In general, the prestress loss caused by anchorage deformation and prestress retraction (σ_l1), friction between prestressed tendons and their surrounding casing pipes (σ_l2), and elastic compression of concrete (σ_l3) is produced in the prestressing stage. The prestress loss caused by the relaxation of prestressed tendons (σ_l4), and concrete shrinkage and concrete creep (σ_l5) is produced in the in-service stage, usually lasting for a long period.

3.2.1. Prestress Loss in the Prestressing Stage

The prestress loss of BFRP tendons with different distribution angles (20°, 25°, 30°, 35°, 40°, and 45°) in the prestressing stage given the slab width of 3.0 m, 4.5 m, 9.0 m, and 12.75 m are summarized in

Table 2. Theoretical prestress loss of BFRP tendons given the slab width of 3.0 m.

Distribution Angle (°)	Length of BFRP Tendon (mm)	Prestress Loss (%)			$\frac{{\mathit{\sigma }}_{\mathit{l}1}}{{\mathit{\sigma }}_{\mathit{l}1}+{\mathit{\sigma }}_{\mathit{l}2}}$ (%)
		${\mathit{\sigma }}_{\mathit{l}1}$	${\mathit{\sigma }}_{\mathit{l}2}$	${\mathit{\sigma }}_{\mathit{l}1}+{\mathit{\sigma }}_{\mathit{l}2}$
20	8771	4.3	3.4	7.8	55.6
25	7099	5.3	2.8	8.1	65.6
30	6000	6.3	2.4	8.7	72.7
35	5230	7.2	2.1	9.3	77.8
40	4667	8.1	1.8	10.0	81.4
45	4243	8.9	1.7	10.6	84.1

,

Table 3. Theoretical prestress loss of BFRP tendons given the slab width of 4.5 m.

Distribution Angle (°)	Length of BFRP Tendon (mm)	Prestress Loss (%)			$\frac{{\mathit{\sigma }}_{\mathit{l}1}}{{\mathit{\sigma }}_{\mathit{l}1}+{\mathit{\sigma }}_{\mathit{l}2}}$ (%)
		${\sigma }_{l1}$	${\sigma }_{l2}$	${\sigma }_{l1}+{\sigma }_{l2}$
20	13,157	2.9	5.1	8.0	36.0
25	10,648	3.6	4.2	7.7	46.0
30	9000	4.2	3.5	7.7	54.3
35	7846	4.8	3.1	7.9	61.0
40	7001	5.4	2.8	8.2	66.2
45	6364	6.0	2.5	8.5	70.3

,

Table 4. Theoretical prestress loss of BFRP tendons given the slab width of 9.0 m.

Distribution Angle (°)	Length of BFRP Tendon (mm)	Prestress Loss (%)			$\frac{{\mathit{\sigma }}_{\mathit{l}1}}{{\mathit{\sigma }}_{\mathit{l}1}+{\mathit{\sigma }}_{\mathit{l}2}}$ (%)
		${\mathit{\sigma }}_{\mathit{l}1}$	${\mathit{\sigma }}_{\mathit{l}2}$	${\mathit{\sigma }}_{\mathit{l}1}+{\mathit{\sigma }}_{\mathit{l}2}$
20	26,314	1.4	10.0	11.4	12.6
25	21,296	1.8	8.2	9.9	17.9
30	18,000	2.1	6.9	9.1	23.2
35	15,691	2.4	6.1	8.5	28.4
40	14,002	2.7	5.4	8.2	33.2
45	12,728	3.0	5.0	7.9	37.5

and

Table 5. Theoretical prestress loss of BFRP tendons given the slab width of 12.75m.

Distribution Angle (°)	Length of BFRP Tendon (mm)	Prestress Loss (%)			$\frac{{\mathit{\sigma }}_{\mathit{l}1}}{{\mathit{\sigma }}_{\mathit{l}1}+{\mathit{\sigma }}_{\mathit{l}2}}$ (%)
		${\mathit{\sigma }}_{\mathit{l}1}$	${\mathit{\sigma }}_{\mathit{l}2}$	${\mathit{\sigma }}_{\mathit{l}1}+{\mathit{\sigma }}_{\mathit{l}2}$
20	37,279	1.0	13.9	14.9	6.8
25	30,169	1.3	11.4	12.6	9.9
30	25,500	1.5	9.7	11.2	13.3
35	22,229	1.7	8.5	10.2	16.7
40	19,835	1.9	7.6	9.5	20.0
45	18,031	2.1	7.0	9.1	23.2

, respectively.

As described in Table 2, the theoretical prestress loss of BFRP tendons in the prestressing stage was between 7.8% and 10.6%, given the slab width of 3.0 m. The greater the distribution angle of the BFRP tendon, the higher the σ_l1 and the lower the σ_l2. When the distribution angle increased from 20° to 45°, σ_l1 rose from 4.3% to 8.9% while σ_l2 reduced from 3.4% to 1.7%, and therefore the proportion of σ_l1 in the total prestress loss in the prestressing stage increased from 55.6% to 84.1%, implying that the main prestress loss of BFRP tendons in the prestressing stage given a 3.0 m wide slab was caused by anchorage deformation and prestress retraction (σ_l1).

It can be illustrated from Table 3 that the total prestress loss of the BFRP tendon in the prestressing stage was between 7.7% to 8.5%, given a 4.5 m wide prestressed concrete slab. With the increase of the distribution angle of the BFRP tendon, σ_l1 increased from 2.9% to 6.0% while σ_l2 experienced a drop of 2.6%, and the proportion of σ_l1 in the prestress loss in the prestressing stage increased from 36.0% to 70.3%, demonstrating that the main prestress loss was caused by the friction between the BFRP tendon and the surrounding casing pipe (σ_l2) with the distribution angle less than 30°. However, when the distribution angle was higher than 30°, the main loss resulted from anchorage deformation and prestress retraction (σ_l1).

For a 9.0 m wide slab, the prestress loss in the prestressing stage decreased from 11.4% to 7.9% when the distribution angle of the BFRP tendon varied from 20° to 45° given a 1.6% increase in σ_l1 and a 5.0% decrease in σ_l2. It is shown in Table 4 that the main prestress loss was caused by the friction between the BFRP tendon and the surrounding casing pipe (σ_l2), since the proportion of σ_l1 was always less than 38%, regardless of the distribution angle.

Similar to the results for the slab width of 9.0 m, the main prestress loss given the slab width of 12.75 m was caused by the friction between the BFRP tendon and the surrounding casing pipe (σ_l2), as shown in Table 5. The total prestress loss varied from 9.1% to 14.9%, with the variation of the distribution angle being between 20° and 45°.

In general, the prestress loss in the prestressing stage (σ_l1 and σ_l2) varied with the distribution angle of the BFRP tendon and the slab width. Given the same slab width, σ_l1 increased and σ_l2 decreased when the distribution angle varied from 20° and 45°, and the proportion of σ_l1 in the total prestress loss in the prestressing stage rose as well. However, given the same distribution angle, the σ_l1 decreased while σ_l2 significantly increased with the increase in slab width, and the proportion of σ_l1 went down gradually.

3.2.2. Prestress Loss during the In-Service Stage

It can be found from Equations (3)–(6) that the length of the prestressed tendon had no impact on the prestress loss during the in-service stage, and as a result, the prestress loss did not vary with the change of the slab width. Given the same properties of prestressed tendon and concrete, the prestress loss during the in-service stage was a fixed value. The prestress loss of the BFRP tendon during the in-service stage is summarized in

Table 6. Theoretical prestress loss of BFRP tendons during the in-service stage.

σl4 (%)	σl5 (%)	σl4 + σl5 (%)
3.2	2.0	5.2

. It can be found that the total prestress loss during the in-service stage (5.2%) was much smaller than that in the prestressing stage.

3.2.3. Total Prestress Loss of BRRP Tendons

The total prestress loss of BFRP tendons at various distribution angles and slab widths is summarized in

Table 7. The total prestress loss of BFRP tendons.

Distribution Angle (°)	Total Prestress Loss (%)
	Slab Width = 3.0 m	Slab Width = 4.5	Slab Width = 9.0 m	Slab Width = 12.75 m
20	12.9	13.2	16.6	20.1
25	13.3	12.9	15.1	17.8
30	13.9	12.9	14.2	16.4
35	14.5	13.1	13.7	15.4
40	15.1	13.4	13.3	14.7
45	15.8	13.6	13.1	14.2

. The smallest prestress loss of the BFRP tendons was 12.9%, given the slab width of 3.0 m and distribution angle of 20°, while the highest prestress loss was 20.1%, given the slab width of 12.75 m and distribution angle of 20°. For the slab width of 9.0 m and 12.75 m, the prestress loss decreased with the rise of the distribution angle, while for the slab width of 4.5 m, the prestress loss decreased first and then increased with the minimum loss of 12.9% when the distribution angle was 30°. In the case of a 3.0 m wide slab, the prestress loss experienced a continuous increase with the rise of the distribution angle.

As expected, given the same distribution angle, the total prestress loss varied with the slab width as well. With a distribution angle of 20°, the greater the slab width, the higher the total prestress loss. However, when the distribution angle was more than 20°, the prestress loss experienced a decrease first and then increased with the increase in slab width, given the fact that the higher the distribution angle of the BFRP tendon, the faster the prestress loss decreased.

4. Comparison of the Prestress Loss with Steel Strands

4.1. Calculation Process of the Prestress Loss for Steel Strands

4.1.1. Prestress Loss Due to Anchorage Deformation and Prestress Retraction

For the prestress loss caused by anchorage deformation and prestress retraction, the calculation process is the same as that for BFRP tendons, as shown in Equation (1).

4.1.2. Prestress Loss from the Friction between Steel Strands and the Surrounding Casing Pipe

Similar to BFRP tendons, friction occurs between the steel strand and the casing pipe during the stretching process of the prestressed steel strand. The calculation method is defined in Equation (8).

$${\sigma }_{l2}=\{\begin{array}{cc}{\sigma }_{\mathrm{c}\mathrm{o}\mathrm{n}}\left(1-\frac{1}{e^{\kappa x+\mu \theta }}\right)\hfill & \hfill \kappa x+\mu \theta >0.3\\ {\sigma }_{\mathrm{c}\mathrm{o}\mathrm{n}}\left(\kappa x+\mu \theta \right)\hfill & \hfill \kappa x+\mu \theta \le 0.3\end{array}$$

(8)

On the basis of the Chinese standard JGJ 92-2016 [25], the value of κ and µ can be assumed to be 0.004 and 0.09, respectively, given the nominal diameter of the steel strand being 9.5 mm, 12.7 mm, 15.2 mm, and 15.7 mm.

4.1.3. Prestress Loss Due to Elastic Compression of Concrete

Like the case of BFRP tendons, the prestress loss caused by elastic compression of concrete can be neglected given the application of the hypertension in cross-tensioned concrete pavements.

4.1.4. Prestress Loss from the Relaxation of Prestressed Steel Strands

For steel strands, the prestress loss caused by relaxation of prestress tendons can be determined on the basis of the relationship between the tension control stress σ_con and the standard tensile strength f_ptk of the prestressed steel strands, as presented in Equation (9). Normally, the tension control stress is around 75% of the standard tensile strength.

$${\sigma }_{l4}=\{\begin{array}{cc}0.20(\frac{{\sigma }_{\mathrm{c}\mathrm{o}\mathrm{n}}}{f_{\mathrm{p}\mathrm{t}\mathrm{k}}}-0.575){\sigma }_{\mathrm{c}\mathrm{o}\mathrm{n}}\hfill & 0.7f_{\mathrm{p}\mathrm{t}\mathrm{k}}<{\sigma }_{\mathrm{c}\mathrm{o}\mathrm{n}}\le 0.8f_{\mathrm{p}\mathrm{t}\mathrm{k}}\hfill \\ 0.125(\frac{{\sigma }_{\mathrm{c}\mathrm{o}\mathrm{n}}}{f_{\mathrm{p}\mathrm{t}\mathrm{k}}}-0.5){\sigma }_{\mathrm{c}\mathrm{o}\mathrm{n}}\hfill & 0.5f_{\mathrm{p}\mathrm{t}\mathrm{k}}<{\sigma }_{\mathrm{c}\mathrm{o}\mathrm{n}}\le 0.7f_{\mathrm{p}\mathrm{t}\mathrm{k}}\hfill \\ 0\hfill & {\sigma }_{\mathrm{c}\mathrm{o}\mathrm{n}}\le 0.5f_{\mathrm{p}\mathrm{t}\mathrm{k}}\hfill \end{array}$$

(9)

4.1.5. Prestress Loss Due to Shrinkage and Creep of Concrete

For steel strands, the prestress loss resulted from the concrete shrinkage and concrete creep can be obtained through Equation (10).

$${\sigma }_{l5}=\frac{55+300\frac{{\sigma }_{\mathrm{p}\mathrm{c}}}{f{\prime }_{\mathrm{c}\mathrm{u}}}}{1+15\rho }$$

(10)

According to Equations (1) and (8)–(10), the total prestress loss for steel strands can be obtained.

4.2. Results for Steel Strands

The same input parameters for concrete slabs and distribution angles of BFRP tendons were used in the calculation of prestress loss for steel strands. The diameter of the steel strands was assumed to be 15.2 mm with the nominal cross-sectional area being 184 mm², and the ultimate tensile strength and elastic modulus of steel strands were 1860 MPa and 195 GPa, respectively. The tension control stress of steel strands was 75% of the ultimate tensile strength, namely, 1395 MPa in this case. Given the distribution angle of 30° and spacing of 1000 mm, the mean longitudinal compressive stress for steel strands was calculated to be 3.85 MPa with Equation (7), and therefore the corresponding spacing of steel strands at each distribution angle (20°, 25°, 30°, 35°, 40°, and 45°) were 1721 mm, 1296 mm, 1000 mm, 780 mm, 609 mm, and 471 mm, respectively.

4.2.1. Prestress Loss in the Prestressing Stage

With Equations (1) and (8), the prestress loss of steel strands in the prestressing stage at different distribution angles (20°, 25°, 30°, 35°, 40°, and 45°) can be obtained given the slab width of 3.0 m, 4.5 m, 9.0 m, and 12.75 m, as presented in

Table 8. Theoretical prestress loss of steel strands given the slab width of 3.0 m.

Distribution Angle (o)	Length of Steel Strand (mm)	Prestress Loss (%)			$\frac{{\mathit{\sigma }}_{\mathit{l}1}}{{\mathit{\sigma }}_{\mathit{l}1}+{\mathit{\sigma }}_{\mathit{l}2}}$ (%)
		${\mathit{\sigma }}_{\mathit{l}1}$	${\mathit{\sigma }}_{\mathit{l}2}$	${\mathit{\sigma }}_{\mathit{l}1}+{\mathit{\sigma }}_{\mathit{l}2}$
20	8771	9.6	3.4	13.0	73.5
25	7099	11.8	2.8	14.6	80.8
30	6000	14.0	2.4	16.3	85.5
35	5230	16.0	2.1	18.1	88.6
40	4667	18.0	1.8	19.8	90.7
45	4243	19.8	1.7	21.5	92.2

,

Table 9. Theoretical prestress loss of steel strands given the slab width of 4.5 m.

Distribution Angle (°)	Length of Steel Strand (mm)	Prestress Loss (%)			$\frac{{\mathit{\sigma }}_{\mathit{l}1}}{{\mathit{\sigma }}_{\mathit{l}1}+{\mathit{\sigma }}_{\mathit{l}2}}$ (%)
		${\mathit{\sigma }}_{\mathit{l}1}$	${\mathit{\sigma }}_{\mathit{l}2}$	${\mathit{\sigma }}_{\mathit{l}1}+{\mathit{\sigma }}_{\mathit{l}2}$
20	13,157	6.4	5.1	11.5	55.4
25	10,648	7.9	4.2	12.0	65.4
30	9000	9.3	3.5	12.9	72.5
35	7846	10.7	3.1	13.8	77.6
40	7001	12.0	2.8	14.7	81.3
45	6364	13.2	2.5	15.7	84.0

,

Table 10. Theoretical prestress loss of steel strands given the slab width of 9.0 m.

Distribution Angle (°)	Length of Steel Strand (mm)	Prestress Loss (%)			$\frac{{\mathit{\sigma }}_{\mathit{l}1}}{{\mathit{\sigma }}_{\mathit{l}1}+{\mathit{\sigma }}_{\mathit{l}2}}$ (%)
		${\mathit{\sigma }}_{\mathit{l}1}$	${\mathit{\sigma }}_{\mathit{l}2}$	${\mathit{\sigma }}_{\mathit{l}1}+{\mathit{\sigma }}_{\mathit{l}2}$
20	26,314	3.2	10.0	13.2	24.2
25	21,296	3.9	8.2	12.1	32.5
30	18,000	4.7	6.9	11.6	40.1
35	15,691	5.3	6.1	11.4	46.8
40	14,002	6.0	5.4	11.4	52.4
45	12,728	6.6	5.0	11.6	57.0

and

Table 11. Theoretical prestress loss of steel strands given the slab width of 12.75 m.

Distribution Angle (°)	Length of Steel Strand (mm)	Prestress Loss (%)			$\frac{{\mathit{\sigma }}_{\mathit{l}1}}{{\mathit{\sigma }}_{\mathit{l}1}+{\mathit{\sigma }}_{\mathit{l}2}}$ (%)
		${\mathit{\sigma }}_{\mathit{l}1}$	${\mathit{\sigma }}_{\mathit{l}2}$	${\mathit{\sigma }}_{\mathit{l}1}+{\mathit{\sigma }}_{\mathit{l}2}$
20	37,279	2.2	13.9	16.1	14.0
25	30,169	2.8	11.4	14.1	19.6
30	25,500	3.3	9.7	13.0	25.3
35	22,229	3.8	8.5	12.3	30.7
40	19,835	4.2	7.6	11.9	35.7
45	18,031	4.7	7.0	11.6	40.1

, respectively.

It can be illustrated from Table 8, Table 9, Table 10 and Table 11 that the prestress loss in the prestressing stage ranged from 11.5 to 21.5%. The main prestress loss was caused by anchorage deformation and prestress retraction (σ_l1) when the slab width was less than 9.0 m, and by the friction between the steel strand and the surrounding casing pipe (σ_l2) when the slab width was higher than 9.0 m.

In general, the relationship between the prestress loss (σ_l1 and σ_l2) and the distribution angle of steel strands with the same slab width was similar to the results of BFRP tendons, given the greater the distribution angle, the higher the σ_l1 and the lower the σ_l2, resulting in the higher proportion of σ_l1 in the prestress loss in the prestressing stage. Conversely, given the same distribution angle, σ_l1 decreased and σ_l2 increased with the increase of the slab width, causing a drop in the proportion of σ_l1 in the prestress loss in the prestressing stage.

4.2.2. Prestress Loss during the In-Service Stage

Similar to BFRP tendons, the prestress loss of steel strands during the in-service stage did not vary with the slab width and distribution angle of steel strands either. The prestress loss of steel strands during the in-service stage is listed in

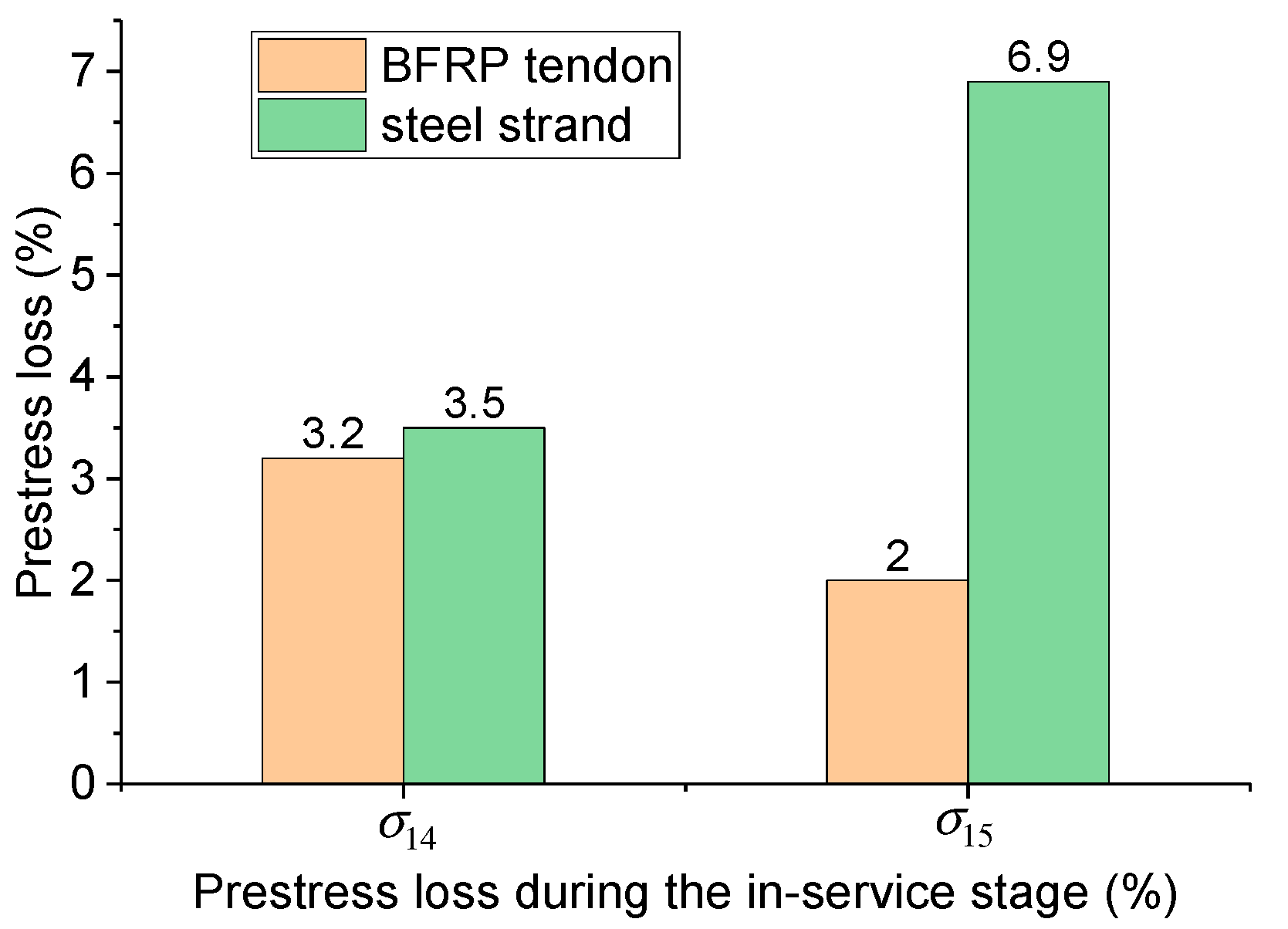
Table 12. Theoretical prestress loss of steel strands during the in-service stage.

σl4 (%)	σl5 (%)	σl4 + σl5 (%)
3.5	6.9	10.4

. The prestress loss caused by concrete shrinkage and creep (σ_l5) was 6.9%, almost twice of that caused due to the relaxation of the prestressed steel strands (σ_l4). As expected, the prestress loss of steel strands during the in-service stage was significantly lower than that in the prestressing stage.

4.2.3. Total Prestress Loss of Steel Strands

The total prestress loss of steel strands at different distribution angles and slab widths is summarized in

Table 13. The total prestress loss of steel strands (%).

Distribution Angle (°)	Total Prestress Loss (%)
	Slab Width = 3.0 m	Slab Width = 4.5 m	Slab Width = 9.0 m	Slab Width = 12.75 m
20	30.8	21.9	23.6	26.5
25	25.0	22.4	22.5	24.5
30	26.7	23.2	22.0	23.4
35	28.5	24.2	21.8	22.7
40	30.2	25.1	21.8	22.2
45	31.8	26.1	21.9	22.0

.

As shown in Table 13, given the slab width ranging from 3.0 m to 12.75 m and the distribution angle from 20° to 45°, the total prestress loss of steel strands was from 21.8% to 31.8%, with the lowest and the highest prestress loss being 21.8% and 31.8%, respectively. For a given distribution angle of steel strands, the total prestress loss reduced first, and then underwent a small increase as the slab width increased. The smaller the distribution angle, the greater the decrease rate.

4.3. Comparison of BFRP Tendons and Steel Strands

4.3.1. Prestress Loss in the Prestressing Stage

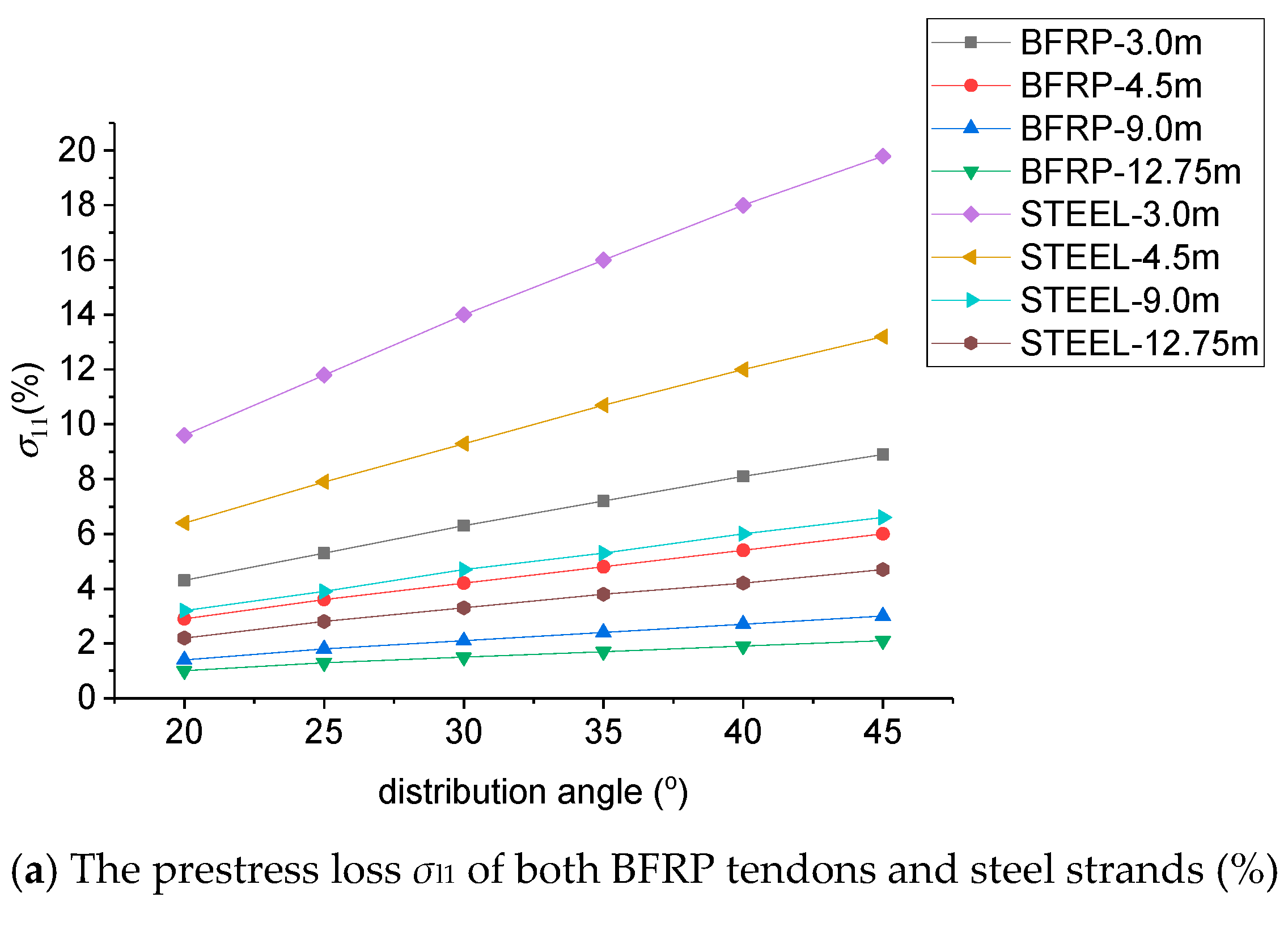
The prestress loss of BFRP tendons and steel strands in the prestressing stage at various distribution angles and with different slab widths is presented in Figure 1. Whether it was BFPR tendon or steel strand, the prestress loss arising from anchorage deformation and prestress retraction (σ_l1) decreased as the slab width increased, and increased as the distribution angle increased, as shown in Figure 1a, signifying that the type of the prestressed tendon had limited impact on the relationship between the prestress loss σ_l1 and the slab width and distribution angle. For the prestress loss resulting from the friction between the prestressed tendon and the surrounding casing pipe (σ_l2), its values for BFRP tendons and steel strands were the same, given the same slab width and distribution angle, as shown in Figure 1b, demonstrating that the properties of the prestressed reinforcement had no impact on the prestress loss σ_l2.

As described in Figure 1, given the same slab width and distribution angle of the prestressed reinforcement, the prestress loss σ_l1 of the BFRP tendon was far lower than that of the steel strand, and the difference showed a tremendous increase with the decrease of the slab width and the increase of the distribution angle. When the slab width was 3.0 m and the distribution angle was 45°, the difference in σ_l1 between the BFRP tendon and steel strand reached the maximum value of 10.9%, which illustrated that the use of BFRP tendon can significantly reduce the prestress loss during the prestressing stage, especially with a smaller slab width and a greater distribution angle.

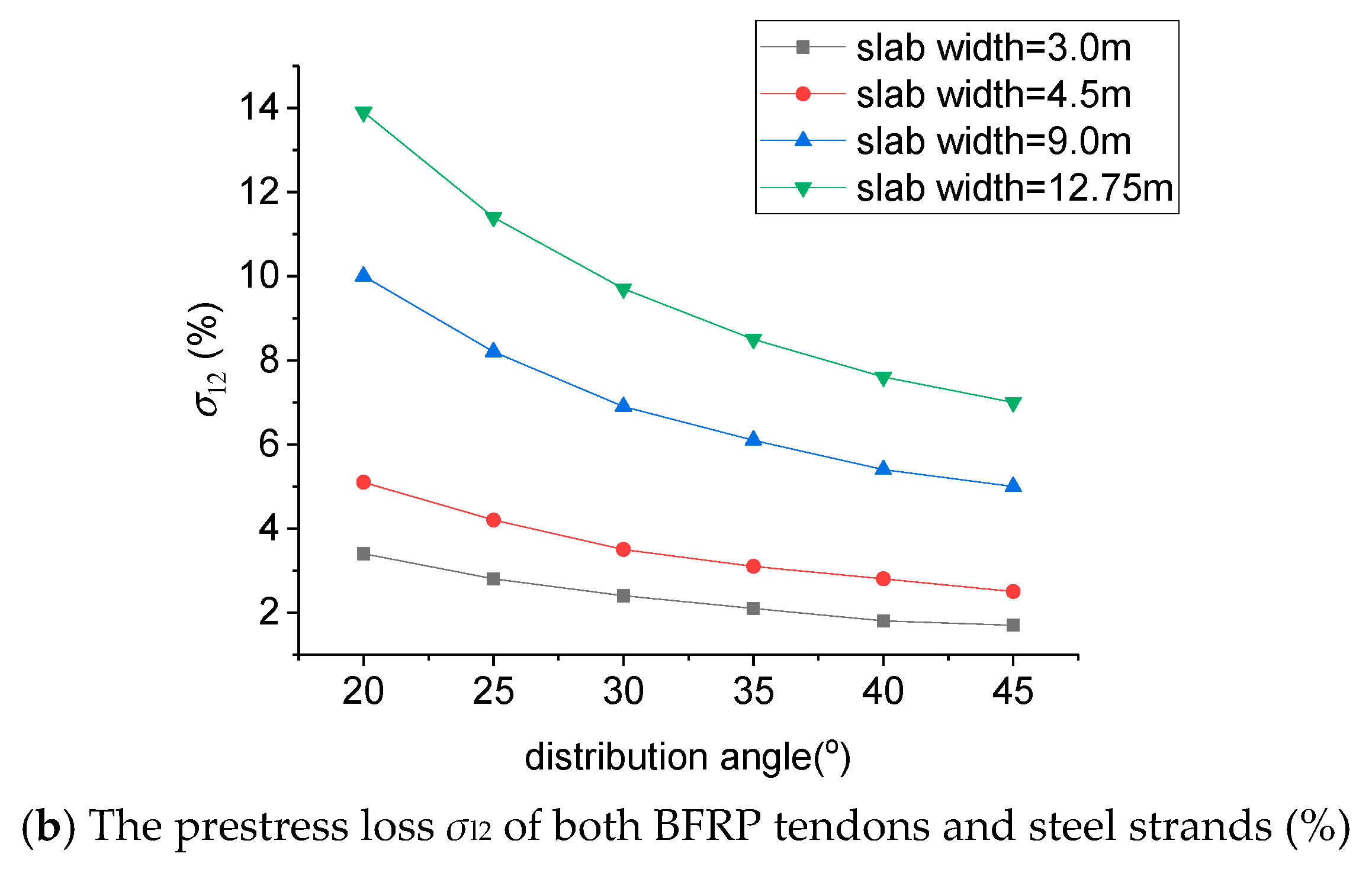
4.3.2. Prestress Loss during the In-Service Stage

Figure 2 presents the prestress loss of both BFRP tendons and steel strands during the in-service stage at various slab widths and distribution angles. Similar to the prestress loss in the prestressing stage, the use of BFRP tendons can greatly reduce the prestress loss during the in-service stage given the prestress loss of BFRP tendons and steel strands of 5.2% and 10.4%, respectively. This was mainly because the application of the BFRP tendon led to a significant decrease in the prestress loss σ_l5, 4.9% less than the prestress loss of steel strands.

4.3.3. Total Prestress Loss

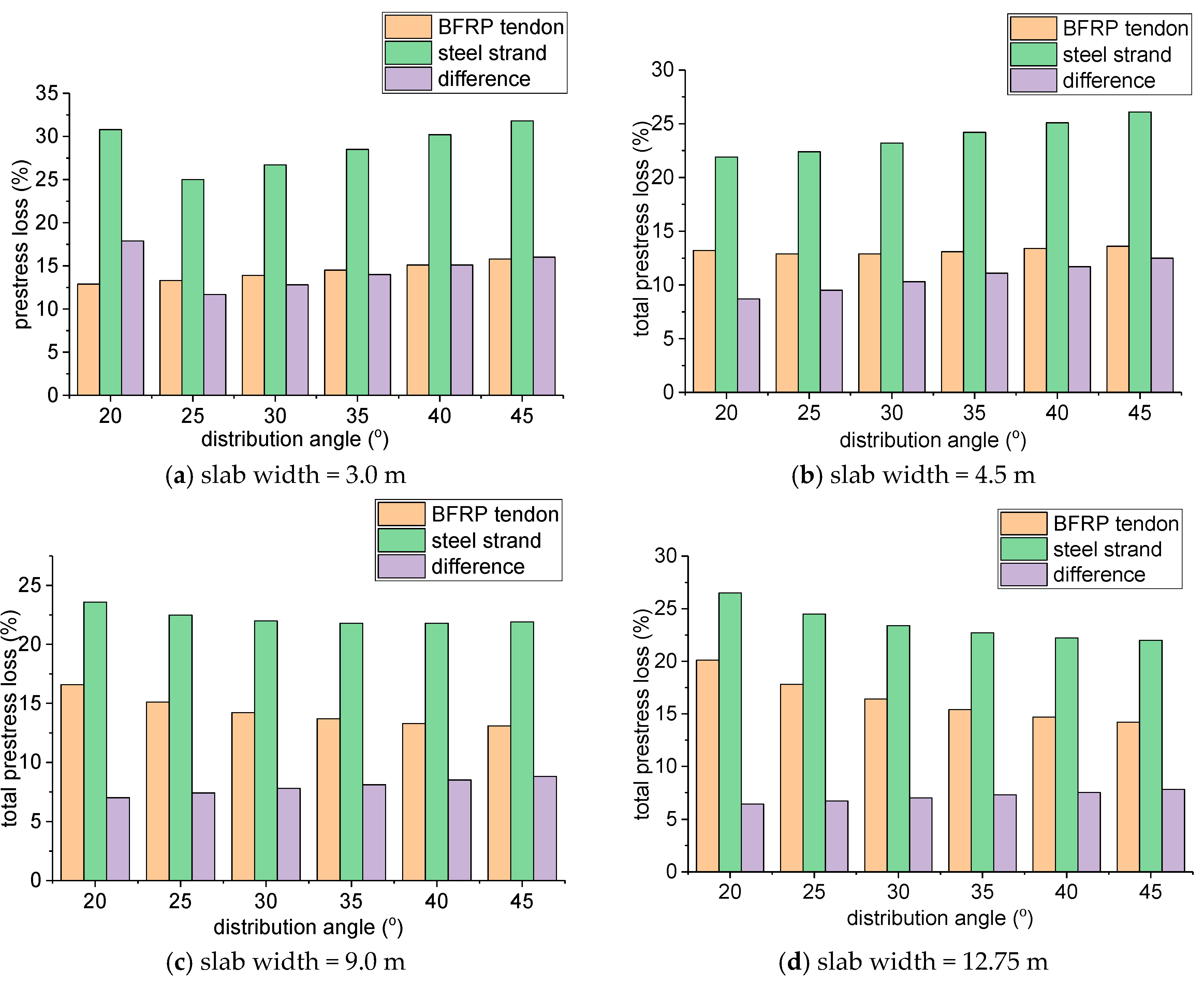
As shown in Figure 3, for a specific slab width (3.0 m, 4.5 m, 9.0 m, and 12.75 m) and distribution angle (20°, 25°, 30°, 35°, 40°, and 45°) of the prestressed tendon, the total prestress loss of the BFRP tendon was always lower than that of the steel strand. The difference between the two prestress losses varied from 6.4% to 16% and it decreased with the increase of the slab width. When the slab width was 3.0 m and the distribution angle was 20°, the difference peaked at 17.9%. When the slab width was 12.75 m and the distribution angle was 20°, the difference reached the minimum value of 6.4%.

In summary, the use of the BFRP tendon in the cross-tensioned concrete pavement can effectively reduce the prestress loss compared to the steel strand, let alone its corrosion resistance, which can increase the durability of the cross-tensioned concrete pavement. Further lab tests and test sections are still needed for better evaluation of prestress loss of BFRP tendons and the performance of the BFRP-reinforced cross-tensioned concrete pavement.

5. Conclusions

This paper proposed a detailed theoretical method and calculation process for determining the prestress loss of the BFRP tendon, a corrosion-resistant and lightweight material, in cross-tensioned concrete pavements with the consideration of the unique relaxation properties of BFRP to improve the durability of the pavement structure. The impact of the slab width and distribution angle of the prestressed tendon on the prestress loss in different stages was studied and compared to the results of traditional steel strands. The conclusions are summarized as follows:

(1) For both BFRP tendons and steel strands, the prestress loss σ_l1 decreased and σ_l2 increased with the increase of the slab width at a given distribution angle of the prestressed tendon, resulting in a lower proportion of σ_l1 in the prestress loss during the prestressing stage. In contrast, given the same slab width, the prestress loss σ_l1 increased and σ_l2 decreased as distribution angle increased, while the prestress loss was a constant value during the in-service stage.

(2) During the prestressing stage, the prestress loss of BFRP tendons was far lower than that of steel strands, given that the difference of prestress loss σ_l1 increased with the decrease of the slab width and the increase of the distribution angle, peaking at 10.9% when the slab width was 3 m and the distribution angle was 45^o.

(3) During the in-service stage, both the prestress losses of BFRP tendons and steel strands were constant, and the former (5.2%) was half of the latter (10.4%).

(4) For a given slab width (3 m, 4.5 m, 9.0 m, and 12.75 m) and distribution angle (20°, 25°, 30°, 35°, 40°, and 45°), the prestress loss of BFRP tendons was always lower than that of steel strands, with the difference ranging from 6.4% to 16%. The smaller the slab width, the greater the difference, indicating that BFRP tendons can effectively reduce the prestress loss in concrete pavements, especially when the slab width is smaller.