Creep Behaviours of Argillaceous Sandstone: An Experimental and Modelling Study

Abstract

Understanding the creep behaviours of rocks is essential for the long-term stability of underground excavations in mining engineering. Creep behaviours are more important when the mining depth is greater, which leads to the emergence of weak rock masses and high in situ stresses. In this study, the creep behaviours of argillaceous sandstone (AS) were systematically investigated. For the experimental investigation, creep tests were conducted on AS with different confining pressures (3, 6, 9, 12, 15, and 18 MPa) using an MTS815.02 rock mechanics test system. The mechanical characteristics of AS were analysed. For the numerical study, a nonlinear creep model of AS under equal and different confining pressures was established based on rock creep theory and plastic theory. The results showed that confining pressure could effectively improve the creep failure strength of AS, accelerating its creep deformation rate and process and reducing the final expansion volume. The nonlinear creep model was embedded in the FLAC3D software, and the experimental and numerical results agreed well. The experimental investigation and proposed creep model can provide important guidance in underground mines for safe long-term stability of underground excavations.

1. Introduction

The long-term behaviors of rock masses around underground structures have received increasing attention from both academia and industry since these behaviors have significant influence on the structures’ stability [1,2,3]. Creep behaviours refer to the continuous re-distribution of stress and displacement that occurs when the shear stress exceeds a threshold. For underground structures in weak rock masses or rock masses under high in situ stresses, creep behaviors are particularly common. Moreover, creep behaviors must be investigated for some underground structures that need to be operated for a long period of time, i.e., thousands to tens of thousands years for repositories for radioactive waste disposal [4].

Significant advances have been achieved towards understanding the creep behaviors of various rock types, such as red sandstone [5], rock salt [6], cataclastic rocks [7], granite [8,9], green tuff [10], and limestone [11]. At present, the investigation of the creep behaviors of rock can be categorized into experimental studies and numerical modelling. Experimental studies are often performed using creep tests on various rock types and under various conditions, such as different confining pressures and temperatures [12]. Creep tests can be conducted in either single-stage or multi-stage manners [13,14,15]. Since single-stage loading is time-consuming, multi-stage loading has been increasingly employed to obtain the complete creep characteristics of rock, including deceleration creep, constant velocity creep and accelerated creep [16]. Despite many investigations on the mechanical properties of argillaceous sandstone (AS), the creep behaviors of AS under different confining pressures have not been well documented.

Numerical modelling is another way to analyze the creep behaviors of rocks. For example, the interaction between rock masses and a backfill body considering the creep behaviors of rock masses be investigated [3]. Possible explanations were provided for in situ anomalies after the introduction of the creep constitutive model. One important issue in numerical modelling is the selection of the constitutive model and the corresponding parameters [17,18,19]. Various constitutive models have been established to represent the creep characteristics of different materials.

The traditional creep constitutive model is established without proper consideration of the tertiary creep stage [20,21]. Towards this end, nonlinear viscoplastic creep models have been proposed [22,23]. For example, Jia proposed a nonlinear elastic viscoplastic damage model based on the modified Mohr–Coulomb criterion and investigated the creep and permeability of clay rock during the construction of a high-level waste repository [24]. Zhao investigated the instantaneous deformation characteristics of rock creep by establishing an elastic–plastic model describing the instantaneous behavior [25]. However, the constitutive creep relations for AS are still in the infancy. In other words, more efforts should be directed to the constitutive modelling of the creep behavior of AS.

Therefore, an intensive study on the creep behaviors of AS under various confining pressures was conducted. Multi-stage creep tests were carried out first on AS specimens with different confining pressures. The creep characteristics of AS were analyzed based on the experimental results. Then, a novel constitutive relation was proposed to describe the creep behaviors of AS, which was embedded into FLAC3D for implementation. Finally, the experimental and numerical results were compared to validate the feasibility of the proposed creep model. A systematic study about experiment, theory model, and numerical calculation of AS’ creep characteristics has been presented in this paper. Furthermore, major rock creep models only stay at the stage of theoretical explanation, this paper embeds the constructed creep model into numerical calculation software to verify its correctness.

2. Creep Tests of AS

2.1. AS Samples

The AS samples were collected in Quandian Coal Mine, which is located in Henan Province, China. The average burial depth of the belt conveying roadway in its 22 mining areas is −700 m. After the excavation of the roadway, it is observed by the “cross point method” that the deformation continues to increase with time after systematic support using “anchor-net-shotcrete”. Thirty days after the excavation of the roadway, the deformation continues and the surrounding rock creep effect is significant; when the roadway was excavated for 70 days, the surrounding rock continued to deform at a high deformation rate. The average deformation rates of the roof subsidence, the convergence of the two sides, and the floor heave were 14.4 mm/d, 12.9 mm/d, and 7.3 mm/d, respectively.

As introduced above, the AS samples were taken from the roof of the belt conveying roadway in Quandian Coal Mine 22. In the AS samples, clay materials account for 35.8%, while sand materials account for 64.2%. After the rock samples were collected in accordance with the International Society for Rock Mechanics (ISRM) recommendations for rock mechanics tests, the samples were processed into cylindrical specimens with a diameter of 50 mm and a height of 100 mm. The parallelism and flatness of the two ends of the processed specimens were controlled to be less than 0.02 mm and 0.5 mm, respectively. Figure 1 shows some AS samples used in this study. The basic physical and mechanical properties of the AS samples are listed in

Table 1. Physical and mechanical properties of AS.

Specimens	No.	ρ/g·cm−3	E/GPa	μ	σc/MPa	σt/MPa	C/MPa	φ/°
AS	1	0.287	2.2	0.22	44.66	4.79	4.8	32
	2	0.289	1.8	0.25	29.01	3.44	5.3	29
	3	0.243	2.6	0.23	37.05	4.65	5.1	30
	Average	0.240	2.2	0.23	36.91	4.29	5.06	30

Note: ρ represents density, E and μ represent Young’s modulus and Poisson’s ratio, respectively, σ_c and σ_t represents the uniaxial compressive strength and uniaxial tensile strength, c and φ represent cohesion and internal friction angle, respectively.

. The equipment used in the test was an MTS815.02 electro-hydraulic servo rock mechanics test system from the United States. Each index of the system was ensured to meet the requirements of uniaxial, triaxial, and creep tests. The test equipment and loading method of AS samples are shown in Figure 2. The circumferential deformation of the sample was measured by a circumferential extensometer.

2.2. Experimental Scenarios

In this study, the creep characteristics of AS specimens under various confining pressures were investigated by the multi-stage loading method. The specific process was as follows: First, the compressive deviatoric strength of the specimens under different confining pressures was tested. Second, according to the compressive deviatoric strength, the specimens were subjected to multi-stage loading. Five-stage loading was employed for each confining pressure, and the loading interval for each stage was 48 h. Finally, the multi-stage loading curve was processed to obtain the stress-strain and mechanical parameters of specimens.

The selection of confining pressures was based on the engineering conditions. The depths of the underground roadway were 644.5–814.7 m. The average minimum in situ stress in the stability zone of the roadway was determined to be 18.23 MPa. Therefore, in order to analyse the creep behaviours in different positions along the roadway, the confining pressure C was set to 3 MPa, 6 MPa, 9 MPa, 12 MPa, 15 MPa, and 18 MPa.

The setup for the multi-stage loading was also determined carefully. The results of triaxial tests showed that the maximum deviatoric stress corresponding to the elastic deformation of specimens under different confining pressures was approximately 60% of the deviatoric strength σ_c. Under different confining pressures, the first-stage loading σ₁ was determined to be 55–59% of the deviatoric strength. The second- to fifth-stage loadings were increased progressively considering the first-stage loading, and each time, the loading was increased by 4 MPa. If the specimens under the fifth-stage load were not damaged, further loading was carried out with the same increment. If the tertiary creep stage occurred before the fifth-stage load was applied and the AS specimens were destroyed, no further loading was applied afterwards.

In the current study, the loading time per stage was determined to be 48 h. Several previous tests determined that the deformation rate of specimens after 24 h was less than 0.002 m/h at each stage when the tertiary creep stage was not reached. Thus, 48 h was considered long enough to reach a stable creep stage.

According to the results of triaxial compression tests, the creep test scenarios of AS samples under different confining pressures are shown in

Table 2. Multi-stage loading for creep tests of AS.

C (Mpa)	σc (MPa)	σi (MPa)
		σI/δ	σII/δ	σIII/δ	σIV/δ	σV/δ
3	42.5	23.5/55.29%	26.9/63.29%	30.3/71.29%	33.7/79.29%	37.1/87.29%
6	47.35	26.4/55.76%	30.7/64.84%	35/73.92%	39.3/83.00%	43.6/92.08%
9	52.75	30.3/57.44%	34.4/65.21%	38.5/72.99%	42.6/80.76%	46.7/88.53%
12	57.37	33.6/58.57%	37.7/65.71%	41.8/72.86%	45.9/80.01%	50.0/87.15%
15	62.92	36.9/58.65%	40.2/63.89%	43.5/69.14%	46.8/74.38%	50.1/79.62%
18	67.3	39.6/58.84%	43.9/65.23%	48.2/71.62%	52.5/78.01%	56.8/84.40%

. In the table, σ_i (i = I, II, …, V) represents creep loadings at different stages, and δ represents the ratio of creep loading σ_i to deviatoric strength σ_c.

2.3. Results and Analysis

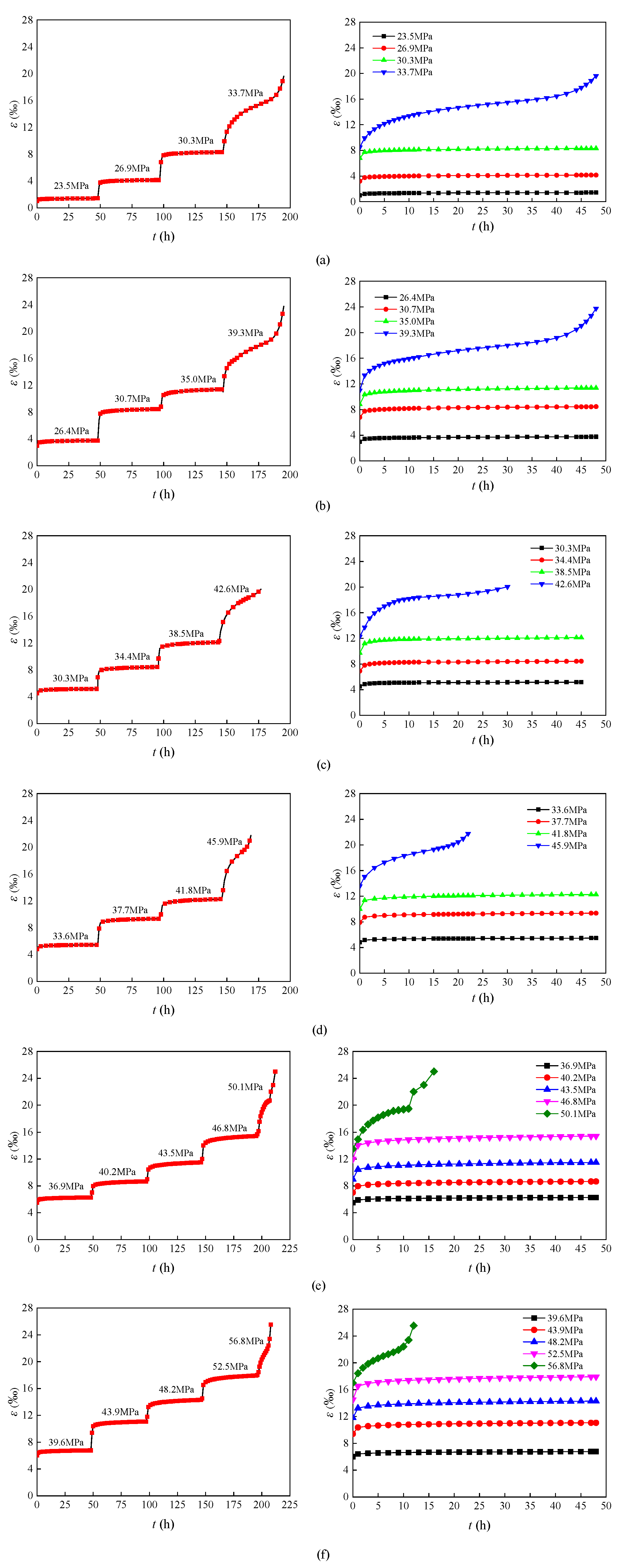
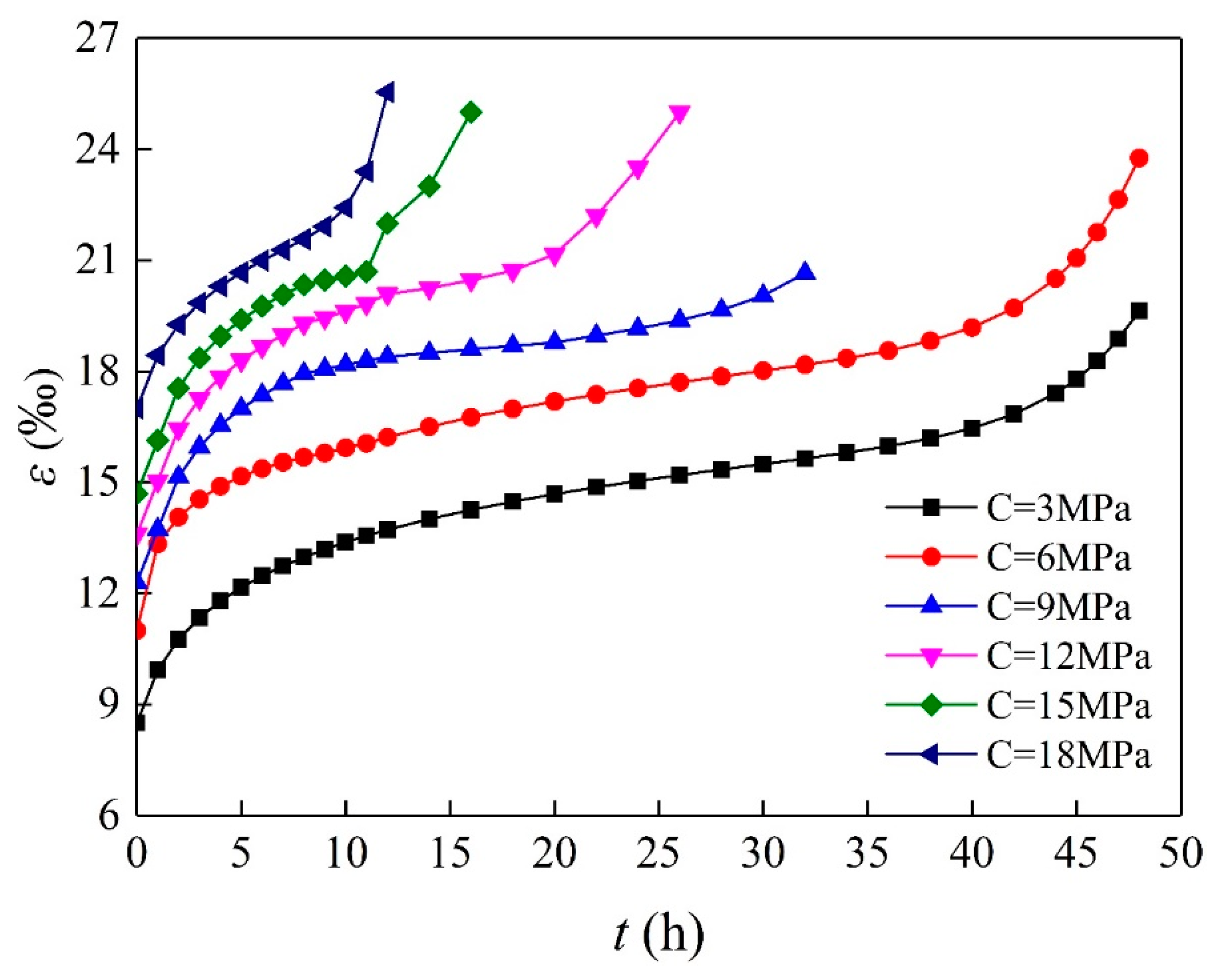
2.3.1. Strain-Time Curves and Creep Characteristic Curves of AS

The strain-time curves of AS samples under different confining pressures were obtained by multi-stage loading tests. According to the principle of the multi-stage loading test, the strain-time curves for each loading stage could be obtained from the strain-time curves. The influence of confining pressures on the strain-time curves and strain-time curves for each loading stage of AS samples is shown in Figure 3. The following conclusions can be drawn from Figure 3.

• Regardless of the confining pressure, the deformation of AS samples at the initial loading stage increased with time, although at a decelerating rate. This stage is known as the primary creep stage. With continuous loading, the strain of the AS samples exhibited a linear response with time, and this stage is known as the secondary creep stage. At the final loading stage, which is known as the tertiary stage, the strain increased exponentially with time until the failure of samples. All AS samples exhibited three complete creep stages.
• For creep tests with the same confining pressure, a certain amount of instantaneous deformation was observed when the stress loading at each stage was applied. Moreover, the deformation magnitude increased with increasing stress level. Instantaneous strain was the main component of the total strain.
• With increasing confining pressure, the total instantaneous strain increased gradually. For example, when the confining pressure was increased from 3 MPa to 6 MPa, 9 MPa, 12 MPa, 15 MPa, and 18 MPa, the ratios of instantaneous strain to total strain were 61.2%, 63.1%, 65.2%, 67.3%, 70.2%, and 73.5%, respectively.
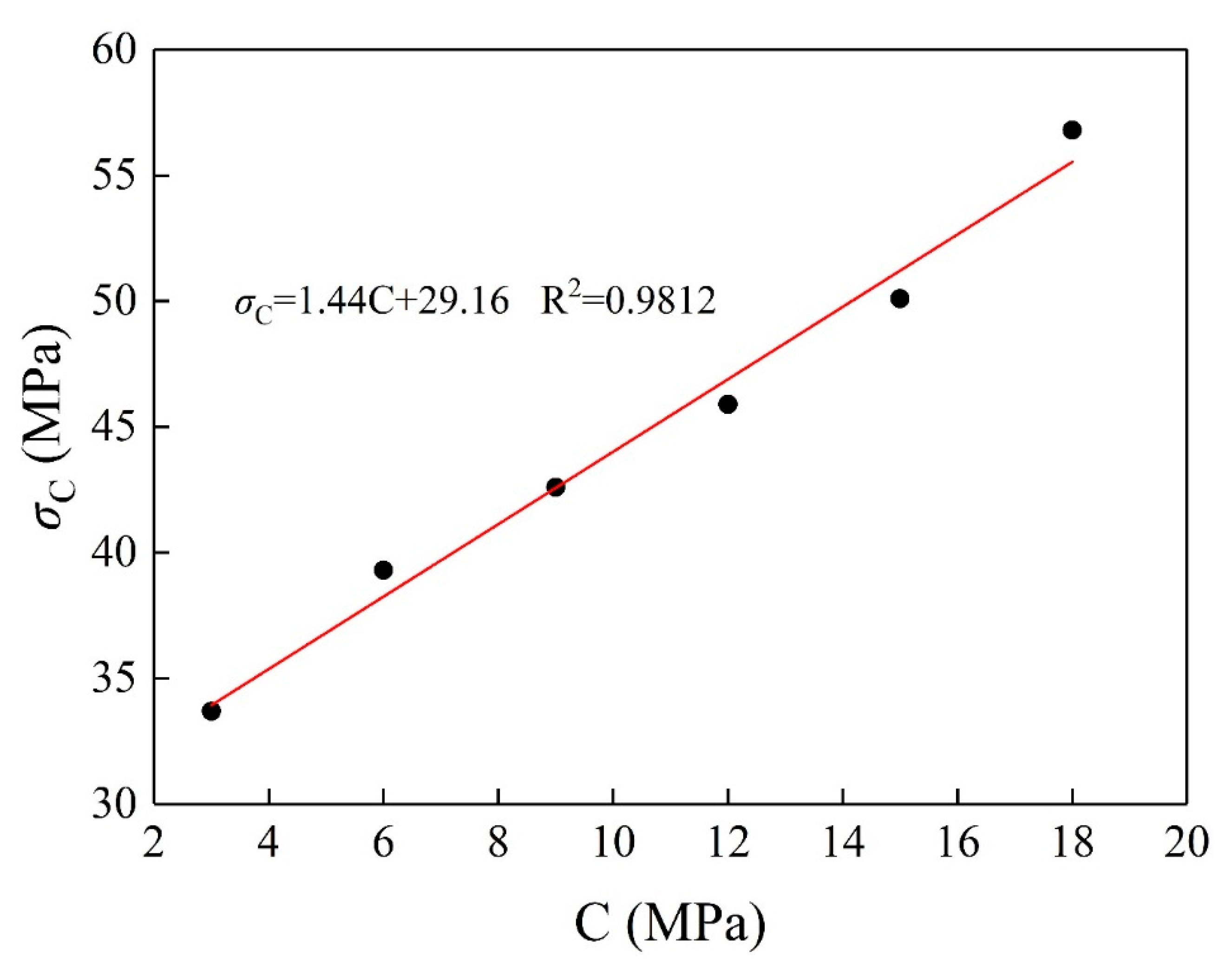
• With increasing confining pressure, the failure load at the tertiary creep stage increased gradually. However, the failure load from the creep tests was less than the corresponding failure load from the conventional triaxial compressive tests.

In summary, Figure 3 shows that all AS samples exhibited four complete creep stages, namely, instantaneous deformation stage, primary creep stage, secondary creep stage and tertiary creep stage. Figure 4 shows a comparison of the strain-time curves at the final loading stage for all confining pressures. The confining pressure had significant influence on the strain-time curves at the tertiary creep stage. With increasing confining pressure, the duration of the tertiary creep stage decreased. In other words, the AS samples were destroyed after a shorter time when the confining pressure was increased.

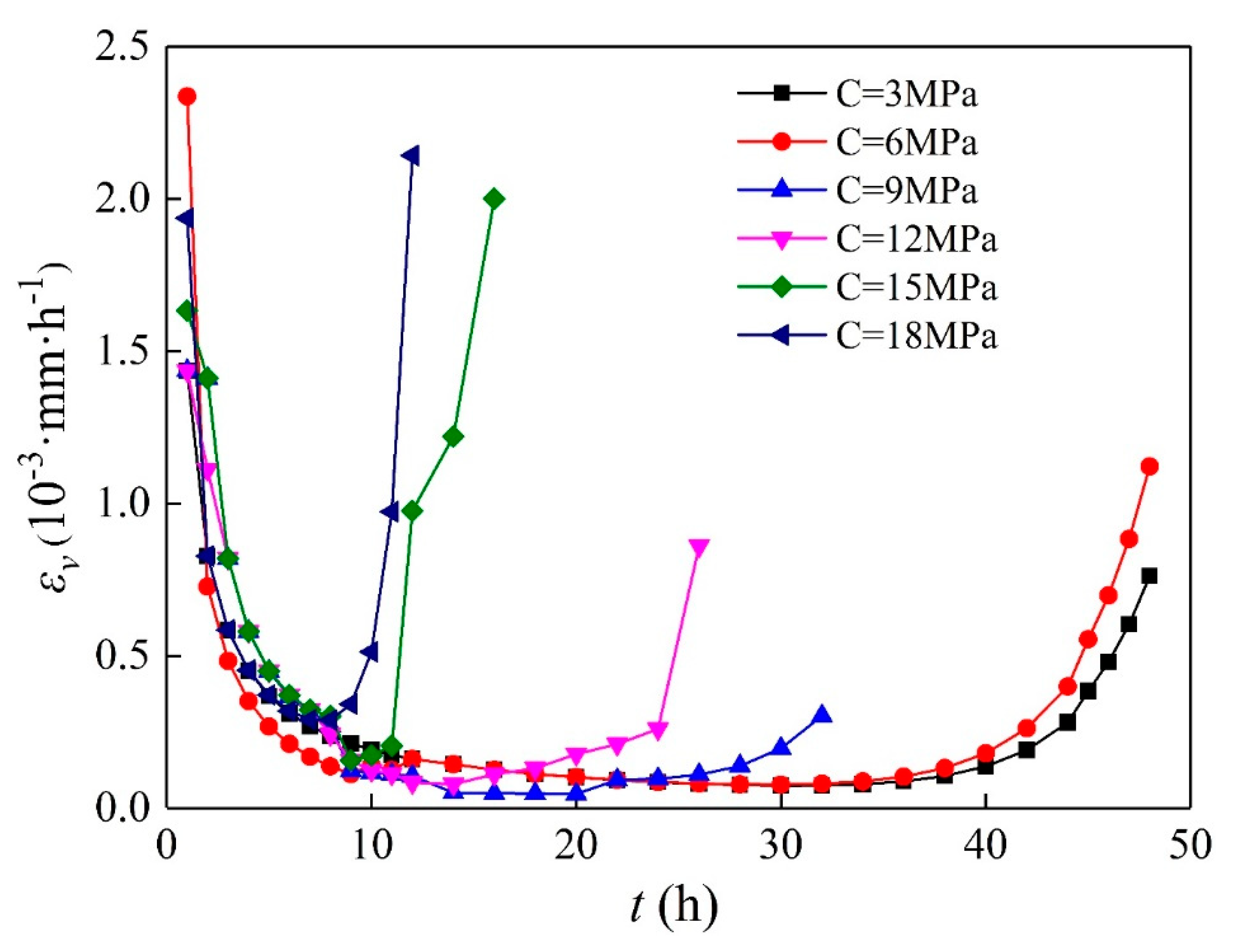
2.3.2. Creep Deformation Rate

Figure 5 shows the creep deformation rates of AS samples under different confining pressures. The authors note that only the creep deformation rate at the final loading stage is provided as an illustration, and similar results could be observed at other loading stages. As shown, the creep deformation rates of AS samples under various confining pressures followed a decreasing-stable-increasing pattern. Detailed conclusions are drawn from Figure 5 as follows:

• Based on different confining pressures, the deformation rates of AS samples showed a fast decrease at the beginning. The deformation rate became stable within 7 to 9 h.
• With increasing confining pressure, the average deformation rates in the stable stage were similar. However, evident differences were observed in the duration of the stable stage, which decreased gradually with increasing confining pressure. For example, when C = 6 MPa, the stable stage lasted approximately 30 h, and the average creep rate was 0.112 × 10⁻³ mm/h. When C = 12 MPa, the stable stage lasted only approximately 5 h, and the average creep rate was 0.08 × 10⁻³ mm/h. An interesting phenomenon was that the stable stage disappeared when C = 18 MPa.
• The influence of the confining pressure on the deformation rate at the acceleration stage was also evident. With increasing confining pressure, the duration of the acceleration stage decreased gradually. Meanwhile, the acceleration rate increased sharply. The nonlinear acceleration stage was due to the expansion of the internal cracks. At high confining pressure, the axial load of the AS samples was high, leading to a high speed of crack expansion. The crack expansion in turn accelerated the creep failure. Thus, the nonlinear acceleration stage of the deformation rate was observed.

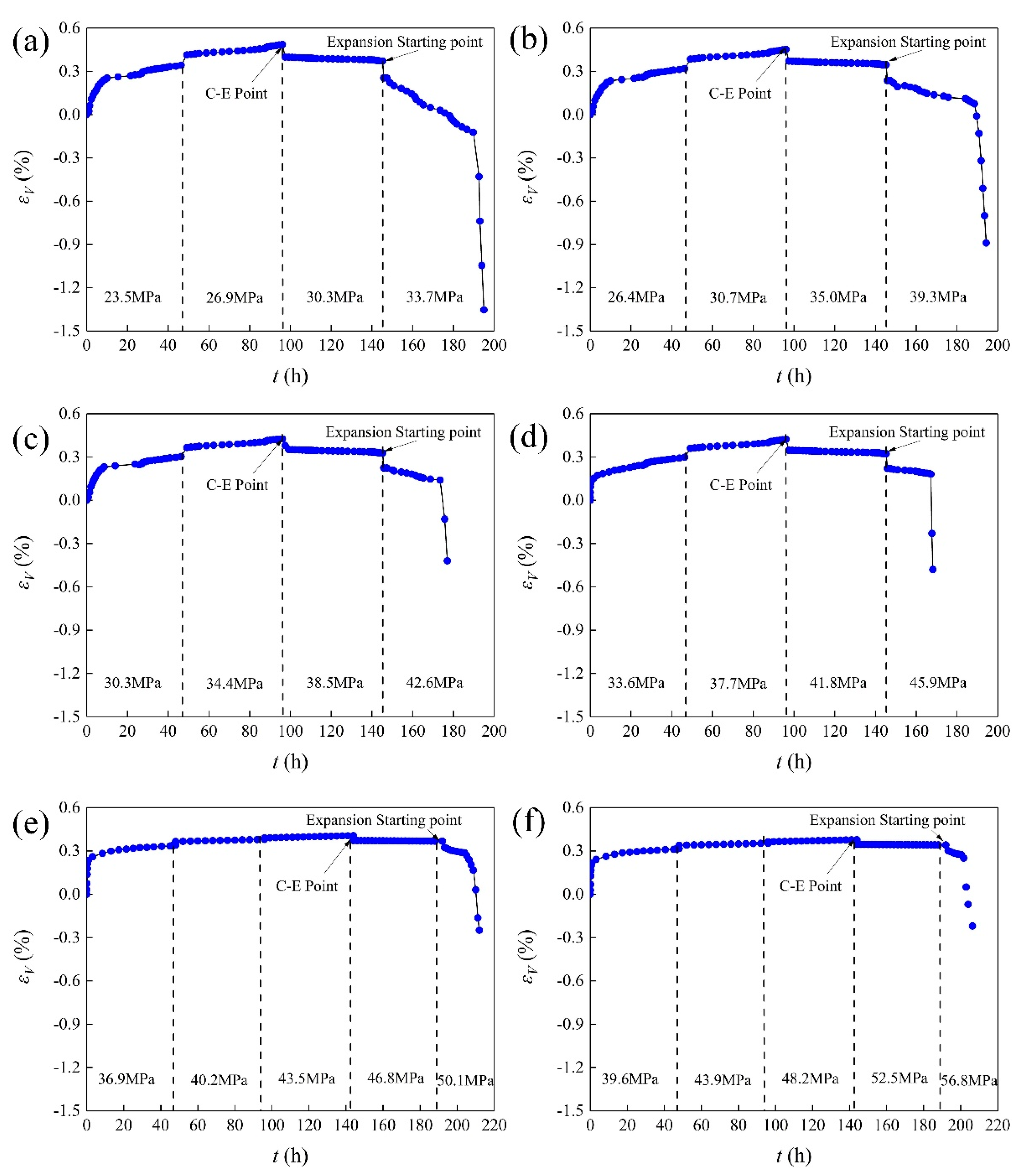
2.3.3. Volume Expansion of AS Samples

During the tests, the circumferential strains of AS samples under different confining pressures were obtained by a circumferential extensometer. Combined with the axial compressive strain data, the variation in the volumetric strain with time was obtained, as shown in Figure 6.

Figure 6 illustrates that the volumetric strains of the AS samples under different confining pressures were basically similar. For each volumetric strain curve, three stages were observed: accelerated volumetric strain stage, stable volumetric strain stage, and dilatant volumetric strain stage. When the stress level was lower than 70% of the deviatoric strength, the volumetric deformation of AS samples was mainly compressive. With the gradual increase of stress level, when it reached approximately 75% of the deviatoric strength, the volume deformation of AS samples was basically maintained at a stable value. When the deviatoric stress level reached 80–85% of the deviatoric strength, the microcracks in AS samples began to expand and gradually penetrate. At this point, the specimen entered the dilatant volumetric strain stage. Moreover, the expansion rate increased gradually with increasing time until AS samples were destroyed. Due to the confining pressure constraint, the final volumetric strain of the AS samples gradually decreased with increasing confining pressure.

2.3.4. Creep Failure Strength

Figure 7 shows the variations in creep failure strength with confining pressure. The figure displays that with increasing confining pressure, the creep failure strength increased linearly. When the confining pressure was increased from 3 MPa to 18 MPa, the creep failure strength increased from 33.7 MPa to 56.8 MPa, which was a 68.55% increase. Thus, the confining pressure could effectively improve the creep failure strength of AS.

3. Nonlinear Creep Model of AS

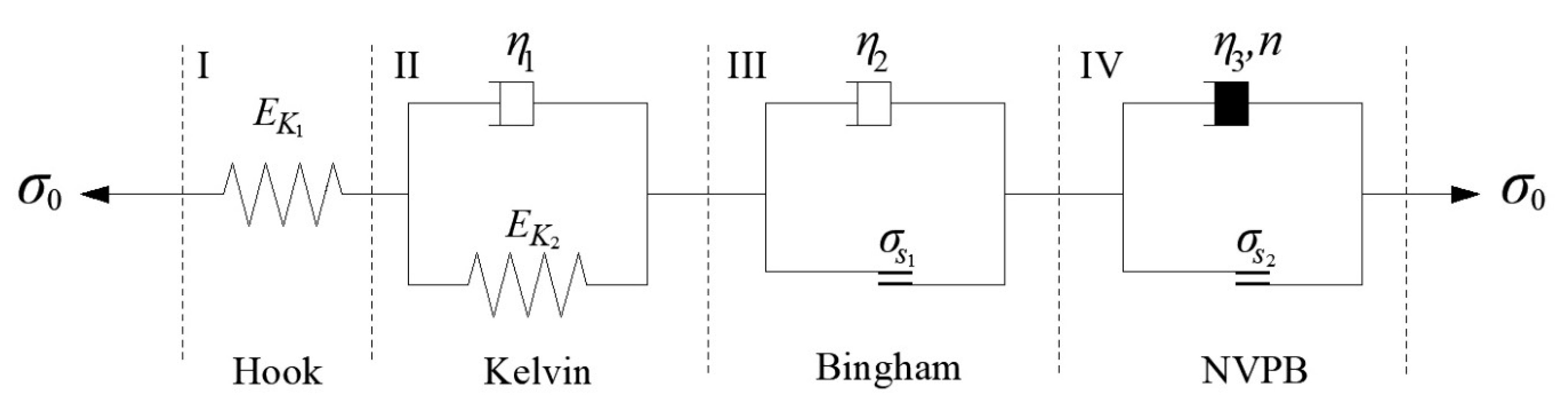
3.1. Establishment of Nonlinear Creep Model

In this paper, the establishment of the nonlinear creep model was conducted by a combination of elemental components. As discussed above, the creep results revealed four stages during the creep tests: instantaneous elastic deformation, primary creep stage, secondary creep stage, and tertiary creep stage. Among them, the instantaneous elastic deformation and primary creep stages could be described by a Hook elastic element (Figure 8I) and Kelvin viscoelastic model (Figure 8II), respectively. When the stress level reached a certain threshold, the surrounding rock began to enter the secondary creep stage, which could be described by the Bingham model (Figure 8III) (Liu et al. 2017). When the stress level was higher than a certain threshold, the creep curves showed the characteristics of accelerated deformation. For conventional rheological elements to accurately describe the accelerated creep stage of AS was difficult. In this paper, the nonlinear volume plasticity Bingham (NVPB) model (Figure 8IV) was introduced to describe the tertiary creep stage. Based on the above analysis, this paper proposes a nonlinear viscoelastic-plastic creep model, as shown in Figure 8, which would be suitable for the description of AS.

In the above models, $E_{K_1}$ and $E_{K_2}$ represent the elastic moduli of elastic elements in Hook and Kelvin–Voigt bodies, respectively; ${\eta }_1$, ${\eta }_2$, and ${\eta }_3$ represent the viscous coefficients of viscous elements in Kelvin, Bingham, and NVPB bodies, respectively; N is the rheological index in the NVPB body, indicating the accelerated rheological rate of rock, $n>0$; ${\sigma }_{s_1}$ and ${\sigma }_{s_2}$ represent the crack initiation stress and the expansion stress of the rock, respectively.

In Figure 8, the physical meaning and constitutive relation of the first three parts are clear and are not discussed in detail in this study. Interested readers can referred to published papers for more detailed information [26,27]. For the NVPB model, the viscosity coefficient ${\eta }_3$ is assumed to satisfy the following equation.

$${\eta }_3(\sigma ,t)=\frac{{\eta }_c}{n}{(\frac{t}{t_0})}^{1-n}$$

(1)

where $t_0$ is the relative reference time with a value of 1 and ${\eta }_c$ is the equivalent viscosity coefficient of the NVPB model, which is closely related to the properties of rock materials.

Then, the constitutive equation of the NVPB model is

$${\sigma }_0-{\sigma }_{s_2}=\frac{{\eta }_c}{n}{(\frac{t}{t_0})}^{1-n}\dot{\epsilon }$$

(2)

The corresponding constitutive equation is

$$\epsilon (t)=\frac{H({\sigma }_0-{\sigma }_{s_2})}{{\eta }_c}\frac{t^n}{t_0^{n-1}}=\frac{H({\sigma }_0-{\sigma }_{s_2})}{{\eta }_c}{t}^n$$

(3)

where $H({\sigma }_0-{\sigma }_{s_2})$ is a plastic switching function, which can be expressed as follows:

$$H({\sigma }_0-{\sigma }_{s_2})=\{\begin{array}{cc}0\hfill & \hfill ({\sigma }_0\le {\sigma }_{s_2})\\ {\sigma }_0-{\sigma }_{s_2}\hfill & \hfill ({\sigma }_0>{\sigma }_{s_2})\end{array}$$

(4)

Equation (4) shows that when ${\sigma }_0\le {\sigma }_{s_2}$, the model can reflect the instantaneous deformation, primary creep stage and secondary creep stage of AS; when ${\sigma }_0>{\sigma }_{s_2}$, the model can fully represent the tertiary creep stage.

Figure 9 shows the strain-time curves of the NVPB model under different rheological indices n. As the rheological index n increased, the deformation rate of the AS samples increased gradually. This property could be used to describe the accelerated creep of AS samples under different confining pressures. According to the series–parallel relationship between components, the following equations can be obtained.

When $\sigma <{\sigma }_{s_1}$, the model degenerates into a Hook body and Kelvin elements in series, and its constitutive relationship is as follows:

$$\frac{\dot{\sigma }}{E_{K_1}}+\frac{E_{K_1}+E_{K_2}}{E_{K_1}{\eta }_1}\sigma =\dot{\epsilon }+\frac{E_{K_2}}{{\eta }_1}\epsilon$$

(5)

When ${\sigma }_{s_1}\le \sigma <{\sigma }_{s_2}$, the model is mainly composed of Hook, Kelvin, and Bingham elements. The constitutive relationship is as follows:

$$\frac{1}{E_{K_1}}\ddot{\sigma }+\frac{E_{K_1}{\eta }_2+E_{K_2}{\eta }_2+E_{K_1}{\eta }_1}{E_{K_1}{\eta }_1{\eta }_2}\dot{\sigma }+\frac{E_{K_2}}{{\eta }_1{\eta }_2}\sigma -\frac{E_{K_2}{\sigma }_{s_1}}{{\eta }_1{\eta }_2}=\ddot{\epsilon }+\frac{E_{K_2}}{{\eta }_1}\dot{\epsilon }$$

(6)

When $\sigma \ge {\sigma }_{s_2}$, the model contains all four elements, and its constitutive relationship is as follows:

$$\begin{array}{l}\frac{\ddot{\sigma }}{E_{K_1}}+(\frac{1}{{\eta }_1}+\frac{1}{{\eta }_2}+\frac{E_{K_2}}{E_{K_1}{\eta }_1}+\frac{n}{{\eta }_c}{t}^{n-1})\dot{\sigma }+[\frac{E_{K_2}}{{\eta }_1{\eta }_2}+\frac{E_{K_2}n}{{\eta }_1{\eta }_c}{t}^{n-1}\\ -\frac{n(1-n)}{{\eta }_c}{t}^{n-2}]\sigma -\frac{E_{K_2}{\sigma }_{s_1}}{{\eta }_1{\eta }_2}-\frac{E_{K_2}n}{{\eta }_1{\eta }_c}{t}^{n-1}{\sigma }_{s_2}\\ +\frac{n(1-n)}{{\eta }_c}{t}^{n-2}{\sigma }_{s_2}=\ddot{\epsilon }+\frac{E_{K_2}}{{\eta }_1}\dot{\epsilon }\end{array}$$

(7)

The simultaneous Equations (5)–(7) are used to obtain the constitutive equation of the nonlinear creep model of AS, as follows:

$$\{\begin{array}{cc}\frac{\dot{\sigma }}{E_{K_1}}+\frac{E_{K_1}+E_{K_2}}{E_{K_1}{\eta }_1}\sigma =\dot{\epsilon }+\frac{E_{K_2}}{{\eta }_1}\epsilon \hfill & \hfill (\sigma <{\sigma }_{s_1})\\ \frac{1}{E_{K_1}}\ddot{\sigma }+\frac{E_{K_1}{\eta }_2+E_{K_2}{\eta }_2+E_{K_1}{\eta }_1}{E_{K_1}{\eta }_1{\eta }_2}\dot{\sigma }+\frac{E_{K_2}}{{\eta }_1{\eta }_2}\sigma -\frac{E_{K_2}{\sigma }_{s_1}}{{\eta }_1{\eta }_2}=\ddot{\epsilon }+\frac{E_{K_2}}{{\eta }_1}\dot{\epsilon }\hfill & \hfill ({\sigma }_{s_1}\le \sigma <{\sigma }_{s_2})\\ \frac{\ddot{\sigma }}{E_{K_1}}+(\frac{1}{{\eta }_1}+\frac{1}{{\eta }_2}+\frac{E_{K_2}}{E_{K_1}{\eta }_1}+\frac{n}{{\eta }_c}{t}^{n-1})\dot{\sigma }+[\frac{E_{K_2}}{{\eta }_1{\eta }_2}+\frac{E_{K_2}n}{{\eta }_1{\eta }_c}{t}^{n-1}-\frac{n(1-n)}{{\eta }_c}{t}^{n-2}]\sigma \hfill & \hfill (\sigma \ge {\sigma }_{s_1})\\ -\frac{E_{K_2}{\sigma }_{s_1}}{{\eta }_1{\eta }_2}-\frac{E_{K_2}n}{{\eta }_1{\eta }_c}{t}^{n-1}{\sigma }_{s_2}+\frac{n(1-n)}{{\eta }_c}{t}^{n-2}{\sigma }_{s_2}=\ddot{\epsilon }+\frac{E_{K_2}}{{\eta }_1}\dot{\epsilon }\hfill & \end{array}$$

(8)

According to Equation (8), the nonlinear creep equation of AS can be obtained as follows:

$$\{\begin{array}{cc}\epsilon (t)=\frac{{\sigma }_0}{E_{K_2}}(1-e^{-\frac{E_{K_2}}{{\eta }_1}t})+\frac{{\sigma }_0}{E_{K_1}}\hfill & \hfill (\sigma <{\sigma }_{s_1})\\ \epsilon (t)=\frac{{\sigma }_0}{E_{K_2}}(1-e^{-\frac{E_{K_2}}{{\eta }_1}t})+\frac{{\sigma }_0}{E_{K_1}}+\frac{{\sigma }_0-{\sigma }_{s_1}}{{\eta }_2}t\hfill & \hfill ({\sigma }_{s_1}\le \sigma <{\sigma }_{s_2})\\ \epsilon (t)=\frac{{\sigma }_0}{E_{K_2}}(1-e^{-\frac{E_{K_2}}{{\eta }_1}t})+\frac{{\sigma }_0}{E_{K_1}}+\frac{{\sigma }_0-{\sigma }_{s_1}}{{\eta }_2}t+\frac{{\sigma }_0-{\sigma }_{s_2}}{{\eta }_c}{t}^n\hfill & \hfill (\sigma \ge {\sigma }_{s_1})\end{array}$$

(9)

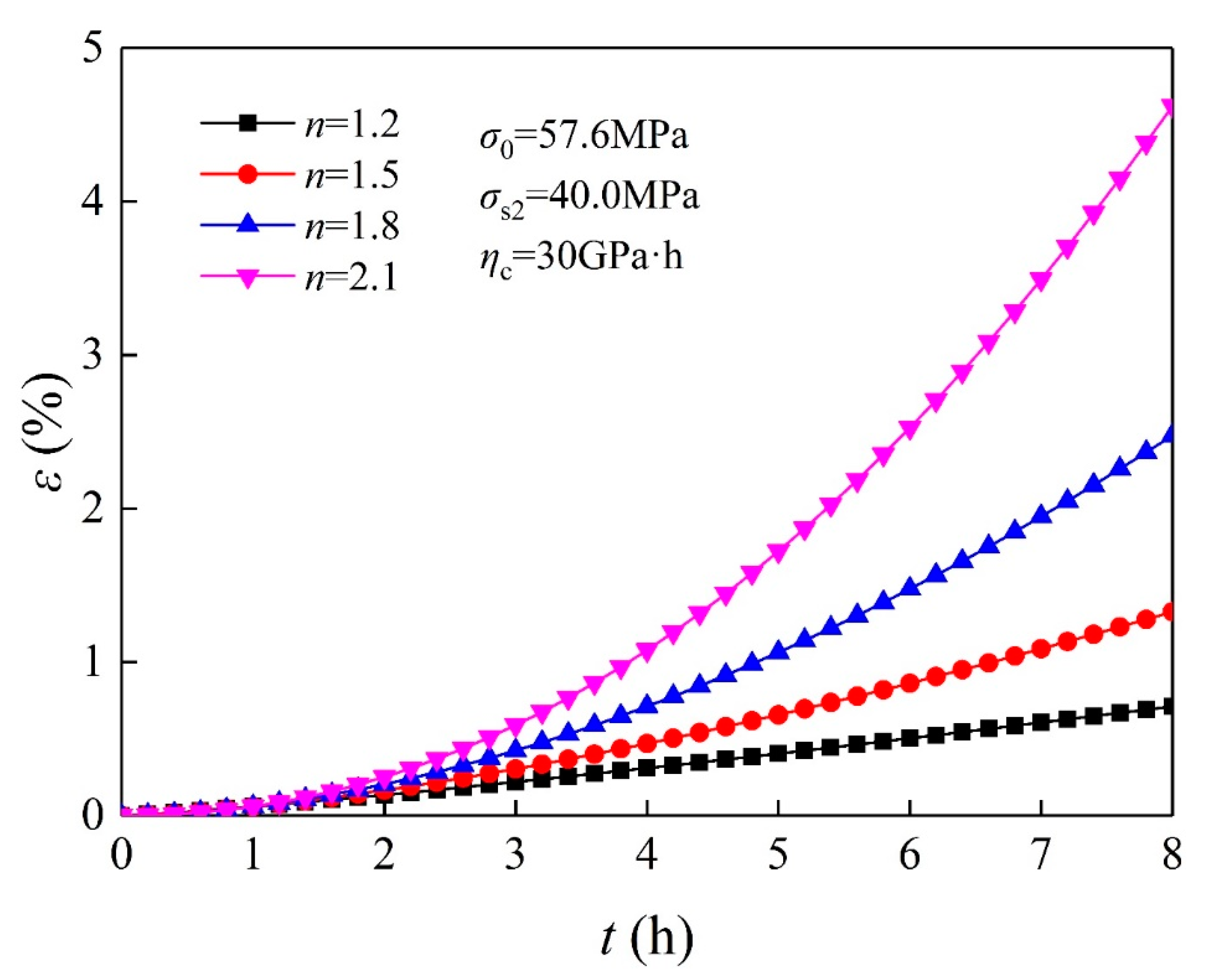
3.2. Nonlinear Creep Model in Three Dimensions

Equations (8) and (9) are actually one-dimensional creep equations for AS. For underground roadways, a one-dimensional constitutive model cannot accurately describe the stress-strain distribution of the surrounding rock masses. Therefore, the model needs to be expanded to three dimensions so that it can be used in 3D stress/displacement analysis.

When the rock is loaded in three dimensions, the stress state of any point in the rock sample can be divided into a stress spherical tensor and a stress deviatoric tensor. The stress spherical tensor can influence only the volume of the cell, and the stress deviatoric tensor can influence the shape of the cell. The stress tensor and strain tensor can be expressed as follows:

$$\{\begin{array}{l}{\sigma }_{ij}={\delta }_{ij}{\sigma }_m+S_{ij}\\ {\epsilon }_{ij}={\delta }_{ij}{\epsilon }_m+e_{ij}\end{array}$$

(10)

where ${\sigma }_m$ and $S_{ij}$ represent the stress spherical tensor and stress deviatoric tensor, respectively, and ${\epsilon }_m$ and $e_{ij}$ represent the strain spherical tensor and strain deviatoric tensor, respectively. ${\sigma }_m$, $S_{ij}$ and ${\epsilon }_m$ can be calculated as follows:

$$\{\begin{array}{c}{\sigma }_m=\frac{{\sigma }_1+{\sigma }_2+{\sigma }_3}{3}=\frac{1}{3}{\sigma }_{kk}\hfill \\ S_{ij}={\sigma }_{ij}-\frac{1}{3}{\delta }_{ij}{\sigma }_{kk}\hfill \\ {\epsilon }_{m=}\frac{{\epsilon }_1+{\epsilon }_2+{\epsilon }_3}{3}=\frac{1}{3}{\epsilon }_{kk}\hfill \end{array}$$

(11)

For the elastomer, the Hook element expression in the three-dimensional force state can be derived from the Hook body expression in the one-dimensional force state as follows:

$$\{\begin{array}{l}{\sigma }_m=3K{\epsilon }_m\\ S_{ij}=2G{e}_{ij}\end{array}$$

(12)

where K and G are the bulk modulus and shear modulus of the rock mass, respectively, as follows:

$$\{\begin{array}{l}K=\frac{E}{3(1-2\mu )}\\ G=\frac{E}{2(1+\mu )}\end{array}$$

(13)

The constitutive relation of the elastomer can be obtained by introducing Equation (11) into Equation (12):

$${\epsilon }_{ij}^e=\frac{S_{ij}}{2G}+\frac{{\sigma }_m}{3K}{\delta }_{ij}$$

(14)

Assume that rock is a homogeneous material, and that creep deformation is caused only by the stress deviatoric tensor. In this case, the creep equation of a three-dimensional viscoelastic body can be obtained by directly replacing ${\sigma }_0$ in a one-dimensional creep equation with ${(S_{ij})}_0$, in which ${(S_{ij})}_0$ is the constant deviatoric stress imposed on the rock sample during creep tests. Therefore, the three-dimensional constitutive relationship of the viscoelastic body is as follows:

$${\epsilon }_{ij}^{v-e}=\frac{1}{2G_1}(1-e^{-\frac{G_1}{{\eta }_1}t})S_{ij}$$

(15)

For a viscoplastic body, the creep behaviors are mainly reflected in the shear deformation. Thus, the constitutive relation under the three-dimensional stress state can be expressed as (Brotóns et al., 2014):

$${\epsilon }_{ij}^{v-p}=\frac{1}{{\eta }_2}\langle \varphi (\frac{g}{g_0})\rangle \frac{\partial F}{\partial {\sigma }_{ij}}t$$

(16)

where $g$ and $g_0$ are the initial values of the yield function and yield function, respectively; F is the plastic potential function; and $\langle \varphi (\frac{g}{g_0})\rangle$ is the model switching function under three-dimensional conditions, which satisfies the conditions:

$$\{\begin{array}{l}If g<0, then\langle \varphi (\frac{g}{g_0})\rangle \ge 0\\ If g\ge 0, then\langle \varphi (\frac{g}{g_0})\rangle \ge 1\end{array}$$

(17)

Based on the above analysis, substitute Equations (13)–(15) into Equation (9); thus, the nonlinear viscoelastic–plastic creep equation of AS under a three-dimensional stress state is obtained:

$$\{\begin{array}{cc}\epsilon (t)=\frac{S_{ij}}{2G_1}(1-e^{-\frac{G_1}{{\eta }_1}t})+\frac{S_{ij}}{2G_0}+\frac{{\sigma }_m}{3K}{\delta }_{ij}\hfill & \hfill (S_{ij}<S_{s_1})\\ \epsilon (t)=\frac{S_{ij}}{2G_1}(1-e^{-\frac{G_1}{{\eta }_1}t})+\frac{S_{ij}}{2G_0}+\frac{{\sigma }_m}{3K}{\delta }_{ij}+\frac{S_{ij}-{\sigma }_{s_1}}{{\eta }_2}t\hfill & \hfill (S_{s_1}\le S_{ij}<S_{s_2})\\ \epsilon (t)=\frac{S_{ij}}{2G_1}(1-e^{-\frac{G_1}{{\eta }_1}t})+\frac{S_{ij}}{2G_0}+\frac{{\sigma }_m}{3K}{\delta }_{ij}+\frac{S_{ij}-{\sigma }_{s_1}}{{\eta }_2}t+\frac{S_{ij}-{\sigma }_{s_2}}{{\eta }_c}{t}^n\hfill & \hfill (S_{ij}\ge S_{s_2})\end{array}$$

(18)

In the current study, the intermediate and minimum principal stresses were equal, i.e., ${\sigma }_2={\sigma }_3$. Therefore, the stress spherical tensor and the stress deviatoric tensor can be expressed as follows:

$$\{\begin{array}{l}{\sigma }_m=\frac{1}{3}({\sigma }_1+2{\sigma }_3)\\ S_{ij}=\frac{2}{3}({\sigma }_1-{\sigma }_3)\end{array}$$

(19)

Introducing Equation (19) into Equation (18), the nonlinear creep model for AS with ${\sigma }_2={\sigma }_3$ is obtained as follows:

$$\{\begin{array}{ll}\epsilon (t)=\frac{{\sigma }_1-{\sigma }_3}{3G_1}(1-e^{-\frac{G_1}{{\eta }_1}t})+\frac{{\sigma }_1-{\sigma }_3}{3G_0}+\frac{{\sigma }_1+2{\sigma }_3}{9K}& \hfill (\sigma <{\sigma }_{s_1})\\ \epsilon (t)=\frac{{\sigma }_1-{\sigma }_3}{3G_1}(1-e^{-\frac{G_1}{{\eta }_1}t})+\frac{{\sigma }_1-{\sigma }_3}{3G_0}+\frac{{\sigma }_1+2{\sigma }_3}{9K}+\frac{{\sigma }_1-{\sigma }_3-{\sigma }_{s_1}}{3{\eta }_2}t& \hfill ({\sigma }_{s_1}\le \sigma <{\sigma }_{s_2})\\ \epsilon (t)=\frac{{\sigma }_1-{\sigma }_3}{3G_1}(1-e^{-\frac{G_1}{{\eta }_1}t})+\frac{{\sigma }_1-{\sigma }_3}{3G_0}+\frac{{\sigma }_1+2{\sigma }_3}{9K}+\frac{{\sigma }_1-{\sigma }_3-{\sigma }_{s_1}}{3{\eta }_2}t+\frac{{\sigma }_1-{\sigma }_3-{\sigma }_{s_2}}{3{\eta }_c}{t}^n& \hfill (\sigma \ge {\sigma }_{s_2})\end{array}$$

(20)

3.3. Determination of Creep Parameters

3.3.1. Cracking Stress ${\sigma }_{s_1}$ and Creep Dilatancy Stress ${\sigma }_{s_2}$

According to the creep test results, when the loading stress reached approximately 80% of the deviatoric stress before failure, the volume of AS samples began to change from compressive to expansive. Therefore, 80% of the loading stress was taken as the value of ${\sigma }_{s_1}$. When the loading stress reached approximately 85% of the final loading stress in the expansion stage, the sample began to expand. Therefore, 85% of the final loading stress in the expansion stage was taken as ${\sigma }_{s_2}$ value. The values of creep parameters ${\sigma }_{s_1}$ and ${\sigma }_{s_2}$ under different confining pressure conditions are shown in

Table 3. The creep parameters ${\sigma }_{s_1}$ and ${\sigma }_{s_2}$ under different confining pressures.

C (MPa)	${\mathit{\sigma }}_{\mathit{v}\mathit{e}}(\mathbf{MPa})/\mathsf{\delta }$	${\mathit{\sigma }}_{{\mathit{s}}_1}(\mathbf{Mpa})$	${\mathit{\sigma }}_{\mathit{d}\mathit{s}}(\mathbf{MPa})/\mathsf{\delta }$	${\mathit{\sigma }}_{{\mathit{s}}_2}(\mathbf{MPa})$
3	30.3/71.29%	24.24	33.7/79.29%	28.65
6	35.0/73.92%	28.00	39.3/83.00%	33.41
9	38.5/72.99%	30.80	42.6/80.76%	36.21
12	41.8/72.86%	33.44	45.9/80.01%	39.02
15	46.8/74.38%	37.44	50.1/79.62%	42.59
18	52.5/78.01%	42.00	56.8/84.40%	48.28

Note: ${\sigma }_{ve}$ represents the stress when the volume changed from compressive to expansive, ${\sigma }_{ds}$ represents the stress level in the volume expansion stage.

.

3.3.2. Determination of the Remaining Creep Parameters

When ${\sigma }_C<{\sigma }_{s_1}$, the parameters to be fitted include $K,G_0,G_1$ and ${\eta }_1$; when ${\sigma }_{s_1}\le {\sigma }_C<{\sigma }_{s_2}$, the parameters to be fitted are $K,G_0,G_1,{\eta }_1$ and ${\eta }_2$; when ${\sigma }_C\ge {\sigma }_{s_2}$, the creep parameters to be fitted are $K,G_0,G_1,{\eta }_1,{\eta }_2$ and the rheological index n. In this study, the least squares method was used to fit the parameters. First, the fitting function was determined.

$$\epsilon =f(t,K,G_0,G_1,{\eta }_1,{\eta }_2,{\eta }_c,n)$$

(21)

Use $b_1$ to $b_7$ to represent the approximate values of parameters $K,G_0,G_1,{\eta }_1,{\eta }_2,{\eta }_c,\mathrm{and}n$ and define:

$$\{\begin{array}{c}{\delta }_1=K-b_1,{\delta }_2=G_0-b_2,{\delta }_3=G_1-b_3,{\delta }_4={\eta }_1-b_4\\ {\delta }_5={\eta }_2-b_5,{\delta }_6={\eta }_c-b_6,{\delta }_7=n-b_7\end{array}$$

(22)

By expanding the Taylor series and extracting only the linear part, we can obtain:

$$\epsilon =f(t,b_1,b_2,b_3,b_4,b_5,b_6,b_{,7})+{\displaystyle \sum }_{j=1}^7{f}_{Bj}^{\prime }(t,b_1,b_2,b_3,b_4,b_5,b_6,b_{,7}){\delta }_j$$

(23)

Then, the following equations can be obtained:

$$f_{B1}^{\prime }=\frac{\partial f}{\partial K},f_{B2}^{\prime }=\frac{\partial f}{\partial G_0},f_{B3}^{\prime }=\frac{\partial f}{\partial G_1},f_{B4}^{\prime }=\frac{\partial f}{\partial {\eta }_1},f_{B5}^{\prime }=\frac{\partial f}{\partial {\eta }_2},f_{B6}^{\prime }=\frac{\partial f}{\partial {\eta }_c},f_{B7}^{\prime }=\frac{\partial f}{\partial n}$$

(24)

According to Equation (24), the objective function of the least squares fitting problem is obtained:

$$Q={{\displaystyle \sum }}^{}{[{\epsilon }_j-f(t_j,K,G_0,G_1,{\eta }_1,{\eta }_2,{\eta }_c,n)]}^2-{{\displaystyle \sum }}^{}{f}_{Bj}(t,K,G_0,G_1,{\eta }_1,{\eta }_2,{\eta }_c,n){\delta }_j$$

(25)

If

$$\frac{\partial Q}{\partial {\delta }_k}=0,(k=1,2,3,4,5,6,7)$$

(26)

Then

$${\displaystyle \sum }_{j=1}^7{a}_{kj}{\delta }_j=C_k,(k=1,2,3,4,5,6,7)$$

(27)

where $a_{kj}$ and $C_k$ in Equation (27) are defined as follows:

$$\{\begin{array}{l}{a}_{kj}={\displaystyle \sum }{f}_{Bk}^{\prime }(t_j,b_1,b_2,b_3,b_4,b_5,b_6,b_7)\cdot f_{Bj}^{\prime }(t_j,b_1,b_2,b_3,b_4,b_5,b_6,b_7)k,j=1,2,\cdots ,7\\ C_k={\displaystyle \sum }[{\epsilon }_j-f(t_j,b_1,b_2,b_3,b_4,b_5,b_6,b_7)]\cdot f_{Bk}^{\prime }(t_j,b_1,b_2,b_3,b_4,b_5,b_6,b_7)k=1,2,\cdots ,7\end{array}$$

(28)

By solving Equation (28), the ${\delta }_j$ values can be obtained, which yield the approximate values of the creep parameters. Equation (28) can be solved as follows:

• Arbitrarily select initial values of a set of coefficients $b_1$ to $b_7$;
• Calculate $a_{kj},C_k$;
• Substitute $a_{kj}$ and $C_k$ into (2 − 46) (28) to obtain ${\delta }_1$ $\mathrm{to}{\delta }_7$;
• Take $b_1+{\delta }_1,b_2+{\delta }_2$, …, $b_7+{\delta }_7$ as the approximate values of the regression coefficients;
• Using $b_1+{\delta }_1,b_2+{\delta }_2$, …, $b_7+{\delta }_7$ as the initial values of the regression coefficients, repeat the above steps until ${\delta }_1$, ${\delta }_2$, …, ${\delta }_7$ are small enough;
• Obtain the final values of the creep model parameters $K,G_0,G_1,{\eta }_1,{\eta }_2,{\eta }_c$ and the rheological index $n$, which are the values of the final iterative regression coefficients $b_1$ to $b_7$.

The nonlinear creep model parameters of AS samples under different confining pressures and loading levels were obtained by the above methods. As shown in

Table 4. Creep parameters of AS under different confining pressures.

C/MPa	${\mathit{\sigma }}_{\mathit{c}}/\mathbf{MPa}$	$\mathit{K}$	${\mathit{G}}_0/\mathbf{GPa}$	${\mathit{G}}_1/\mathbf{GPa}$	${\mathit{\eta }}_1/\mathbf{GPa}·\mathbf{h}$	${\mathit{\eta }}_2/\mathbf{GPa}·\mathbf{h}$	${\mathit{\eta }}_{\mathit{c}}/\mathbf{GPa}·\mathbf{h}$	$\mathit{n}$
3	23.5	9.33	8.31	48.32	865.71	-	-	-
	26.9	17.52	2.43	23.24	280.35	-	-	-
	30.3	3.14	2.17	17.57	215.63	3.6	-	-
	33.7	8.57	5.70	188.23	670.53	1660.12	51.31	2
6	26.4	9.98	7.83	281.56	755.48	-	-	-
	30.7	10.37	6.72	260.34	691.35	-	-	-
	35.0	9.84	6.02	210.73	466.83	3434.97	-
	39.3	9.96	5.87	169.85	349.77	556.42	49.10	3
9	30.3	10.55	6.73	281.53	841.71	-	-	-
	34.4	10.78	5.75	226.87	768.69	-	-	-
	38.5	10.63	5.15	189.38	647.36	1436.64	-	-
	42.6	10.63	4.83	167.38	527.84	690.32	50.44	4
12	33.6	11.35	6.47	298.46	954.37	-	-	-
	37.7	12.02	6.68	260.14	857.67	-	-	-
	41.8	11.15	5.53	210.35	724.68	2857.64	-	-
	45.9	10.86	5.66	170.75	687.63	1557.86	57.48	4
15	36.9	12.12	7.56	360.93	1033.75	-	-	-
	40.2	12.45	7.54	326.67	957.34	-	-	-
	43.5	11.55	7.01	291.64	890.48	-	-	-
	46.8	11.68	6.82	242.88	824.35	3687.85	-	-
	50.1	11.48	5.82	190.51	783.42	1868.52	58.81	5
18	39.6	12.13	8.37	409.65	1247.55	-	-	-
	43.9	12.84	7.87	341.67	1001.58	-	-	-
	48.2	12.69	6.36	317.64	1034.75	-	-	-
	52.5	11.77	6.82	271.53	977.46	2436.32	-	-
	56.8	12.03	6.52	217.32	960.73	1982.54	55.53	6

, the model could reflect the creep behaviors of AS. A comparison between the experimental data and the fitting value is shown in Figure 10.

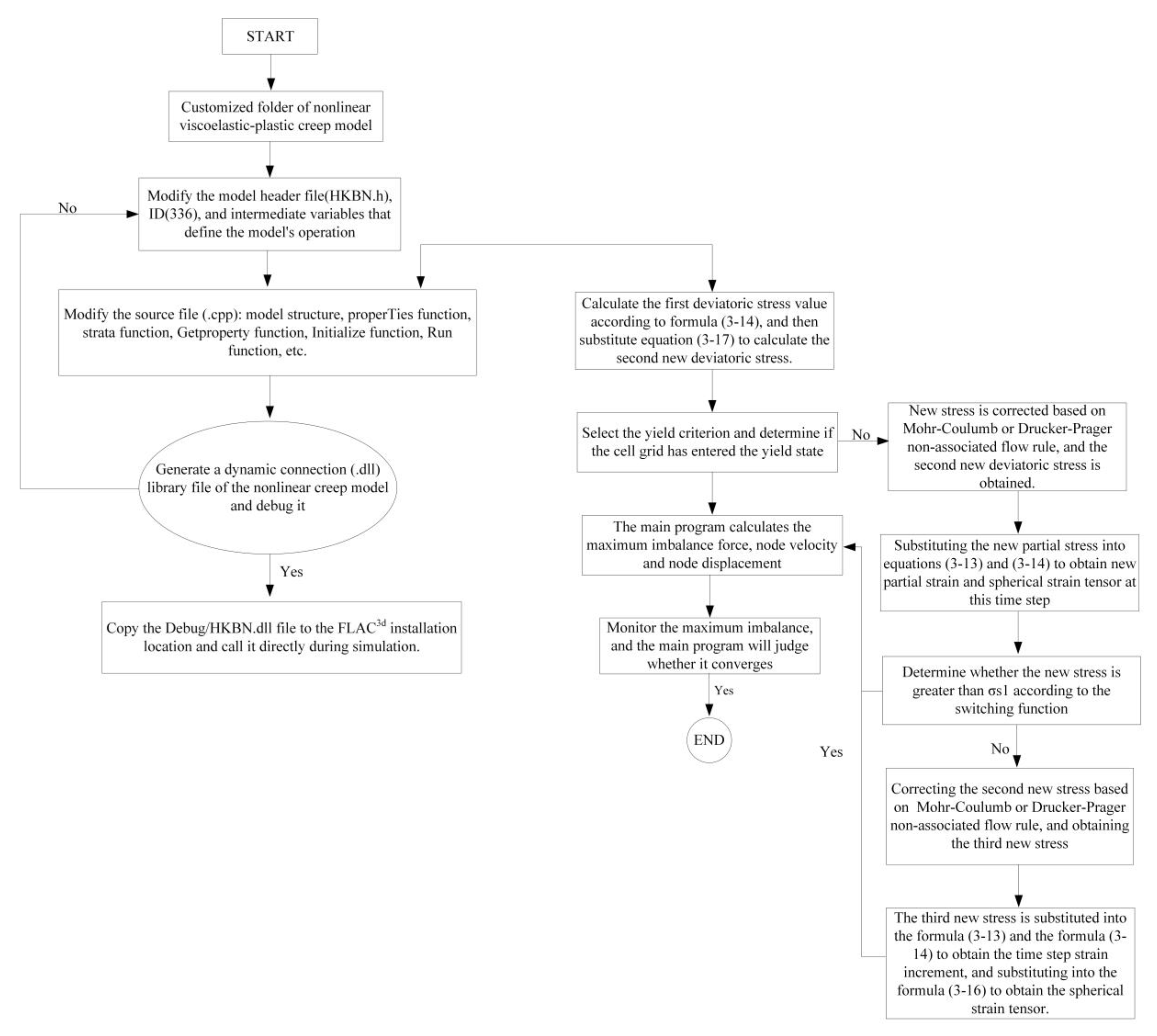
4. Numerical Implementation of the Nonlinear Creep Model of AS

4.1. Finite Difference Form of the Nonlinear Creep Model

According to the components of the nonlinear model, the total deviatoric stress and the total deviatoric strain tensors can be expressed as follows:

$$\{\begin{array}{c}{e}_{ij}=e_{ij}^H+e_{ij}^K+e_{ij}^B+e_{ij}^N\hfill \\ S_{ij}=S_{ij}^H+S_{ij}^K+S_{ij}^B+S_{ij}^N\hfill \end{array}$$

(29)

where $e_{ij}^H,e_{ij}^K,e_{ij}^B$ and $e_{ij}^N$ represent the partial strains of Hook, Kelvin, Bingham, and NVPB, respectively; $S_{ij}^K,S_{ij}^H,S_{ij}^B$ and $S_{ij}^N$ represent the deviatoric (partial) stress of Hook, Kelvin, Bingham, and NVPB, respectively.

According to the superposition principle, the total deviatoric strain rate of the nonlinear creep model is as follows:

$${\dot{e}}_{ij}={\dot{e}}_{ij}^H+{\dot{e}}_{ij}^K+{\dot{e}}_{ij}^B+{\dot{e}}_{ij}^N$$

(30)

Equation (30) is converted to an incremental expression as follows:

$$\mathsf{\Delta }{e}_{ij}=\mathsf{\Delta }{e}_{ij}^H+\mathsf{\Delta }{e}_{ij}^K+\mathsf{\Delta }{e}_{ij}^B+\mathsf{\Delta }{e}_{ij}^N$$

(31)

The Hook element deviatoric stress is expressed as

$$S_{ij}^H=2G_0\mathsf{\Delta }{e}_{ij}^H$$

(32)

The stress-strain relationship of the combined model of the Hook element and Kelvin element is as follows:

$$S_{ij}^K=2G_1{e}_{ij}^K+2\eta {\dot{e}}_{ij}^K$$

(33)

The strain rate of the Bingham viscoplastic element in three-dimensional form is as follows:

$${\dot{e}}_{ij}^B=\frac{H(g)}{2\eta }\frac{\partial F}{\partial {\sigma }_{ij}}$$

(34)

Furthermore, the deviatoric strain rate of the Bingham viscoplastic element is as follows:

$${\dot{e}}_{ij}^B=\frac{H(g)}{2\eta }\frac{\partial F}{\partial {\sigma }_{ij}}-\frac{{\dot{e}}_{ij}^B}{3}{\delta }_{ij}$$

(35)

Based on the assumption in plastic mechanics, the plastic deformation of rock would not change the volume, and the volumetric stress results only from elastic volumetric strain; thus, the following equation can be obtained:

$${\dot{\sigma }}_m=K_B{\dot{e}}_{kk}^B+K_H{\dot{e}}_{kk}^H$$

(36)

where $K_B$ and $K_H$ both represent the bulk modulus of the rock.

Based on the principle of centre difference, Equation (33) can be transformed into

$${\overline{S}}_{ij}^K\mathsf{\Delta }t=2G_1{e}_{ij}^K+2\eta {\stackrel{\mathsf{\Delta }}{e}}_{ij}^K\mathsf{\Delta }t$$

(37)

where $\mathsf{\Delta }t$ represents a time increment step and ${\overline{S}}_{ij}$ and ${\overline{e}}_{ij}$ represent the average deviating stress and bias strain in a time increment, respectively. Among these parameters,

$$\{\begin{array}{c}{\overline{S}}_{ij}=\frac{(S_{ij}^N+S_{ij}^O)}{2}\hfill \\ {\overline{e}}_{ij}=\frac{(e_{ij}^N+e_{ij}^O)}{2}\hfill \end{array}$$

(38)

where the superscript symbols N and O represent the new and old values in a computing time step, respectively.

Substituting Equation (38) into Equation (37), the following equation can be obtained:

$$e_{ij}^{B-N}=\frac{1}{1+\frac{G_2}{2\eta }\mathsf{\Delta }t}[(1-\frac{G_2}{2\eta }\mathsf{\Delta }t)e_{ij}^{B-O}+\frac{\mathsf{\Delta }t}{4\eta }(S_{ij}^N+S_{ij}^O)]$$

(39)

The first part of the spherical strain expression of Equation (39) can be calculated as follows:

$$e_m^{B-N}=\frac{1}{1+\frac{K_B}{2\eta }\mathsf{\Delta }t}[(1-\frac{K_B}{2\eta }\mathsf{\Delta }t)e_m^{B-O}+\frac{\mathsf{\Delta }t}{6K_B}({\sigma }_{ij}^N+{\sigma }_{ij}^O)]$$

(40)

By substituting Equations (37) and (40) into Equation (31), the following results can be obtained:

$$S_{ij}^N=\frac{1}{A_1}[\mathsf{\Delta }{e}_{ij}-\mathsf{\Delta }{e}_{ij}^B-\mathsf{\Delta }{e}_{ij}^N-(\frac{1-\frac{G_2}{2\eta }\mathsf{\Delta }t}{1+\frac{G_2}{2\eta }\mathsf{\Delta }t}-1)e_{ij}^{K-O}+A_2{S}_{ij}^O]$$

(41)

$$\{\begin{array}{l}{A}_1=\frac{1}{2G_0}+\frac{\mathsf{\Delta }t}{4(1+\frac{G_2}{2\eta }\mathsf{\Delta }t)\eta }\\ A_2=\frac{1}{2G_0}-\frac{\mathsf{\Delta }t}{4(1+\frac{G_2}{2\eta }\mathsf{\Delta }t)\eta }\end{array}$$

(42)

When $\sigma <{\sigma }_{s_1}$,

$$S_{ij}^N=\frac{1}{A_1}[\mathsf{\Delta }{e}_{ij}-(\frac{1-\frac{G_2}{2\eta }\mathsf{\Delta }t}{1+\frac{G_2}{2\eta }\mathsf{\Delta }t}-1)e_{ij}^{K-O}+A_2{S}_{ij}^O]$$

(43)

When ${\sigma }_{s_1}\le \sigma <{\sigma }_{s_2}$,

$$S_{ij}^N=\frac{1}{A_1}[\mathsf{\Delta }{e}_{ij}-\mathsf{\Delta }{e}_{ij}^B-(\frac{1-\frac{G_2}{2\eta }\mathsf{\Delta }t}{1+\frac{G_2}{2\eta }\mathsf{\Delta }t}-1)e_{ij}^{K-O}+A_2{S}_{ij}^O]$$

(44)

At the same time, the total stress spherical tensor of the entire nonlinear viscoelastic–plastic creep model is

$${\sigma }_m^N=K_B{e}_{kk}^B+K_H{e}_{kk}^H+{\sigma }_m^O$$

(45)

Both Equations (43) and (44) can obtain new values in a calculation step according to the calculation value of the previous step. Thus, cumulative calculation can be achieved.

4.2. Numerical Implementation in FLAC3D

FLAC3D numerical simulation of the nonlinear creep model of AS was achieved using the C++ programming language to connect it to the secondary development interface of FLAC3D. Its process included main three steps: modifying the header file (.h file), modifying the program source file (.cpp file) and generating the dynamic connection or linking library file (.dll format).

(1) Modifying the header file

This part mostly modified some basic information about the new constitutive model. The modification included mainly the name of the model, the ID version, basic parameters of the nonlinear creep model and the intermediate variables during the operation of the program. The primary purpose of the above modifications was to ensure that the embedded files and parameters were correctly identified by the FLAC3D software. In the current secondary development process, the model header file was named HKBN.h, the file was named HKBN, and the model ID was changed to 336.

(2) Modifying the source file (.cpp file)

At this stage, the Properties function, the Strata function, the Getproperty function, the Initialize function, and the Run function were modified so that essential functions, such as identification and initialization, could be used. Its main contents included the following steps:

Modify the model structure: The constitutive model is actually an empty function. The main purpose is to assign the initial value to the derived new member in the custom HKBN.h header file. In general, the initial value is set to 0.

Customize the Properties function: This function converts creep parameters in the nonlinear creep model into a series of strings. During FLAC3D operation, new parameters can be assigned to the relevant definitions through the string.

Modify the Strata function, Getproperty function and SetProperty function: The Strata function is the unit status indicator, which realizes the precise positioning of the unit state. The main function of the Getproperty function and SetProperty function is to realize the assignment of creep parameters to the model parameters in the derived class.

Modify the Initialize function: The main function of this function is to initialize the unit status indicator and related parameter assignments and assign values to the private variables of the custom nonlinear creep model defined in the derived class.

Modify the Run function: The main purpose of this function is to realize the cumulative calculation process of defining a new model; that is, to calculate the strain increment in each cycle and convert it into a stress increment. Then, the new stress value of the calculation unit body is superimposed.

Modify the Save.Restore function: The calculation results can be saved after this modification.

(3) Generating dynamic link library (.dll format) file of nonlinear creep model

The dynamic link library is a necessary part of the normal call of the nonlinear creep model. The main steps are as follows. First, the user defined map (UDM) folder is named HKBN and copied to the FLAC3D installation location. Then, the Visual Studio software is run, and the udm.veproj file is opened. Second, the UDM command is executed to modify the output file named Debug/HKBN.dll. The file is a dynamic connection library of the nonlinear creep model. Finally, the solution command is run to check whether the dynamic library file has been successfully exported. If the export is successful, it is copied to the FLAC3D installation location and invoked directly during simulation. Otherwise, it is checked and modified, and the above steps are repeated after modification. The entire process is shown in Figure 11.

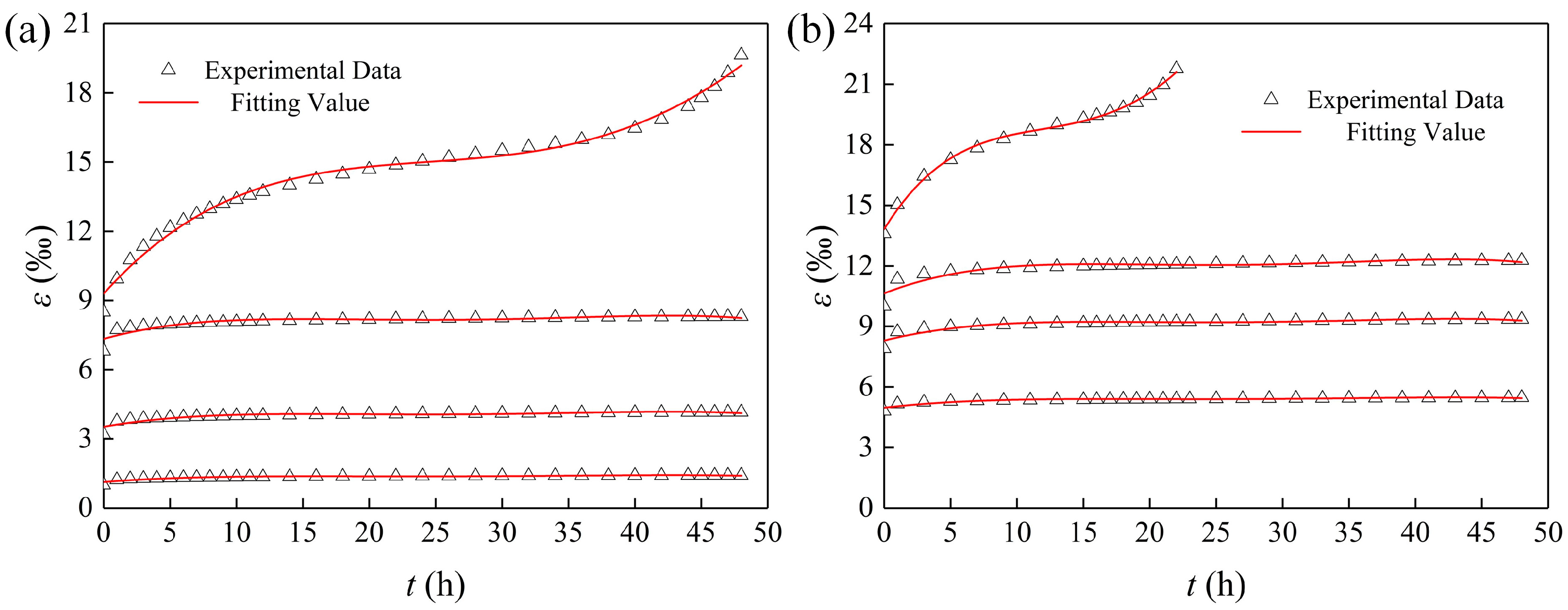
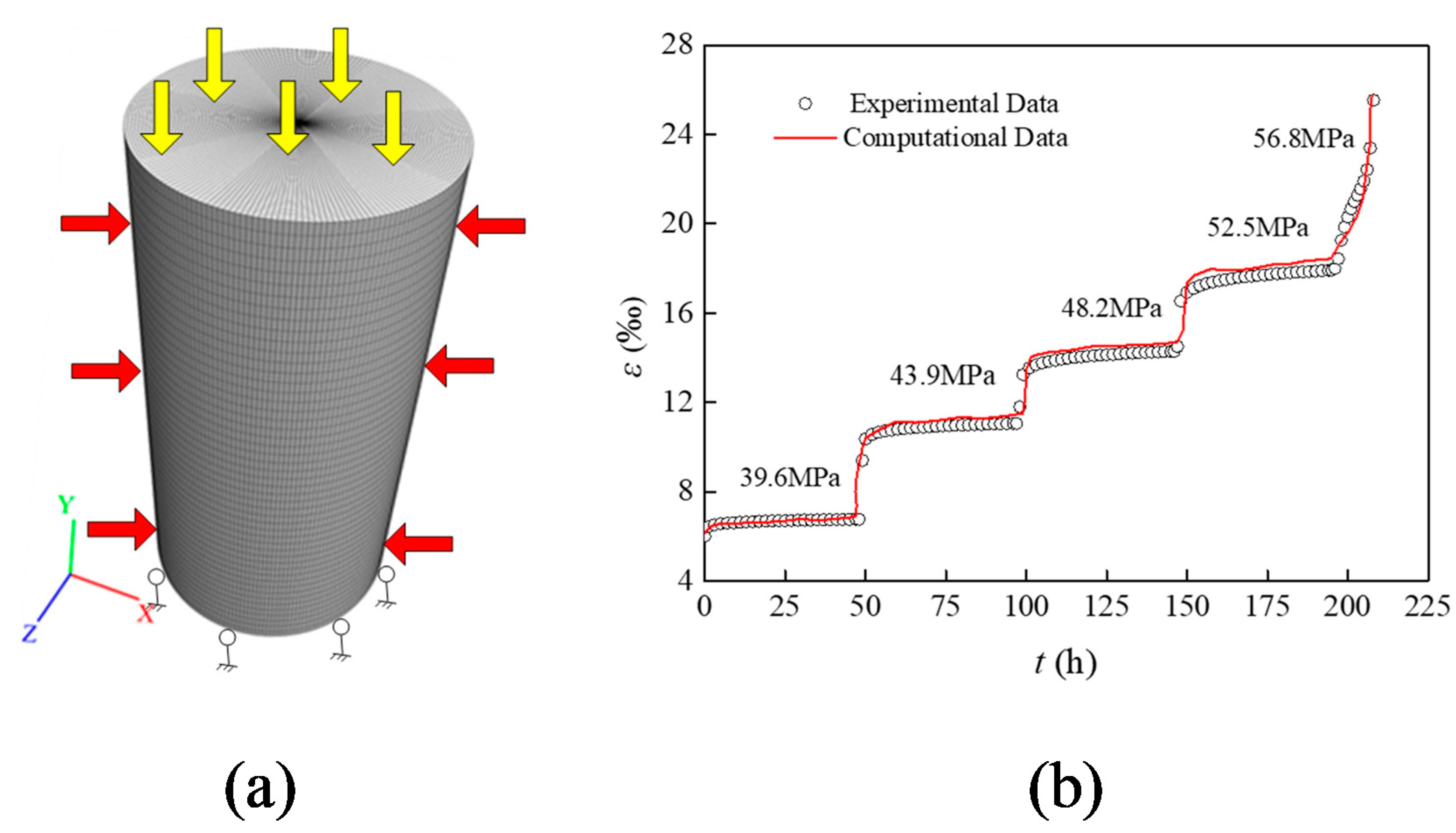
4.3. Numerical Model Verification

To verify the accuracy of the secondary development of the nonlinear creep model, a numerical calculation model that was consistent with the creep test of AS was established. The size of the simulation model was a 50 mm × 100 mm cylinder with a total of 14,280 units and 14,686 nodes. A vertical uniform stress was applied at the top of the model, and a fixed circumferential stress was applied on both sides to simulate the confining pressure. A displacement constraint was applied at the bottom in the vertical direction. Displacement constraints, specific numerical models and boundary conditions are shown in Figure 12a. The parameters of the model were the material parameters of AS. In this simulation, the axial load was applied by means of fixed confining pressure and stepwise loading. The confining pressure was set to 18 MPa, and the creep time of each stage was 48 h. The axial load deviatoric stresses of successive stages were 39.6 MPa, 43.9 MPa, 48.2 MPa, 52.5 MPa, and 56.8 MPa.

In the numerical simulation, the rock parameters were taken as the average values from the conventional triaxial compression tests. The variations in the specimen axial displacement with time under different loading stresses are shown in Figure 12b. The deformation curves obtained by the numerical calculation agree well with the experimental results. The good agreement between the numerical simulation and lab experiments indicates that the nonlinear creep model developed by FLAC3D can reflect the creep behaviors of the surrounding rock, which can be used in future analysis of Quandian Coal Mine 22.

5. Conclusions

In this study, the creep behaviors of AS were investigated both experimentally and numerically. Multi-stage creep tests were conducted on AS samples under different confining pressures (3, 6, 9, 12, 15, and 18 MPa). The creep characteristics of AS were analyzed. Based on the experimental results, a new nonlinear creep model was proposed. The nonlinear creep model was implemented in the FLAC3D software, and the procedure for the model parameter determination was presented. A comparison between the numerical and experimental results was also conducted for numerical modelling validation. Based on the above results, the following conclusions can be drawn:

• During the creep tests, the AS samples under various confining pressures exhibited four stages: instantaneous deformation, primary creep, secondary creep, and tertiary creep. With increasing confining pressure, the acceleration rate of the AS samples increased, and the creep failure strength gradually increased. However, due to the confining effect of confining pressure, the final volume gradually decreased.
• The nonlinear creep model of AS was constructed by adding another element, the NVPB element, to the traditional Nishihara model. The three-dimensional form of the creep model was deduced to simulate the rock creep problem under the equal confining pressure of surrounding rock masses. The parameters of the creep model could be obtained by fitting the least squares method.
• Based on the principle of finite difference, the finite difference form of the nonlinear creep model of AS was derived, and the model was embedded in the FLAC3D software. The numerical calculation model of AS was established. The creep behaviors of specimens under a confining pressure of 18 MPa were calculated and verified with experimental data. A good agreement was observed between the numerical and experimental results, indicating the feasibility of the creep model.
• The creep and rupture process of rock is a process of damage accumulation essentially, which is not only related to the confining pressure, but also closely affiliated with factors such as loading rate and initial damage degree etc. In this paper, as the dominant factor in the engineering case, the confining pressure is used as a variable to carry out creep test research, which has certain limitations and will be supplemented in the future.