Abstract
This paper discusses the numerical solution of the generalized non-Hermitian eigenvalue problem. It provides a comprehensive comparison of existing algorithms, as well as of available free and open-source software tools, which are suitable for the solution of the eigenvalue problems that arise in the stability analysis of electric power systems. The paper focuses, in particular, on methods and software libraries that are able to handle the large-scale, non-symmetric matrices that arise in power system eigenvalue problems. These kinds of eigenvalue problems are particularly difficult for most numerical methods to handle. Thus, a review and fair comparison of existing algorithms and software tools is a valuable contribution for researchers and practitioners that are interested in power system dynamic analysis. The scalability and performance of the algorithms and libraries are duly discussed through case studies based on real-world electrical power networks. These are a model of the All-Island Irish Transmission System with 8640 variables; and, a model of the European Network of Transmission System Operators for Electricity, with 146,164 variables.
1. Introduction
Eigenvalue analysis is a fundamental component of electric power system Small-Signal Stability Analysis (SSSA). It is utilized in order to determine the stability of the operating points of the system [1,2], design controllers [3], determine machine clusters and reduced equivalent models [4], and evaluate the properties of the transmission grid [5]. On the other hand, there is rich literature on numerical algorithms that determine the full or a partial solution of a given eigenvalue problem. Relevant monographs on the topic are, for example [6,7]. However, not all available algorithms are suitable for the SSSA of power systems.
The vast majority of numerical algorithms, in fact, solve exclusively symmetric, Hermitian, or tridiagonal Hermitian eigenvalue problems, which arise in many engineering, physics, and computer applications. Such algorithms are, for example, the Davidson [8], the implicitly restarted Lanczos [9], and the locally optimal block preconditioned conjugate gradient [10] methods. However, the matrices that describe a linearized power system model are typically non-symmetric. When compared to symmetric problems, non-symmetric eigenvalue problems are more difficult and computationally demanding to solve. This is also due to the fact that symmetric eigenvalue problems are generally well-conditioned, while non-symmetric eigenvalue problems are not. Consequently, the available free and open-source software libraries that solve non-symmetric eigenvalue problems are a small subset of all existing libraries.
The scalability of the numerical solution of eigenvalue problems is also very important, since real-world electrical power networks are large-scale dynamic systems. Unfortunately, the most reliable methods for finding the full spectrum of an eigenvalue problem are dense-matrix methods, and their computational complexity and memory requirements increase more than quadratically (in some cases even cubically) as the size of the matrix increases. As a matter of fact, the largest ever eigenvalue analysis with a dense algorithm to date was the solution of a problem in about 1 h, and it was carried out in 2014 by the Japanese K computer in Riken. To be able to obtain this result, the K computer includes 88,000 processors that draw a peak power of 12.6 MW, while its operation costs annually US$10 million. The solution of large-scale power system eigenvalue problems is challenging even when using sparse matrices and limiting the search to a subset of the spectrum.
A coarse taxonomy of existing algorithms for the solution of non-symmetric eigenvalue problems is as follows:
- Vector iteration methods, which, in turn, are separated to single and simultaneous vector iteration methods. Single vector iteration methods include the power method [11] and its variants, such as the inverse power and Rayleigh quotient iteration. Simultaneous vector iteration methods include the subspace iteration method [12] and its variants, such as the inverse subspace method. Regarding the application of vector iteration methods in power systems, the inverse power iteration was first discussed in [13]. A Rayleigh quotient iteration based algorithm was proposed in [14,15], while recent studies have provided subspace accelerated and deflated versions of the same algorithm [16,17,18]. Finally, simultaneous vector iteration methods were studied in [19,20].
- Schur decomposition methods, which mainly include the QR algorithm [21], the QZ algorithm [22], and their variants, such as the QR algorithm with shifts. Schur decomposition based methods have been the standard methods employed for the eigenvalue analysis of small to medium size power systems [23,24].
- Krylov subspace methods, which basically include the Arnoldi iteration [25] and its variants, such as the implicitly restarted Arnoldi [26] and the Krylov–Schur method [27]. In this category also belong preconditioned extensions of the Lanczos algorithm, such as the non-symmetric versions of the Generalized Davidson and the Jacobi–Davidson method. In power systems, different versions of the Arnoldi method were proposed in [19,28,29], while a parallel version of the Krylov–Schur method was implemented very recently, in [30]. The Jacobi-Davidson method and an inexact version of the same method were discussed in [31,32], respectively.
- Contour integration methods, which basically include a moment-based Hankel method [33] and a Rayleigh–Ritz-based projection method [34] proposed by Sakurai; and, the FEAST algorithm [35]. Contour integration for power system eigenvalue analysis was only very recently discussed [36,37].
The main objective of this paper is to provide a state-of-art reference of eigenvalue numerical algorithms that can be actually utilized for the analysis of large power system models. To this aim, we have carefully selected only methods for non-Hermitian matrices for which open-source numerical libraries are available and that we were able to test and that were successful to solve relatively “large” eigenvalue problems. In particular, the paper provides a fair comparison of algorithms that have been proposed for power system analysis only very recently, such as versions of the parallel Krylov–Schur and contour integration methods discussed in [30,37], as well as of state-of-art implementations of standard algorithms for unsymmetric dense and sparse matrices, such as the QR and Arnoldi method. The paper provides an overview and comparison of the state-of-art open-source libraries that solve the non-symmetric eigenvalue problem. These are Linear Algebra PACKage (LAPACK) [38] and its GPU-based version, namely Matrix Algebra for GPU and Multicore Architectures (MAGMA) [39]; ARnoldi PACKage (ARPACK) [40]; Anasazi [41]; Scalable Library for Eigenvalue Problem computations (SLEPc) [42]; FEAST [43]; and, z-PARES [44].
The remainder of the paper is organized, as follows. Section 2 provides the background and problem formulation of power system eigenvalue analysis and a description of matrix pencil spectral transforms. Section 3 outlines the most relevant numerical algorithms for the eigenvalue analysis of power systems. Open-source libraries that implement state-of-art implementations of these methods are presented in Section 4. The examined algorithms are comprehensively tested through two real-world power system models in the case studies discussed in Section 5. Finally, conclusions are drawn in Section 6.
2. Background
2.1. Power System Model
Electric power system models for transient stability analysis can be formulated as a set of non-linear Differential Algebraic Equation (DAEs), as follows [45]:
where , ; , , are the state variables, , , are the algebraic variables; , , are assumed to be constant matrices; and is the simulation time. Finally, denotes the zero matrix of dimensions . For the purpose of analysis and, for sufficiently small disturbances, (1) can be linearized around an equilibrium , as follows:
where , ; , , , , are the Jacobian matrices calculated at . This system can be rewritten in the following form:
where
the linear system (2) is often reduced to a system of Ordinary Differential Equation (ODEs), by elimination of algebraic variables. The linearized ODE power system model can be described, as follows:
where is the state matrix, and where we have assumed that , are non-singular.
2.2. Eigenvalue Problem
In this paper, we are concerned with finding the eigenvalues of the following system:
where , . Matrix in (5) can be:
The stability of (5) can be assessed by calculating its eigenvalues, which are defined as the roots of the characteristic equation:
where denotes the complex Laplace variable. In (6), is called the matrix pencil and the characteristic polynomial of system (5). In this paper, we assume that , where is polynomial of order equal or less than r, in which case is called a regular pencil [46]. In general, analytical solution of (6) is possible only if . For higher degrees, general formulas do not exist and only the application of a numerical method is possible. In addition, algorithms that explicitly determine the characteristic polynomial and then numerically calculate its roots, may be extremely slow, even for small problems. Alternatively, the eigenvalues of can be found from the solution of the Generalized Eigenvalue Problem (GEP):
where and . Every value of s that satisfies (7) is an eigenvalue of the pencil , with the vectors , being the corresponding right and left eigenvectors, respectively. Thus, the solution of the GEP consists in calculating the eigenpairs, i.e., eigenvalues and eigenvectors, which satisfy (7). It may be required that only right (or left) or both right and left eigenvectors are calculated, depending on the analysis that needs to be carried out. In general, the pencil has finite eigenvalues and the infinite eigenvalue with multiplicity . Note that, if is singular, then the pencil will have the infinite eigenvalue with multiplicity of at least one.
2.3. Spectral Transforms
In general, the solution of the eigenvalue problem involves finding the full or partial spectrum of the pencil . However, depending on the applied numerical method as well as on the structure of the system matrices, it is common that the eigenvalues are not found by directly using , but through the pencil that arises from the application of a proper spectral transform. Spectral transforms are utilized by eigenvalue numerical methods usually for one of the following reasons:
- To find the eigenvalues of interest. Some numerical methods, for example vector iteration-based methods, find the Largest Magnitude (LM) eigenvalues, whereas the eigenvalues of interest in SSSA are typically the ones with Smallest Magnitude (SM) or Largest real Part (LRP). Thus, it is necessary to apply a spectral transform, e.g., the invert or shift & invert.
- Address a singularity issue. A GEP with singular left hand side coefficient matrix can create problems to many numerical methods. Applying a Möbius transform can help address singularity issues.
- Accelerate convergence. Eigenvalues that are not very close to each other can lead to large errors and slow convergence of eigensolvers. Spectral transforms can help to magnify the eigenvalues of interest and speed up convergence.
We describe here the Möbius transformation, which is a general variable transformation that includes as special cases all spectral transforms used in practice by eigenvalue algorithms. The formulation of the Möbius transformation is:
The restriction in (9) is necessary, because, if , then s is constant which is not possible. Applying the transform (9) in (6) we obtain
or, equivalently, by using determinant properties
or, equivalently,
which is the Characteristic equation characteristic equation of a linear dynamical system
with pencil . System (5) will be referred as the prime system, and the family of systems (10) will be defined as the proper “M-systems”. An important property is that the solutions and stability properties of system (5) can be studied through (10) without resorting to any further computations, see [47]. The utilities of the family of systems of type (10) have been further emphasized by the features of some particular special cases. Table 1 summarizes the most commonly employed Möbius transforms and the corresponding matrix pencils for the GEP. The values of the parameters that lead to each of these transforms are given in Table 2. In the case that , the Cayley transform is equivalent to the bilinear transform , where . The choice of the best transform for a specific system and eigenvalue problem is a challenging task to solve, since the selection of shift values is always more or less heuristic. Finally, note that the importance of such spectral transforms for the eigenvalue analysis has also been identified in power system literature, see [48,49].

Table 1.
Common linear spectral transforms.

Table 2.
Coefficients of special Möbius transformations.
3. Description of Numerical Algorithms
This section provides an overview of the following classes of eigenvalue numerical methods: vector iteration methods, Schur decomposition methods, Krylov subspace methods, and contour integration methods. These are, in fact, the methods implemented by the open-source software libraries that are compared in Section 4 and in the case studies of Section 5 of this paper.
3.1. Single Vector Iteration Methods
The vector iteration or power method is the oldest and probably the simplest and most intuitive numerical method for solving an eigenvalue problem. Consider the LEP (8) with matrix pencil . The main idea of the power method is that, if one starts with a vector and repeatedly multiplies by , then the subsequence
converges to a multiple of the right eigenvector that corresponds to the eigenvalue of with LM. More strictly put, under the assumption that the magnitude of the largest eigenvalue is larger than that of all other eigenvalues, (11) linearly converges to a multiple of the corresponding right eigenvector . In order to guarantee the convergence, it is also required that the initial vector is selected with a non-zero component in the direction of . Applying the above idea, the method starts with an initial vector , which is updated at each step of the iteration through multiplication with and normalization. The k-th step of the iteration is as follows:
Finally, under the assumptions discussed above, converges to the vector , which corresponds to the eigenvalue of LM . Given , an estimation of the eigenvalue is given by the Rayleigh quotient. In general, given a right eigenvector , the Rayleigh quotient provides an estimate of the corresponding eigenvalue , as follows:
where is the conjugate transpose of .
The power method finds an eigenvector that corresponds to the eigenvalue of LM. However, the eigenvalue of LM is typically not of interest for SSSA. The inverse power method addresses this issue by using instead of in (12), where the spectral shift represents an initial guess of an eigenvalue . The k-th step of the inverse power method is as follows:
Provided that is a good initial guess of , converges to the corresponding right eigenvector . Hence, the inverse power method is able to calculate the eigenvector that corresponds to any single eigenvalue, by computing the dominant eigenvector of . Then, the eigenvalue is approximated by the Rayleigh quotient that is given by (13).
A bad selection of the spectral shift leads to very slow convergence, or convergence to a different eigenvector than the one desired, despite the ability of the inverse power method to compute any eigenpair (). The Rayleigh quotient iteration method is an extension of the inverse power method that updates the applied spectral shift at each step of the iteration. Starting from an initial eigenpair guess (, ), the k-th step, , of the Rayleigh quotient iteration is:
The method is able to converge to any eigenpair , depending on the initial guess.
For the sake of simplicity, numerical methods were presented in (12), (14), (15) for the solution of the LEP; however, they can be modified to handle also the GEP. For example, considering the GEP (7), the inverse power method for finding an eigenvector of the pencil can be described as:
The methods that are described above calculate a single eigenvector in one iteration and, for this reason, they are referred in the literature as single vector iteration methods. Calculating multiple eigenpairs with a single vector iteration method is possible by applying a deflation technique and repeating the iteration.
3.2. Simultaneous Vector Iteration Methods
Simultaneous vector iteration or subspace method is a vector iteration method that calculates multiple eigenvectors simultaneously in one iteration. Suppose that we want to compute the p LM eigenvalues of the LEP (8) with pencil . Extending the idea of the power method, consider the subsequence (11), where now is not a vector, but . As it is, the subsequence does not converge, as we would desire, to a matrix with columns the p eigenvectors of . However, convergence to these eigenvectors can be achieved by ensuring that the columns of the k-th element are orthonormal vectors. Subsequently, we say that the columns of span the subspace:
The steps of the subspace iteration algorithm are the following.
- The iteration starts with an initial matrix , , with orthonormal columns, i.e., .
- At the k-th step of the iteration, :
- (a)
- Matrix , , is formed as:
- (b)
- Matrix is updated by maintaining column-orthonormality, through the QR decomposition of matrix :where is a unitary matrix and is an upper triangular matrix.
The columns of eventually converge to p right eigenvectors that correspond to the p LM eigenvalues.
Note that the LM eigenvalues may not be the important ones for the needs of SSSA. Similarly to the discussion of the inverse power method, finding the eigenvalues of smallest magnitude is possible by forming an inverse subspace iteration.
The convergence of the subspace iteration is, in general, slow and, thus, its use is avoided for complex problems. Still, acceleration of the speed of convergence is possible by combining the method with the Rayleigh-Ritz procedure. Because the utility of the Rayleigh-Ritz procedure goes far beyond the subspace iteration, we describe it separately in Appendix A.
3.3. Schur Decomposition Methods
Schur decomposition-based methods take advantage of the fact that, for any matrix , there always exists a unitary matrix , such that:
where , , is an upper triangular matrix with diagonal elements all the eigenvalues of the pencil . Decomposition (20) is known as the Schur decomposition of , and matrix as the Schur form of . It appears that the most efficient algorithm for computing the Schur decomposition of a given matrix is the QR algorithm. In an analogy to the previously described methods, the QR algorithm can be understood as a nested subspace iteration or as a nested sequence of r power iterations [50]. Starting with matrix , the main steps of the QR algorithm at k-th iteration, are:
where is orthogonal and is upper triangular. The QR decomposition (21) is computed by applying Householder transformations, see [51].
If converges, say, after steps, then . The diagonal elements of are the eigenvalues of . The corresponding right eigenvectors are found as the columns of the matrix:
where . Notice that, throughout the algorithm, matrices , are similar and, thus, they have the same eigenvalues with the same multiplicities. The QR algorithm uses a complete basis of vectors and computes all of the eigenvalues of the matrix pencil . In practice, the QR algorithm is not typically used as it is, but multiple shifts are applied to accelerate convergence, which leads to the implicitly shifted QR algorithm [52].
The analog of the QR algorithm for the GEP is the QZ algorithm. The QZ algorithm takes advantage of the fact that for any matrices , , there always exist unitary matrices , , such that:
are upper triangular, and the eigenvalues of the pencil are the ratios of the diagonal elements of , , respectively. The decomposition (24) is known as generalized Schur decomposition. From the implementation viewpoint, the algorithm computes all of the eigenvalues of the matrix pencil by first reducing , , to upper Hessenberg and upper triangular form, respectively, through Householder transformations. The method can be perceived as equivalent to applying the implicitly shifted QR algorithm to , without, nonetheless, explicitly computing [52].
3.4. Krylov Subspace Methods
The power method consists in the calculation of the products , , , and so on, until convergence. The method utilizes the converged vector, let us say , which corresponds to the LM eigenvalue. However, the power iteration discards the information of all vectors calculated in the meantime. The main idea of Krylov subspace eigenvalue methods is to utilize this intermediate information in order to calculate the p LM eigenvalues of . The Krylov subspace that corresponds to and vector is defined as:
Subspace (25) is spanned by the columns of the Krylov matrix, which is defined as:
The matrix-vector multiplications typically render the columns of linearly dependent. Thus, these columns require orthonormalization. The orthonormalized vectors can be then employed in order to provide approximations of the eigenvectors that correspond to the p eigenvalues of LM. The eigenvalues are extracted by projecting onto the Krylov subspace, typically through the Rayleigh–Ritz procedure (see the Appendix A).
3.4.1. Arnoldi Iteration
The Arnoldi iteration finds the p LM eigenvalues of . In particular, it employs the Gram–Schmidt process in order to find an orthonormal basis of the Krylov subspace. Subsequently, the eigenvalues are extracted by applying the Rayleigh–Ritz procedure. Starting from an initial normalized vector , the vector at the k-th step is calculated, as follows:
where , .
At the k-th step, the Arnoldi relation is formulated, as follows:
where , , is the matrix with columns ; , , is in Hessenberg form and it has elements ; denotes the k-th column of the identity matrix . The algorithm stops when , suppose when . Then, relation (28) becomes:
where is an orthonormal basis of the Krylov subspace. Following the Rayleigh–Ritz procedure, the eigenvalue , , of is also eigenvalue of . Moreover, if is eigenvector of , the Ritz vector is a eigenvector that corresponds to .
The Arnoldi iteration converges quickly if the initial vector has larger entries at the direction of desired eigenvalues. This is usually not the case and, thus, it is common that many iterations are required. On the other hand, the ability to compute the columns of is constrained, because of its high memory requirements. For this reason, in practice, the Arnoldi iteration is typically restarted after a number of steps, while using a new, improved initial vector. The restarts can be explicit or implicit. The idea of explicit restarts is to utilize the information of the most recent factorization in order to produce a better initial vector. This is usually combined with a locking technique, i.e., a technique to ensure that converged vectors do not change in successive runs of the algorithm. On the other hand, the idea of the Implicitly Restarted (IR) Arnoldi iteration is to combine the Arnoldi iteration with the implicitly shifted QR algorithm.
3.4.2. Krylov-Schur Method
A more recently proposed idea that achieves the effect of the implicit restart technique in a simpler way is the Krylov–Schur method, which is a generalization of the Lanczos thick restart [53] for non-Hermitian matrices. The method considers the Arnoldi relation (28) and applies the QR algorithm to bring matrix to its Schur form, i.e., , where is an upper triangular matrix with diagonal elements the eigenvalues of (Ritz values). Subsequently, (28) becomes:
or equivalently,
where , . Decomposition (31) is reordered in order to separate undesired Ritz values from the desired ones. The part that corresponds to the desired Ritz values is kept and the rest is discarded:
where , , and represent the parts of , and that correspond to the desired Ritz values after the reordering, respectively. Subsequently, the reduced decomposition (32) is expanded to order k. The above process is repeated until convergence to an invariant subspace is achieved.
3.4.3. Generalized Eigenvalue Problem
Krylov subspace methods above were described for the solution of the LEP. Using the Krylov subspace methods for the solution of the GEP is usually done by employing a spectral transform. For example, applying the shift & invert transform to the pencil , the Arnoldi relation becomes:
where, in this case, it is . Each eigenvalue obtained after the convergence of (33) to an invariant subspace, is then transformed in order to find the corresponding eigenvalue of the original problem as .
3.5. Contour Integration Methods
Contour integration methods find the eigenvalues of the pencil that are inside a given, user-defined domain of the complex plane. The method that was proposed by Sakurai and Sugiura [33] and its variants [34,54], are the most characteristic examples of this class.
Suppose that p distinct eigenvalues are located inside positively oriented simple closed curve in . The contour integration method with Hankel matrices (CI-Hankel) applies a moment-based approach in order to reduce the problem of finding the p eigenvalues of to finding the eigenvalues of a matrix pencil. For a non-zero vector , consider the moments:
where ; is a user-defined point that lies in . A standard case is to define as a circle with center and radius .
The moments are used to construct the Hankel matrices and . Subsequently, the eigenvalues of the matrix pencil are given by , , …, . The corresponding eigenvectors are found through the contour integral:
where . Given the eigenvectors associated to , , …, , the eigenvectors of are retrieved through a simple vector manipulation. In practice, integrals (34), (35) are approximated through a numerical integration technique. For example, the following approximations of (34), (35) are obtained while using the N-point trapezoidal rule when is defined as the circle with center and radius :
where ; , . In order to compute (36), (37), the following linear systems need to be solved:
Systems (38) are independent for each j, and hence, they can be solved in parallel. A parallel implementation can significantly improve the computational efficiency, especially if the dimensions of , are large.
In the case that some eigenvalues in the defined region are very close, the accuracy of the CI-Hankel method decreases, as the associated Hankel matrices become ill-conditioned. An alternative approach is to use contour integration to construct a subspace that is associated to the eigenvalues in , and then extract the eigenpairs from such subspace while using the Rayleigh–Ritz procedure. The resulting method is the CI-RR (Contour Integration with Rayleigh–Ritz).
Based on (35), it can be proven that, if the column vectors form an orthonormal basis of , then the eigenvalues and the corresponding eigenvectors , can be extracted while using the basis and applying the Rayleigh–Ritz procedure for the pencil . In order to construct the orthonormal basis , the contour integral (35) is first approximated through the N-point trapezoidal rule. In practice, an orthonormal basis with size larger than p may be used to improve accuracy. When compared to the Hankel method, the CI-RR method is typically more accurate and, thus, is preferred most of the time.
Finally, another promising contour integration algorithm is FEAST. FEAST was first proposed in [35] for the solution of symmetric eigenvalue problems, but it was later extended to include non-symmetric eigenvalue problems. The algorithm can be understood as an accelerated subspace iteration method combined with the Rayleigh–Ritz procedure [55] and, from this point of view, it has some similarities with the CI-RR method. The unique characteristic of the FEAST algorithm is that it implements an acceleration through a rational matrix function that approximates the spectral projector onto the subspace.
4. Open-Source Libraries
This section provides an overview of—to the best of our knowledge—all of the open-source numerical eigensolvers that implement state-of-art numerical algorithms for non-symmetric eigenvalue problems. These are LAPACK, ARPACK, Anasazi, SLEPc, FEAST, and z-PARES.
4.1. LAPACK
- Summary: LAPACK [38] is a standard library aimed at solving problems of numerical linear algebra, such as systems of linear equations and eigenvalue problems.
- Eigenvalue Methods: QR and QZ algorithms.
- Matrix Formats: cannot handle general sparse matrices, but is functional with dense matrices. In fact, LAPACK is the standard dense matrix data interface used by all other eigenvalue libraries.
- Returned Eigenvectors: LAPACK algorithms are 2-sided, i.e., return both right and left eigenvectors.
- Dependencies: a large part of the computations required by the routines of LAPACK are performed by calling the BLAS (Basic Linear Algebra Subprograms) [56]. In general, BLAS functionality is classified in three levels. Level 1 defines routines that carry out simple vector operations; Level 2 defines routines that carry out matrix-vector operations; and, Level 3 defines routines that carry out general matrix-matrix operations. Modern optimized BLAS libraries, such as ATLAS (Automatically Tuned Linear Algebra Software) [57] and Intel MKL (Math Kernel Library), typically support all three levels for both real and complex data types.
- GPU-based version: MAGMA [39] provides hybrid CPU/GPU implementations of LAPACK routines. It depends on NVidia CUDA. For general non-symmetric matrices, MAGMA includes the QR algorithm for the solution of the LEP, but does not support the solution of the GEP.
- Parallel version: ScaLAPACK (Scalable LAPACK) [58] provides implementations of LAPACK routines for parallel distributed memory computers. Similarly to the dependence of LAPACK on BLAS, ScaLAPACK depends on PBLAS (Parallel BLAS), which, in turn, depends on BLAS for local computations and BLACS (Basic Linear Algebra Communication Subprograms) for communication between nodes.
- Development: as a eigensolver, LAPACK is the successor of EISPACK [59]. The first version of LAPACK was released in 1992. When compared to EISPACK, LAPACK was restructured to include the block forms of QR and QZ algorithms, which allows for exploiting Level 3 BLAS and leads to improved efficiency [60]. The latest version of LAPACK is 3.7 and it was released in 2016.
4.2. ARPACK
- Summary: ARPACK [40] is a library developed for solving large eigenvalue problems with the IR-Arnoldi method.
- Eigenvalue Methods: IR-Arnoldi iteration.
- Matrix Formats: ARPACK supports the Reverse Communication Interface (RCI), which provides to the user the freedom to customize the matrix data format as desired. In particular, with RCI, whenever a matrix operation has to take place, control is returned to the calling program with an indication of the task required and the user can, in principle, choose the solver for the specific task independently from the library.
- Returned Eigenvectors: only right eigenvectors are calculated.
- Dependencies: ARPACK depends on a number of subroutines from LAPACK/BLAS. Moreover, ARPACK requires to be linked to a library that factorizes matrices. This can be either dense or sparse. In the simulations that are described in this paper, we linked ARPACK to the efficient library KLU, which is part of SuiteSparse [61], and that is particularly suited for sparse matrices whose structure originates from an electrical circuit.
- GPU-based version: to the best of the authors’ knowledge, a library that provides a functional GPU-based implementation of ARPACK is not available to date.
- Parallel version: PARPACK is an implementation of ARPACK for parallel computers. The message parsing layers supported by PARPACK are MPI (Message Passing Interface) [62] and BLACS.
- Development: the first version of ARPACK became available on Netlib in 1995. The last few years, ARPACK has stopped getting updated by Rice University. The library has been forked into ARPACK-NG, a collaborative effort among software developers, including Debian, Octave, and Scilab, to put together their own improvements and fixes of ARPACK. The latest version of ARPACK-NG is 3.7.0 and it was released in 2019.
4.3. Anasazi
- Summary: Anasazi [41] is a library that implements block versions of algorithms for the solution of large-scale eigenvalue problems.
- Eigenvalue Methods: the library includes methods for both symmetric and non-symmetric problems. Regarding non-symmetric problems, it provides a block extension of the Krylov–Schur method and the Generalized Davidson (GD) method.
- Matrix Formats: Anasazi depends on LAPACK as an interface for dense matrix and on Epetra as an interface for sparse CSR matrix formats.
- Returned Eigenvectors: only right eigenvectors are calculated.
- Dependencies: Anasazi depends on Trilinos [41] and LAPACK/BLAS.
- GPU-based version: Currently not supported.
- Parallel version: a parallel version of Anasazi is not currently available. On the other hand, the library has an abstract structure, which is, in principle, compatible with parallel implementations.
- Development: the latest version of Anasazi was released in 2014.
4.4. SLEPc
- Summary: SLEPc [42] is a library that focuses on the solution of large sparse eigenproblems.
- Eigenvalue Methods: SLEPc includes a variety of methods, for both symmetric and non-symmetric problems. For non-symmetric problems, it provides the following methods: power/inverse power/Rayleigh quotient iteration with deflation, in a single implementation; Subspace iteration with Rayleigh-Ritz projection and locking; Explicitly Restarted and Deflated (ERD) Arnoldi; Krylov–Schur; GD; Jacobi–Davidson (JD); CI-Hankel; and, CI-RR methods.
- Matrix Formats: SLEPc depends on LAPACK as an interface for dense matrix and on MUMPS [63] as an interface for sparse Compressed Sparse Row (CSR) matrix formats. In addition, it supports custom data formats, enabled by RCI.
- Returned Eigenvectors: only the power method and Krylov–Schur method implementations are two-sided. All other algorithms return only right eigenvectors.
- Dependencies: SLEPc depends on PETSc (Portable, Extensible Toolkit for Scientific Computation) [64]. By default, the matrix factorization routines that are provided by PETSc are utilized by SLEPc but, at the compilation stage, SLEPc can be linked to other more efficient solvers, e.g., MUMPS, which is recommended by SLEPc developers and exploits parallelism.
- GPU-based version: SLEPc supports GPU computing, which depends on NVidia CUDA.
- Parallel version: SLEPc includes a parallel version that depends on MPI. The parallel version employs MUMPS as its linear sparse solver.
- Development: the first version of SLEPc (2.1.1) was released in 2002. The latest version is SLEPc 3.13 and it was released in 2020.
4.5. FEAST
- Summary: FEAST [43] is the eigensolver that implements the FEAST algorithm, which was first proposed in [35]. Among other characteristics, the package includes the option to switch to IFEAST, which uses an inexact iterative solver to avoid direct matrix factorizations. This feature is particularly useful if the sparse matrices are very large and carrying out direct factorization is very expensive.
- Eigenvalue Methods: FEAST.
- Arithmetic: both real and complex types.
- Matrix Formats: FEAST depends on LAPACK as an interface for dense matrix, on SPIKE as an interface for banded matrix and on MKL-PARDISO [65] for sparse CSR matrix formats. In addition, FEAST includes RCI and, thus, data formats can be customized by the user. Using the sparse interface requires linking FEAST with Intel MKL. Linking the library with BLAS/LAPACK and not with MKL is possible, but seriously impacts the performance and the results of the library.
- Returned Eigenvectors: the FEAST algorithm implementation is two-sided.
- Dependencies: FEAST requires LAPACK/BLAS.
- GPU-based version: currently not supported.
- Parallel version: PFEAST and PIFEAST are the parallel implementations of FEAST and IFEAST, respectively. Both support three-Level MPI message parsing layer, with available options for the MPI library being Intel MPI, OpenMPI, and MPICH. PFEAST and PIFEAST employ MKL-Cluster-PARDISO and PBiCGStab, respectively, as their parallel linear sparse solvers.
- Development: the first version of FEAST (v1.0) was released in 2009 and supported only symmetric matrices. Through the years FEAST added many functionalities, such as support for non-symmetric matrices, parallel computing, and support for polynomial eigenvalue problems. Since 2013, Intel MKL has adopted FEAST v2.1 as its extended eigensolver. The latest version is FEAST v4.0, which was released in 2020.
4.6. z–PARES
- Summary: z-PARES [44] is a complex moment-based contour integration eigensolver for GEPs that finds the eigenvalues (and corresponding eigenvectors) that lie into a contour path defined by the user.
- Eigenvalue Methods: CI-Hankel, CI-RR.
- Matrix Formats: z-PARES depends on LAPACK for dense matrices and on MUMPS for sparse CSR matrices. In addition, it supports custom data formats, enabled by RCI.
- Returned Eigenvectors: only right eigenvectors are calculated.
- Dependencies: z-PARES requires BLAS/LAPACK to be installed.
- GPU-based version: currently not supported.
- Parallel version: z-PARES includes a parallel version, which exploits two-Level MPI layer and employs MUMPS as its sparse solver.
- Development: the latest version of z-PARES is v0.9.6a and it was released in 2014.
4.7. Summary of Library Features
Table 3 and Table 4 provide a synoptic summary of the methods and relevant features of open-source libraries that solve non-symmetric eigenvalue problems. All of the libraries can handle both real and complex arithmetic types.

Table 3.
Methods of open-source libraries for non-symmetric eigenvalue problems.

Table 4.
Relevant features of open-source libraries for non-symmetric eigenvalue problems.
As it can be seen from Table 4, not all libraries provide algorithms that allow for calculating both left and right eigenvectors at once. However, in order to calculate participation factors, which are an important tool of power system SSSA [66,67,68], both right and left eigenvectors are required. With this regard, a formula to directly calculate left eigenvectors from right ones was proposed in [69]. In general, which is the most efficient solution for the calculation of the left eigenvalues depends on the library and the eigenvalue problem.
5. Case Studies
This section presents simulation results based on two real-world size power system models. The first system is a detailed model of the All-Island Irish Transmission System (AIITS), which includes 1443 state variables and 7197 algebraic variables. The second system is a dynamic model of the European Network of Transmission System Operators for Electricity (ENTSO-E) system, which includes 49,396 state variables and 96,770 algebraic variables. Table 5 summarizes the versions and dependencies of the open-source libraries considered in this section. Note that we only consider the open-source libraries that we managed to compile and install on Linux and Mac OS X operating systems and that worked for relatively “large” eigenvalue problems.

Table 5.
Versions and dependencies of open-source libraries for non-symmetric eigenvalue problems.
All of the simulations are obtained using the Python-based software tool Dome [70]. The Dome version utilized for this paper is based on Fedora Linux 28, Python 3.6.8, CVXOPT 1.1.9, and KLU 1.3.9. Regarding the computing times reported in both examples, we have two comments. First, all of the simulations were executed on a server mounting two quad-core Intel Xeon 3.50 GHz CPUs, 1 GB NVidia Quadro 2000 GPU, 12 GB of RAM, and running a 64-bit Linux OS. Second, since not all method implementations include two-sided versions and, in order to provide as a fair comparison as possible, all of the eigensolvers are called so as to return only the calculated eigenvalues and not eigenvectors.
5.1. All-Island Irish Transmission System
In this case study, we consider a real-world model of the AIITS. The topology and the steady-state operation data of the system have been provided by the Irish transmission system operator, EirGrid Group, whereas the dynamic data have been defined based on our knowledge about the technology of the generators and the controllers. The dynamic model has been also validated while using frequency data from a severe event that occurred in the real system in 2018, see [71]. The system consists of 1479 buses, 796 lines, 1055 transformers, 245 loads, 22 synchronous machines, with Automatic Voltage Regulator (AVRs) and Turbine Governor (TGs), 6 Power System Stabilizer (PSSs), and 176 wind generators. In total, the dynamic model has n = 1443 state variables and m = 7197 algebraic variables.
The results of the eigenvalue analysis of the AIITS are discussed for both LEP and GEP and for a variety of different numerical methods, namely, QR and QZ algorithms by LAPACK, GPU-based QR algorithm by MAGMA, subspace iteration, ERD-Arnoldi, and Krylov–Schur methods by SLEPc, IR-Arnoldi by ARPACK; and, CI-RR by z-PARES. In particular, we provide, for each method, the rightmost eigenvalues, as well as the time that is required to complete the solution of the eigenvalue problem. The dimensions of the LEP and GEP for the AIITS are shown in Table 6.

Table 6.
AIITS: dimensions of the LEP and GEP.
5.1.1. Dense Algorithms
Table 7 presents the results obtained with Schur decomposition methods. Both QR and QZ algorithms find all 1443 finite eigenvalues of the system. For the GEP, the QZ algorithm also finds the additional infinite eigenvalue with its algebraic multiplicity. The obtained rightmost eigenvalues are the same for both LEP and GEP. Since LAPACK is the most mature software tool among those considered in this paper, the accuracy of the eigenvalues found with all other libraries is evaluated by comparing them with the reference solution that was computed with LAPACK. Figure 1 shows the system root loci plot.

Table 7.
AIITS: Schur decomposition methods, LEP and GEP.
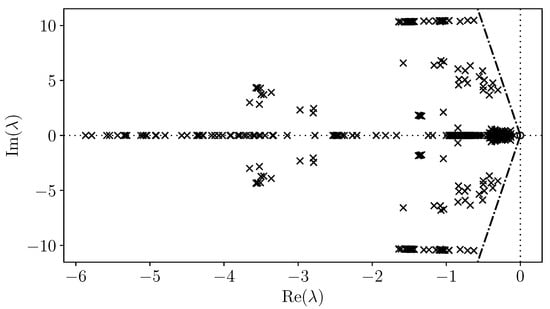
Figure 1.
AIITS: root loci computed with LAPACK.
Regarding the computational time, we see that, for the LEP, both LAPACK and the GPU-based MAGMA are very efficient at this scale, with MAGMA only providing a marginal speedup. On the other hand, when it comes to solving the GEP with LAPACK’s QZ method, scalability becomes a serious issue, since the problem is solved in 3669.77 s, which is computationally cumbersome.
5.1.2. Möbius Transform Image of the Spectrum
We show the image of the spectrum of the AIITS system for a couple of common special Möbius transforms, in particular for the shift & invert and the Cayley transform. Figure 2 and Figure 3 present the results, in which denotes an eigenvalue of the transformed pencil. These results refer to the LEP, and they are obtained using LAPACK. In each figure, the stable region is shaded, while the stability boundary is indicated with a solid line. The 5% damping boundary is indicated with a dash-dotted line.

Figure 2.
AIITS: shift & invert transform image of the spectrum, .
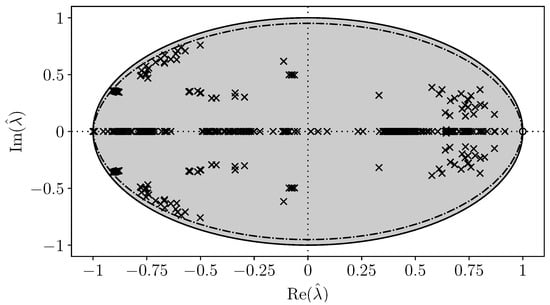
Figure 3.
AIITS: Cayley transform image of the spectrum, .
For the shift & invert transform, the stability boundary is defined by the circle with center and radius . If , wgucg is the case of Figure 2, stable eigenvalues are mapped outside the circle. On the other hand, if , stable eigenvalues are mapped inside the circle. If , we obtain the dual pencil with the corresponding invert transform, and the stable region is the full negative right have plane. Finally, Figure 3 shows the image of the Cayley transform of the AIITS for . All of the stable eigenvalues are located inside the unit circle with center the origin.
5.1.3. Sparse Algorithms
The implementation of the subspace iteration by SLEPc only finds the desired number of LM eigenvalues. However, in the s-domain, the relevant eigenvalues from the stability point of view are not the LM ones, but the ones with LRP or SM. Especially for the GEP, the LM eigenvalue is infinite and, hence, does not provide any meaningful information on the system dynamics. For this reason and for the needs of power system SSSA, the subspace method and, in general, any method that looks for LM eigenvalues must always be combined with a spectral transform. For the needs of this example, we apply the invert transform and pass to SLEPc the pencil of the dual system, i.e., . Subsequently, the method looks for the 50 LM eigenvalues of the dual system, which correspond to the 50 SM eigenvalues of the prime system. With this setup, the eigenvalues found by the subspace iteration for the GEP are shown in Table 8. As can be seen, the pair is not captured, since its magnitude is larger than the magnitudes of the 50 SM eigenvalues. In order to also obtain this pair, one can customize the spectral transform or simply increase the number of the eigenvalues to be returned. However, the best setup is not known a priori and, thus, some heuristic parameter tuning is required. Finally, the method does not scale well, since the solution of the GEP is completed in s.

Table 8.
AIITS: subspace iteration method, GEP.
The rightmost eigenvalues found with Krylov subspace methods for the LEP and GEP are shown in Table 9 and Table 10, respectively. For the LEP, ARPACK is set up in order to find the 50 LRP eigenvalues. Although all of the eigenvalues shown in Table 9 for ARPACK are actual eigenvalues of the system, some of the LRP ones are missed. Furthermore, no correct eigenvalues were found for the GEP, which we attribute to the fact that a non-symmetric is not supported. In SLEPc methods, both for LEP and GEP and in order to obtain the eigenvalues with good accuracy, we use the option “Target Real Part” (TRP), which allows targeting eigenvalues with specified real part. In particular, we set the TRP parameter to , and apply a shift & invert transform with . ERD-Arnoldi and Krylov–Schur methods are both able to accurately capture all rightmost eigenvalues. For the sake of completeness, we mention that the eigenvalues obtained with SLEPc, when compared to the ones that were found by LAPACK, appeared to be shifted by a constant offset , i.e., was returned instead of 0, and so on. The results shown in Table 9 and Table 10 take into account such a shift by adding to all output values that were returned by SLEPc. Finally, the Krylov subspace methods by SLEPc appear to be more efficient than ARPACK’s IR-Arnoldi. When compared to Schur decomposition methods, at this scale, Krylov methods, although they require some tuning, appear to be by far more efficient for the GEP, but less efficient for the LEP.

Table 9.
AIITS: Krylov subspace methods, LEP.

Table 10.
AIITS: Krylov subspace methods, GEP.
Table 11 presents the results that are produced by z-PARES’ CI-RR method for the LEP and GEP. The method is set to look for solutions in the circle with center the point and radius . In both cases, the eigenvalues found by z-PARES are actual eigenvalues of the system, although the eigenvalues found for the GEP include noticeable errors, when compared to the results that were obtained with LAPACK.

Table 11.
AIITS: contour integration method, LEP and GEP.
The most relevant issue is that the eigenvalues obtained with z-PARES are not the most important ones for the stability of the system, which means that critical eigenvalues are missed. This issue occurs despite the defined search contour being reasonable. Of course, there may be some region for which the critical eigenvalues are captured, but this can not be known a priori. Regarding the simulation time, the method for the AIITS is faster than SLEPc’s Krylov subspace methods for the LEP, but slower for the GEP. Figure 4 shows the search contour and the location of the characteristic roots that are found by z-PARES for the LEP.

Figure 4.
AIITS: root loci obtained with z-PARES, LEP.
5.2. European Network of Transmission System Operators for Electricity
This example presents the simulation results for a dynamic model of the ENTSO-E. The system includes 21,177 buses (1212 off-line); 30,968 transmission lines and transformers (2352 off-line); 1144 zero-impedance connections (420 off-line); 4828 power plants represented by 6-th order and 2-nd order synchronous machine models; and, loads (364 off-line), modeled as constant active and reactive power consumption. Synchronous machines that are represented by 6-th order models are also equipped with dynamic AVR and TG models. The system also includes 364 PSSs.
The system has, in total, state variables and m = 96,770 algebraic variables, as summarized in Table 12. The pencil has dimensions 146,166 × 146,166 and the matrix has 654,950 non-zero elements, which represent the of the total number of elements of the matrix.

Table 12.
ENTSO-E: statistics.
Neither the LEP nor GEP could be solved while using Schur decomposition methods. At this scale, the dense matrix representation that is required by LAPACK and MAGMA libraries leads to massive memory requirements, and a segmentation fault error is returned by the CPU. Among the algorithms that support sparse matrices, here we only test the contour-integration based methods, which, in fact, were the ones that were able to tackle this large eigenvalue problem on the available hardware.
The effect of changing the search region of the z-PARES CI-RR method on the eigenvalue analysis of the ENTSO-E system is shown in Table 13. Interestingly, simulations showed that shrinking the defined contour may lead to a marginal increase of the computation time. Although not intuitive, this result indicates that the large size of the ENTSO-E system mainly determines the mass of the computational burden, and that, at this scale, smaller subspaces are not necessarily constructed faster by the CI-RR algorithm. Regarding the number of eigenvalues obtained, using a region that is too small leads, as expected, to missing an important number of critical eigenvalues.

Table 13.
ENTSO-E: impact of the search region of the CI-RR method.
We test the impact of applying spectral transforms to the matrix pencil , on the eigenvalue analysis of the ENTSO-E with z-PARES’ CI-RR. In particular, we test the invert transform that yields the dual pencil ; and, the inverted Cayley transform, i.e., , which yields the pencil . Table 14 shows the results. Passing the transformed matrices to z-PARES provides a marginal speedup to the eigenvalue computation. In addition, when considering either the prime system or the inverted Cayley transform with , results in finding the same number of eigenvalues, whereas, when the dual system is considered, a number of eigenvalues is missed.

Table 14.
ENTSO-E: impact of spectral transforms of the CI-RR method.
5.3. Remarks
The following remarks are relevant:
- With regard to dense matrix methods, their main disadvantage is that they are computationally expensive. In addition, they generate complete fill-in in general sparse matrices and, therefore, cannot be applied to large sparse matrices simply because of massive memory requirements. Even so, LAPACK is the most mature among all computer-based eigensolvers and, as opposed to basically all sparse solvers, requires practically no parameter tuning. For small to medium size problems, the QR algorithm with LAPACK remains the standard and most reliable algorithm for finding the full spectrum for the conventional LEP.
- As for sparse matrix methods, convergence of vector iteration methods can be very slow and, thus, in practice, if not completely avoided, these algorithms should only be used for the solution of simple eigenvalue problems. An application where vector iteration methods may be more relevant, is in correcting eigenvalues and eigenvectors that have been computed with low accuracy, i.e., as an alternative to Newton’s method [69]. With regard to Krylov subspace methods, the main shortcoming of ARPACK’s implementation is the lack of support for general, non-symmetric left-hand side coefficient matrices, which is the form that commonly appears when dealing with the GEP of large power system models. On the other hand, the implementations of ERD-Arnoldi and Krylov–Schur by SLEPc do not have this limitation and exploit parallelism while providing good accuracy, although some parameter tuning effort is required. In addition, for the scale of the AIITS system and the GEP, these methods appear to be by far more efficient than LAPACK. Moreover, the implementation of contour integration by z-PARES is very efficient and can handle systems at the scale of the ENTSO-E. An interesting result is that, at this scale, smaller contour search regions, even if properly setup, do not necessarily imply faster convergence or, equivalently, smaller subspaces are not necessarily constructed faster by the CI-RR algorithm. The most relevant issue for z-PARES is that, depending on the problem, it may miss some critical eigenvalues, despite the defined search contour being reasonable. Although there may be some parameter settings for which this problem does not occur, those can not be known a priori.
- Finally, the presented comparison of numerical methods and libraries is not specific of power system problems, but it is relevant to any system with unsymmetric matrices. A relevant problem of the eigenvalue analysis for any dynamical system is to utilize its physical background in order to obtain an efficient approximation to some (components of) the eigenvectors. A computer algorithm that has successfully addressed this problem for conventional, synchronous machine dominated power systems is AESOPS [23,72], a heuristic quasi Newton–Raphson based method that aimed at finding dominant electromechanical oscillatory modes. On the other hand, how to effectively exploit the physical structure of modern, high-granularity power systems to shape efficient numerical algorithms is a challenging problem and an open research question.
6. Conclusions
The paper provides a comprehensive comparison of algorithms and open-source software tools for the numerical solution of the non-Hermitian eigenvalue problems that arise in power systems. In particular, the paper considers state-of-art implementations of methods that are based on Schur decomposition, vector iteration, Krylov subspace, and contour integration.
The most robust and reliable method for the solution of the LEP for small to medium size problems is the QR algorithm with LAPACK. For large-scale problems, which is the case of real-world power systems, the only option is to use software tools that exploit matrix sparsity. While different options exist, such methods are less mature than the QR algorithm. The simulation results discussed in this paper recommend that, among the available options, the most promising for power systems are the parallel versions of the Krylov-Schur method by SLEPc and CI-RR method by z-PARES. In particular, SLEPc’s Krylov–Schur provides the best accuracy, while z-PARES’s CI-RR was the only one that was able to tackle the 146,166 × 146,166 GEP of the European Network of Transmission System Operators for Electricity (ENTSO-E).
Author Contributions
Formal analysis, G.T., I.D., M.L. and F.M.; Methodology, G.T., I.D., M.L. and F.M.; Writing—original draft, G.T., I.D., M.L. and F.M. The authors claim to have contributed equally and significantly in this paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by: Science Foundation Ireland (Grant No. SFI/15/IA/3074), by funding Georgios Tzounas, Ioannis Dassios, Muyang Liu, and Federico Milano; Georgios Tzounas and Federico Milano are also supported by European Union’s Horizon 2020 research and innovation programme (Grant No. 883710).
Conflicts of Interest
The authors declare no conflict of interest.
Notation
| vector | |
| matrix | |
| matrix conjugate transpose (Hermitian) | |
| complex numbers | |
| Hessenberg matrix | |
| identity matrix of dimensions | |
| j | unit imaginary number |
| Hankel matrix | |
| upper triangular matrix of QR decomposition | |
| real numbers | |
| s | complex Laplace variable |
| upper triangular matrix of Schur decomposition | |
| right eigenvector | |
| left eigenvector | |
| vector of state variables | |
| vector of algebraic variables | |
| z | spectral transform |
| center of circular contour in the complex plane | |
| eigenvalue | |
| moment associated to matrix pencil | |
| spectral anti-shift | |
| radius of circular contour in the complex plane | |
| spectral shift | |
| contour integrals associated to matrix pencil | |
| zero matrix of dimensions |
Appendix A
The Rayleigh-Ritz procedure is a numerical technique used by many solvers to extract eigenvalue approximations from an associated to these eigenvalues subspace. The eigenvalues are extracted by projecting the matrix pencil onto the constructed subspace. In particular, given a subspace associated to p eigenvalues of , the Rayleigh-Ritz procedure for the LEP consists of the following steps:
- Construct an orthonormal basis , , which represents the subspace associated to p eigenvalues.
- Compute . Matrix is the projection of onto the subspace .
- Compute the eigenvalues and eigenvectors , of . The eigenvalues are called Ritz values and are also eigenvalues of .
- Form the vector , for . Each vector is called Ritz vector and corresponds to the eigenvalue .
In case that a GEP is to be solved, then the Rayleigh-Ritz procedure consists in finding the p eigenvalues of . Then, steps 2 and 3 have to be modified as follows:
- 2.
- Compute and .
- 3.
- Compute the eigenvalues and eigenvectors , of . The p eigenvalues found are called Ritz values and are also eigenvalues of .
References
- Sauer, P.W.; Pai, M.A. Power System Dynamics and Stability; Prentice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Milano, F. Power System Modelling and Scripting; Springer: New York, NY, USA, 2010. [Google Scholar]
- Gibbard, M.; Pourbeik, P.; Vowles, D. Small-Signal Stability, Control and Dynamic Performance of Power Systems; University of Adelaide Press: Adelaide, Australia, 2015. [Google Scholar]
- Chow, J.H.; Cullum, J.; Willoughby, R.A. A Sparsity-Based Technique for Identifying Slow-Coherent Areas in Large Power Systems. IEEE Trans. Power Appar. Syst. 1984, PAS-103, 463–473. [Google Scholar] [CrossRef]
- Gao, B.; Morison, G.K.; Kundur, P. Voltage Stability Evaluation Using Modal Analysis. IEEE Trans. Power Syst. 1992, 7, 1529–1542. [Google Scholar] [CrossRef]
- Saad, Y. Numerical Methods for Large Eigenvalue Problems—Revised Edition; SIAM: Philadelphia, PA, USA, 2011. [Google Scholar]
- Kressner, D. Numerical Methods for General and Structured Eigenvalue Problems, 4th ed.; Springer: New York, NY, USA, 2015. [Google Scholar]
- Davidson, E.R. The iterative calculation of a few of the lowest eigenvalues and corresponding eigenvectors of large real-symmetric matrices. J. Comput. Phys. 1975, 17, 87–94. [Google Scholar] [CrossRef]
- Sorensen, D.C. Implicit Application of Polynomial Filters in a k-Step Arnoldi Method. SIAM J. Matrix Anal. Appl. 1992, 13, 357–385. [Google Scholar] [CrossRef]
- Knyazev, A.V. Toward the Optimal Preconditioned Eigensolver: Locally Optimal Block Preconditioned Conjugate Gradient Method. SIAM J. Sci. Comput. 2001, 23, 517–541. [Google Scholar] [CrossRef]
- von Mises, R.; Pollaczek-Geiringer, H. Praktische Verfahren der Gleichungsauflösung. Z. Angew. Math. Mech. 1929, 9, 152–164. [Google Scholar] [CrossRef]
- Bathe, K.J.; Wilson, E.L. Solution Methods for Large Generalized Eigenvalue Problems in Structural Engineering. Int. J. Numer. Methods Eng. 1973, 6, 213–226. [Google Scholar] [CrossRef]
- Martins, N. Efficient eigenvalue and frequency response methods applied to power System small-signal Stability Studies. IEEE Trans. Power Syst. 1986, 1, 217–224. [Google Scholar] [CrossRef]
- Martins, N.; Lima, L.T.G.; Pinto, H.J.C.P. Computing dominant poles of power system transfer functions. IEEE Trans. Power Syst. 1996, 11, 162–170. [Google Scholar] [CrossRef]
- Martins, N. The dominant pole spectrum eigensolver [for power system stability analysis]. IEEE Trans. Power Syst. 1997, 12, 245–254. [Google Scholar] [CrossRef]
- Rommes, J.; Martins, N. Efficient computation of transfer function dominant poles using subspace acceleration. IEEE Trans. Power Syst. 2006, 21, 1218–1226. [Google Scholar] [CrossRef]
- Gomes, S., Jr.; Martins, N.; Portela, C. Sequential Computation of Transfer Function Dominant Poles of s-Domain System Models. IEEE Trans. Power Syst. 2009, 24, 776–784. [Google Scholar]
- Rommes, J.; Martins, N.; Freitas, F.D. Computing Rightmost Eigenvalues for Small-Signal Stability Assessment of Large-Scale Power Systems. IEEE Trans. Power Syst. 2010, 25, 929–938. [Google Scholar] [CrossRef]
- Wang, L.; Semlyen, A. Application of sparse eigenvalue techniques to the small signal stability analysis of large power systems. IEEE Trans. Power Syst. 1990, 5, 635–642. [Google Scholar] [CrossRef]
- Campagnolo, J.M.; Martins, N.; Falcao, D.M. Refactored bi-iteration: A high performance eigensolution method for large power system matrices. IEEE Trans. Power Syst. 1996, 11, 1228–1235. [Google Scholar] [CrossRef]
- Francis, J.G.F. The QR transformation A unitary analogue to the LR transformation—Part 1. Comput. J. 1961, 4, 265–271. [Google Scholar] [CrossRef]
- Moler, C.B.; Stewart, G.W. An algorithm for generalized matrix eigenvalue problems. SIAM J. Numer. Anal. 1973, 10, 241–256. [Google Scholar] [CrossRef]
- Kundur, P.; Rogers, G.J.; Wong, D.Y.; Wang, L.; Lauby, M.G. A comprehensive computer program package for small signal stability analysis of power systems. IEEE Trans. Power Syst. 1990, 5, 1076–1083. [Google Scholar] [CrossRef]
- Milano, F.; Dassios, I. Primal and Dual Generalized Eigenvalue Problems for Power Systems Small-Signal Stability Analysis. IEEE Trans. Power Syst. 2017, 32, 4626–4635. [Google Scholar] [CrossRef]
- Arnoldi, W.E. The principle of minimized iterations in the solution of the matrix eigenvalue problem. Q. Appl. Math. 1951, 9, 17–29. [Google Scholar] [CrossRef]
- Lehoucq, R.B.; Sorensen, D.C. Deflation Techniques for an Implicitly Restarted Arnoldi Iteration. SIAM J. Matrix Anal. Appl. 1996, 17, 789–821. [Google Scholar] [CrossRef]
- Stewart, G.W. A Krylov–Schur Algorithm for Large Eigenproblems. SIAM J. Matrix Anal. Appl. 2002, 23, 601–614. [Google Scholar] [CrossRef]
- Chung, C.Y.; Dai, B. A Combined TSA-SPA Algorithm for Computing Most Sensitive Eigenvalues in Large-Scale Power Systems. IEEE Trans. Power Syst. 2013, 28, 149–157. [Google Scholar] [CrossRef]
- Liu, C.; Li, X.; Tian, P.; Wang, M. An improved IRA algorithm and its application in critical eigenvalues searching for low frequency oscillation analysis. IEEE Trans. Power Syst. 2017, 32, 2974–2983. [Google Scholar] [CrossRef]
- Li, Y.; Geng, G.; Jiang, Q. An efficient parallel Krylov-Schur method for eigen-analysis of large-scale power Systems. IEEE Trans. Power Syst. 2016, 31, 920–930. [Google Scholar] [CrossRef]
- Du, Z.; Liu, W.; Fang, W. Calculation of Rightmost Eigenvalues in Power Systems Using the Jacobi–Davidson Method. IEEE Trans. Power Syst. 2006, 21, 234–239. [Google Scholar] [CrossRef]
- Du, Z.; Li, C.; Cui, Y. Computing Critical Eigenvalues of Power Systems Using Inexact Two-Sided Jacobi-Davidson. IEEE Trans. Power Syst. 2011, 26, 2015–2022. [Google Scholar] [CrossRef]
- Sakurai, T.; Sugiura, H. A projection method for generalized eigenvalue problems using numerical integration. J. Comput. Appl. Math. 2003, 159, 119–128. [Google Scholar] [CrossRef]
- Sakurai, T.; Tadano, H. CIRR: A Rayleigh-Ritz type method with contour integral for generalized eigenvalue problems. Hokkaido Math. J. 2007, 36, 745–757. [Google Scholar] [CrossRef]
- Polizzi, E. Density-matrix-based algorithm for solving eigenvalue problems. Phys. Rev. B Am. Phys. Soc. 2009, 79, 115112. [Google Scholar] [CrossRef]
- Li, Y.; Geng, G.; Jiang, Q. A Parallel Contour Integral Method for Eigenvalue Analysis of Power Systems. IEEE Trans. Power Syst. 2017, 32, 624–632. [Google Scholar] [CrossRef]
- Li, Y.; Geng, G.; Jiang, Q. A parallelized contour integral Rayleigh–Ritz method for computing critical eigenvalues of large-scale power systems. IEEE Trans. Smart Grid 2018, 9, 3573–3581. [Google Scholar] [CrossRef]
- Angerson, E.; Bai, Z.; Dongarra, J.; Greenbaum, A.; McKenney, A.; Croz, J.D.; Hammarling, S.; Demmel, J.; Bischof, C.; Sorensen, D. LAPACK: A portable linear algebra library for high-performance computers. In Proceedings of the 1990 ACM/IEEE Conference on Supercomputing, New York, NY, USA, 12–16 November 1990. [Google Scholar]
- Tomov, S.; Dongarra, J.; Baboulin, M. Towards dense linear algebra for hybrid GPU accelerated manycore systems. Parallel Comput. 2010, 36, 232–240. [Google Scholar] [CrossRef]
- Lehoucq, R.B.; Sorensen, D.C.; Yang, C. ARPACK Users Guide: Solution of Large Scale Eigenvalue Problems by Implicitly Restarted Arnoldi Methods; SIAM: Philadelphia, PA, USA, 1997. [Google Scholar]
- Baker, C.; Hetmaniuk, U.; Lehoucq, R.; Thornquist, H. Anasazi software for the numerical solution of large-scale eigenvalue problems. ACM Trans. Math. Softw. 2009, 36, 351–362. [Google Scholar] [CrossRef]
- Hernandez, V.; Roman, J.E.; Vidal, V. SLEPc: A scalable and flexible toolkit for the solution of eigenvalue problems. ACM Trans. Math. Softw. 2005, 31, 351–362. [Google Scholar] [CrossRef]
- Polizzi, E. FEAST Eigenvalue Solver v4.0 User Guide. arXiv 2020, arXiv:2002.04807. [Google Scholar]
- Futamura, Y.; Sakurai, T. z-Pares Users’ Guide Release 0.9.5; University of Tsukuba: Tsukuba, Japan, 2014. [Google Scholar]
- Milano, F. Semi-implicit formulation of differential-algebraic equations for transient stability analysis. IEEE Trans. Power Syst. 2016, 31, 4534–4543. [Google Scholar] [CrossRef]
- Gantmacher, R. The Theory of Matrices I, II; Chelsea: New York, NY, USA, 1959. [Google Scholar]
- Dassios, I.; Tzounas, G.; Milano, F. The Möbius transform effect in singular systems of differential equations. Appl. Math. Comput. 2019, 361, 338–353. [Google Scholar] [CrossRef]
- Uchida, N.; Nagao, T. A new eigen-analysis method of steady-state stability studies for large power systems: S matrix method. IEEE Trans. Power Syst. 1988, 3, 706–714. [Google Scholar] [CrossRef]
- Lima, L.T.G.; Bezerra, L.H.; Tomei, C.; Martins, N. New methods for fast small-signal stability assessment of large scale power systems. IEEE Trans. Power Syst. 1995, 10, 1979–1985. [Google Scholar] [CrossRef]
- Parlett, B.N.; Poole, W.G. A geometric theory for QR, LU and power iteration. SIAM J. Numer. Anal. 1973, 10, 389–412. [Google Scholar] [CrossRef]
- Householder, A.S. Unitary triangularization of a nonsymmetric Matrix. J. ACM 1958, 5, 339–342. [Google Scholar] [CrossRef]
- Golub, G.H.; Loan, C.F.V. Matrix Computations, Fourth Edition; The Johns Hopkins University Press: Baltimore, MD, USA, 2013. [Google Scholar]
- Wu, K.; Simon, H. Thick-Restart Lanczos Method for Large Symmetric Eigenvalue Problems. SIAM J. Matrix Anal. Appl. 2000, 22, 602–616. [Google Scholar] [CrossRef]
- Asakura, J.; Sakurai, T.; Tadano, H.; Ikegami, T.; Kimura, K. A numerical method for nonlinear eigenvalue problems using contour integrals. JSIAM Lett. 2009, 1, 52–55. [Google Scholar] [CrossRef]
- Tang, P.T.P.; Polizzi, E. FEAST As A Subspace Iteration Eigensolver Accelerated By Approximate Spectral Projection. SIAM J. Matrix Anal. Appl. 2014, 35, 354–390. [Google Scholar] [CrossRef]
- Lawson, C.L.; Hanson, R.J.; Kincaid, D.R.; Krogh, F.T. Basic Linear Algebra Subprograms for FORTRAN Usage; Technical Report; University of Texas at Austin: Austin, TX, USA, 1977. [Google Scholar]
- Clint Whaley, R.; Petitet, A.; Dongarra, J.J. Automated empirical optimizations of software and the ATLAS project. Parallel Comput. 2001, 27, 3–35. [Google Scholar] [CrossRef]
- Blackford, L.S.; Choi, J.; Cleary, A.; D’Azevedo, E.; Demmel, J.; Dhillon, I.; Dongarra, J.; Hammarling, S.; Henry, G.; Petitet, A.; et al. ScaLAPACK Users’ Guide; SIAM: Philadelphia, PA, USA, 1997. [Google Scholar]
- Garbow, B.S. EISPACK—A package of matrix eigensystem routines. Comput. Phys. Commun. 1974, 7, 179–184. [Google Scholar] [CrossRef]
- Anderson, E.; Bai, Z.; Bischof, C.; Blackford, L.S.; Demmel, J.; Dongarra, J.J.; Du Croz, J.; Hammarling, S.; Greenbaum, A.; McKenney, A.; et al. LAPACK Users’ Guide, 3rd ed.; SIAM: Philadelphia, PA, USA, 1999. [Google Scholar]
- Davis, T.A. Direct Methods for Sparse Linear Systems; SIAM: Philadelphia, PA, USA, 2006. [Google Scholar]
- Snir, M.; Otto, S.; Huss-Lederman, S.; Walker, D.; Dongarra, J. MPI—The Complete Reference, Volume 1: The MPI Core; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Amestoy, P.; Duff, I.S.; Koster, J.; L’Excellent, J.Y. A fully asynchronous multifrontal solver using distributed dynamic scheduling. SIAM J. Matrix Anal. Appl. 2001, 23, 15–41. [Google Scholar] [CrossRef]
- Argonne National Laboratory. PETSc Users Manual; Argonne National Laboratory: Lemont, IL, USA, 2020. [Google Scholar]
- Schenk, O.; Gartner, K. Solving Unsymmetric Sparse Systems of Linear Equations with PARDISO. J. Future Gener. Comput. Syst. 2004, 20, 475–487. [Google Scholar] [CrossRef]
- Pérez-Arriaga, I.J.; Verghese, G.C.; Schweppe, F.C. Selective Modal Analysis with Applications to Electric Power Systems, PART I: Heuristic Introduction. IEEE Trans. Power Appar. Syst. 1982, PAS-101, 3117–3125. [Google Scholar]
- Tzounas, G.; Dassios, I.; Milano, F. Modal Participation Factors of Algebraic Variables. IEEE Trans. Power Syst. 2020, 35, 742–750. [Google Scholar] [CrossRef]
- Dassios, I.; Tzounas, G.; Milano, F. Participation Factors for Singular Systems of Differential Equations. Circuits Syst. Signal Process. 2020, 39, 83–110. [Google Scholar] [CrossRef]
- Semlyen, A.; Wang, L. Sequential computation of the complete eigensystem for the study zone in small signal stability analysis of large power systems. IEEE Trans. Power Syst. 1988, 3, 715–725. [Google Scholar] [CrossRef]
- Milano, F. A Python-based software tool for power system analysis. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013. [Google Scholar]
- Murad, M.A.A.; Tzounas, G.; Liu, M.; Milano, F. Frequency control through voltage regulation of power system using SVC devices. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019. [Google Scholar]
- Byerly, R.T.; Bennon, R.J.; Sherman, D.E. Eigenvalue Analysis of Synchronizing Power Flow Oscillations in Large Electric Power Systems. IEEE Trans. Power Appar. Syst. 1982, PAS-101, 235–243. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).