An Optimization Model for Operational Planning and Turnaround Maintenance Scheduling of Oil and Gas Supply Chain
Abstract
1. Introduction
2. Materials and Methods
2.1. Problem Statement
2.2. Mathematical Model
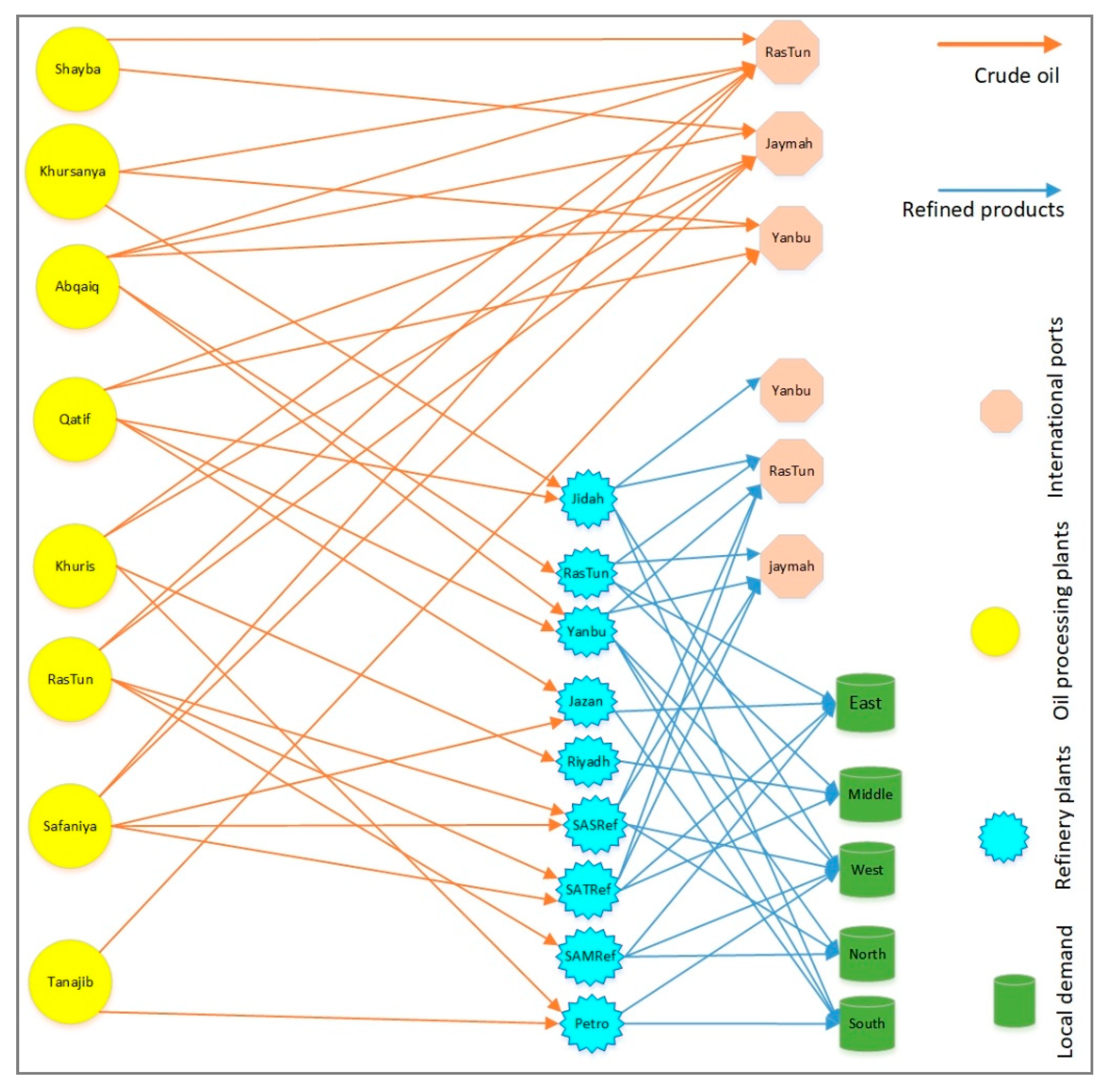
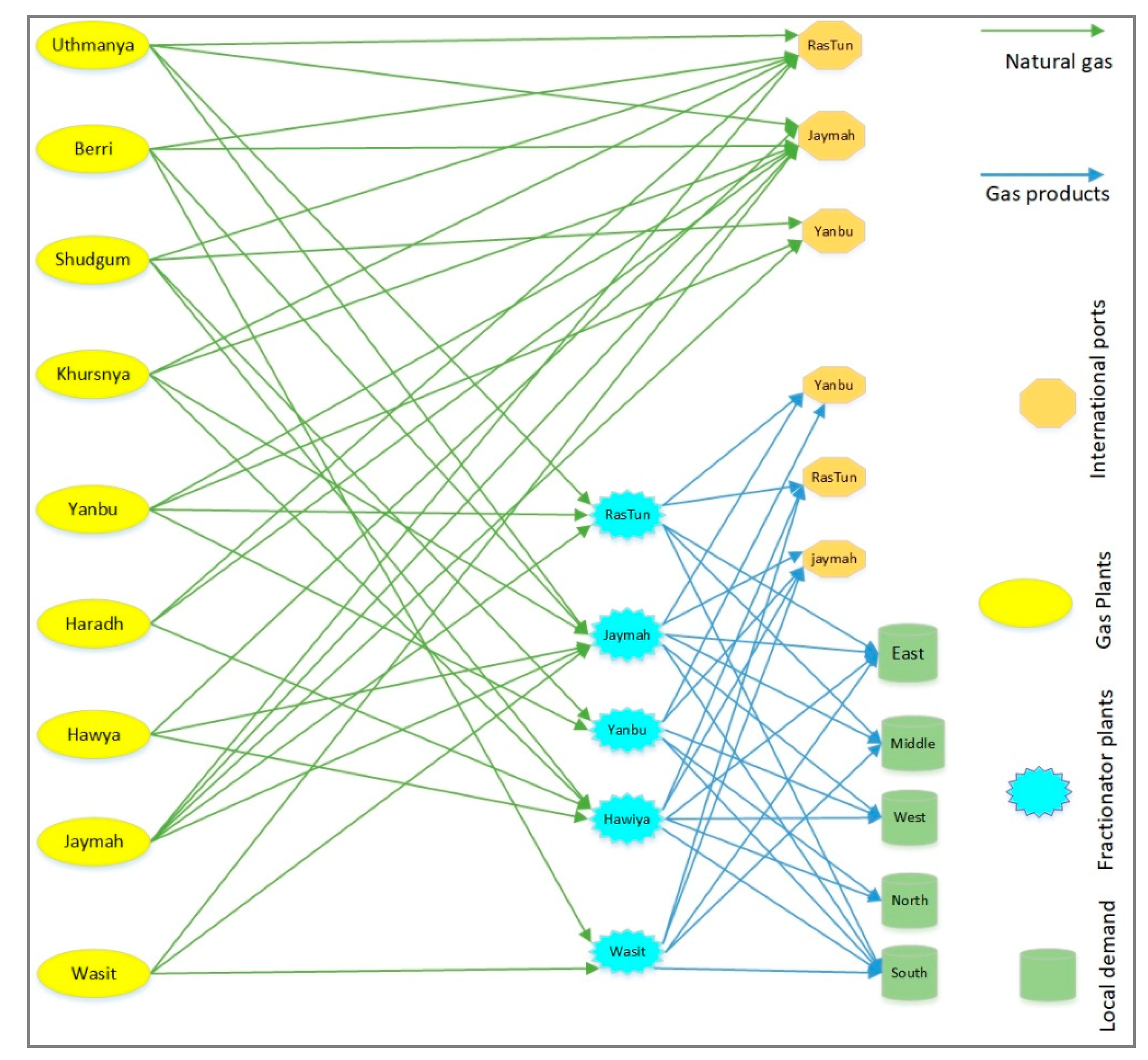
2.3. Case Study
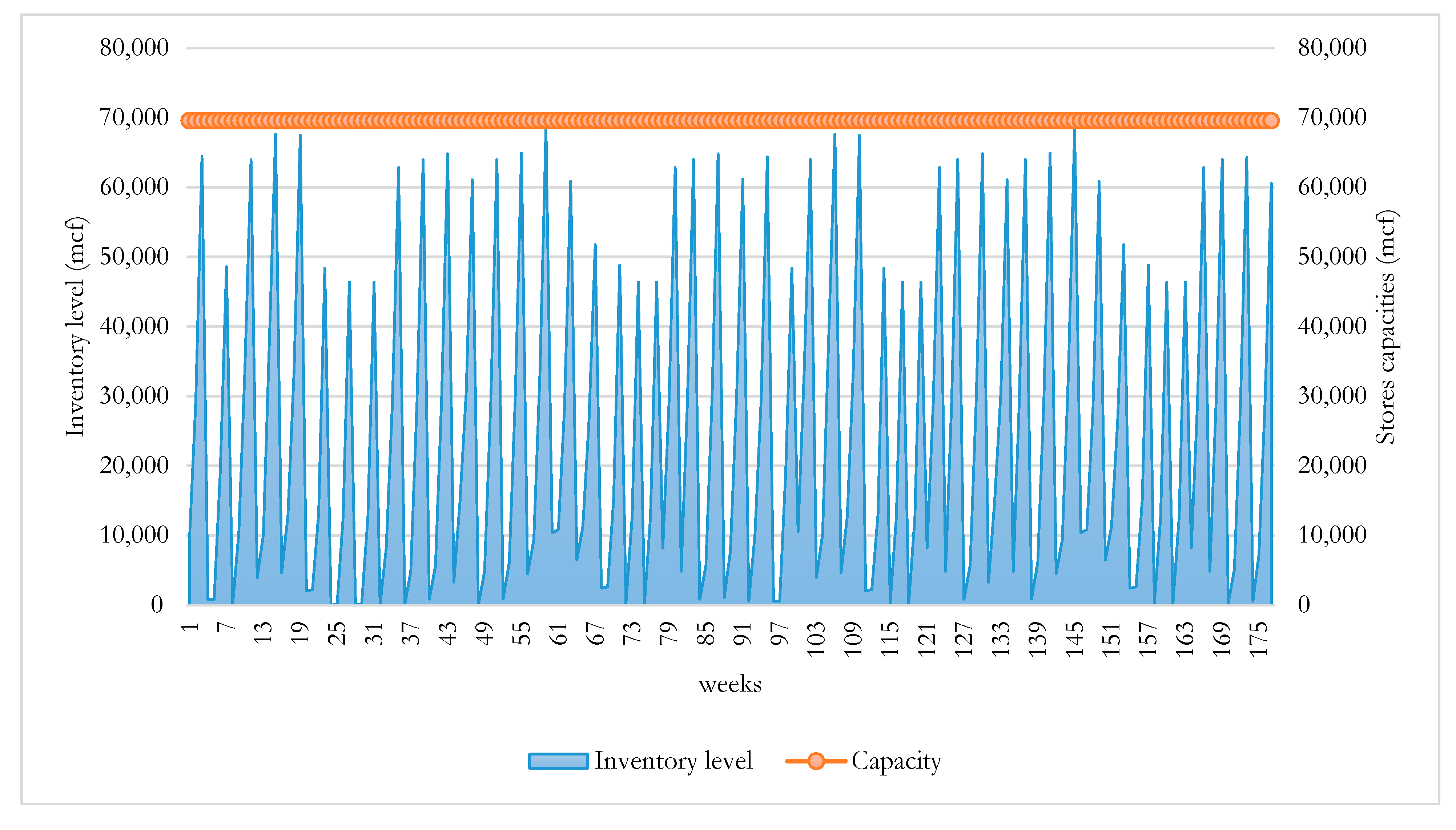
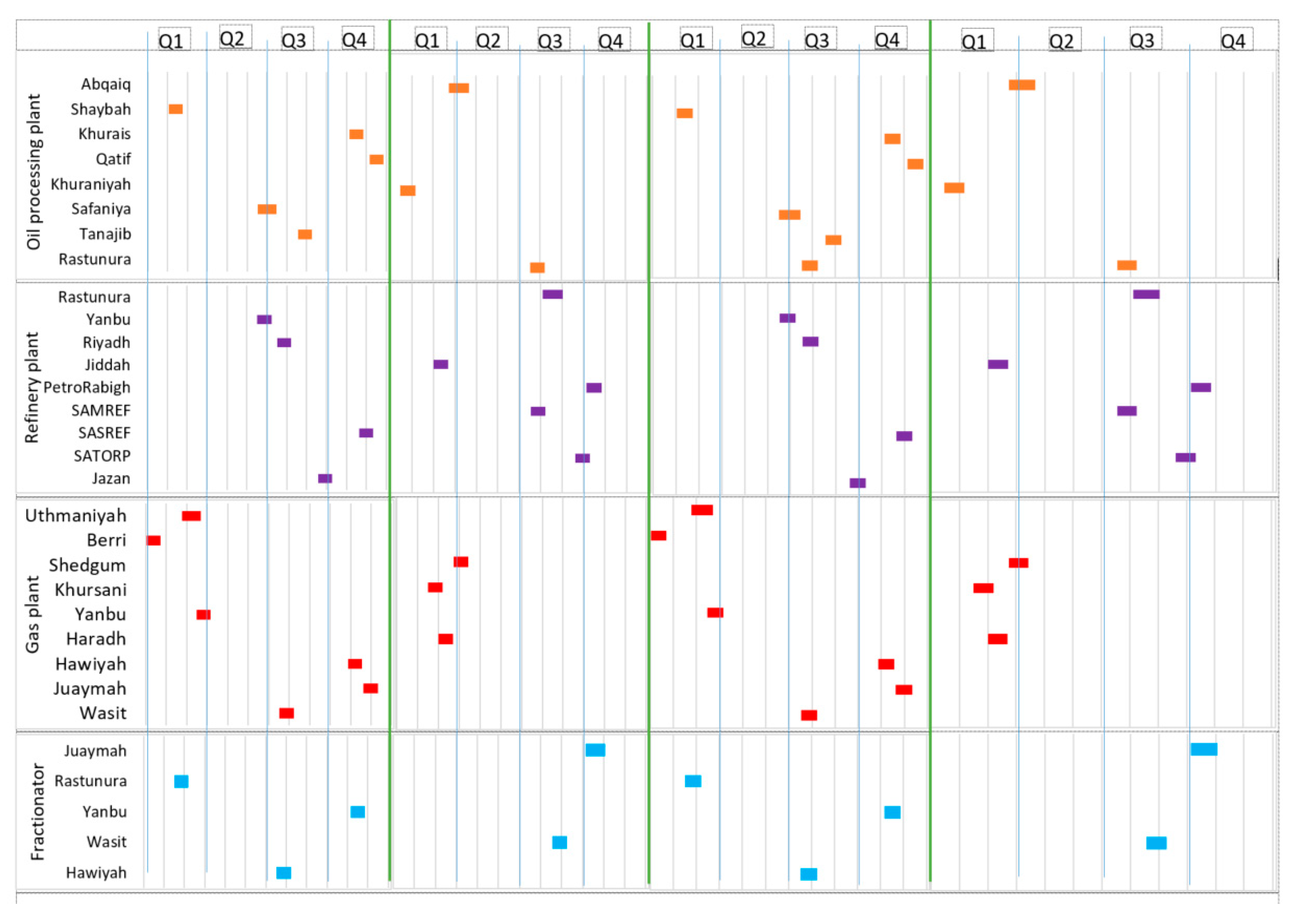
3. Results
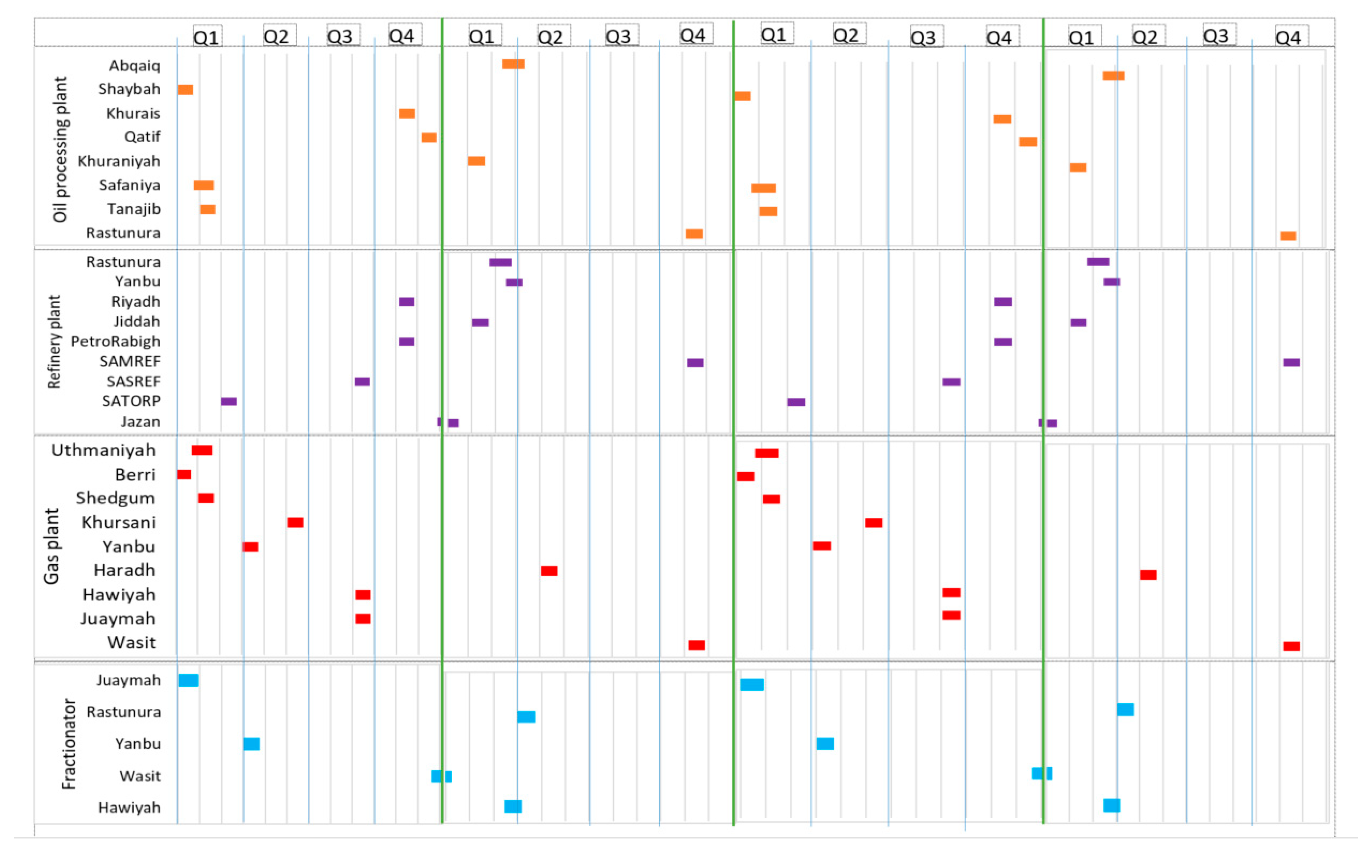
- It was observed that the proposed model distributes maintenance activities uniformly and perfectly among the HCSC plants along the time horizon of four years.
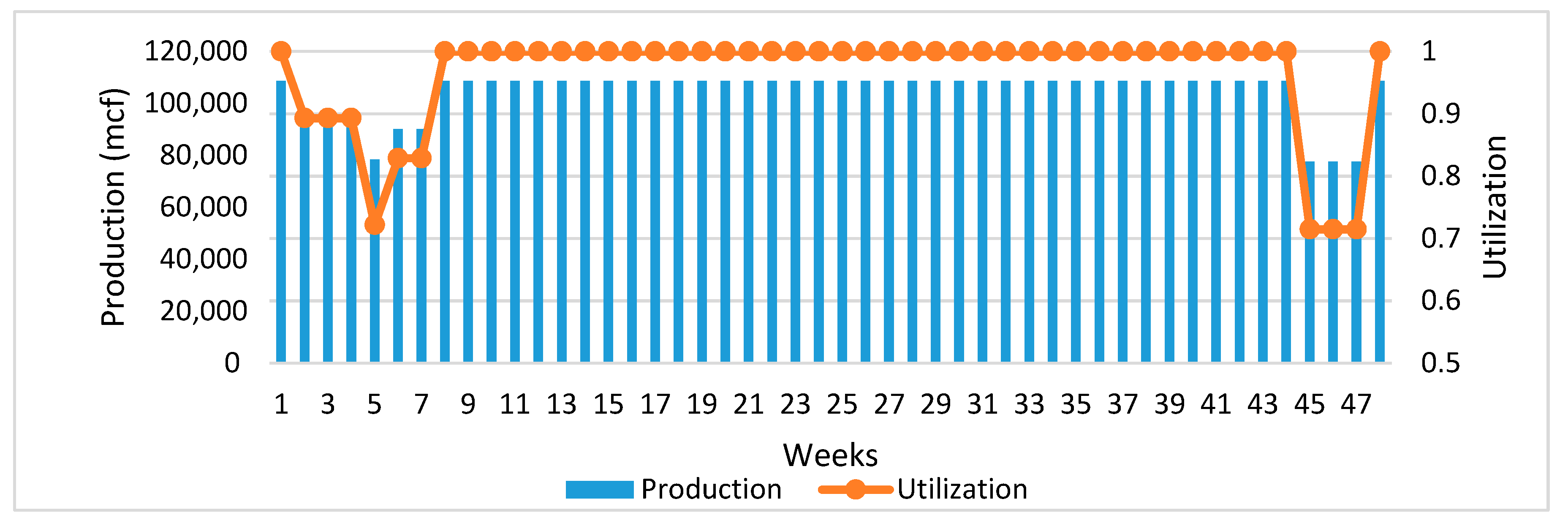
- In addition, it is shown that the model minimizes the amount of lost sales by forcing most of HCSC units to be maintained during the months of low demand. Almost all HCSC units are taken for maintenance during the quarters of low demand (quarters 1, 2, and 4). The third quarter is the summer period, which represents the months of high demand.
- The HCSC is a complex network that involves multi-connections where each plant belongs to the upstream is connected to more than one downstream plant and even to more than one demand node. Similarly, each plant has tanks with enough capacity to feed the associated downstream plants during the maintenance period. This situation provides flexibility for choosing maintenance timing. Therefore, the majority of HCSC plants were taken for maintenance randomly at different times.
- Few connected plants have been taken for maintenance at the same time. For instance, Abqaiq oil processing plant and RasTunura refinery plant are maintained simultaneously. Similarly, both the Tanajib oil processing plants and PetroRabigh refinery plant are maintained at the same time.
- For natural gas plants, maintenance tasks are decoupled; almost all connected upstream and downstream plants are maintained randomly because each downstream plant has connections with more than one upstream unit, and the storage capacity is enough during the maintenance time. In the sensitivity analysis section, the impact of upstream storage capacities on maintenance schedule and arrangement will be investigated.
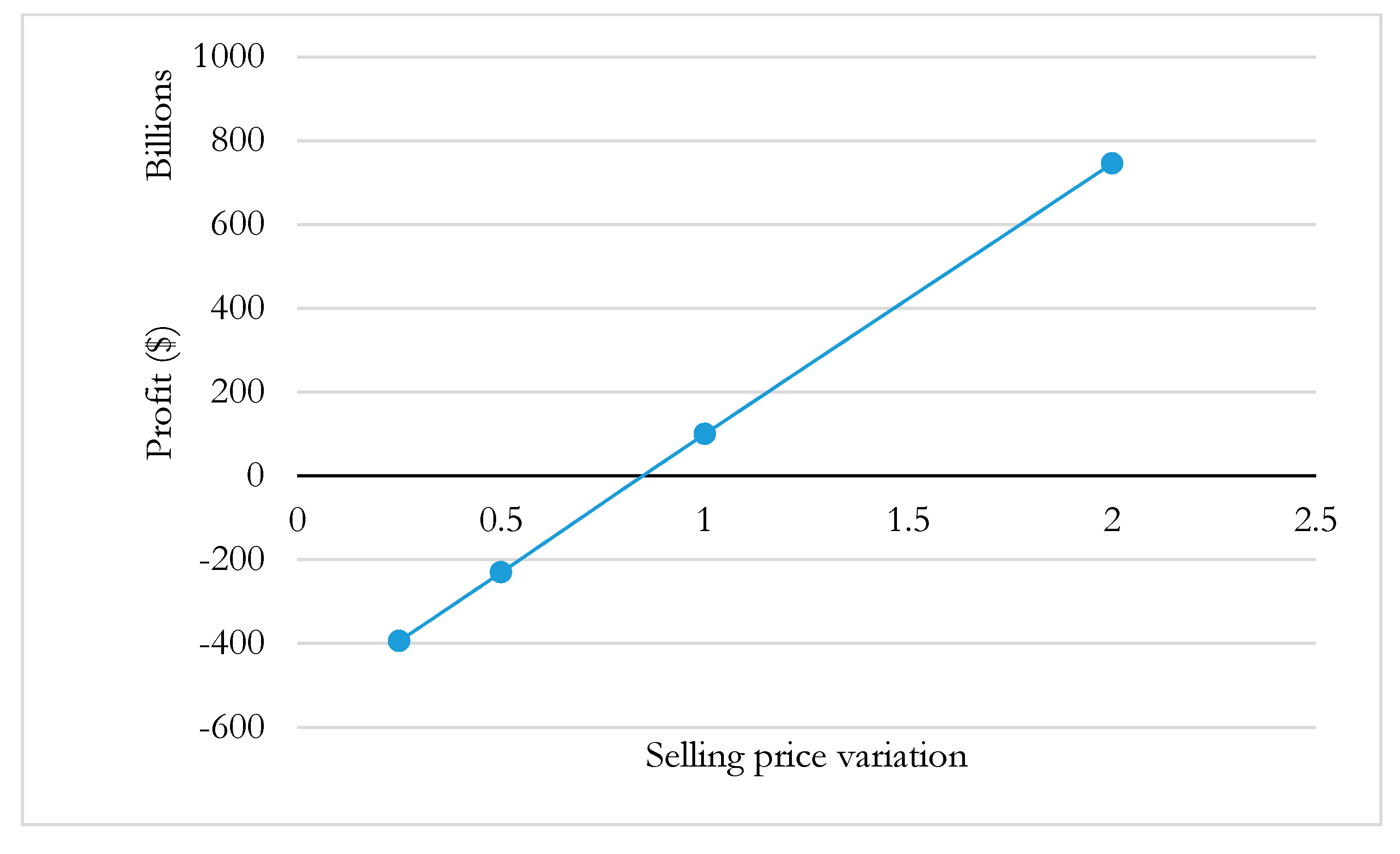
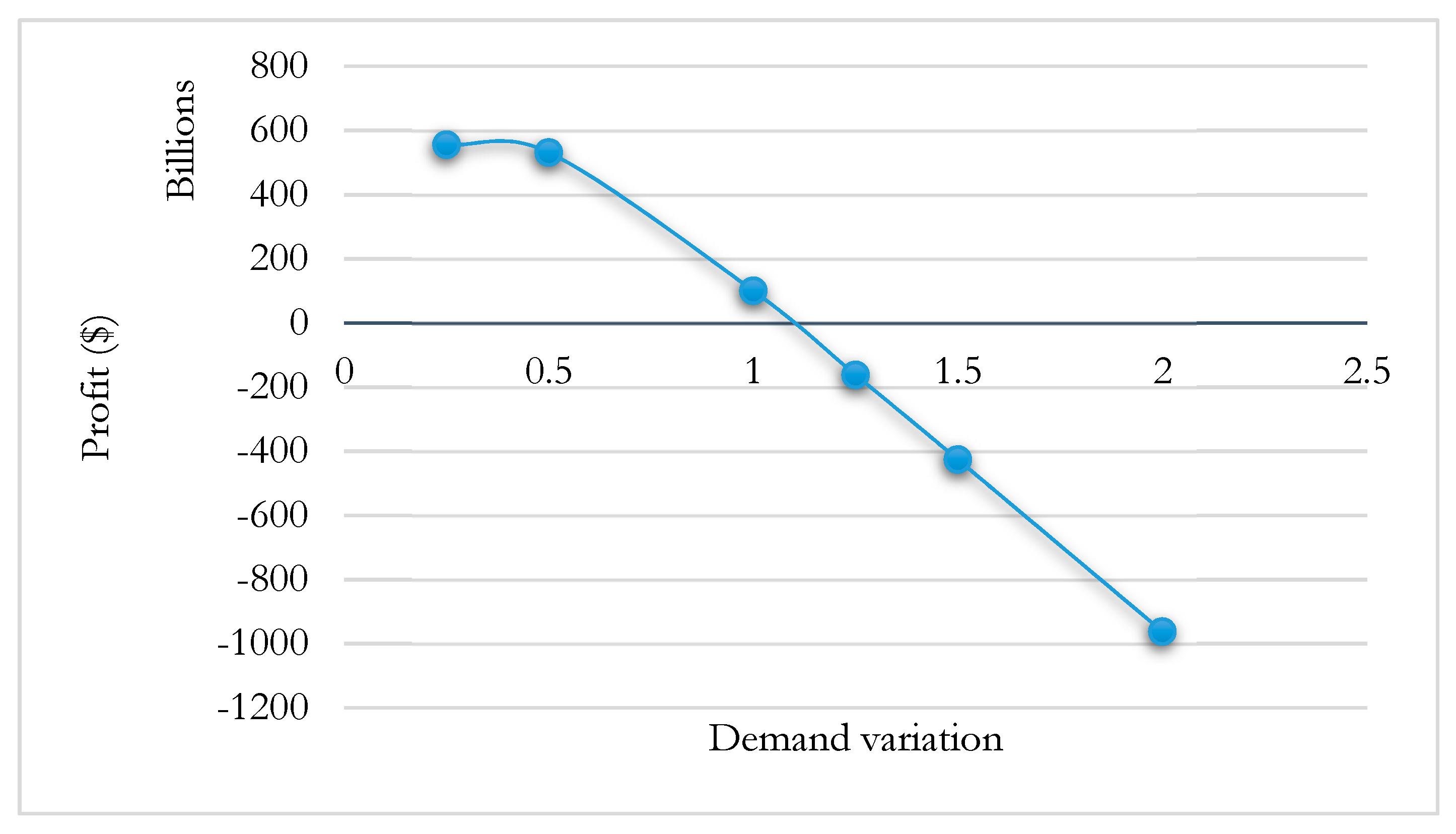
Sensitivity Analysis
- The maintenance activities were distributed uniformly and perfectly among HCSC plants and over the study period.
- The majority of petroleum plants are taken for maintenance during the quarters of low demands.
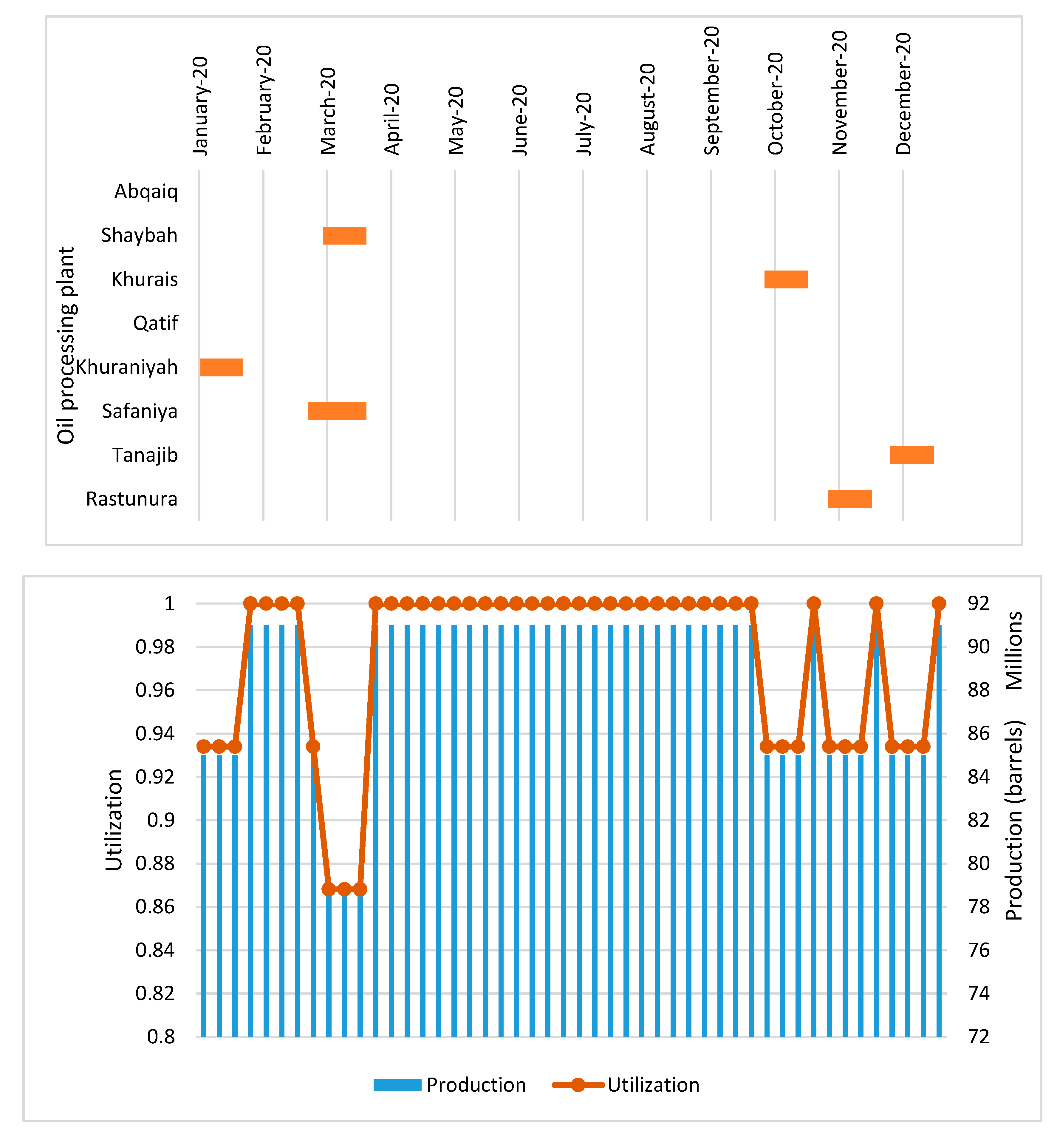
- Due to the reducing storage capacities of upstream plants, most of the connected plants have been taken for maintenance at the same time because the storage capacity of the upstream units is not sufficient to feed downstream units. For instance, the Jiddah refinery plant and Khurasaniya oil processing plant have been maintained in the same period. Similarly, both Riyadh and PetroRabigh refinery plants are maintained with Khurais oil processing plant.
- Likewise, RasTunura and Yanbu refinery plants were maintained exchangeably; Rastunura is maintained during the first two weeks of the Abqaiq oil processing plant’s maintenance time, and then Yanbu is maintained during the last two weeks of the Abqaiq oil processing plant’s maintenance period because during the first two weeks of maintaining the Abqaiq plant, inventory capacity is sufficient to feed only RasTunura refinery plant and vice versa for Yanbu refinery plant.
- For natural gas petroleum plants, Jaymah fractionation plant is recommended to be maintained with Uthmaniya and Berri gas plants. Similarly, the Yanbu fractionation plant and Yanbu gas plants are maintained at the same time.
4. Discussion
Funding
Acknowledgments
Conflicts of Interest
References
- Ghaithan, A.M.; Attia, A.; Duffuaa, S.O. Multi-objective optimization model for a downstream oil and gas supply chain. Appl. Math. Model. 2017, 52, 689–708. [Google Scholar] [CrossRef]
- Alkhamis, T.M.; Yellen, J. Refinery units maintenance scheduling using integer programming. Appl. Math. Model. 1995, 19, 543–549. [Google Scholar] [CrossRef]
- Mendez, C.A.; Grossmann, I.E.; Harjunkoski, I.; Kaboré, P. A simultaneous optimization approach for off-line blending and scheduling of oil-refinery operations. Comput. Chem. Eng. 2006, 30, 614–634. [Google Scholar] [CrossRef]
- Göthe-Lundgren, M.; Lundgren, J.T.; Persson, J.A. An optimization model for refinery production scheduling. Int. J. Prod. Econ. 2002, 78, 255–270. [Google Scholar] [CrossRef]
- Antomarioni, S.; Bevilacqua, M.; Potena, D.; Diamantini, C. Defining a data-driven maintenance policy: An application to an oil refinery plant. Int. J. Qual. Reliab. Manag. 2019. [Google Scholar] [CrossRef]
- Bertolini, M.; Bevilacqua, M.; Ciarapica, F.E.; Giacchetta, G. Development of risk-based inspection and maintenance procedures for an oil refinery. J. Loss Prev. Process Ind. 2009, 22, 244–253. [Google Scholar] [CrossRef]
- Aissani, N.; Beldjilali, B.; Trentesaux, D. Dynamic scheduling of maintenance tasks in the petroleum industry: A reinforcement approach. Eng. Appl. Artif. Intell. 2009, 22, 1089–1103. [Google Scholar] [CrossRef]
- Amaran, S.; Sahinidis, N.V.; Sharda, B.; Morrison, M.; Bury, S.J.; Miller, S.; Wassick, J.M. Long-term turnaround planning for integrated chemical sites. Comput. Chem. Eng. 2015, 72, 145–158. [Google Scholar] [CrossRef]
- Awad, M.; Ertem, M. Stochastic scheduling of workforce-constrained preventive maintenance activities in petroleum plants. In Proceedings of the 2017 Annual Reliability and Maintainability Symposium (RAMS), Orlando, FL, USA, 23–26 January 2017; pp. 1–5. [Google Scholar]
- Xu, J.; Qu, H.; Wang, S.; Xu, Q. A new proactive scheduling methodology for front-end crude oil and refinery operations under uncertainty of shipping delay. Ind. Eng. Chem. Res. 2017, 56, 8041–8053. [Google Scholar] [CrossRef]
- Qu, H.; Wang, S.; Xu, Q. Integrated Proactive and Reactive Scheduling for Refinery Front-end Crude Movement with Consideration of Unit Maintenance. Ind. Eng. Chem. Res. 2019, 58, 12192–12206. [Google Scholar] [CrossRef]
- Rosenblatt, M.J.; Lee, H.L. Economic production cycles with imperfect production processes. IIE Trans. 1986, 18, 48–55. [Google Scholar] [CrossRef]
- Joshi, S.; Gupta, R. Scheduling of routine maintenance using production schedules and equipment failure history. Comput. Ind. Eng. 1986, 10, 11–20. [Google Scholar] [CrossRef]
- Pintelon, L. Performance reporting and decision tools for maintenance management. Ph.D. Thesis, Department of Industrial Management, Catholic University of Leuven, Leuven, Belgium, 1990. (Unpublished). [Google Scholar]
- Ashayeri, J.; Teelen, A.; Selenj, W. A production and maintenance planning model for the process industry. Int. J. Prod. Res. 1996, 34, 3311–3326. [Google Scholar] [CrossRef]
- Rahim, M.A.; Ben-Daya, M. Integrated Models in Production Planning, Inventory, Quality, and Maintenance; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Iravani, S.M.; Duenyas, I. Integrated maintenance and production control of a deteriorating production system. IIE Trans. 2002, 34, 423–435. [Google Scholar] [CrossRef]
- Cassady, C.R.; Kutanoglu, E. Integrating preventive maintenance planning and production scheduling for a single machine. IEEE Trans. Reliab. 2005, 54, 304–309. [Google Scholar] [CrossRef]
- Cassady, C.R.; Kutanoglu, E. Minimizing job tardiness using integrated preventive maintenance planning and production scheduling. IIE Trans. 2003, 35, 503–513. [Google Scholar] [CrossRef]
- Darwish, M.A.; Ben-Daya, M. Effect of inspection errors and preventive maintenance on a two-stage production inventory system. Int. J. Prod. Econ. 2007, 107, 301–313. [Google Scholar] [CrossRef]
- Aghezzaf, E.H.; Jamali, M.A.; Ait-Kadi, D. An integrated production and preventive maintenance planning model. Eur. J. Oper. Res. 2007, 181, 679–685. [Google Scholar] [CrossRef]
- Aghezzaf, E.-H.; Najid, N.M. Integrated production planning and preventive maintenance in deteriorating production systems. Inf. Sci. 2008, 178, 3382–3392. [Google Scholar] [CrossRef]
- Zied, H.; Sofiene, D.; Nidhal, R. An optimal production/maintenance planning under stochastic random demand, service level and failure rate. In Proceedings of the 2009 IEEE International Conference on Automation Science and Engineering, Bangalore, India, 22–25 August 2009; pp. 292–297. [Google Scholar]
- Berrichi, A.; Amodeo, L.; Yalaoui, F.; Châtelet, E.; Mezghiche, M. Bi-objective optimization algorithms for joint production and maintenance scheduling: Application to the parallel machine problem. J. Intell. Manuf. 2009, 20, 389. [Google Scholar] [CrossRef]
- Ayed, S.; Sofiene, D.; Nidhal, R. Joint optimisation of maintenance and production policies considering random demand and variable production rate. Int. J. Prod. Res. 2012, 50, 6870–6885. [Google Scholar] [CrossRef]
- Fitouhi, M.-C.; Nourelfath, M. Integrating noncyclical preventive maintenance scheduling and production planning for multi-state systems. Reliab. Eng. Syst. Saf. 2014, 121, 175–186. [Google Scholar] [CrossRef]
- Yalaoui, A.; Chaabi, K.; Yalaoui, F. Integrated production planning and preventive maintenance in deteriorating production systems. Inf. Sci. 2014, 278, 841–861. [Google Scholar] [CrossRef]
- Assid, M.; Gharbi, A.; Hajji, A. Joint production, setup and preventive maintenance policies of unreliable two-product manufacturing systems. Int. J. Prod. Res. 2015, 53, 4668–4683. [Google Scholar] [CrossRef]
- Khosrojerdi, A.; Zegordi, S.H.; Allen, J.K.; Mistree, F. A method for designing power supply chain networks accounting for failure scenarios and preventive maintenance. Eng. Optim. 2016, 48, 154–172. [Google Scholar] [CrossRef]
- Cheng, G.Q.; Zhou, B.H.; Li, L. Joint optimisation of production rate and preventive maintenance in machining systems. Int. J. Prod. Res. 2016, 54, 6378–6394. [Google Scholar] [CrossRef]
- Ettaye, G.; El Barkany, A.; El Khalfi, A. Integrating production and maintenance for a multi-lines system. Int. J. Perform. Eng. 2017, 13, 29. [Google Scholar] [CrossRef]
- Géhan, M.; Castanier, B.; Lemoine, D. Integration of maintenance in the tactical production planning process under feasibility constraint. In IFIP International Conference on Advances in Production Management Systems; Springer: Berlin/Heidelberg, Germany, 2014; pp. 467–474. [Google Scholar]
- Liu, Q.; Lv, W. Multi-component manufacturing system maintenance scheduling based on degradation information using genetic algorithm. Ind. Manag. Data Syst. 2015, 115, 1412–1434. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, L.; Zheng, Y. Integrating production planning and maintenance: An iterative method. Ind. Manag. Data Syst. 2014, 114, 162–182. [Google Scholar] [CrossRef]
- Hnaien, F.; Yalaoui, F.; Mhadhbi, A.; Nourelfath, M. A mixed-integer programming model for integrated production and maintenance. IFAC-Pap. 2016, 49, 556–561. [Google Scholar] [CrossRef]
- Askri, T.; Hajej, Z.; Rezg, N. Jointly production and correlated maintenance optimization for parallel leased machines. Appl. Sci. 2017, 7, 461. [Google Scholar] [CrossRef]
- Amiri, S.; Honarvar, M. Providing an integrated Model for Planning and Scheduling Energy Hubs and preventive maintenance. Energy 2018, 163, 1093–1114. [Google Scholar] [CrossRef]
- Khatab, A.; Diallo, C.; Aghezzaf, E.-H.; Venkatadri, U. Integrated production quality and condition-based maintenance optimisation for a stochastically deteriorating manufacturing system. Int. J. Prod. Res. 2019, 57, 2480–2497. [Google Scholar] [CrossRef]
- Rinaldi, G. An integrated Operation and Maintenance Framework for Offshore Renewable Energy. Ph.D. Thesis, University of Exeter, Exeter, UK, 2019. [Google Scholar]
- Martin, R.; Lazakis, I.; Barbouchi, S.; Johanning, L. Sensitivity analysis of offshore wind farm operation and maintenance cost and availability. Renew. Energy 2016, 85, 1226–1236. [Google Scholar] [CrossRef]
- Rinaldi, G.; Pillai, A.C.; Thies, P.R.; Johanning, L. Multi-objective optimization of the operation and maintenance assets of an offshore wind farm using genetic algorithms. Wind Eng. 2020, 44, 390–409. [Google Scholar] [CrossRef]
- Helsen, J.; Peeters, C.; Doro, P.; Ververs, E.; Jordaens, P.J. Wind farm operation and maintenance optimization using big data. In Proceedings of the 2017 IEEE Third International Conference on Big Data Computing Service and Applications (BigDataService), San Francisco, CA, USA, 6–9 April 2017; pp. 179–184. [Google Scholar]
- Nielsen, J.J.; Sørensen, J.D. On risk-based operation and maintenance of offshore wind turbine components. Reliab. Eng. Syst. Saf. 2011, 96, 218–229. [Google Scholar] [CrossRef]
- Dinwoodie, I. Modelling the Operation and Maintenance of Offshore Wind Farms. Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 2014. [Google Scholar]
- Seyr, H.; Muskulus, M. Decision support models for operations and maintenance for offshore wind farms: A review. Appl. Sci. 2019, 9, 278. [Google Scholar] [CrossRef]
- Murray, S. Energy to the World: The Story of Saudi Aramco; Aramco Services Company: Houston, TX, USA, 2011. [Google Scholar]
- Attia, A.M.; Ghaithan, A.M.; Duffuaa, S.O. Data on upstream segment of a hydrocarbon supply chain in Saudi Arabia. Data Brief 2019, 27, 104804. [Google Scholar] [CrossRef]
- Attia, A.M.; Ghaithan, A.M.; Duffuaa, S.O. A multi-objective optimization model for tactical planning of upstream oil & gas supply chains. Comput. Chem. Eng. 2019, 128, 216–227. [Google Scholar]
- Manual, C.U. IBM ILOG CPLEX Optimization Studio. Version 1987, 12, 1987–2018. [Google Scholar]
- Brook, A.; Kendruck, D.; Meeraus, A. GAMS—General Algebraic Modeling System: A User’s Guide; Scientific Press: Redwood City, CA, USA, 1988. [Google Scholar]




| Sets | ||
|---|---|---|
| : | All nodes; | |
| : | Set of petroleum plants belong to the first level of the supply chain; | |
| : | Set of petroleum plants belong to the second level of the supply chain; | |
| : | Set of demand nodes; | |
| : | Set of storage tanks belong to the first level of the supply chain; | |
| : | Set of storage tanks belong to the second level of the supply chain; | |
| R | : | Set of raw material imported from upstream of the supply chain to the first level; |
| P | : | Set of products processed at level 1; |
| B | : | Set of products processed at level 2; |
| : | Time horizon. | |
| Indices | ||
| t | : | Time periods in weeks,; |
| r | : | Raw material imported from upstream, ; |
| p | : | Product produced at level 1, ; |
| b | : | Product produced at level 2, . |
| Decision Variables | ||
| : | Supply of raw material from upstream to plants belong to first level at time ; | |
| : | Flow of product p from plant i to customer/plant j at time t; | |
| : | Flow of by-product b from plant i to customer/plant j at time t; | |
| : | Inventory level of product p at time t at plants of level 1; | |
| : | Inventory level of product p at time t at plants of level 2; | |
| : | Amount of product p produced above, below the demand of demand node i during time ; | |
| : | Amount of product b produced above, below the demand of demand node i during time ; | |
| : | . | |
| Parameters | ||
| : | The duration of maintenance for the plant i. | |
| : | The manpower required for maintaining plant i during time t. | |
| : | The total manpower available for plant i during time t. | |
| : | Capacity of plant i. | |
| : | Capacity of storage tank i. | |
| : | Capacity of route connecting plant with plant/customer j. | |
| : | Demand quantities of product at demand node at time t. | |
| : | Demand quantities of by-product at demand node at time t. | |
| : | Lost sales of products p at demand node at time t; | |
| : | Lost sales of by-products b at demand node at time t; | |
| : | Cost of maintaining plant i at time t; | |
| : | Cost of processing raw material r at plant i at time t; | |
| : | Cost of processing product stream coming from plant i and processed at plant j at time t; | |
| : | Cost of shipping product p from plant i to customer/plant j at time t; | |
| : | Cost of shipping by-product b from plant i to customer/plant j at time t; | |
| : | Cost incurred due to producing product more than, less than the demand of node at time ; | |
| : | Cost incurred due to producing product more than, less than the demand of node at time ; | |
| : | Inventory holding cost of product p per period t at plants i of level 1; | |
| : | Inventory holding cost of product b per period t at plants i of level 2; | |
| : | Selling price of product p at demand node at time t; | |
| : | Selling price of by-product b at demand node at time t; | |
| : | Composition of product p obtained from raw materials streaming from upstream to the plant i at time t; | |
| : | Composition of by-product b obtained from product p streaming from plant i to plant j at time t; | |
| : | Market share of crude oil specified to an oil production country at time t. | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghaithan, A.M. An Optimization Model for Operational Planning and Turnaround Maintenance Scheduling of Oil and Gas Supply Chain. Appl. Sci. 2020, 10, 7531. https://doi.org/10.3390/app10217531
Ghaithan AM. An Optimization Model for Operational Planning and Turnaround Maintenance Scheduling of Oil and Gas Supply Chain. Applied Sciences. 2020; 10(21):7531. https://doi.org/10.3390/app10217531
Chicago/Turabian StyleGhaithan, Ahmed M. 2020. "An Optimization Model for Operational Planning and Turnaround Maintenance Scheduling of Oil and Gas Supply Chain" Applied Sciences 10, no. 21: 7531. https://doi.org/10.3390/app10217531
APA StyleGhaithan, A. M. (2020). An Optimization Model for Operational Planning and Turnaround Maintenance Scheduling of Oil and Gas Supply Chain. Applied Sciences, 10(21), 7531. https://doi.org/10.3390/app10217531





