Calculation of Loads on Carrying Structures of Articulated Circular-Tube Wagons Equipped with New Draft Gear Concepts

Lovska, Alyona; Fomin, Oleksij; Kučera, Pavel; Píštěk, Václav

doi:10.3390/app10217441

Open AccessArticle

Calculation of Loads on Carrying Structures of Articulated Circular-Tube Wagons Equipped with New Draft Gear Concepts

¹

Department of Wagons, Ukrainian State University of Railway Transport, Feuerbach sq., 7, 61050 Kharkiv, Ukraine

²

Department of Cars and Carriage Facilities, State University of Infrastructure and Technologies, Kyrylivska str., 9, 04071 Kyiv, Ukraine

³

Institute of Automotive Engineering, Brno University of Technology, Technická 2896/2, 616-69 Brno, Czech Republic

^*

Author to whom correspondence should be addressed.

Appl. Sci. 2020, 10(21), 7441; https://doi.org/10.3390/app10217441

Submission received: 23 September 2020 / Revised: 15 October 2020 / Accepted: 18 October 2020 / Published: 23 October 2020

(This article belongs to the Section Mechanical Engineering)

Download

Browse Figures

Versions Notes

Abstract

:

Featured Application

The research results will inspire technicians to design modern railway vehicles with higher operational efficiency.

Abstract

This article deals with the dynamic load and strength of the carrying structures of articulated circular-tube wagons. The study was conducted on the carrying structures of wagons equipped with new draft gear concepts. The accelerations on the carrying structures of wagons were determined using mathematical modeling. The results of modeling show that implementation of the draft gear concept can decrease the dynamic load of wagons by about 10% in comparison with that of a typical SA-3 coupler. Using the created computational models, the service life of the structure of the proposed articulated wagons was also determined. This research will encourage engineers to design modern structures of railway vehicles of higher operational efficiency.

Keywords:

wagon; articulated wagon; carrying structure; draft gear; dynamic load; strength; transport mechanics

1. Introduction

Higher operational efficiency, as a precondition for maintaining the leading position in the global transportation market, can be achieved through the introduction of articulated wagons on railways. A special feature of such wagons is the two-section carrying structure resting on three bogies. The sections interact through a joint assembly.

The lower material capacity of the carrying structure of a wagon, under observance of the conditions of strength and operational reliability, can be achieved with the use of circular tubes in the carrying structure elements. Previous research enabled us to conclude that such implementation could decrease the tare weight of a wagon by 3–5% in comparison with that of a prototype wagon. However, the problem of determining the fatigue strength under operation remains unsolved. It is known that one of the most considerable loads on a wagon in operation is the dynamic load, and the main devices absorbing the kinetic energy that affects the carrying structure of a wagon are automatic couplers or buffer devices. However, they cannot fully absorb the kinetic energy under increased normative values of dynamic loads. It causes damage to the carrying structures of wagons in operation and requires off-schedule repairs. Therefore, there is a need to develop and implement new draft gear concepts for rail vehicles.

The structural and design features of a universal long-base wagon for intermodal transportation in Europe are presented in [1], which provides the results of strength calculations for the carrying structure of a wagon. However, the study does not propose any measures to decrease the dynamic load under operation at the design stage.

The Department for Mechanics and Applied Information of the Military University of Technology (Poland) has developed a specialized wagon with a low rotary loading platform [2]. The wagon is intended for transportation of trucks by rail. A previous study [3] presented the calculation of dynamic indices for this wagon. The factor of safety against wagon overturning was studied when the wagon entered a curve at various traffic speeds. However, the issue of improving the coupling device of the wagon to reduce its dynamic load in these works was not studied.

Some measures to improve the carrying structure of a wagon are proposed in [4]. The study provides the results of a strength calculation for the carrying structure of a wagon realized in LIRA software. The authors considered the normative load values on a wagon in operation for the strength calculation but the study does not give refined dynamic load values on the improved wagon structure.

The mean dynamic load on transport under a longitudinal impact is presented in [5]. The study used accelerations as dynamic load components for the experimental variable. The authors did not propose measures for improving the wagon coupler to lower the dynamic load during operation.

The structures of the BCNHL wagons are analyzed in [6]. The authors discuss some possible ways to improve the technical and economic parameters of wagons for higher operational efficiency.

The results of the structural finite element analysis of a freight wagon using the finite element method are presented in [7]. The research was conducted using the BOXN25 open wagon used by Indian Railways.

The objective of this study was to demonstrate some peculiarities in computation of the dynamic load and strength of the carrying structure of an articulated wagon of circular tubes. To achieve the objective, the following tasks were set:

To propose techniques for lowering the dynamic load on articulated wagons in operation,
To conduct mathematic modeling of dynamic loads on the carrying structure of a circular-tube articulated wagon, and
To determine the basic strength parameters of the carrying structure of an articulated circular-tube wagon.

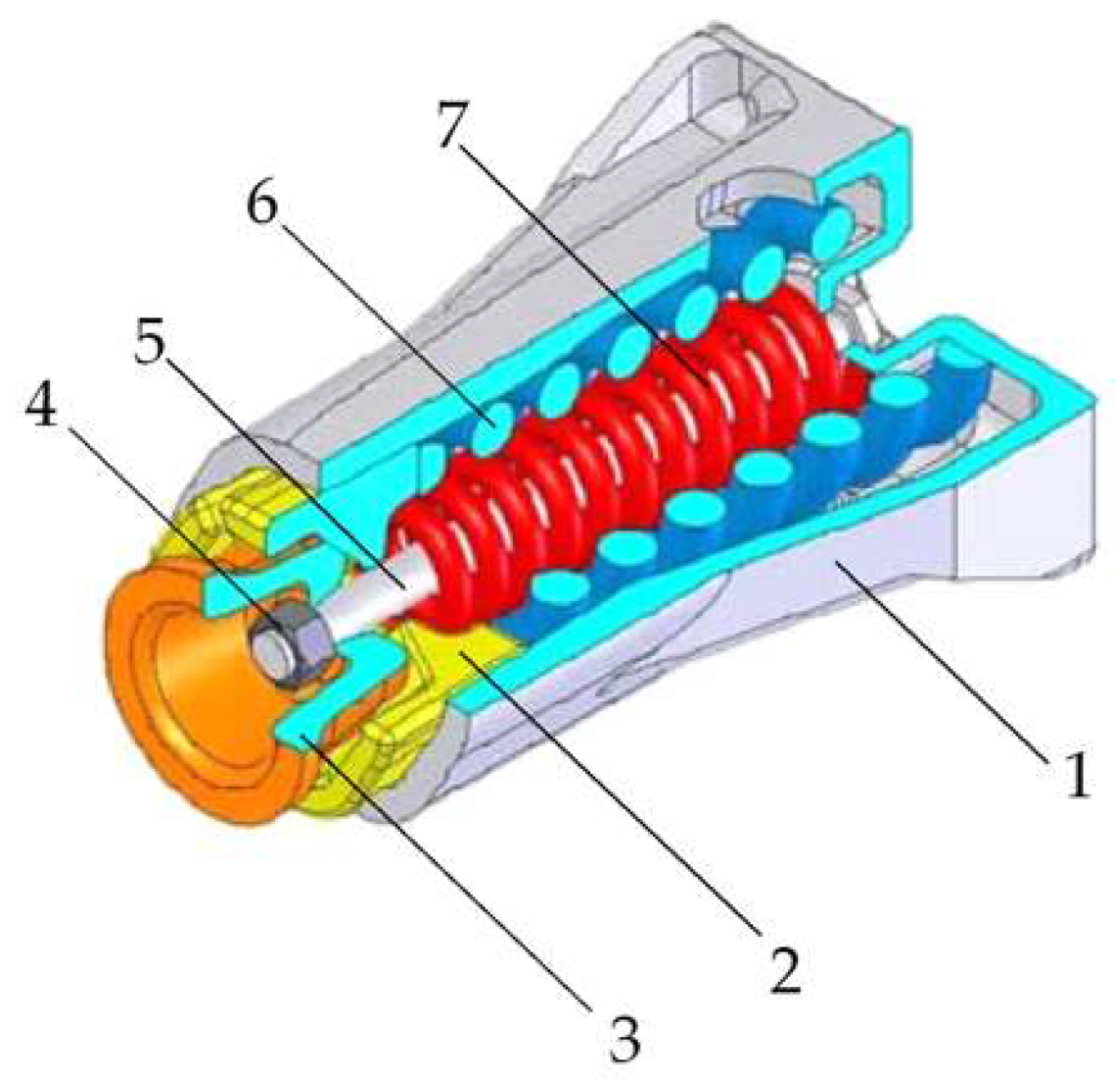
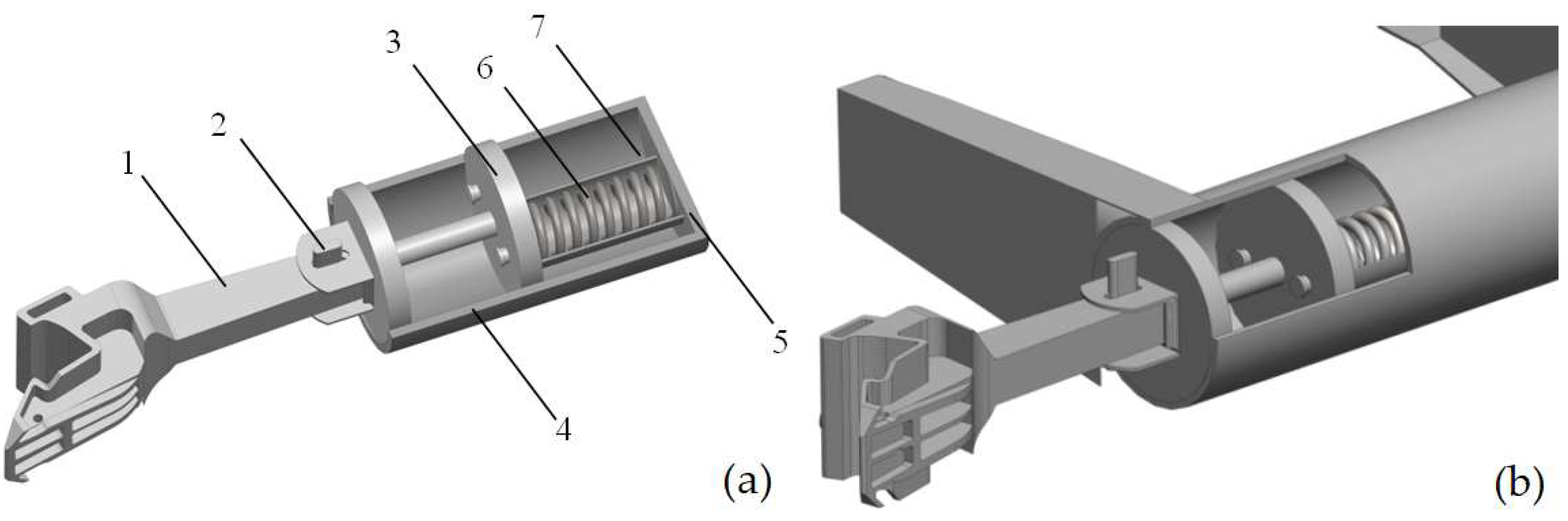
2. Improvement of the Draft Gear for Articulated Circular-Tube Wagons

The absorber of the autocoupling device of the wagon is designed to mitigate the longitudinal (tensile and compressive) forces arising in the train during operation and transfer them to the supporting structure of the car. Sh-2-V-90 draft gears are used on wide-gauge freight wagons (Figure 1).

The acting forces are decreased due to transformation of the kinetic energy of the masses of the interacting wagons into the work of the friction forces of the friction wedges and into the potential energy of the springs. The draft gear protects the carriage, as well as the cargo transported in it, from harmful dynamic effects. This is especially important at the present time in connection with the increases in the masses and speeds of trains, as well as the increase in the intensity of shunting operations.

This type of draft gear has significant disadvantages in operation, such as the technological complexity of manufacturing, as well as technical maintenance, limited energy dissipation, and insufficient reliability in operation. As such, it is necessary to develop alternative designs of draft gears for the automatic couplers of wagons.

We propose a draft gear concept for a lower dynamic load on wagons under operational modes (Figure 2).

The kinetic impact energy is absorbed through its transformation into the work of viscous dissipated forces. The resistance is formed when the piston transfers the viscous liquid through the throttle openings by the operational principle of a hydraulic damper. The system returns to its initial state with release of a spring in the telescopic element.

This draft gear concept can be used for railway vehicles with closed-section center sills. This engineering solution can be used, for example, for wagons with circular-tube carrying elements (Figure 3). The frames of such wagons are presented in Figure 4.

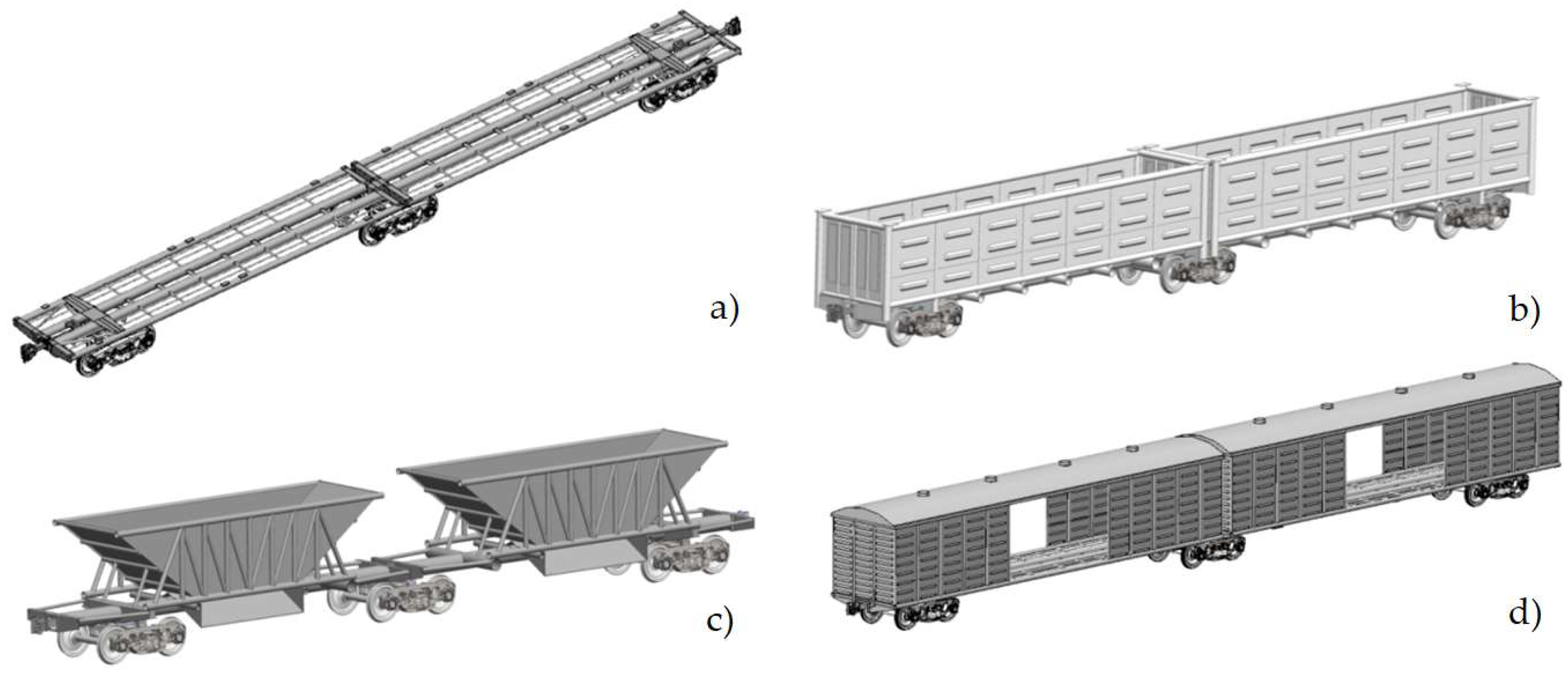
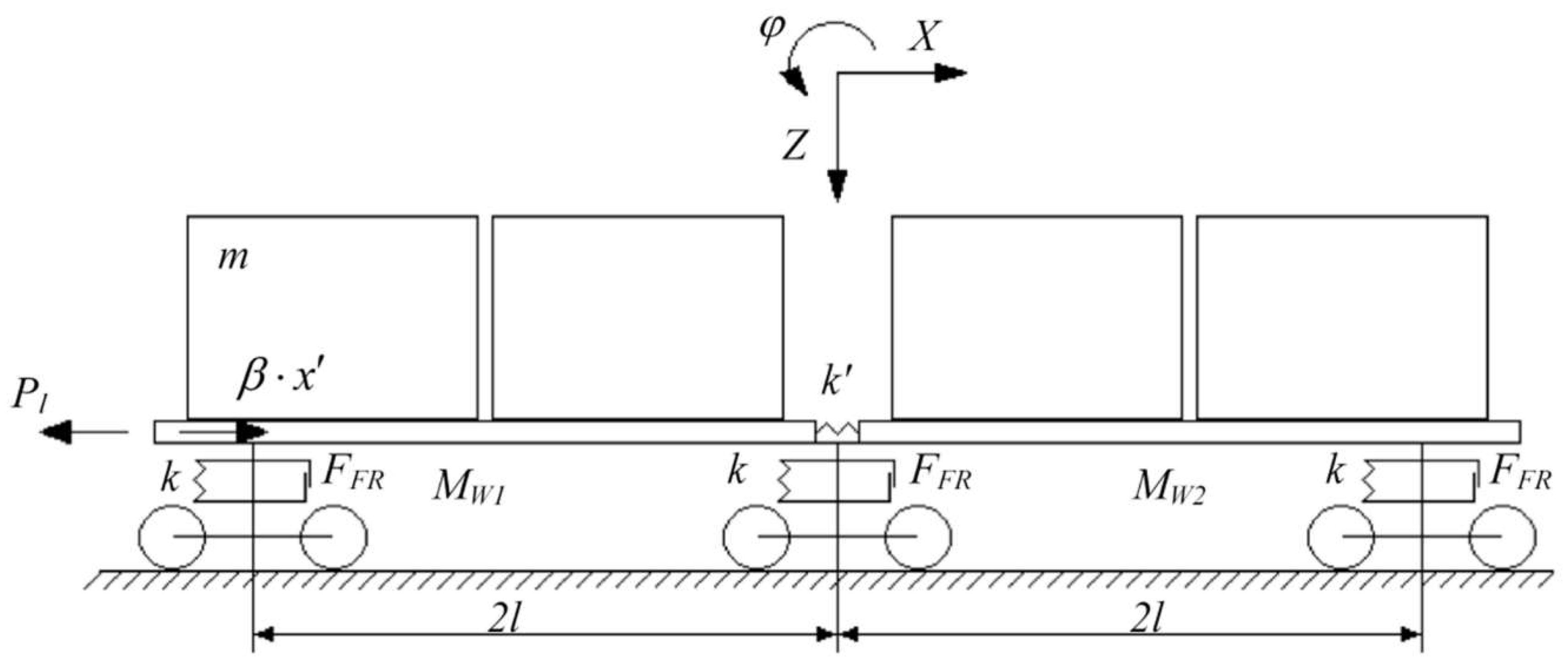
3. Dynamic Load Mathematical Modeling of the Load-Bearing Structures of Articulated Circular-Tube Wagons

The dynamic load of the carrying structure of a wagon with the draft gear concept was defined with the mathematic functional notation of dynamic load under a longitudinal force on the front draft gear stop (tension-jerk). The calculation was conducted using an example of an articulated flat wagon, which is one of the most popular types of articulated wagons in service. The design diagram is presented in Figure 5.

M_{w_{1}}^{'} \cdot {\ddot{x}}_{w_{1}} + M_{W_{1}} \cdot h \cdot {\ddot{φ}}_{W_{1}} + k^{'} (x_{w_{1}} - x_{w_{2}}) = P_{l} - β \cdot {\dot{x}}_{w_{1}},

(1)

I_{w_{1}} \cdot {\ddot{φ}}_{w_{1}} + M_{W_{1}} \cdot h \cdot {\ddot{x}}_{w_{1}} - g \cdot φ_{w_{1}} \cdot M_{W_{1}} \cdot h = l \cdot F_{F R} (s i g n {\dot{Δ}}_{1}^{W_{1}} - s i g n {\dot{Δ}}_{2}^{W_{1}}) + l (k_{1} \cdot {\dot{Δ}}_{1}^{W_{1}} - k_{2} \cdot {\dot{Δ}}_{2}^{W_{1}}),

(2)

M_{w_{1}} \cdot {\ddot{z}}_{w_{1}} = k_{1} \cdot Δ_{1}^{W_{1}} + k_{2} \cdot Δ_{2}^{W_{1}} - F_{F R} (s i g n {\dot{Δ}}_{1}^{W_{1}} - s i g n {\dot{Δ}}_{2}^{W_{1}}),

(3)

m_{i} \cdot {\ddot{x}}_{w_{1}} + (m_{i} \cdot z_{c_{i}}) \cdot {\ddot{φ}}_{w_{1}} = 0,

(4)

I_{i} \cdot {\ddot{φ}}_{w_{1}} + (m_{i} \cdot z_{c_{i}}) \cdot {\ddot{x}}_{w_{1}} - g (m_{i} \cdot z_{c_{i}}) \cdot φ_{w_{1}} = 0,

(5)

m_{i} \cdot {\ddot{z}}_{w_{1}} = 0,

(6)

M_{w_{2}}^{'} \cdot {\ddot{x}}_{w_{2}} + M_{W_{2}} \cdot h \cdot {\ddot{φ}}_{W_{2}} - k^{'} (x_{w_{1}} - x_{w_{2}}) = 0,

(7)

I_{w_{2}} \cdot {\ddot{φ}}_{w_{2}} + M_{W_{2}} \cdot h \cdot {\ddot{x}}_{w_{2}} - g \cdot φ_{w_{2}} \cdot M_{W_{2}} \cdot h = l \cdot F_{F R} (s i g n {\dot{Δ}}_{1}^{W_{2}} - s i g n {\dot{Δ}}_{2}^{W_{2}}) + l (k_{1} \cdot {\dot{Δ}}_{1}^{W_{2}} - k_{2} \cdot {\dot{Δ}}_{2}^{W_{2}}),

(8)

M_{w_{2}} \cdot {\ddot{z}}_{w_{2}} = k_{1} \cdot Δ_{1}^{W_{2}} + k_{2} \cdot Δ_{2}^{W_{2}} - F_{F R} (s i g n {\dot{Δ}}_{1}^{W_{2}} - s i g n {\dot{Δ}}_{2}^{W_{2}}),

(9)

m_{i} \cdot {\ddot{x}}_{w_{2}} + (m_{i} \cdot z_{c_{i}}) \cdot {\ddot{φ}}_{w_{2}} = 0,

(10)

I_{i} \cdot {\ddot{φ}}_{w_{2}} + (m_{i} \cdot z_{c_{i}}) \cdot {\ddot{x}}_{w_{2}} - g (m_{i} \cdot z_{c_{i}}) \cdot φ_{w_{2}} = 0,

(11)

m_{i} \cdot {\ddot{z}}_{w_{2}} = 0,

(12)

where

Δ_{1}^{i} = z_{w_{1}} - l \cdot φ_{w_{1}}

,

Δ_{2}^{i} = z_{w_{2}} + l \cdot φ_{w_{2}}

, M’_Wi is the gross mass of the ith section of a flat wagon, M_Wi is the mass of the carrying structure of the ith section of a flat wagon, I_Wi is the inertia moment of the ith section of a flat wagon, P_l is the longitudinal force on the automatic coupler, β is the viscous resistance coefficient formed by the draft gear concept, l is the half-base of a flat wagon section, F_FR is the absolute value of the dry force in a spring group, k’ is the rigidity of the connection between the sections, k₁ and k₂ are the stiffness of the springs in the spring group of a flat wagon’s bogie (of Model 18-100), m_i is the container mass, z_ci is the height of the container’s center of gravity, I_i is the inertia moment of the i-th container, and x_i, ϕ_i and z_i are coordinates corresponding to displacements of the flat wagon sections relative to the appropriate axels.

The research was conducted in the plane coordinates [8]. The sections had elastic interaction between them. The longitudinal load on the carrying structure of a flat wagon was taken as 2.5 MN [9,10]. The initial displacements and speeds were taken as zero. Differential Equations (1)–(12) were solved using algorithms created by the authors based on the Runge–Kutta method, considering the specifics of the task using the approaches described in [11,12,13,14,15,16,17,18]. We found that the stability of the numerical solution is achieved at the integration step h = 0.0001 s.

The results of calculation showed that accelerations on the carrying structure of the first section of a flat wagon from the force action were 34.9 m/s², and 34.2 m/s² on the second section (Figure 6). The viscous resistance coefficient formed by the draft gear concept should exceed 70 kN s/m.

The acceleration curve of the sections under the action of the longitudinal load on the wagon at the initial moment of time is explained by the first section receiving the impact through the viscous link in the draft gear and the load being transferred to the second section through the elastic link, which simulates the joint of the sections with each other. Thus, application of the draft gear concept for an articulated flat wagon makes it possible to reduce the dynamic load by about 10%. The calculation was also completed for other types of articulated circular-tube wagons. The numerical values of the accelerations are listed in Table 1. The research conducted proved the efficiency of the draft gear concept for railway vehicles (Figure 7, Figure 8 and Figure 9).

4. Results of Computational Modeling

We also computed strength factors for the carrying structures of circular-tube wagons. Let us consider some peculiarities of strength calculations for the carrying structure of an articulate flat wagon with the finite element method realized in CosmosWorks software [19,20,21,22,23,24]. The design diagram of the carrying structure of a flat wagon for design mode I (jerk) is given in Figure 10. A longitudinal load of 2.5 MN was applied to the front stops.

We considered that each section of the flat wagon was loaded with two 20-foot containers. The vertical load from the containers was applied to the horizontal surfaces of fitting stops in the form of the remote load, with consideration of the center of gravity of the container.

A finite element model of the carrying structure of a flat wagon was built with spatial isoparametric tetrahedrons. The optimal number of elements in the mesh was determined with the graph-analytical method. The number of elements in the mesh was 5,406,526 and the number of nodes was 1,538,366. The maximum size of an element in the mesh was 15 mm, the minimum size was 3 mm, and the maximum element side ratio was 3078.9. The percentage of elements with a side ratio less than 3 was 87.6% and the percentage with more than 10 was 0.212%. The number of elements in the circle was 8 and the element size gain ratio was 1.7. The model was fixed in the zones where the carrying structure rested on the gearing parts.

The results of the strength calculation for the carrying structure for a flat wagon are given below. The maximum equivalent stresses were concentrated in the end parts of the center sill and accounted for about 180 MPa; thus, they did not exceed the admissible values (Figure 11).

The maximum displacements in the structural nodes were taken in the middle sections; they accounted for 3.4 mm (Figure 12). The maximum strain was 2.3 × 10⁻³.

Strength calculations were also conducted for other types of articulated wagon (Table 2).

The method described in [25] was used to determine the design life of wagons designed using the developed computational models:

T_{n} = \frac{(σ_{- 1 D} / {[n]}^{m} \cdot N_{0})}{B \cdot f_{e} \cdot σ_{a}^{m}},

(13)

where

σ_{- 1 D}

is the average value of strength endurance of a detail, n is the admissible safety factor, m is the degree of fatigue curve, N₀ is the number of tests, B is the coefficient characterizing a period of continuous work of an object,

f_{e}

is the effective frequency of dynamic load, and

σ_{a}^{m}

is the amplitude of equivalent dynamic loads. The calculation results showed that the design lifetime of the proposed carrying structure models of the wagons exceeded 32 years.

5. Discussion

In Section 1, the goal was to reduce the dynamic load of the load-bearing structures of articulated circular-tube wagons in operation. This goal was achieved by improving of the automatic coupler of the wagon. The introduction of this device is possible in wagons whose central frame support has a closed cross-section. To substantiate the proposed solution, we mathematically modeled the dynamic load on the wagon under the influence of longitudinal loads. The results of the calculation led to the conclusion that, by considering the new draft gear concept in articulated wagons, a reduction in dynamic load of almost 10% is possible (Table 1).

The obtained results were used in strength calculations of articulated wagons. The calculation was carried out in the CosmosWorks software package using the finite element method. The calculation results showing the strength of the load-bearing structures of articulated wagons are provided in Table 2.

The limitations of this study are that the strength calculations did not consider the elastic bonds in the bearing zones of the wagons on the chassis. These restrictions will be taken into account in further investigations in this direction.

These investigations will help to reduce the dynamic load on the load-bearing structures of articulated wagons during operation, ensuring the strength of the supporting structures of articulated wagons and reducing the costs of unscheduled repairs. Studies have also been carried out that will help to create innovative new-generation wagons that will improve the efficiency of the transportation industry.

6. Conclusions

We propose a draft gear concept for lowering the dynamic load of wagons under operational modes. The draft gear concept can be implemented for rail vehicles with closed-section center sills (e.g., for the carrying structure of a circular-tube wagon). The peculiarity of the concept is the possibility to transform the impact kinetic energy into the work of viscous resistance forces emerging in the concept.

We focused on the mathematical modeling of dynamic loads on the carrying structure of an articulated circular-tube wagon. The strength of a flat wagon structure was also calculated. The results of the calculation showed that the accelerations on the carrying structure of the first section of a flat wagon from the action force were 34.9 m/s² and those on the second section were 34.2 m/s². For an open wagon, the accelerations that acted on the first section from the side of the longitudinal force were 28.3 m/s² and those on the second were 27.9 m/s². For the boxcar and the hopper wagon, the accelerations acting on the first section are 25.7 and 28.5 m/s², respectively, and 25.2 and 28.1 m/s² for the second, respectively.

We established that the use of the draft gear concept for articulated wagons can help decrease the dynamic load by about 10%.

This study presents the basic strength parameters of the carrying structure of an articulated circular-tube wagon. The strength of a flat wagon structure was also calculated. We established that the maximum equivalent stresses emerging in the end parts of the center sills accounted for 180 MPa and, thus, they did not exceed the admissible values. The maximum displacements in the nodes of the carrying structure were 3.4 mm. The maximum equivalent stresses acting on the supporting structure of the open wagon were 298 MPa and the displacement in the nodes of the structure was 3.2 mm. For a boxcar and a hopper wagon, the maximum equivalent stresses were, respectively, 297 and 280 MPa and the displacements were 4.0 and 5.6 mm.

The results of strength calculations for the carrying structure of other wagons also confirmed the effectiveness of the design solutions.

The research conducted will encourage engineers to design modern structures for railway vehicles with higher efficiency in service.

Author Contributions

Conceptualization, A.L.; methodology, A.L. and O.F.; software, P.K.; validation, P.K.; writing—review and editing, V.P. All authors have read and agreed to the published version of the manuscript.

Funding

The authors gratefully acknowledge funding from the specific research on “Innovative principles for creating resource-saving structures of railroad cars based on the refined dynamic loads and functionally adaptive flash-concepts”, which was funded from the state budget of Ukraine in 2020. The authors gratefully acknowledge funding from the specific research on BUT FSI-S-20-6267.

Acknowledgments

The authors thank the Ukrainian State University of Railway Transport, the State University of Infrastructure and Technologies, and Brno University of Technology for support.

Conflicts of Interest

The authors declare no conflict of interest.

References

Marton, P.; Gerlici, J.; Fabián, P. Versatile, efficient and long wagon for intermodal transport in Europe. Communications 2013, 2, 118–123. [Google Scholar]
Krasoń, W.; Niezgoda, T.; Stankiewicz, M. Innovative Project of Prototype Railway Wagon and Intermodal Transport System. Transp. Res. Procedia 2016, 14, 615–624. [Google Scholar]
Niezgoda, T.; Krasoń, W.; Stankiewicz, M. Simulations of motion of prototype railway wagon with rotatable loading floor wagonsried out in MSC Adams software. J. KONES 2015, 19, 495–502. [Google Scholar] [CrossRef]
Vatulia, G.; Falendysh, A.; Orel, Y.; Pavliuchenkov, M. Structural improvements in a tank wagon with modern software packages. Procedia Eng. 2017, 187, 301–307. [Google Scholar] [CrossRef]
Zamecnik, J.; Jagelcak, J. Evaluation of wagon impact tests by various measuring equipment and influence of impacts on cargo stability. Communications 2015, 4, 21–27. [Google Scholar]
Shukla, C.-P.; Bharti, P.-K. Study and Analysis of Doors of BCNHL Wagons. Int. J. Eng. Res. Technol. (IJERT) 2015, 4, 1195–1200. [Google Scholar]
Harak, S.S.; Sharma, S.C.; Harsha, S.P. Structural Dynamic Analysis of Freight Railway Wagon Using Finite Element Method. Procedia Mater. Sci. 2014, 6, 1891–1898. [Google Scholar] [CrossRef] [Green Version]
Fomin, O.; Lovska, A.; Píštěk, V.; Kučera, P. Dynamic load computational modelling of containers placed on a flat wagon at railroad ferry transportation. Vibroeng. Procedia 2019, 29, 118–123. [Google Scholar]
Freight Wagons. General Requirements for the Calculations and Design of New and Upgraded 1520 mm (Non-Self-Propelled) Rail Cars; DSTU 7598: 2014; Ukrainian Scientific Railway Car Building Research Institute: Kremenchuk, Ukraine, 2014. [Google Scholar]
Freight Wagons. Strength and Dynamic Quality Requirements; GOST 33211-2014; Standartinform: Moscow, Russia, 2014. [Google Scholar]
Kostek, R.; Aleksandrowicz, P. Effect of contact parameters on the pattern of vehicle collisions with a round pillar. In Proceedings of the 23rd International Conference Engineering Mechanics, Svratka, Czech Republic, 15–18 May 2017; pp. 490–493. [Google Scholar]
Kostek, R.; Aleksandrowicz, P. Simulation of car collision with an impact block. In Proceedings of the 11th International Congress of Automotive and Transport Engineering, Pitesti, Romania, 8–10 November 2017; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
Puškár, M.; Bigoš, P. Output Performance Increase of Two-stroke Combustion Engine with Detonation Combustion Optimization. Strojarstvo 2010, 52, 577–587. [Google Scholar]
Puškár, M.; Kopas, M.; Puškár, D.; Lumnitzer, J.; Faltinová, E. Method for reduction of the NOX emissions in marine auxiliary diesel engine using the fuel mixtures containing biodiesel using HCCI combustion. Mar. Pollut. Bull. 2018, 127, 752–760. [Google Scholar] [CrossRef]
Puškár, M.; Kopas, M. System based on thermal control of the HCCI technology developed for reduction of the vehicle NOX emissions in order to fulfil the future standard Euro 7. Sci. Total Environ. 2018, 643, 674–680. [Google Scholar]
Sapronova, S.; Tkachenko, V.; Fomin, O.; Hatchenko, V.; Maliuk, S. Research on the safety factor against derailment of railway vehicles. East. Eur. J. Enterp. Technol. 2017, 6, 19–25. [Google Scholar] [CrossRef] [Green Version]
Drápal, L.; Vopařil, J. Shape Design of a Piston Ring. In Proceedings of the Transport Means 2016—Proceedings of the 20th International Scientific Conference, Kaunas, Lithuania, 5–7 October 2016; pp. 767–771. [Google Scholar]
Drápal, L.; Vopařil, J. Design Concept of a Crankshaft for Reduction of Main Bearings Power Losses and a Deep Skirt Engine Block Load. In Proceedings of the 18th International Conference on Mechatronics—Mechatronika (ME) 2018, Brno, Czech Republic, 5–7 December 2018; pp. 533–536. [Google Scholar]
Okorokov, A.M.; Fomin, O.V.; Lovska, A.O.; Vernigora, R.V.; Zhuravel, I.L.; Fomin, V.V. Research into a possibility to prolong the time of operation of universal semi-wagon bodies that have exhausted their standard resource. East.-Eur. J. Enterp. Technol. 2018, 3, 20–26. [Google Scholar] [CrossRef] [Green Version]
Lovskaya, A.; Ryibin, A. The study of dynamic load on a wagon-platform at a shunting collision. East.-Eur. J. Enterp. Technol. 2016, 3, 4–8. [Google Scholar] [CrossRef]
Fomin, O.; Lovska, A.; Píštěk, V.; Kučera, P. Research of stability of containers in the combined trains during transportation by railroad ferry. MM Sci. J. 2020, 1, 3728–3733. [Google Scholar] [CrossRef]
Kitov, Y.; Verevicheva, M.; Vatulia, G.; Orel, Y.; Deryzemlia, S. Design Solutions for Structures with Optimal Internal Stress Distribution; EDP Sciences: Paris, France, 2017; p. 133. [Google Scholar]
Alyamovsky, A.A. SolidWorks/COSMOSWorks 2006–2007—Engineering Analysis by the Finite Element Method; DMK: Moscow, Russia, 2007. (In Russian) [Google Scholar]
Fomin, O.; Lovska, A.; Radkevych, V.; Horban, A.; Skliarenko, I.; Gurenkova, O. The dynamic loading analysis of containers placed on a flat wagon during shunting collisions. ARPN J. Eng. Appl. Sci. 2019, 14, 3747–3752. [Google Scholar]
Ustich, P.A.; Karpych, V.A.; Ovechnikov, M.N. Reliability of Non-Traction Rail Rolling Stock; IG “Variant”: Moscow, Russia, 1999. (In Russian) [Google Scholar]

Figure 1. Sh-2-B-90 absorbing mechanism: 1, body; 2, friction wedge; 3, pressure cone; 4, nut; 5, bolt; 6, external spring; 7, internal spring.

Figure 2. Draft gear concept for the automatic coupler: (a) concept components; (b) location on wagon frame. 1, automatic coupler frame; 2, wedge; 3, adapter; 4, circular-tube center sill; 5, bottom; 6, spring; 7, telescopic element.

Figure 3. Spatial computer models of freight wagons: (a) flat wagon, (b) open wagon, (c) boxcar, and (d) hopper wagon.

Figure 4. Spatial computer models of freight wagon frames: (a) flat wagon, (b) open wagon, (c) boxcar, and (d) hopper wagon.

Figure 5. Design diagram of an articulated flat wagon.

Figure 6. Accelerations on the carrying structure of the articulated flat wagon: (a) first and (b) second sections of the flat wagon from longitudinal force.

Figure 7. Accelerations on the carrying structure of the articulated open wagon: (a) first and (b) second sections of the flat wagon from longitudinal force.

Figure 8. Accelerations on the carrying structure of the articulated boxcar: (a) first and (b) second sections of the flat wagon from longitudinal force.

Figure 9. Accelerations on the carrying structure of the articulated hopper wagon: (a) first and (b) second sections of the flat wagon from longitudinal force.

Figure 10. Design diagram of the carrying structure of the flat wagon.

Figure 11. Stress state of the articulated flat wagon section.

Figure 12. Displacements in nodes of the articulated flat wagon section.

Table 1. Numerical values of accelerations on the carrying structure of articulated circular-tube wagons.

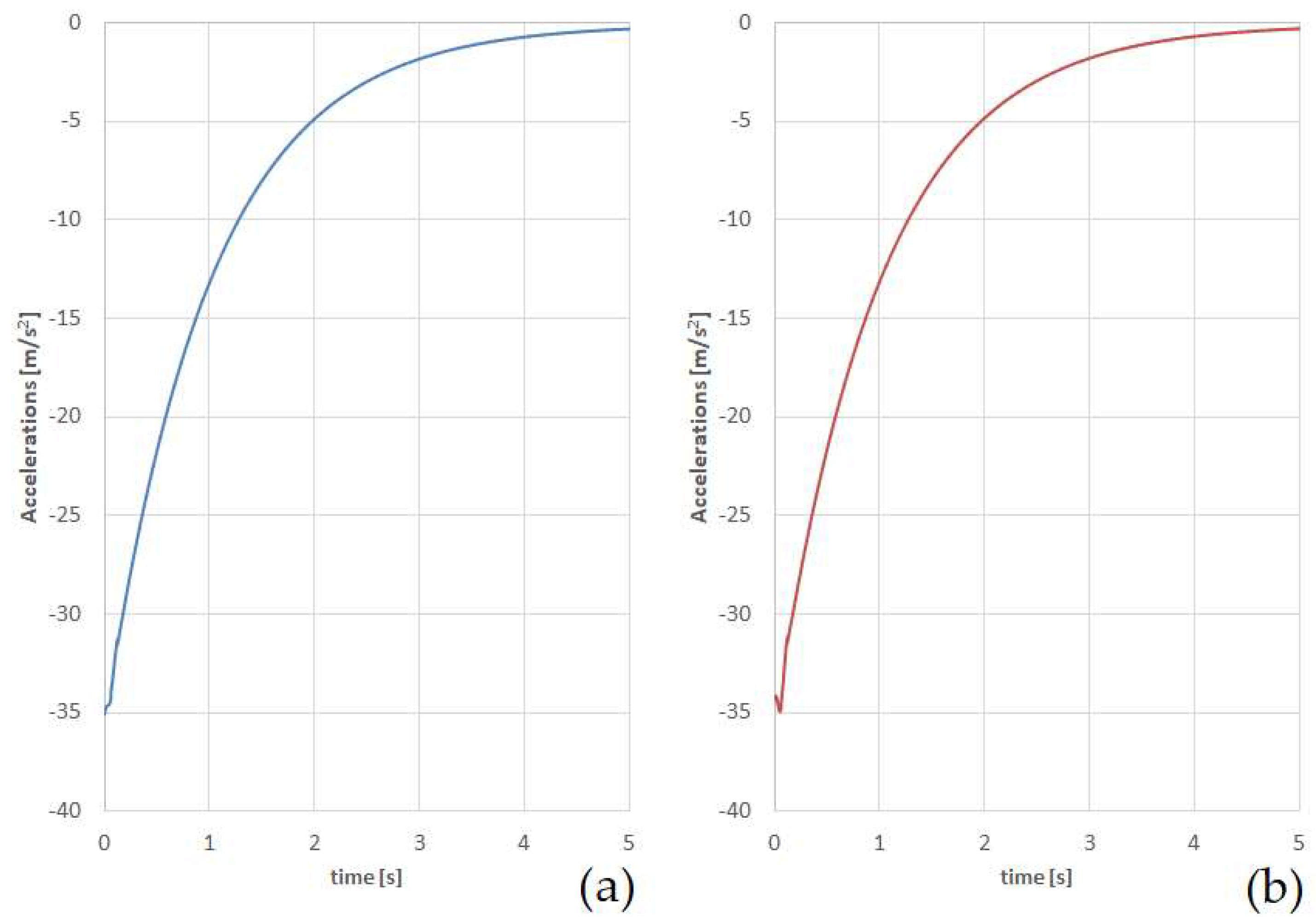
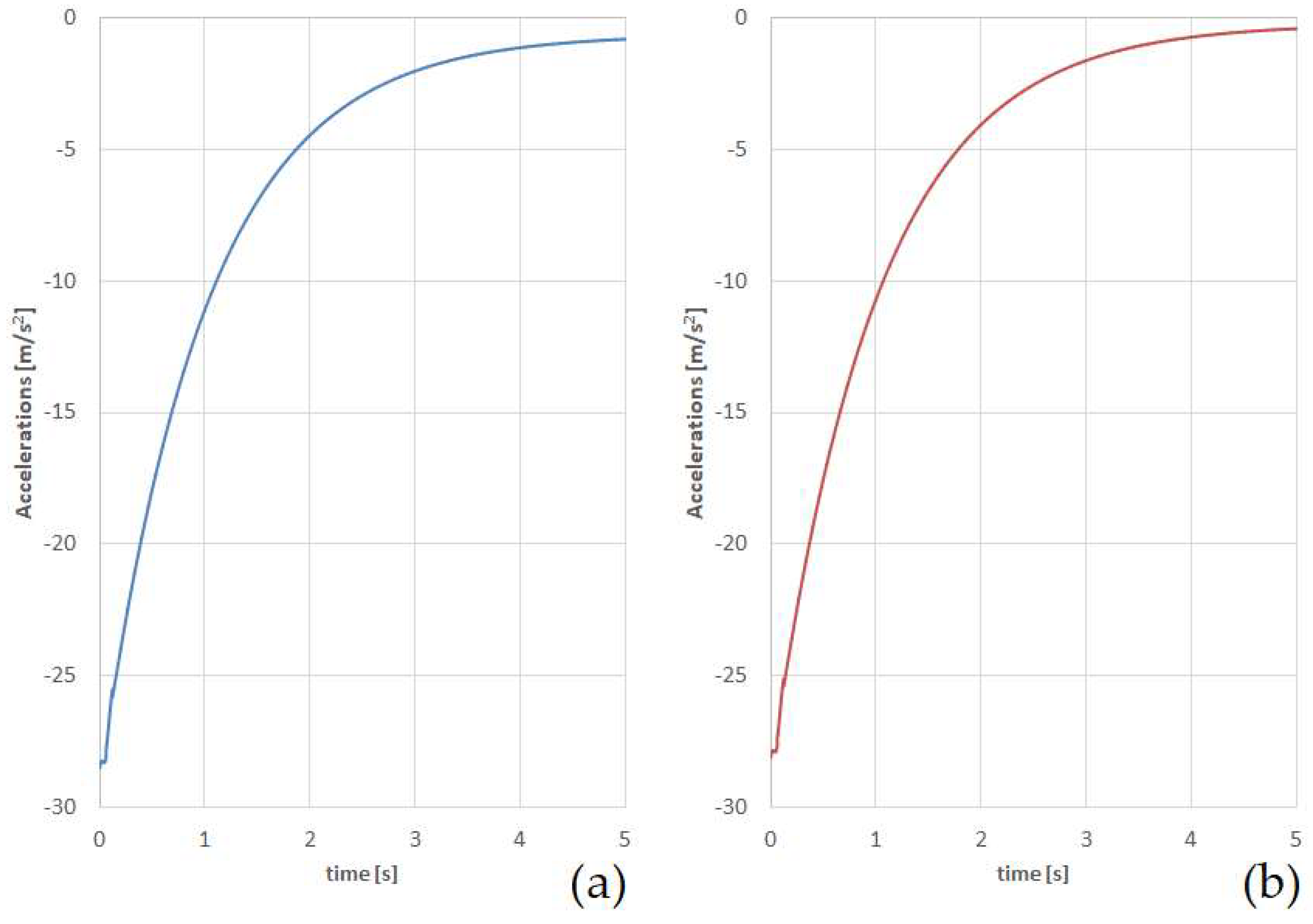
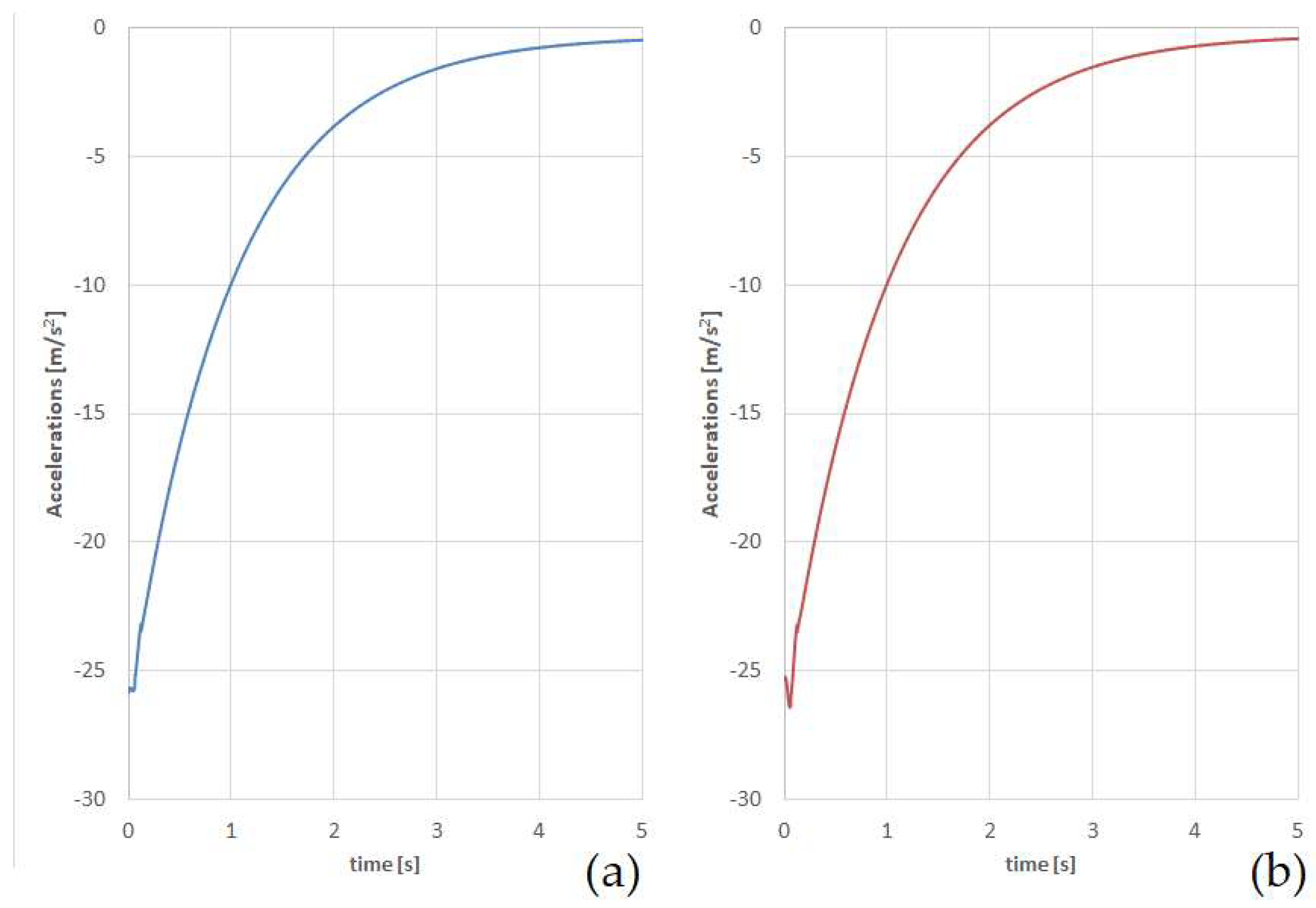
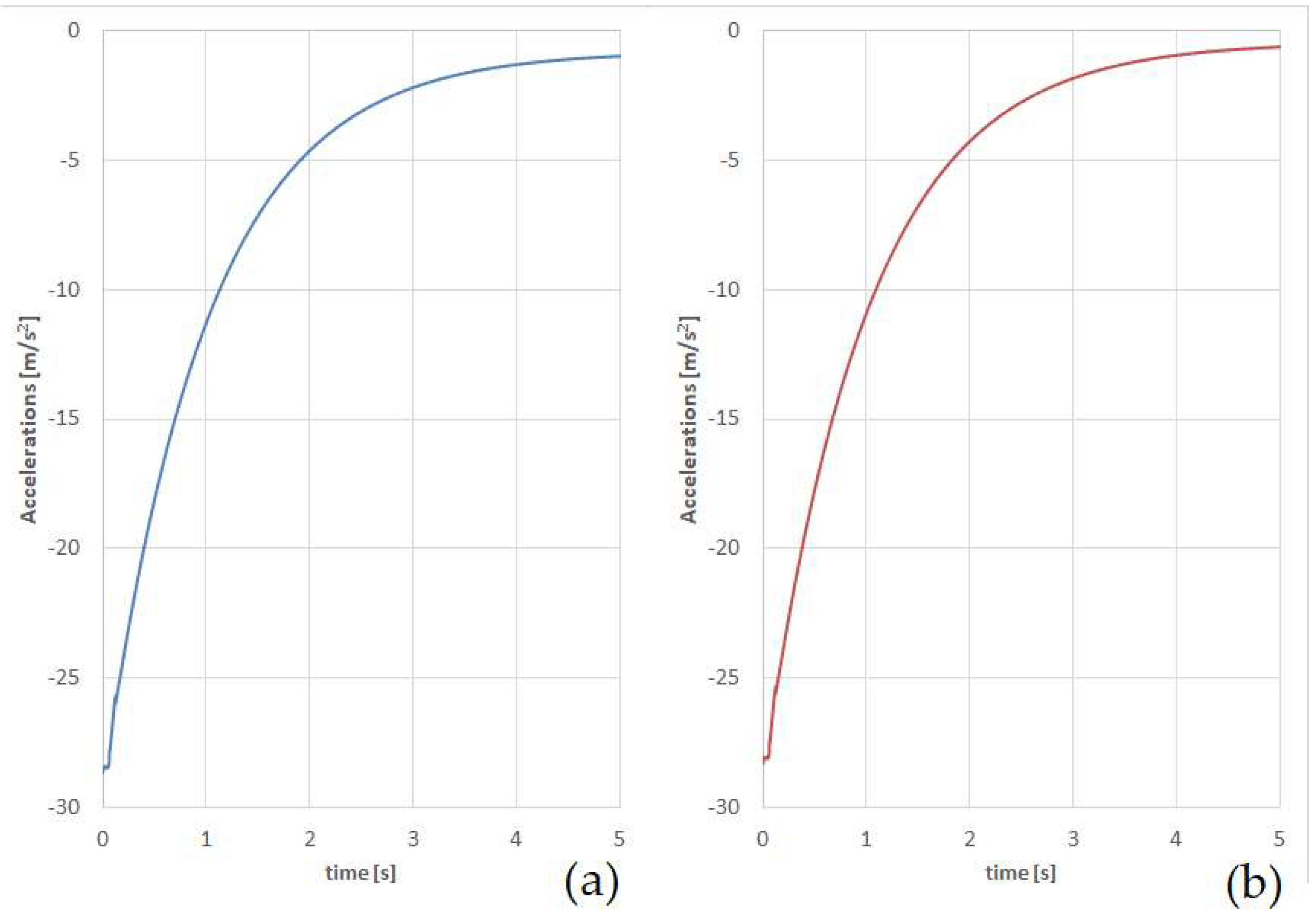
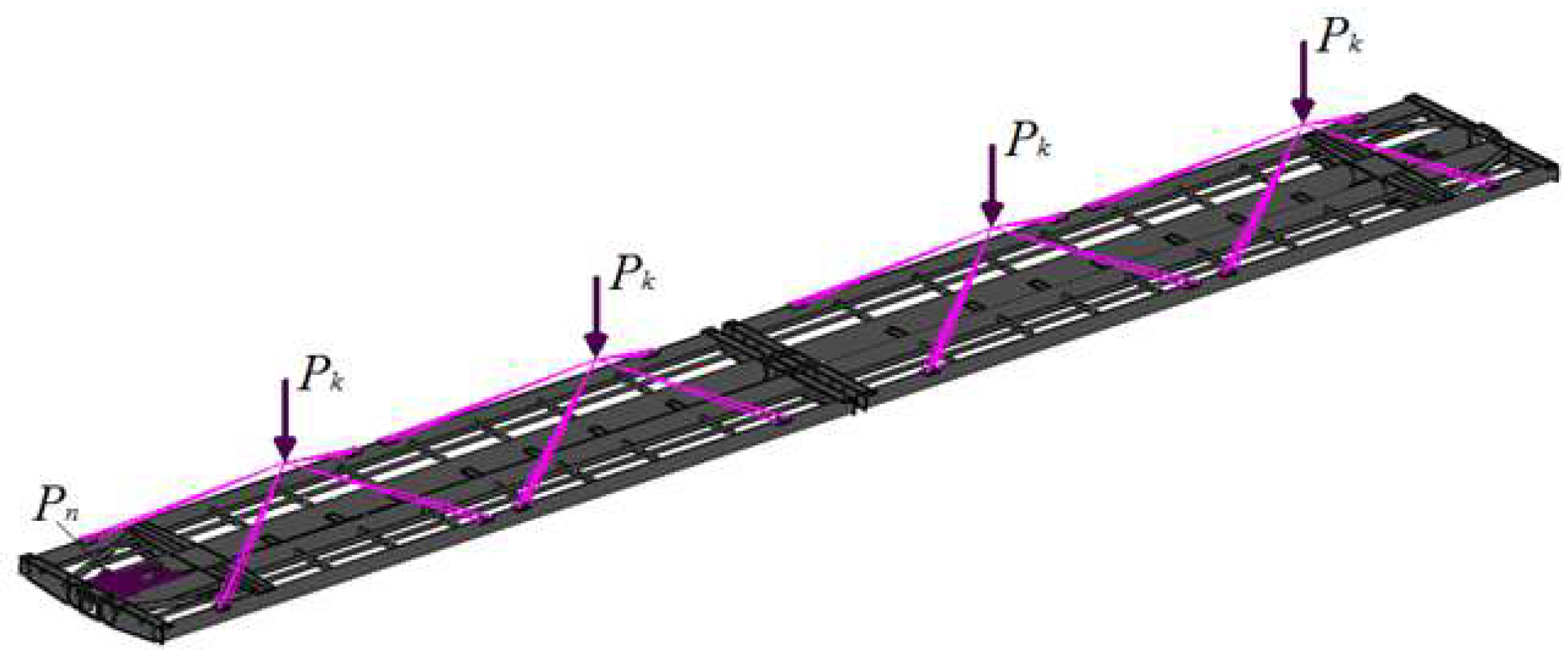
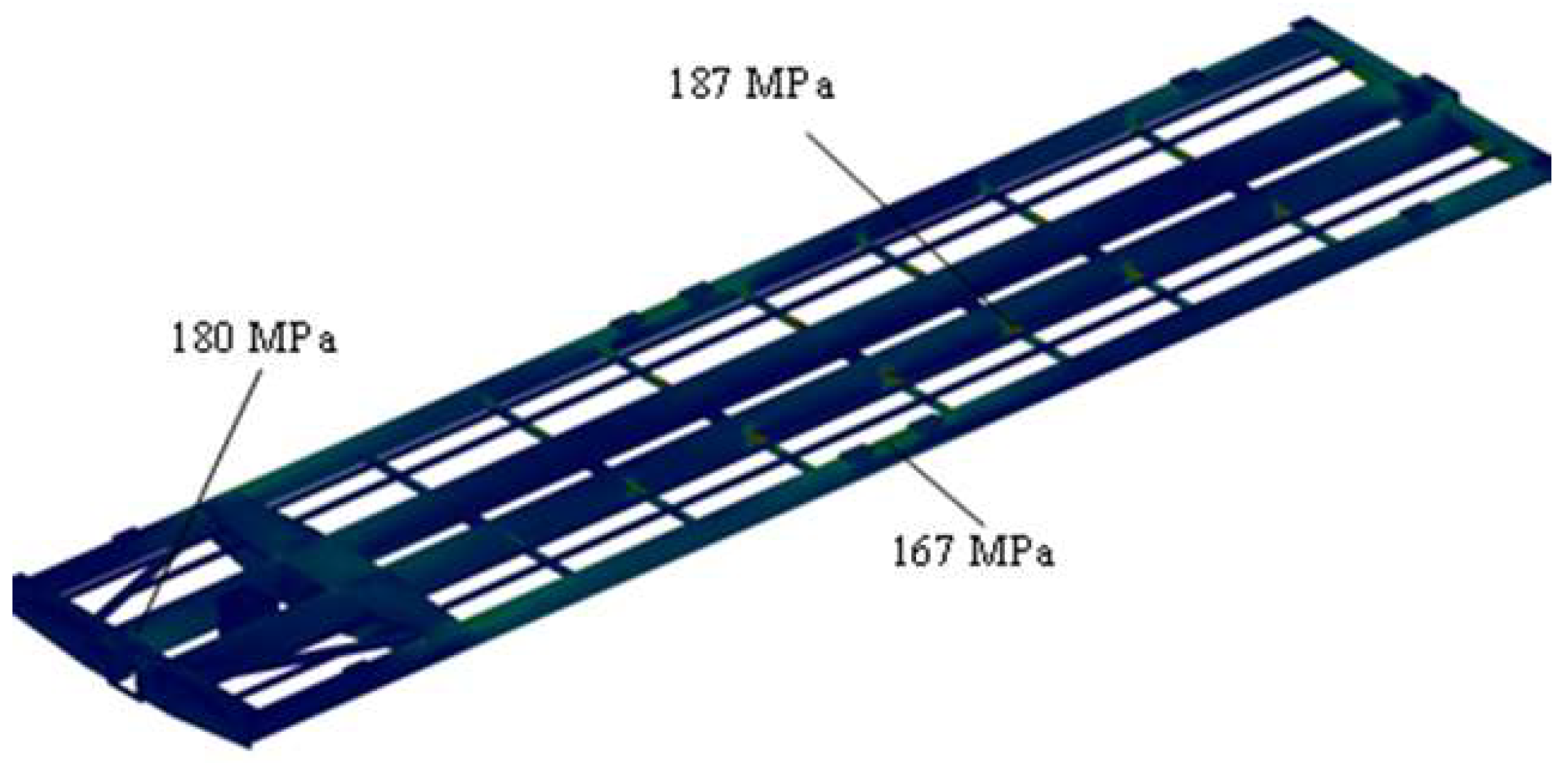
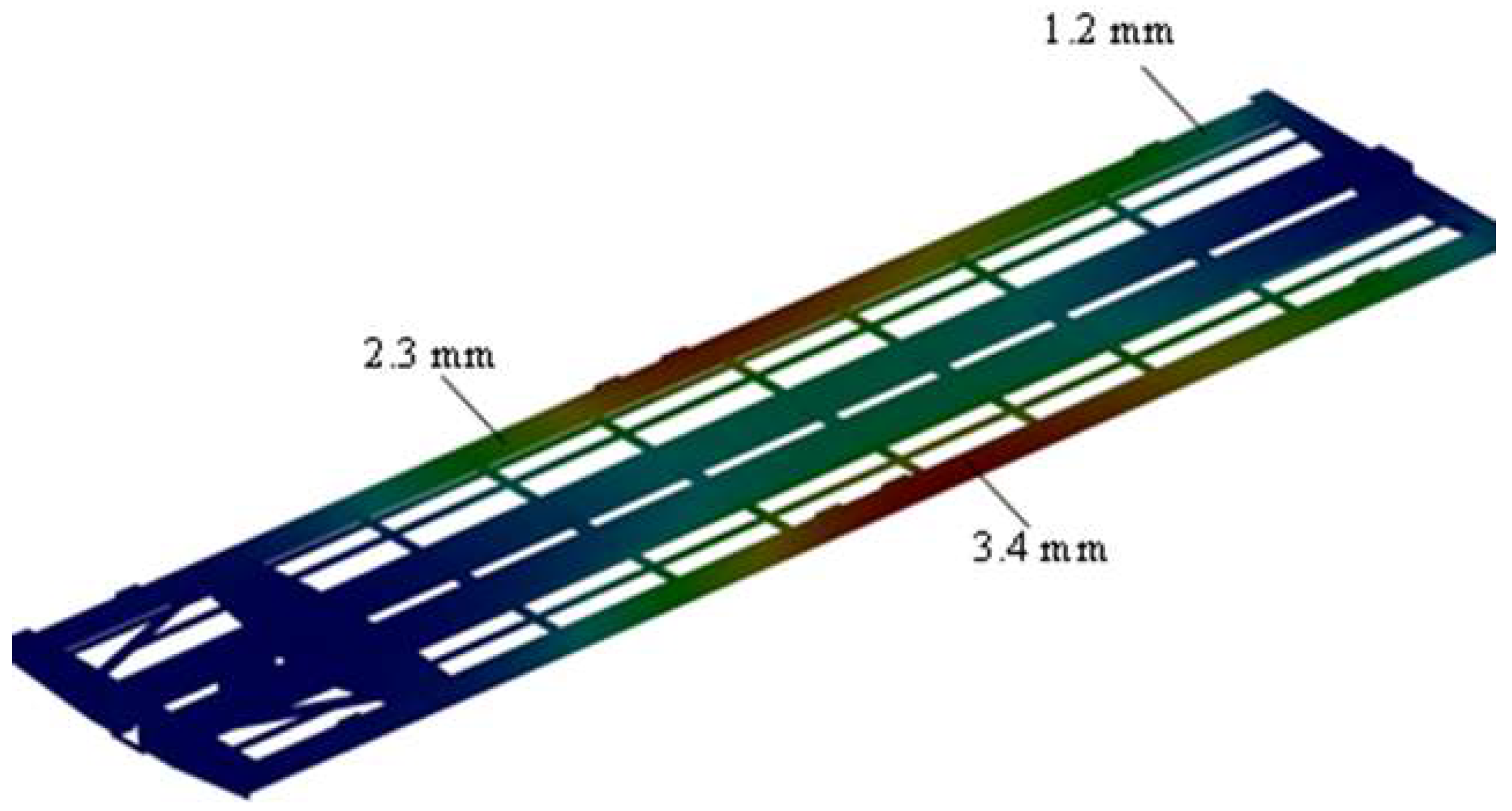
Wagon Type	Accelerations on First Section from Force Action (m/s²)	Accelerations on Second Section from Force Action (m/s²)
Open	28.3	27.9
Boxcar	25.7	25.2
Hopper	28.5	28.1

Table 2. Basic strength parameters of the carrying structures of articulated circular-tube wagons.

Wagon Type	Maximum Equivalent Stresses (MPa)	Displacements in Structural Nodes (mm)
Open	298	3.2
Boxcar	297	4.0
Hopper	280	5.6

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Share and Cite

MDPI and ACS Style

Lovska, A.; Fomin, O.; Kučera, P.; Píštěk, V. Calculation of Loads on Carrying Structures of Articulated Circular-Tube Wagons Equipped with New Draft Gear Concepts. Appl. Sci. 2020, 10, 7441. https://doi.org/10.3390/app10217441

AMA Style

Lovska A, Fomin O, Kučera P, Píštěk V. Calculation of Loads on Carrying Structures of Articulated Circular-Tube Wagons Equipped with New Draft Gear Concepts. Applied Sciences. 2020; 10(21):7441. https://doi.org/10.3390/app10217441

Chicago/Turabian Style

Lovska, Alyona, Oleksij Fomin, Pavel Kučera, and Václav Píštěk. 2020. "Calculation of Loads on Carrying Structures of Articulated Circular-Tube Wagons Equipped with New Draft Gear Concepts" Applied Sciences 10, no. 21: 7441. https://doi.org/10.3390/app10217441

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Menu

Calculation of Loads on Carrying Structures of Articulated Circular-Tube Wagons Equipped with New Draft Gear Concepts

Abstract

Featured Application

Abstract

1. Introduction

2. Improvement of the Draft Gear for Articulated Circular-Tube Wagons

3. Dynamic Load Mathematical Modeling of the Load-Bearing Structures of Articulated Circular-Tube Wagons

4. Results of Computational Modeling

5. Discussion

6. Conclusions

Author Contributions

Funding

Acknowledgments

Conflicts of Interest

References

Share and Cite

Article Metrics

Article Access Statistics

Further Information

Guidelines

MDPI Initiatives

Follow MDPI