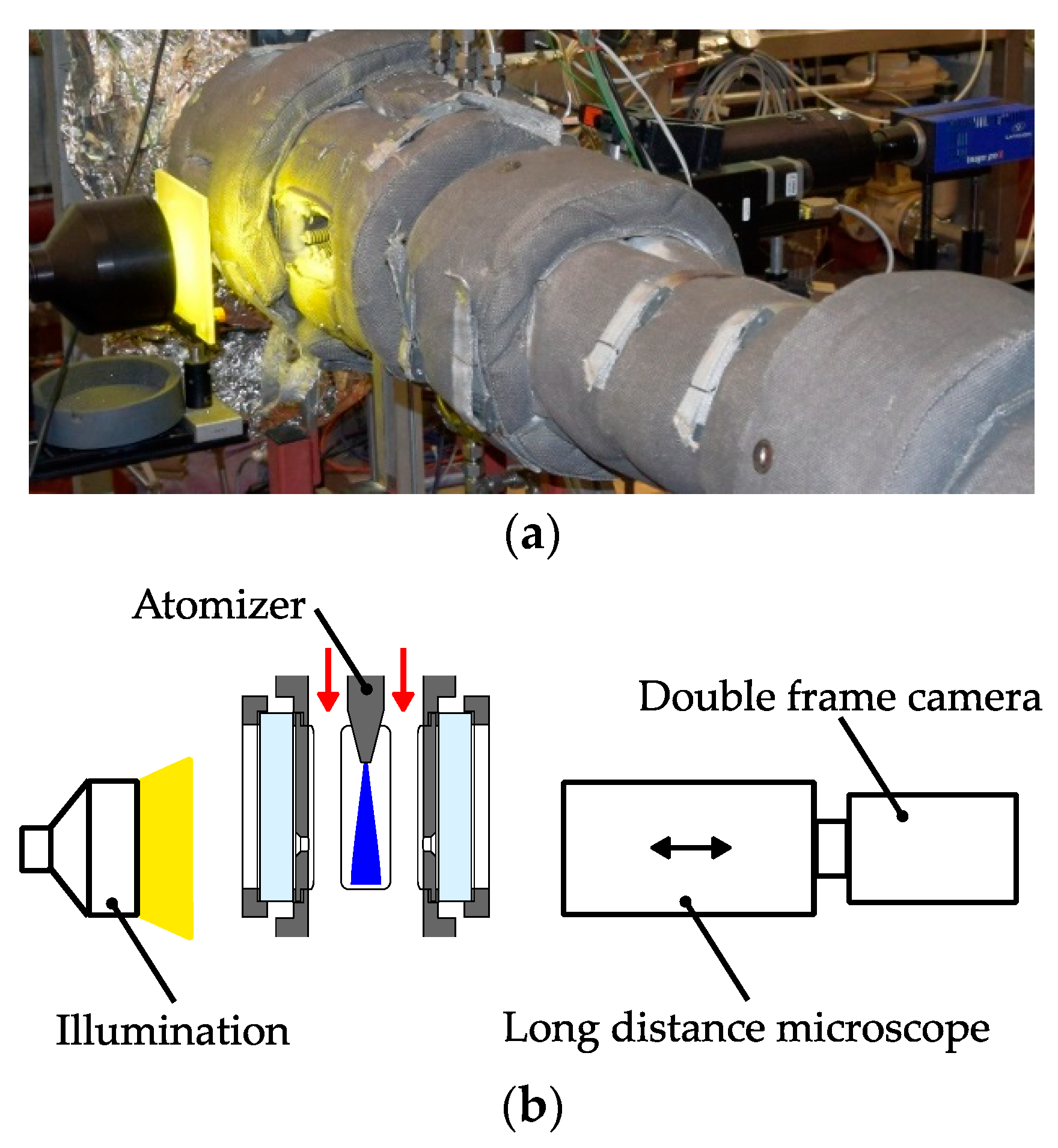
In the following subsections, the characteristics of the gas jet and the spray will be discussed in detail. At first, the propagation of the expanding gas jet and the influence of the turbulence model will be evaluated. After that, the ability of the model to predict the measured droplet characteristics like velocity and size are reviewed critically. Finally, the evaporation of the urea-water solution (UWS) will be discussed briefly.
3.1. Characteristics of the Gas Jet
The simulations of the gas jet were carried out on the computational mesh shown in
Figure 3. Before the gas jet is initialized, the hot gas flow in the test bench was calculated to provide a well-converged flow field. During these flow simulations, the time step is increased from 1 µs to 10 µs in order to speed up the calculation time. A resulting flow field is shown exemplarily for OP 2 in
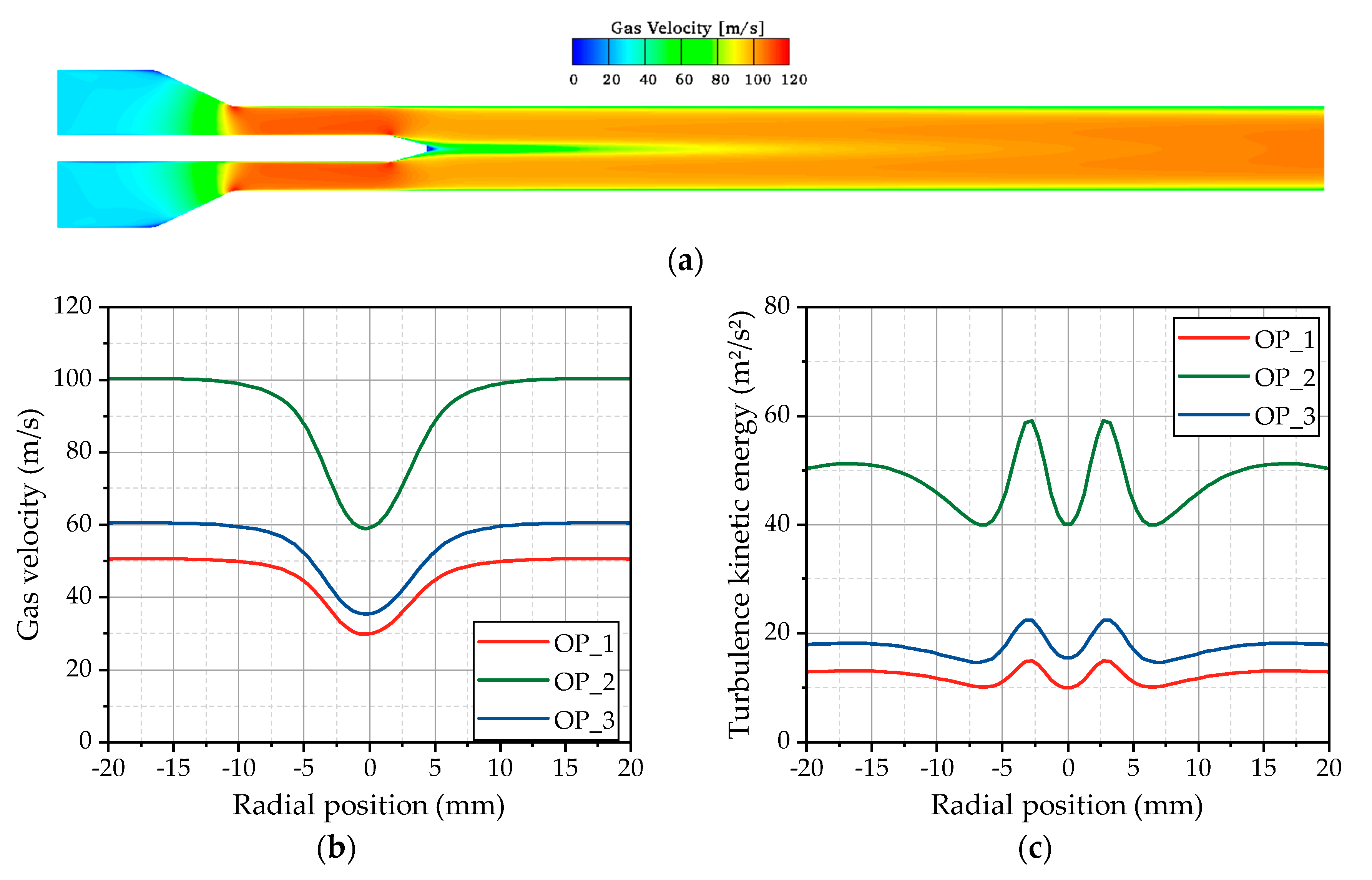
Figure 6a, whereby the gas velocity is illustrated on a plane cut through the center axis of the test bench. Downstream of the inlet of the computational domain, the gas is accelerated in the tapered cross section to velocities over 100 m/s. Passing the injector shaft mounted in the center of the pipe, the flow detaches from the injector cone and starts to recombine downstream of the nozzle exit. At the first measurement position, at a distance of 50 mm downstream, the nozzle the flow is still not completely recombined, resulting in the radial profiles of the gas velocity shown in
Figure 6b. For OP 2, the velocity decreases from 100 m/s in the outer area to 60 m/s in the center of the pipe, which has to be considered for the evaluation of the gas jet and the spray characteristics. The velocity reduction is, for all operating points, in the range of 40%. Obviously, this velocity gradient is followed by the formation of a shear layer, which locally increases the turbulence. This behavior is clarified by the radial profiles of the turbulence kinetic energy depicted in
Figure 6c. Thereby, two peaks are detectable ±3 mm away from the center axis, indicating the position of the shear layer. An unchanged position of these peaks can be found in all three operating points, even if the flow velocity and the turbulence level are completely different. The reason for these phenomena is the preservation of the Reynolds number by means of choosing the conditions for the hot gas flow by Lieber et al. [
17].
Starting from the simulations of the hot gas flow, the gas jet is initialized in the outflow channel of the nozzle. The gas flow inside the channel is in a subsonic state and accelerates to supersonic speed downstream of the nozzle exit, which is characteristic for under-expanded nozzles. Thereby, flow velocities over 400 m/s are present in the vicinity of the nozzle exit. The flow velocity on a plane cut through the center axis of the test bench and an isoline representing a Mach number (Ma) of one are depicted in
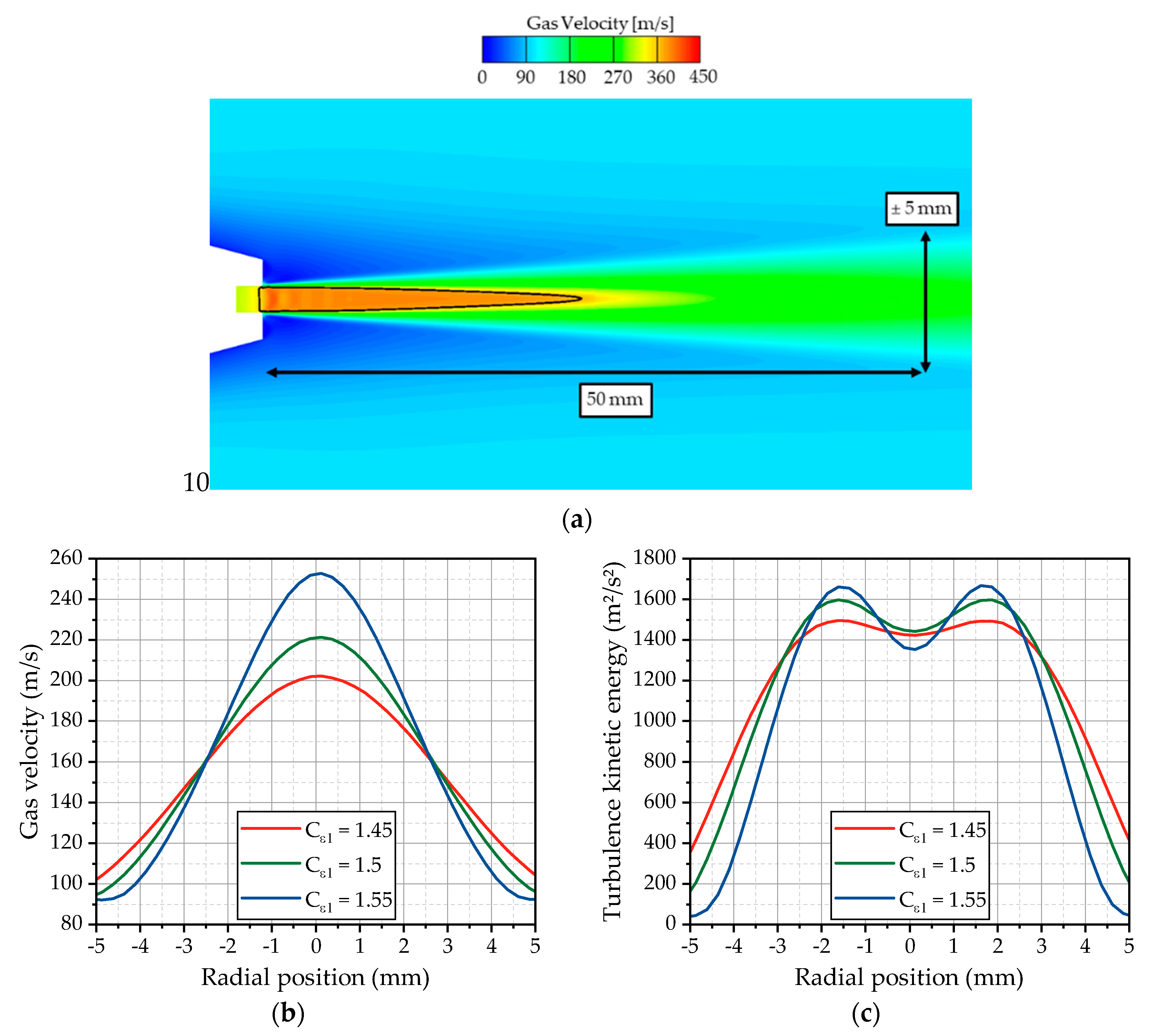
Figure 7a. The expanding gas jet preserves a supersonic core up to 25 mm downstream the nozzle. Further downstream of the nozzle, the jet is rapidly decelerated on its center axis by radial momentum flux, leading to the widening of the radial velocity profile. The spreading rate determines the resulting velocity profile at the first measurement position and is strongly influenced by the choice of the turbulence model and the discretization.
For the investigation of the impact of the used k-ε turbulence model on the spreading rate, the model parameter
Cε1, which controls the influence of the production term P in the transport equation of the dissipation rate, is adjusted, as already discussed in
Section 2.2.2. In
Figure 7b, the velocity profiles for three different values of the
Cε1 parameter are plotted for OP 2. Obviously, the spreading rate of the jet is very sensitive to this parameter. Higher
Cε1 values lead to a smaller spreading rate and a narrower profile. Lower values result in a wider velocity profile. According to the fact that the standard k-ε model predicts a too-high spreading rate [
25], the model constant
Cε1 is adapted to 1.49, which was found suitable to achieve a good agreement with the experimentally observed droplet velocities discussed in
Section 3.2. The value of 1.49 is slightly lower than the often literature-proposed values of 1.55 and 1.6 [
7,
28]. Further on, the influence on the turbulence kinetic energy is investigated. The radial profiles of the turbulence kinetic energy are illustrated in
Figure 7c for OP 2. For higher values of
Cε1, significant peaks appear at the radial positions ±1.5 mm, while, for lower values close to the standard model, the peaks seem to disappear. Lower values also lead to a wider spreading of the turbulence kinetic energy, which is consistent with the observations from the flow velocity.
3.2. Evaluation of Droplet Velocities
The following section covers the investigation of the droplet velocities derived from the experiment and the simulation. Thereby, the quality and the predictivity of the computational method will be discussed. Starting from the simulation of the gas jet, the droplets are released into the computational domain according to the initial conditions derived in
Section 2.2.4. The droplet velocities were evaluated at the first measurement position 50 mm downstream of the nozzle exit in the radial direction. A traverse system was applied in the experiment to shift the measurement volume, starting from −5 mm to 5 mm, in 1 mm steps through the spray (see
Section 2.1). Due to the higher signal-to-noise ratio, less droplets are detectable in the range of 0 mm to 5 mm, leading to less statistical significance and an asymmetric velocity profile. To overcome this, and to improve the comparability with the almost symmetric simulation data, the average of both sides is calculated and mirrored at the center axis [
17].
The spray data derived from the simulations is processed using a MATLAB
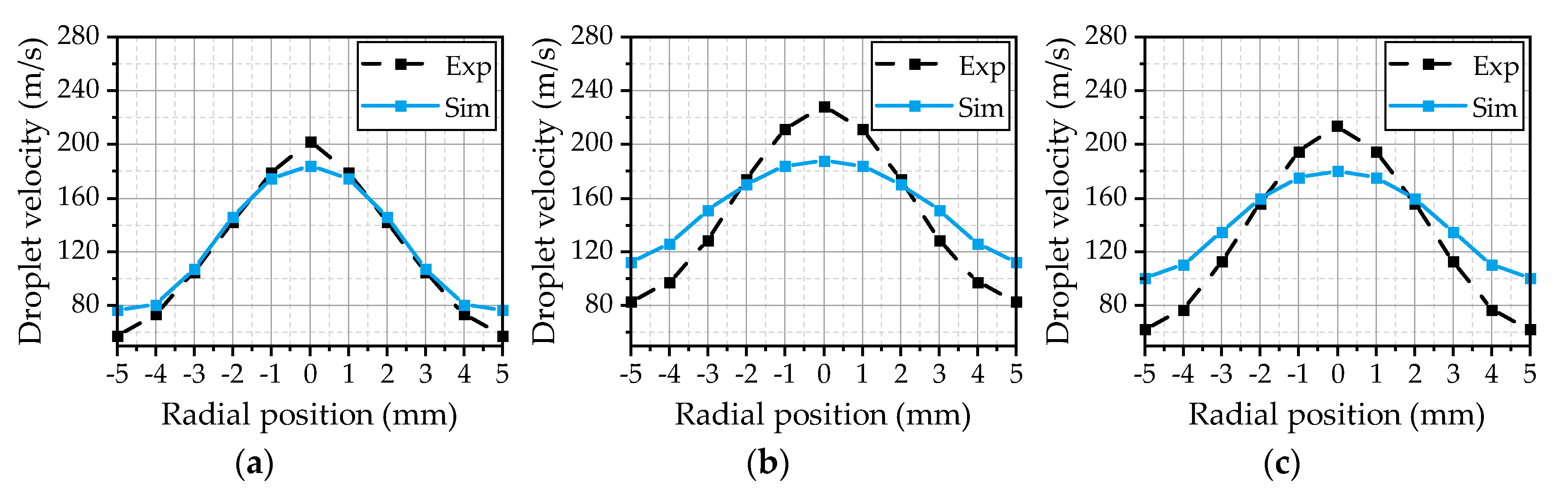
® (R2019b, The MathWorks, Inc., Natick, MA, USA) routine. Thereby, the data comprises the properties of every parcel in the simulation domain exported at different time steps. At first, the data is filtered to extract the parcels in the experimental measurement volume at the corresponding measurement positions. Subsequently, the temporal averages of the properties of different droplet size classes are calculated. This procedure is similar to the evaluation of the experimental data, where the derived values represent the temporal average of the detected droplets from the recorded images. The evaluated velocities of the droplets with a diameter of 5 µm for the three investigated operating points are illustrated in
Figure 8. This size class is slightly above the smallest detectable droplet size of the experimental methodology and gives an insight into the gas velocity due to a small Stokes number. Overall, the simulation results are in a good agreement with the experiment for all three operating points. The best fit could be achieved for OP 2 (
Figure 8b), which served as a reference point for the model calibration. Thus, the
Cε1 parameter of the turbulence model seems to be chosen appropriately. Starting from a maximum value at the center axis, the velocity decreases with the radial distance until it reaches the range of the gas velocity at ±5 mm. For OP 1 (
Figure 8a), the simulated curve is a little wider than experimentally observed, resulting in a reduced maximum in the center. This may result from an overestimation of the spreading rate of the gas jet due to a higher gas mass flow and an increase of the ambient density from 0.54 kg/m³ (OP 2) to 1.08 kg/m³ (OP 1). Further on, there are no 5 µm droplets detected at the radial positions ±4 mm and ±5 mm in the simulation. This behavior is suspected to be a result of underestimated turbulent transport phenomena inside the spray, since the turbulent fluctuations are not resolved. Small droplets will follow the turbulent motion inside the spray plume, which distributes the droplets inside the spray. By means of RANS simulations, the turbulent dispersion is modeled as described in
Section 2.2.3. due to the fact that RANS solutions provide an averaged flow field that contains no detailed information about the turbulent fluctuations. A deeper insight into the turbulent transport phenomena could be achieved using a large eddy simulation that resolves the largescale turbulence structures.
A further validation of the simulation is performed using the measured droplets with a diameter of 8 µm. These droplets possess a higher inertia and respond to an acceleration or a deacceleration of the gas flow with some delay. The radial velocity profiles of the droplets with a diameter of 8 µm are illustrated in
Figure 9 for the three investigated operating points. The simulation results show a good correlation with the experimental data for all operating points, which suggests a predictivity of the model in the present range of the operating conditions. Droplets are also detected at a radial position of ±4 mm in the simulation. Thus, those droplets are less-aligned to the center of the spray by the high gas velocity inside the gas jet. However, at a radial position of ±5 mm, there are still no 8 µm droplets detectable in the simulation.
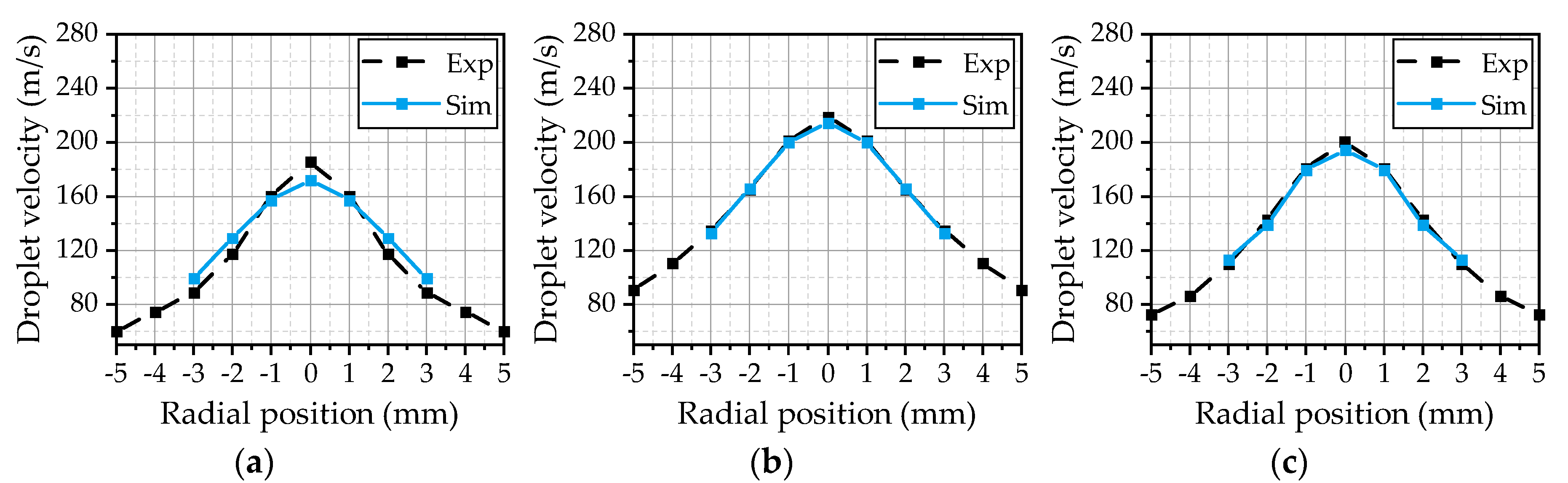
The velocity profiles of droplets with diameters greater than 15 µm are illustrated in
Figure 10. These droplets represent large droplets in the present spray. In this case, the comparability of the simulation with the experiment is dependent on the conformity of the droplet spectra, due to the dependence of the droplet velocity on the droplet size. The simulated velocity profile for OP 1 (
Figure 10a) is in a good agreement with the experimentally observed velocities. The maximum velocity in the center of the spray is slightly underpredicted. For OP 2 (
Figure 10b) and OP 3 (
Figure 10c), the velocity profile is predicted significantly wider by the simulation than in the experiment. This is followed by an overestimation of the droplet velocity in the outer area of the jet. The lower density of the hot gas in OP 2 and OP 3 results in a reduction of the momentum transfer between the gas phase and the liquid phase. This results in an underestimation of the deacceleration of larger droplets in the outer area and of the acceleration of larger droplets in the center of the spray.
One must consider the initial velocity imprinted on the droplets in the simulation for a more detailed interpretation of these phenomena. All droplets are initialized with a constant velocity. Imprinting the corresponding velocity for each size class on the initial droplets according to
Section 2.2.4 may improve the results. This way, small droplets will emerge from the nozzle with a higher velocity, while larger droplets will emerge with a lower velocity. This will enhance the momentum transfer between the gas phase and larger droplets due to a reduction of the momentum flux to smaller droplets due to smaller relative velocities. Nevertheless, the estimated droplet initial conditions, in combination with the tuning of the turbulence model, provide reasonable results for a wide range of droplet sizes that are in good agreement with the experimentally determined velocity profiles.
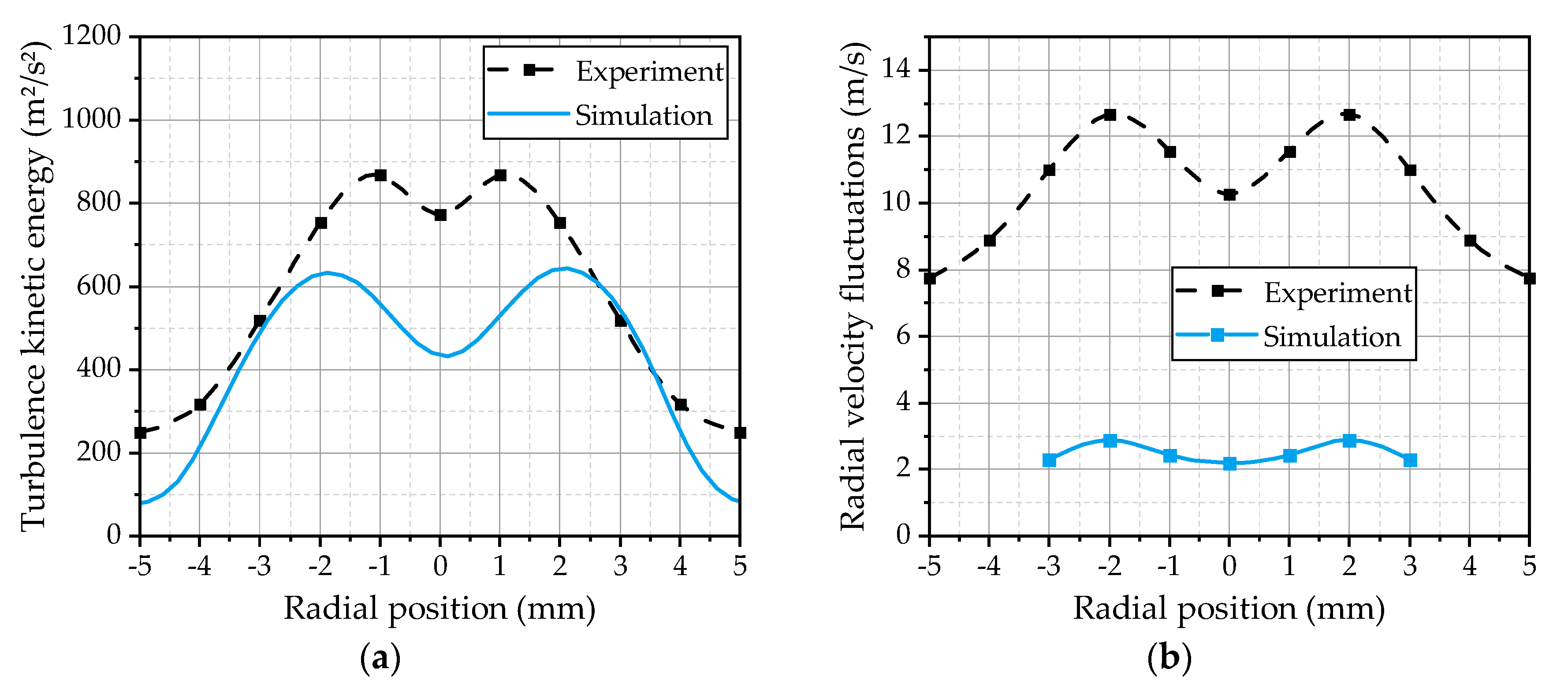
In addition to the mean velocities, the turbulent fluctuations inside the spray are of interest, because they represent the basis for the turbulent dispersion of the droplets. Further on, the turbulence enhances the heat and mass transfers, which increase the evaporation rate of the spray. Therefore, the turbulence kinetic energy calculated by the turbulence model in the gas phase is compared with the experimentally estimated turbulence kinetic energy from the velocity fluctuations of the 5 µm droplets. This droplet class can be used as an indicator for the turbulent fluctuations of the gas phase, as demonstrated in [
17]. The radial profiles of the simulated and the experimentally evaluated turbulence kinetic energy at the first measurement position are depicted in
Figure 11a. The shape of the two curves is qualitatively in a good agreement, while the absolute values in the center and the outer area of the spray are underestimated by the simulation. The contour of the simulated turbulence indicates that the value chosen for the
Cε1 parameter of the turbulence model is suitable. As shown in
Figure 7c, the choice of
Cε1 strongly influences the profile of the turbulence kinetic energy. In addition, the radial components of the droplet velocity fluctuations are compared in
Figure 11b. The simulation and the experimental results are represented by the velocity fluctuations of the 5 µm droplets. It becomes apparent that the velocity fluctuations of the droplets are much lower in the simulation, while the shapes of the two curves are qualitatively in good agreement. Even the position of the maxima is correctly predicted. This may be an indication of an underestimation of the turbulent dispersion effects inside the spray plume. One has also to consider that the information of the radial velocity fluctuations of the gas velocity is not provided by the RANS solution. Therefore, they have to be estimated by the turbulent dispersion model using the modeled turbulence kinetic energy, which will lead to uncertainties. More complex turbulence models like Reynolds stress models could be an interesting alternative for a more detailed modeling of the turbulent dispersion phenomena due to the fact that they are able to consider anisotropic turbulence. However, the turbulent transport inside the spray is a significant issue for further investigations.
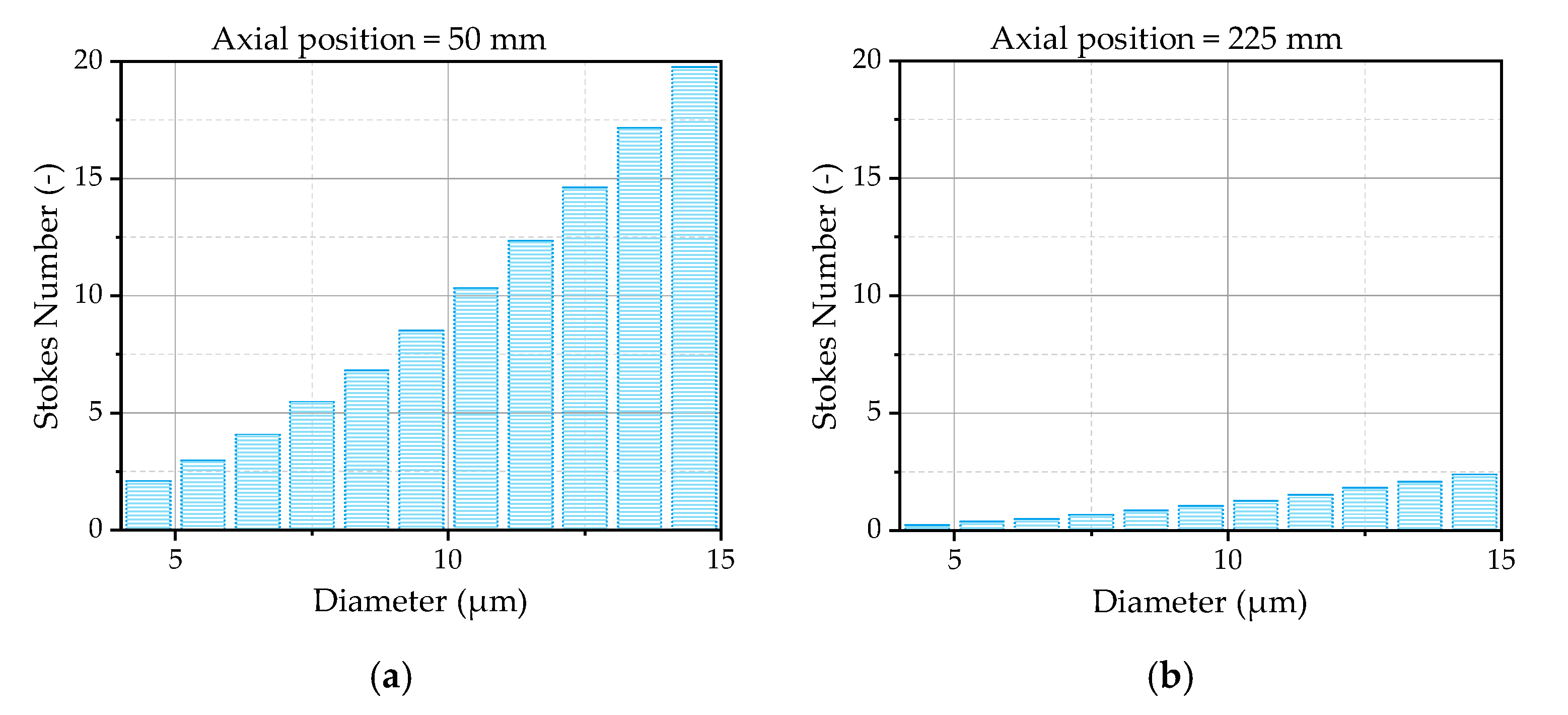
The Stokes number of the droplets is, as generally discussed in
Section 2.2.3, a decisive parameter to evaluate a droplet’s response to the turbulent motion of the gas phase. Therefore, the Stokes number of the droplets is analyzed by means of the simulation results at the first two measurement positions downstream of the nozzle.
Figure 12a illustrates the Stokes number as a function of the droplet size averaged in radial direction from -3 mm to 3 mm at the first measurement position. The radial positions are chosen due to the fact that there are still small droplets detectable, as previously discussed. The Stokes number increases with an increasing droplet diameter, which is mainly driven by a higher relaxation time due to a higher inertia of bigger droplets. The smallest droplets are in a range of a Stokes number of 2.5 and are, therefore, less affected by the turbulent motions of the gas phase, as expected. One reason for this behavior is the small eddy lifetime at this position. Further downstream the nozzle exit, the Stokes number decreases due to an increasing eddy lifetime, shown in
Figure 12b for the second measurement position. At this position, the Stokes numbers of the smallest droplets are lower than unity, resulting in a high impact of the turbulent motion on the droplet trajectories. If the findings of Klose et al. [
37] are considered, the Gosman and Ioannides model [
31], applied for the modeling of the turbulent dispersion, provides good results in a narrow area of Stokes numbers ~2. The model should be able to describe the turbulent dispersion shortly after the first measurement position. In the area upstream the first measurement position, the Stokes numbers are higher, leading to uncertainties in the modeling. One has still to consider that, to finally judge the quality of the selected dispersion model, more detailed information about the initial conditions of the droplets at the nozzle exit is necessary.
3.3. Discussion of Droplet Sizes
In addition to the droplet velocities, the diameter distribution of the spray is of interest for the assessment of the quality of the model. Therefore, the arithmetic diameter (D
10), the Sauter mean diameter (D
32) and diameter at the 90% volumetric quantile (D
V90), depicting the characteristic parameters of a droplet spectrum, are evaluated in the radial direction at the first measurement position 50 mm downstream of the nozzle. This is conducted by means of a MATLAB
® routine, as described in
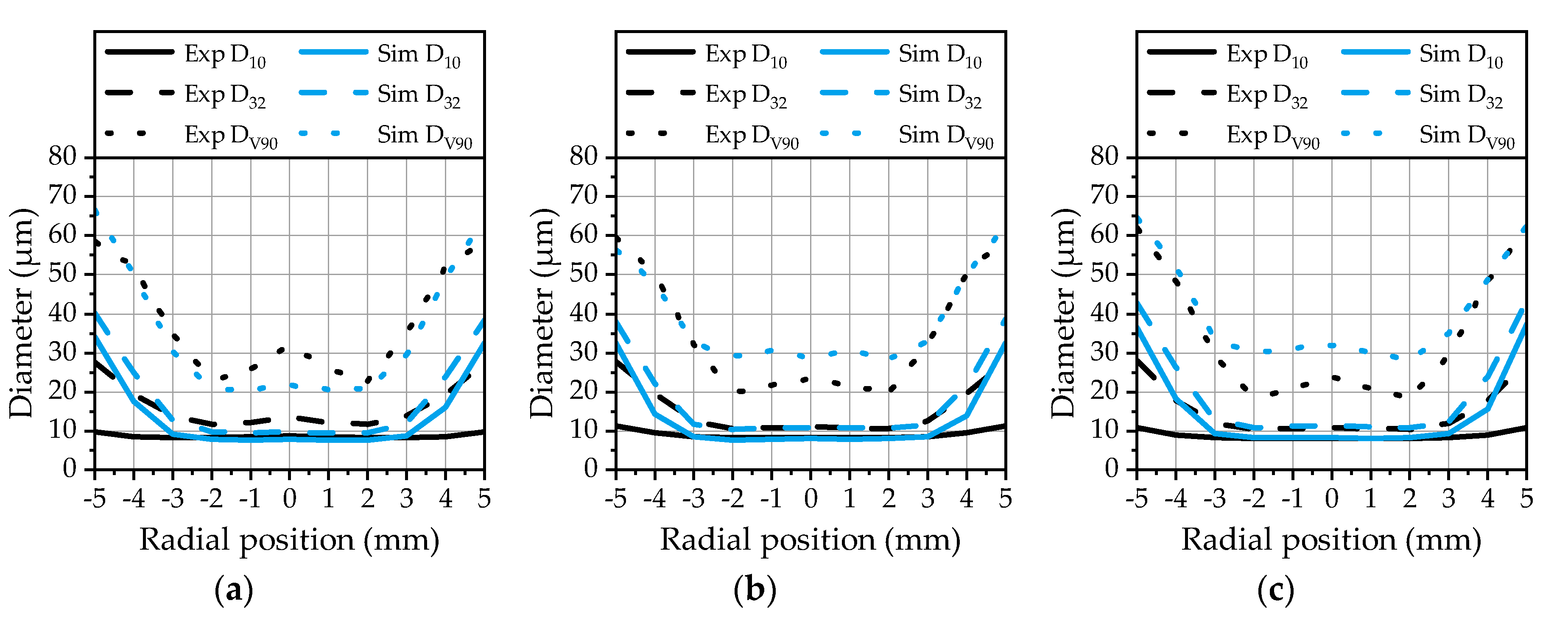
Section 3.2. The radial profiles of the characteristic parameters are plotted in
Figure 13 for the three investigated operating points. The arithmetic diameter and the Sauter mean diameter calculated from the simulation data are in good agreement with the experimental data in the core region of the spray. In the outer area, starting from ±3 mm, the arithmetic diameter is overestimated by the model.
An explanation for this behavior is the absence of small droplets in this area as already presented in
Figure 8. The Sauter mean diameter is in a range of 10 µm to 14 µm in the spray center for all three operating points, which confirms a continuously good atomization. The SMD is also correctly predicted by the model in the core zone, while it is overestimated in the outer area. Finally, the DV
90 from the simulation data is in a good agreement with the experiment over the whole radial distance for OP 1 (
Figure 13a). For OP 2 (
Figure 13b) and OP 3 (
Figure 13c), there is a slight overestimation in the core area recognizable. The DV
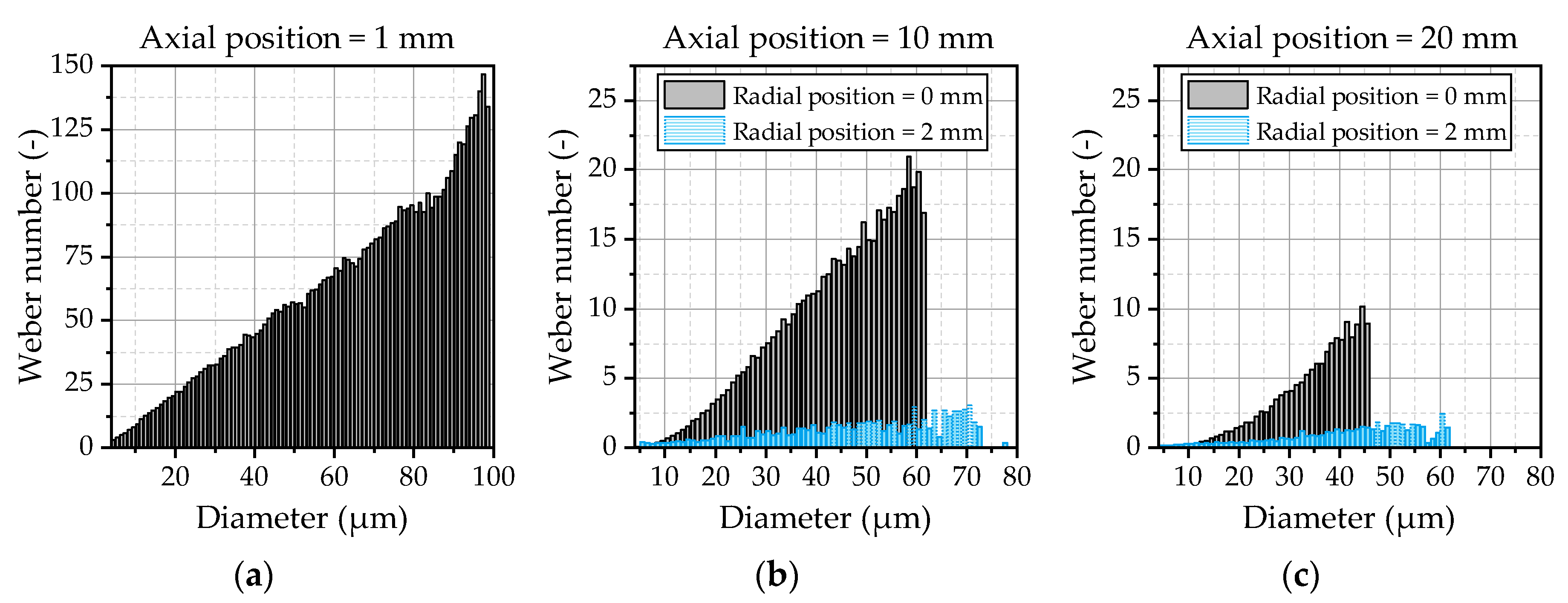
90 depicts a sensitive parameter that can be strongly influenced by a small number of larger droplets. The correlation with the experimental data achieved by the model demonstrates that the droplet breakup and kinematics are predicted correctly. Large droplets emerging at the spray center are immediately broken up in the vicinity of the nozzle due to high relative velocities, while they persist in the outer area of the spray. This behavior can be analyzed by an evaluation of the Weber number of the droplets. The Weber number of the droplets at three different positions downstream of the nozzle exit is illustrated
Figure 14. Further on, the Weber number is depicted in the spray center and the outer area of the spray at distances of 10 mm (
Figure 14b) and 20 mm (
Figure 14c) downstream the nozzle.
In the vicinity of the nozzle (
Figure 14a), high Weber numbers up to 150 occur due to the high relative velocities of the droplets and the escaping gas jet. This results in an immediate breakup of the droplets that is also known from high-pressure injections. At the axial position of 20 mm (
Figure 14c), the Weber numbers are smaller than 10, indicating that the main part of the secondary atomization is completed. The droplets in the outer area of the spray represented by the radial position of 2 mm in
Figure 14b,c quickly leave the core region of the gas jet, resulting in Weber numbers smaller than 3 even for bigger droplets in the area of 50 µm to 70 µm. Those droplets are not atomized and are preserved at the spray boarders, resulting in the observed behavior of the DV
90 in
Figure 13, which could be predicted quite well by the applied WAVE breakup model.
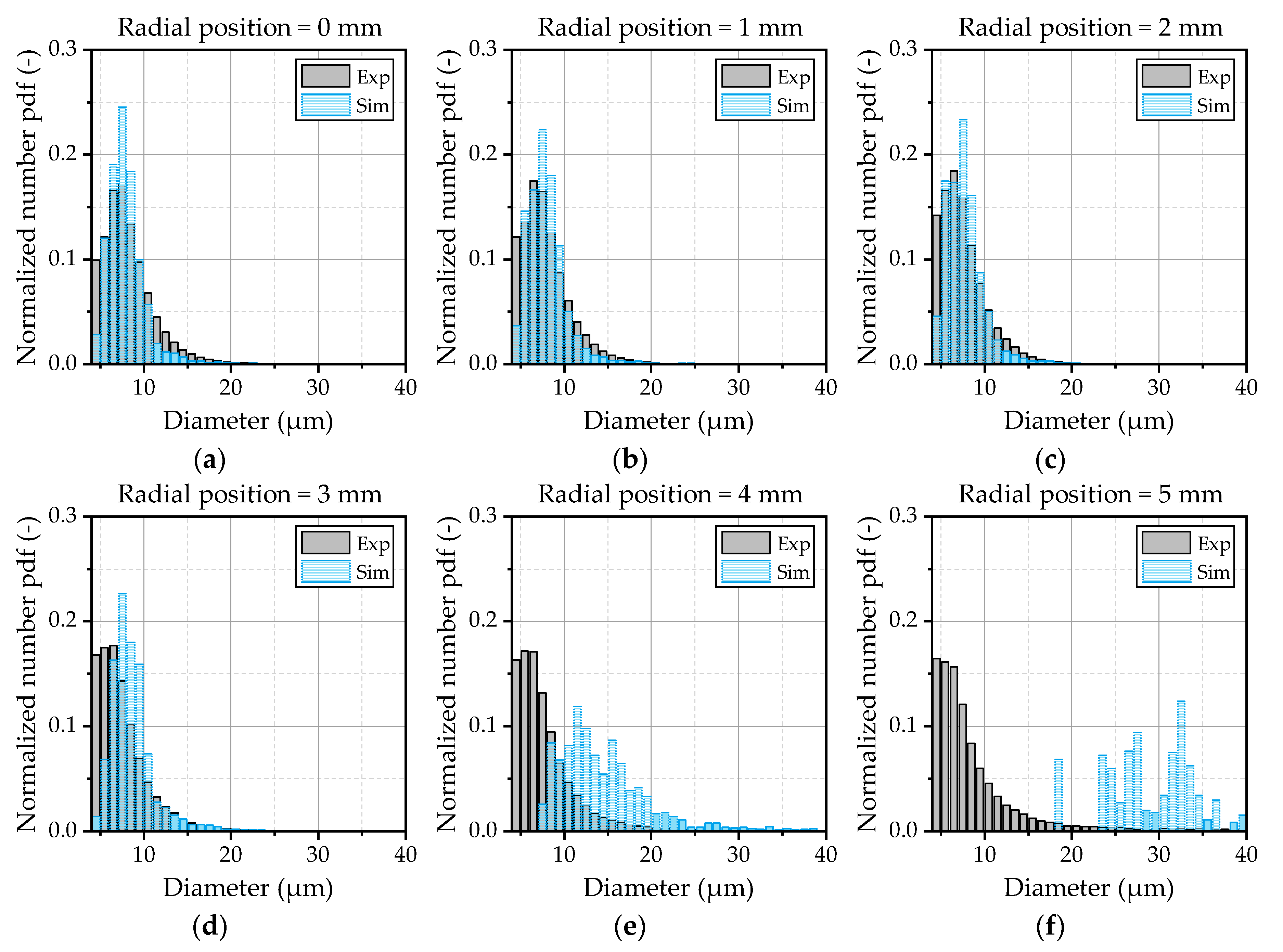
Apart from the characteristic parameters of the spray, the droplet spectra are evaluated in the following to get a deeper insight into the observed behavior of smaller droplets. Therefore, the filtered data from the simulation and the data of the single droplets detected in the experiment are processed with a MATLAB
® routine. Thus, the processing of the data is the same for the simulation and experiment, ensuring good comparability. One has to consider that the statistical significance of the experiment is considerably higher than of the simulation, due to the fact that the measured droplet spectrum at a given measurement position consists of 10
4 to 10
5 single droplets, which are represented by a few hundred to thousand detected parcels in the simulation. The droplet spectra at different radial positions are illustrated as number-based distributions in
Figure 15 for OP 2.
In the center zone of the spray depicted by
Figure 15a–c, the spectrum is well-predicted by the model. In the outer area, starting from 3 mm (
Figure 15d) up to 5 mm (
Figure 15f) the deviations between the experiment and simulation increased. The already discussed lack of small droplets at the edge of the spray cone becomes obvious by means of this illustration. Based on these results, further investigations should be conducted to get a deeper insight into the turbulent transport phenomena inside the jet and the breakup of the droplets inside the shear layer of the gas flow. Further on, a detailed investigation of the initial conditions of the droplets at the nozzle exit is necessary to provide well-defined boundary conditions for the validation of the turbulent dispersion. Thereby, large eddy simulations in combination with a volume-of-fluid approach could serve as a suitable method to gain detailed information about the turbulent structures and the formation of the initial droplets.
3.4. Evaporation of the Urea-Water Droplets
Prior to evaluating the predicted evaporation characteristics of the spray, the evaporation process of urea-water droplets will be discussed briefly. The evaporation can be subdivided into two main stages: The first stage is characterized by an almost exclusive evaporation of water. This means that there will be no evident difference between the evaporation of pure water and urea-water droplets. Once the water of the urea-water droplet is consumed by evaporation, the thermolysis and evaporation of urea sets in. This is the second stage, which can be described as an evaporation process with a considerably lower evaporation rate in comparison to water. At the same time, the droplet temperature increases drastically. A detailed investigation of the evaporation process of urea-water droplets is given by Birkhold [
33].
The important conclusion from the brief discussion of the evaporation process is that a designated droplet size exists during the lifetime of each urea-water droplet at which, the evaporation rate is drastically reduced. This distinct feature of the evaporation process was used to define the droplet size at the limit of water evaporation as a criterion for determining the progress of spray evaporation in a previous study [
17]. Using this criterion, the comparison of experimental results to numerical predictions is straightforward, which will be directly demonstrated in the following paragraphs.
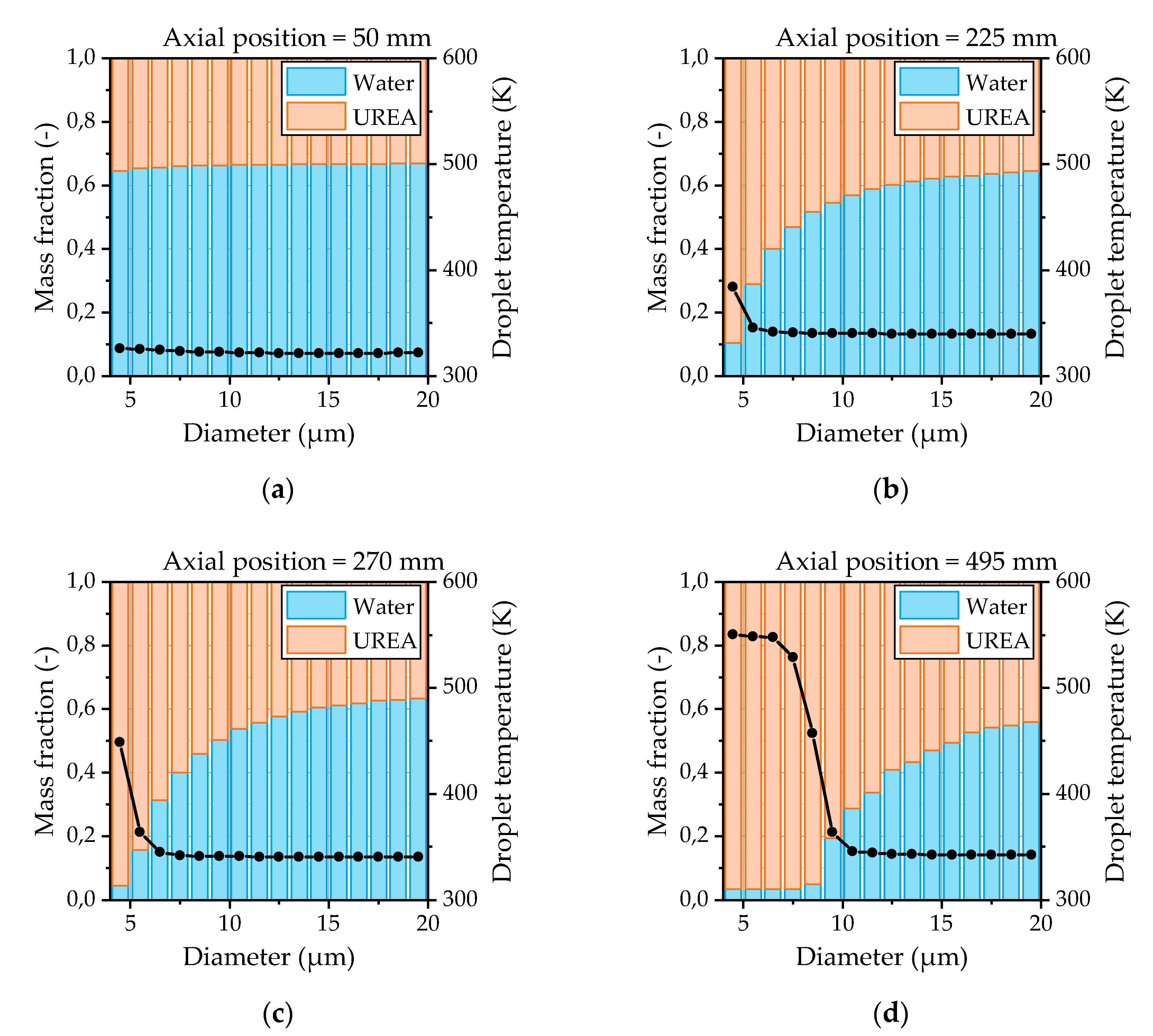
The evaporation characteristics of the urea-water droplets are evaluated from the simulations by means of the droplet temperature and the droplet composition. Thereby, the droplet composition provides information about whether a droplet undergoes water evaporation or urea thermolysis. The composition and temperatures of the droplets as a function of the droplet size and the distance from the nozzle are depicted in
Figure 16 for OP 2. At the first measurement position shown in
Figure 16a, there is no significant evaporation recognizable. Only the smallest droplets start to evaporate. This behavior also proves the suitability to apply an averaged droplet spectrum from the first measurement position as the initial condition at the nozzle exit in the CFD model. After the droplets are heated up, the water evaporation is present for almost all droplet sizes shown in
Figure 16b. The urea thermolysis indicated by a rapid rise of the droplet temperature and a significant reduction of the water content has already begun for the smallest droplets at this position. Further downstream of the nozzle, the droplet diameter from which the urea thermolysis is present increases continuously, as illustrated in
Figure 16c,d. Thereby, the droplet temperature reaches a steady state for droplets smaller than 7 µm at the last measurement position 495 mm downstream of the nozzle.
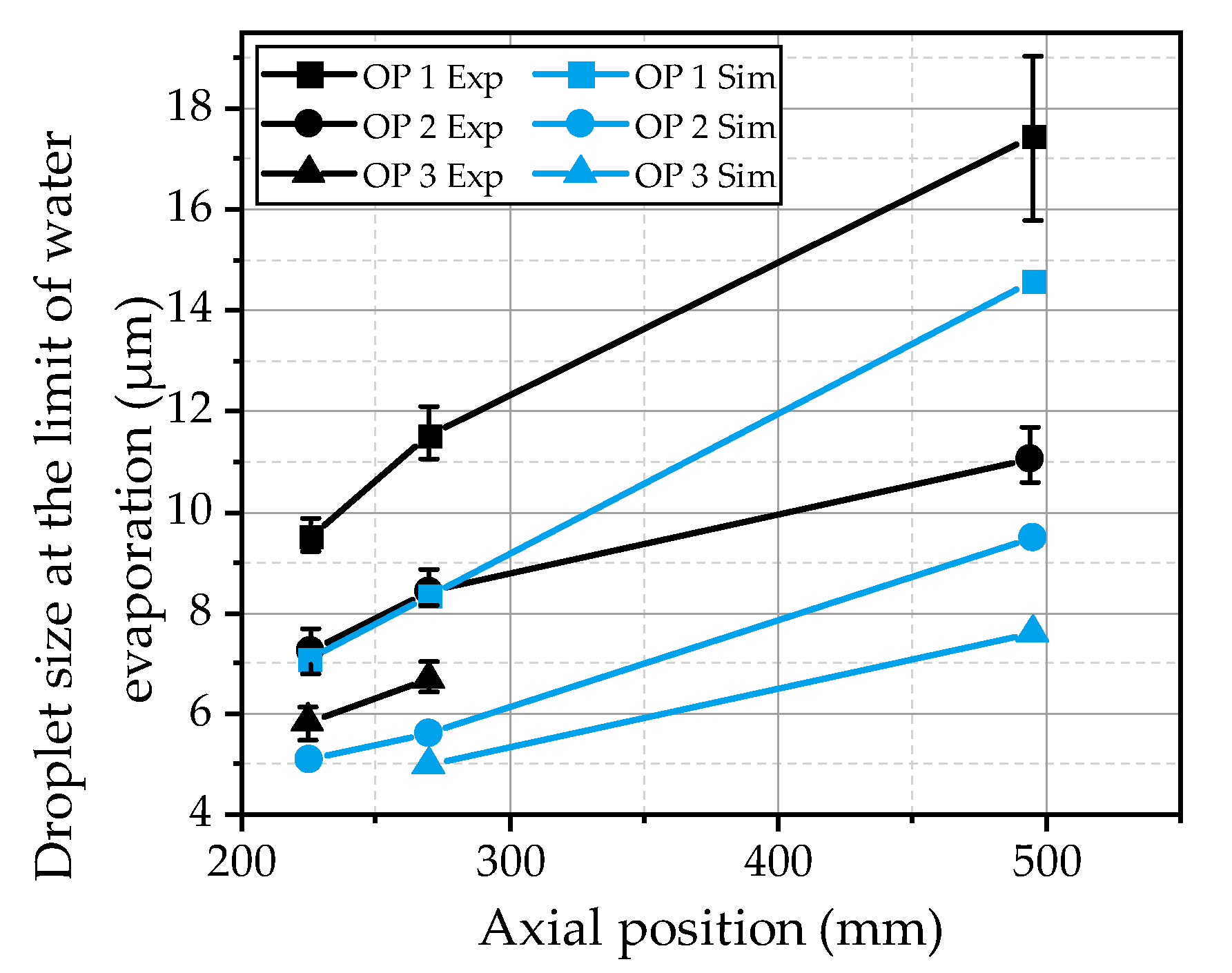
To compare the findings from the simulations with the experimental observations, the characteristic diameter at which the urea thermolysis starts is evaluated. The evaluation is conducted by the increase of the droplet temperature as a function of the droplet diameter. In the case of a strong rise above 10 K from size class to size class, the corresponding droplet size is determined as the diameter at the limit of water evaporation. The results are compared with the experimental data in
Figure 17 for the three investigated operating points as a function of the axial distance from the nozzle. It is obvious that the progress of the evaporation process of the present urea-water spray is underpredicted by the model. The diameter at the limit of water evaporation is approximately 2 µm to 3 µm below the experimental results. Nevertheless, the effects of the three hot gas operating conditions are predicted correctly. The evaporation rate is significantly decreased from OP 1 to OP 2 due to a decrease in the ambient density. For OP 3, the evaporation rate is further decreased due to a considerably lower ambient temperature. The underestimation of the evaporation process in the simulations may be explained by the turbulent dispersion, which is quite lower in the simulations. The turbulent dispersion imprints an additional fluctuation velocity on the droplets, increasing the relative velocity of the droplets, which results in higher evaporation rates. Further on, the smallest droplets are more homogenously distributed over the spray plume, reducing the temperature decrease in the center of the spray in the experiment. However, to finally assess the observed deviations between the simulation and experiment, further investigations of the evaporation process are necessary.