Dynamic Load Modelling within Combined Transport Trains during Transportation on a Railway Ferry
Abstract
1. Introduction
- -
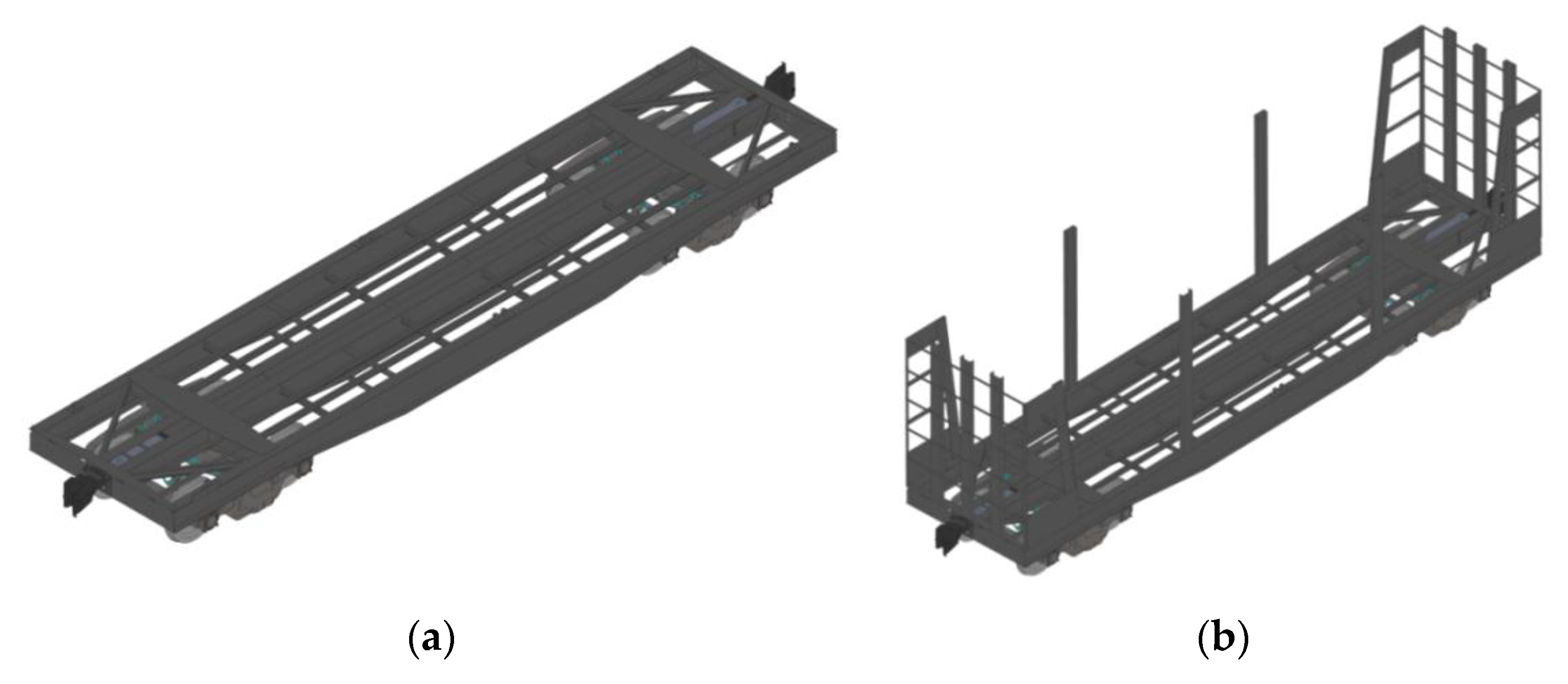
- To improve the load-bearing structure of the flat wagon in order to ensure the stability of containers during transportation by a railway ferry. This is done by placing removable superstructures on the wagon-supporting structure. At the same time, on the inner surface of the superstructures, there is a material with viscous energy-absorbing properties
- -
- To conduct mathematical modelling of the dynamic load of containers, taking into account the new scheme of interaction with the flat wagon. The simulation results will make it possible to determine the more precise definition of the dynamic load, which acts on the supporting structure of the flat wagon during transportation by sea
- -
- To conduct a computer simulation of the dynamic load of containers, taking into account the new scheme of interaction with the flat wagon. The results of computational modelling will make it possible to determine the numerical values of accelerations and their dislocation fields on the supporting structure of a flat wagon with containers, as well as to check the adequacy of the developed mathematical model.
2. Improvement of the Load-Bearing Structure of the Flat Wagon
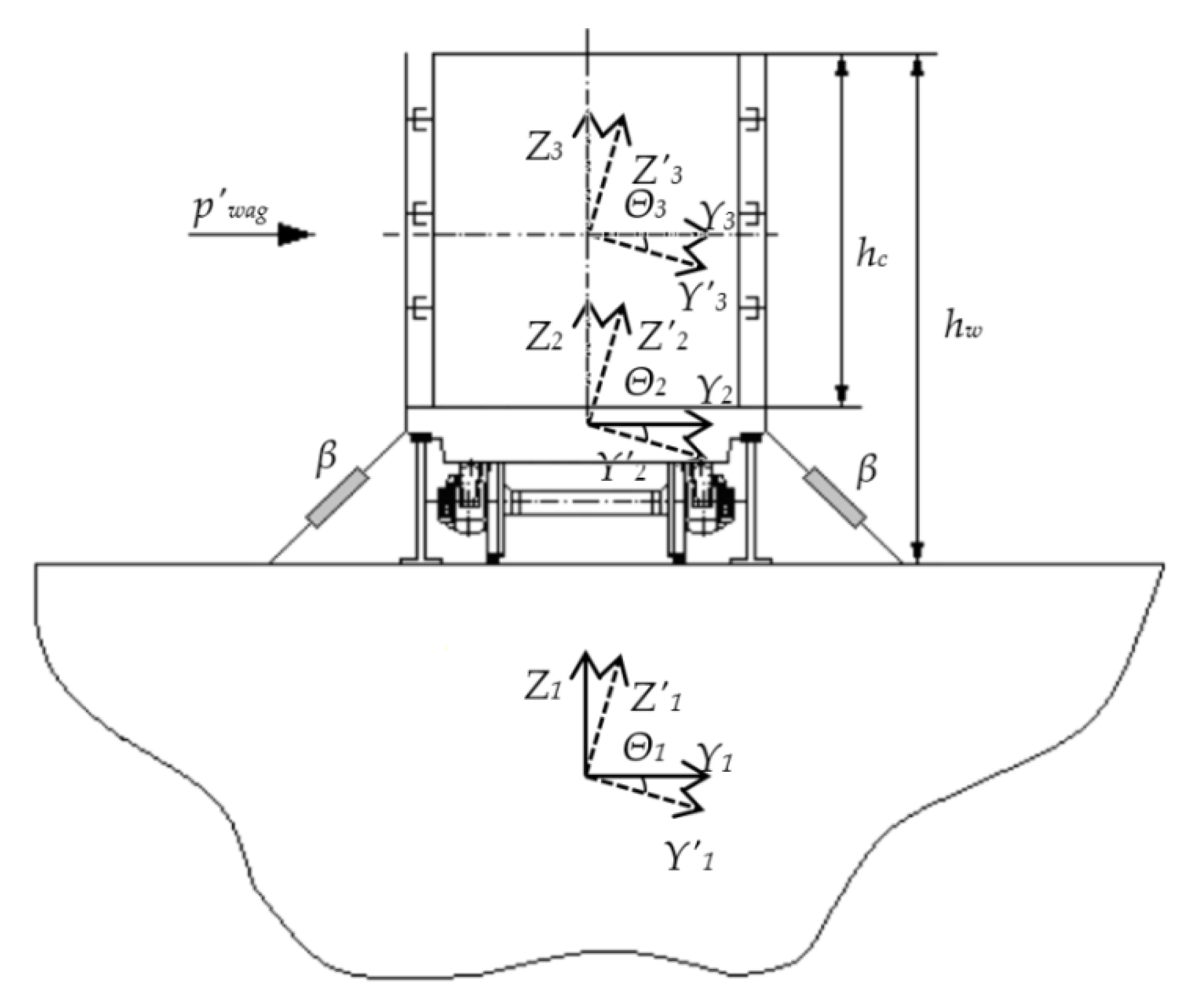
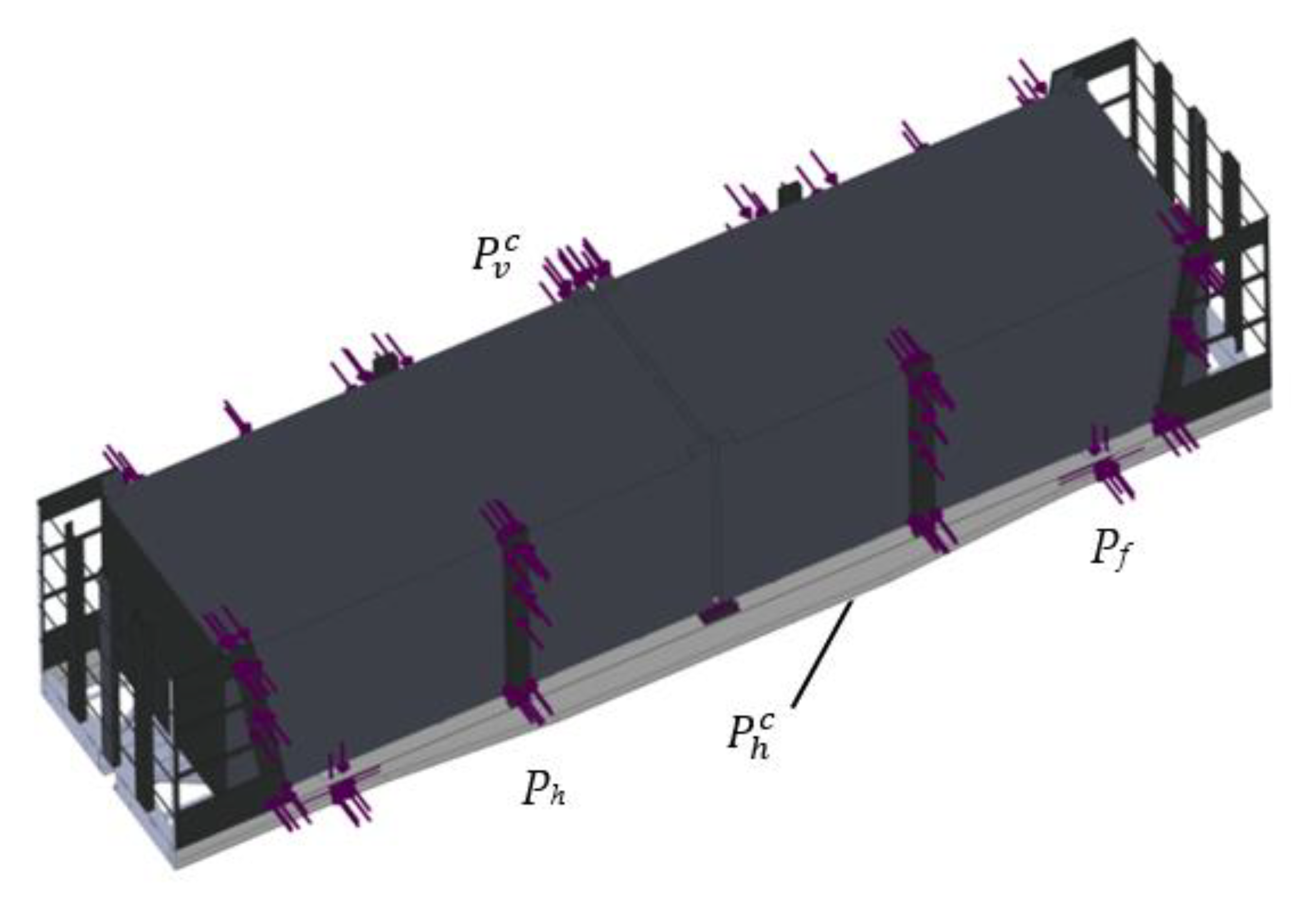
3. Mathematical Modelling of the Dynamic Load of Containers
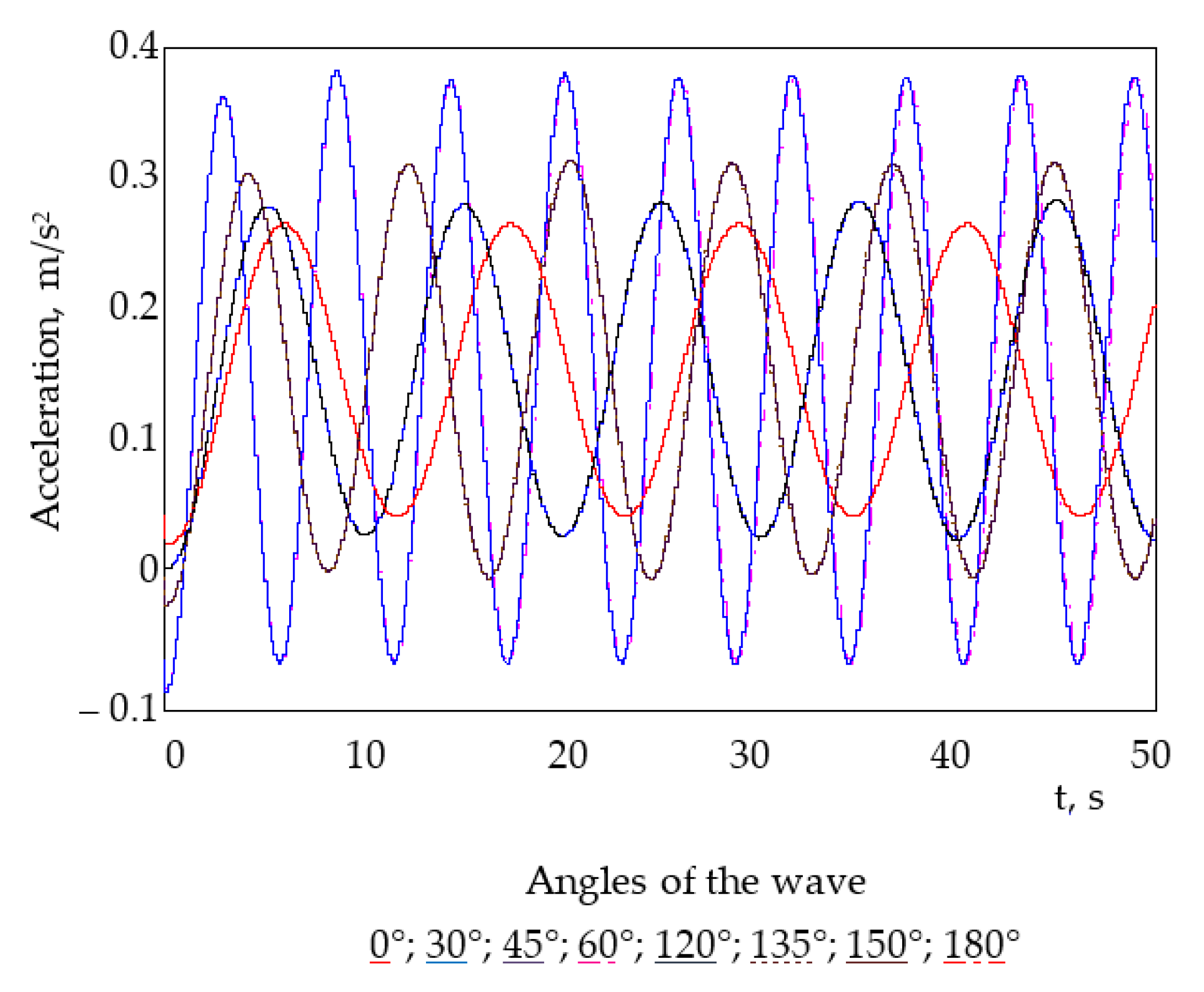
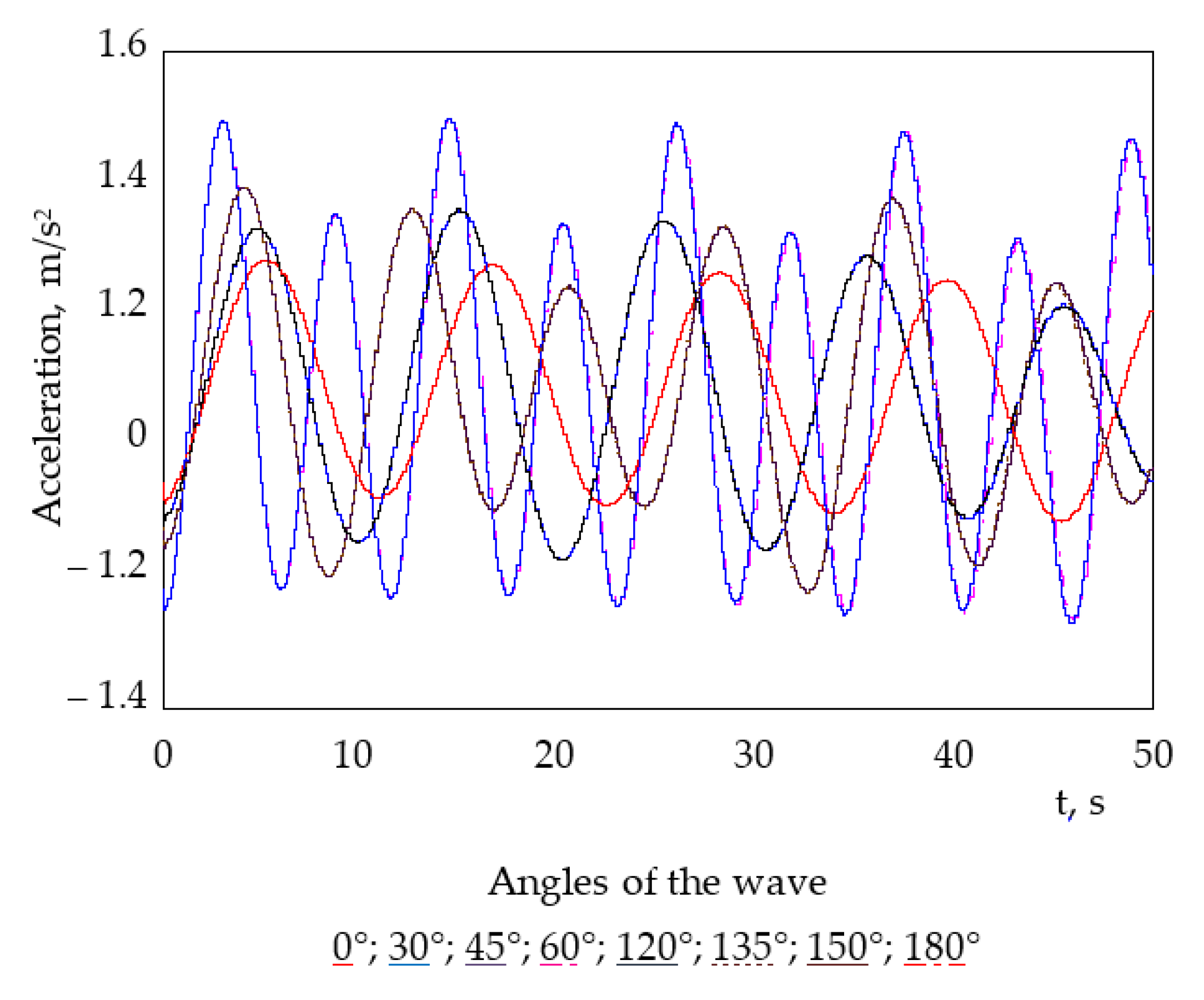
4. Results
5. The Discussion of the Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Iris, Ç.; Christensen, J.M.; Pacino, D.; Ropke, s. Flexible ship loading problem with transfer vehicle assignment and scheduling. Transp. Res. Part B Methodol. 2018, 111, 113–134. [Google Scholar] [CrossRef]
- Iris, C.; Pacino, D.; Ropke, S. Improved formulations and an adaptive large neighbourhood search heuristic for the integrated berth allocation and quay crane assignment problem. Transp. Res. Part E Logist. Transp. Rev. 2017, 105, 123–147. [Google Scholar] [CrossRef]
- Iris, Ç.; Pacino, D.; Ropke, S.; Larsen, A. Integrated Berth Allocation and Quay Crane Assignment Problem: Set partitioning models and computational results. Transp. Res. Part E Logist. Transp. Rev. 2015, 81, 75–97. [Google Scholar] [CrossRef]
- Azab, A.; Karam, A.; Eltawil, A.B. A simulation-based optimization approach for external trucks appointment scheduling in container terminals. Int. J. Model. Simul. 2019, 1–18. [Google Scholar] [CrossRef]
- Karam, A.; Eltawil, A.B.; Reinau, K.H. Energy-Efficient and Integrated Allocation of Berths, Quay Cranes, and Internal Trucks in Container Terminals. Sustainability 2020, 12, 3202. [Google Scholar] [CrossRef]
- Karam, A.; Attia, E.A. Integrating collaborative and outsourcing strategies for yard trucks assignment in ports with multiple container terminals. Int. J. Logist. Syst. Manag. 2019, 32, 372–391. [Google Scholar] [CrossRef]
- Review of the Marine Market. United Nations Conference on Trade and Development UNCTAD/RMT/2018; United Nations Publications: New York, NY, USA, 2018. (In Russian) [Google Scholar]
- Fomin, O.; Lovska, A.O.; Pistek, V.; Kucera, P. Research of Stability of Containers in the Combined Trains During Transportation by Railroad Ferry. MM Sci. J. 2020, 2020, 3728–3733. [Google Scholar] [CrossRef]
- Ceyhun, G.C. The impact of shipping accidents on marine environment: A study of Turkish seas. Eur. Sci. J. 2014, 10, 10–23. [Google Scholar]
- Bell, R.; Kirtman, B. Extreme environmental forcing on the container ship SS El Faro. J. Oper. Oceanogr. 2019, 1–16. [Google Scholar] [CrossRef]
- Battershill, C.; Ross, P. Schiel the MV Rena shipwreck: Time-critical scientific response and environmental legacies. N. Z. J. Mar. Freshw. Res. 2016, 50, 173–182. [Google Scholar] [CrossRef]
- Kamm, N. An Overview of Pollution from Shipwrecks. Ph.D. Thesis, University of Cape Town, Cape Town, South Africa, 2014. [Google Scholar]
- The Impact of Sea and River Transport on the Environment as an Urgent Problem of Our Time. Available online: https://greenologia.ru/eko-problemy/gidrosfera/rechnoi-transport.html (accessed on 23 January 2020). (In Russian).
- Death of “Mercury—2”. How It Was…. Available online: https://www.pravda.ru/accidents/9720-parom/ (accessed on 1 November 2002). (In Russian).
- In the Pacific Ocean, a Ship with Passengers on Board Sank. Available online: https://www.rbc.ru/spb_sz/07/08/2009/5592c21c9a79473b7f4bc1a8 (accessed on 7 August 2009). (In Russian).
- Steamers on Fire… Part 2. Available online: https://moremhod.info/index.php/library-menu/24-v-mire-interesnogo/131-riverkat2?showall=1 (accessed on 31 January 2011). (In Russian).
- Typhoon No. 15 (Maria) Struck—The Destruction of the Toya Maru Ferry. Available online: http://www.infoflotforum.ru (accessed on 3 March 2008). (In Russian).
- Kvyatkovsky, I.A. Man and Ship; Gidrometizdat: Leningrad, Russia, 1972. (In Russian) [Google Scholar]
- Nikitchenko, A.; Artiukh, V.; Shevchenko, D.; Prakash, R. Evaluation of Interaction between Flat Wagons and Container at Dynamic Coupling of Flat Wagons. In MATEC Web of Conferences; EDP Sciences: Paris, France, 2016; Volume 7. [Google Scholar] [CrossRef]
- Wojcik, K.; Małachowski, J.; Baranowski, P.; Mazurkiewicz, Ł.; Damaziak, K.; Krasoń, W. Multi-Body Simulations of Railway Wagon Dynamics. J. KONES 2015, 19, 499–506. [Google Scholar] [CrossRef]
- Chłus, K.; Krasoń, W. Numerical standard tests of railway carriage platform. J. KONES Powertrain Transp. 2012, 19, 59–64. [Google Scholar] [CrossRef]
- Šťastniak, P.; Kurčík, P.; Pavlík, A. Design of a new railway wagon for intermodal transport with the adaptable loading platform. In MATEC Web of Conferences; EDP Sciences: Paris, France, 2018; p. 235. [Google Scholar]
- Lovskaya, A.A. The definition of freight pressure which influence upon the wall of open-top wagon under transportation with railway-ferry boat. Collect. Sci. Works Ukr. State Acad. Railw. Transp. 2014, 143, 54–57. [Google Scholar]
- Eremin, V.; Semennikova, L. The Study of the Stress-Strain State of the Container Body Using the APM WinMachine Software Package; CAD and Graphics: Foster, CA, USA, 2004; Volume 7, pp. 23–28. (In Russian) [Google Scholar]
- Ibragimov, N.N.; Rahimov, R.V.; Hadzhimuhamedova, M.A. Development of the design of a container for transportation of fruits and vegetables. Molod. Uchenyiy 2015, 21, 168–173. (In Russian) [Google Scholar]
- Tiernan, S.; Fahy, M. Dynamic FEA modelling of ISO tank containers. J. Mater. Process. Technol. 2002, 124, 126–132. [Google Scholar] [CrossRef]
- Rzeczycki, A.; Wisnicki, B. Strength Analysis of Shipping Container Floor with Gooseneck Tunnel under Heavy Cargo Load. Solid State Phenom. 2016, 252, 81–90. [Google Scholar] [CrossRef]
- Zemlezin, I.N. Methodology for Calculating and Studying the Forces Acting on a Wagon during Transportation by Sea Ferries; Transport: Moscow, Russia, 1970. (In Russian) [Google Scholar]
- Shmakov, M.G. Special Ship Devices; Shipbuilding: Leningrad, Russia, 1975. (In Russian) [Google Scholar]
- Manual on Securing Cargo for the Ship “Petrovsk”; Marine Engineering Bureau: Odessa, Ukraine, 2005. (In Russian)
- Cargo Secuaring Menual m/v “Geroite na Sevastopol”; Navigation Maritime Bulgare: Varna, Bulgaria, 1997. (In Bulgarian)
- Cargo Secuaring Menual Transocean Line a/s ms “Greifswald”; Germanischer Lloyd: Hamburg, Germany, 2001.
- Blagoveshchensky, S.N.; Kholodilin, A.N. A Reference Book on the Statics and Dynamics of a Ship; Shipbuilding: Leningrad, Russia, 1975. (In Russian) [Google Scholar]
- Makov, Y.L. Pumping of Ships; Kaliningrad State Technical University: Kaliningrad, Russia, 2007. (In Russian) [Google Scholar]
- Vasiliev, V. Railway ferries for the line Illichivsk—Varna. Navy 1976, 12, 16. [Google Scholar]
- Davidan, N.I. Wind and Waves in Oceans and Seas: Reference Data; Transport: Leningrad, Russia, 1974. (In Russian) [Google Scholar]
- Lovska, A.O.; Ryibin, A. The study of dynamic load on a wagon–platform at a shunting collision. East. Eur. J. Enterp. Technol. 2016, 3, 4. [Google Scholar] [CrossRef]
- Fomin, O.; Lovska, A.; Kulbovskyi, I.; Holub, H.; Kozarchuk, I.; Kharuta, V. Determining the dynamic loading on a semi-wagon when fixing it with a viscous coupling to a ferry deck. East. Eur. J. Enterp. Technol. 2019, 2, 6–12. [Google Scholar] [CrossRef]
- Lovskaya, A.; Gerlici, J.; Fomin, O.; Kravchenko, K.; Prokopenko, P.; Lack, T. Improvement of the bearing structure of the wagon-platform of the articulated type to ensure the reliability of the fixing on the deck of the railway ferry. In MATEC Web of Conferences; EDP Sciences: Paris, France, 2019; p. 254. [Google Scholar]
- Fomin, O.; Gerlici, J.; Lovskaya, A.; Kravchenko, K.; Burlutski, O.; Hauser, V. Peculiarities of the mathematical modelling of dynamic loading on containers in flat wagons transportation. In MATEC Web of Conferences; EDP Sciences: Paris, France, 2019; p. 254. [Google Scholar]
- Kondratiev, A.; Prontsevych, O. Stabilization of physical-mechanical characteristics of honeycomb filler based on the adjustment of technological techniques for its fabrication. East. Eur. J. Enterp. Technol. 2018, 5, 71–77. [Google Scholar] [CrossRef]
- Aleksandrowicz, P. Verifying a truck collision applying the SDC method. In Proceedings of the 58th International Conference of Machine Design Departments, Praque, Czech Republic, 6–8 September 2017; pp. 14–19. [Google Scholar]
- Kostek, R.; Aleksandrowicz, P. Effect of contact parameters on the pattern of vehicle collisions with a round pillar. In Proceedings of the 23rd International Conference Engineering Mechanics, Svratka, Czech Republic, 15–18 May 2017; pp. 490–493. [Google Scholar]
- Kapitsa, M.; Mikhailov, E.; Kliuiev, S.; Semenov, S.; Kovtanets, M. Study of rail vehicles movement characteristics improvement in curves using fuzzy logic mechatronic systems. In MATEC Web of Conferences; EDP Sciences: Paris, France, 2019; p. 294. [Google Scholar]
- Fomin, O.; Lovska, A.; Píštěk, V.; Kučera, P. Dynamic load computational modelling of containers placed on a flat wagon at railroad ferry transportation. Vibroengineering Procedia 2019, 29, 118–123. [Google Scholar]
- Alyamovsky, A.A. SolidWorks/COSMOSWorks 2006–2007—Engineering Analysis by the Finite Element Method; DMK: Moscow, Russia, 2007. (In Russian) [Google Scholar]
- Kurowski, P. Engineering Analysis with SOLIDWORKS Simulation 2019; SDC Publications: Mission, KS, USA, 2019. [Google Scholar]
- Weber, M.; Verma, G. SolidWorks Simulation 2015 Black Book II Editio; SDC Publications: Mission, KS, USA, 2015. [Google Scholar]
- Vatulia, G.; Falendysh, A.; Orel, Y.; Pavliuchenkov, M. Structural Improvements in a Tank Wagon with Modern Software Packages. Procedia Eng. 2017, 187, 301–307. [Google Scholar] [CrossRef]
- Tkachenko, V.; Sapronova, S.; Kulbovskiy, I.; Fomin, O. Research of resistance to the motion of vehicles related to the direction by railway. East. Eur. J. Enterp. Technol. 2017, 5, 65–72. [Google Scholar]
- Kitov, Y.; Verevicheva, M.; Vatulia, G.; Orel, Y.; Deryzemlia, S. Design solutions for structures with optimal internal stress distribution. In MATEC Web of Conferences; EDP Sciences: Paris, France, 2017; Volume 133. [Google Scholar]
- Freight Wagons. General Requirements for the Calculations and Design of New and Upgraded 1520 mm (Non-Self-Propelled) Rail Cars; DSTU 7598: 2014; Ukrainian Scientific Railway Car Building Research Institute: Kremenchuk, Ukraine, 2014. [Google Scholar]
- Freight Wagons. Strength and Dynamic Quality Requirements; GOST 33211-2014; Standartinform: Moscow, Russia, 2014. [Google Scholar]
- Freight Wagons. Railway Applications—Structural Requirements of Railway Vehicle Bodies—Part 2; EN 12663-2; BSI: Sofia, Bulgaria, 2010. [Google Scholar]
- Christensen, J.M.; Pacino, D. A matheuristic for the Cargo Mix Problem with Block Stowage. Transp. Res. Part E Logist. Transp. Rev. 2017, 97, 151–171. [Google Scholar] [CrossRef]
- Iris, Ç.; Lam, J.S.L. A review of energy efficiency in ports: Operational strategies, technologies and energy management systems. Renew. Sustain. Energy Rev. 2019, 112, 170–182. [Google Scholar] [CrossRef]



| Parameter Name | Value |
|---|---|
| Length, m: | |
| Maximum | 184.25 |
| Between perpendiculars | 170 |
| Width | 26 |
| Height, m: | |
| To the upper deck | 15.2 |
| To the main deck | 9 |
| Draft, m | 6.5 |
| Deadweight, t | 12,889 |
| Displacement, t | 23,744 |
| Speed, knots | 18.6 |
| Wagon capacity, pcs. | 108 |
| Parameter Name | Numerical Value |
|---|---|
| Sea wave height, m | 8 |
| Sea wave period, s | 9 |
| Heading angle of a wave, degree | 0–180 |
| Wind pressure on the surface projection of the vessel, kPa | 1.47 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lovska, A.; Fomin, O.; Píštěk, V.; Kučera, P. Dynamic Load Modelling within Combined Transport Trains during Transportation on a Railway Ferry. Appl. Sci. 2020, 10, 5710. https://doi.org/10.3390/app10165710
Lovska A, Fomin O, Píštěk V, Kučera P. Dynamic Load Modelling within Combined Transport Trains during Transportation on a Railway Ferry. Applied Sciences. 2020; 10(16):5710. https://doi.org/10.3390/app10165710
Chicago/Turabian StyleLovska, Alyona, Oleksij Fomin, Václav Píštěk, and Pavel Kučera. 2020. "Dynamic Load Modelling within Combined Transport Trains during Transportation on a Railway Ferry" Applied Sciences 10, no. 16: 5710. https://doi.org/10.3390/app10165710
APA StyleLovska, A., Fomin, O., Píštěk, V., & Kučera, P. (2020). Dynamic Load Modelling within Combined Transport Trains during Transportation on a Railway Ferry. Applied Sciences, 10(16), 5710. https://doi.org/10.3390/app10165710








