1. Introduction
Electricity power is an essential part of today’s life, and it is the backbone of modern civilization [
1]. The generation of power for daily life is crucial in every country. Different challenges worldwide in economics, environment, and growing populations require electrical systems that operate efficiently and continually all around the year. Therefore, electrical load forecasting is one of the critical tools for policymakers to make the right decision in expanding and managing the electric grid and for the management of the existing powerplants. Energy forecasting provides vital information for generating capacity, control and planning, system management, distribution, and maintenance scheduling. Accurate forecasting assures an efficient capacity planning for the growing population and increasing demand for electricity that avoids over or underestimating of utility expansion plans. In addition, it would allow proper and data-driven economic and environmental management and planning. Different planning horizons of electrical load forecasting are investigated in various publications, which are traditionally categorized into short-term, medium-term, and long-term forecasting [
2,
3,
4,
5,
6]. First, the short-term forecasting investigates the sub-hourly, hourly, daily, and weekly predictions. Second, the medium-term forecasting that includes weekly, monthly, and quarterly forecasting. Lastly, long-term forecasting contains periods of a year or beyond. Each one of these planning horizons is important; however, the long-term forecasting can be considered the most critical horizon due to the consequences of the strategic and costly decisions, such as the expansion of utility plants. An overestimation of electricity demand, especially in the long-term forecasting, will result in a significant increase in the construction of unnecessary electricity generation plants. In contrast, an underestimation of electricity demand forecasting will result in a shortage of electricity production and customer dissatisfaction. Therefore, the study of this research will focus on long-term electricity demand forecasting and the use of models that give the most accurate predictions.
An enormous number of research in electrical load forecasting is found in the literature that tackles the different challenges faced by the power industry and provides a superior forecasting method for predicting the demand of the electrical load. Various types of models and methodologies are implemented for electrical load forecasting in the literature with several parameters in a range of complexity degrees to achieve the best load forecasting accuracy. The methods can be categorized into several groups, but for simplicity, it can be divided into two main groups, namely the group of conventional models and the group of artificial intelligence (AI) models [
1,
2,
3,
4,
5,
6]. Conventional methods include models, such as regression models, time series models, exponential smoothing, and gray models [
2,
4]. In contrast, artificial intelligence models include models such as artificial neural network (ANN)-based models, support vector regression (SVR), genetic algorithm (GA) models, machine learning (ML) models, and deep learning (DL) models [
1,
2,
3,
4]. These models were used as simple or hybrid models or as a combination of more than one method, whether conventional or artificial intelligence models. Generally, the artificial intelligence models are more complex than conventional models. During the last two decades, the application of the AI models in the forecasting processes was rapidly increasing compared to the conventional models, and that can be attributed to the development of different AI models and the advancement of the computers [
2]. However, a relatively recent review [
3] depicted that the conventional methods, such as regression and/or multiple regression, are still widely efficiently used, especially for long-term forecasting despite their simplicity.
Researchers globally tackled the long-term forecasting challenges by using different models and methodologies to achieve superior and accurate forecasting. For example, Dudic et al. [
7] used a linear regression model to forecast the monthly and yearly electricity consumption for the German market, taking into account some factors, especially the higher efficiency of electricity usage from year to year. Filik et al. [
8] proposed a nested combination of three subsections for modeling to reduce the forecasting error and can be used for several years ahead. Mohammed [
9] examined the correlation of actual load supply with factors, such as population, gross national product, consumer price index, and weather temperature of Iraq using linear logarithmic and ANN models. García-Díaz and Trull [
10] presented multiple Holt–Winters models to improve the forecasting electricity demand of the Spanish national electricity market for very short-term forecasting. Taylor [
11] showed the superiority of triple seasonal methods of Holt–Winters and auto regressive moving average (ARMA) models for Short-Term Electricity Demand Forecasting. Recently, Trull et al. [
12] proposed a new method to initialize the level, seasonality, and trend in multiple seasonal Holt–Winters models. Bianco et al. [
13] used a trigonometric grey model with a rolling mechanism and Holt–Winters smoothing method to predict long-term non-residential electricity consumption for ten years up to the year 2020 and showed low average deviation. Hussain et al. [
14] employed Holt–Winters and Autoregressive Integrated Moving Average (ARIMA) models using real data from the year 1980 to 2011 to forecast the electricity consumption for Pakistan up to the year 2020 and showed better results for the Holt–Winters model than ARIMA model. Ali et al. [
15] employed a fuzzy logic model for long-term load forecasting of one year based on temperature and humidity in addition to historical load data. Ouedraogo [
16] developed a scenario-based model for the African power system using the Schwartz methodology in this context and showed an increase in electricity demand of 4% by 2040. Liu et al. [
17] proposed a least squares support vector machine optimized by two different models to forecast the demand of electric load in the multi-energy coupling mode. More examples can be found in several reviews carried out by Kuster et al. [
3], Wei et al. [
4], Ahmad et al. [
5], Deb et al. [
18], Khuntia et al. [
19], Runge and Zmeureanu [
20], and Su et al. [
21]. A relatively new method called Prophet is introduced by Taylor and Letham [
22] for forecasting, which has a high potential to be used in electric load forecasting. Different implementations were found for this model in recent years. For example, Yenidogan et al. [
23] compared two models: ARIMA and Prophet in Bitcoin forecasting. The results show that Prophet had an accuracy of about 94.5%, which was much better than ARIMA, which had an accuracy of only 68%. In addition, Ashwini Chaudhari [
24] used three models: ARIMA, Prophet, and long-short term memory (LSTM) recurrent neural networks in forecasting the prices of cryptocurrencies: Bitcoin, Ethereum, and Litecoin. The results show that the application of LSTM and Prophet led to very high accuracy between 93% and 99% for the three currencies, while the accuracy of the ARIMA model ranges between 82% and 66% only. In addition, Bianchi et al. [
25] carried a comparative for heat short-term demand forecasting methods using the Autoregressive Model (ARM), Non-Autoregressive Model (NARM), and Prophet based on real data of an Italian utility company. The ARM was superior to the other models in short-term forecasting. A thorough recent study carried out by Das [
26] where five different forecasting models (Simple Exponential Smoothing, ARIMA, Dynamic Harmonic Regression, Neural Network, and Prophet) were used for prediction of wind speed in two states in India (Tamil Nadu and Maharashtra). The neural network model provided the best results. However, the Prophet model showed promising results, and it was recommended to be used in the future.
Different studies about long-term forecasting for Kuwait were carried out. Almeshaiei and Soltan [
27] proposed a methodology to be used as a guide for constructing electric power load forecasting models based on segmentation and decomposition of the load time series and used real daily load data from the Kuwaiti electric network and a model with a mean absolute percentage error (MAPE) value of 3.84% was reported. Al-Rashidi and El-Naggar [
28] employed the particle swarm optimization to minimize the error associated with the estimated model parameters for annual peak load forecasting for Kuwaiti and Egyptian powerplants using the least error squares estimation technique to forecast the annual peak load for the years 2006 to 2010. Alhajeri et al. [
29] used the cuckoo search algorithm to minimize the error associated with the estimated parameters of three long-term forecasting methods used to forecast the annual peak demands. Al-Hamad and Qamber [
30] presented long-term forecasting for peak loads of Gulf Cooperation Council (GCC) countries using Multiple Linear Regression (MLR) and Adaptive Neuro-Fuzzy Inference System (ANFIS) methods. A recent study for the residential sector in Kuwait was carried out by Alajmi, and Phelan [
31] created a baseline using a bottom-up approach for the end-use energy profile for the residential sector in Kuwait until 2040.
With reference to the aforementioned relevant literature, research to date has not yet investigated the performance of the Prophet model in long-term forecasting of maximum load. In this paper, real recorded data from the National Control Center (NCC) in Kuwait were used for long-term electric load forecasting using the Prophet model. The proposed method is simple yet powerful in prediction because of its features of adjusting parameters without exploring the specifications of the underlying model [
22]. It consists of a decomposable time series model with three main model components: seasonality, trend, and holidays. The model is compared with a well-established Holt–Winters model for evaluation and to obtain the best forecasting model.
This study aims to contribute to the literature by investigating long-term maximum peak load forecasting performance of Kuwait peak loads using the Prophet method based on comparative quantitative analysis with the Holt–Winters forecasting method. To the best of our knowledge, no prior study has investigated the use of Prophet model in long-term forecasting of the maximum electricity load either in Kuwait’s electrical national grid or elsewhere. Furthermore, the generalizability and robustness of the Prophet and Holt–Winters methods for the long-term electric peak loads forecasting are explored and presented.
2. Methodologies
A dataset of the maximum load of Kuwait between January 2010 and May 2020 was acquired from the Ministry of Electricity and Water (MEW) to support this research.
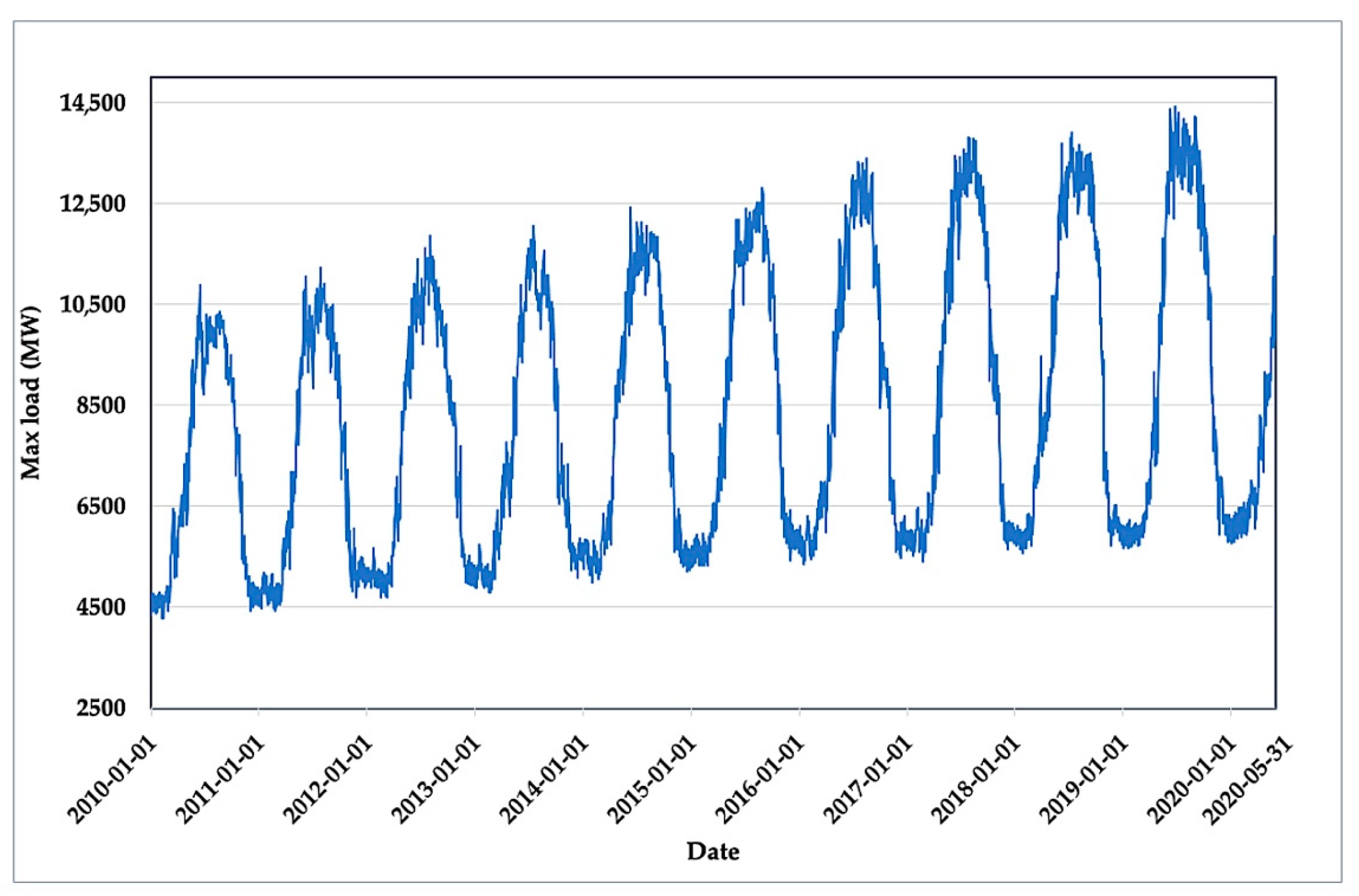
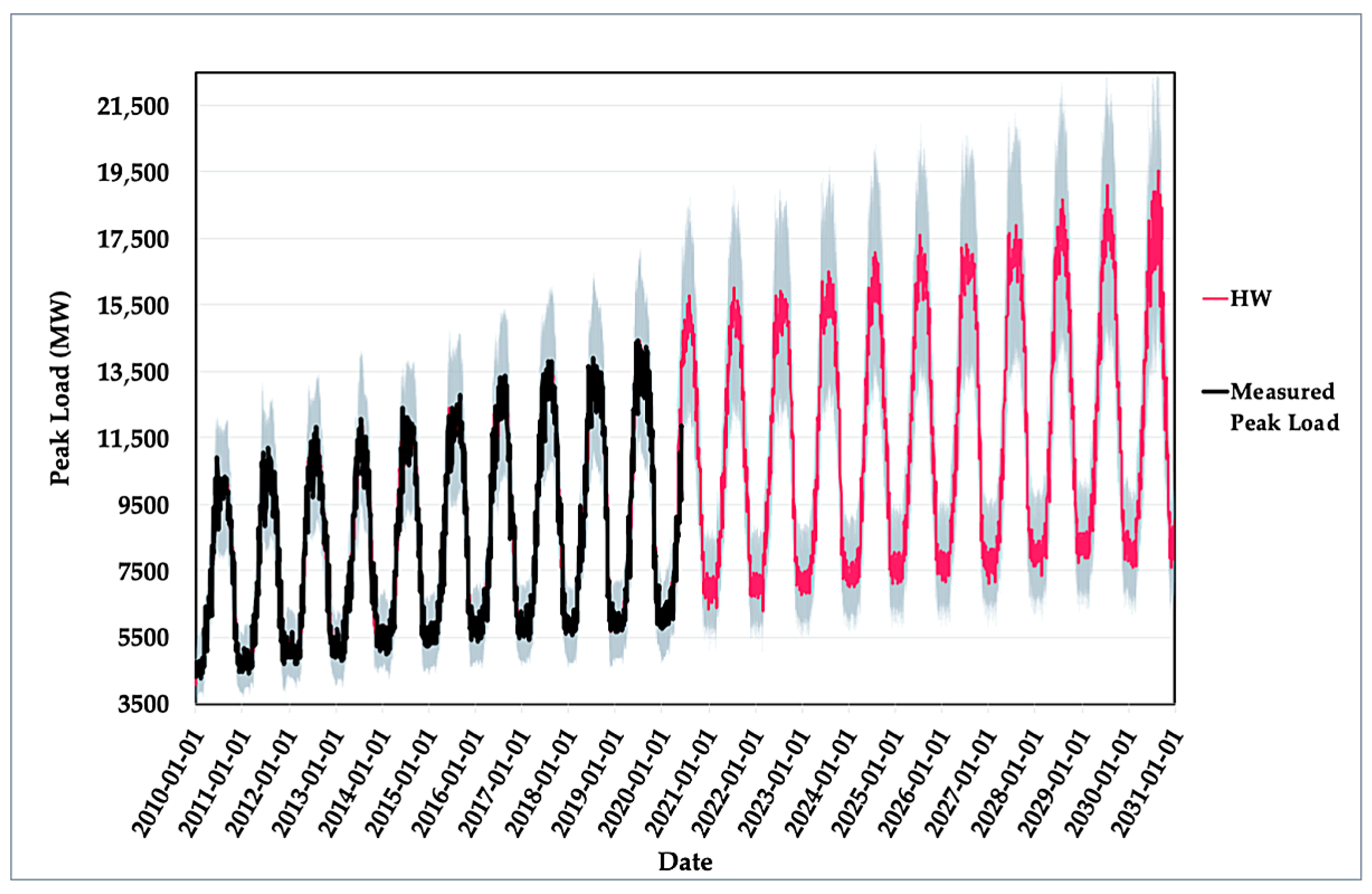
Figure 1 presents the maximum load (MW) of Kuwait for the past ten years. With reference to
Figure 1, a yearly seasonality of the maximum load can be clearly observed. The maximum load peaks are within the summer period between June and August each year due to the subtropical weather nature of Kuwait with extreme temperatures in summer and cold winter seasons. In addition, the maximum load takes an increasing trend. The gradual and steady trend increase is likely to continue for the upcoming years due to the fact of the increasing population, increased factories, and the expansion of the urban and residential areas.
In order to forecast the maximum load of Kuwait for the upcoming years, forecasting models that incorporate seasonality and trends are required to ensure a well-fitted model to the actual data. In this work, Facebook’s Prophet and Holt–Winters forecasting models have been utilized in this research for the long-term forecasting of the maximum load in Kuwait.
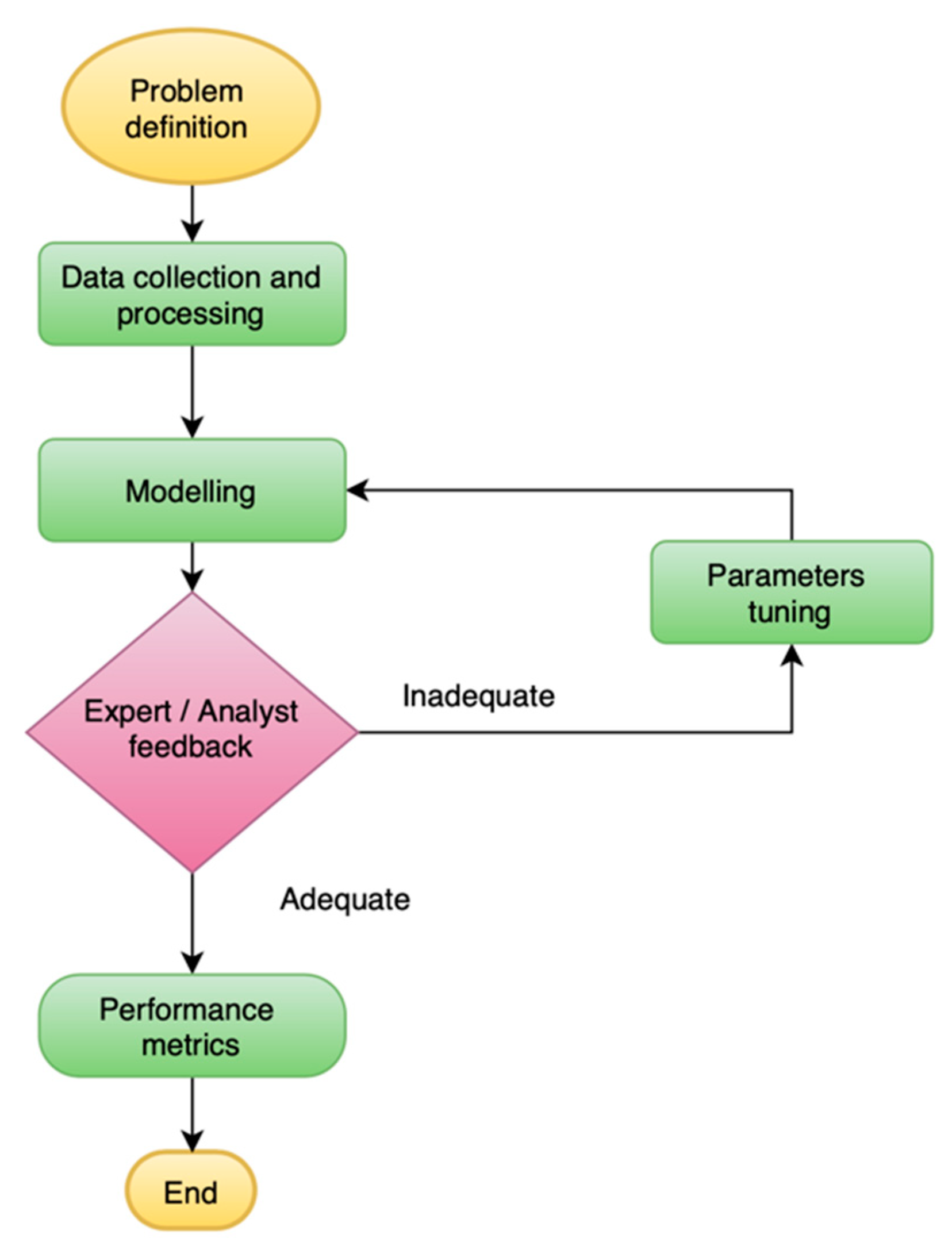
The Prophet forecasting model that is used for forecasting the maximum load is a relatively new modular forecasting method based on various tunable parameters by analyst-in-the-loop, as shown in
Figure 2. One of the Prophet forecasting method’s strengths is that it was designed to have intuitive tuning of the parameters and does not require knowledge of the underlying model. However, to date, long-term maximum load forecasting using Prophet has not been reported in the literature. Whereas, the Holt–Winters model, or else known as triple exponential smoothing, has been excessively reported in the relevant literature and was proven to be effective in forecasting energy consumption with high accuracy [
32,
33,
34]. In addition, unlike the Holt–Winters method, the Prophet forecasting method is robust to missing data and does not require data interpolation. Furthermore, seasonality with multiple periods can be incorporated in the Prophet forecasting method to provide flexibility in modeling complex data using an analyst-in-the-loop experience. The Prophet method also enables the user to use extra regressors to present multivariate forecasting to explore the effects of different variables with a very fast-fitting procedure. In the next sections, the implementation of the Prophet and Holt–Winters forecasting methods is presented in detail.
2.1. Prophet Forecasting Method
Prophet forecasting model incorporates data trends, seasonality, and holidays that allow the possibility of modeling complicated time-series features. Multiple seasonality can be fitted as daily, weekly, and yearly patterns. The mathematical representation of the decomposed time series model is hence described as:
where g(t) represents the data trend function, s(t) represents the seasonality, and h(t) represents holidays effect that can be added within specific points of the data. The error term,
εt, represents any distinctive features of the data that are not fitted by the model.
Prophet trend function,
g(t), can be represented by a piecewise linear growth model or a saturating growth model. Since the maximum load data do not exhibit a saturating growth, a piecewise linear growth model is utilized as:
where
is the growth rate,
is adjustment rate,
is the offset parameter, and
represents the trend changepoints,
, and is set as
, with
defined as:
The change points allow the growth model to change the trend and can be utilized by the analyst-in-the-loop to fit the model better and produce reliable data forecasts. The Prophet model allows the user to specify the flexibility of the trend by the adjustment rate. It can also automatically detect the change points, or the data analyst can manually adjust them to describe trend-altering events in the time series.
For the seasonality function,
, the time series’ multiperiod seasonality can be modeled using the Fourier series to represent the daily, weekly, and yearly seasonality. The seasonality function is hence written as:
with P = 354.25 for yearly seasonality or P=7 for weekly seasonality. Lastly, to include holiday effects by the holiday function,
, the user can define a matrix list of holidays with dates to be incorporated into the time series as a matrix of regressors,
Z(t), defined as:
with
D as the set of holiday dates,
with
as the holiday smoothing parameter.
2.2. Holt–Winters Forecasting Model
There are two variations of the Holt–Winters forecasting method: the additive and multiplicative models of the seasonal variations. The multiplicative model is suitable for a time series with an increasing seasonal pattern that is proportional to the data level. In contrast, the additive model is suitable for fitting a time series with a constant seasonal variation. In this work, the multiplicative method is utilized for forecasting the maximum load of Kuwait.
The Holt–Winters model consists of forecast equation and smoothing equations of the level, trend, and seasonality of the time series. Assuming that
represents the seasonality,
to represent the trend and that
corresponds to the level with smoothing parameters of
, and
. Therefore, the Holt–Winters multiplicative forecast model can be expressed as:
where
m denotes the seasonality period and the smoothing parameters defined as:
In the Holt–Winters multiplicative method, the seasonality component is expressed relatively, and the time series can be seasonally adjusted by dividing through by the seasonality component. Equation (8) corresponds to the level, and it is expressed as a weighted average between the seasonal term and the non-seasonal term . While Equation (9) corresponds to the trend of the time series, which is expressed as a weighted average of the trend between the level and previous slope . Equation (10) corresponds to the seasonality and is calculated by the weighted average between the current and previous seasonal components of the time series.
2.3. Validation Approach
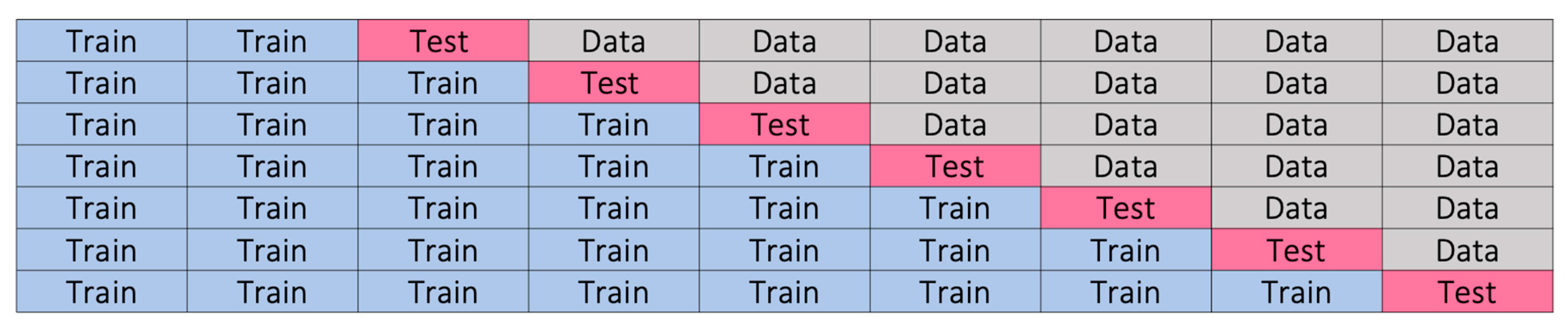
In order to validate the performance of the prediction of the models, a simulated historical forecast (SMH) approach is conducted. SMH is based on the rolling origin cross-validation approach, or otherwise known as forward chaining, where the data are split into training and testing sets and each day is tested based on the prior training data. However, this method would be computationally intensive due to conducting tests each day and would result in more forecasts that are likely to have correlated estimates of errors. While with SMH, fewer forecasts can be defined at cut-off dates and the total error can be evaluated based on all the forecast horizons.
Figure 3 illustrates the process of the rolling origin cross-validation. This approach would allow the models to train on a dataset and test on another unseen dataset of the time series. Moreover, the SMH approach could be used as an indicator of the models’ generalizability in forecasting the maximum load.
In addition, to assess the performance of each model in terms of accuracy, various statistical metrics were adopted, such as root mean square error (RMSE), the mean absolute percentage error (MAPE), coefficient of determination (R
2), mean absolute error (MAE), and coefficient of variation of root mean square error (CVRMSE) that can be expressed as in the following equations:
where
and
represent the measured, predicted, and averaged values respectively.
3. Results and Discussion
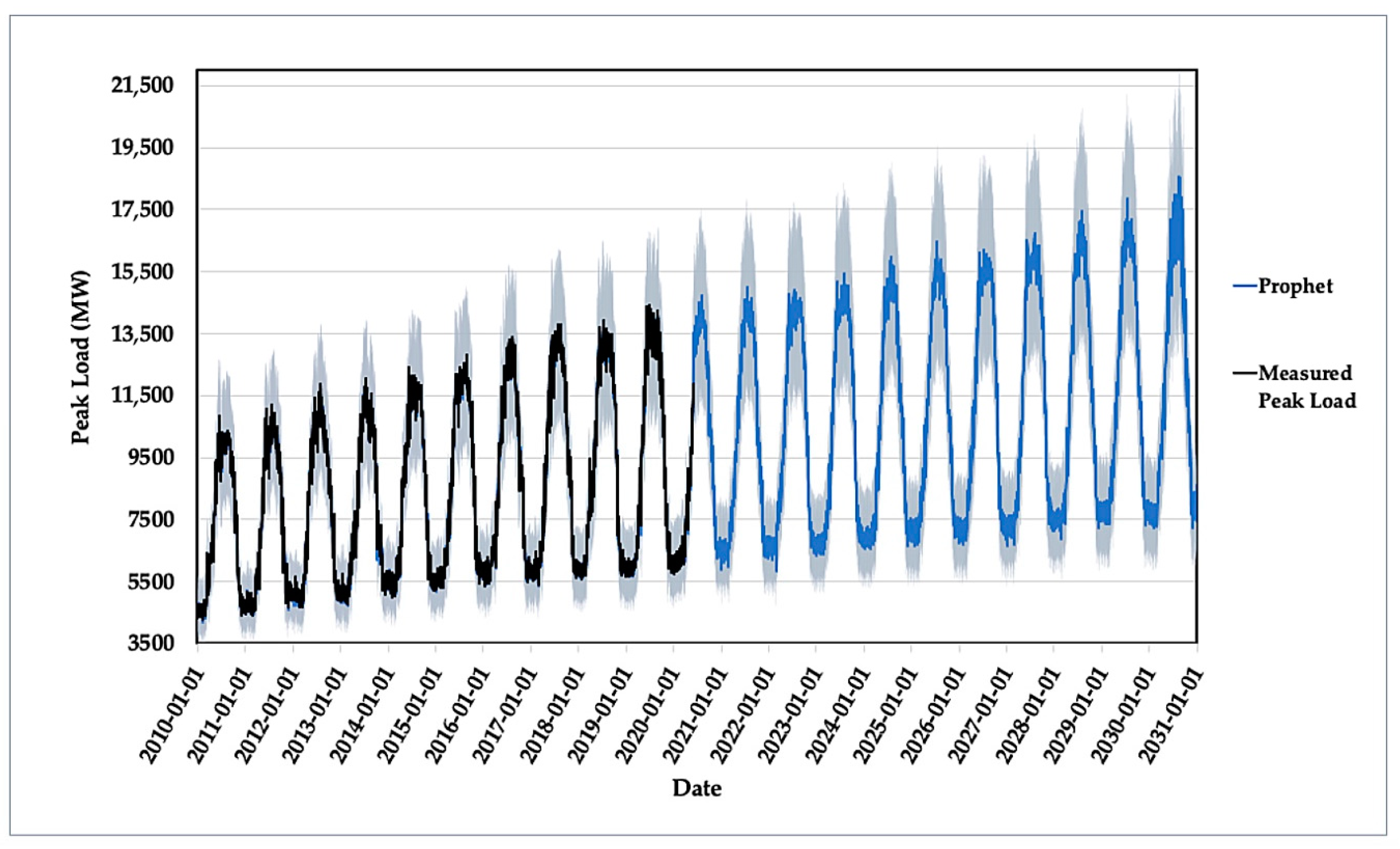
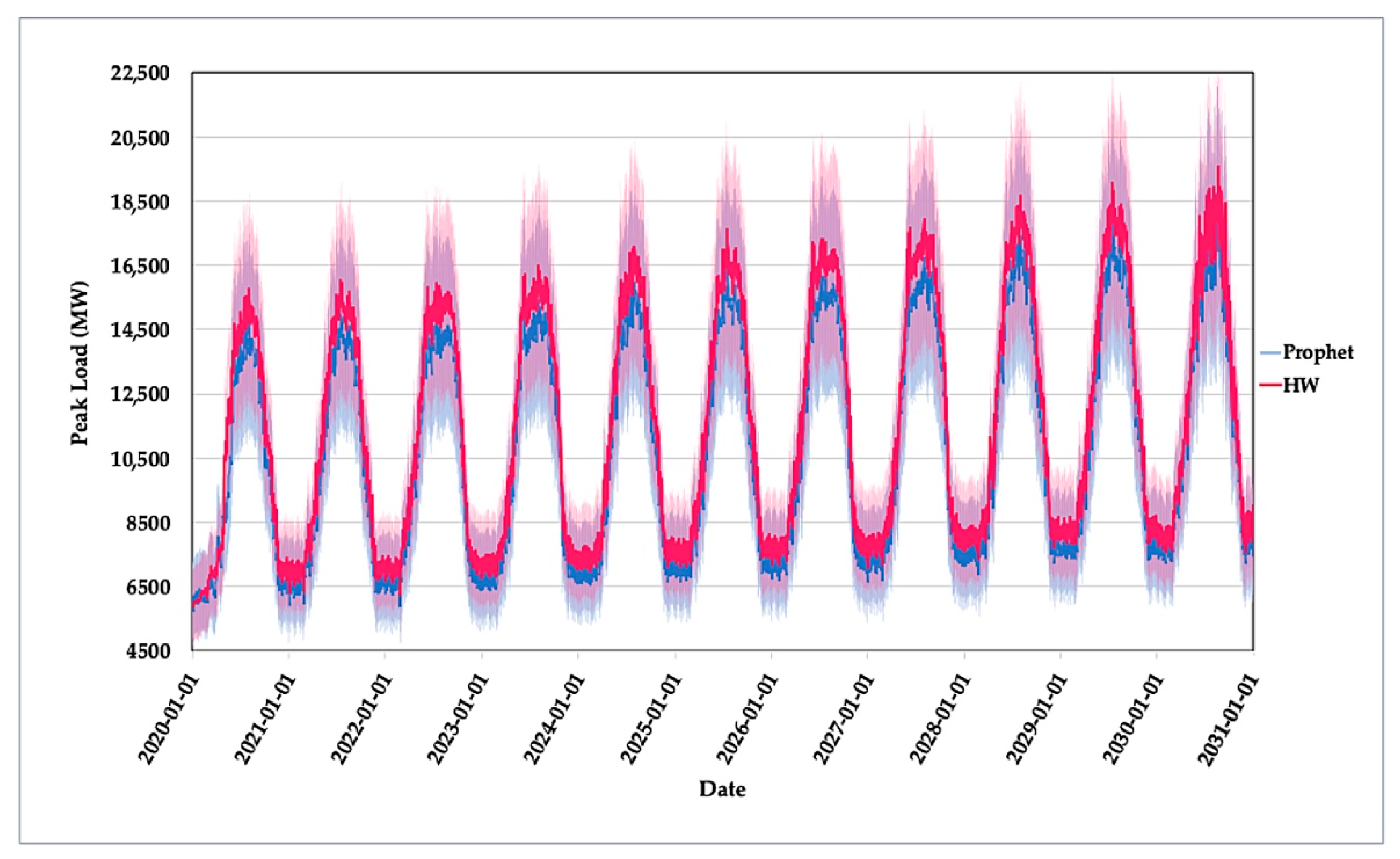
The Prophet and Holt–Winters models are implemented in R and Python, using real data of electrical daily peak load from Kuwaiti powerplants from 2010 to 2020. The two models’ outputs are plotted in
Figure 4 and
Figure 5, along with the real electrical peak of daily loads. The data include Kuwait’s peak loads from 2010 to 2020. Moreover, the forecasted from 2020 to 2030, along with a 99% confidence interval, are included. The forecasted region of this period is enlarged and presented in
Figure 6, along with the 99% confidence interval for both models.
The graphs in the previous figures demonstrate that there has been a steady increase in the values of daily peak loads with a yearly seasonality for both models. The two models share several key features, such as trend similarity of the forecasted maximum and minimum peaks. However, the Holt–Winters model generally shows a higher magnitude of the forecasted maximum and minimum peaks than the Prophet model. The superiority of the models is assessed from different aspects by three indicators: accuracy, generalization, and robustness. Also, the future peak loads forecasting for Kuwait is discussed, and the maximum capacity needed by 2030 is investigated.
3.1. Model Accuracy
Various accuracy and statistical performance metrics were used in this study, which include MAPE, MAE, RMSE, CVRMSE, and the coefficient of determination R2. MAE demonstrates the gap between the estimated value and the real value using the absolute error. RMSE assesses the instability of model response regarding variance and sensitivity to large errors. CVRMSE normalizes the forecasted error and provides a unitless metric that evaluates the variability of the errors between real and predicted values. The advantage of using these statistical indicators is to explore various aspects of the presented models.
Table 1 presents the calculated values of five statistical performance metrics (MAPE, MAE, RMSE, CVRMSE, and R
2) for both the Prophet and Holt–Winters models using the equations aforementioned in the methodology section. MAPE is one of the most used tools for measuring the accuracy of models [
35]. MAPE is proposed in [
4] as a reference range for evaluating the performance of energy consumption forecasting at different horizons. Highly accurate models are considered when the MAPE is less than 10%, as benchmarked in [
36]. The highly accurate models were divided into levels into four sublevels for each planning horizon. For example, the long-term forecasting is divided into these sublevels: I (≤1.2%), II (1.2–2.8%), III (2.8–4.6%), and IV (4.6–10%) [
4].
Accurate values of MAPE were achieved by the Prophet and Holt–Winters methods with superiority by the Prophet model. The values of MAPE were 1.75% and 4.17% for Prophet and Holt–Winters models, respectively. Both values indicate an accurate prediction of the values of both models with relatively low MAPE values. Based on the sublevels of accuracy mentioned above and in [
4], the Prophet model falls within sublevel II, whereas the Holt–Winters model falls within sublevel III accuracy.
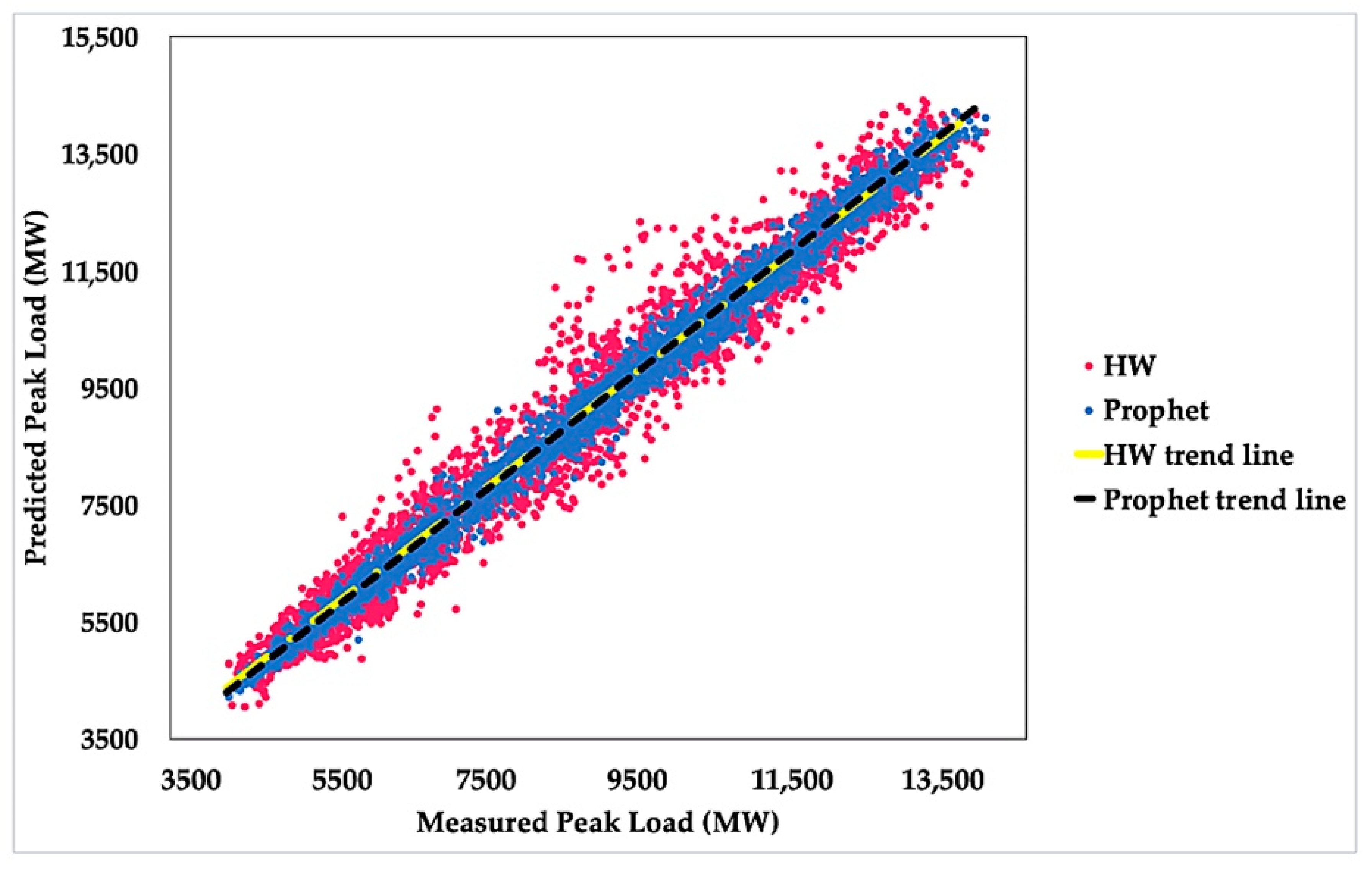
Figure 7 depicts the coefficient of determination, R
2, and illustrates the variations between the forecasted and real data values for both the Prophet and Holt–Winters models. Both models achieved high values of the coefficient of determination R
2 equal to 0.9942 and 0.9694 for the Prophet and Holt–Winters models, respectively. The MAE of the Prophet model is reported as 147.89, whereas the value of MAE for Holt–Winters model is 343.33, which is approximately more than the double of the Prophet model MAE. In addition, the Prophet model results in a better RMSE value than the Holt–Winters model with a value of 205.64. Moreover, the CVRMSE percentage of the Prophet model is less than the Holt–Winters model with values of 7.61% and 17.59%, respectively.
It is clear that the Prophet model has a superior fitting to the real data and has better performance and accuracy than the Holt–Winters model. From the five different statistical metrics, both the Prophet and Holt–Winters models show high accuracy with the superiority of the Prophet model over the Holt–Winters model.
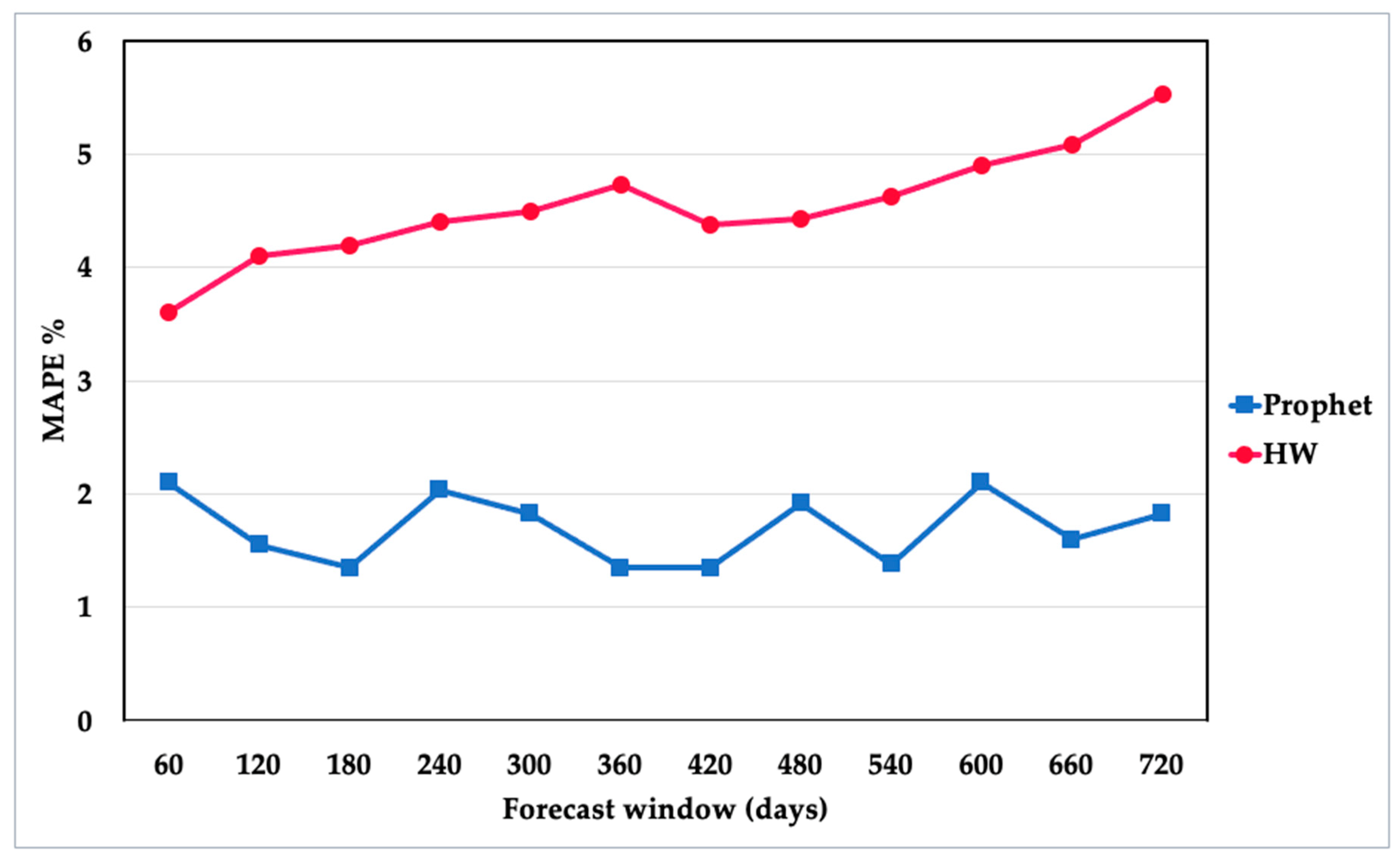
Another measure to assess the accuracy of the models is to use the simulated historical forecast (SHF) [
22,
37], as depicted in
Figure 8. The Prophet model forecasts have a considerably lower prediction error than the Holt–Winters model. The Prophet model’s MAPE values are limited within the range between 1.3 and 2.1 approximately, and there is no clear trend of MAPE with the forecast window. The MAPE values of the Holt–Winters model across the different forecasting periods were generally good but higher than the Prophet model. The Holt–Winters model showed a generally increasing trend of MAPE values with the increase in the forecast horizon. These results are evidence that both models exhibit a great extent of accuracy in long-term energy forecasting.
3.2. Model Generalization
The model’s generalization is assessed by the model’s ability to forecast samples beyond the training range.
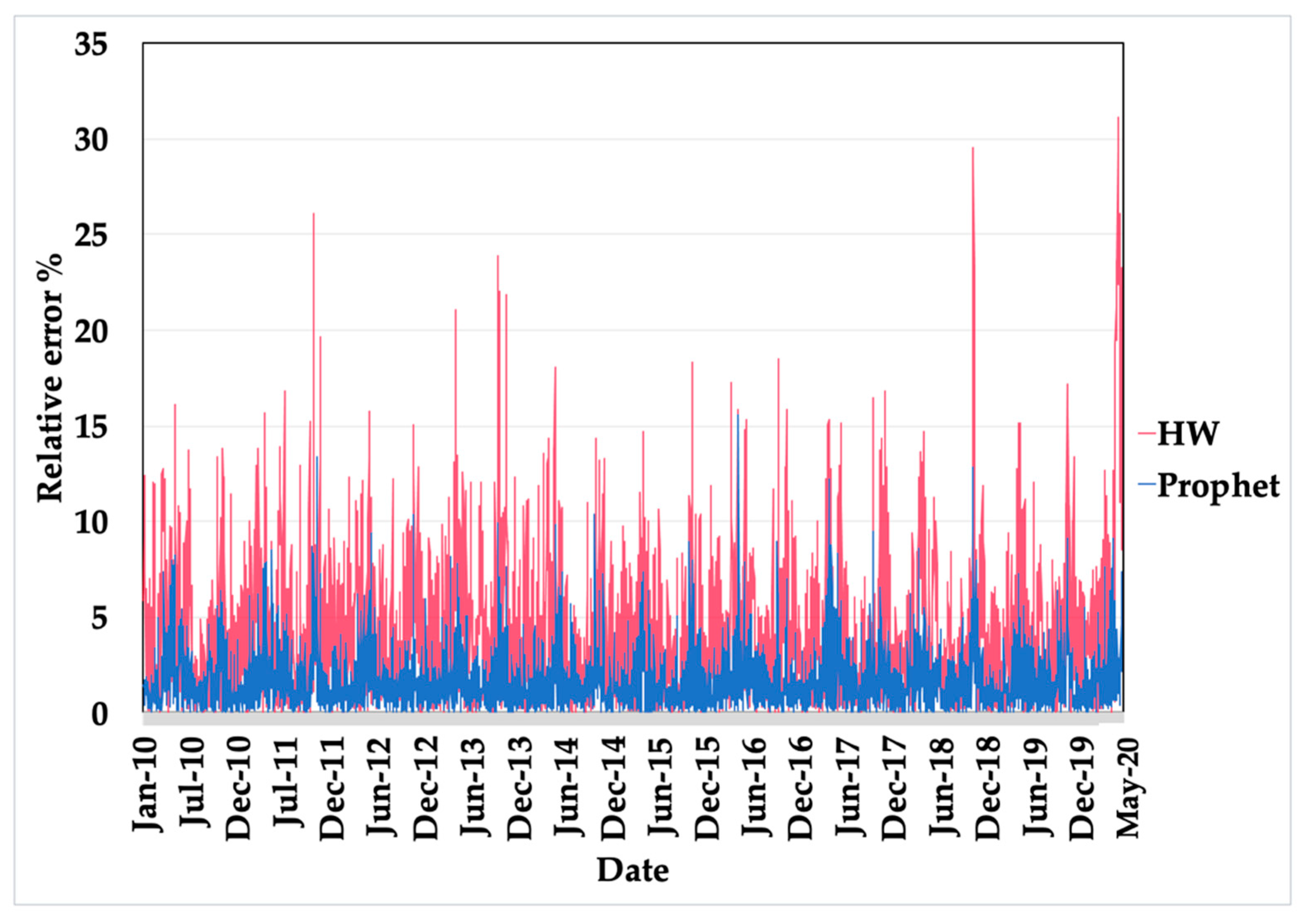
Figure 9 depicts the relative error variation in each of the Prophet and Holt–Winters models. The relative error percentage of the Prophet model outperforms the Holt–Winters model. The percentage of maximum relative error in the Prophet model is less than 16%, whereas the Holt–Winters model’s relative error reached 30%. Besides, the SHF results can be used to show the generalizability of both models. The Prophet model shows better generalizability than the Holt–Winters model, as suggested by the MAPE values and the relative error percentage.
3.3. Model Robustness
To test the model robustness, Gaussian white noise with different intensities is utilized and added into testing data sets of actual data. This approach has been utilized by relevant literature, such as in [
38,
39]. The data is split into training dataset and multiple testing sets with each set corresponding to a defined noisy intensity. Gaussian white noise is generated with four different intensities of 20%, 40%, 60%, and 80% to assess the robustness of the Prophet and Holt–Winter models. The generated Gaussian white noise samples are distributed randomly at each testing data set, with the corresponding noise intensity, and model robustness is evaluated by the effect of the noise intensity over the accuracy of the model, measured by the coefficient of determination R
2. Low variance in R
2 indicates high robustness where high variance indicates low robustness.
Table 2 presents the results of the R
2 of both models under various noise intensities.
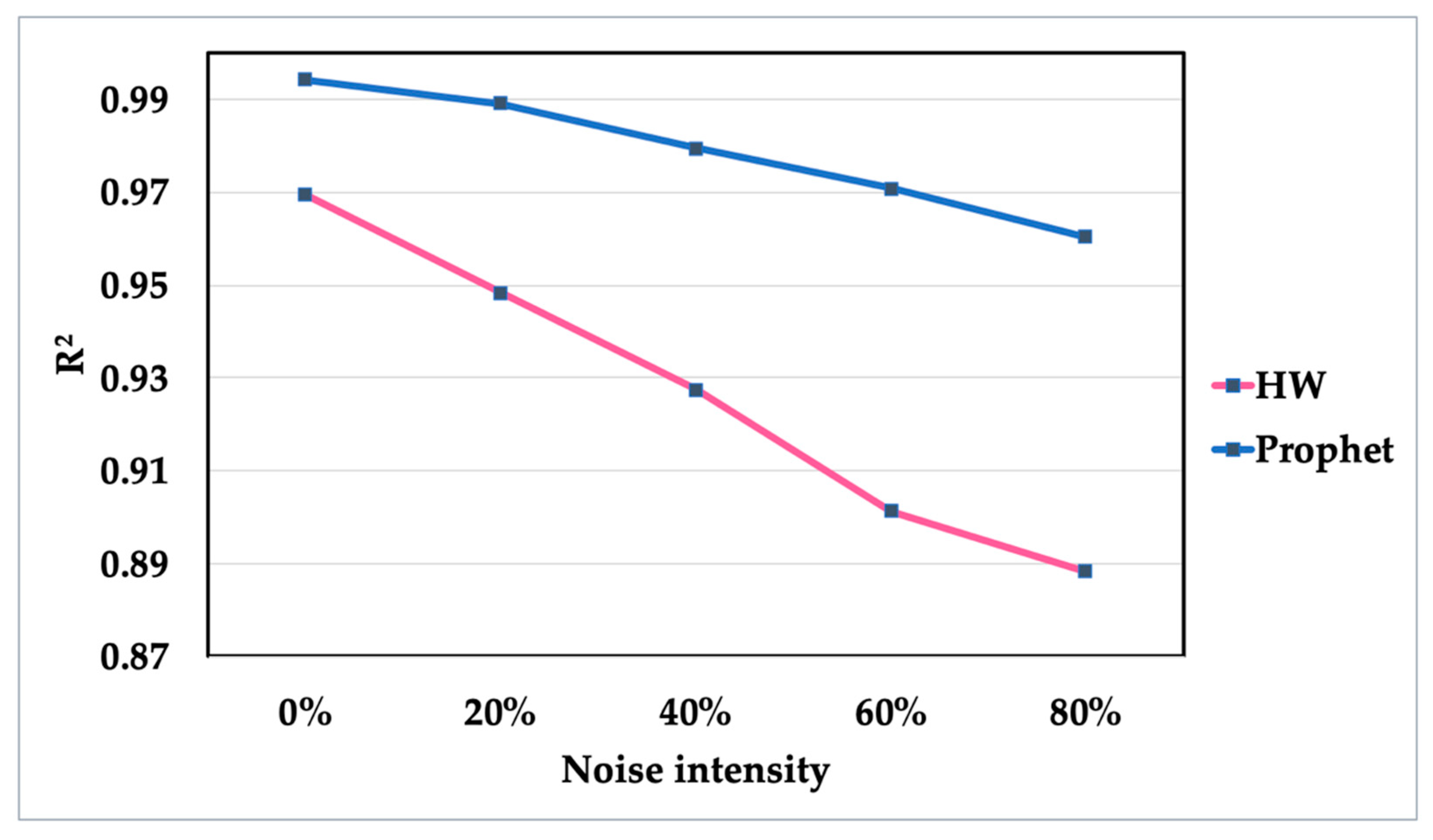
A reduction in the coefficient of determination is associated with the increase in the noise level, as depicted in
Figure 10. The Prophet model showed high R
2 values across the different noise intensities with a minimum value of 0.9604 at 80% noise intensity. On the other hand, the Holt–Winters model showed high values of R
2 but relatively lower than the Prophet model. The minimum value of R
2 for Holt–Winters was 0.8883 at 80% noise intensity. The results indicate that the Prophet model is more robust than the Holt–Winters model under various Gaussian white noise intensities.
3.4. Future Peak Loads Forecasting
According to the assessment of the two models, the Prophet model outperforms the Holt–Winters model and, therefore, should provide more reliable forecasting. The real data of daily peak loads consumption from 2010 to the end of May 2020 are used to forecast the daily peak load from June 2020 to 31-12-2030, with results plotted in
Figure 4 and
Figure 5. The forecasting plots also provide essential information about the yearly maximum peak demand. Estimating the maximum peak demand is crucial for long-term strategic decisions in terms of electricity capacity expansion plans to withstand the foreseen maximum loads. Soares et al. [
40] reported that the electric peak demand is expected to reach 30,000 MW by 2030. Al-Hamad and Qamber [
30] applied the Adaptive Neuro-Fuzzy Inference System (ANFIS) and Multiple Linear Regression (MLR) methods to forecast the peak loads for Kuwait in three scenarios according to the expected growth rates of the gross domestic product (GDP) for the years 2014–2024. The three sceneries were associated with high, average, and low growth of GDP. The high, average, and low growth of GDP models were increasing in different rates reaching maximum forecasted loads of 18,700, 27,300, and 44,500 MW, respectively, for the year 2024. Alhajeri et al. [
41] showed that the expected demand in Kuwait is increasing by an average of 2.8% annually by 2030, and the installed capacity should be higher than 21.8 GW. Past studies [
30,
40,
41,
42,
43] about the maximum peak loads forecasting showed a clear increasing trend for peak loads in the coming years, reaching about 30 GW by 2030. On the other hand, the recent study and the new forecast of MEW show a similar trend but lower in magnitude.
The long-term forecasting provides daily, monthly, and annual maximum peaks.
Table 3 presents a comparison between actual maximum peak load data and forecasted demand from the MEW in different years (2017–2019) [
42,
43,
44], Prophet, and Holt–Winters models. The MEW forecasting showed variations in the percentage increase in annual maximum load from 2017 to 2019 with a decreasing trend. In the year 2017, there was a yearly increase in the maximum peak load by an average of 5.4%. The average increase was reduced in the forecast for 2018 to reach 4.7% annually. However, the growth became more conservative in the statistical book of the year 2019 and reached 1% only. The forecasting for years between 2020 and 2030 by the Prophet and Holt–Winters models showed an increasing trend with varying percentages for each year, reaching a maximum peak load of 18,550 and 19,588 MW by the year 2030, respectively. The magnitude of the increase in the Prophet model is between the value of the maximum peaks of MEW in the year 2019 and the Holt–Winters model that suggests the Prophet model is more reliable when compared with the actual data. It is a common practice to have a capacity reservoir to withstand any sharp increase in the daily consumption of electricity. Accordingly, the 99% confidence interval can be used to be the capacity reservoir. As a result, the capacity reservoir should reach up to 22.1 and 23.3 GW for the Prophet and Holt–Winters models to tolerate any failure or disruption of the electrical system during the maximum peak load time by 2030.
On the other hand,
Table 4 presents the monthly forecasted maximum load peaks for 17 months from August 2020 to December 2021. The data provided in
Table 4 are essential for monthly planning in the powerplants. It offers a clear vision for the expected maximum consumption of power by proposing the monthly maximum load peaks, which is essential for planning activity in powerplants, such as maintenance scheduling. Optimum planning for the maintenance schedule is vital for unit availability and avoiding any unexpected failures or shutdowns. Preventive maintenance is a cost-effective option that can be implemented when planning is accurate. The monthly maximum load peaks indicate that the best months for scheduling maintenance are from November 2020 until March 2021 for both models. Even with 99% confidence interval, the maximum peaks do not exceed 10,000 MW and 10,500 MW for the Prophet and Holt–Winters models. Additional months can be alternatives, such as October 2020 and April 2021 but with some low risk.