1. Introduction
Electromyography (EMG) is a method used to record electrical signals generated by muscular activities. EMG is related to muscle contraction and extension which can easily be recorded from the surface of the skin. Owing to these features, EMG is widely studied in various research fields, such as biomechanics, rehabilitation, and clinical diagnosis [
1,
2,
3,
4,
5]. These applications require muscle activity information related to contraction or extension, and this information can be obtained by confirming the activation of EMG signals. Therefore, the muscle activity detection through EMG signal is a basic but crucial part of EMG applications [
5,
6].
The muscle activity detection aims to obtain both the onset and offset timing of EMG activity. The onset is defined as the beginning of a muscle contraction or extension, while the offset represents the end of a muscle contraction or extension. An easy technique to detect muscle activity is through visual inspection [
7,
8]. However the visual inspection by experts is accurate but complex. Thus, various methods for automatic onset and offset detection have been studied [
9,
10,
11,
12,
13,
14,
15,
16,
17].
Most automatic detection methods are based on a threshold [
9,
10,
11,
12]. These methods detect the event timing by comparing the mean of EMG signals in a sliding window with a certain threshold. The onset detection using the generalized likelihood ratio test has been studied [
9,
10]. A single threshold is used for the onset detection only during a series of rapid upper limb movements [
11]. Further, the onset detection based on Teager–Kaiser Energy method has been studied [
12]. Bonato introduced a double threshold method where two thresholds were used to detect onsets of muscles from eight different locations under the waist [
13]. Unlike the single threshold method, this method reduces the false alarm rate. Furthermore, other double threshold-based methods have been developed to increase the robustness to a noise level using EMG recorded from the upper and lower limbs [
14,
15,
16,
17]. In addition, Xu selected threshold based on the likelihood ratio test [
10] where the optimal threshold was calculated via a likelihood ratio test. Rashid has attempted to achieve parameter optimization and then proposed an extended double threshold algorithm as a variant of the double threshold method [
13]. However, these methods require optimization and an additional training process for parameter selection, thereby increasing the complexity of algorithm. Moreover, these conventional threshold-based algorithms are unable to accurately detect the offset timing.
In this study, we proposed a novel method used to detect the precise onset and offset timing of muscle activity, during hand-close and hand-open movements. The adaptive threshold was determined using the constant false alarm rate (CFAR) algorithm, and the EMG signal is refined by morphological hole filling that closes up and fills out the missing information. To evaluate the performance, we calculated the estimated error of the onset and offset timing. Furthermore, the results were compared with the two conventional methods based on the double thresholds. The experimental results indicate that the estimated errors for both onset and offset detection are lower than those occurring in the two conventional methods. In addition, the proposed method does not require a training process unlike conventional training-based methods.
2. Data Acquisition
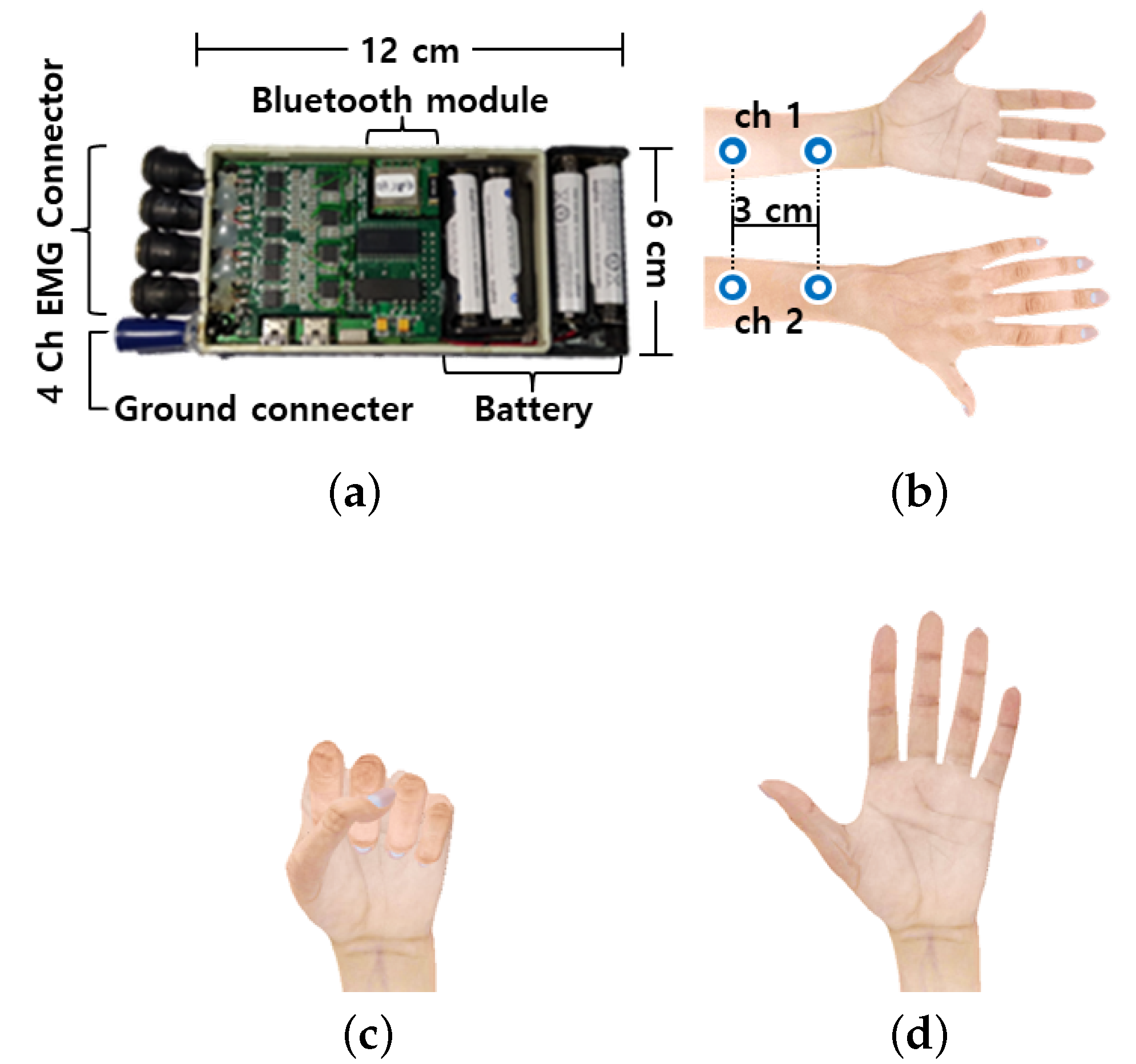
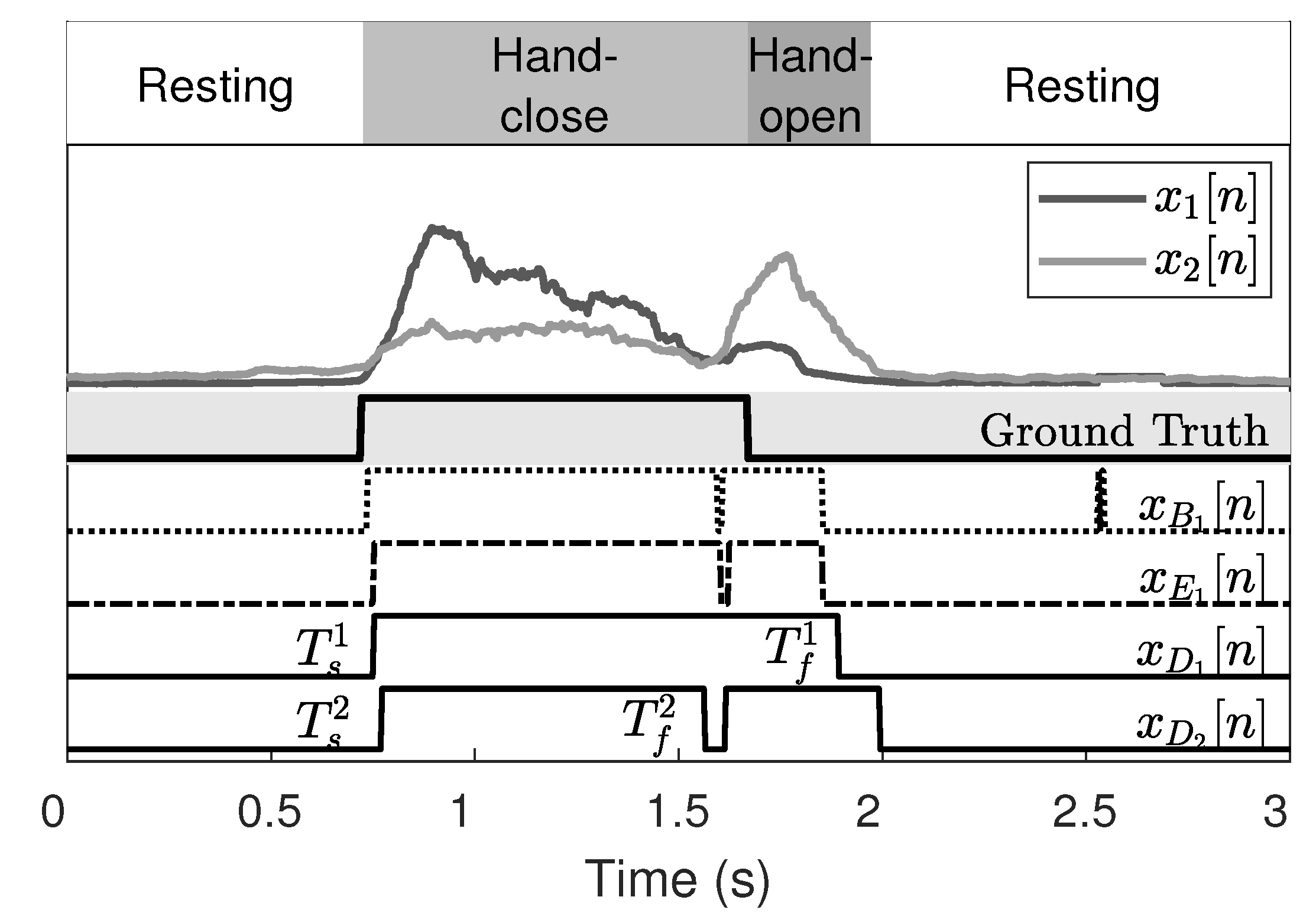
Figure 1a shows the self-made wrist-type wearable device, which is used to measure EMG data. This device is composed of a four-channel EMG sensor and connecter, six axis motion sensor module, battery, Bluetooth module, and micro controller unit. The EMG signals and motion sensor data can be recorded simultaneously with a sampling rate of 256 Hz. Bipolar Ag-AgCl snap electrodes were used, and two channels were located in the inner and outer part of the left forearm. A reference electrode was attached to the backside of the neck. Then, gyroscope sensor data were simultaneously recorded from the middle finger of a subject, for the evaluation of the proposed algorithm. The gyroscope is used to obtain the ground truth of the onset and offset timing. One female and nine male subjects were asked to repeat the finger folding sequence. They had to contract all their fingers and maintain this for a certain second (close state), extend all their fingers very quickly (open state), and subsequently relax all their fingers (resting state). The subjects were also instructed to maintain the close stage during two different time intervals, and each trial was repeated 60 times.
3. Proposed Algorithm
Let be the EMG signal and be the absolute value after the DC removal (i.e., ) where is the mean of during the resting period.
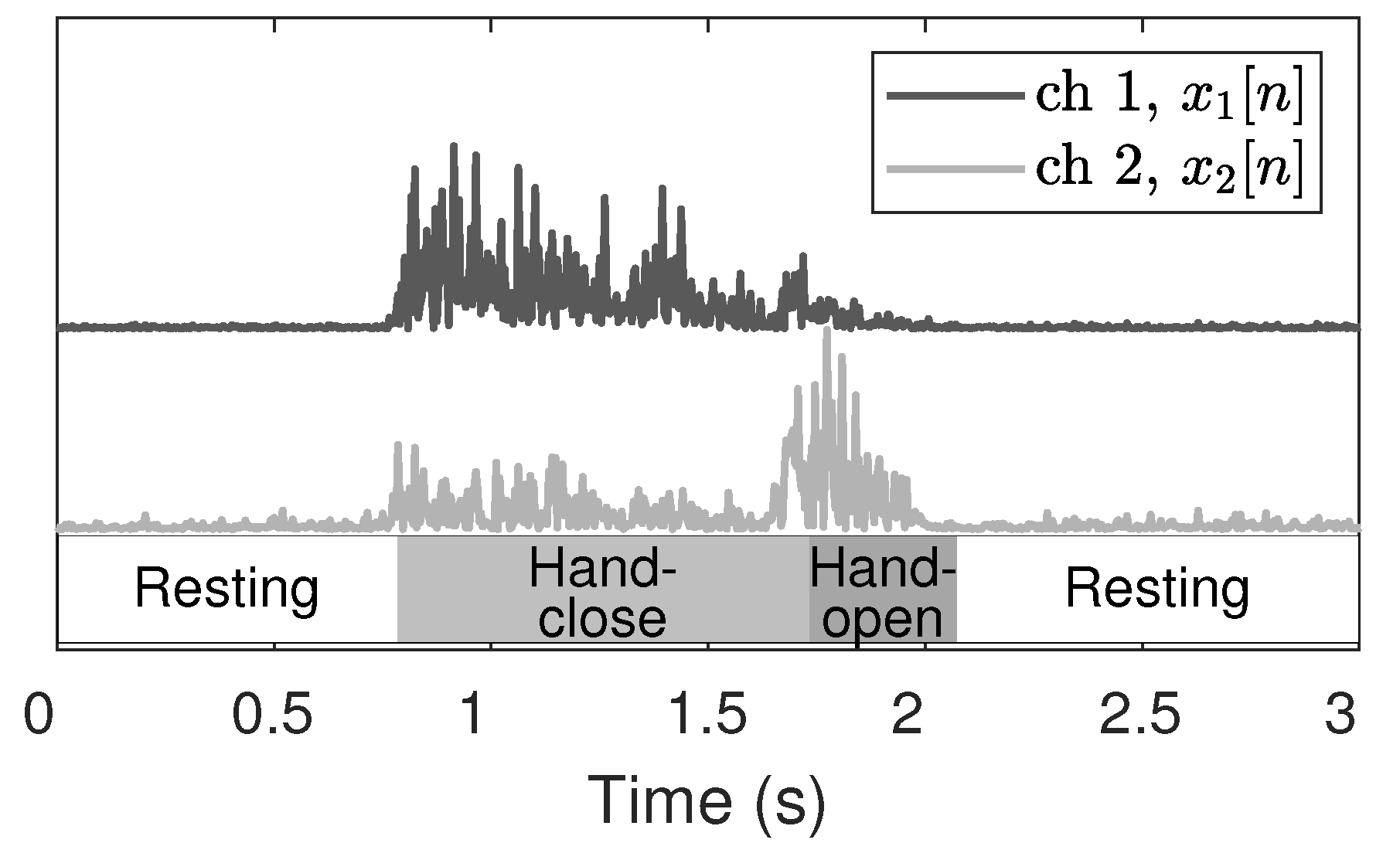
Figure 2 depicts the absolute value of EMG signals without the DC component for various states. Evidently, the activation of the inner channel (
) is greater than that of the outer channel (
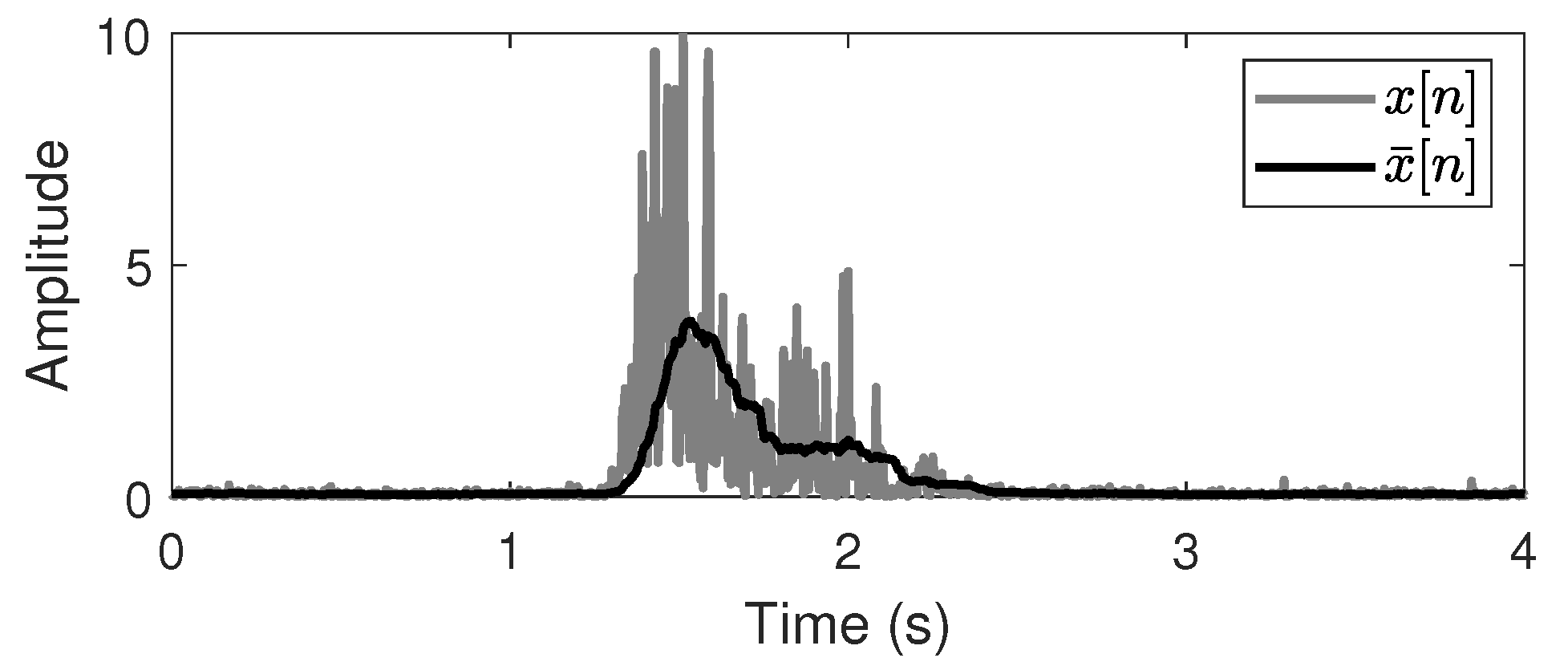
) during finger contraction (close state), and vice versa for finger extension (open state). The ideal onset and offset timings are the start and the end points of the close state, respectively. The mean absolute value (MAV) is the most common feature in EMG analysis owing to its computational simplicity and is calculated for every sliding window. The MAV for the channel
c,
is obtained as
and is illustrated in
Figure 3.
3.1. CFAR-Based EMG Binarization
First, we detect the activation of the EMG signal by using the modified CFAR threshold. The CFAR is an algorithm, which sets a threshold to maintain a false alarm rate constantly. We use the median CFAR detector to calculate the decision threshold. Let be the training cell, and let be the test cell for the channel c, where and N represent the guard and the training cell length, respectively.
Subsequently, the CFAR threshold is calculated as
where
. Here,
denotes the false alarm rate and is set to
. The CFAR threshold
is modified by setting the upper limit to
where
represents the upper limit. The EMG signal is binarized using this threshold. When the EMG signal is activated, the state is mapped to 1, and when the EMG signal is inactivated, the state is mapped to 0, that is,
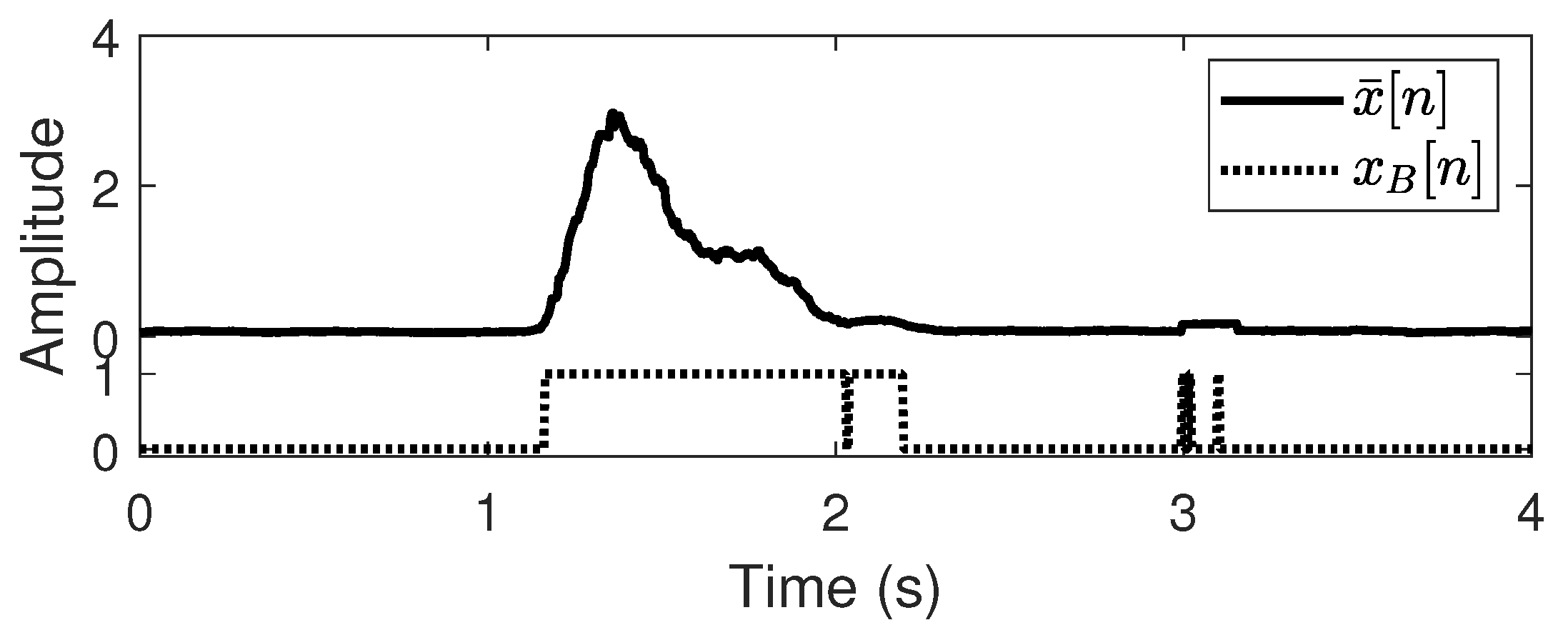
Figure 4 illustrates the binarized EMG using the modified CFAR threshold. There is a notable existence of abnormal peaks and holes that disturb the detection of activation. Morphological hole filling is adopted to refine the binarized EMG, thereby removing these abnormal peaks and holes.
3.2. Refinement of the Binarized EMG
Morphological hole filling is a signal processing algorithm using for closing up and filling out the missing information. The algorithm consists of two steps: erosion and dilation.
The erosion step is calculated as
Although the erosion step may remove abnormal peaks, it also enlarges holes. Therefore, dilation is applied to fill holes. The dilation is calculated as
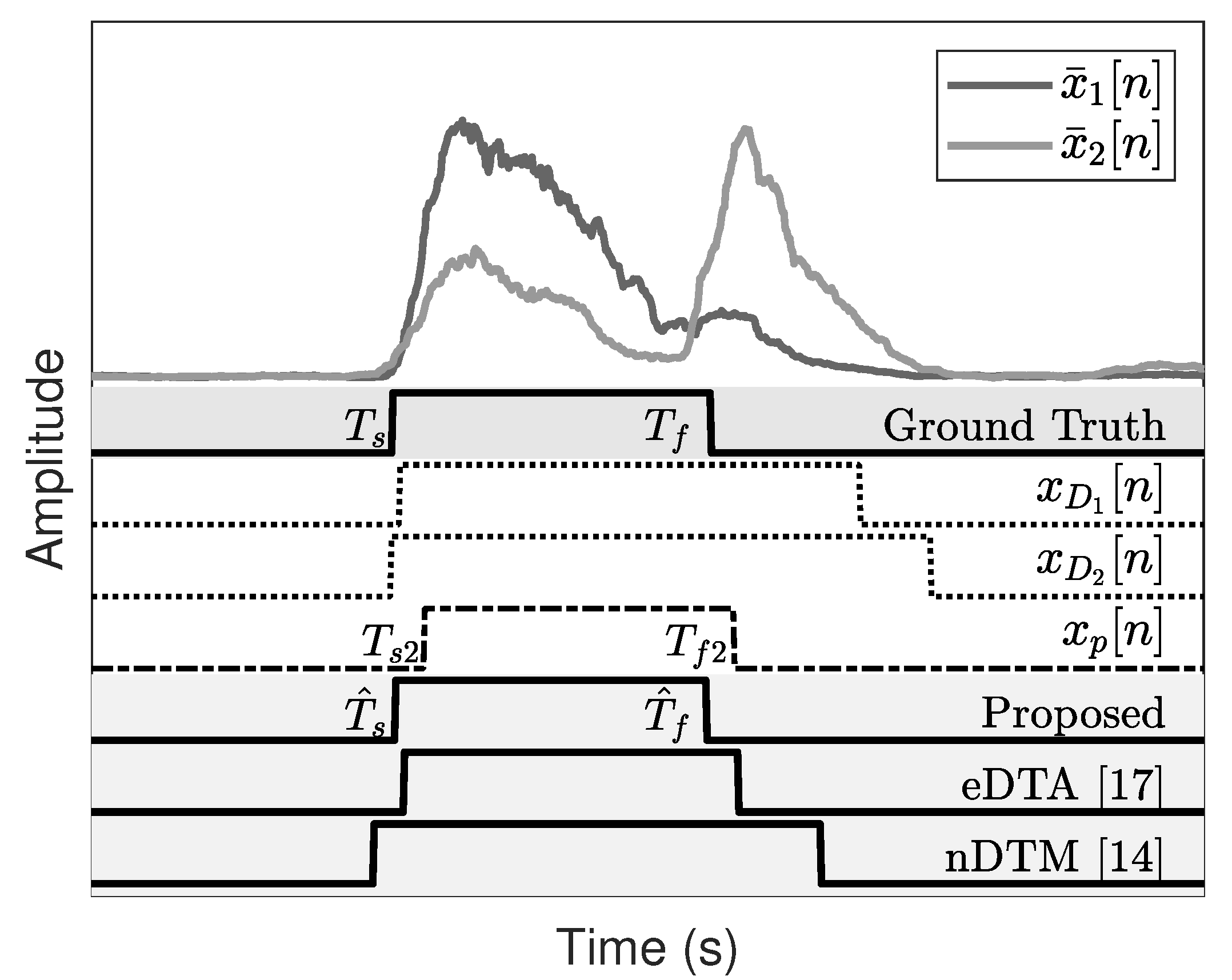
The start and end of the activation are detected from the channel dilation results, , and they are denoted by and , respectively.
Figure 5 displays the EMG refinement results and shows that the peaks and holes disappear after the morphological hole filling. From
and
, we obtain
and
by selecting the minimum and maximum values for each channel, that is,
and
3.3. Onset and Offset Detection
Since they are both activated during the hand-close movement, the onset detection can be easily achieved using either
or
. However, the offset, which is the end time of the hand-close movement or the start time of the hand-open movement, is more difficult to detect than the onset. This is because EMG signals are sustained even after the completion of hand-close movements. Thus the offset detection becomes inaccurate [
14,
17]. This phenomenon can be observed in
Figure 5. In the hand-close movement,
is clearly higher than
and vice versa in the hand-open movement. Thus, if we investigate the EMG amplitude ratio of
and
, we can successfully detect the time taken to transition from the hand-close to the hand-open movement. The transition time is the same as the offset time, the end point of the hand-close movement. To do this, we calculate the EMG ratio,
as
Then
is defined as
where
is the mean of
; that is,
Further,
is a standard deviation of
during resting period. Using
, we calculate
and
as
and
Finally, by compensating for the delay occurred by sliding windows from
, and
, the onset,
, and the offset time,
, are estimated as
and
Here,
means the compensation value calculated as
.
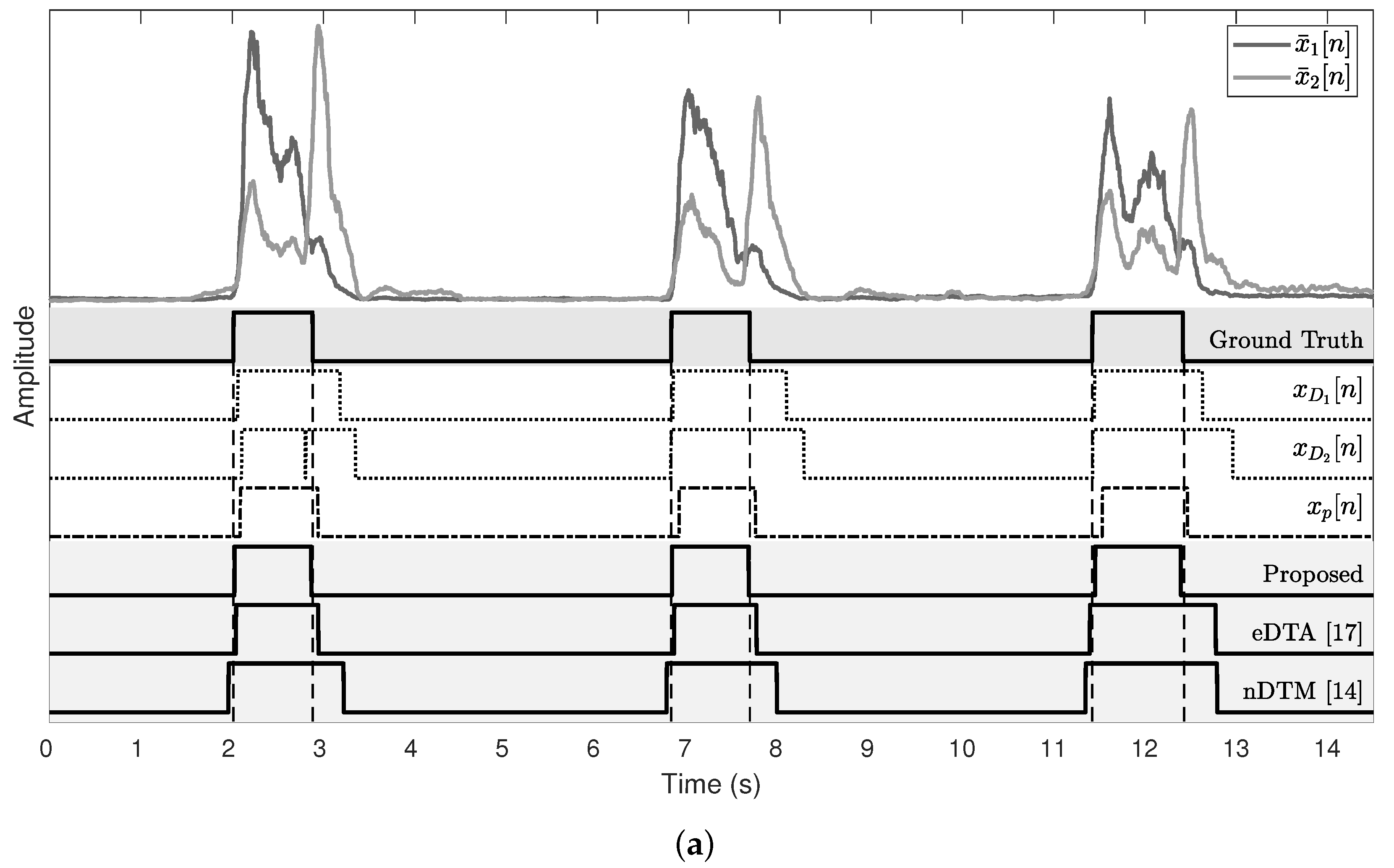
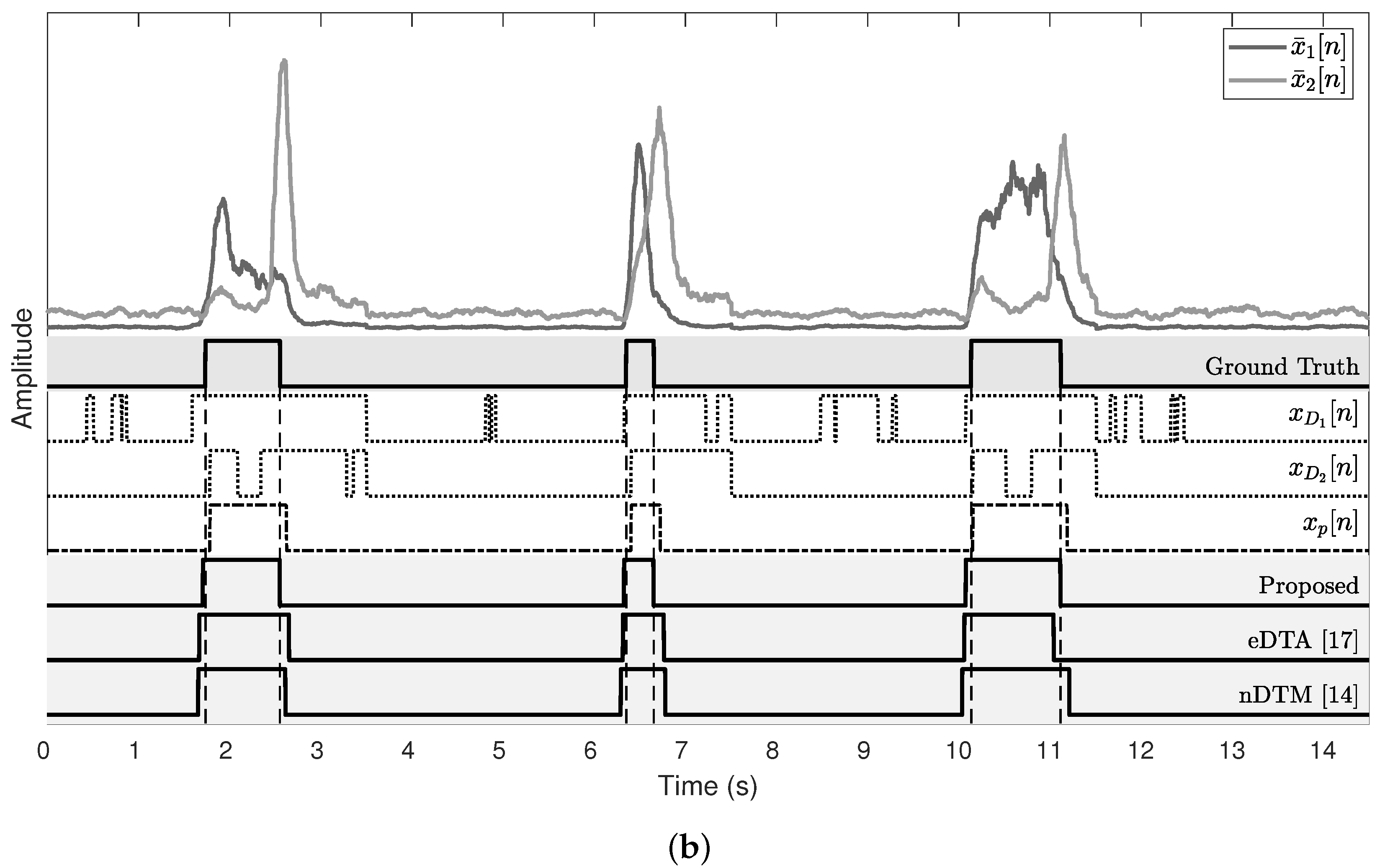
Figure 7 presents the onset and offset detection results of the two subjects. These results are compared with those obtained through conventional methods.
4. Experimental Results
We compared the results of the proposed algorithm with the novel double threshold method (nDTM) [
14] and the extended double threshold algorithm (eDTA) [
17] to evaluate the performance of the proposed algorithm. Both conventional algorithms are based on the original double threshold method [
13], which is a simple but widely used method for muscle activity detection. In the experiments, we set
, and
.
Figure 7 verifies that the proposed algorithm is more accurate than the eDTA or nDTM.
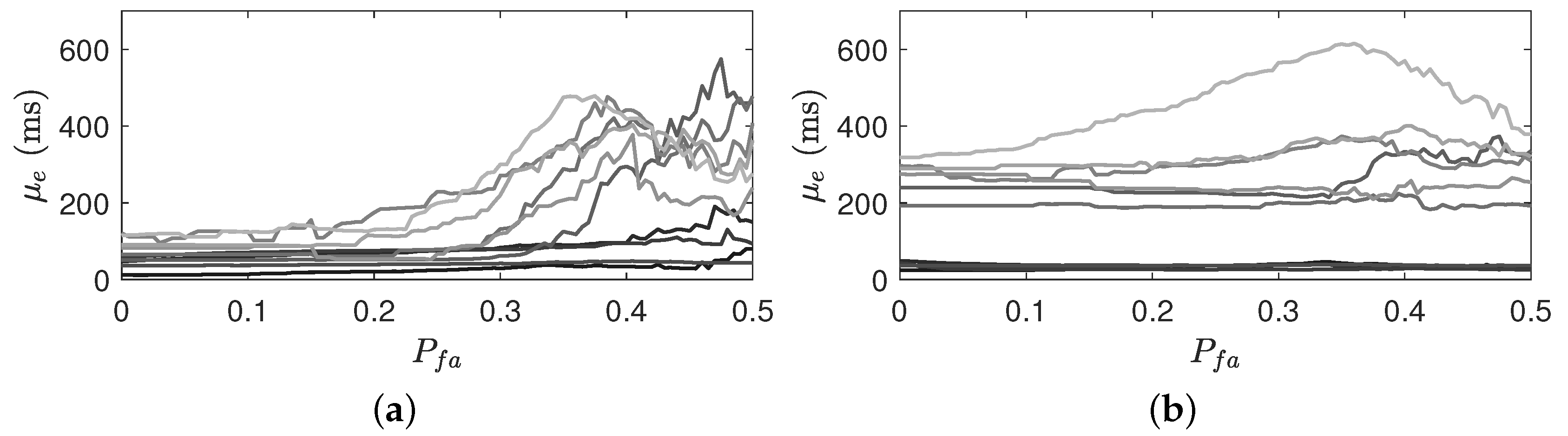
Figure 8 shows the effect of the
selection on the estimate error by varying from 0 to 0.5 for 10 subjects. Althouogh
higher than 0.3 results in the increased estimated error,
smaller than 0.2 results in the steady performace.
To quantify the accuracy, we have computed the estimation error as
where
represents the ground truth of the onset or the offset and
is estimated. The performance of the onset and the offset detection are separately evaluated.
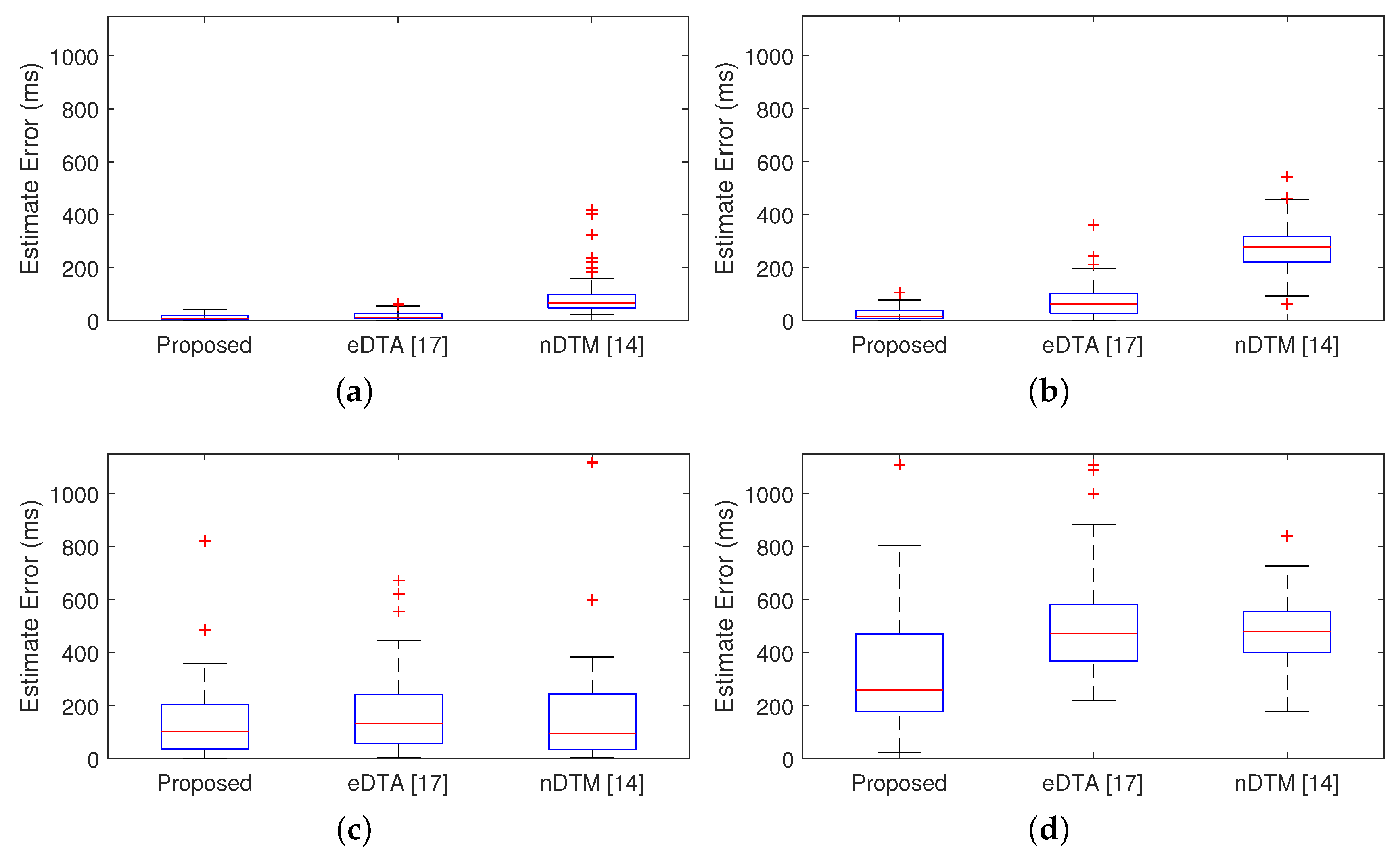
Figure 9 shows the results of subjects who show the best and the worst detection performance. For the onset detection, the proposed algorithm and eDTA reveal a similar estimate error, whereas nDTM exhibits a higher estimate error both in the best and the worst cases. It is noticeable that the offset detection result of the proposed algorithm is better than both of conventional methods.
The means and the standard deviations of the estimated error for the 10 subjects are listed in
Table 1. For the onset detection, the proposed algorithm exhibits better or similar estimated errors compared to conventional methods for all the subjects. Regarding the offset detection, the proposed algorithm demonstrates the better performance than conventional methods. This indicates that the proposed algorithm can detect the onset and the offset of muscle activation more accurately than eDTA and nDTM.
5. Conclusions
In this study, we investigated a precise onset and offset detection algorithm for muscle activation by using two channel EMG signals. In controlling prosthetic devices or smart user interface, user’s intended gestures or motions are usually predicted by EMG signals. The onset and offset timing as well as types of gestures are very important to control prosthetic devices or smart user interface accurately. Since inaccurate onset or offset detection may result in non-causal or delayed response, the accurate onset and offset detection are required.
We significantly enhanced the offset detection performance by exploiting the EMG amplitude ratio in two channels. The estimated onset and offset errors have been calculated separately for the performance evaluation. The results have been compared with those of two conventional methods, which are based on the double threshold method. For onset detection, the proposed algorithm is comparable to eDTA and nDTM, whereas for offset detection, the proposed algorithm exhibits a performance that surpasses that of conventional ones.
Author Contributions
Conceptualization, H.-C.S.; methodology, K.K. and K.R.; software, K.K.; validation, K.K., K.R. and H.-C.S.; writing—original draft preparation, K.K.; writing—review and editing, K.K. and H.-C.S.; visualization, K.K. and K.R.; supervision, project administration, and funding acquisition, H.-C.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the BK21 Plus (Software Security Program, Dept. of Software Convergence, Soongsil Univ.) through the National Research Foundation (NRF) of Korea funded by the Ministry of Science and ICT.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| EMG | Electromyography |
| CFAR | Constant false alarm rate |
| DC | Direct current |
| MAV | Mean absolute value |
| nDTM | Novel double threshold method |
| eDTA | Extended double threshold algorithm |
References
- Bojanic, D.M.; Petrovacki-Balj, B.D.; Jorgovanovic, N.D.; Ilic, V.R. Quantification of dynamic EMG patterns during gait in children with cerebral palsy. J. Neurosci. Methods 2011, 198, 325–331. [Google Scholar] [CrossRef]
- Benedetti, M.G.; Bonato, P.; Catani, F.; D’Alessio, T.; Knaflitz, M.; Marcacci, M.; Simoncini, L. Myoelectric activation pattern during gait in total knee replacement: Relationship with kinematics, kinetics, and clinical outcome. IEEE Trans. Rehabil. Eng. 1999, 7, 140–149. [Google Scholar] [CrossRef] [PubMed]
- Castellini, C.; van der Smagt, P. Surface EMG in advanced hand prosthetics. Biol. Cybern. 2009, 100, 35–47. [Google Scholar] [CrossRef] [PubMed]
- Frigo, C.; Crenna, P. Multichannel SEMG in clinical gait analysis: A review and state-of-the-art. Clin. Biomech. 2009, 24, 236–245. [Google Scholar] [CrossRef] [PubMed]
- Kawakami, M.; Fujiwara, T.; Ushiba, J.; Nishimoto, A.; Abe, K.; Honaga, K.; Nishimura, A.; Mizuno, K.; Kodama, M.; Masakado, Y.; et al. A new therapeutic application of brain-machine interface (BMI) training followed by hybrid assistive neuromuscular dynamic stimulation (HANDS) therapy for patients with severe hemiparetic stroke: A proof of concept study. Restor. Neurol. Neurosci. 2016, 34, 789–797. [Google Scholar] [CrossRef] [PubMed]
- Micera, S.; Vannozzi, G.; Sabatini, A.M.; Dario, P. Improving detection of muscle activation intervals. IEEE Eng. Med. Biol. Mag. 2001, 20, 38–46. [Google Scholar] [CrossRef] [PubMed]
- Hodges, P.W.; Moseley, G.L.; Gandevia, S.C. Experimental muscle pain changes feedforward postural responses of the trunk muscles. Exp. Brain Res. 2003, 151, 262–271. [Google Scholar] [CrossRef] [PubMed]
- Worsley, P.; Warner, M.; Mottram, S.; Gadola, S.; Veeger, H.E.J.; Hermens, H.; Morrissey, D.; Little, P.; Cooper, C.; Carr, A. Motor control retraining exercises for shoulder impingement: Effects on function, muscle activation, and biomechanics in young adults. J. Shoulder Elb. Surg. 2013, 22, e11–e19. [Google Scholar] [CrossRef] [PubMed]
- Micera, S.; Sabatini, A.M.; Dario, P. An algorithm for detecting the onset of muscle contraction by EMG signal processing. Med. Eng. Phys. 1998, 20, 211–215. [Google Scholar] [CrossRef]
- Xu, Q.; Quan, Y.; Yang, L.; He, J. An adaptive algorithm for the determination of the onset and offset of muscle contraction by emg signal processing. IEEE Trans. Neural Syst. Rehabil. Eng. 2013, 21, 65–73. [Google Scholar] [CrossRef] [PubMed]
- Hodges, P.W.; Bui, B.H. A comparison of computer-based methods for the determination of onset of muscle contraction using electromyography. Electroencephalogr. Clin.Neurophysiol./Electromyogr. Motor Control 1996, 101, 511–519. [Google Scholar]
- Yang, D.; Zhang, H.; Gu, Y.; Liu, H. Accurate EMG onset detection in pathological, weak and noisy myoelectric signals. Biomed. Signal Proc. Control 2017, 33, 306–315. [Google Scholar] [CrossRef]
- Bonato, P.; D’Alessio, T.; Knaflitz, M. A statistical method for the measurement of muscle activation intervals from surface myoelectric signal during gait. IEEE Trans. Biomed. Eng. 1998, 45, 287–299. [Google Scholar] [CrossRef] [PubMed]
- Severini, G.; Conforto, S.; Chmid, M.S.; D’alessio, T. Novel Formulation of A Double Threshold Algorithm for the Estimation of Muscle Activation Intervals Designed for Variable Snr Environments. J. Electromyogr. Kinesiol. 2012, 22, 878–885. [Google Scholar] [CrossRef] [PubMed]
- Di Nardo, F.; Mengarelli, A.; Burattini, L.; Maranesi, E.; Agostini, V.; Nascimbeni, A.; Knaflitz, M.; Fioretti, S. Normative EMG patterns of ankle muscle co-contractions in school-age children during gait. Gait Posture 2016, 46, 161–166. [Google Scholar] [CrossRef] [PubMed]
- Strazza, A.; Mengarelli, A.; Fioretti, S.; Burattini, L.; Agostini, V.; Knaflitz, M.; Di Nardo, F. Surface-EMG analysis for the quantification of thigh muscle dynamic co-contractions during normal gait. Gait Posture 2017, 51, 228–233. [Google Scholar] [CrossRef] [PubMed]
- Rashid, U.; Niazi, I.K.; Signal, N.; Farina, D.; Taylor, D. Optimal automatic detection of muscle activation intervals. J. Electromyogr. Kinesiol. 2019, 48, 103–111. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).