Building Geometry Simplification for Improving Mesh Quality of Numerical Analysis Model
Abstract
1. Introduction
2. Literature Review
3. Mesh Quality
4. Automatic Geometry Simplification Method for FVM
4.1. Preprocess
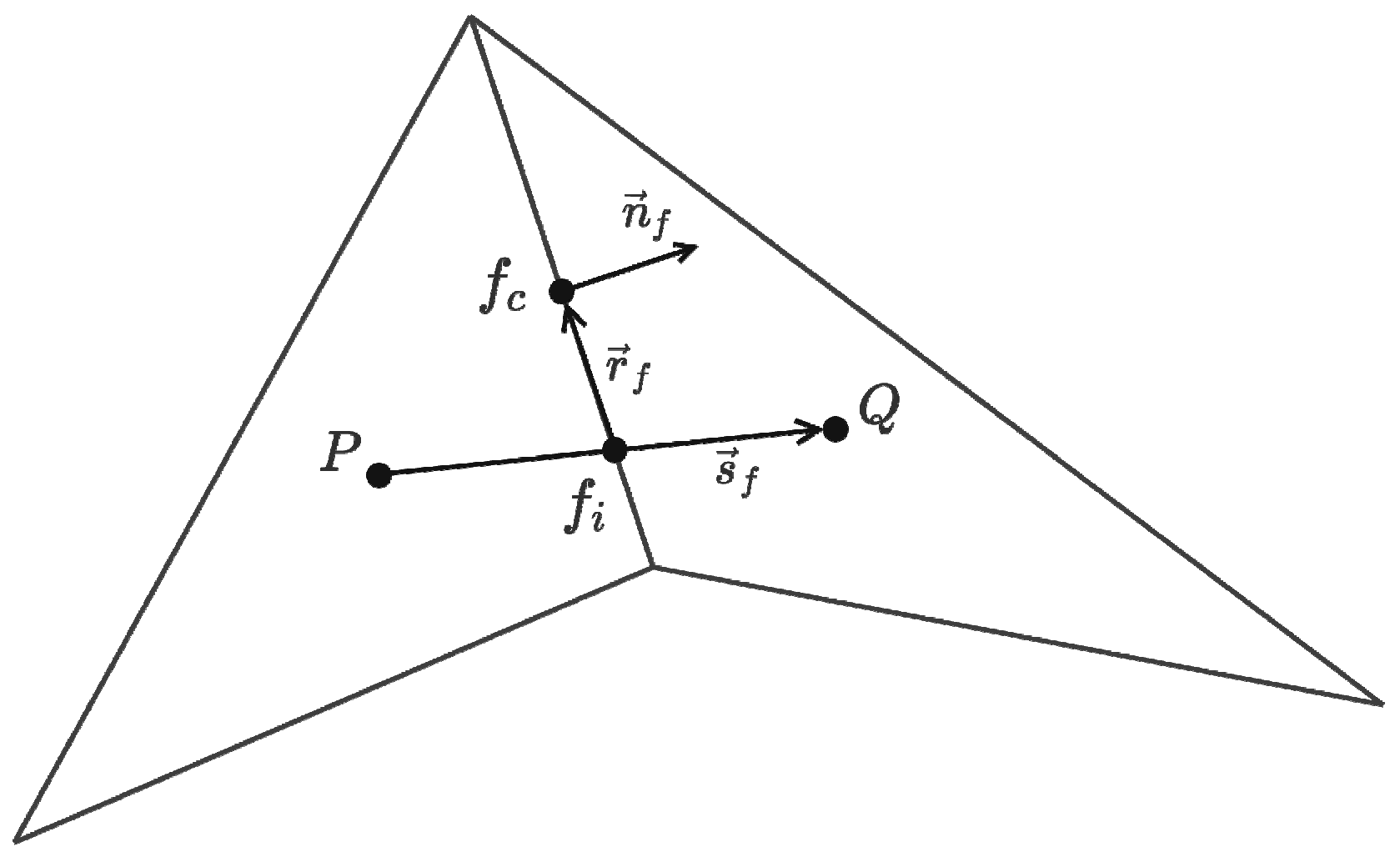
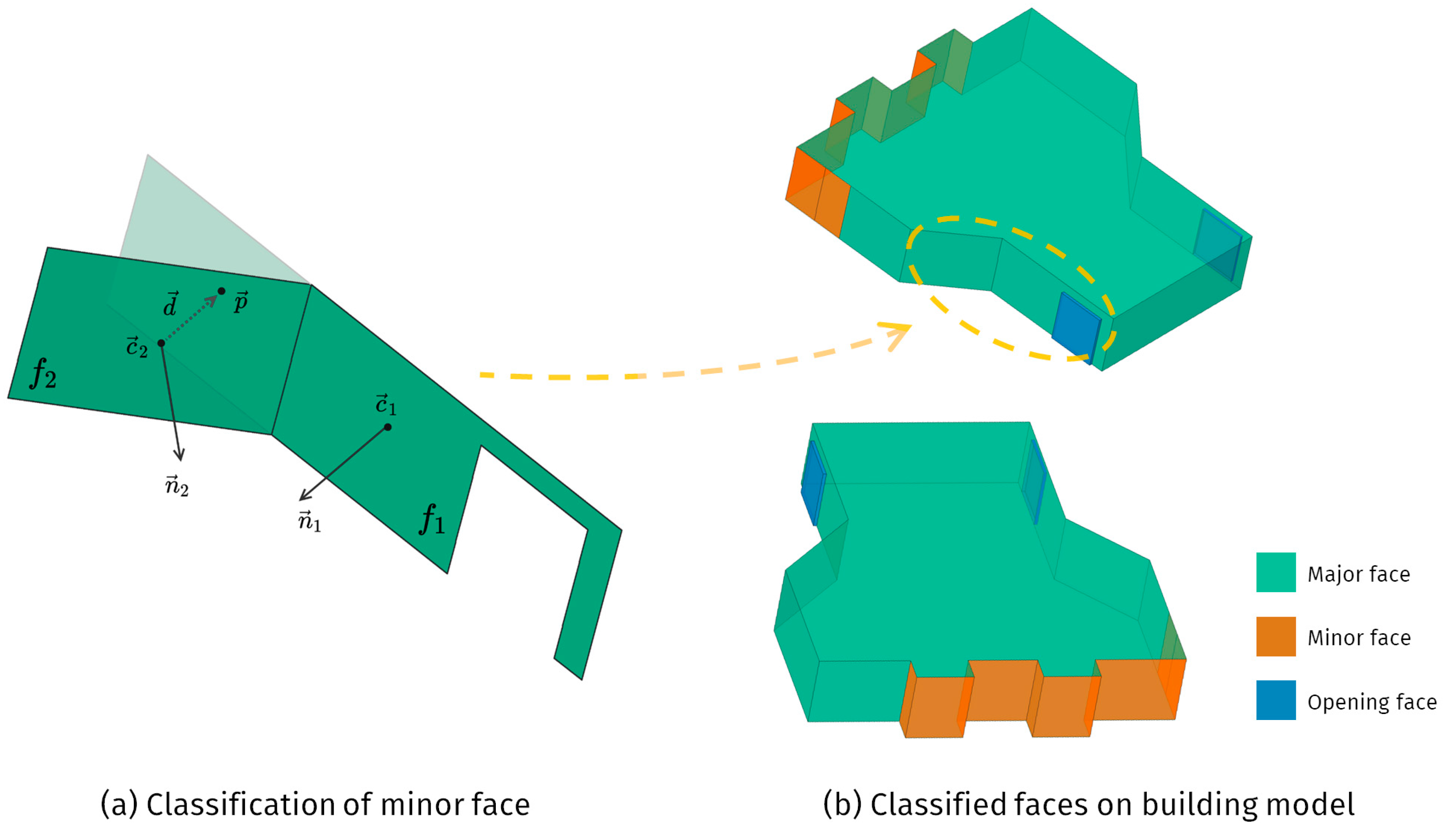
4.2. Face Classification
| Algorithm 1 Pseudocode for face classification |
| Input: : Set of geometry solids of the target model : Set of geometry solids to preserve : Angle threshold of simplification : Distance threshold of simplification |
| Output: : Set of major faces of target geometry |
| Algorithm: (Note that is area, is geometric center, is unit normal of face ) Sequence of faces on Set of faces on Sort by and in descending order FOR EACH in IF and FOR EACH in IF and and RETURN |
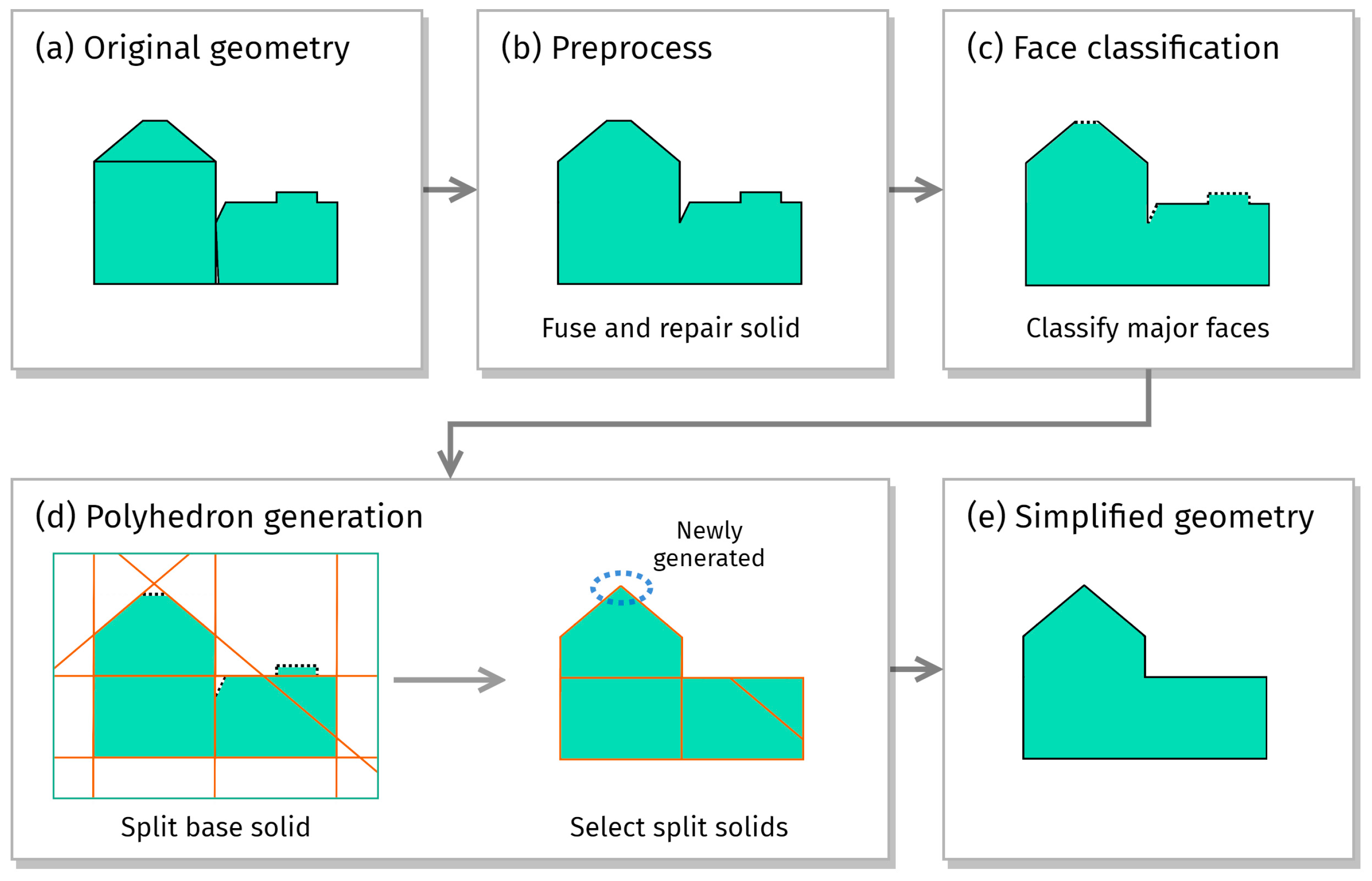
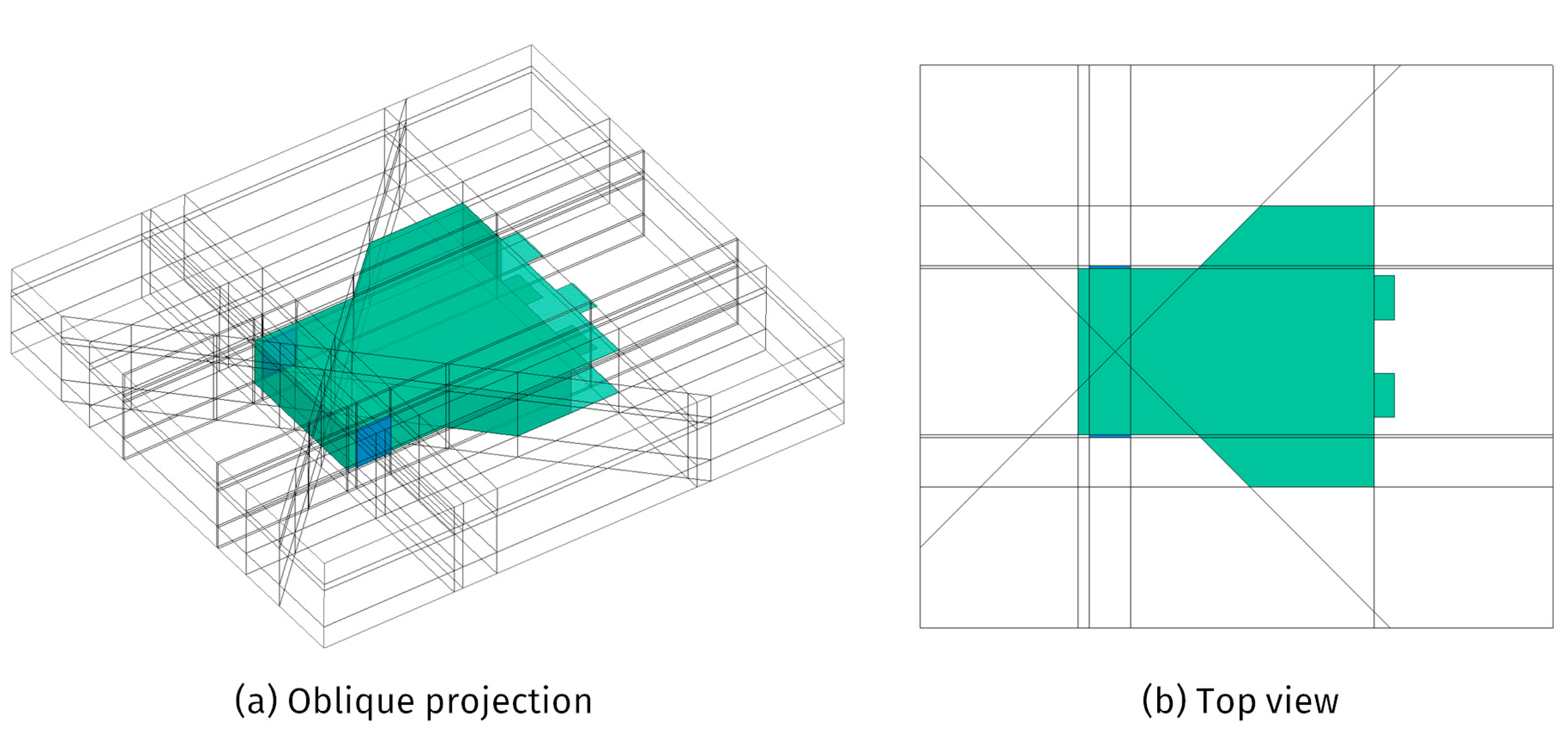
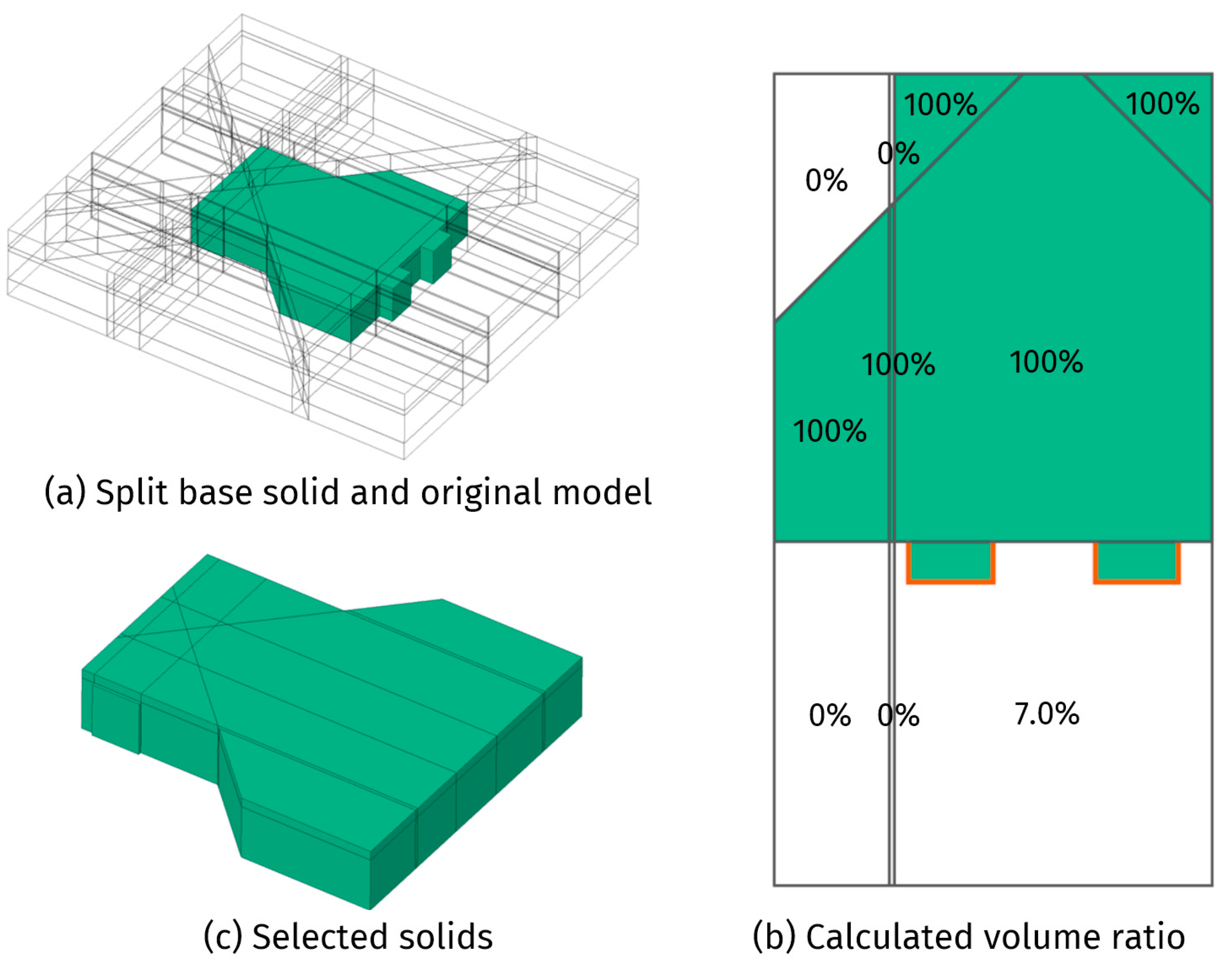
4.3. Polyhedron Generation
| Algorithm 2 Pseudocode for polyhedron generation |
| Input: : Set of geometry solids of the target model : Set of major faces of target geometry |
| Output: : Solids of simplified geometry |
| Algorithm: Plane containing Bounding volume of Split by each plane in into FOR EACH solid in IF Union of solids in RETURN |
5. Evaluation of Simplification Effect
5.1. Geometrical Properties
5.1.1. Shape Similarity
5.1.2. Meshing Complexity
5.2. Building Geometry Dataset
5.3. Implementation and Mesh Design
5.4. Experiment Settings and Analysis
6. Results and Discussion
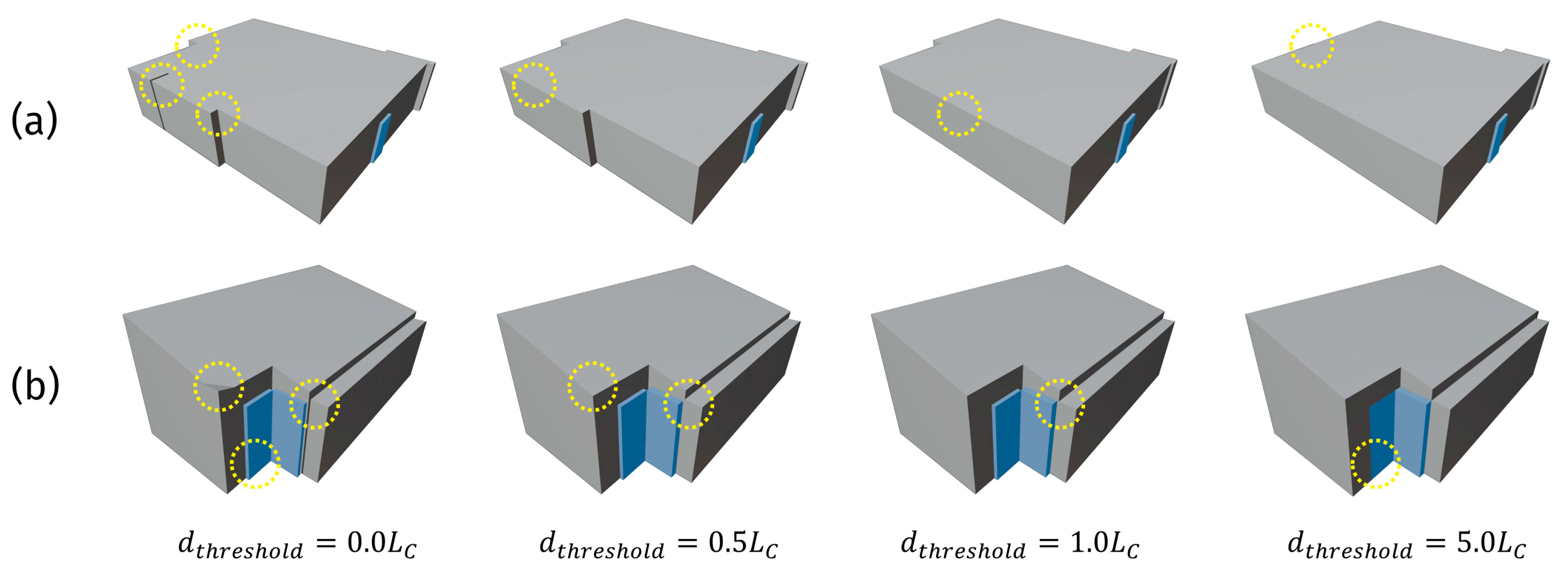
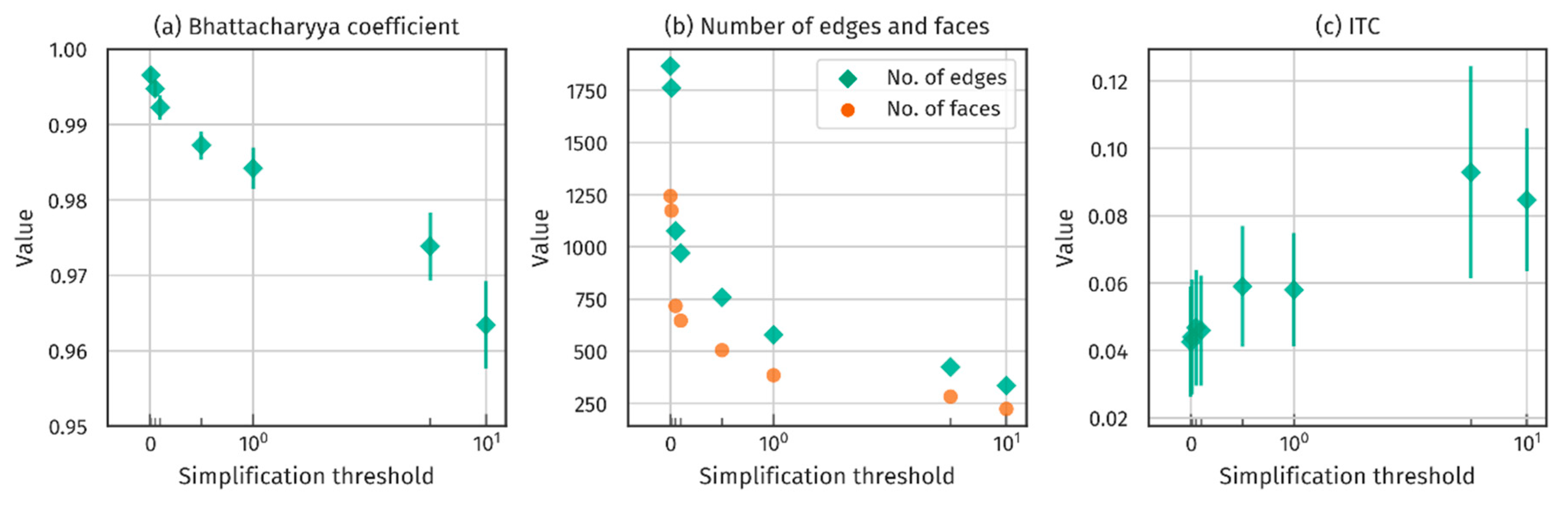
6.1. Simplification of Building Geometry
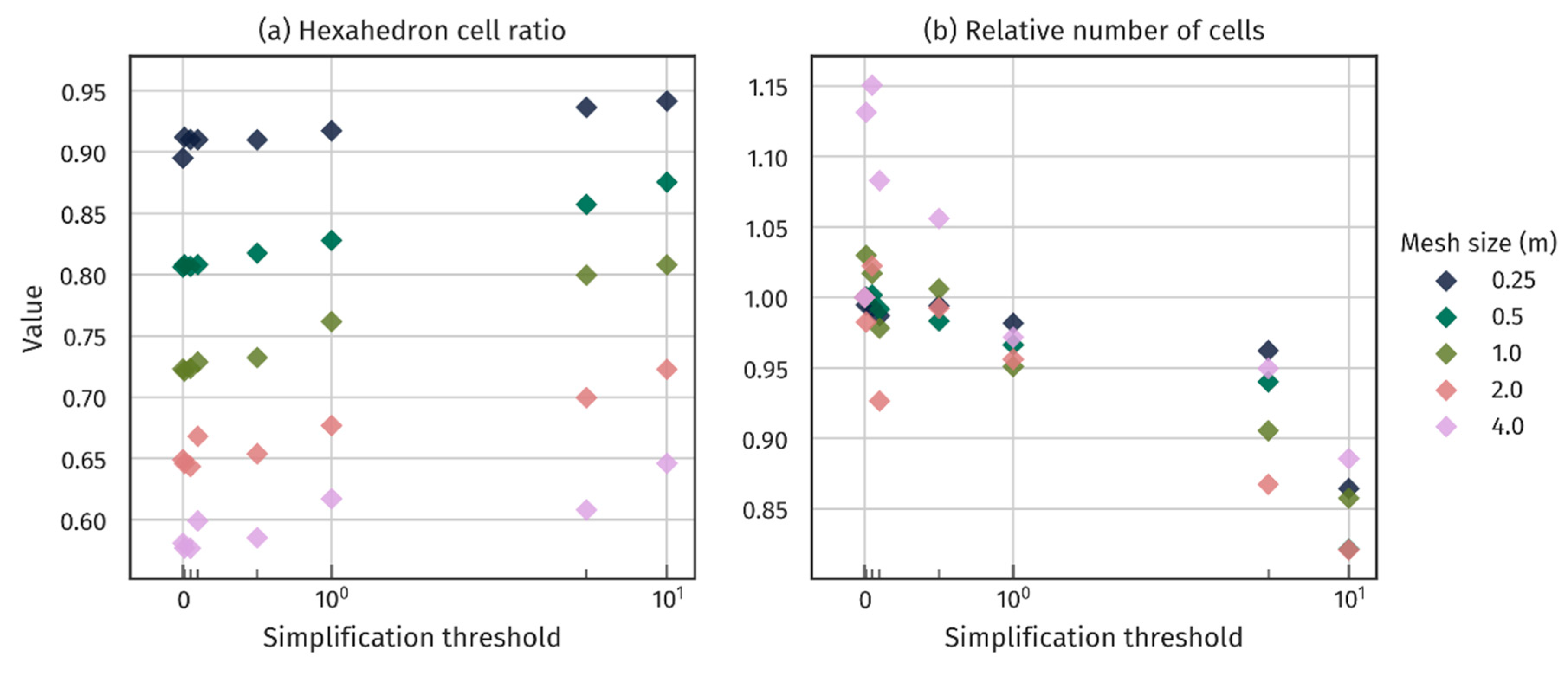
6.2. Mesh Quality Improvement by Geometry Simplification
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Eymard, R.; Gallouët, T.; Herbin, R. Finite volume methods. Handb. Numer. Anal. 2000, 7, 713–1018. [Google Scholar]
- McGrattan, K.; Hostikka, S.; McDermott, R.; Floyd, J.; Weinschenk, C.; Overholt, K. Fire dynamics simulator user’s guide. NIST Spec. Publ. 2013, 1019. [Google Scholar]
- Krykowski, T.; Zybura, A. Modelling of reinforced concrete element damage as a result of reinforcement corrosion. Procedia Eng. 2013, 57, 614–623. [Google Scholar] [CrossRef][Green Version]
- Hendrickx, R.; De Clercq, H. Heat and moisture simulations of repair mortars: Benchmark experiments and practical cases in conservation. In Historic Mortars; Springer: Berlin/Heidelberg, Germany, 2019; pp. 319–336. [Google Scholar]
- Nielsen, P.V. Fifty years of CFD for room air distribution. Build. Environ. 2015, 91, 78–90. [Google Scholar] [CrossRef]
- Knupp, P. Remarks on Mesh Quality; Sandia National Lab.(SNL-NM): Albuquerque, NM, USA, 2007. [Google Scholar]
- Burkhart, T.A.; Andrews, D.M.; Dunning, C.E. Finite element modeling mesh quality, energy balance and validation methods: A review with recommendations associated with the modeling of bone tissue. J. Biomech. 2013, 46, 1477–1488. [Google Scholar] [CrossRef] [PubMed]
- Denner, F.; van Wachem, B.G.M. Compressive VOF method with skewness correction to capture sharp interfaces on arbitrary meshes. J. Comput. Phys. 2014, 279, 127–144. [Google Scholar] [CrossRef]
- Ishigaki, M.; Abe, S.; Sibamoto, Y.; Yonomoto, T. Influence of mesh non-orthogonality on numerical simulation of buoyant jet flows. Nucl. Eng. Des. 2017, 314, 326–337. [Google Scholar] [CrossRef]
- Ricci, A.; Kalkman, I.; Blocken, B.; Burlando, M.; Freda, A.; Repetto, M.P. Local-scale forcing effects on wind flows in an urban environment: Impact of geometrical simplifications. J. Wind Eng. Ind. Aerodyn. 2017, 170, 238–255. [Google Scholar] [CrossRef]
- Ali, Z.; Tyacke, J.; Watson, R.; Tucker, P.; Shahpar, S. Efficient preprocessing of complex geometries for CFD simulations. Int. J. Comput. Fluid Dyn. 2019, 1–17. [Google Scholar] [CrossRef]
- Heok, T.K.; Daman, D. A review on level of detail. In Proceedings of the International Conference on Computer Graphics, Imaging and Visualization, 2004 (CGIV 2004), Penang, Malaysia, 2 July 2004; IEEE: New York, NY, USA, 2004; pp. 70–75. [Google Scholar]
- Li, X.; Yan, Y.; Tu, J. The simplification of computer simulated persons (CSPs) in CFD models of occupied indoor spaces. Build. Environ. 2015, 93, 155–164. [Google Scholar] [CrossRef]
- Yan, Y.; Li, X.; Yang, L.; Tu, J. Evaluation of manikin simplification methods for CFD simulations in occupied indoor environments. Build. Environ. 2016, 127, 611–626. [Google Scholar] [CrossRef]
- Forberg, A.; Mayer, H. Simplification of 3D building data. 3D building data. ZFV-Zeitschrift fur Geodasie, Geoinformation und Landmanagement 2006, 131, 148–152. [Google Scholar]
- Kada, M. 3D building generalization based on half-space modeling. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 58–64. [Google Scholar]
- Rau, J.-Y.; Chen, L.; Tseng, D.-C. Automatic Generalization of Digital Building Models. In Proceedings of the Asian Association on Remote Sensing—26th Asian Conference on Remote Sensing and 2nd Asian Space Conference (ACRS 2005), Hanoi, Vietnam, 7–11 November 2005; Volume 2. [Google Scholar]
- He, S.; Moreau, G.; Martin, J.-Y. Footprint-based generalization of 3D building groups at medium level of detail for multi-scale urban visualization. Int. J. Adv. Softw. 2012, 5, 377–387. [Google Scholar]
- Zhao, J.; Zhu, Q.; Du, Z.; Feng, T.; Zhang, Y. Mathematical morphology-based generalization of complex 3D building models incorporating semantic relationships. ISPRS J. Photogramm. Remote Sens. 2012, 68, 95–111. [Google Scholar] [CrossRef]
- Geiger, A.; Benner, J.; Haefele, K.H. Generalization of 3D IFC building models. In 3D Geoinformation Science; Springer: Berlin/Heidelberg, Germany, 2015; pp. 19–35. [Google Scholar]
- Ayala, P.; Cantizano, A.; Gutiérrez-Montes, C.; Rein, G. Influence of atrium roof geometries on the numerical predictions of fire tests under natural ventilation conditions. Energy Build. 2013, 65, 382–390. [Google Scholar] [CrossRef]
- Piepereit, R.; Deininger, M.; Kada, M.; Pries, M.; Voß, U. A Sweep-plane Algorithm For The Simplification Of 3d Building Models In The Application Scenario Of Wind Simulations. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-4/W10, 151–156. [Google Scholar] [CrossRef]
- Gullberg, R. Computational Fluid Dynamics in OpenFOAM. 2017. Available online: http://folk.ntnu.no/preisig/HAP_Specials/AdvancedSimulation_files/2017/project%20reports/CFD/Rebecca%20Gullberg%20-%20CFD_Mesh_Report.pdf (accessed on 30 June 2020).
- Greenshields, C.J. OpenFOAM user guide. OpenFOAM Found. Ltd Version 2015, 3, e2888. [Google Scholar]
- Hefny, M.M.; Ooka, R. CFD analysis of pollutant dispersion around buildings: Effect of cell geometry. Build. Environ. 2009, 44, 1699–1706. [Google Scholar] [CrossRef]
- Sosnowski, M.; Gnatowska, R.; Grabowska, K.; Krzywański, J.; Jamrozik, A. Numerical Analysis of Flow in Building Arrangement: Computational Domain Discretization. Appl. Sci. 2019, 9, 941. [Google Scholar] [CrossRef]
- Butlin, G.; Stops, C. CAD data repair. In Proceedings of the 5th International Meshing Roundtable, Pittsburgh, PA, USA, 10–11 October 1996; pp. 7–12. [Google Scholar]
- Guo, J.; Ding, F.; Jia, X.; Yan, D.-M. Automatic and high-quality surface mesh generation for CAD models. Comput.-Aided Des. 2019, 109, 49–59. [Google Scholar] [CrossRef]
- Wang, J.; Yu, Z. A novel method for surface mesh smoothing: Applications in biomedical modeling. In Proceedings of the 18th international meshing roundtable, Salt Lake City, UT, USA, 25–28 October 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 195–210. [Google Scholar]
- Osada, R.; Funkhouser, T.; Chazelle, B.; Dobkin, D. Matching 3D models with shape distributions. In Proceedings of the International Conference on Shape Modeling and Applications, Genoa, Italy, 7–11 May 2001; IEEE: New York, NY, USA, 2001; pp. 154–166. [Google Scholar]
- Osada, R.; Funkhouser, T.; Chazelle, B.; Dobkin, D. Shape distributions. ACM Trans. Graph. 2002, 21, 807–832. [Google Scholar] [CrossRef]
- Wohlkinger, W.; Vincze, M. Ensemble of shape functions for 3D object classification. In Proceedings of the 2011 IEEE International Conference on Robotics and Biomimetics, Phuket, Thailand, 7–11 December 2011; pp. 2987–2992. [Google Scholar]
- Bhattacharyya, A. On a measure of divergence between two statistical populations defined by their probability distributions. Bull. Calcutta Math. Soc. 1943, 35, 99–109. [Google Scholar]
- White, D.R.; Saigal, S.; Owen, S.J. Meshing complexity: Predicting meshing difficulty for single part CAD models. Eng. Comput. 2005, 21, 76–90. [Google Scholar] [CrossRef]
- DURAARK Datasets. Available online: http://duraark.eu/data-repository/ (accessed on 27 April 2020).
- East, E.W. Common Building Information Model Files and Tools. Available online: https://www.nibs.org/page/bsa_commonbimfiles (accessed on 27 April 2020).
- Dimyadi, J.; Dimalen, D. Open IFC Model Repository. Available online: http://openifcmodel.cs.auckland.ac.nz/ (accessed on 27 April 2020).
- Krijnen, T. IfcOpenShell. 2011. Available online: http://ifcopenshell.org (accessed on 30 June 2020).
- OPEN CASCADE Company. Open CASCADE Technology; OPEN CASCADE Company: Guyancourt, France, 2019. [Google Scholar]
- Paviot, T.; Feringa, J. pythonOCC; 3D CAD/CAE/PLM Development Framework for the Python Programming Language. 2018. Available online: https://github.com/tpaviot/pythonocc (accessed on 30 June 2020).
- Juretić, F. cfMesh User Guide. Creat. Fields Ltd. 2015. Available online: http://cfmesh.com (accessed on 30 June 2020).
- Lee, W.; Kim, D.; Park, Y.; Huh, K.Y. Development of a Web-Based Open Source CAE Platform for Simulation of IC Engines. Int. J. Automot. Technol. 2020, 21, 169–179. [Google Scholar] [CrossRef]
- Hoyle, B.; Rau, M.M.; Paech, K.; Bonnett, C.; Seitz, S.; Weller, J. Anomaly detection for machine learning redshifts applied to SDSS galaxies. Mon. Not. R. Astron. Soc. 2015, 452, 4183–4194. [Google Scholar] [CrossRef]


| Properties | Volume (m3) | Surface Area (m2) | Characteristic Length (m) | ITC |
| Average | 170.4 | 233.6 | 0.592 | 4.25e-2 |
| Standard deviation | 210.8 | 228.7 | 0.223 | 0.101 |
| Minimum | 0.960 | 37.6 | 1.47e-2 | 6.46e-4 |
| Maximum | 1062.6 | 1251.7 | 1.025 | 0.583 |
| Multiple R2 | Adjusted R2 | F-Statistic | p-Value |
| 0.2369 | 0.2363 | 363.9 | <2.2e-16 |
| Variable | Coefficient | Standard Error | p-Value |
| (Intercept) | 0.9918288 | 0.0006793 | <2e-16 |
| −0.0031480 | 0.0001650 | <2e-16 |
| Multiple R2 | Adjusted R2 | F-Statistic | p-Value |
| 0.3806 | 0.3784 | 169.7 | <2.2e-16 |
| Variable | Coefficient | Standard Error | p-Value |
| (Intercept) | 0.706601 | 0.014671 | <2e-16 |
| 0.012601 | 0.001138 | <2e-16 | |
| −0.174158 | 0.012044 | <2e-16 | |
| 0.030040 | 0.002733 | <2e-16 | |
| 0.320294 | 0.026096 | <2e-16 | |
| 0.234317 | 0.016826 | <2e-16 |
| Multiple R2 | Adjusted R2 | F-Statistic | p-Value |
| 0.2143 | 0.2120 | 94.21 | <2.2e-16 |
| Variable | Coefficient | Standard Error | p-Value |
| (Intercept) | 103.5349 | 2.3859 | <2e-16 |
| −2.3652 | 0.2556 | <2e-16 | |
| −22.6681 | 2.7056 | <2e-16 | |
| 3.9979 | 0.6139 | 1.04e-10 | |
| −84.6206 | 5.8553 | <2e-16 |
| Multiple R2 | Adjusted R2 | F-Statistic | p-Value |
| 0.2370 | 0.2343 | 85.81 | <2.2e-16 |
| Variable | Coefficient | Standard Error | p-Value |
| (Intercept) | 3.01519 | 0.16625 | <2e-16 |
| −0.11820 | 0.01290 | <2e-16 | |
| −1.20214 | 0.13649 | <2e-16 | |
| 0.21268 | 0.03097 | 9.86e-12 | |
| −4.63938 | 0.29573 | <2e-16 | |
| −0.71985 | 0.19068 | 0.000167 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, G.; Kim, C.; Lee, M.; Choi, C. Building Geometry Simplification for Improving Mesh Quality of Numerical Analysis Model. Appl. Sci. 2020, 10, 5425. https://doi.org/10.3390/app10165425
Park G, Kim C, Lee M, Choi C. Building Geometry Simplification for Improving Mesh Quality of Numerical Analysis Model. Applied Sciences. 2020; 10(16):5425. https://doi.org/10.3390/app10165425
Chicago/Turabian StylePark, Gwanyong, Changmin Kim, Minhyung Lee, and Changho Choi. 2020. "Building Geometry Simplification for Improving Mesh Quality of Numerical Analysis Model" Applied Sciences 10, no. 16: 5425. https://doi.org/10.3390/app10165425
APA StylePark, G., Kim, C., Lee, M., & Choi, C. (2020). Building Geometry Simplification for Improving Mesh Quality of Numerical Analysis Model. Applied Sciences, 10(16), 5425. https://doi.org/10.3390/app10165425





