Machine-Learning Based Optimal Seismic Control of Structure with Active Mass Damper
Abstract
1. Introduction
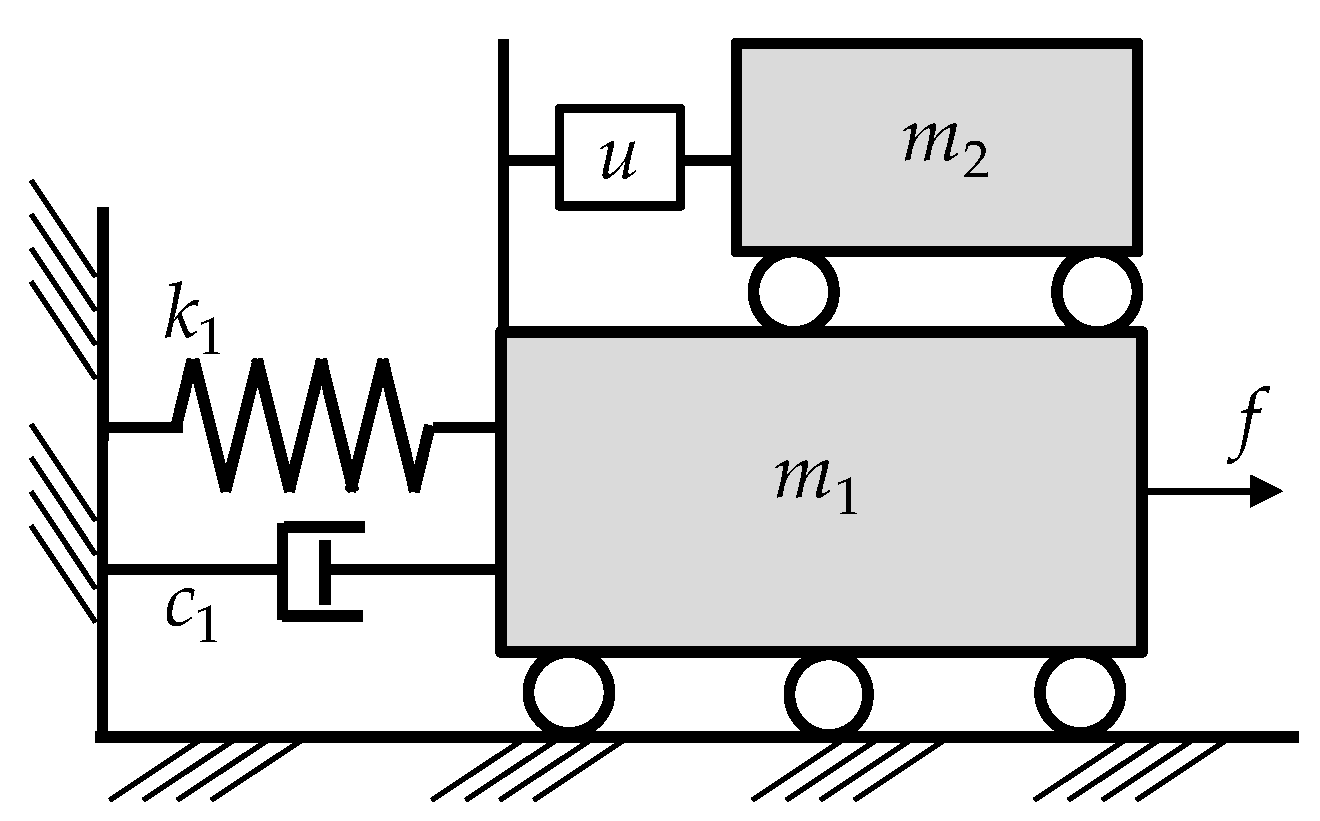
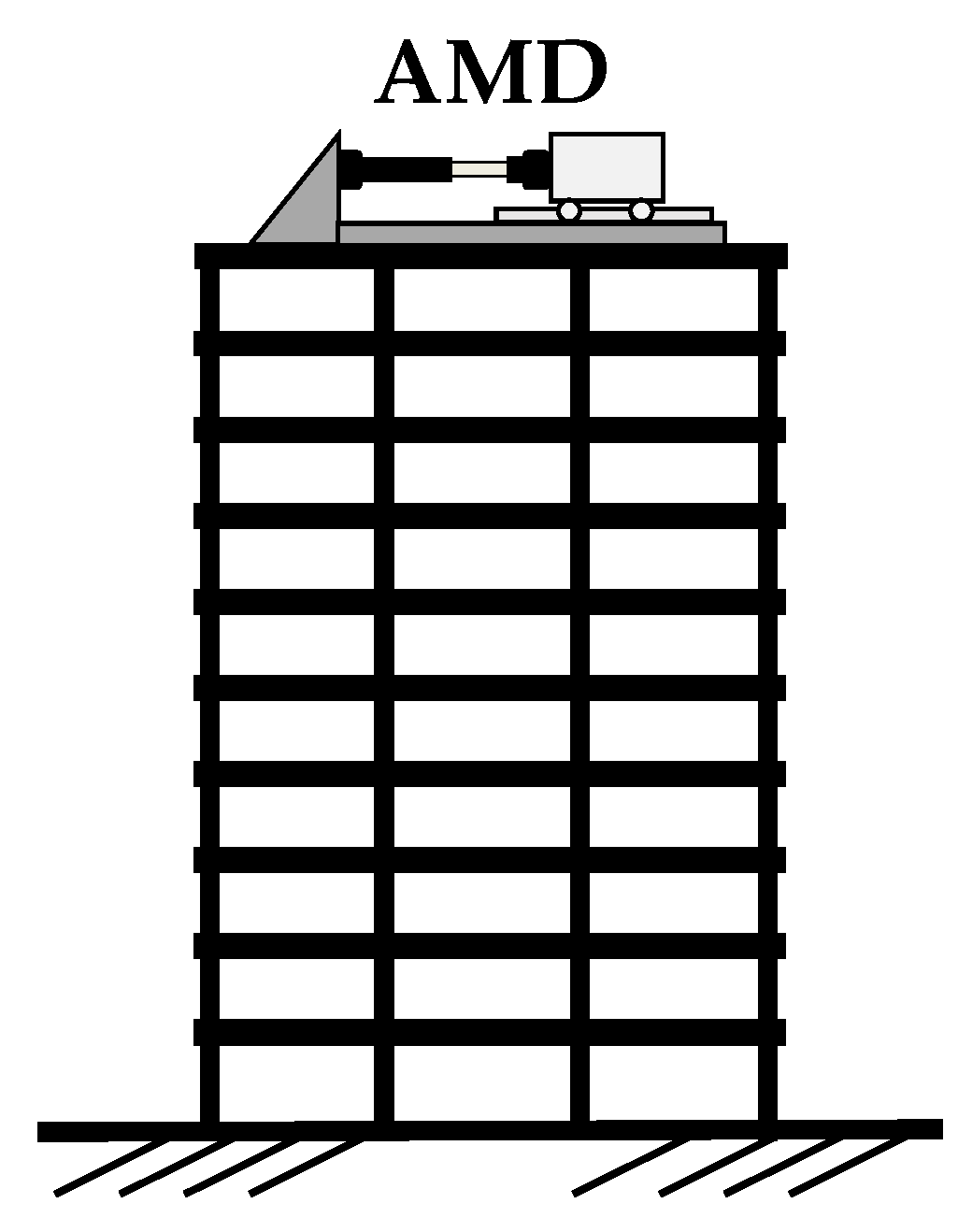
1.1. Active Mass Damper
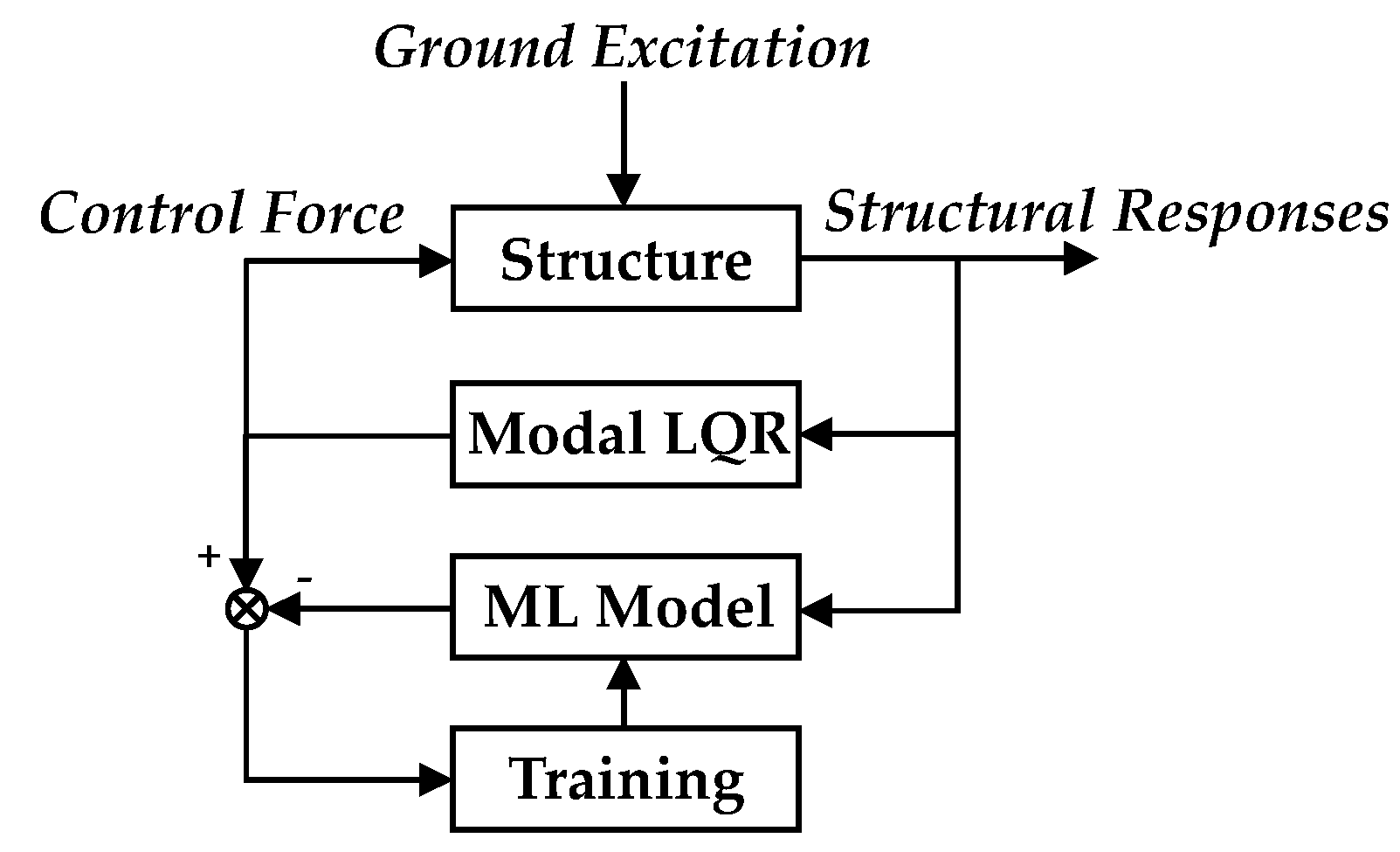
1.2. Motivation
2. Modal LQR with Optimized Weighting Matrices
2.1. Modal LQR
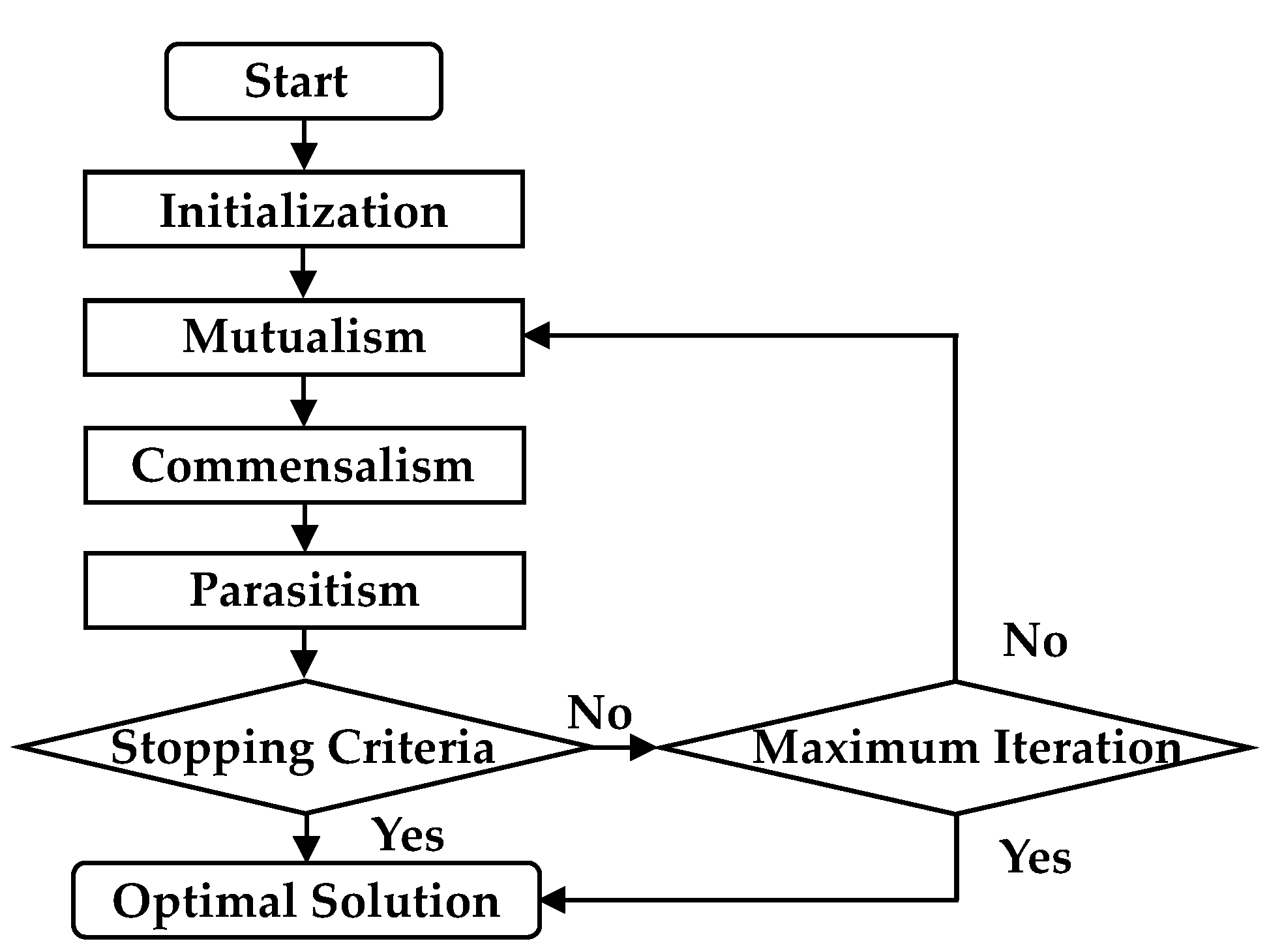
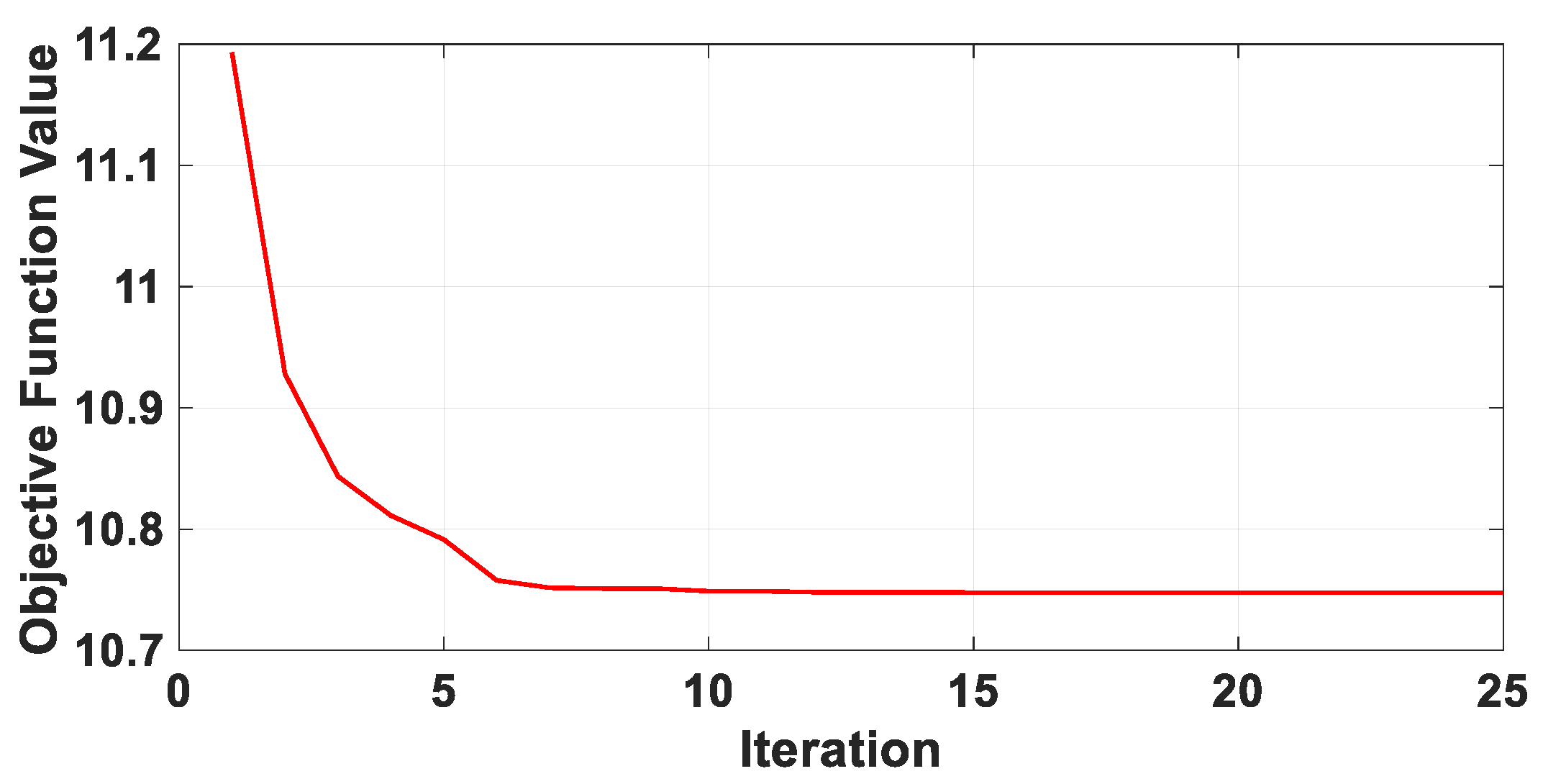
2.2. Symbiotic Organisms Search
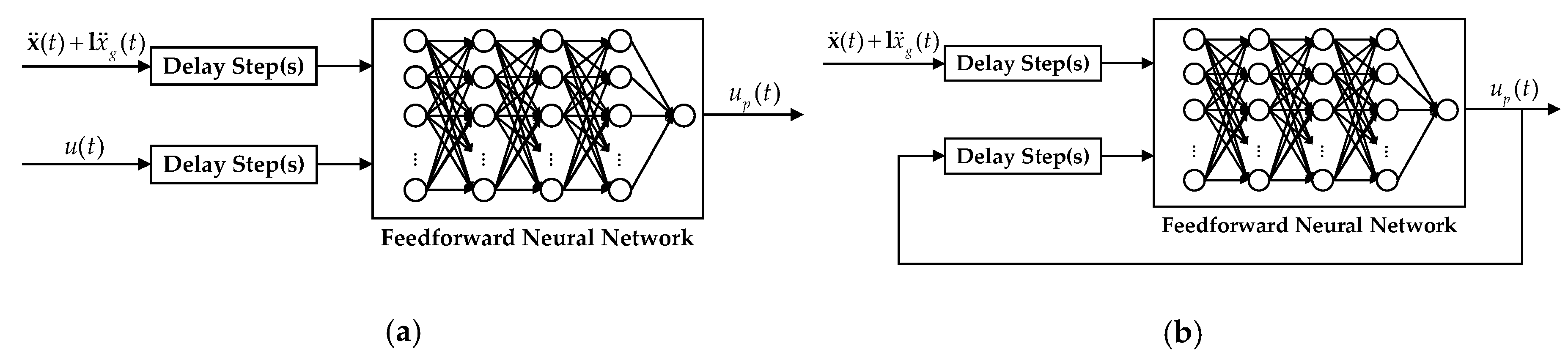
3. Neural Network Models
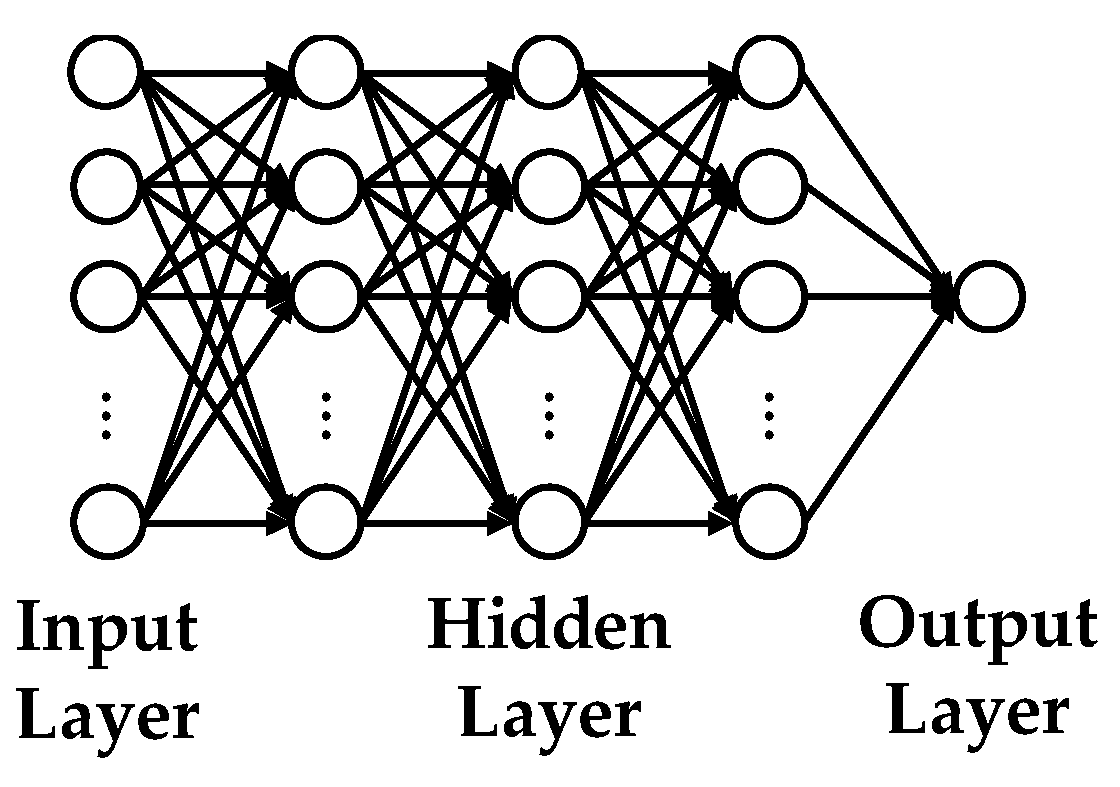
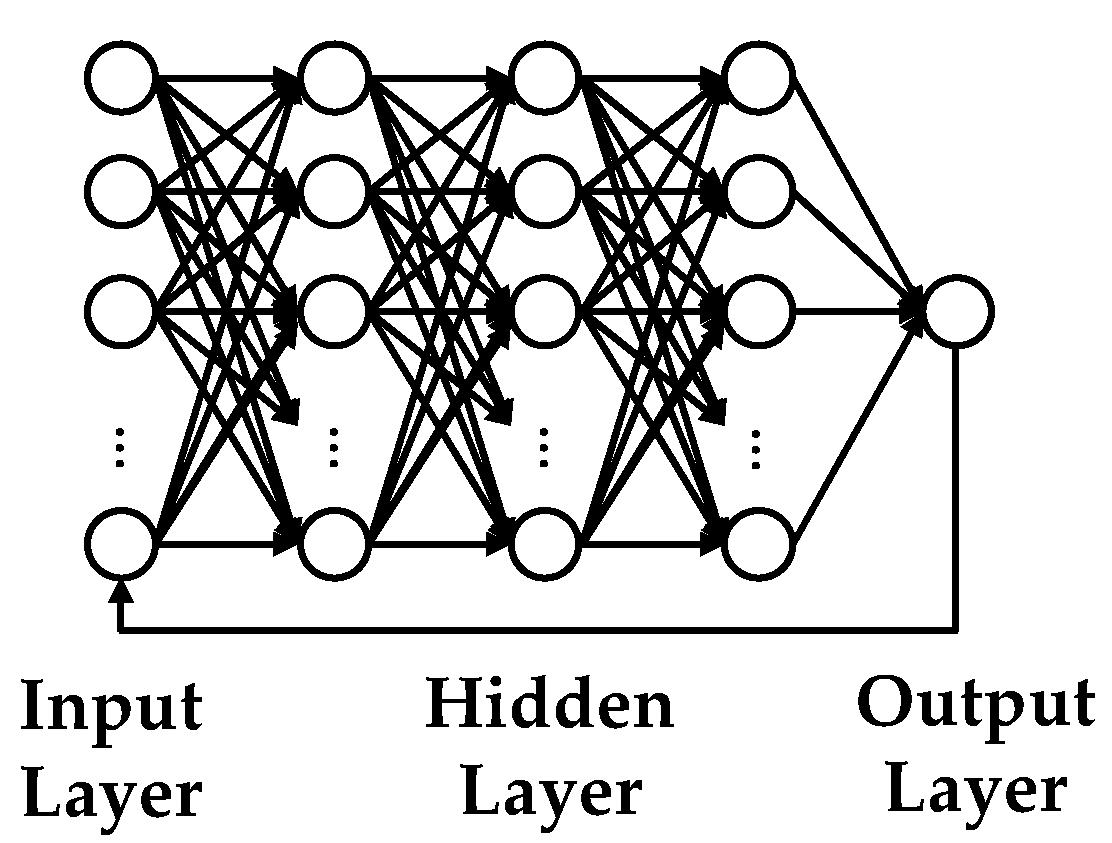
3.1. Multilayer Perceptron Model
3.2. Autoregressive Exogenous with Exogenous Inputs Model
4. Numerical Study: A 10-Story Shear Building
4.1. Modal LQR with Optimized Weighting Matrices
4.2. Training and Validating of MLP Model
4.3. Training and Validating of ARX Model
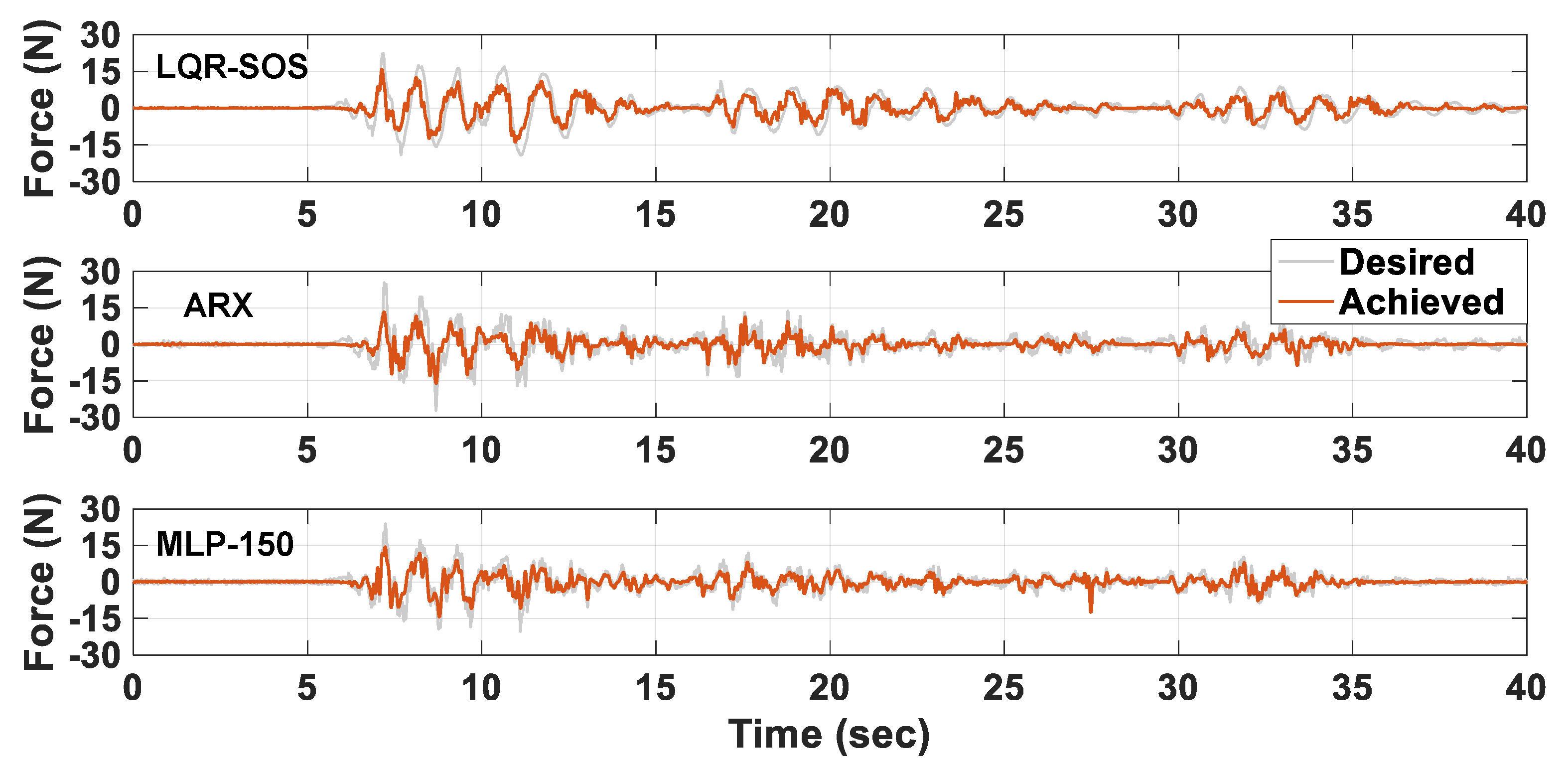
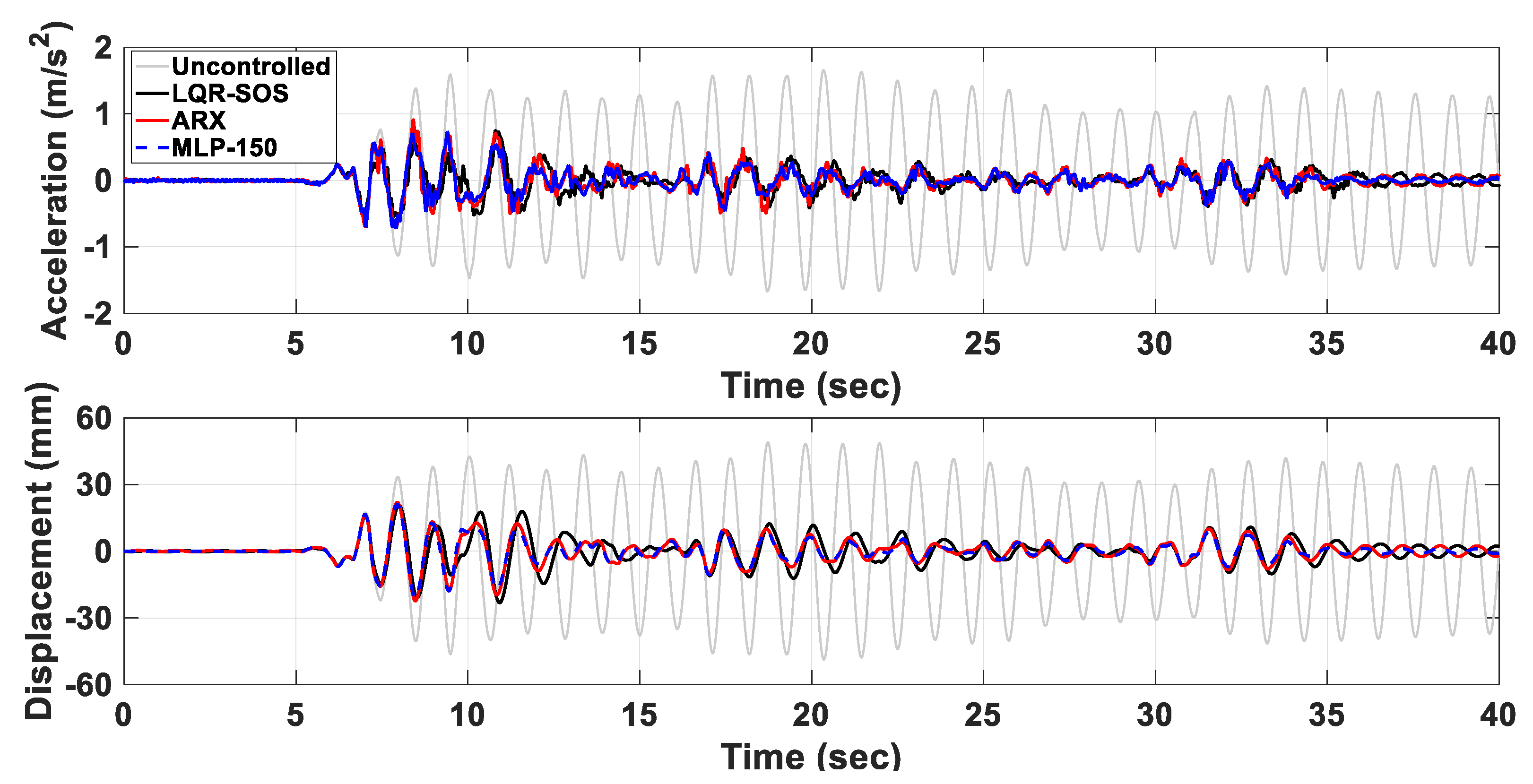
4.4. Comparison of Seismic Control Performance
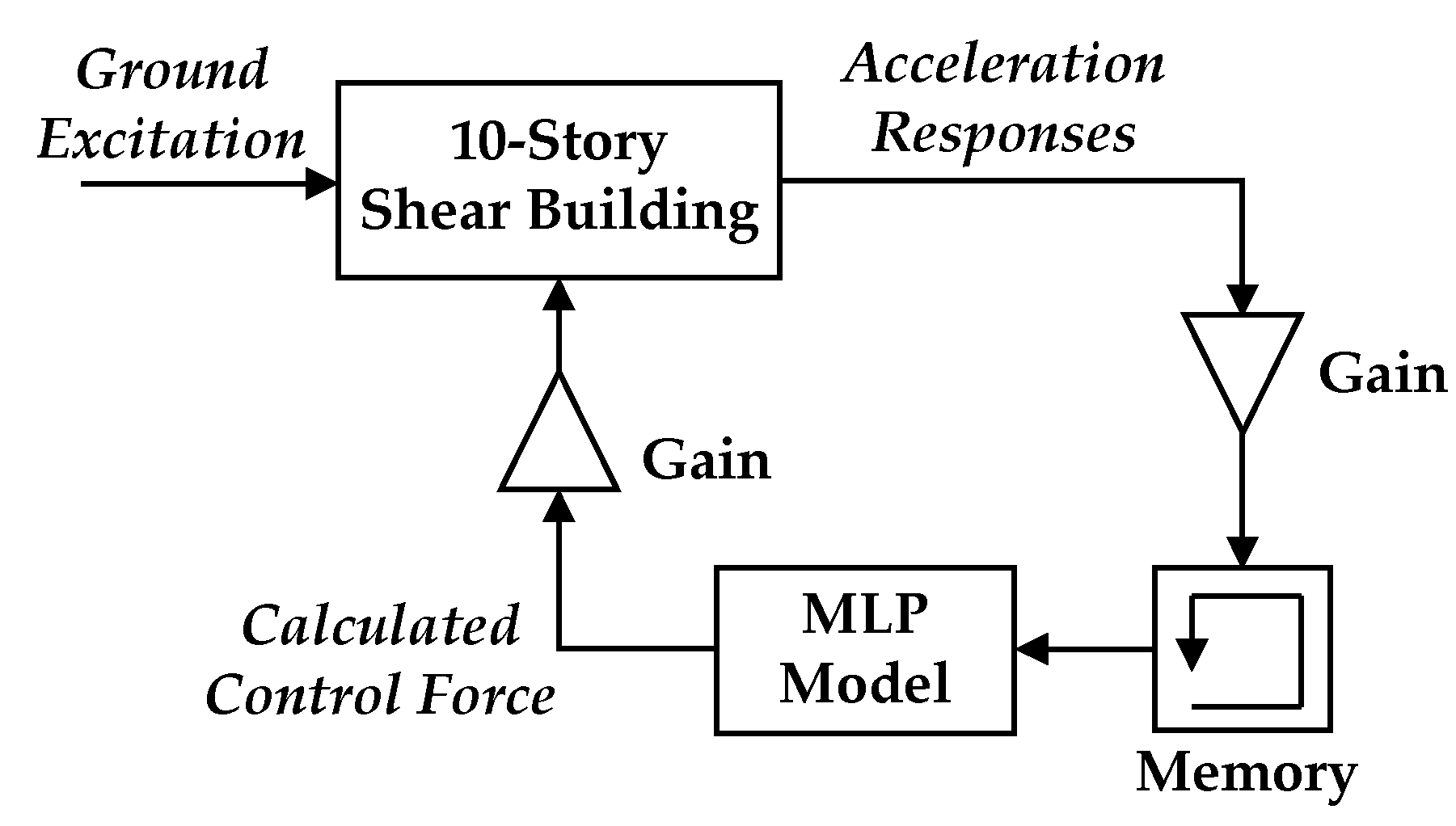
5. Experimental Validation
5.1. Experimental Setup
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Saaed, T.E.; Nikolakopoulos, G.; Jonasson, J.E.; Hedlund, H. A state-of-the-art review of structural control systems. J. Sound Vib. 2015, 21, 919–937. [Google Scholar] [CrossRef]
- Chang, C.C.; Yang, H.T.Y. Control of buildings using active tuned mass damper. J. Eng. Mech. 1995, 121, 355–366. [Google Scholar] [CrossRef]
- Cao, H.; Reinhorn, A.M.; Soong, T.T. Design of active mass damper for a tall TV tower in Nanjing China. Eng. Struct. 1998, 20, 134–143. [Google Scholar] [CrossRef]
- Dyke, S.J.; Spencer, B.F., Jr.; Quast, P.; Kaspari, D.C., Jr.; Sain, M.K. Implementation of an active mass driver using acceleration feedback control. Microcomput. Civ. Eng. 1996, 11, 305–323. [Google Scholar] [CrossRef]
- Wu, J.C.; Yang, J.N. Active control of transmission tower under stochastic wind. J. Struct. Eng. 1998, 124, 1302–1312. [Google Scholar] [CrossRef]
- Ghaboussi, J.; Joghataie, A. Active control of structures using neural networks. J. Eng. Mech. 1995, 121, 555–567. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Chen, H.M.; Tsai, K.H.; Qi, G.Z.; Yang, J.C.S. Neural network for structure control. J. Comput. Civ. Eng. 1995, 9, 168–176. [Google Scholar] [CrossRef]
- Bani-Hani, K.; Ghaboussi, J. Nonlinear structural control using neural networks. J. Eng. Mech. 1998, 124, 319–327. [Google Scholar] [CrossRef]
- Kim, J.T.; Jung, H.J.; Lee, I.W. Optimal structural control using neural networks. J. Eng. Mech. 2000, 126, 201–205. [Google Scholar] [CrossRef]
- Hung, S.L.; Kao, C.Y.; Lee, J.C. Active pulse structural control using artificial neural networks. J. Eng. Mech. 2000, 126, 839–849. [Google Scholar] [CrossRef]
- Cho, H.C.; Fadali, S.M.; Saiidi, M.S.; Lee, K.S. Neural network active control of structures with earthquake excitation. Int. J. Control Autom. Syst. 2005, 3, 202–210. [Google Scholar]
- Lin, T.K.; Chang, K.C.; Chung, L.L.; Lin, Y.B. Active control with optical fiber sensors and neural networks. I: Theoretical analysis. J. Struct. Eng. 2006, 132, 1293–1303. [Google Scholar] [CrossRef]
- Bani-Hani, K. Vibration control of wind-induced response of tall buildings with an active tuned mass damper using neural networks. Struct. Control Health Monit. 2007, 14, 83–108. [Google Scholar] [CrossRef]
- Setio, H.D.; Gunawan, A.S. Numerical study of active mass damper application on cable-stayed bridge structure using artificial neural network algorithm. Int. J. Civ. Environ. Eng. 2017, 17, 1–17. [Google Scholar]
- Chen, C.J.; Yang, S.M. Application neural network controller and active mass damper in structural vibration suppression. J. Intell. Fuzzy Syst. 2014, 27, 2835–2845. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Prayogo, D. Symbiotic organisms search: A new metaheuristic optimization algorithm. Comput. Struct. 2014, 139, 98–112. [Google Scholar] [CrossRef]
- Amini, F.; Hazaveh, N.K.; Rad, A.A. Wavelet PSO-based LQR algorithm for optimal structural control using active tuned mass dampers. Comput.-Aided Civ. Infrastruct. Eng. 2013, 28, 542–557. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam, A method for stochastic optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Jansen, L.M.; Dyke, S.J. Semiactive control strategies for MR dampers: Comparative study. J. Eng. Mech. 2000, 126, 795–803. [Google Scholar] [CrossRef]
- Chen, P.C.; Ting, G.C.; Li, C.H. A versatile small-scale structural laboratory for novel experimental earthquake engineering. Earthq. Struct. 2020, 18, 337–348. [Google Scholar] [CrossRef]




| 1st Mode | 2nd Mode | 3rd Mode | 4th Mode | 5th Mode |
|---|---|---|---|---|
| 0.336 | 1.002 | 1.644 | 2.250 | 2.807 |
| Number of Acceleration Steps | ||||||
|---|---|---|---|---|---|---|
| 10 | 50 | 100 | 120 | 150 | 200 | |
| Training RMSE (%) | 1.95 | 0.40 | 0.62 | 0.68 | 0.89 | 0.87 |
| Simulation RMSE (%) | N.A. | N.A. | N.A. | 1.77 | 1.82 | 1.70 |
| Earthquakes | J1 | J2 | J3 | J4 |
|---|---|---|---|---|
| El Centro | 0.434 | 0.523 | 0.803 | 0.020 |
| Chichi | 0.472 | 0.814 | 0.690 | 0.016 |
| Kobe | 0.531 | 0.584 | 0.645 | 0.029 |
| Meinong | 0.686 | 0.747 | 0.655 | 0.049 |
| Northridge | 0.553 | 0.655 | 0.895 | 0.025 |
| Kumamoto | 0.543 | 0.718 | 0.648 | 0.020 |
| Capemendocino | 0.557 | 0.677 | 0.684 | 0.028 |
| Parkfield | 0.702 | 0.797 | 0.732 | 0.022 |
| Chuetsu Oki | 0.605 | 0.549 | 0.674 | 0.030 |
| Montenegro | 0.778 | 0.812 | 0.701 | 0.030 |
| Imperial Valley | 0.553 | 0.531 | 0.606 | 0.040 |
| Taipei | 0.501 | 0.487 | 0.462 | 0.047 |
| El Mayor | 0.584 | 0.618 | 0.569 | 0.030 |
| Darfield | 0.846 | 0.896 | 0.744 | 0.033 |
| Average | 0.596 | 0.672 | 0.679 | 0.030 |
| Earthquakes | J1 | J2 | J3 | J4 | RMSE |
|---|---|---|---|---|---|
| El Centro | 0.433 | 0.523 | 0.801 | 0.020 | 0.018 |
| Chichi | 0.471 | 0.813 | 0.690 | 0.016 | 0.019 |
| Kobe | 0.531 | 0.582 | 0.643 | 0.030 | 0.017 |
| Meinong | 0.686 | 0.747 | 0.656 | 0.049 | 0.011 |
| Northridge | 0.553 | 0.655 | 0.890 | 0.025 | 0.009 |
| Kumamoto | 0.543 | 0.720 | 0.645 | 0.020 | 0.016 |
| Capemendocino | 0.558 | 0.677 | 0.686 | 0.028 | 0.016 |
| Parkfield | 0.702 | 0.791 | 0.731 | 0.022 | 0.015 |
| Chuetsu Oki | 0.604 | 0.549 | 0.670 | 0.030 | 0.015 |
| Montenegro | 0.779 | 0.812 | 0.699 | 0.030 | 0.012 |
| Imperial Valley | 0.552 | 0.531 | 0.597 | 0.040 | 0.010 |
| Taipei | 0.501 | 0.485 | 0.450 | 0.047 | 0.008 |
| El Mayor | 0.583 | 0.615 | 0.572 | 0.030 | 0.013 |
| Darfield | 0.847 | 0.897 | 0.739 | 0.033 | 0.011 |
| Average | 0.596 | 0.671 | 0.676 | 0.030 | 0.014 |
| Earthquakes | J1 | J2 | J3 | J4 | RMSE |
|---|---|---|---|---|---|
| El Centro | 0.433 | 0.523 | 0.801 | 0.020 | 0.013 |
| Chichi | 0.471 | 0.813 | 0.690 | 0.016 | 0.015 |
| Kobe | 0.532 | 0.583 | 0.644 | 0.029 | 0.014 |
| Meinong | 0.687 | 0.747 | 0.655 | 0.049 | 0.010 |
| Northridge | 0.553 | 0.655 | 0.891 | 0.025 | 0.008 |
| Kumamoto | 0.543 | 0.720 | 0.646 | 0.020 | 0.011 |
| Capemendocino | 0.559 | 0.677 | 0.687 | 0.028 | 0.013 |
| Parkfield | 0.703 | 0.790 | 0.731 | 0.022 | 0.015 |
| Chuetsu Oki | 0.605 | 0.550 | 0.669 | 0.030 | 0.011 |
| Montenegro | 0.779 | 0.812 | 0.699 | 0.030 | 0.011 |
| Imperial Valley | 0.553 | 0.531 | 0.600 | 0.040 | 0.008 |
| Taipei | 0.501 | 0.487 | 0.453 | 0.047 | 0.007 |
| El Mayor | 0.583 | 0.615 | 0.573 | 0.030 | 0.011 |
| Darfield | 0.847 | 0.897 | 0.736 | 0.033 | 0.009 |
| Average | 0.596 | 0.671 | 0.677 | 0.030 | 0.011 |
| Earthquakes | J1 | J2 | J3 | J4 | RMSE |
|---|---|---|---|---|---|
| El Centro | 0.434 | 0.524 | 0.803 | 0.020 | 0.013 |
| Chichi | 0.471 | 0.813 | 0.690 | 0.016 | 0.015 |
| Kobe | 0.532 | 0.583 | 0.645 | 0.029 | 0.016 |
| Meinong | 0.687 | 0.747 | 0.656 | 0.049 | 0.011 |
| Northridge | 0.554 | 0.655 | 0.893 | 0.025 | 0.010 |
| Kumamoto | 0.543 | 0.720 | 0.645 | 0.020 | 0.011 |
| Capemendocino | 0.559 | 0.677 | 0.688 | 0.028 | 0.013 |
| Parkfield | 0.703 | 0.791 | 0.731 | 0.022 | 0.016 |
| Chuetsu Oki | 0.605 | 0.550 | 0.671 | 0.030 | 0.011 |
| Montenegro | 0.779 | 0.812 | 0.699 | 0.029 | 0.012 |
| Imperial Valley | 0.553 | 0.531 | 0.601 | 0.040 | 0.008 |
| Taipei | 0.502 | 0.488 | 0.455 | 0.047 | 0.008 |
| El Mayor | 0.583 | 0.617 | 0.573 | 0.030 | 0.012 |
| Darfield | 0.847 | 0.897 | 0.738 | 0.033 | 0.010 |
| Average | 0.596 | 0.672 | 0.678 | 0.030 | 0.012 |
| Earthquakes | J1 | J2 | J3 | J4 | RMSE |
|---|---|---|---|---|---|
| El Centro | 0.431 | 0.522 | 0.799 | 0.020 | 0.045 |
| Chichi | 0.472 | 0.809 | 0.686 | 0.016 | 0.054 |
| Kobe | 0.527 | 0.576 | 0.632 | 0.030 | 0.049 |
| Meinong | 0.685 | 0.747 | 0.654 | 0.048 | 0.032 |
| Northridge | 0.553 | 0.655 | 0.894 | 0.025 | 0.037 |
| Kumamoto | 0.541 | 0.722 | 0.647 | 0.020 | 0.039 |
| Capemendocino | 0.557 | 0.677 | 0.682 | 0.028 | 0.043 |
| Parkfield | 0.696 | 0.770 | 0.733 | 0.022 | 0.045 |
| Chuetsu Oki | 0.602 | 0.549 | 0.662 | 0.030 | 0.031 |
| Montenegro | 0.779 | 0.809 | 0.696 | 0.029 | 0.040 |
| Imperial Valley | 0.549 | 0.531 | 0.577 | 0.039 | 0.026 |
| Taipei | 0.500 | 0.483 | 0.438 | 0.046 | 0.027 |
| El Mayor | 0.579 | 0.611 | 0.556 | 0.029 | 0.039 |
| Darfield | 0.845 | 0.899 | 0.714 | 0.032 | 0.034 |
| Average | 0.594 | 0.669 | 0.669 | 0.030 | 0.039 |
| Controller | J1 | J2 | J3 | J4 | RMSE |
|---|---|---|---|---|---|
| LQR-SOS | 0.596 | 0.672 | 0.679 | 0.030 | 0 |
| MLP-120 | 0.596 | 0.671 | 0.676 | 0.030 | 0.014 |
| MLP-150 | 0.596 | 0.671 | 0.677 | 0.030 | 0.011 |
| MLP-200 | 0.596 | 0.672 | 0.678 | 0.030 | 0.012 |
| ARX | 0.594 | 0.669 | 0.669 | 0.030 | 0.039 |
| Controller | LQR-SOS | MLP-150 | ARX | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Earthquakes | J1/J2 | J3 | J4 | J1/J2 | J3 | J4 | J1/J2 | J3 | J4 |
| El Centro | 0.473 | 0.455 | 0.036 | 0.431 | 0.437 | 0.033 | 0.456 | 0.544 | 0.036 |
| Chichi | 0.668 | 0.690 | 0.021 | 0.672 | 0.752 | 0.026 | 0.693 | 0.728 | 0.027 |
| Kobe | 0.447 | 0.438 | 0.056 | 0.519 | 0.567 | 0.042 | 0.525 | 0.515 | 0.036 |
| Northridge | 0.899 | 0.885 | 0.030 | 0.776 | 0.841 | 0.032 | 0.843 | 0.832 | 0.038 |
| Parkfield | 0.449 | 0.414 | 0.039 | 0.389 | 0.446 | 0.036 | 0.441 | 0.501 | 0.031 |
| Montenegro | 0.671 | 0.641 | 0.043 | 0.613 | 0.616 | 0.035 | 0.635 | 0.642 | 0.034 |
| Meinong | 0.637 | 0.616 | 0.048 | 0.644 | 0.621 | 0.033 | 0.647 | 0.679 | 0.045 |
| Capemendocino | 0.743 | 0.685 | 0.041 | 0.764 | 0.839 | 0.051 | 0.790 | 0.787 | 0.041 |
| Average | 0.623 | 0.603 | 0.039 | 0.601 | 0.640 | 0.036 | 0.629 | 0.653 | 0.036 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, P.-C.; Chien, K.-Y. Machine-Learning Based Optimal Seismic Control of Structure with Active Mass Damper. Appl. Sci. 2020, 10, 5342. https://doi.org/10.3390/app10155342
Chen P-C, Chien K-Y. Machine-Learning Based Optimal Seismic Control of Structure with Active Mass Damper. Applied Sciences. 2020; 10(15):5342. https://doi.org/10.3390/app10155342
Chicago/Turabian StyleChen, Pei-Ching, and Kai-Yi Chien. 2020. "Machine-Learning Based Optimal Seismic Control of Structure with Active Mass Damper" Applied Sciences 10, no. 15: 5342. https://doi.org/10.3390/app10155342
APA StyleChen, P.-C., & Chien, K.-Y. (2020). Machine-Learning Based Optimal Seismic Control of Structure with Active Mass Damper. Applied Sciences, 10(15), 5342. https://doi.org/10.3390/app10155342





