Abstract
In this paper, a seven-parameter spectral/hp finite element model to obtain natural frequencies in shell type structures is presented. This model accounts for constant and variable thickness of shell structures. The finite element model is based on a Higher-order Shear Deformation Theory, and the equations of motion are obtained by means of Hamilton’s principle. Analysis is performed for isotropic linear elastic shells. A validation of the formulation is made by comparing the present results with those reported in the literature and with simulations in the commercial code ANSYS. Finally, results for shell like structures with variable thickness are presented, and their behavior for different ratios and is studied.
1. Introduction
During the last several decades, studies of refined shell finite elements have taken importance due to their use in modeling variety of structures, mainly to study complex materials (e.g., laminated and functionally graded materials) and their applications in distinct areas of engineering. Consequently, many researchers have shown a strong interest in new and robust shell formulations, which require no artificial fixes such as reduced integration and stabilization. Through these developments, the performance of shell elements have been enhanced significantly. Continuous improvement of underlying mathematical models and computer implementations have been an area of significant research. Due to the amount of works in literature about shells, a detailed review is not presented here; the review of literature is limited to the present focus, namely, free vibration studies of shells.
Through the years, different theories of shells have been proposed and the most used can be classified as follows: Classical Theories (CT), First-order Shear Deformation Theories (FSDT), and High-order Shear Deformation Theories (HSDT). The latest theories have been developed with the intention to avoid locking (of various kinds) present in the numerical solution of some shell theories, to enhance the performance of the elements, and to eliminate limitations (e.g., the thickness inextensibility) of these theories. The classical theories are based on the Kirchhoff–Love’s hypothesis in which lines normal to the undeformed mid-surface remain straight and normal to the surface after deformation [1]; the kinematics of these theories is defined using three displacements in each direction of a point located on the mid-surface [2]. The use of formulations based on CT is limited to thin shells, mainly because such assumption underestimates the effects of normal and shear strains in the thickness direction [3]. In addition, often one neglects rotatory inertia in CT and thus overestimates natural frequencies of moderately thick shells [2].
The FSDT is developed [4] to overcome the limitations of CT [2]; nevertheless, FSDT still presents a few limitations and exhibits shear locking (in addition to thickness and membrane locking present in the CT). Here, the term locking refers to the stiffening effects created by the use of low-order interpolation functions or by the kinematic assumptions. Generally, the shell kinematic is described with five parameters, three displacements in each coordinate direction at the mid-surface, and two rotations about the mid-surface coordinates (one can include the drilling degree of freedom or rotation about the transverse normal, as needed). In addition, this theory often is known as theory of five parameters. Limitation of this theory lies in its application to thin shells, need for shear correction factors, and transverse inextensibility. The shear correction factors are difficult to determine since they depend on the shell geometry, boundary conditions, and loads applied [3,5]. Results obtained are accurate while the shell does not show significant deformation through its thickness [2]. This is due to the fact that the theory is based on zero normal strain [6]. The good accuracy obtained with FSDT, with respect to CT, is a result of taking into account the effects of transverse shear strain and rotatory inertia [7]. The numerical implementation of FSDT exhibits locking phenomena (e.g., shear locking [8,9]), which is caused by the zero shear strains [10]. Some remedies to avoid locking phenomenon are the use of the method of assumed natural strain (ANS) [8], reduced integration techniques [9], and mixed formulations [11].
In HSDT, the displacement expansions considered are of high-order, and they can be applied to thick shells. These theories are developed using either polynomial or nonpolynomial expansions through thickness coordinate. The HSDT were introduced to avoid the use of shear correction factors needed in the FSDT [3]. Papers with high-order formulations can be found in the works of Sansour [12], Bischoff & Ramm [8], Hahn & Kikuchi [13], Payette & Reddy [14], and Amabili [2]. Among the finite element formulations based on these theories is the seven-parameter formulation with the drilling degree of freedom, the seventh parameter being the thickness stretch (see Arciniega & Reddy [11]). In addition, seven-parameter formulations were developed with the intention to eliminate the phenomenon of Poisson locking presented in six-parameter formulations (i.e., three displacements and three rotations). The Poisson locking arises when a constant state of normal strain through the thickness is assumed, and this phenomenon is due to the mathematical model and not to finite element model discretization [15]; in other words, a mesh refinement does not alleviate the locking.
There are numerous works related to shells in the literature. Finite element formulations to perform different types of analyses (e.g., static, dynamic and vibration or wave propagation analysis) can also be found. These finite element models can be classified as follows [14]: facet-shell elements, 2D elements based on shell theories, 3D elasticity elements, and continuum or degenerated elements. Often, these formulations are restricted to model elements with particular geometries, such as shallow shells, doubly curved shells, circular cylindrical shells, and so on. In addition, in general, formulations for dynamic analysis, free vibration, or transient response are developed for specific cases of materials (e.g., laminated shells and functionally graded materials). Examples related to these formulations can be found in the works of Cugnoni et al. [16], Park et al. [17], Jung & Han [18], Sahoo et al. [19], Hirwani et al. [20], Biswal & Mohanty [21], Moita et al. [22], among others. A review for plates and shells fabricated with FGM can be found in the work of Thai & Kim [3].
Kant et al. [23] presented a dynamic analysis model by means of degenerated shell elements, where the discretization of the 3D elasticity equations is made in terms of mid-surface nodal variables. In this formulation, five parameters were used to define the shell kinematic; however, they do not present any analysis to determine natural frequencies. Bardell et al. [24] reported a free vibration analysis of isotropic, open conical panels using the hp version of the finite element method (i.e., a refinement in the mesh size h and the order p of the polynomial interpolation functions) based on Kirchhoff–Love thin shell equations, and they assumed cones of uniform thickness. They presented natural frequencies and mode shapes, and compared their results with those obtained using a commercial finite element code and experimental results. Lee & Han [25] determined natural frequencies for plates and shells by means of a nine-node degenerated element with six degrees of freedom, which was developed by them based on assumptions of the FSDT, and using the ANS approach to mitigate the locking phenomena. In the work of Lee & Han [26], a similar formulation to the one presented by these authors in 2001 [25] is used, but this time it is applied to laminated composite plates and shells. Recently, Bahrami et al. [27] reported a vibration analysis of thin shallow shells with the spectral interpolation functions and subjected to impact loads. Tornabene et al. [28] presented formulations based on differential and integral quadrature methods for the free vibration analysis of composite plates and shells; they considered nonuniform thickness. Żak & Krawczuk [29] presented a finite element with six degrees of freedom and spectral interpolation functions for dynamic analysis of isotropic shell-like structures; the transverse deformation was considered and the structures studied were of uniform thickness.
Additionally, many works related to the calculation of natural frequencies for plates and shells can be found in the literature; these use different numerical approaches, than the finite element method, and considered structures; see Ganesan & Sivadas [30] and Sivadas & Ganesan [31]. Both papers reported a semi-analytic finite element analysis of free vibration for thin circular isotropic cylindrical shells with variable thickness based on Kirchhoff–Love’s shell theory, but Ganesan & Sivadas [30] reported analysis of cantilevered cylindrical shells. Kang & Leissa [32] presented a three-dimensional vibration analysis to determine natural frequencies of thick spherical shell panels with variable thickness using the Ritz method. El-Kaabazi & Kennedy [33] determined natural frequencies and vibration modes of cylindrical shells with variable thickness based on the assumptions of Donell, Timoshenko, and Flüge shell theories; the natural frequencies were found using the Wittrick–Williams algorithm. Dai et al. [34] presented an exact series solution for the vibration analysis of circular cylindrical shells by means of the Flüge shell theory. Bacciocchi et al. [35] performed free vibration analysis of variable thickness plates and shells using the Generalized Differential Quadrature method.
The aim of this work is to implement a seven-parameter finite element formulation (with thickness stretch as the seventh degree of freedom) to determine natural frequencies and mode shapes of arbitrary isotropic shell structures with uniform and nonuniform thicknesses. In this formulation, a continuum element with the hp spectral interpolation functions (see the text of Karniadakis & Sherwin [36]) is used. The description of shell kinematics with seven parameters, higher-order spectral interpolation of all variables, and the use of three-dimensional constitutive equations avoids all types of locking. By means of hp spectral interpolation functions, the errors in the numerical interpolation are reduced, achieving great accuracy and avoiding the Runge’s effect (more details about this effect can be found in the works of Reddy [15] and Pozrikidis [37]). The seven-parameter formulation was presented by Payette & Reddy [14] for static nonlinear analyses of isotropic, FGM, and laminated composite shells, and Gutierrez Rivera & Reddy [38] extended the work to thermo-mechanical nonlinear analysis of FGM plates and shells. Numerical results obtained were compared with those available in the literature for constant thickness formulations and with those obtained by means of the commercial code ANSYS.
2. Theoretical Formulation
In this work, the 3D geometry is approximated using a continuum shell element; in other words, the shell element presented in Figure 1 is modeled only by means of its mid-surface (shaded area). The shell element shown in figure has constant thickness and radii, and ; however, in reality, thickness can vary. In Figure 2, a discretization of shell’s mid-surface using spectral nodes can be observed; in this case, an element with polynomial order is shown. In both figures, the reference system is Cartesian , and the local system is curvilinear () and it is attached to the mid-surface.
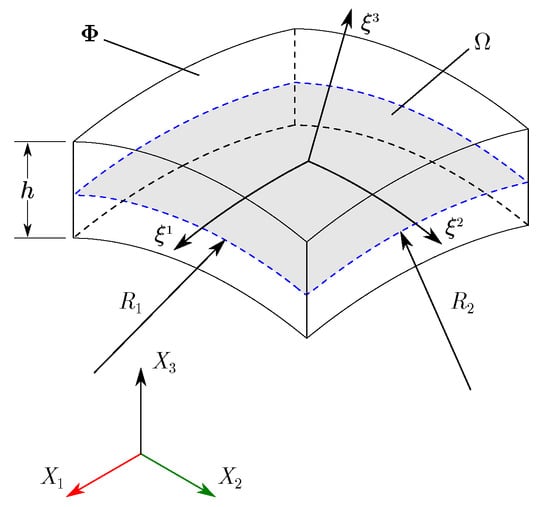
Figure 1.
Shell element and its mid-surface.
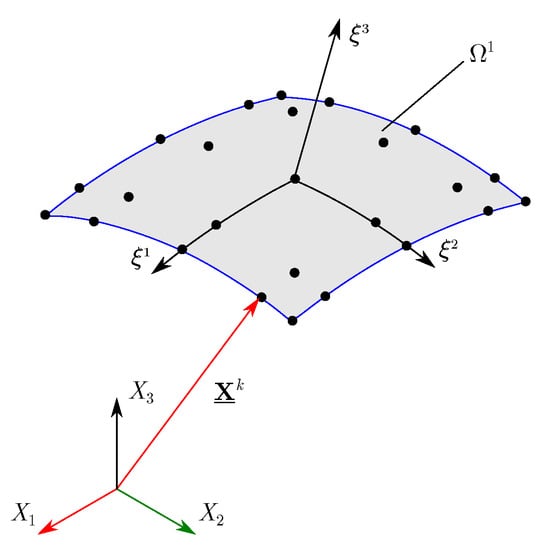
Figure 2.
Finite element discretization of shell mid-surface.
The position vector , shown in Figure 2, describes the mid-surface coordinates of the kth spectral node. The spectral nodes, which are not equally spaced, are distributed in positions that correspond to the roots of orthogonal polynomial families, in this case, the Legendre polynomials (more detailed information may be consulted in the work of Payette & Reddy [14]). Additionally, it is necessary to know the unit normal vector at each node, which is denoted by . Both vectors are in terms of the reference system. In addition, the thickness at each node is denoted with . All these geometric parameters define the spectral element and correspond to the code’s input data. In Section 2.1, the approximation of these parameters will be described.
2.1. Geometric Parameters
The position vector of a point located on the element’s mid-surface is approximated as follows:
where is the position vector of the kth spectral node, is the kth interpolation function of order p (i.e., isoparametric formulation is used). The total number of nodes n per element is given by .
In this formulation, the normal vector of a point located on the element’s mid-surface is approximated as
where is the unit normal vector of the kth spectral node.
Now, using the position vector in Equation (1) and scaling the normal vector in Equation (2) by a factor of (half of the thickness), the position of a typical point in the element is given as
In addition to the above approximations, the covariant basis vectors for each point in the element must be defined:
The covariant basis vectors in Equation (4), by means of Equation (3), can be separated as follows:
where the subindex can take values of . Furthermore, the vector is given by
A differential line element in the typical shell element, in terms of the curvilinear coordinates, can be expressed as
where is the Jacobian matrix with determinant J. In conjunction with the covariant basis vectors, a contravariant set of basis vectors is defined as follows:
2.2. Displacement Field
By definition, the displacement of a particle with position vector , in the reference configuration, to a point in the current configuration is given by the vector
The displacement vector can be expanded using the Taylor’s series in terms of the thickness coordinate () as follows:
where .
In this work, following the ones of Arciniega & Reddy [11] and Payette & Reddy [14], the displacement field is expanded upto the quadratic term in thickness direction:
where the generalized displacements , and are defined as follows:
and denotes the unit basis vectors in the fixed orthogonal Cartesian coordinate system.
The vector is associated with the displacements at mid-surface, is the difference vector, and it gives the change in the mid-surface director, and the vector is defined by scaling the normal vector with the parameter . Both vectors and have three components (i.e., six degrees of freedom), and the term is the seventh parameter and it denotes the thickness stretch, which is used to mitigate the phenomenon of Poisson’s locking that appears in six-parameter formulation [14,39].
For a harmonic motion, the displacement field is assumed to be a periodic function in time and, in general, its solution can be treated as the product of a function of and a time function (see text of Reddy [40]):
where is the vibration mode vector associated with the frequency of natural (or free) vibration, .
2.3. Strains
The strains in the element are obtained by means of the Green–Lagrange strain tensor, which is defined as
In terms of the covariant components, it can be written as [12]
Considering only the linear part, the covariant components in the above equation are given as
If the scalar products are computed, the covariant components can be expanded in terms of the thickness coordinate as
This expansion is based on the assumed displacement field, which was taken to be a quadratic function of .
3. Constitutive Equations
This formulation considers only isotropic linear elastic materials. For these materials, the fourth-order elasticity tensor, in terms of contravariant vectors, is defined as
where the contravariant components are determined by
In the above expression, and are the Lamé parameters, which can be expressed in terms of Young’s modulus, E, and Poisson’s ratio, , as
Here, denotes the contravariant components of the Riemannian metric tensor in the reference configuration, given as .
The mechanical behavior of material is assumed to follow Hooke’s Law; then, the relation between the Second Piola–Kirchhoff stress tensor and the Green–Lagrange strain tensor is given by
where the contravariant components of could be determined by .
4. Equations of Motion
The equations of motion for the finite element model are obtained by means of the Hamilton’s principle [41]:
where represents the virtual kinetic energy, is the virtual strain energy, and is the virtual potential energy due to the external loads.
Hamilton’s principle allows us to directly derive the finite element equations (i.e., the mass matrix is obtained with the virtual kinetic energy, the stiffness matrix with the virtual strain energy, and the load vector with the virtual potential energy). For natural vibration, it is only necessary to determine the stiffness and mass matrices. The matrix calculation procedure is explained in Section 5.
The virtual kinetic energy is given by
where is the density. Substituting the displacement field and the differential volume element in the above equation, expressions for the mass matrix coefficients can be obtained. Integrating along yields
where are the mass inertias defined as follows:
and is the norm of the normal vector .
The virtual strain energy is computed by
Substituting the Green–Lagrange tensor and the fourth-order elasticity tensor, an expression to determine the stiffness matrix is obtained:
where the contravariant components are the effective extensional, extensional-bending coupling, and bending fourth-order stiffness tensor components [14]. These components are calculated as
5. Finite Element Model
For natural vibration, the generalized displacements in Equation (9) are assumed of the form
where represents the frequency of natural vibration, , and the finite element approximations of the displacements are given by
being the Lagrange interpolation functions of order p.
Substituting the approximations in the virtual kinetic energy of Equation (25) and in the virtual strain energy of Equation (27), the mass and the stiffness matrices are obtained. It is important to mention that the terms involved in the stiffness matrix are extensive, and a computer program of algebraic manipulation is required; in this case, they were obtained using Maple.
Finally, the finite element model to estimate the natural frequencies and the vibration modes of a shell is an eigenvalue problem of the form
where and denote the stiffness and mass matrices of the e element, respectively, denotes the natural frequency, and is the vibration mode vector associated with . In this work, the solution to the resulting eigenvalue problem is obtained by means of Eigen, a C++ template library for linear algebra [42].
6. Numerical Results
This section is divided into three different parts. In the first one, a convergence study is presented. Then, in the second one, a numerical comparison with the results available on the literature is developed. Finally, in the third one, the relation between some geometrical parameters with the natural frequencies is studied for shell like structures with variable thickness.
In order to describe the boundary conditions, the nomenclature used to label them is given by the letters C for clamped edge, F for free edge, and S for simply supported edge. For open geometries, the description of the boundary conditions starts with the nearest edge to the plane, and the others are listed using the left-hand rule. Figure 3 shows two examples of this terminology applied to open geometries, a CFCF condition for a plate, and an SCSF condition for a cylindrical panel.
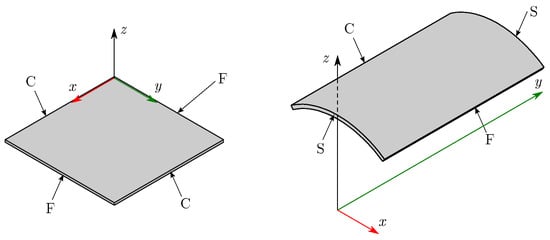
Figure 3.
Examples of boundary conditions for open geometries.
In cases where closed geometries are analyzed, the applied boundary conditions are described listing the nearest edge to the reference system and then the other edge. Figure 4 shows two examples of this convention, an annular plate under CF condition and an open ended cylinder with SC condition.
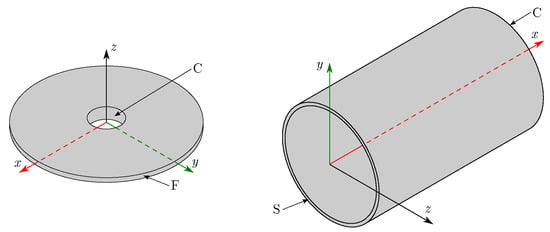
Figure 4.
Examples of boundary conditions for closed geometries.
6.1. Convergence Study
First, a convergence study is performed to determine the mesh size and the element degree needed to obtain the eigenvalues (i.e., natural frequencies) with good accuracy. In this work, square meshes are used for all the cases studied. In general, an element with polynomial degree is used and, if the convergence is slow, the polynomial degree is increased to . In this study, the relative error between each mesh size is calculated as follows:
where is the relative error in percentage, is the natural frequency obtained with the previous mesh, and is the natural frequency calculated with the current mesh i. This study is divided in two parts. The first one presents results for plates and the second one for shells.
6.1.1. Plates
In the convergence study, the material properties considered are: , GPa, and kg/m. The natural frequencies for rectangular plates, with dimensions , are reported using a dimensionless parameter defined in reference [35] as
where f is the natural frequency expressed in Hz and h represents the thickness of the geometry. In the case of a plate with variable thickness, h takes the value of the smallest thickness.
First, the present formulation is tested to model square plates with ratio , and constant thickness. For this geometry, the convergence study is performed for the following boundary conditions:
- I.
- All edges simply-supported (SSSS)
- II.
- Two opposite edges simply-supported and the other two clamped (SCSC)
- III.
- All edges clamped (CCCC)
Table 1 contains results using different mesh sizes for Cases I, II, and III. In all the studies, the relative error for the last mesh refinement (from 36 to 64 elements) is less than 0.12%. For that reason, a mesh size of 36 elements is used on the verification section to model plates with constant thickness.

Table 1.
Convergence of dimensionless frequency parameter for square plates of ratio .
In addition, the present formulation is tested to model plates with variable thickness in one direction along its mid-surface. Thickness variation is considered as follows:
where is the maximum thickness, is the tapered ratio, and b is the length of the side along y axis. Thus, the dimensionless frequency parameter , given by Equation (34), is calculated using the maximum thickness. Additionally, for this variation, the minimum thickness in the plate can be calculated setting in Equation (38), which gives
Table 2 contains the frequency parameter values obtained in the convergence study performed by applying each case of the boundary conditions given in Equations (35)–(37) to a plate with variable thickness. From those values, it is concluded that the results obtained using 36 elements are converged, and this mesh size will be used for the numerical verification.

Table 2.
Convergence of dimensionless frequency parameter for square plates of variable thickness.
In addition to the plates with linear variable thickness, a square plate with parabolic thickness variation is analyzed. The thickness variation used is the same presented by Bacciocchi et al. [35], and it is given as follows:
This plate is subject to the boundary conditions given in Case III, Equation (37), with a ratio and . Table 2 also presents the convergence study of plates with linear and parabolic thickness variation, LTV and PTV denote a linear and parabolic thickness variation, respectively. The values obtained for the last refinement are in the order of 0.1%. For that reason, a mesh with 36 elements is used for the numerical validation.
6.1.2. Shells
Here, two cases for truncated half hemispheres and three cases for cylinders are studied. In Figure 5, the revolution profiles of (a) a truncated hemisphere, (b) a cylinder with linear variation, and (c) a cylinder with linear symmetric variation [30] are shown. The important geometric parameters are shown in these figures. Note that an angle , not shown, lies in the -plane for the hemisphere and in the -plane for the cylinder.

Figure 5.
Revolution profiles for (a) hemispherical, and (b,c) cylindrical shells.
The dimensionless frequency parameter for the hemispheres is denoted by (see Bacciocchi et al. [35])
where G is the shear modulus. In addition, for these kinds of geometries, the following boundary conditions are considered:
- IV.
- All free edges (FF)
On the the other hand, for cylinders, the boundary conditions are:
- V.
- All clamped edges (CC)
- VI.
- A clamped edge and a free edge (CF)
The first case studied is a truncated hemisphere with constant thickness, where its geometrical parameters are taken from the work by Kang and Leissa [32], and those correspond to , and . The second case analyzed is a truncated hemisphere with linear variable thickness, and its geometric parameters are given by , and , where corresponds to the mean thickness defined as . The thickness variation is determined as [35]
Note that this expression works for a thickness ratio , where .
Table 3 contains the results of the convergence study, using elements with , for the truncated hemispheres with constant and variable thicknesses. In both cases, the errors for the last increment are in general below of 0.43%. Thus, the study shows that a good convergence can be achieved with a mesh size of 49 elements.

Table 3.
Convergence of dimensionless parameter for a truncated hemisphere with FF boundary conditions.
The geometrical parameters of the cylinder with constant thickness are taken from Dai et al. [34], which correspond to , , and , while the material properties are , , and . The study of convergence is realized for two types of boundary conditions, Cases V and VI given by Equations (43) and (44), respectively, and using elements with polynomial order . The results are presented in Table 4. In both cases, the relative errors are below of 0.1 order for the last increment. For that reason, it is concluded that a convergence can be achieved with a mesh size of nine elements.

Table 4.
Convergence of natural frequencies of cylinder with constant thickness.
The cylinders with linear and linear symmetric thickness variations have the geometrical parameters reported in the work by Ganesan & Sivadas [30], which are: , , and . For these cases, the material properties are: , , and . Additionally, the boundary conditions applied correspond to Case VI, given by Equation (44), where the edge with the maximum thickness is clamped. For both models, the mesh is made using elements . Table 5 presents the convergence studies for these cylinders. It is concluded that good convergence is achieved in both cases using 25 elements.

Table 5.
Convergence of natural frequencies for a cylinder of ratio and CF boundary conditions.
6.2. Numeric Validation
In order to validate the numerical results obtained by means of the present finite element model, a comparison with results previously reported in the literature is performed. The number of spectral elements used for comparison are the ones obtained in the previous section, when convergence is achieved for each case. The natural frequencies obtained by means of the present formulation are reported in the column labeled as Present. In addition, for each case of study, a three-dimensional model is made in the commercial code ANSYS, using an eight node brick element (SOLID185). The number of brick elements used for the solid finite element models are shown below of the label 3D in each table.
6.2.1. Plates
In this section, comparisons for plates with constant, linear, and parabolic variations in thickness are presented. Table 6, Table 7 and Table 8 present the results for the boundary conditions listed on Cases I, II, and III, applied to squares plates with constant thickness. The values shown in parentheses represent the relative error in percentage. In general, a good agreement is observed with the results previously reported and those obtained by means of solid elements, with relative errors smaller than 5.8%.

Table 6.
Comparison of results for a square plate of ratio and SSSS boundary conditions.

Table 7.
Comparison of results for a square plate of ratio and SCSC boundary conditions.

Table 8.
Comparison of results for a square plate of ratio and CCCC boundary conditions.
Table 9, Table 10 and Table 11 present the results for the boundary conditions listed for Cases I, II, and III, applied to square plates with linear thickness variation. The highest relative errors between the presented formulation and solid elements is on the order of 3.92%. However, the highest errors are obtained when the present formulation is compared with the FSDT presented by Shufrin & Eisenberg [47], having a value of 4.11%.

Table 9.
Comparison of results for a square plate of ratio and SSSS boundary conditions.

Table 10.
Comparison of results for a square plate of ratio and SCSC boundary conditions.

Table 11.
Comparison of results for a square plate of ratio and CCCC boundary conditions.
Table 12 shows a comparison for the natural frequencies for a square plate with the parabolic thickness variation given in Equation (40), and its four edges clamped. The relative errors between the present formulation and solid elements have a maximum value of 2.97%. The maximum relative error is found when the present formulation is compared with the FSDT presented in the work by Bacciocchi et al. [35], with a value of 3.73%.

Table 12.
Comparison of results for a square plate of ratio , parabolic variation and CCCC boundary conditions.
6.2.2. Shells
Within this section, comparisons between the presented formulation and results available in the literature and those obtained by means of solid elements in ANSYS, for truncated hemispheres and cylinders, are presented. In these comparisons, values of natural frequencies and dimensionless parameters written in bold font represent even frequencies, that is, frequencies with identical value but different vibration mode.
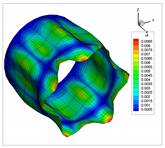
Table 13 presents comparisons for a truncated hemisphere with constant and linear variable thickness. For constant thickness, the relative errors are below 5.10%. For linear thickness variation, frequencies of the present formulation are approximated of those reported in references [35,51] with maximum errors of 6.04% and 5.70%, respectively. The comparison with the 3D model gives a maximum error of 5.59%.

Table 13.
Comparison of results for a truncated hemisphere with FF boundary conditions.
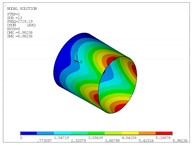
Table 14 presents a comparison for the natural frequencies of a cylinder with constant thickness, subjected to CC and CF boundary conditions. For these boundary conditions, the maximum relative errors are obtained when the present formulation is compared with the three-dimensional models; having values of 1.21% and 1.43%, respectively.

Table 14.
Comparison of results for a cylinder with constant thickness.
A comparison of the natural frequencies for cylinders with linear and linear symmetric thickness variations subjected to CF boundary conditions is presented in Table 15. For the linear thickness variation, the relative errors are smaller than 2.5%, when the results obtained using the present formulation are compared with those reported by Ganesan & Sivadas [30], and below 8% when the comparison is made with solid elements. On the other hand, for the cylinder with linear symmetric thickness variation, the results obtained with the present formulation have relative errors lower than 5%, except for the natural frequency , when those are compared with the results presented by Ganesan & Sivadas [30]. The frequencies obtained with solid elements present errors below 4.4%.

Table 15.
Comparison of results for cylinders of ratio , with thickness variation and CF boundary conditions.
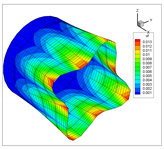
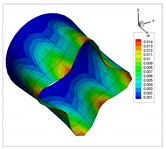
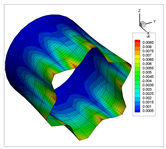
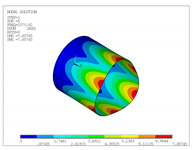
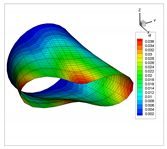
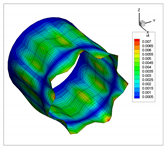
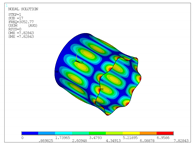
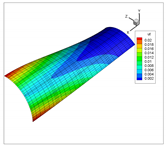
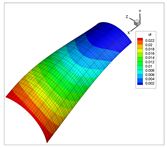
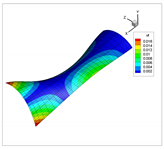
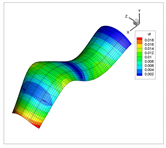
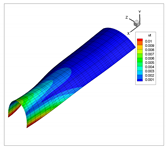
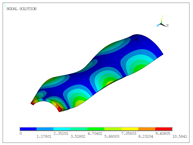
In addition to the comparison presented in Table 15, for the cylinder with linear thickness variation, the vibration modes calculated using the presented formulation and solid elements in ANSYS are reported in Table 16. The plotted contours correspond to the resultant displacement vector. In this case, the fundamental frequency is even; therefore, two modes are shown in the table with illustrative purposes. From now on, for even frequencies, a single vibration mode will be shown. Note that the axes are rotated, and that the scaling factors may be different. A detailed inspection shows that almost all the vibration modes are almost equal, except for 4 and 5, which are interchanged. This difference is attributed to the closeness of the values of frequencies obtained, since in ANSYS and using the presented formulation, which are almost identical. Since the eigenvalues are almost the same, the eigenvectors associated are very similar (vibration modes).

Table 16.
Vibration modes of a cylinder with linear thickness variation and CF boundary conditions.
6.3. Numeric Results
This section presents a study of the geometric parameters on the natural frequencies. Although the formulation is capable of modeling arbitrary shapes, in this study, the natural frequencies for the following geometries are obtained:
- Hemisphere with linear variable thickness, .
- Cylinder with linear variable thickness, .
- Fraction of cylinder with linear variable thickness, .
In addition, for each case of study, a three-dimensional model is made in the commercial code ANSYS, using the element SOLID185. The number of brick elements used for the solid finite element models are shown below of the label 3D in each table.
6.3.1. Hemisphere
A hemisphere with linear thickness variation is analyzed for different ratios of radius to mean thickness: . For these cases, the thickness ratio remains constant and FF boundary conditions are applied. Table 17 presents the natural frequencies, written using the dimensionless parameter defined for the hemispheres. The results obtained with the present formulation, using a mesh with 16 elements and a polynomial degree , are shown in columns labeled as 7-PL. Note that the ratios are more closely to be thick shells, and, for these cases, the parameter increases as this ratio decreases. Values of the relative errors suggest that the model has a good performance for ratios less than 20.

Table 17.
Dimensionless natural frequencies parameter for an hemisphere with linear thickness variation and FF boundary conditions, .
6.3.2. Cylinder
Cylinders with linear thickness variation, and subjected to CC and CF boundary conditions are studied for different radius to thickness ratios, in order to determine a valid work range for the present formulation. For these geometries, the radius-thickness ratio is calculated using the minimum thickness, and the natural frequencies are represented by the dimensionless parameter , which is obtained by [50]
The number of spectral p shell elements used for this geometry is shown in Tables below the label 7-PL. In all the cases, elements with a polynomial degree were used.
Table 18 presents the natural frequencies for a cylinder with both edges clamped and for different ratios. The ratio length to radius remains fixed and its value is . From these results, a raise in the parameter can be observed as the shell becomes thicker. The highest error values are obtained when thicker shells are analyzed (), having a maximum error of 6.0%.

Table 18.
Dimensionless natural frequencies parameter for cylinders with linear thickness variation and CC boundary conditions, .
Table 19 presents the dimensionless parameter for a cantilevered cylinder with linear thickness variation, where the edge with maximum thickness is clamped. In this case, for a fixed aspect ratio , the natural frequencies rise for thick shells, and the relative errors also increase.

Table 19.
Dimensionless natural frequencies parameter for cylinders with linear thickness variation and CF boundary conditions, .
6.3.3. Fraction of Cylinder
A quarter of cylinder, with different radius to thickness () and length to radius () ratios, is analyzed. The geometry is in cantilever, where the edge with the maximum thickness is clamped. The natural frequencies are presented using the dimensionless parameter . Table 20 shows the results for different ratios. It is observed that the highest error is presented for relatively thick shells () with a variation of 10.02%, when the present formulation is compared with solid elements.

Table 20.
Dimensionless parameter for a quarter of cylinder with linear thickness variation.
From the previous results, the geometry with is chosen to vary the ratio . The ratio is near to be a thick shell and, in general, the frequencies of the present formulation have good behavior for greater ratios. The natural frequencies for different aspect ratios of a partial cylinder are presented in Table 21. From these results, an increment on the frequencies is observed when the ratio is decreased. The relative errors increase when the geometries have aspect ratios less than 4, with maximum values at .

Table 21.
Dimensionless parameter for a quarter of cylinder with linear thickness variation, .
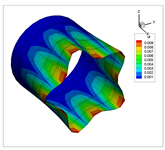
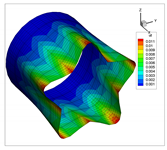
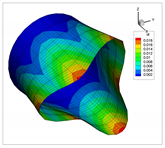
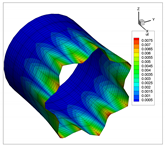
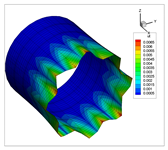
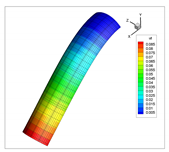
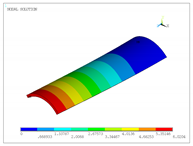
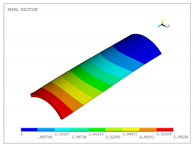
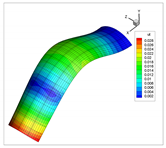
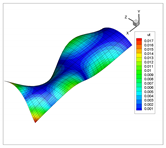
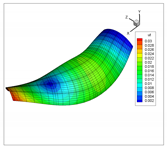
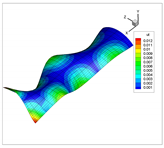
The vibration modes for a cantilevered quarter of cylinder, with ratio , are shown in Table 22. In addition, the modes obtained using solid elements in the commercial code ANSYS are shown. In general, the modes of each natural frequency are in agreement. Note that the Cartesian system is rotated clockwise around the y-axis.

Table 22.
Vibration modes for a cantilevered quarter of cylinder with linear thickness variation, .
Finally, based on the results presented in Table 17, Table 18, Table 19, Table 20 and Table 21, the following limits for the presented formulation are set:
- Truncated hemisphere: ,
- Cylinder: ,
- Fraction of cylinder: .
These parameter ranges demonstrate the capability of the spectral element presented to model thin and moderate thick shells with constant and variable thickness.
7. Conclusions
In the present work, a seven-parameter spectral finite element has been used to determine natural frequencies in shell structures. This formulation allows for modeling thin and moderate thick structures with constant and variable thicknesses, and avoids the use of shear correction factor. The spectral element is validated to model plates, truncated hemispheres, cylinders, and cylindrical panels. Other types of shell geometries can be analyzed. The numerical verification is presented for different types of boundary conditions.
The natural frequencies obtained with the present formulation are in agreement with analytic results, having relative errors less than 9%. For the cases where exact solutions are not available, a comparison with the results obtained by means of solid elements is performed, having a maximum error of 15.12% for a thick shell ( and ).
It is important to note that the presented formulation could be used to model arbitrary geometries and boundary conditions, contrary to other solutions found in the literature where those are restricted to specific cases. Furthermore, the computational time is smaller, compared to the one used to model the same problems using solid elements, even when the current formulation calculated all the frequencies and vibration modes in the finite element model, while using solid elements in the commercial code only forty were computed.
In a numerical model, the number of natural frequencies obtained corresponds to the number of unrestricted degrees of freedom on the finite element model. The fundamental frequency can be computed with a coarse mesh, but a refinement is needed to determine higher frequencies accurately. Refined meshes also yield an accurate fundamental frequency. The determination of the vibration modes requires a close examination of the numerical results.
Author Contributions
The authors C.V.M., M.G.R., and J.N.R. contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Secretaría de Educación Pública (SEP) Grant No. UGTO-PTC-643.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Reddy, J.N. Theory and Analysis of Elastic Plates and Shells, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Amabili, M. Nonlinearities in rotation and thickness deformation in a new third-order thickness deformation theory for static and dynamic analysis of isotropic and laminated doubly curved shells. Int. J. Non-Linear Mech. 2015, 69, 109–128. [Google Scholar] [CrossRef]
- Thai, H.T.; Kim, S.E. A review of theories for the modeling and analysis of functionally graded plates and shells. Compos. Struct. 2015, 128, 70–86. [Google Scholar] [CrossRef]
- Mindlin, R.D. Influence of rotatory inertia and shear in flexural motions of isotropic elastic plates. J. Appl. Mech. 1951, 18, 31–38. [Google Scholar]
- Thai, H.T.; Nguyen, T.K.; Vo, T.P.; Ngo, T. A new simple shear deformation plate theory. Compos. Struct. 2017, 171, 277–285. [Google Scholar] [CrossRef]
- Carrera, E.; Brischetto, S. Analysis of thickness locking in classical, refined and mixed theories for layered shells. Compos. Struct. 2008, 85, 83–90. [Google Scholar] [CrossRef]
- Wang, Q.; Shao, D.; Qin, B. A simple first-order shear deformation shell theory for vibration analysis of composite laminated open cylindrical shells with general boundary conditions. Compos. Struct. 2018, 184, 211–232. [Google Scholar] [CrossRef]
- Bischoff, M.; Ramm, E. Shear deformable shell elements for large strains and rotations. Int. J. Numer. Methods Eng. 1997, 40, 4427–4449. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Chapelle, D.; Bathe, K.J. The Finite Element Analysis of Shells—Fundamentals, 2nd ed.; Springer: Berlin/Heidelberg, Geramny, 2011. [Google Scholar]
- Arciniega, R.A.; Reddy, J.N. Tensor-based finite element formulation for geometrically nonlinear analysis of shell structures. Comput. Methods Appl. Mech. Eng. 2007, 196, 1048–1073. [Google Scholar] [CrossRef]
- Sansour, C. A theory and finite element formulation of shells at finite deformations involving thickness change: Circumventing the use of a rotation tensor. Arch. Appl. Mech. 1995, 65, 194–216. [Google Scholar] [CrossRef]
- Hahn, Y.; Kikuchi, N. Mixed shell element for seven-parameter formulation. Int. J. Numer. Methods Eng. 2005, 64, 95–124. [Google Scholar] [CrossRef][Green Version]
- Payette, G.S.; Reddy, J.N. A seven-parameter spectral/hp finite element formulation for isotropic, laminated composite and functionally graded shell structures. Comput. Methods Appl. Mech. Eng. 2014, 278, 664–704. [Google Scholar] [CrossRef]
- Reddy, J.N. An Introduction to Nonlinear Finite Element Analysis: With Applications to Heat Transfer, Fluid Mechanics, and Solid Mechanics, 2nd ed.; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Cugnoni, J.; Gmur, T.; Schorderet, A. Identification by modal analysis of composite structures modelled with FSDT and HSDT laminated shell finite elements. Compos. Part A Appl. Sci. Manuf. 2004, 35, 977–987. [Google Scholar] [CrossRef]
- Park, T.; Kidu, K.; Han, S. Linear static and dynamic analysis of laminated composite plates and shells using a 4-node quasi-conforming shell element. Compos. Part B Eng. 2005, 37, 237–248. [Google Scholar] [CrossRef]
- Jung, W.Y.; Han, S.C. Transient analysis of FGM and laminated composite structures using a refined 8-node ANS shell element. Compos. Part B Eng. 2014, 56, 372–383. [Google Scholar] [CrossRef]
- Sahoo, S.S.; Panda, S.K.; Mahapatra, T.R. Static, free vibration and transient response of laminated composite curved shallow panel – An experimental approach. Eur. J. Mech. A/Solids 2016, 59, 95–113. [Google Scholar] [CrossRef]
- Hirwani, C.K.; Patil, R.K.; Panda, S.K.; Mahapatra, S.S.; Mandal, S.K.; Srivastava, L.; Buragohain, M.K. Experimental and numerical analysis of free vibration of delaminated curved panel. Aerosp. Sci. Technol. 2016, 54, 353–370. [Google Scholar] [CrossRef]
- Biswal, D.K.; Mohanty, S.C. Free vibration and damping characteristics study of doubly curved sandwich shell panels with viscoelastic core and isotropic/laminated constraining layer. Eur. J. Mech. A/Solids 2018, 72, 424–439. [Google Scholar] [CrossRef]
- Moita, J.S.; Araújo, A.L.; Soares, C.M.M.; Soares, C.A.M. Vibration analysis of functionally graded material sandwich structures with passive damping. Compos. Struct. 2018, 183, 407–415. [Google Scholar] [CrossRef]
- Kant, T.; Kumar, S.; Singh, U. Shell dynamics with three-dimensional degenerate finite elements. Comput. Struct. 1994, 50, 135–146. [Google Scholar] [CrossRef][Green Version]
- Bardell, N.S.; Dunsdon, J.M.; Langley, R.S. Free vibration of thin, isotropic, open, conical panels. J. Sound Vib. 1998, 217, 297–320. [Google Scholar] [CrossRef]
- Lee, S.J.; Han, S.E. Free-vibration analysis of plates and shells with a nine-node assumed natural degenerated shell element. J. Sound Vib. 2001, 241, 605–633. [Google Scholar] [CrossRef]
- Lee, W.H.; Han, S.C. Free and forced vibration analysis of laminated composite plates and shells using a 9-node assumed strain shell element. Comput. Mech. 2006, 39, 41–58. [Google Scholar] [CrossRef]
- Bahrami, S.; Shirmohammadi, F.; Saadatpour, M.M. Vibration analysis of thin shallow shells using spectral element method. Appl. Math. Model. 2017, 44, 470–480. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. The local GDQ method for the natural frequencies of doubly-curved shells with variable thickness: A general formulation. Compos. Part B Eng. 2016, 92, 265–289. [Google Scholar] [CrossRef]
- Żak, A.; Krawczuk, M. A higher order transversely deformable shell-type spectral finite element for dynamic analysis of isotropic structures. Finite Elem. Anal. and Des. 2018, 142, 17–29. [Google Scholar] [CrossRef]
- Ganesan, N.; Sivadas, K.R. Free vibration of cantilever circular cylindrical shells with variable thickness. Comput. Struct. 1990, 34, 669–677. [Google Scholar] [CrossRef]
- Sivadas, K.R.; Ganesan, N. Free vibration of circular cylindrical shells with axially varying thickness. J. Sound Vib. 1991, 147, 73–85. [Google Scholar] [CrossRef]
- Kang, J.H.; Leissa, A.W. Three-dimensional vibrations of thick spherical shell segments with variable thickness. Int. J. Solids Struct. 2000, 37, 4811–4823. [Google Scholar] [CrossRef]
- El-Kaabazi, N.; Kennedy, D. Calculation of natural frequencies and vibration modes of variable thickness cylindrical shells using the Wittrick–Williams algorithm. Comput. Struct. 2012, 104, 4–12. [Google Scholar] [CrossRef]
- Dai, L.; Yang, T.; Du, J.; Li, W.L.; Brennan, M.J. An exact series solution for the vibration analysis of cylindrical shells with arbitrary boundary conditions. Appl. Acoust. 2013, 74, 440–449. [Google Scholar] [CrossRef]
- Bacciocchi, M.; Eisenberger, M.; Fantuzzi, N.; Tornabene, F.; Viola, E. Vibration analysis of variable thickness plates and shells by the Generalized Differential Quadrature method. Compos. Struct. 2016, 156, 218–237. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Sherwin, S. Spectral/hp Element Methods for CFD; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Pozrikidis, C. Introduction to Finite and Spectral Element Methods Using MATLAB; Chapman and Hall/CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Gutierrez Rivera, M.; Reddy, J.N. Nonlinear transient and thermal analysis of functionally graded shells using a seven-parameter shell element. J. Modeling Mech. Mater. 2017, 1. [Google Scholar] [CrossRef]
- Gutierrez Rivera, M.; Reddy, J.N. Stress analysis of functionally graded shells using a 7-parameter shell element. Mech. Res. Commun. 2016, 78, 60–70. [Google Scholar] [CrossRef]
- Reddy, J.N. An Introduction to the Finite Element Method, 3rd ed.; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Reddy, J.N. Energy Principles and Variational Methods in Applied Mechanics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Guennebaud, G.; Jacob, B. Eigen v3. Available online: http://eigen.tuxfamily.org (accessed on 24 July 2020).
- Reddy, J.N.; Phan, N.D. Stability and vibration of isotropic, orthotropic and laminated plates according to a higher-order shear deformation theory. J. Sound Vib. 1985, 98, 157–170. [Google Scholar] [CrossRef]
- Liew, K.M.; Xiang, Y.; Kitipornchai, S.; Wang, C.M. Vibration Of Thick Skew Plates Based On Mindlin Shear Deformation Plate Theory. J. Sound Vib. 1993, 168, 39–69. [Google Scholar] [CrossRef]
- Liew, K.M.; Hung, K.C.; Lim, M.K. A continuum three-dimensional vibration analysis of thick rectangular plates. Int. J. Solids Struct. 1993, 30, 3357–3379. [Google Scholar] [CrossRef]
- Shufrin, I.; Eisenberger, M. Stability and vibration of shear deformable plates –first order and higher order analyses. Int. J. Solids Struct. 2005, 42, 1225–1251. [Google Scholar] [CrossRef]
- Shufrin, I.; Eisenberger, M. Vibration of shear deformable plates with variable thickness – first-order and higher-order analyses. Int. J. Solids Struct. 2006, 290, 465–489. [Google Scholar] [CrossRef]
- Chopra, I.; Durvasula, S. Natural frequencies and modes of tapered skew plates. Int. J. Mech. Sci. 1971, 13, 935–944. [Google Scholar] [CrossRef]
- Mizusawa, T. Vibration of rectangular Mindlin plates with tapered thickness by the spline strip method. Comput. Struct. 1993, 46, 451–463. [Google Scholar] [CrossRef]
- Blevins, R.D. Formulas for Natural Frequency and Mode Shape; RE Krieger: Malabar, FL, USA, 1979. [Google Scholar]
- Kang, J.H.; Leissa, A.W. Corrigendum to “Three-dimensional vibrations of thick spherical shell segments with variable thickness” [International Journal of Solids and Structures 37 (2000) 4811-4823]. Int. J. Solids Struct. 2006, 43, 2848–2851. [Google Scholar] [CrossRef][Green Version]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).