Abstract
The feature extraction of composite fault of gearbox in mining machinery has always been a difficulty in the field of fault diagnosis. Especially in strong background noise, the frequency of each fault feature is different, so an adaptive time-frequency analysis method is urgently needed to extract different types of faults. Considering that the signal after complementary ensemble empirical mode decomposition (CEEMD) contains a lot of pseudo components, which further leads to misdiagnosis. The article proposes a new method for actively removing noise components. Firstly, the best scale factor of multi-scale sample entropy (MSE) is determined by signals with different signal to noise ratios (SNRs); secondly, the minimum value of a large number of random noise MSE is extracted and used as the threshold of CEEMD; then, the effective Intrinsic mode functions(IMFs) component is reconstructed, and the reconstructed signal is CEEMD decomposed again; finally, after multiple iterations, the MSE values of the component signal that are less than the threshold are obtained, and the iteration is terminated. The proposed method is applied to the composite fault simulation signal and mining machinery vibration signal, and the composite fault feature is accurately extracted.
1. Introduction
In industrial production, the normal operation of mining machinery is the guarantee for the economic growth of enterprises. The gear and bearing in the gearbox are the most important transmission parts. When one of them fails, complex mechanical behavior will appear. In the unbalanced mechanical environment, other parts will appear fatigued, and further develop into the weak fault and significant fault. At the same time, their vibration signals are coupled with each other. In the case of strong noise environments and complex transmission paths, weak fault noises are submerged, and further leakage or misdiagnosis occurs [1,2,3,4,5]. Mechanical intelligence fault diagnosis usually includes three links. (1) Signal acquisition: Obtain multi-physical monitoring signals radiated by mechanical equipment to reflect the health status of equipment. (2) Feature extraction: By analyzing the acquired monitoring data, extract features to reveal fault information. (3) Fault identification and prediction: Based on the extracted features, faults are identified and predicted through artificial intelligence models and methods.
Over decades, with the development of computer science, a series of different time-frequency analysis methods have emerged. In 1998, empirical mode decomposition (EMD) was proposed, and then a large number of applications in signal processing [6,7,8], but it has endpoint effects and mode aliasing phenomena. In 2005, ensemble empirical mode decomposition (EEMD) was proposed [9,10,11]; it can not only overcome the endpoint effects of EMD but also weaken the mode aliasing phenomenon, so it has been applied in industrial production by a large number of scholars. However, it needs to set the times of additions and the amplitude of white noise; so far, no formula can adaptively determine the white noise amplitude value. At the same time, the number of additions is also not adaptive. When the number is too large, the calculation amount is too large; otherwise, the noise cannot be effectively averaged [12,13,14]. In order to improve the decomposition efficiency, complementary ensemble empirical mode decomposition (CEEMD) was proposed, which weakens the effect of the contained noise on the original signal by adding different positive and negative white noise multiple times [15], and is widely used in fault diagnosis [16,17,18]. CEEMD can improve the decomposition efficiency of EEMD, but the noise part of the original signal still exists. In other words, the noise component of the original signal still exists in the multiple Intrinsic mode functions(IMFs) decomposed. If it is not removed in time, it will lead to leakage or misdiagnosis. So, it is necessary to propose an effective method to eliminate noise components. In recent years, variable mode decomposition (VMD) [19,20,21] has been applied to fault diagnosis. It can decompose the original signal into several different time scale functions from low frequency to high frequency. The center frequency of each time scale is different, so its decomposition efficiency is higher than the EEMD and CEEMD. However, the method is limited to the choice of the number of decomposition layers and the penalty factor. So far there is still no suitable method to adaptively determine these two parameters. Therefore, in order to adaptively reduce the noise of complex vibration signals, this article uses the CEEMD decomposition method.
In strong background noise, each fault feature frequency is different [22,23,24,25,26,27,28,29], so an adaptive time-frequency analysis method is urgently needed to extract different types of faults. The article employs CEEMD to adaptively reduce the noise of complex vibration signals, but CEEMD has the problem of mode aliasing and the difficulty of removing noise components. Considering that the multi-scale sample entropy (MSE) [30,31,32] can estimate the complexity of time series, accurately measuring the complexity of different modal functions with strong noise resistance ability and excellent consistency, and at the same time, a stable entropy value can be obtained by using fewer data segments. Therefore, the MSE is used as the basis for eliminating the noise component, but the accuracy of the MSE is related to the scale factor. So, a method is proposed to determine the best scale factor in the MSE by the simulation signal with different signal to noise ratio (SNR), and the best factor is placed in the multi-scale sample entropy to calculate the MSE value of random noise, simulation signal, and vibration signal. This is firstly done by calculating the multiscale sample entropy value of 10,000 sets of random noise, extracting the minimum value and using it as the threshold of the noise component in CEEMD; then, the effective IMFs component is reconstructed, and the reconstructed signal is CEEMD decomposed again; this is followed by calculating the MSE value of each component signal, comparing the obtained MSE values with the threshold value, and if there are IMFs component signals greater than the threshold value, remove them, then reconstruct the remaining signal and perform CEEMD decomposition again; after multiple iterations, the MSE values of the component signal that are less than the threshold can be obtained, and the iteration is terminated. Finally, the resulting signal is analyzed by the spectrum to determine the fault characteristics. The proposed method is applied to the composite fault simulation signal and mining machinery vibration signal, and the composite fault feature is accurately extracted. At the same time, the feasibility of the method is verified by comparison with the traditional CEEMD.
2. Basic Theory
2.1. CEEMD
To solve the mode aliasing problem caused by EMD, EEMD uses the characteristics that white noise can be evenly distributed in the spectrum. Adding white noise to EMD improves the mode aliasing phenomenon; however, the residual white noise also brings reconstruction error problems. Inspired by EEMD, adding white noise to equalize the noise in the original signal, Yeh J R [15] proposed a new time-frequency analysis method CEEMD. The CEEMD method adds a pair of positive and negative white noise to the original signal for EMD decomposition to achieve the purpose of eliminating residual white noise in the reconstructed signal. In addition, the added white noise improves the mode aliasing problem, and the number of CEEMD noise addition is lower, which improves the calculation efficiency.
The CEEMD method is as follows:
- (1)
- Two new signals are formed by adding white noise with a certain standard deviation and equal length and opposite signs to the original signal.where S+i is the sum of the original signal and the positive white noise signal, S(t) is the original signal, n+i is the positive white noise; S-i is the sum of the original signal and the negative white noise signal, and n-i is the negative white noise.
- (2)
- EMD decomposition of S+i and S-i to obtain IMF+(i,j) and IMF-(i,j), then the first-order IMF is
- (3)
- Repeat the above steps to add Gaussian white noise 2N times.
- (4)
- Finally, the decomposition results of multiple component combinations are obtained:where N is the number of pairs added with white noise, IMFj is the j-th component obtained by CEEMD decomposition, and IMF(i,j) is the i-th IMF component of the j-th signal.
The decomposition process of CEEMD is shown in Figure 1.
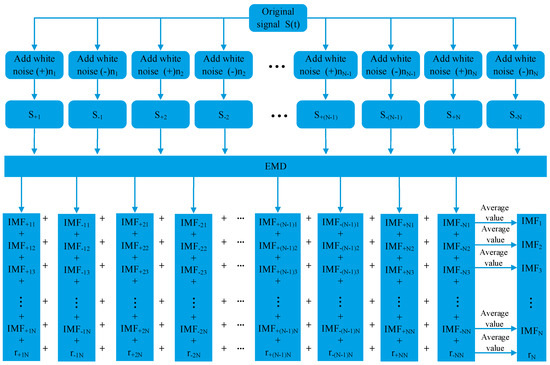
Figure 1.
Complementary ensemble empirical mode decomposition (CEEMD) flowchart.
2.2. Multi-Scale Sample Entropy (MSE)
Fault signals detected in rotating machinery are usually embedded in multi-scale structures. However, the sample entropy (SE) [33,34] only analyzes the single scale signal and ignores much useful information. This limits its performance in extracting embedded fault features [35]. In order to solve the shortcomings of sample entropy, Costa [36] proposed multi-scale sample entropy as an effective complexity measure of time series on different time scales. For a time series {x1, x2, …, xN‒1, xN}, MSE constructs multiple coarse-graining time series. The process of coarse-graining scale factor Q is obtained by averaging the internal structure of the time series, but without overlapping the length of the scale factor. Figure 2 shows the coarse-graining examples of processes. Therefore, the coarse-graining time series can be obtained from Equation (4):
where Q is the scale factor and is a positive integer. When Q = 1, the coarse-graining time series is the original time series. j is the length of the coarse-graining time series.
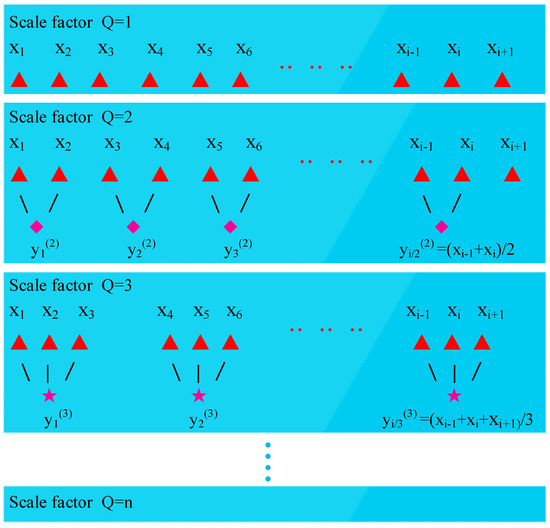
Figure 2.
Coarse graining process.
The next step is to calculate the multi-scale sample entropy and scale factor Q for each newly reconstructed coarse-graining time-series signal yQ. The multi-scale sample entropy is calculated as follows:
- (1)
- From N/Q-m+1 to vector (i)where m is the length of the sequence to be compared.
- (2)
- Calculate the maximum norm between two vectors dm[(i), (j)].
- (3)
- Define function Bwhere r is the tolerance of the acceptance matrix, um(i) is equal to dm[(i), (j)], and dm[(i), (j)] ≤ r, i ≠ j.
- (4)
- Define function Awhere υm+1 is equal to dm+1[(i), (j)], and dm+1[(i), (j)] ≤ r, i ≠ j.
- (5)
- Then calculate the probability of matching pointswhere Bm(r) and Am(r) represent the probability of two sequences matching m and m + 1 points, respectively.
- (6)
- The theoretical value of multiscale sample entropy is defined asWhen the data point N/Q is a finite number, the estimate of sample entropy is given by the following formula:It can be seen from Equation (12) that the value of SampEn is related to the value of m,r. At present, there is no definite value, and the empirical value is m = 2, r ∈ (0.1SD~0.5SD). SD is the standard deviation of the original data. In this paper, when studying the complexity of time series, m = 1, r = 0.25SD is taken.
2.3. Optimized CEEMD Method
CEEMD is an improved method based on the EMD method to add a pair of positive and negative white noise; there is also a mode aliasing phenomenon, and there is still noise in the decomposed IMF component. In order to eliminate the influence of noise on the decomposition results, this paper uses multi-scale sample entropy to remove the IMF with more noise components, reconstruct the signal, and perform the Fast Fourier transform(FFT) transform to obtain the fault feature signal to achieve the purpose of optimizing CEEMD. The flow chart is shown in Figure 3, the method is as follows:
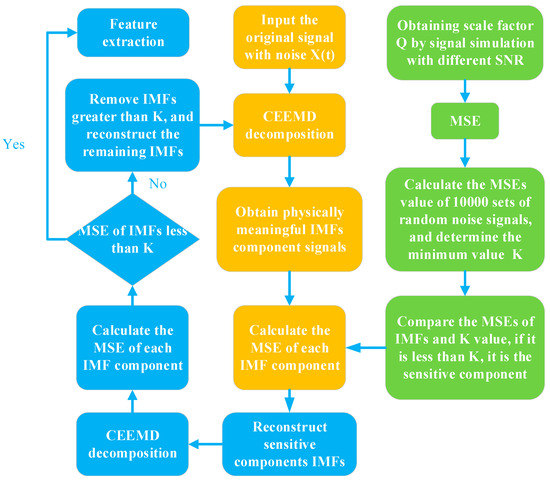
Figure 3.
Optimized CEEMD method flow chart.
- (1)
- Employing the CEEMD method to decompose the original signal X(t) containing noise to obtain a series of IMFs.
- (2)
- The selection of the scale factor Q of the MSE will affect the multiscale sample entropy value of each IMF. According to the decomposition characteristics of the IMF, the noise content of each layer is different. In order to better distinguish each layer of signals, this paper chooses a scale factor of 1–20 and signals with different SNRs for simulation to determine the best scale factor Q.
- (3)
- Substitute m = 2, r = 0.25SD, and the Q that was determined in step (2) into the MSE, calculate the multiscale sample entropy value of 10,000 sets of random noise signals, and obtain the minimum value K of the noise multiscale sample entropy.
- (4)
- Calculate the multi-scale sample entropy value of each IMF component, compare the obtained value with K, remove components greater than K value, and reconstruct the remaining IMFs components.
- (5)
- Perform CEEMD decomposition on the reconstructed signal again, and then calculate the multiscale sample entropy value of each IMF component.
- (6)
- Compare the MSE value of each IMF component with the minimum value K, if there is more than K worth of IMF, repeat (2–6); otherwise, continue.
- (7)
- The signal is FFT transformed to obtain the fault signal.
3. Simulation
3.1. Construct a Simulation Signal
The collected gearbox signal appears in the form of a mixture of the modulation signal of the gear mesh and the impact signal of the bearing rotation, and the signal contains noise in the working environment. As a result, this paper establishes a mathematical model containing a mixture of impact signal, modulation signal, and noise signal for signal simulation. The mathematical model established is as follows:
where Am = 3.0, g = 0.01, Tm = 1/13, fc = 130 Hz, fn1 = 10 Hz, and fz = 50 Hz. randn(t) is random noise. The number of sampling points is 1024 and the sampling frequency is 2048 Hz. Figure 4 is the time domain diagram and frequency domain diagram of the simulation signal, where the frequency domain diagram is obtained by performing FFT transformation on the time domain signal.
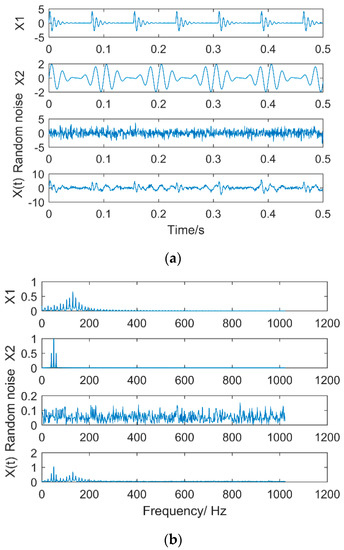
Figure 4.
Simulation signal. (a) Time domain of simulation signal, (b) Frequency domain of simulation signal.
Among them, X1 is the impact signal of bearing rotation, X2 is the modulation signal of gear mesh, and X(t) is the mixed signal of impact signal, modulation signal, and random noise signal. It can be observed from the figure that the X(t) signal contains a lot of noise signals.
3.2. Optimized CEEMD Method
The simulation signal X(t) is decomposed by CEEMD, and the decomposed time and frequency domain diagram is shown in Figure 5. Impact signals can be observed in the time-domain diagram. The signal in the frequency-domain diagram still has mode aliasing and contains some noise, which will affect the extraction of fault feature signals. Therefore, this paper proposes to use MSE to optimize the decomposition of CEEMD.
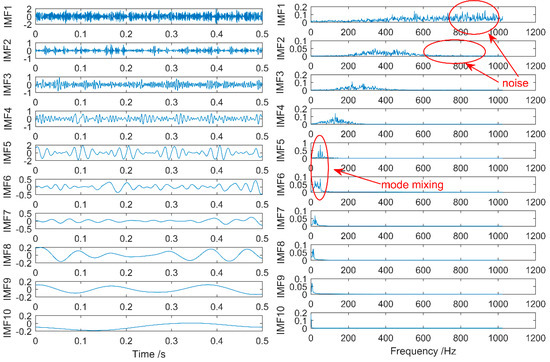
Figure 5.
Simulation signal decomposed by CEEMD.
The scale factor Q of the multi-scale sample entropy will affect the MSE value, and different Q values have different MSE values. According to the decomposition characteristics of CEEMD, each layer of IMF has a different SNR. In order to accurately determine the MSE value of each IMF, the different IMFs must be accurately distinguished. In this paper, the values of the scale factor Q range from 1 to 20 are taken, and the SNR is respectively taken as −30 dB, −20 dB, −10 dB, 1 dB, and 10 dB for simulation. The results are shown in Figure 6. The signals with the same SNR in the figure have different MSE values due to different Q values. Taking the SNR −30dB as an example, when the scale factor takes different values, MSE only has large fluctuations, and the fluctuation range is 1.6–2.5. For MSE with the same scale factor, there are different values of MSE due to different SNRs. Multi-scale sample entropy measures the complexity of the signal, the more noise in the signal, the greater the MSE value. In Figure 6, when the scale factor is taken as 10, MSE values are arranged in the order that the noise content in the signal is more or less. There is no situation where the MSE value of the low-noise signal is greater than the MSE of the high-noise signal, and the signal can be distinguished. Therefore, we choose the scale factor Q = 10 to calculate the MSE value of each layer of the IMF.
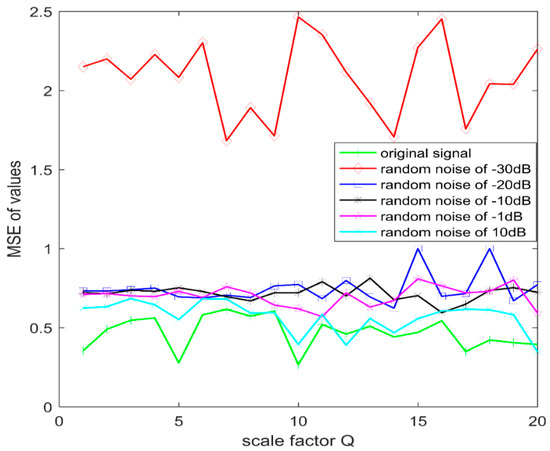
Figure 6.
Scale factor Q.
To eliminate the signal with larger MSE value in IMFs, it is necessary to determine the appropriate threshold. In this paper, the MSE values of 10,000 sets of noise signals (the signal length of each group of random noise is the same as the simulated signal) are calculated separately. The signal length of each group of random noise is the same as the vibration signal and the values are normalized, and the graph is drawn in Figure 7. The MSE value of the noise signal in Figure 7 varies from 0.55 to 1.0. In this paper, the minimum value of the MSE value in the 10,000 sets of noise signals is selected as the threshold for eliminating IMFs. 10,000 sets of random noise are randomly obtained, so the threshold in this paper is a dynamically changing value. After a lot of simulation, the minimum threshold fluctuates in a small range, so it is reasonable to choose the minimum value of 10,000 groups of noise as the threshold in this paper.
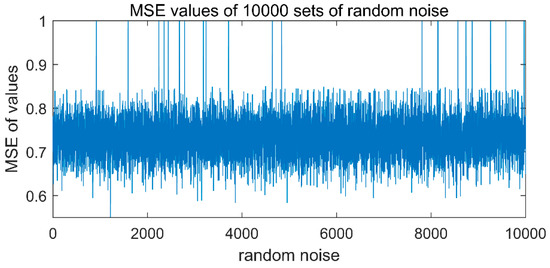
Figure 7.
Multi-scale sample entropy (MSE) values of 10,000 sets of random noise.
In this paper, the scale factor Q = 10 is used to calculate the MSE values of IMFs and 10,000 sets of random noise, at the same time, the minimum value of 10,000 sets of random noise is used as the threshold, and Figure 8 is drawn. In Figure 8, the pink line is the minimum value of 10,000 groups of random noise, and the red bar is the MSE value of each IMF. In this paper, IMFs signals larger than the threshold are eliminated, so the IMF1–IMF4 signals are eliminated. Reconstruct the remaining IMF5–IMF10 signals and perform FFT transformation to obtain Figure 9. In Figure 9, the red line is the reconstructed signal, and the blue is the original signal. It can be seen that the high-frequency noise part of the signal is removed from 400 Hz to 1000 Hz, which achieves the purpose of noise reduction.
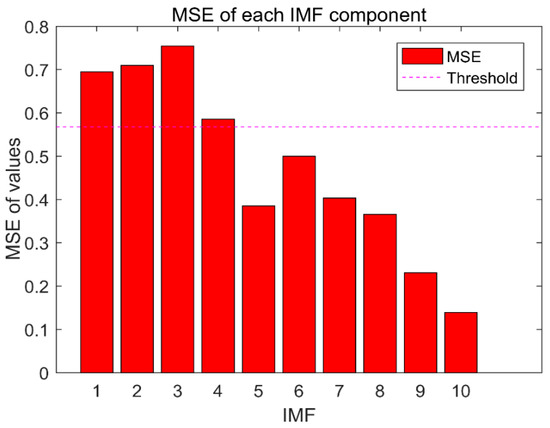
Figure 8.
MSE of each IMF component.
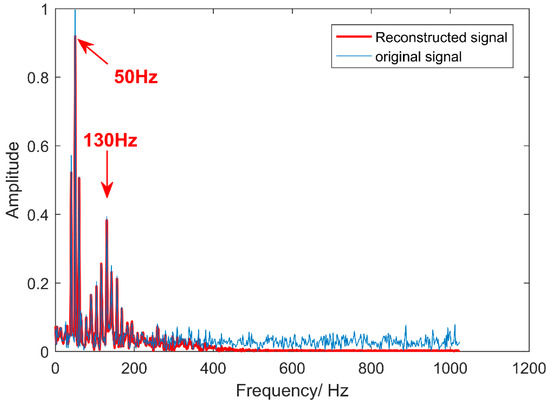
Figure 9.
Comparison of the original signal and reconstructed signal.
According to the method mentioned in this article, the reconstructed signal needs to be decomposed again by the CEEMD method, and the MSE value of each component signal is calculated. The MSE value is compared with the dynamic threshold value, and if there is an IMFs component signal greater than the threshold, it is removed, and the remaining signal is reconstructed and CEEMD decomposition is performed again. After multiple iterations, it is finally obtained that there is no case where the MSE value of the component signal is greater than the threshold, so the iteration is terminated. The time and frequency domain diagrams of signal decomposition at the end of the iteration are shown in Figure 10. The fault frequencies of 50 Hz and 130 Hz of the simulated signal in Figure 10 were extracted, which verified the effectiveness of the proposed method. Finally, the relationship between the MSE value of each signal component and the dynamic threshold is shown in Figure 11. In Figure 11, the MSE values of IMF1–IMF10 are all smaller than the dynamic threshold.
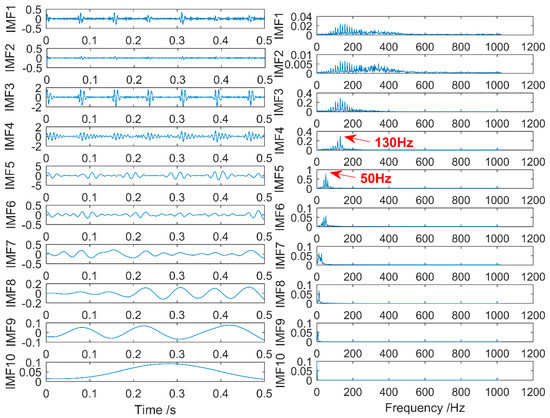
Figure 10.
CEEMD decomposition reconstructed signals.
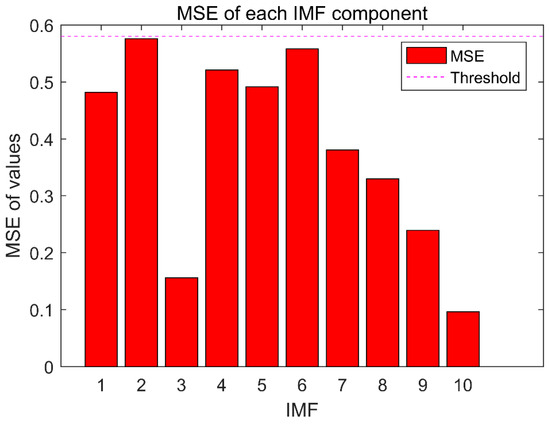
Figure 11.
MSE value of the component signal (reconstructed signal is decomposed by CEEMD).
4. Experimental Verification
To verify the feasibility of the proposed method in engineering application, it is planned to use the gearbox fault test bench for experiments. The experiment bench is shown in Figure 12, which includes a triple-phase asynchronous motor, connector, gear speed increaser, torque and rotational speed sensor, planetary reducer, triaxial acceleration sensor, and magnetic powder loader. The magnetic powder loader is used to adjust the load. The triaxial acceleration sensor model is YD77SA, the sensitivity is 0.01 V/ms‒2, and the sensor placement is shown in Figure 12.

Figure 12.
Experiment bench, 1—Magnetic Powder Loader; 2—Gear speed Increaser; 3—Torque and Rotational Speed Sensor; 4—Planetary Reducer; 5—Triaxial Acceleration Sensor #1; 6—Triaxial Acceleration Sensor #2; and 7—Triple-phase Asynchronous Motor.
During the test, the original bearing was replaced by a bearing with cracks in the inner ring and flaking of the inner ring. The bearing types are NJ210 and NJ405, as shown in Figure 13. The bearing speed is 1500 rmp. According to the calculation formula of the bearing inner ring fault frequency, the fault frequencies of NJ405 and NJ210 are 147.66 Hz and 231 Hz, respectively, as shown in Table 1.

Figure 13.
Faulty bearing. (a) NJ405 bearing. (b) NJ210 bearing.

Table 1.
Failure frequency.
The time and frequency domain of vibration signals in the experiment are shown in Figure 14. In Figure 14a, the periodic impact of the collected vibration signal is not very obvious. Figure 14b is the frequency domain diagram obtained by the FFT transformation of the vibration signal. It can be seen that the fault period is submerged by noise and it failed to judge the existence of the fault. The vibration signals are processed by CEEMD and the method proposed in this article, and the effects of each method are compared.
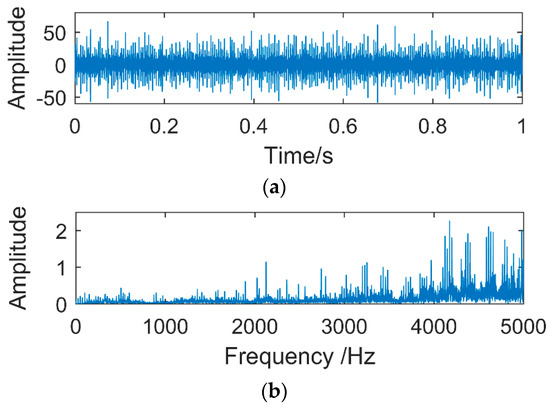
Figure 14.
Time-domain and frequency-domain graphs of experimentally acquired signals. (a) Time domain. (b) Frequency domain.
Figure 15a is the time domain diagram of the vibration signal decomposed by CEEMD, and Figure 15b is the frequency domain diagram of the vibration signal obtained by FFT. The signal in the figure is decomposed into 15 layers in total, and from the time domain diagram and frequency domain diagram in the corresponding diagram, we can observe that the component signals, IMF1–IMF5, are high-frequency noise signals. Bearing failure signals are not obtained in the IMF6–IMF15 component signals, so the vibration signal fails to extract the bearing failure signal through traditional CEEMD decomposition.
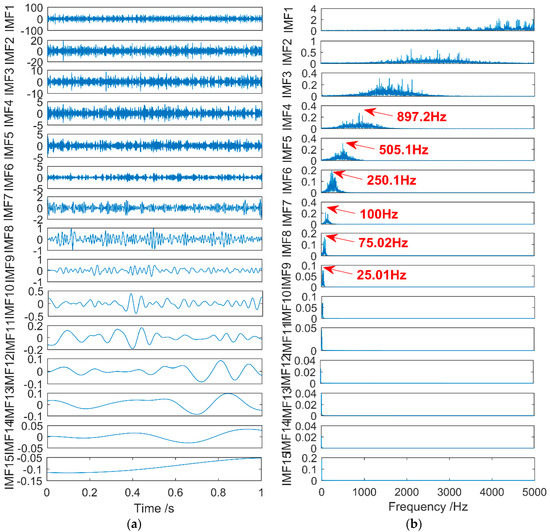
Figure 15.
CEEMD decomposes vibration signals. (a) Time domain. (b) Frequency domain.
Employing the method proposed in this paper to decompose the vibration signal. The threshold needs to be determined, so this paper uses the scale factor Q = 10 to calculate the MSE value of 10,000 sets of random noise. The signal length of each set of random noise is consistent with the vibration signal. The result is shown in Figure 16. The MSE value of the noise signal in Figure 16 varies from 0.705 to 0.745.
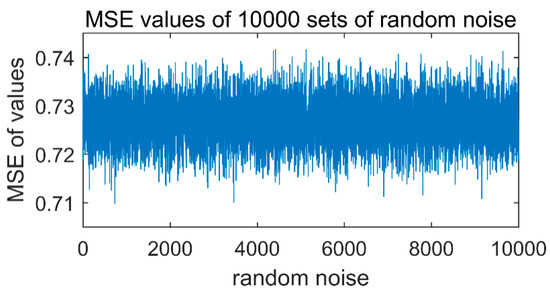
Figure 16.
MSE value of 10,000 sets of random noise signals (the signal length is consistent with the vibration signal).
In this paper, the scale factor Q = 10 is used to calculate the MSE values of IMFs and 10,000 sets of random noise, and the minimum value of 10,000 sets of random noise is used as the threshold, and Figure 17 is drawn. The pink line in Figure 17 is the minimum value of 10,000 sets of random noise, and the red bar is the MSE value of each IMF. In this paper, IMFs signals larger than the threshold are eliminated, so the IMF1–IMF3 signals in the figure below are eliminated. Reconstruct the remaining IMF4–IMF15 signals and perform FFT transformation to obtain Figure 18. In Figure 18, red is the reconstructed signal and blue is the original signal. It can be seen that the high-frequency noise part of the signal from 3000 Hz to 5000 Hz has been removed, which achieves the purpose of noise reduction. In Figure 18, 148 Hz is closest to the fault signal 147.66 Hz; 230.6 Hz is closest to the fault signal 231.2 Hz. Considering that the bearing operating environment has errors, which are allowed, so the method proposed in this article is effective.
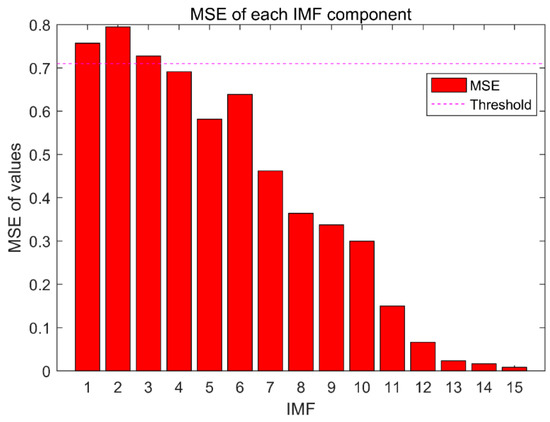
Figure 17.
MSE value of each component of vibration signal decomposed by CEEMD.
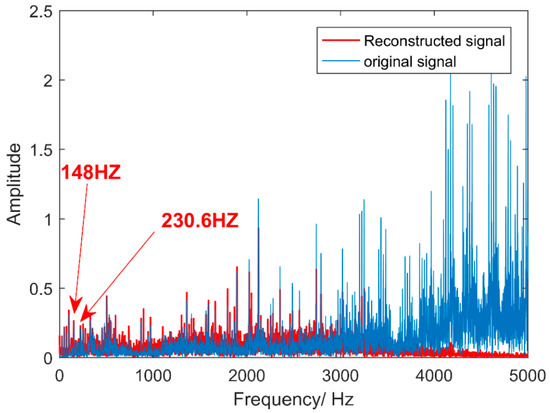
Figure 18.
Vibration signal reconstruction.
In Figure 18, the failure frequency of the reconstructed signal is not obvious. According to the method proposed in this paper, the reconstructed signal needs to be decomposed by the CEEMD method, and the MSE value of each component signal be calculated. The MSE value is compared with the dynamic threshold value, and if there is an IMFs component signal greater than the threshold, it is removed, the remaining signal is reconstructed, and CEEMD decomposition is performed again. After multiple iterations, if it is finally obtained that there is no case where the MSE value of the component signal is greater than the threshold, then the iteration is terminated. The time and frequency domain diagrams of signal decomposition at the end of the iteration are shown in Figure 19. In Figure 19, the reconstructed vibration signal is decomposed into 14 layers, of which IMF1–IMF5 are high-frequency noise signals; IMF6 is the failure frequency of the inner ring of NJ210 bearings; IMF7 is the failure frequency of the inner ring of NJ405 bearings; IMF8–IMF14 are meaningless interference components. Therefore, fault features are extracted, which verifies the effectiveness of the proposed method. The relationship between the multi-scale sample entropy of each signal component and the dynamic threshold is shown in Figure 20. In Figure 20, the MSE values of IMF1–IMF14 are all smaller than the dynamic threshold.
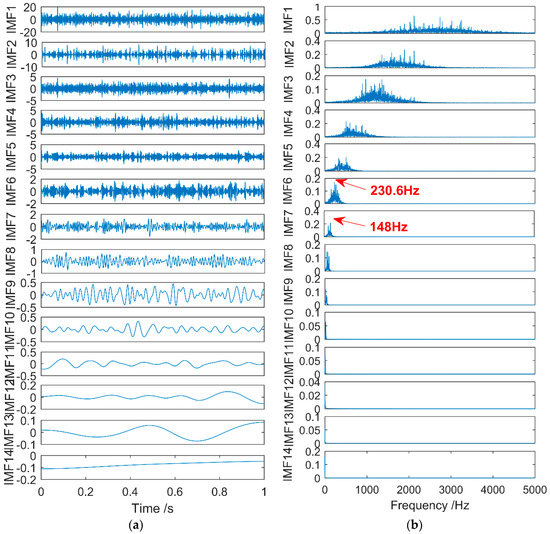
Figure 19.
The time and frequency domain of reconstructed signal by CEEMD decomposition. (a) Time domain. (b) Frequency domain.
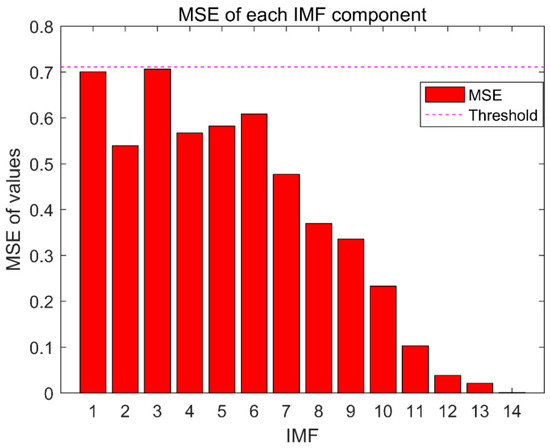
Figure 20.
MSE value of the component signal (reconstructed signal is decomposed by CEEMD).
5. Conclusions
In this paper, the CEEMD method is used to adaptively reduce the noise of complex vibration signals, but the pseudo components after CEEMD decomposition seriously reduce the diagnostic efficiency. The article proposes a new method of adaptively removing noise components, applying the proposed method to the composite fault simulation signal and the vibration signal of mining machinery, accurately extracting the composite fault characteristics, and verifying the feasibility of the method by comparing it with the traditional CEEMD. Finally, the following conclusions are obtained:
- (1)
- Determine the best scale factor Q = 10 in the MSE by simulation signals with different SNR, and then employ it to calculate the MSE values of noise signals, simulation signals, and vibration signals, which provide support for optimizing the CEEMD method.
- (2)
- Calculate the MSE value of 10,000 sets of random noise, and use the minimum value as the threshold, remove the IMFs component signal greater than the threshold, achieve the purpose of CEEMD noise reduction, and verify the feasibility of the minimum value as the threshold.
- (3)
- Through CEEMD decomposition of the reconstructed signal, the MSE value of each component signal is calculated. The MSE value is compared with the dynamic threshold value, and if there is an IMFs component signal greater than the threshold, it is removed, the remaining signal is reconstructed, and CEEMD decomposition is performed again. After multiple iterations, when it is finally shown that there is no case where the MSE value of the component signal is greater than the threshold, the iteration is terminated. Finally, the obtained signal is analyzed by the frequency spectrum to determine the fault characteristics.
Author Contributions
W.G. conceived and designed the experiments; R.L. and J.Z. performed the experiments; and W.G. and Y.K. wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key Research and Development Program of Shanxi Province (International Cooperation) (201903D421051, 201803D421028); Youth Fund Project of Shanxi Province (201901D211210).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xu, J.; Wang, Z.; Tan, C.; Si, L.; Zhang, L.; Liu, X. Adaptive Wavelet Threshold Denoising Method for Machinery Sound Based on Improved Fruit Fly Optimization Algorithm. Appl. Sci. 2016, 6, 199. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, J.; Wang, J.; Du, W.; Wang, J.; Han, X.; He, G.; Du, W. A Novel Fault Diagnosis Method of Gearbox Based on Maximum Kurtosis Spectral Entropy Deconvolution. IEEE Access 2019, 7, 29520–29532. [Google Scholar] [CrossRef]
- Wang, Z.; Du, W.; Wang, J.; Zhou, J.; Han, X.; Zhang, Z.; Huang, L. Research and application of improved adaptive MOMEDA fault diagnosis method. Measurement 2019, 140, 63–75. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Cai, W.; Zhou, J.; Du, W.; Wang, J.; He, G.; He, H. Application of an Improved Ensemble Local Mean Decomposition Method for Gearbox Composite Fault Diagnosis. Complexity 2019, 2019, 1–17. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, H.J. Mining Machinery System Remote Monitoring-Early Warning and Fault Diagnosis. Disaster Adv. 2012, 5, 1709–1712. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A: Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Xu, C.; Du, S.; Gong, P.; Li, Z.; Chen, G.; Song, G. An Improved Method for Pipeline Leakage Localization with a Single Sensor Based on Modal Acoustic Emission and Empirical Mode Decomposition with Hilbert Transform. IEEE Sensors J. 2020, 20, 5480–5491. [Google Scholar] [CrossRef]
- Taheri, B.; Hosseini, S.A.; Askarian-Abyaneh, H.; Razavi, F. Power swing detection and blocking of the third zone of distance relays by the combined use of empirical-mode decomposition and Hilbert transform. IET Gener. Transm. Distrib. 2020, 14, 1062–1076. [Google Scholar] [CrossRef]
- Wu, Z.H.; Huang, N.E. Ensemble empirical mode decomposition: A noise assisted date analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Zhang, Y.; Ji, J.; Ma, B. Fault diagnosis of reciprocating compressor using a novel ensemble empirical mode decomposition-convolutional deep belief network. Measurement 2020, 156, 107619. [Google Scholar] [CrossRef]
- Wang, L.; Shao, Y. Fault feature extraction of rotating machinery using a reweighted complete ensemble empirical mode decomposition with adaptive noise and demodulation analysis. Mech. Syst. Signal Process. 2020, 138, 106545. [Google Scholar] [CrossRef]
- Liu, Z.; Li, X.; Zhang, Z. Quantitative Identification of Near-Fault Ground Motions Based on Ensemble Empirical Mode Decomposition. KSCE J. Civ. Eng. 2020, 24, 922–930. [Google Scholar] [CrossRef]
- Xue, S.; Tan, J.; Shi, L.; Deng, J. Rope Tension Fault Diagnosis in Hoisting Systems Based on Vibration Signals Using EEMD, Improved Permutation Entropy, and PSO-SVM. Entropy 2020, 22, 209. [Google Scholar] [CrossRef]
- Hassan, S.; Alireza, E.; Mohammadhassan, D.K. Energy-based damage localization under ambient vibration and non-stationary signals by ensemble empirical mode decomposition and Mahalanobis-squared distance. J. Vib. Control 2019, 26, 1012–1027. [Google Scholar]
- Yeh, J.-R.; Shieh, J.-S.; Huang, N.E. complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Zhan, L.; Ma, F.; Zhang, J.; Li, C.; Li, Z.; Wang, T. Fault Feature Extraction and Diagnosis of Rolling Bearings Based on Enhanced Complementary Empirical Mode Decomposition with Adaptive Noise and Statistical Time-Domain Features. Sensors 2019, 19, 4047. [Google Scholar] [CrossRef]
- Chen, D.; Lin, J.; Li, Y. Modified complementary ensemble empirical mode decomposition and intrinsic mode functions evaluation index for high-speed train gearbox fault diagnosis. J. Sound Vib. 2018, 424, 192–207. [Google Scholar] [CrossRef]
- Imaouchen, Y.; Kedadouche, M.; Alkama, R.; Thomas, M. A Frequency-Weighted Energy Operator and complementary ensemble empirical mode decomposition for bearing fault detection. Mech. Syst. Signal Process. 2017, 82, 103–116. [Google Scholar] [CrossRef]
- Zhang, X.; Miao, Q.; Zhang, H.; Wang, L. A parameter-adaptive VMD method based on grasshopper optimization algorithm to analyze vibration signals from rotating machinery. Mech. Syst. Signal Process. 2018, 108, 58–72. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, J.; Hu, B.; Tang, J. Intelligent fault diagnosis of rolling bearings using variational mode decomposition and self-organizing feature map. J. Vib. Control. 2020. [CrossRef]
- Vikas, S.; Anand, P. Extraction of weak fault transients using variational mode decomposition for fault diagnosis of gearbox under varying speed. Eng. Failure Anal. 2020, 107, 104204. [Google Scholar]
- Liang, P.; Deng, C.; Wu, J.; Yang, Z.; Zhu, J.; Zhang, Z. Single and simultaneous fault diagnosis of gearbox via a semi-supervised and high-accuracy adversarial learning framework. Knowl. Based Syst. 2020, 198, 105895. [Google Scholar] [CrossRef]
- Wang, Z.; He, G.; Du, W.; Zhou, J.; Han, X.; Wang, J.; He, H.; Guo, X.; Wang, J.; Kou, Y. Application of Parameter Optimized Variational Mode Decomposition Method in Fault Diagnosis of Gearbox. IEEE Access 2019, 7, 44871–44882. [Google Scholar] [CrossRef]
- Wang, Z.; Zheng, L.; Du, W.; Cai, W.; Zhou, J.; Wang, J.; Han, X.; He, G. A Novel Method for Intelligent Fault Diagnosis of Bearing Based on Capsule Neural Network. Complexity 2019, 2019, 1–17. [Google Scholar] [CrossRef]
- Chen, X.; Feng, Z. Induction motor stator current analysis for planetary gearbox fault diagnosis under time-varying speed conditions. Mech. Syst. Signal Process. 2020, 140, 106691. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, M.; Yi, Y.; Lin, J. Application of sparsity-oriented VMD for gearbox fault diagnosis based on built-in encoder information. ISA Trans. 2020, 99, 496–504. [Google Scholar] [CrossRef]
- Wang, Z.; Zheng, L.; Wang, J.; Du, W. Research on Novel Bearing Fault Diagnosis Method Based on Improved Krill Herd Algorithm and Kernel Extreme Learning Machine. Complexity 2019, 2019, 1–19. [Google Scholar] [CrossRef]
- Zheng, L.; Wang, Z.; Zhao, Z.; Wang, J.; Du, W. Research of Bearing Fault Diagnosis Method Based on Multi-Layer Extreme Learning Machine Optimized by Novel Ant Lion Algorithm. IEEE Access 2019, 7, 89845–89856. [Google Scholar] [CrossRef]
- Kim, Y.; Park, J.; Na, K.; Yuan, H.; Youn, B.D.; Kang, C.-S. Phase-based time domain averaging (PTDA) for fault detection of a gearbox in an industrial robot using vibration signals. Mech. Syst. Signal Process. 2020, 138, 106544. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, L.; Cai, Y. Rolling bearing fault diagnosis using generalized refined composite multiscale sample entropy and optimized support vector machine. Measurement 2020, 156, 107574. [Google Scholar] [CrossRef]
- Mao, X.; Shang, P. A new method for tolerance estimation of multivariate multiscale sample entropy and its application for short-term time series. Nonlinear Dyn. 2018, 94, 1739–1752. [Google Scholar] [CrossRef]
- Zhang, N.; Lin, A.; Ma, H.; Shang, P.; Yang, P. Weighted multivariate composite multiscale sample entropy analysis for the complexity of nonlinear times series. Phys. A: Stat. Mech. its Appl. 2018, 508, 595–607. [Google Scholar] [CrossRef]
- Li, X.; Dai, K.; Wang, Z.; Han, W. Lithium-ion batteries fault diagnostic for electric vehicles using sample entropy analysis method. J. Energy Storage 2020, 27, 101121. [Google Scholar] [CrossRef]
- Shang, Y.; Lu, G.; Kang, Y.; Zhou, Z.; Duan, B.; Zhang, C. A multi-fault diagnosis method based on modified Sample Entropy for lithium-ion battery strings. J. Power Sources 2020, 446, 227275. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Liu, Z.; Liang, X.; Si, S. The Entropy Algorithm and Its Variants in the Fault Diagnosis of Rotating Machinery: A Review. IEEE Access 2018, 6, 66723–66741. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale Entropy Analysis of Complex Physiologic Time Series. Phys. Rev. Lett. 2002, 89, 705–708. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).