Abstract
The detection of a brain tumor through magnetic resonance imaging (MRI) is still challenging when the image is in low quality. Image segmentation could be done to provide a clear brain tumor area as the region of interest. In this study, we propose an improved model-based clustering approach for MRI-based image segmentation. The main contribution is the use of the adaptive neo-normal distributions in the form of a finite mixture model that could handle both symmetrical and asymmetrical patterns in an MRI image. The neo-normal mixture model (Nenomimo) also resolves the limitation of the Gaussian mixture model (GMM) and the generalized GMM (GGMM), which are limited by the short-tailed form of their distributions and their sensitivity against noise. Model estimation is done through an optimization process using the Bayesian method coupled with a Markov chain Monte Carlo (MCMC) approach, and it employs a silhouette coefficient to find the optimum number of clusters. The performance of the Nenomimo was evaluated against the GMM and the GGMM using the misclassification ratio (MCR). Finally, this study discovered that the Nenomimo provides better segmentation results for both simulated and real data sets, with an average MCR for MRI brain tumor image segmentation of less than 3%.
1. Introduction
We chose brain tumor detection as the topic for this study since a brain tumor is the 15th most deadly disease in Indonesia, a comparison that includes all types of cancer. The World Health Organization noted that during 2018, Indonesia had 5323 cases of brain and nervous system tumors, with 4229 cases of mortality [1]. This high mortality rate also occurs in Surabaya, where cases of brain tumors are increasing from year to year. The Dr. Soetomo General Hospital (RSUD) in Surabaya provides radiological examination services for brain tumor patients, including brain scanning with the 3 Tesla and 1.5 Tesla magnetic resonance imaging (MRI) scanners. The higher Tesla power provides better quality MRI images. However, the 1.5 Tesla service is still in high demand due to its low cost; moreover, this service is also covered by the Indonesian government’s social security (BPJS). A high-quality MRI image is needed to provide an accurate tumor location for medical surgery. This study tried to employ the image segmentation technique to enhance brain tumor images from the 1.5 Tesla MRI scanner. Segmentation is done by separating the tumor area (which is known as the region of interest—ROI) from the healthy brain. This helps medical surgery by providing a clear boundary to the parts of the tumor area that must be taken away without damaging healthy parts of the brain.
Various image segmentation techniques have been proposed in the form of clustering algorithms. Traditional methods include hierarchical clustering and the partitioning algorithm [2]. In hierarchical clustering, objects are grouped by forming a cluster tree or dendrogram, while partitioning algorithms are based on objective functions that are optimized to obtain clustering and cluster centers. These methods are mostly heuristics, so they are not based on formal models. The hierarchical clustering for image segmentation was implemented by Bruse et al. [3] and Pestunov et al. [4]. Several partitioning algorithm techniques used in image segmentation are K-means cluster [5], K-medoids [6], and fuzzy-based clustering techniques such as Fuzzy C-means (FCM) [7]. Raftery [8] stated that traditional methods are in great demand because of their simplicity. However, Greeve et al. [9] evaluated the traditional methods and found that those methods were unable to represent real data patterns. Model-based clustering is the most appropriate tool to overcome this problem, especially when facing a limited number of data. One of the methods is known as the Gaussian mixture model (GMM) [10].
In image segmentation, the GMM has several limitations. One of them is the usage of Gaussian distributions, which have symmetry and short-tailed properties. They make the GMM inflexible to overcome several cases of image segmentation that tend to have diverse patterns [11]. Some methods developed to overcome this problem include the use of distributions other than Gaussian, e.g., the Student’s t mixture model (SMM) [12] and the Laplace mixture model (LMM) [13]. A similar idea is also seen in the generalized GMM (GGMM), which utilizes the flexibility of form parameters from the Gaussian distribution [14]. However, the use of a Gaussian distribution still leaves problems regarding the short-tailed form of distribution. The existence of a pattern with a long tail must be approached with more Gaussian distribution components that must compile the Gaussian mixture so that the parsimony of the model is less intact. Some of the mentioned models still apply distributions with rules of symmetry and set the mean as the cluster center; therefore, their sensitivity to noise is still high.
Another problem that often arises in image segmentation is the existence of different distributions in the mixture model. Therefore, using a mixture approach from a similar distribution is not adequate. Motivated by a previous study by Rasmussen [10] and Deledalle et al. [14], we propose the use of mixture models with adaptive distributions that can adaptively accommodate a variety of symmetrical and asymmetrical patterns. Despite those facts, these distributions could also handle the limitations related to the short tail form and the lack of robustness of a Gaussian distribution. These adaptive distributions—which are called nearly normal or neo-normal—have symmetrical properties, as with the Gaussian distribution, but can be more pointed or tilted. Some of the distributions in the neo-normal family are Fernandez–Steel skew normal (FSSN) [15] and modified stable to normal from Burr (MSNBurr) [16]. This study used the FSSN and MSNBurr distributions to develop our mixture model, and we named it the Nenomimo. The used FSSN mixture model followed the research of Iriawan et al. [17], which also applied it to MRI image segmentation. The Bayesian method coupled with the Markov chain Monte Carlo (MCMC) approach was employed in model estimation, since the analytical solutions were considered complicated. The proposed models were compared with the GMM and the GGMM for segmenting the simulated and MRI brain tumor image sets. The cluster validation was done by calculating the silhouette coefficient, and the best model was decided by the minimum value of the misclassification ratio.
In the next section, we discuss the Nenomimo, and in Section 3, we continue with the estimation of the purposed models (FSSN and MSNBurr mixture models). Section 4 discusses the cluster validation and model comparison tools. Section 5 shows the discussion of segmentation results performed for the normal model and the Nenomimo in simulated and real data sets. Finally, Section 6 presents some conclusions and directions for future work.
2. Neo-Normal Mixture Model
In this section, we present the mixture model based on neo-normal distributions that were applied in segmenting the MRI brain tumor images. This is explained, as are the finite mixture model and the neo-normal family distributions.
2.1. Finite Mixture Model
This study used MRI images as the input data. MRI images are grayscaled digitized image, in which each pixel has gray color intensities. The grayscale intensities in the pixels describe the level of color from black to white. The lower the intensity value, the darker the gray level, and vice versa.
Suppose we have random variable , where denotes the grayscale intensity of -th pixel observation, and we assume that there are pixels in an image that groups into clusters; then, the finite mixture model is a superposition of specific distributions whose form is given by [11]:
where is the mixture densities with parameters and , and is the density of specific univariate distribution with parameter . The terms are the proportions of the mixture component density that must satisfy the following constraints:
The likelihood of the N data can be written as:
where and are assumed to be conditional independence , and come from identical distributions. This formulation is a general finite K components mixture model. In a specific way, we can provide a certain distribution in the form of . If it is a normal density, then the model becomes a normal or Gaussian mixture model. Likewise, if is the neo-normal distribution, then the model becomes a neo-normal mixture model or the Nenomimo.
2.2. Neo-Normal Distribution
The neo-normal distribution family consists of the adaptive distributions that has symmetrical properties, but it can also accommodate skewed or asymmetrical patterns; moreover, it can also be sharper or gentler [18]. These distributions slightly deviate from normal or Gaussian distributions but set their mode as the location parameter. Some of the distributions included in the neo-normal model are the exponential power distribution and Azalini skew normal distribution. The exponential power distribution is similar to the Gaussian distribution, but it can be more pointed and has a thick tail [19]. The Azalini skew normal distribution can accommodate symmetrical or skewed characteristics of a distribution, but this distribution’s mode is not stable in its location parameters [20].
Fernandez and Steel [15] overcame the weakness of the Azalini’s distribution by introducing another skew normal distribution. This distribution is able to maintain the stability of modes in its location parameters—whether it is symmetrical or skewed—by adding the transformation parameters. This distribution is called the FSSN. Another distribution that is also stable in mode is the MSNBurr by Iriawan [16]. The advantage of using the MSNBurr is that the distribution can accommodate long-tail data, as in an MRI image’s pattern. This study used the FSSN and MSNBurr distributions to build the mixture models. The cluster center was more robust since these distributions are stable in their modes.
Supposing the random variable follows the FSSN distribution, Iriawan et al. [17] provided the density as:
where is a location parameter, is a dispersion parameter, and is a skewness parameter. This distribution transforms the symmetrical normal distribution using inverse scale factors in the positive and negative axes. It loses its symmetry when , skews to the left when , and skews to the right when . By substituting Equation (3) as in Equation (1), we were able to obtain the FSSN mixture model.
The MSNBurr distribution idea was designed for the skewed distribution, which ensures that the modes of the Burr II distribution for all values of its skewness parameter, , remain at its location parameter. Iriawan [16] defined the density function (p.d.f) for the MSBurr family as:
where and are location and dispersion parameters, respectively, and is a scale factor. The distribution in Equation (5) is called the MSNBurr , with the value of is as Equation (5):
The MSNBurr mixture model is built by substituting Equation (4) as in Equations (1) and (2) with parameter .
3. Bayesian Coupled with Markov Chain Monte Carlo Approach
The fully Bayesian method coupled with MCMC approach was employed to estimate the model parameters and conduct inferences. Bayesian MCMC estimates parameters using full conditional posterior distribution through a sample average approach that is stochastically optimized [21]. In this section, we present the inference with Bayesian for the FSSN and MSNBurr mixture models, and we construct the algorithm.
Suppose denotes the number of pixels of the MRI image and denotes the number of the mixture component; then, we assume that each pixel belongs to a single cluster that is indexed by label . For each observation, label is assumed to be independent, and the value is given by:
where:
For each , there is only one of that equals to 1, and the rest are 0. For a certain , therefore, . Single-trial results for each in exactly one of possible mixture components have the probabilities , , . Since ’s are independent, the joint density of the variable is:
Let be an i.i.d random sample drawn from neo-normal mixture density. The likelihood of the mixture density is given by Equation (2). By integrating the label to the likelihood, we can rewrite the likelihood as:
where is the set of the neo-normal parameters.
3.1. Bayesian Approach for FSSN Mixture Model
The Bayesian approach was employed to perform the estimation, owing to the non-close form of the posterior distribution that acts as the multiplication between the likelihood function in Equation (8) and the prior distribution. We designed the prior distribution for the FSSN mixture model (FSSN-MM) following Iriawan et al. [17]. The prior distribution of mixture parameters were discussed by Gelman et al. [22].
The value of hyperparameters were calculated from the data. The hyperparameter and , where represents all data that belongs to the cluster. We also set , , , and . By employing these priors as independent priors and contaminating them with the likelihood, the joint posterior can be constructed easily by multiplying them together. This derivation and the Gibbs sampling algorithm for the FSSN mixture model were adopted from Iriawan et al. [17].
The full conditional posterior was conducted to generate the parameter values. It was derived from multiplying the likelihood and the prior distribution of parameters, which were estimated [23]. The full conditional posterior of each parameter is given below (for simplicity, all equations are written in logarithm and all parts of equation that do not contain the estimated parameter are summed as a constant).
- (a)
- The full conditional posterior for the location parameter , is given by:
- (b)
- The full conditional posterior for parameter , is given by Equation (10):
- (c)
- Equation (11) shows the full conditional posterior for parameter , :
- (d)
- Equation (12) shows the full conditional posterior distribution parameter , :This is a Dirichlet distribution.
- (e)
- The label , and , only has two possible values, i.e., 0 or 1. For each , there are possible mixture components, so follows the multinomial distribution where:
To estimate the parameter of the FSSN-MM, the Gibbs sampling framework as the process of Bayesian approach was applied. Algorithm 1 states the steps of the Gibbs sampling algorithm.
| Algorithm 1: Gibbs sampling for the Fernandez–Steel skew normal-mixture model (FSSN-MM) |
|
3.2. Bayesian Approach for MSNBurr Mixture Model
The prior distribution for MSNBurr was discussed by Iriawan [16]. The proportion of the mixture components follows the Dirichlet distribution, as in the FSSN-MM. The following are prior distributions for each parameter of the MSNBurr mixture model (MSNBurr-MM):
The hyperparameters value are given as in the FSSN-MM; however, we set the hyperparameter for prior by , , and . By setting these priors as independent priors and multiplying them with the likelihood, its joint posterior could be found easily (see Appendix A). The full conditional posterior distributions for each parameter are discussed below. For simplicity, the formulas are shown as logarithms (some derivations are shown in Appendix B) and all parts of the equation that do not contain the estimated parameter are assembled as a constant.
- (a)
- The full conditional posterior for , is shown in Equation(14):
- (b)
- The following Equation (15) shows the full conditional posterior for , :
- (c)
- The full conditional posterior of , is given bellow:
- (d)
- The full conditional posterior for , is as shown in Equation (12).
- (e)
- The full conditional posterior of the label follows the multinomial distribution, where , as in Equation (13).
The Gibbs sampling algorithm was constructed with a full conditional posterior for each parameter. The step of Gibbs sampling for the MSNBurr-MM is presented in Algorithm 2.
| Algorithm 2: Gibbs sampling for the modified stable to normal from Burr-mixture model (MSNBurr-MM). |
|
Both Algorithm 1 and Algorithm 2 were used as a basis for programming via MATLAB. The generation of samples in both algorithms, we used the acceptance rejection sampling method. All programs were run under the computer specification of Intel Core i7, 8GB RAM, 256 GB SSD, without GPU and VRAM. For the sake of reproducibility of our results, we made our MATLAB code for the MSNBurr-MM available online at https://github.com/anindya364/nenomimo.
4. Cluster Validation and Comparison Tools
Cluster validation was done by employing the silhouette coefficient . The value of determines the optimum number of clusters. is formulated in Equation (17) [24]:
where is the value for all data at the cluster, is the average squared Euclidean distance that denotes how similar the data are to their cluster, and indicates how similar the data are to the other clusters. The of a cluster in Equation (18) is the average value of all the data included in the cluster, . The overall () of the image is the average of all of all clusters formulated in Equation (19):
The has a range of values from −1 to 1. The closer the is to 1, the more likely the data should be in the cluster.
The comparison measurement tool used for the segmentation result was the misclassification ratio . The calculates the differences between the segmentation results with the ground truth (GT) image. The smaller the value of , the better the segmentation results [17]. The formula of is given by Equation (20):
5. Result and Discussion
In this section, we compare the proposed models with the GMM by Rasmussen [10] and the GGMM by Deledalle et al. [14]. The GMM and the GGMM represented the model-based normal distribution, while the FSSN-MM and the MSNBurr-MM represented the Nenomimo.
5.1. Application for Data Simulation
The data simulation used in this study were synthetic images and natural images. For synthetic images, original images were also set for the GT. To add more challenge in segmentation, we provided noise (Gaussian noise, salt-paper noise, and speckle noise) to each image. The synthetic images (SI01 and SI02) and natural images (NI01 and NI02) with their GT are visualized in Figure 1.

Figure 1.
Synthetic images: (a) SI01 and (b) SI01. Natural images: (c) NI01 and (d) NI02.
The segmentation results of each method for SI01, SI02, NI01, and NI02 are shown in Figure 2, Figure 3, Figure 4 and Figure 5. The methods run under two clusters for SI01 and NI01, while SI02 and NI02 run under three clusters.

Figure 2.
Segmentation result of SI01 for different methods.
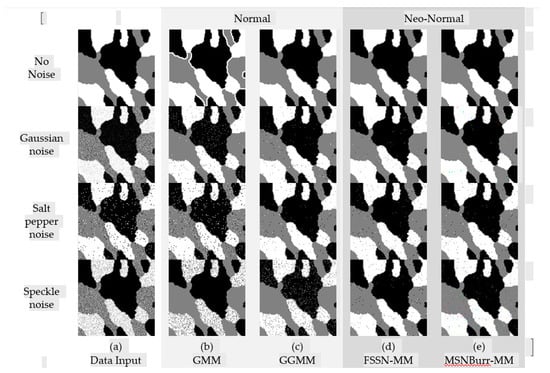
Figure 3.
Segmentation result of SI02 for different methods.

Figure 4.
Segmentation result of NI01 for different methods.
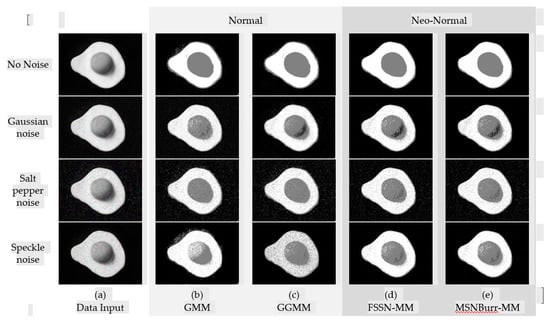
Figure 5.
Segmentation result of NI02 for different methods.
The accuracy of segmentation results was shown by the . As visualized in Figure 6, the minimum was shown by the Nenomimo (FSSN-MM and MSNBurr-MM). For different types of noise, the Nenomimo gave a better performance in segmenting both the synthetic images and natural images. This indicated that the Nenomimo is more robust in handling noise than the GMM and the GGMM. Overall, for the simulation dataset, the Nenomimo segmented the images more precisely than the model-based normal distribution.
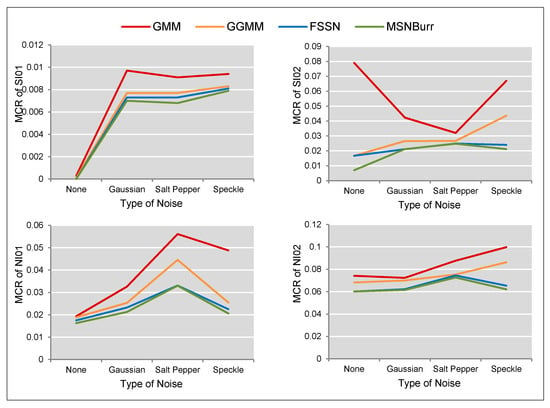
Figure 6.
The misclassification ratio (MCR) comparison for SI01, SI02, NI01, and NI02 segmentation results.
The next application was for a real dataset. The MRI-based brain tumor segmentation was also done under the Nenomimo, the GMM, and the GGMM.
5.2. Application for MRI-Based Brain Tumor
The real datasets were from the Dr. Soetomo General Hospital (RSUD), Surabaya. The MRI sequences in this study were from T1 MEMP + C and T2 FLAIR; both were from the axial point of view. T1 MEMP + C was the MRI sequence in which the tumor area was enhanced by contrast media, which is the material given to patients, either orally or injected, before doing MRI scanning. T2 FLAIR was the MRI sequence without contrast media; this sequence visualized the swelling or edema of the brain tumor more visibly; therefore, the ROI of T2 FLAIR was usually larger than T1 MEMP + C.
We tried to segment about 75 images from the T1 MEMP + C and T2 FLAIR sequences. The tumor area was set as the ROI, while another area was set as a non-ROI. All sequences used in this study passed medical approval, and the GT was also conducted under medical judgment. All MRI images were analyzed under normal and neo-normal models. This paper only displays four sample images. The sample datasets are visualized in Figure 7, while the histograms are shown in Figure 8.
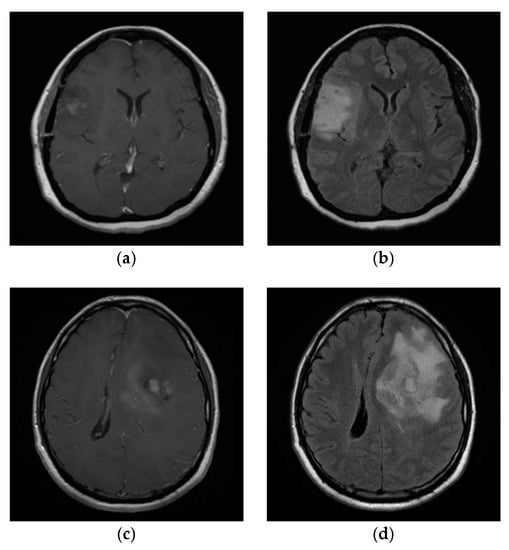
Figure 7.
The real dataset from medical consent: (a) IM01, (b) IM02, (c) IM03, and (d) IM04.
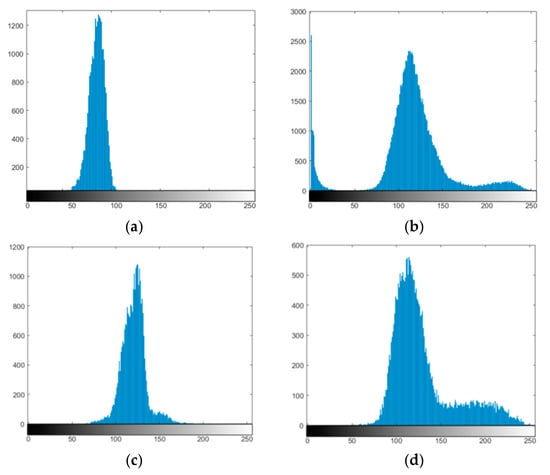
Figure 8.
The histograms of (a) IM01, (b) IM02, (c) IM03, and (d) IM04 after preprocessing.
Figure 7a,c includes the sample from the T1 MEMP + C sequence, while Figure 7b,d is the sample from the T2 FLAIR sequence. The sample data images are named IM01, IM02, IM03, and IM04. The first applied procedure was preprocessing. It was done to eliminate the fat around the skull, which could have interfered with the segmentation process. Figure 8 shows the image histogram after preprocessing. Unlike Figure 8b–d, the multimodality in Figure 8a is not clearly visible since the frequency of the other modes was very small. Due to the multimodalities present in the MRI data pattern, applying the mixture model framework was considered appropriate for this case.
The 75 datasets were segmented under the GMM, the GGMM, the FSSN-MM, and the MSNBurr-MM. The OSC was calculated to provide the optimum number of clusters. Table 1 shows the sample of the OSC for IM01–04. The optimum value of the OSC led to the optimum number of clusters. The optimum number of clusters for the Nenomimo for IM01 and IM03 was , while IM02 and IM04 reached the optimum number at . Various results were found with the GMM; for IM01, the optimum number of clusters was , while IM02 and IM04 reached the optimum number at , and IM03 reached the optimum number at . The GGMM had the cluster optimum at for IM01 and IM04, for IM02, and for IM03. The segmentation results for the optimum clusters are visualized in Figure 9.

Table 1.
The summary of overall silhouette coefficients (OSCs) for the sample image. GMM: Gaussian mixture model; GGMM: generalized Gaussian mixture model.
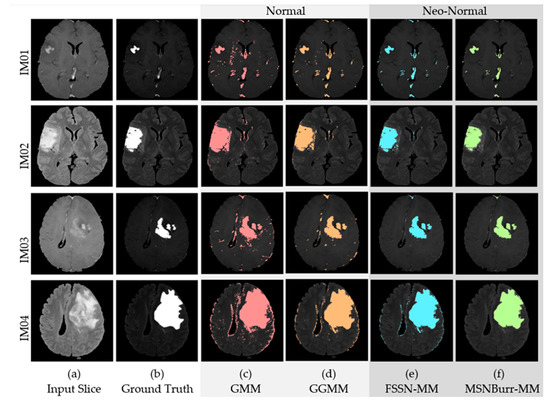
Figure 9.
The region of interest (ROI) of (a) input slice in different layers compared with (b) the ground truth (GT) for the (c) GMM, (d) GGMM, (e) FSSN-MM, and (f) MSNBurr-MM algorithms.
Based on segmentation results in Figure 9, we can see that the ROI from the GMM still contained more noise than the GGMM, the FSSN-MM, and the MSNBurr-MM. For empirical comparison, the from 75 dataset was found. Figure 10 shows the comparison of the for all dataset using different methods. The MCR from Figure 10 shows that the minimum value was reached by the MSNBurr-MM, while the FSSN-MM gave similar results. This indicated that the Nenomimo have a better performance than the model-based normal distribution. The average value of the for the FSSN-MM was about 0.02761, while the MSNBurr-MM had an average value of about 0.02644. This value showed that the Nenomimo could segment the real dataset with a misclassification ratio of less than 3%.
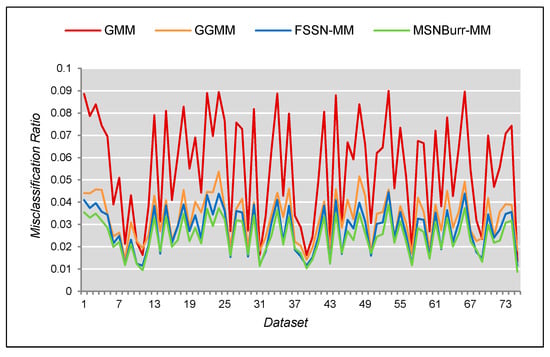
Figure 10.
The comparison of the MCR for each image and each method.
The parameter of the Nenomimo for optimum clusters is shown in Table 2. In Table 2, the ROI for each dataset is denoted by the last cluster. For example, in IM01, for the FSSN-MM, the ROI had a cluster center at a grayscale intensity of 165 with the range of intensity dispersion at about 6.719. The pixel in the ROI was about 5.4% from all MRI areas. Different results were provided by the MSNBurr-MM, which had a cluster center at a grayscale intensity of about 163, an intensity dispersion of 7.138, and the ROI pixel just 6.3% from the MRI areas. Both the FSSN-MM and the MSNBurr-MM had skewness parameters in the first and third clusters, indicating that the distribution of the grayscale intensities was right skewed. The skewness parameter in the second cluster of IM01 indicated the left skew of the distribution.

Table 2.
The parameter of the Nenomimo for the sample image.
Figure 11 shows the historically generated parameter for the Nenomimo iteration. Under the computer specification with processor Intel Core i7, 8GB RAM, 256GB SSD, without GPU and VRAM, the average running time for clustering the MRI images with the FSSN-MM took about six minutes of computer processing, while the MSNBurr-MM took about four minutes. Figure 11 we can see that parameters from both the FSSN-MM and the MSNBurr-MM reached convergence fast. The steady state for the historical mean plotted in Figure 6 was reached before 100 iterations.

Figure 11.
Historically generated the Nenomimo parameter for sample MRI images.
6. Conclusions
In this paper, we presented an improved method for image segmentation, namely the neo-normal mixture model (Nenomimo). The parameter estimation of the Nenomimo employs the Bayesian method coupled with an MCMC framework via Gibbs sampling. The algorithm ran well when using a computer with processor Intel Core i7, 8GB RAM, 256GB SSD, without GPU and VRAM, and it reached convergence quickly. The proposed method successfully overcame the limitation of mixture models based on the normal distribution. The Nenomimo gave a better performance than the GMM and the GGMM on both simulated and real datasets. For segmenting MRI brain tumor images, the Nenomimo showed powerful results, with the value of the misclassification ratio being less than 3%.
In the present work, segmentation results for MRI brain tumors using the Nenomimo still had a little noise, which was identified as the ROI. Therefore, for future research, it is recommended to continue to develop the Nenomimo model that considers pixel spatial dependencies for image segmentation.
Author Contributions
A.A.P., N.I., K.F., S.W.P., I., and W.F. understood and designed the research; A.A.P. collected the data, analyzed the data, and drafted the paper. All authors critically read and revised the draft and approved the final paper. All authors have read and agreed to the published version of the manuscript.
Funding
The authors are grateful to the Directorate for Research and Community Service (DRPM) Ministry of Research, Technology, and Higher Education Indonesia, which supports this research under PT research grant no. 1311/PKS/ITS/2020. This research is also partially funded by the Indonesian Ministry of Research, Technology, and Higher Education under World Class University (WCU) Program managed by Institut Teknologi Bandung.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Joint Posterior Density for Nenomimo
Assuming that each parameter in the Nenomimo, and , is independent (where , , ), then is the pixels in the MRI image. Therefore, the joint prior density for each and is given by:
Via the Bayes theorem, the joint posterior density of the Nenomimo is:
Substituting the joint density for each prior in MSNBurr-MM, we then obtain:
Since:
We then get the following in detail.
- (a)
- The prior density for is:where and are the mean and variance from the data, respectively; and .
- (b)
- The prior density for is given by:
- (c)
- The prior density for is:where , , , and
- (d)
- Prior density for .Assume that , with ; then, we can get the prior density as:where the normalized constant is a multinomial beta function that could be expressed as the following gamma function:
Appendix B. Some Direction for the Derivation of Full Conditional Posterior
Appendix B gives an example of a derivation to get the full conditional posterior for one of the MSNBurr-MM parameters. For example, we derived the full conditional posterior for parameter . The full conditional posterior for certain cluster is given by:
To simplify the derivation, we processed Equation (A2) in the form of the logarithm as follows:
Equation components that do not contain can be simplified into constants; therefore, Equation (A3) can be written as:
In the same way, a full conditional posterior for parameter and can be obtained.
References
- Global Cancer Observatory. Available online: http://gco.iarc.fr/today/data/factsheets/populations/360-indonesia-fact-sheets.pdf (accessed on 16 April 2020).
- Grün, B. Model-based Clustering. Model-based Clsutering. In Handbook of Mixture Analysis; CRC Press: Boca Raton, FL, USA, 2018; pp. 163–198. [Google Scholar]
- Bruse, J.L.; Zuluaga, M.A.; Khushnood, A.; McLeod, K.; Ntsinjana, H.N.; Hsia, T.; Sermesant, M.; Pennec, X.; Taylor, A.M.; Schievano, S. Detecting Clinically Meaningful Shape Clusters in Medical Image Data: Metrics Analysis for Hierarchical Clustering Applied to Healthy and Pathological Aortic Arches. IEEE Trans. Biomed. Eng. 2017, 64, 2373–2383. [Google Scholar] [CrossRef] [PubMed]
- Pestunov, I.A.; Rylov, S.A.; Berikov, V.B. Hierarchical Clustering Algorithms for Segmentation of Multispectral Images. Optoelectron. Instrum. Data Process. 2015, 51, 329–338. [Google Scholar] [CrossRef]
- Rohith, J.; Ramesh, H. Colour Based Segmentation of a Landsat Image Using K-Means Clustering Algorithm. J. Imag. Process. Pattern Recogn. Progress 2017, 4, 31–38. [Google Scholar]
- Muruganandham, S.K.; Sobya, D.; Nallusamy, S.; Mandal, D.K.; Chakraborty, P.S. Study on Leaf Segmentation using K-Means and K-Medoid Clustering Algorithm for Identification of Disease. Indian J. Public Health Res. Dev. 2018, 9, 289–293. [Google Scholar] [CrossRef]
- Huang, H.; Meng, F.; Zhou, S.; Jiang, F.; Manogaran, G. Brain Image Segmentation based on FCM Clustering Algorithm and Rough Set. IEEE Access 2019, 7, 12386–12396. [Google Scholar] [CrossRef]
- Oh, M.S.; Raftery, A.E. Model-Based Clustering with Dissimilarities: A Bayesian Approach. J. Comput. Graph. Stat. 2007, 16, 559–585. [Google Scholar] [CrossRef]
- Greve, B.; Pigeot, I.; Huybrechts, I.; Pala, V.; Börnhorst, C.A. Comparison of Heuristic and Model-based Clustering Methods for Dietary Pattern Analysis. Public Health Nutr. 2016, 19, 255–264. [Google Scholar] [CrossRef] [PubMed]
- Rasmussen, C.E. The Infinite Gaussian mixture model. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2000; pp. 554–560. [Google Scholar]
- Ji, Z.; Huang, Y.; Sun, Q.; Cao, G.A. Spatially Constrained Generative Asymmetric Gaussian mixture model for Image Segmentation. J. Vis. Commun. Image Represent. 2016, 40, 600–626. [Google Scholar] [CrossRef]
- Zhu, H.; Pan, S.; Xie, Q. Image Segmentation by Student’s-t Mixture Models Based on Markov Random Field and Weighted Mean Template. Int. J. Signal. Process. Imag. Process. Pattern Recogn. 2016, 9, 313–322. [Google Scholar]
- Franczak, B.C.; Browne, P.; McNicholas, P. Mixtures of Shifted Asymmetric Laplace Distribution. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1149–1157. [Google Scholar] [CrossRef] [PubMed]
- Deledalle, C.A.; Parameswaran, S.; Nguyen, T.Q. Image denoising with generalized Gaussian mixture model patch priors. SIAM J. Imag. Sci. 2018, 11, 2568–2609. [Google Scholar] [CrossRef]
- Fernandez, C.; Steel, M.F.J. On Bayesian Modelling of Fat Tails and Skewness. J. Am. Stat. Assoc. 1998, 93, 359–371. [Google Scholar] [CrossRef]
- Iriawan, N. Computationally Intensive Approaches to Inference in Neo-Normal Linear Models. Ph.D. Thesis, Curtin University of Technology, Perth, Australia, 2000. [Google Scholar]
- Iriawan, N.; Pravitasari, A.A.; Fithriasari, K.; Irhamah; Purnami, S.W.; Ferriastuti, W. Comparative Study of Brain Tumor Segmentation using Different Segmentation Techniques in Handling Noise. In Proceedings of the 2018 International Conference on Computer Engineering, Network and Intelligent Multimedia (CENIM), Surabaya, Indonesia, 26–27 November 2018; IEEE: Surabaya, Indonesia, 2018; pp. 289–293. [Google Scholar]
- Choir, A.S.; Iriawan, N.; Ulama, B.; Dokhi, M. MSEpBurr Distribution: Properties and Parameter Estimation. Pakistan J. Stat. Oper. Res. 2019, 15, 179–193. [Google Scholar] [CrossRef]
- Box, G.P.E.; Tiao, G.C. Bayesian Inference in Statistical Analysis, 1st ed.; Addison Wesley Publishing Company: Reading, UK, 1973. [Google Scholar]
- Azzalini, A.A. Class of Distribution which Includes the Normal Ones. Scand. J. Stat. 1985, 12, 171–178. [Google Scholar]
- Anderson, E.; Nguyen, H. When can we improve on sample average approximation for stochastic optimization? Oper. Res. Lett. 2020, 48, 566–572. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Prasetyo, R.B.; Kuswanto, H.; Iriawan, N.; Ulama, B.S.S. Binomial Regression Models with a Flexible Generalized Logit Link Function. Symmetry 2020, 12, 221. [Google Scholar] [CrossRef]
- Pravitasari, A.A.; Iriawan, N.; Safa, M.A.I.; Irhamah; Fithriasari, K.; Purnami, S.W.; Ferriastuti, W. MRI-Based Brain Tumor Segmentation using Modified Stable Student’s t from Burr Mixture Model with Bayesian Approach. Malays. J. Math. Sci. 2019, 13, 297–310. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).