Enhancing Bitcoin Price Fluctuation Prediction Using Attentive LSTM and Embedding Network
Abstract
1. Introduction
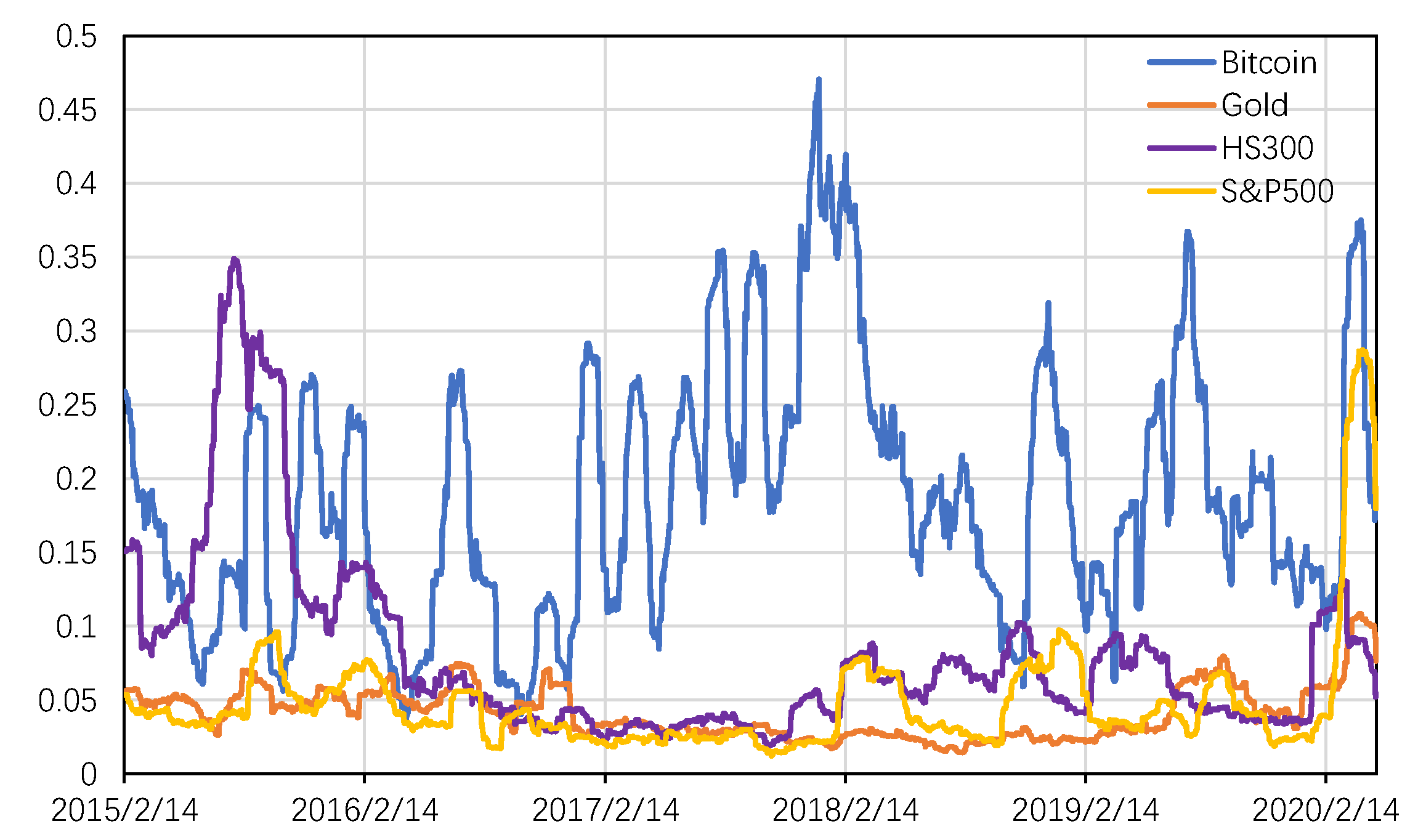
1.1. Motivation
1.2. Contributions
- In this paper, we investigate the Bitcoin price fluctuation prediction problem. Meanwhile, we give a clear problem definition and introduce three kinds of features. This work can enrich the research in Bitcoin and provide investors with more tools for investment analyses.
- A novel model namely ALEN is proposed to solve the fluctuation prediction of Bitcoin price. In particular, an attentive LSTM network is used to capture the time-dependency features of Bitcoin price and an embedding network is proposed to capture the hidden representations from related cryptocurrencies.
- We empirically demonstrate the effectiveness of our ALEN on the real-world cryptocurrency market. Moreover, ALEN achieves superior state-of-the-art performance among all baselines.
2. Related Work
2.1. Bitcoin
2.2. Bitcoin Price
3. Problem Definition and Features Designation
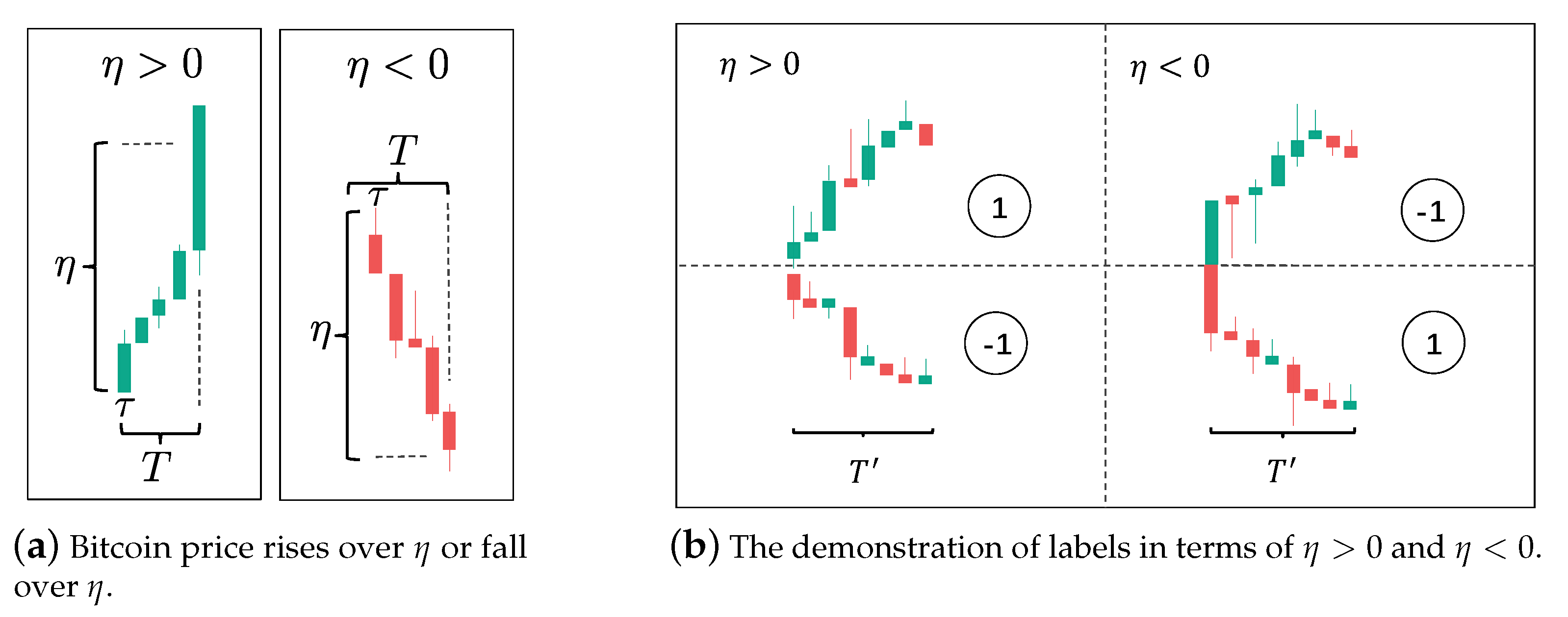
3.1. Problem Definition
3.2. Features for Bitcoin Price Fluctuation Prediction
3.2.1. Basic Features
3.2.2. Technical Trading Indicators
3.2.3. Denoising Autoencoders Features
| Algorithm 1 DAEs |
| Require: |
| time series . |
| encoder parameters . |
| decoder parameters . |
| Ensure: |
| hidden features . |
| for each t in {} do |
| adds tiny noise to , obtain ; |
| Encoder: ; |
| Decoder: ; |
| Training: ; |
| end for |
| return ; |
4. Our Approach
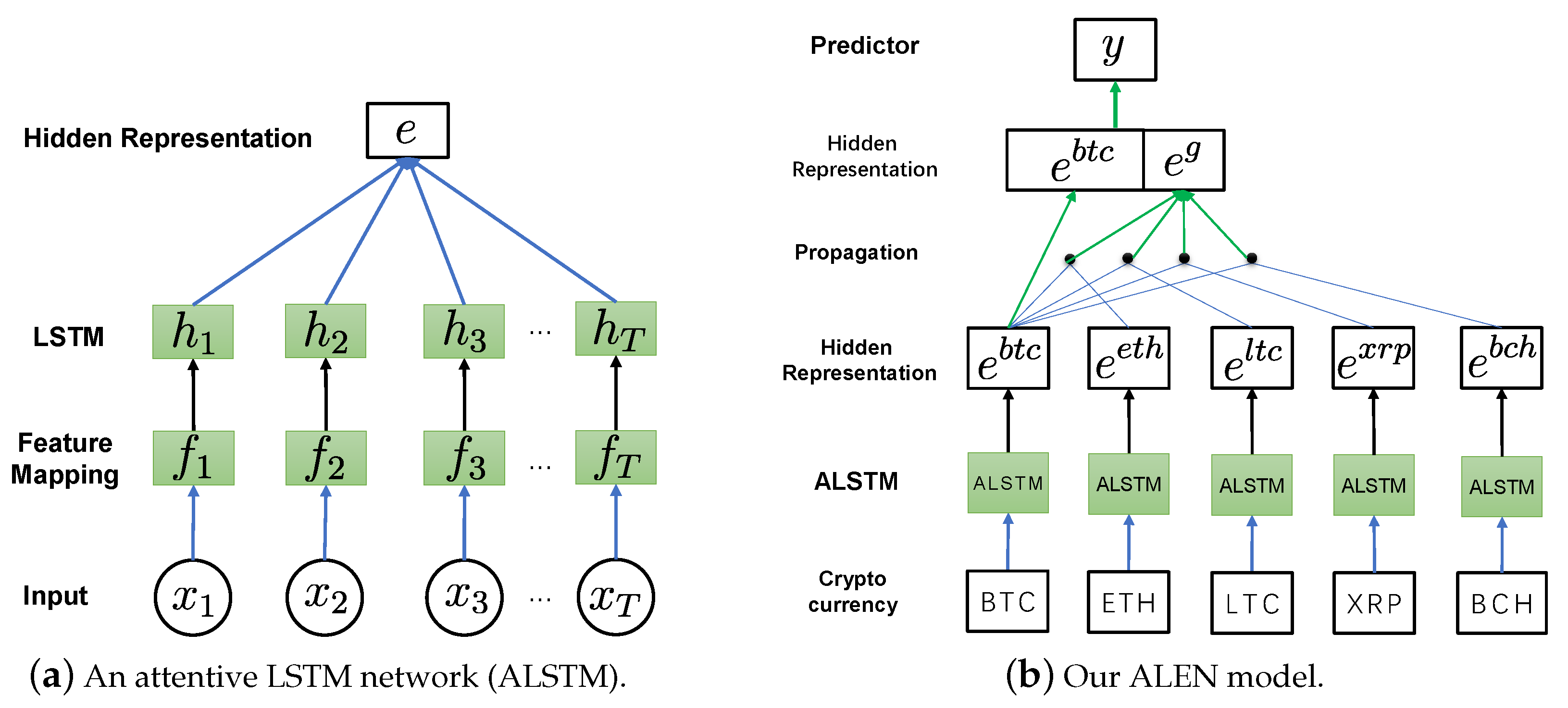
4.1. Attentive LSTM
4.2. Embedding Network
4.3. Prediction Layer
5. Experiments
5.1. Datasets
5.2. Experimental Settings
5.3. Baselines
5.4. Training Protocol
5.5. Experimental Results
- The accuracy of ATrue predictor is related to the percentage of positive samples. The RAND predictor achieves accuracy around 50/50 percent as we expect. Meanwhile, classic machine learning classifiers perform better than random guess. Meanwhile, LSTM and GRU models [28] perform better than traditional machine learning methods, such as RF and SVM, since they can use the time dependency features well. However, XGB outperforms LSTM and GRU, the main reason may be the sufficient use of our designed features. It is not surprising that ALSTM outperforms LSTM since ALSTM can capture the importance of each timestamps; this observation was shown in [7,8]. Notably, ALEN achieves the best result compared to all baselines with accuracy, precision, recall, and F1 score except ATrue. ALEN outperforms the best baseline ALSTM 6.0% on accuracy and 7.0% on F1 score except ATrue.
- It is clear that the technical trading indicators are better than the features generated by DAEs when comparing the results of ALEN with those of ALEN . The reason may own to the fact that the technical trading indicators can capture the inherent regular of the specific time series. Moreover, all three kinds of features can contribute to the results since ALEN achieves the best performance compared to ALEN and ALEN .
- It demonstrates that incorporation with other related cryptocurrencies can contribute to the prediction of Bitcoin price fluctuation prediction problem when compared ALUE with ALSTM. It also demonstrates the effectiveness of the embedding network when compared ALEN with ALUE . ALEN uses network embedding method but ALUE uses uniform embedding method. In particular, ALEN outperforms ALUE 3.3% on accuracy and 3.2% on F1 score.
5.6. Further Analyses
- RQ1: What is the difference between fluctuation prediction problem and traditional price movement prediction problem?
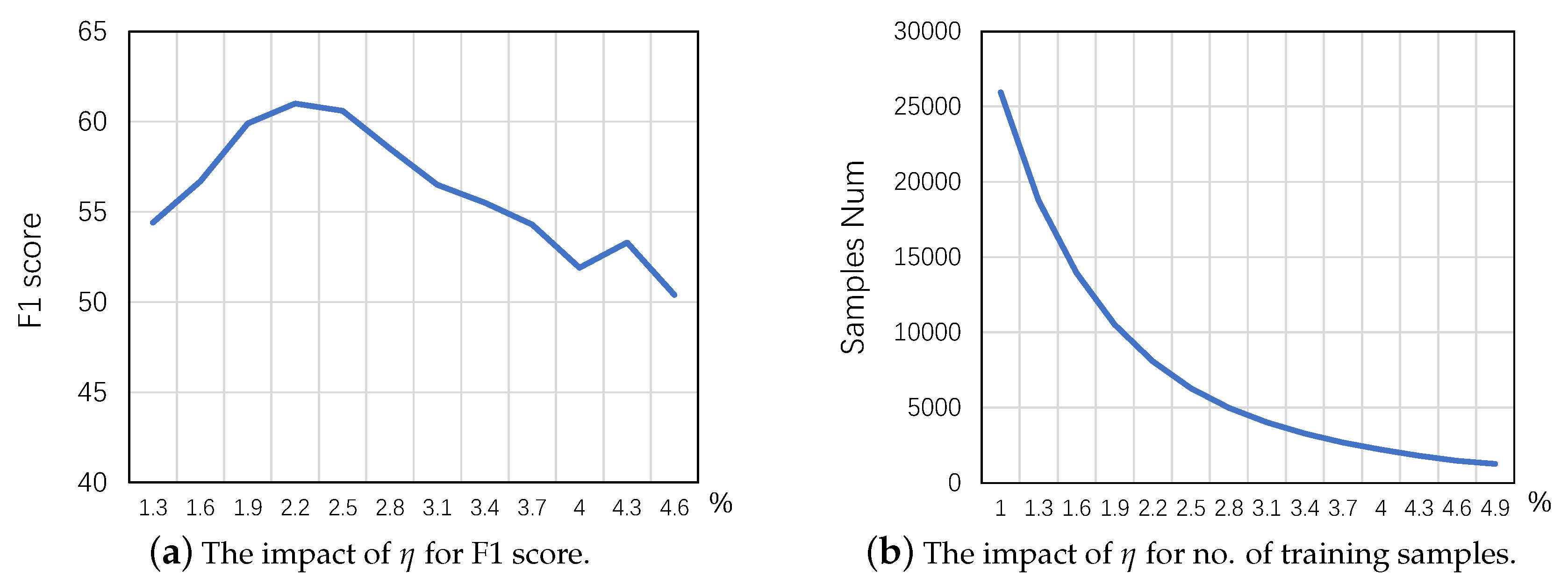
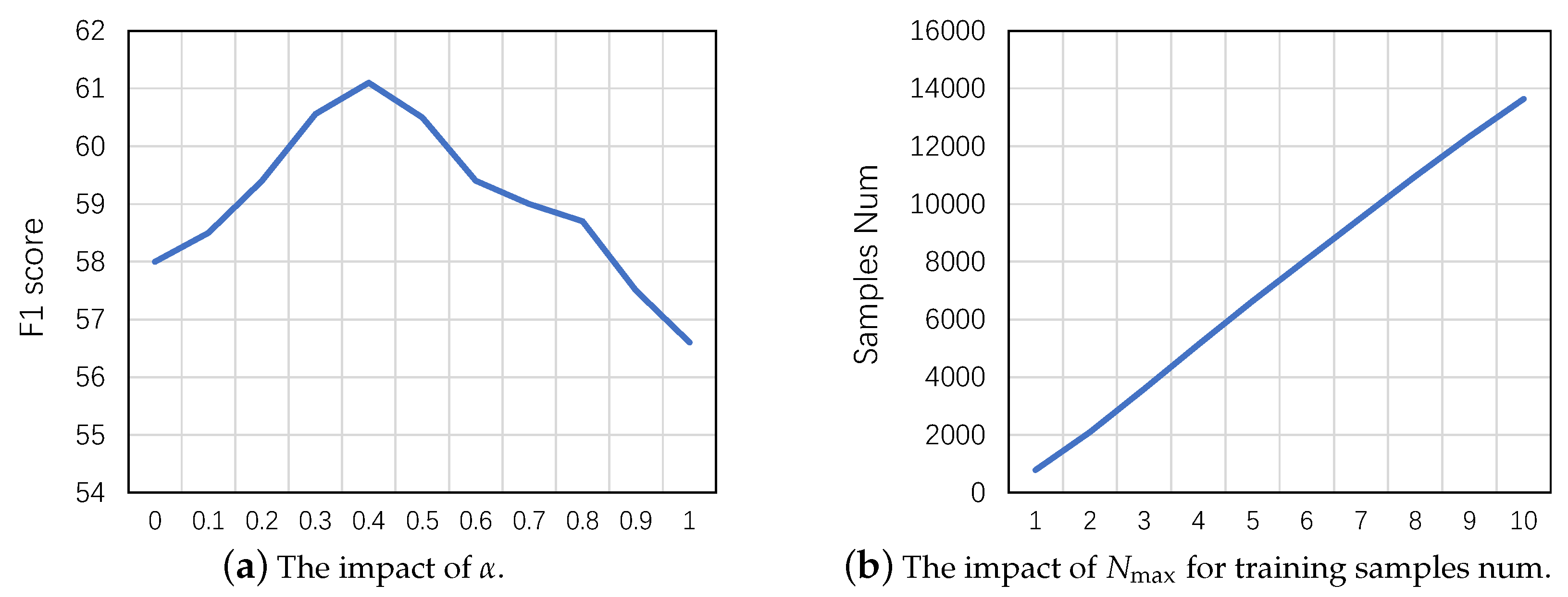
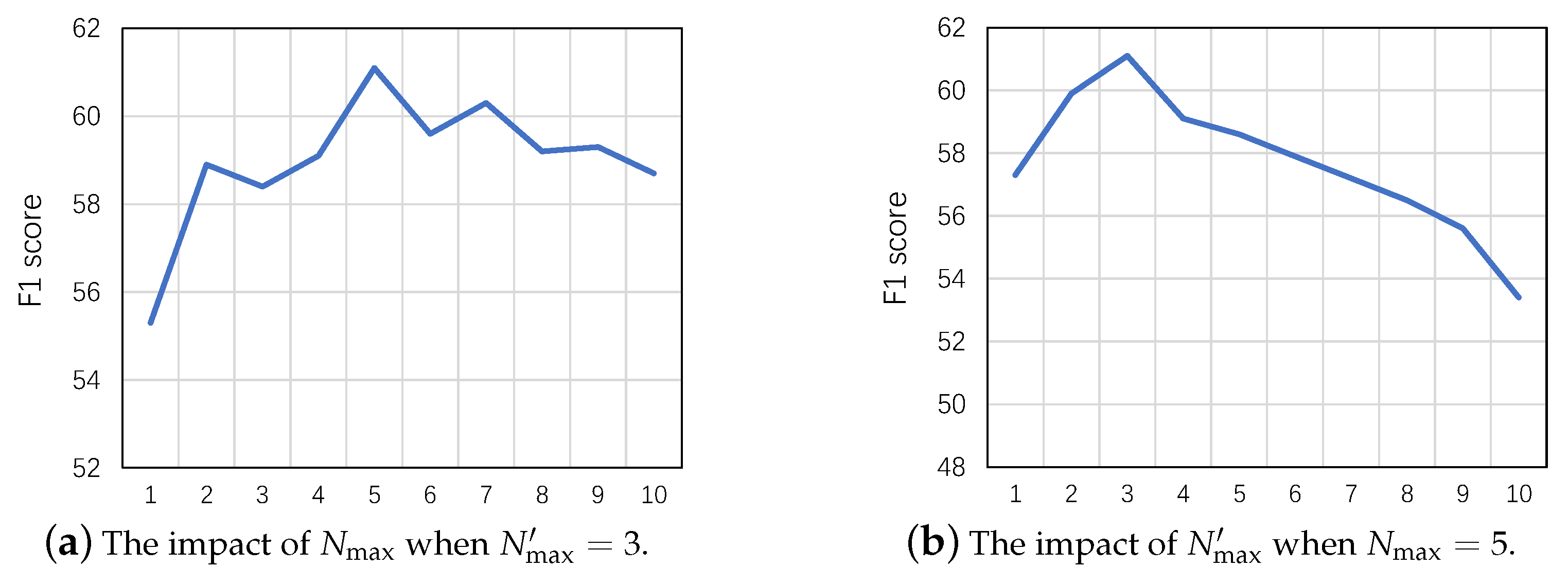
- RQ2: Are the parameters in fluctuation prediction problem sensitive?
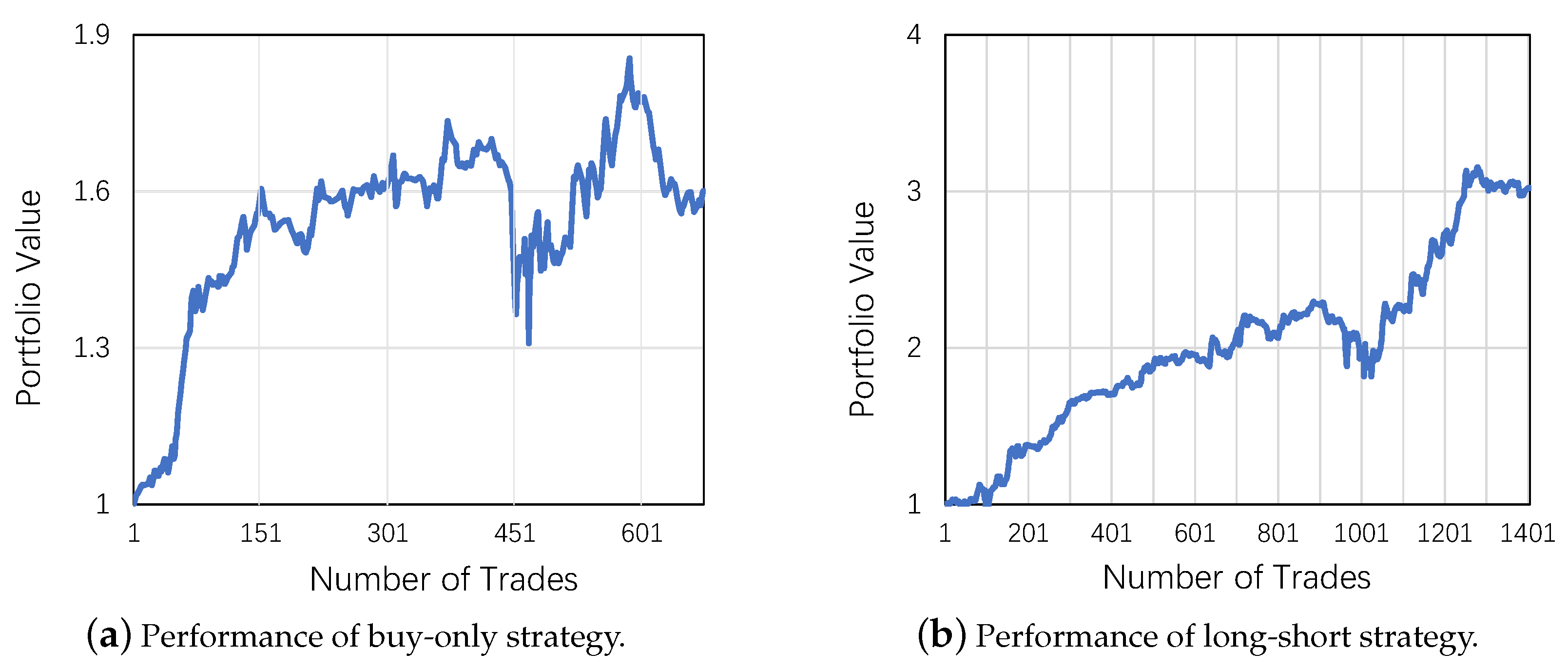
- RQ3: How our research could be used by practitioners in the field?
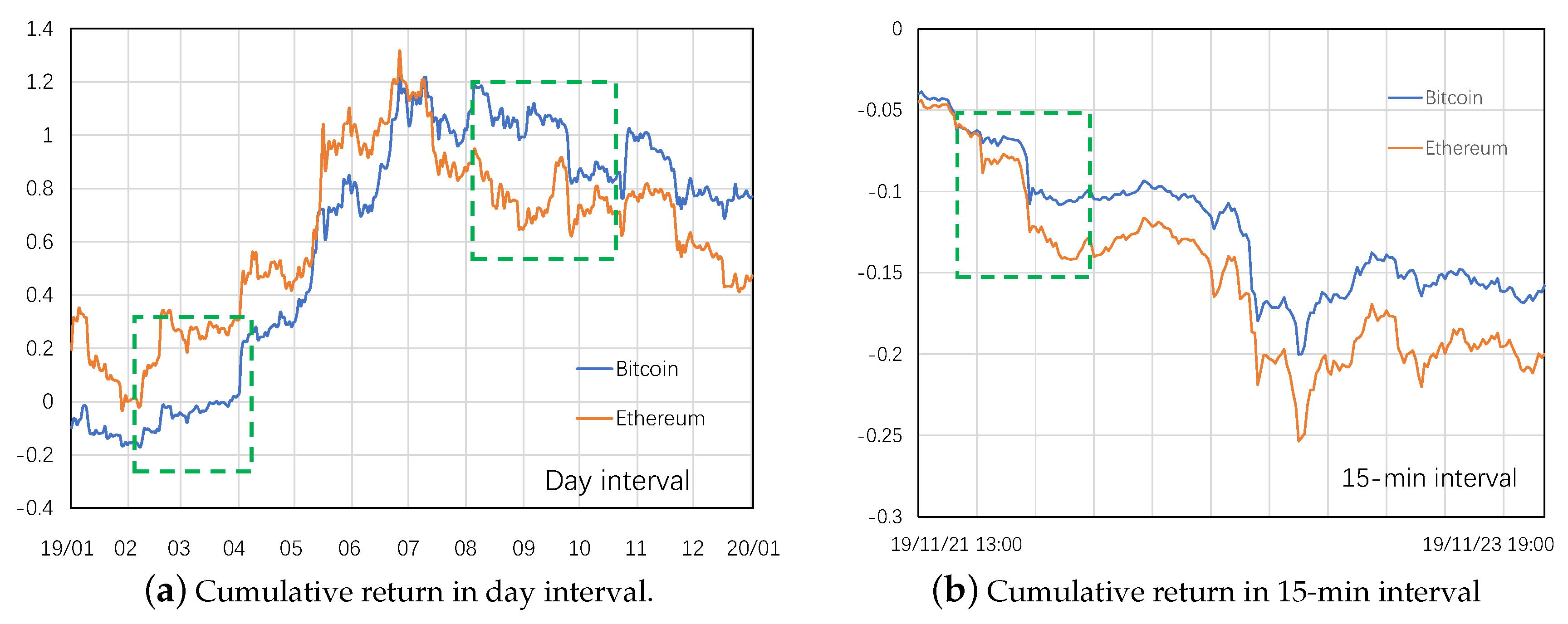
5.6.1. Study of RQ1
5.6.2. Study of RQ2
5.6.3. Study of RQ3
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nakamoto, S. Bitcoin: A Peer-To-Peer Electronic Cash System. Bitcoin. 2008. Available online: https://git.dhimmel.com/bitcoin-whitepaper/ (accessed on 15 March 2018).
- Corbet, S.; Lucey, B.; Urquhart, A.; Yarovaya, L. Cryptocurrencies as a financial asset: A systematic analysis. Int. Rev. Financ. Anal. 2019, 62, 182–199. [Google Scholar] [CrossRef]
- Zheng, Z.; Xie, S.; Dai, H.; Chen, X.; Wang, H. An overview of blockchain technology: Architecture, consensus, and future trends. In Proceedings of the 2017 IEEE International Congress on Big Data (BigData Congress), Honolulu, HI, USA, 25–30 June 2017; pp. 557–564. [Google Scholar]
- Zheng, Z.; Xie, S.; Dai, H.N.; Chen, X.; Wang, H. Blockchain challenges and opportunities: A survey. Int. J. Web Grid Serv. 2018, 14, 352–375. [Google Scholar] [CrossRef]
- Chen, W.; Wu, J.; Zheng, Z.; Chen, C.; Zhou, Y. Market Manipulation of Bitcoin: Evidence from Mining the Mt. Gox Transaction Network. In Proceedings of the IEEE INFOCOM 2019-IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019; pp. 964–972. [Google Scholar]
- Wang, L.X. Dynamical models of stock prices based on technical trading rules part I: The models. IEEE Trans. Fuzzy Syst. 2014, 23, 787–801. [Google Scholar] [CrossRef]
- Qin, Y.; Song, D.; Cheng, H.; Cheng, W.; Jiang, G.; Cottrell, G.W. A dual-stage attention-based recurrent neural network for time series prediction. In Proceedings of the 26th International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 2627–2633. [Google Scholar]
- Feng, F.; Chen, H.; He, X.; Ding, J.; Sun, M.; Chua, T.S. Enhancing stock movement prediction with adversarial training. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; AAAI Press: Menlo Park, CA, USA, 2019; pp. 5843–5849. [Google Scholar]
- Feng, F.; He, X.; Wang, X.; Luo, C.; Liu, Y.; Chua, T.S. Temporal relational ranking for stock prediction. ACM Trans. Inf. Syst. (TOIS) 2019, 37, 1–30. [Google Scholar] [CrossRef]
- Zheng, Z.; Xie, S.; Dai, H.N.; Chen, W.; Chen, X.; Weng, J.; Imran, M. An Overview on Smart Contracts: Challenges, Advances and Platforms. Future Gener. Comput. Syst. 2020, 105, 475–491. [Google Scholar] [CrossRef]
- Xie, S.; Zheng, Z.; Chen, W.; Wu, J.; Dai, H.N.; Imran, M. Blockchain for cloud exchange: A survey. Comput. Electr. Eng. 2020, 81, 106526. [Google Scholar] [CrossRef]
- Dyhrberg, A.H. Bitcoin, gold and the dollar—A GARCH volatility analysis. Financ. Res. Lett. 2016, 16, 85–92. [Google Scholar] [CrossRef]
- Katsiampa, P. Volatility estimation for Bitcoin: A comparison of GARCH models. Econ. Lett. 2017, 158, 3–6. [Google Scholar] [CrossRef]
- Baur, D.G.; Dimpfl, T.; Kuck, K. Bitcoin, gold and the US dollar—A replication and extension. Financ. Res. Lett. 2018, 25, 103–110. [Google Scholar] [CrossRef]
- Chu, J.; Chan, S.; Nadarajah, S.; Osterrieder, J. GARCH modelling of cryptocurrencies. J. Risk Financ. Manag. 2017, 10, 17. [Google Scholar] [CrossRef]
- Eyal, I.; Sirer, E.G. Majority is not enough: Bitcoin mining is vulnerable. In Proceedings of the International Conference on Financial Cryptography and Data Security, Christ Church, Barbados, 3–7 March 2014; pp. 436–454. [Google Scholar]
- Gandal, N.; Hamrick, J.; Moore, T.; Oberman, T. Price manipulation in the Bitcoin ecosystem. J. Monet. Econ. 2018, 95, 86–96. [Google Scholar] [CrossRef]
- Cheah, E.T.; Fry, J. Speculative bubbles in Bitcoin markets? An empirical investigation into the fundamental value of Bitcoin. Econ. Lett. 2015, 130, 32–36. [Google Scholar] [CrossRef]
- Chen, Z.; Li, C.; Sun, W. Bitcoin price prediction using machine learning: An approach to sample dimension engineering. J. Comput. Appl. Math. 2020, 365, 112395. [Google Scholar] [CrossRef]
- Alessandretti, L.; ElBahrawy, A.; Aiello, L.M.; Baronchelli, A. Anticipating cryptocurrency prices using machine learning. Complexity 2018, 2018, 8983590. [Google Scholar] [CrossRef]
- Jain, A.; Tripathi, S.; DharDwivedi, H.; Saxena, P. Forecasting Price of Cryptocurrencies Using Tweets Sentiment Analysis. In Proceedings of the 2018 Eleventh International Conference on Contemporary Computing (IC3), Noida, India, 2–4 August 2018; pp. 1–7. [Google Scholar]
- Kumar, D.; Rath, S. Predicting the Trends of Price for Ethereum Using Deep Learning Techniques. In Artificial Intelligence and Evolutionary Computations in Engineering Systems; Springer: Berlin/Heidelberg, Germany, 2020; pp. 103–114. [Google Scholar]
- Livieris, I.E.; Pintelas, E.; Stavroyiannis, S.; Pintelas, P. Ensemble Deep Learning Models for Forecasting Cryptocurrency Time-Series. Algorithms 2020, 13, 121. [Google Scholar] [CrossRef]
- Ji, S.; Kim, J.; Im, H. A comparative study of Bitcoin price prediction using deep learning. Mathematics 2019, 7, 898. [Google Scholar] [CrossRef]
- Huisu, J.; Lee, J.; Ko, H.; Lee, W. Predicting bitcoin prices by using rolling window lstm model. In Proceedings of the KDD Data Science in Fintech Workshop, London, UK, 19–23 August 2018. [Google Scholar]
- McNally, S.; Roche, J.; Caton, S. Predicting the price of bitcoin using machine learning. In Proceedings of the 2018 26th Euromicro International Conference on Parallel, Distributed and Network-based Processing (PDP), Cambridge, UK, 21–23 March 2018; pp. 339–343. [Google Scholar]
- Wu, C.H.; Lu, C.C.; Ma, Y.F.; Lu, R.S. A new forecasting framework for bitcoin price with LSTM. In Proceedings of the 2018 IEEE International Conference on Data Mining Workshops (ICDMW), Singapore, 17–20 November 2018; pp. 168–175. [Google Scholar]
- Dutta, A.; Kumar, S.; Basu, M. A Gated Recurrent Unit Approach to Bitcoin Price Prediction. J. Risk Financ. Manag. 2020, 13, 23. [Google Scholar] [CrossRef]
- Greaves, A.; Au, B. Using the Bitcoin Transaction Graph to Predict the Price of Bitcoin; Stanford University: Stanford, CA, USA, 2015. [Google Scholar]
- Kurbucz, M.T. Predicting the price of Bitcoin by the most frequent edges of its transaction network. Econ. Lett. 2019, 184, 108655. [Google Scholar] [CrossRef]
- Jang, H.; Lee, J. An empirical study on modeling and prediction of bitcoin prices with bayesian neural networks based on blockchain information. IEEE Access 2017, 6, 5427–5437. [Google Scholar] [CrossRef]
- Achelis, S.B. Technical Analysis from A to Z; McGraw Hill: New York, NY, USA, 2001. [Google Scholar]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.A. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Zheng, W.; Zheng, Z. Deep Robust Reinforcement Learning for Practical Algorithmic Trading. IEEE Access 2019, 7, 108014–108022. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Khaidem, L.; Saha, S.; Dey, S.R. Predicting the direction of stock market prices using random forest. arXiv 2016, arXiv:1605.00003. [Google Scholar]
- Huang, W.; Nakamori, Y.; Wang, S.Y. Forecasting stock market movement direction with support vector machine. Comput. Oper. Res. 2005, 32, 2513–2522. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
| Features | Features’ Dimension | Details |
|---|---|---|
| 4 | , , , | |
| 8 | ||
| 4 | ||
| 4 | short ∈ , long ∈ | |
| 10 | hidden representation |
| Models | Accuracy % | Precision % | Recall % | F1 % |
|---|---|---|---|---|
| ATrue | 51.00 | 51.00 | 1.0 | 67.55 |
| RAND | 49.11 | 50.03 | 49.48 | 49.75 |
| RF | 54.66 | 54.48 | 54.13 | 54.39 |
| SVM | 53.21 | 53.32 | 53.01 | 53.16 |
| XGB | 56.65 | 56.28 | 57.01 | 56.64 |
| LSTM | 55.19 | 55.16 | 55.44 | 55.30 |
| GRU | 55.10 | 55.06 | 55.31 | 55.18 |
| ALSTM | 57.58 | 57.14 | 57.02 | 57.07 |
| ALEN | 60.68 | 60.58 | 60.33 | 60.45 |
| ALEN | 60.46 | 60.17 | 60.31 | 60.23 |
| ALUE | 59.15 | 59.16 | 59.03 | 59.09 |
| ALEN | 61.15 | 61.10 | 60.93 | 61.01 |
| Problem | Accuracy % | Precision % | Recall % | F1 % |
|---|---|---|---|---|
| SMP1 | 52.34 | 52.16 | 52.31 | 52.23 |
| SMP | 54.34 | 54.44 | 54.22 | 54.33 |
| BFD | 61.15 | 61.10 | 60.93 | 61.01 |
| Interval | % | Accuracy % | Precision % | Recall % | F1 % |
|---|---|---|---|---|---|
| 1 min | 0.64 | 56.03 | 56.25 | 56.47 | 56.36 |
| 5 min | 1.4 | 59.15 | 60.15 | 58.01 | 59.06 |
| 15 min | 2.2 | 61.15 | 61.10 | 60.93 | 61.01 |
| 30 min | 2.5 | 59.86 | 59.04 | 59.99 | 59.51 |
| 1 h | 2.7 | 57.86 | 57.64 | 57.11 | 57.37 |
| 4 h | 2.9 | 57.75 | 57.24 | 58.24 | 57.73 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zheng, Z.; Dai, H.-N. Enhancing Bitcoin Price Fluctuation Prediction Using Attentive LSTM and Embedding Network. Appl. Sci. 2020, 10, 4872. https://doi.org/10.3390/app10144872
Li Y, Zheng Z, Dai H-N. Enhancing Bitcoin Price Fluctuation Prediction Using Attentive LSTM and Embedding Network. Applied Sciences. 2020; 10(14):4872. https://doi.org/10.3390/app10144872
Chicago/Turabian StyleLi, Yang, Zibin Zheng, and Hong-Ning Dai. 2020. "Enhancing Bitcoin Price Fluctuation Prediction Using Attentive LSTM and Embedding Network" Applied Sciences 10, no. 14: 4872. https://doi.org/10.3390/app10144872
APA StyleLi, Y., Zheng, Z., & Dai, H.-N. (2020). Enhancing Bitcoin Price Fluctuation Prediction Using Attentive LSTM and Embedding Network. Applied Sciences, 10(14), 4872. https://doi.org/10.3390/app10144872






