A Vibration Isolation System Using the Negative Stiffness Corrector Formed by Cam-Roller Mechanisms with Quadratic Polynomial Trajectory
Abstract
:1. Introduction
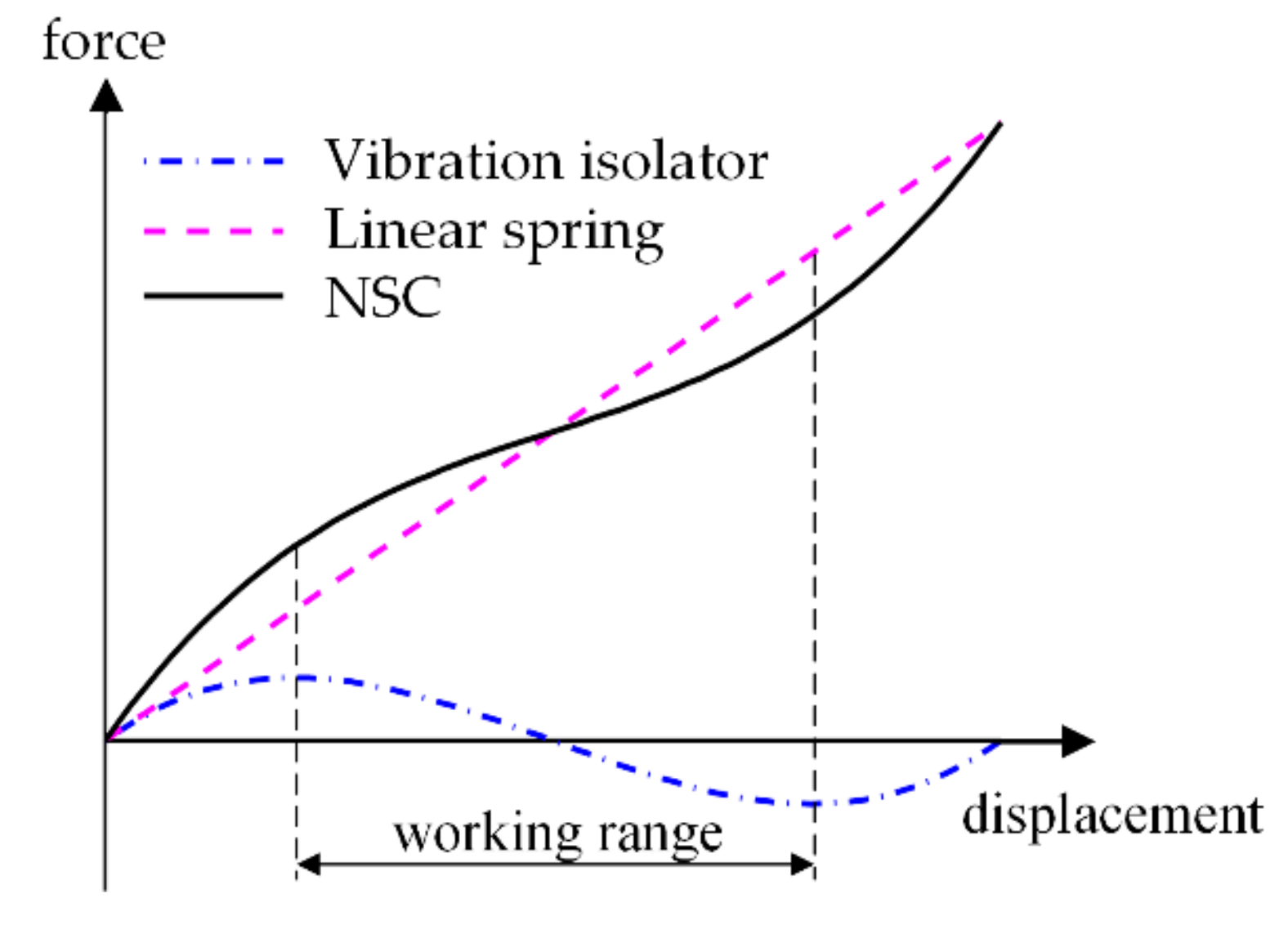
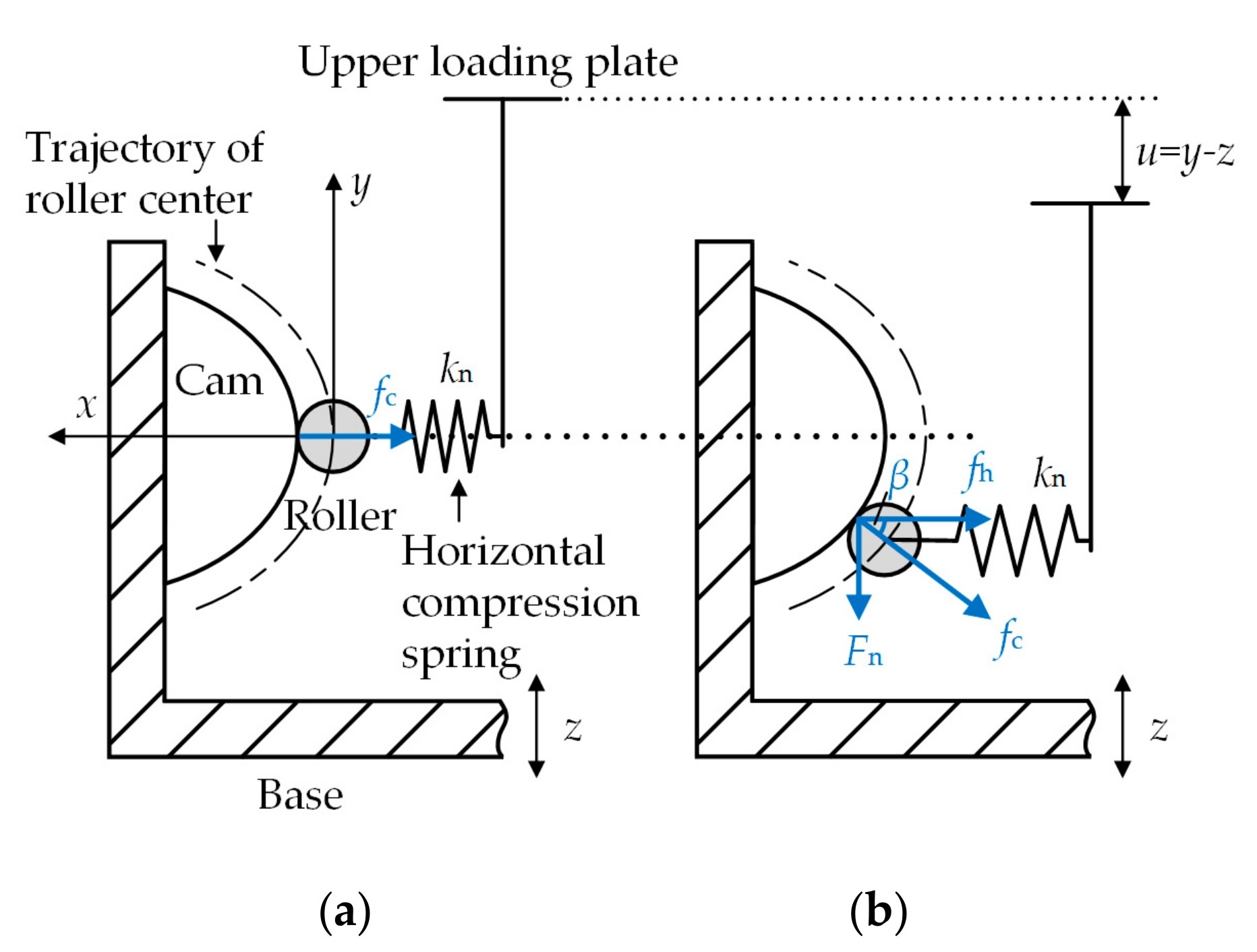
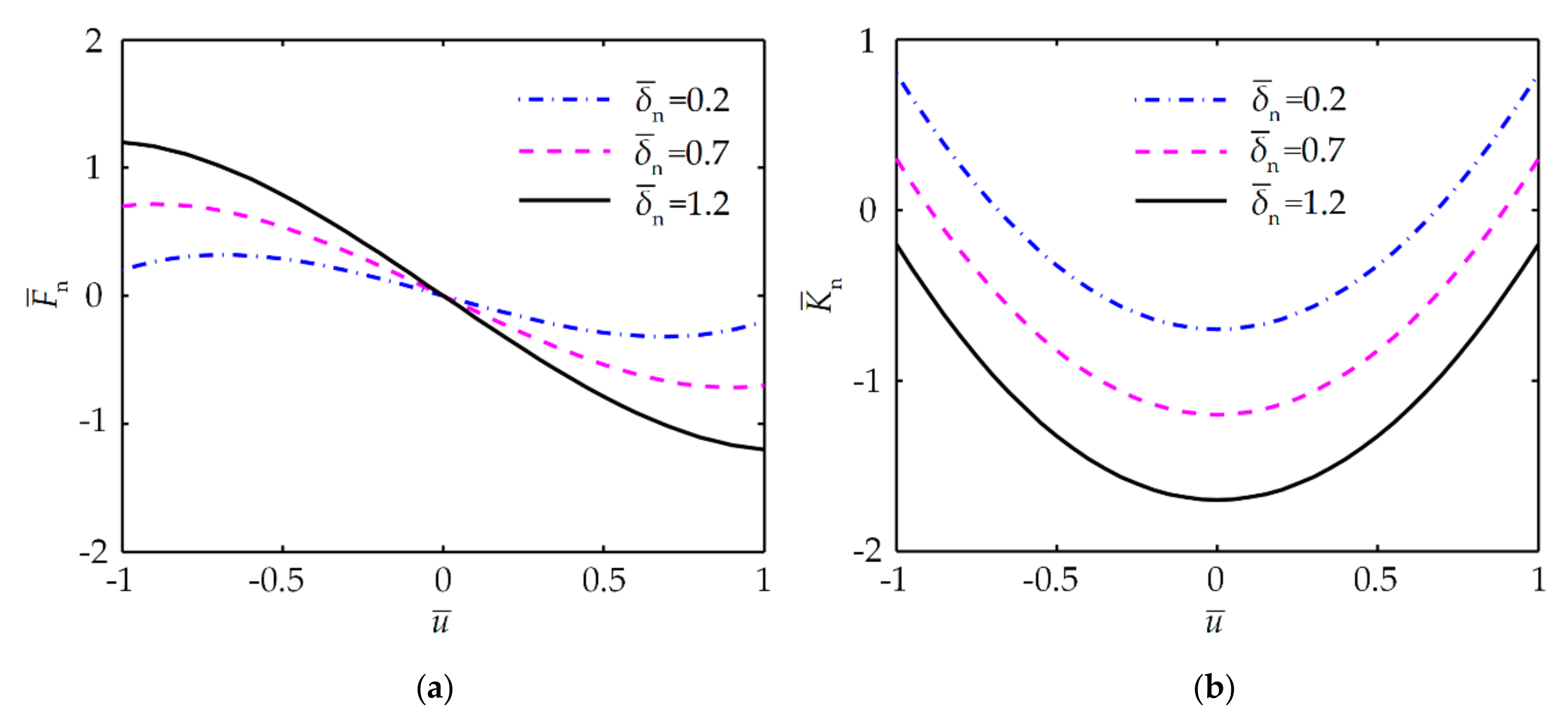
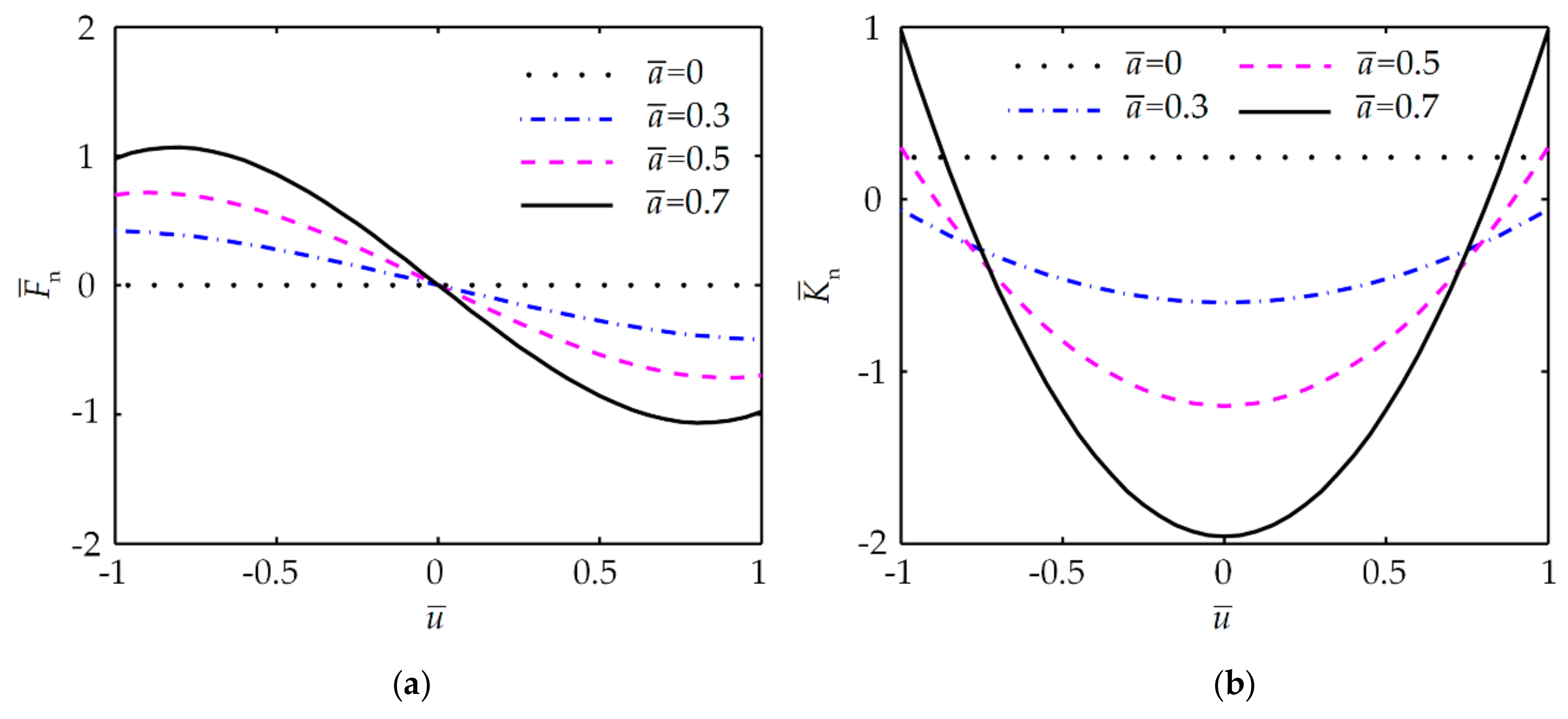
2. NSC Formed by CRMs with Quadratic Polynomial Trajectory
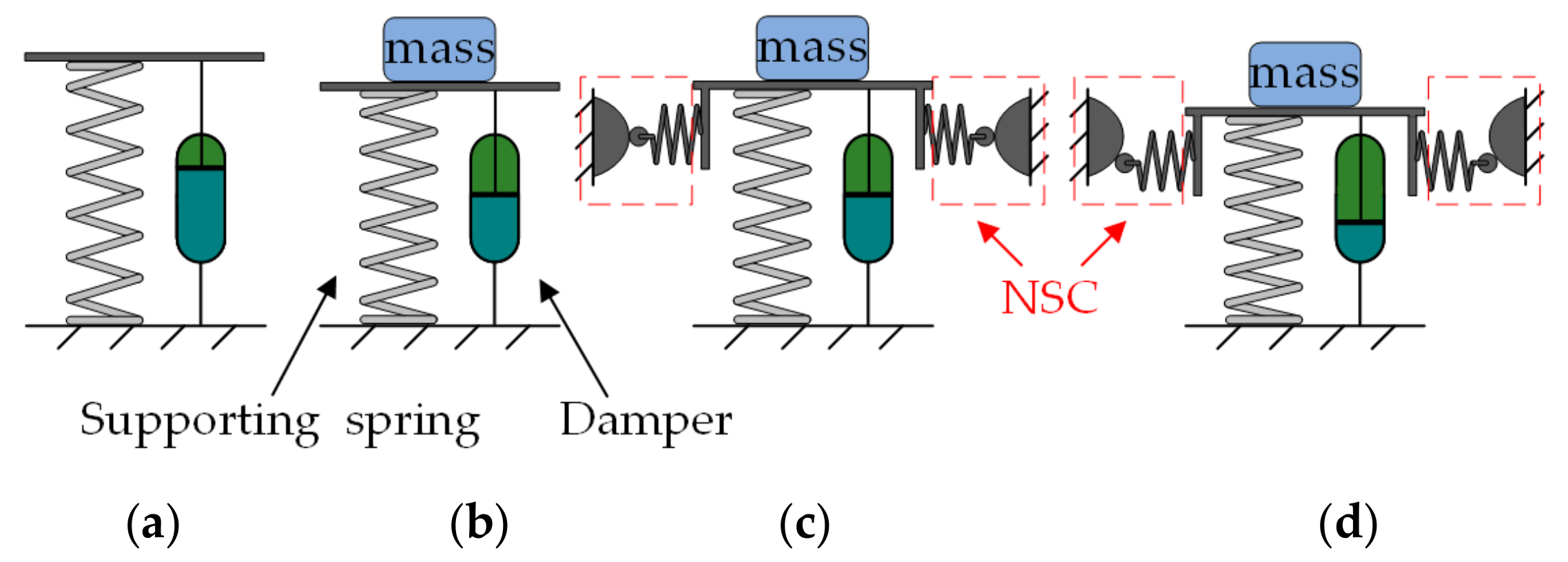
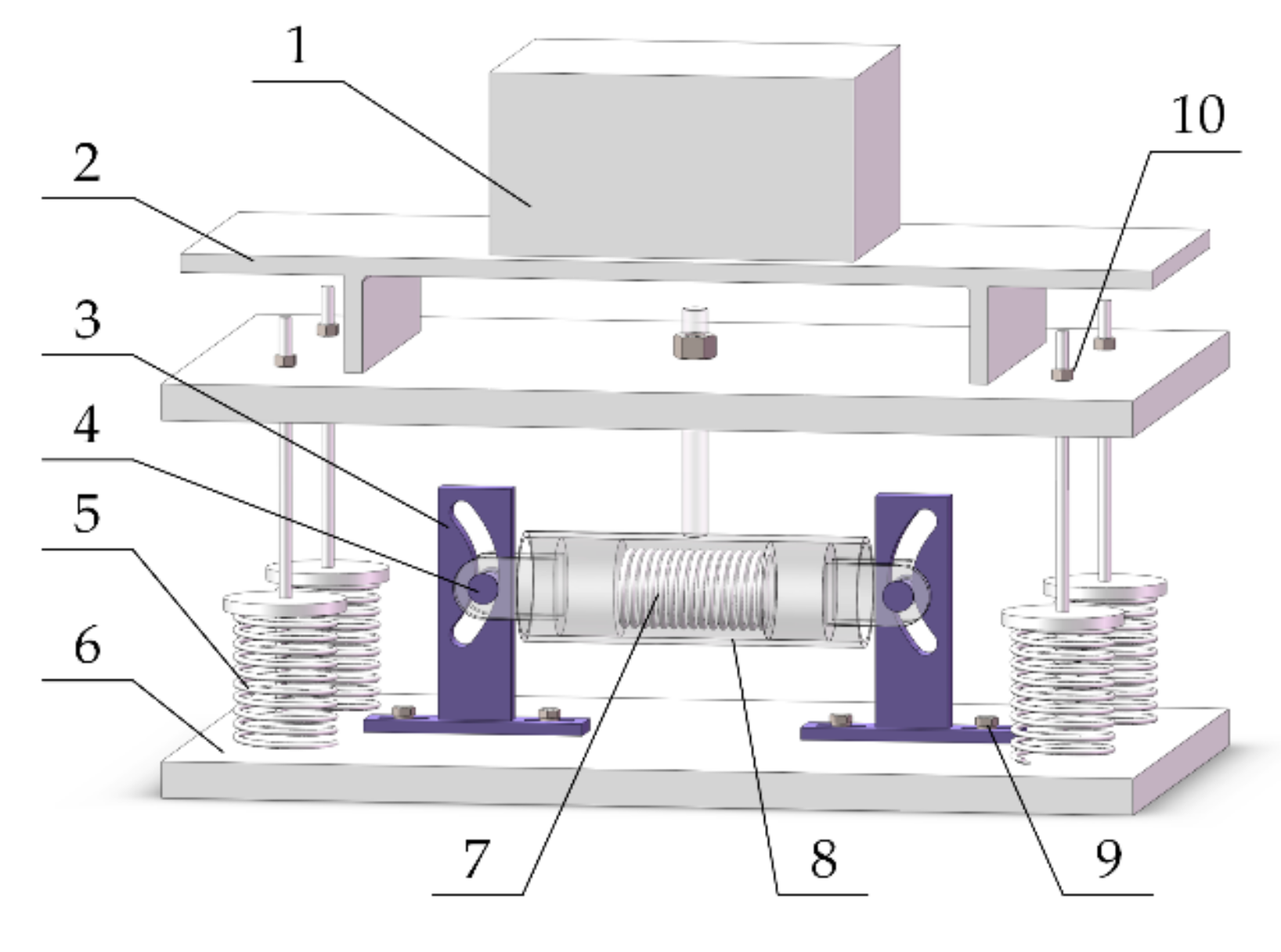
3. Nonlinear Vibration Isolator with Negative Stiffness Corrector
3.1. Modelling of Nonlinear Vibration Isolator
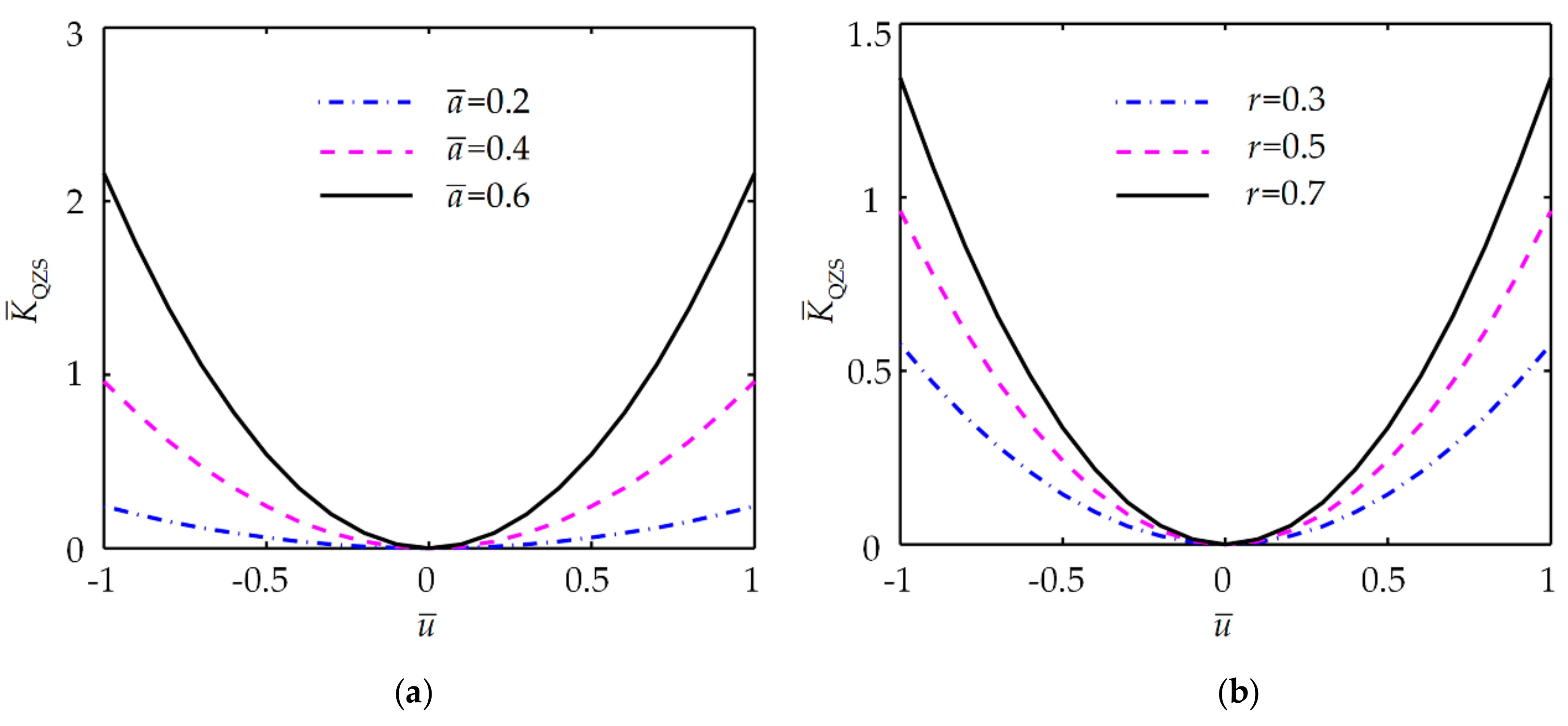
3.2. Condition for Quasi-Zero Stiffness
4. Dynamics and Isolation Performance of the Vibration Isolator
4.1. Dynamic Equation
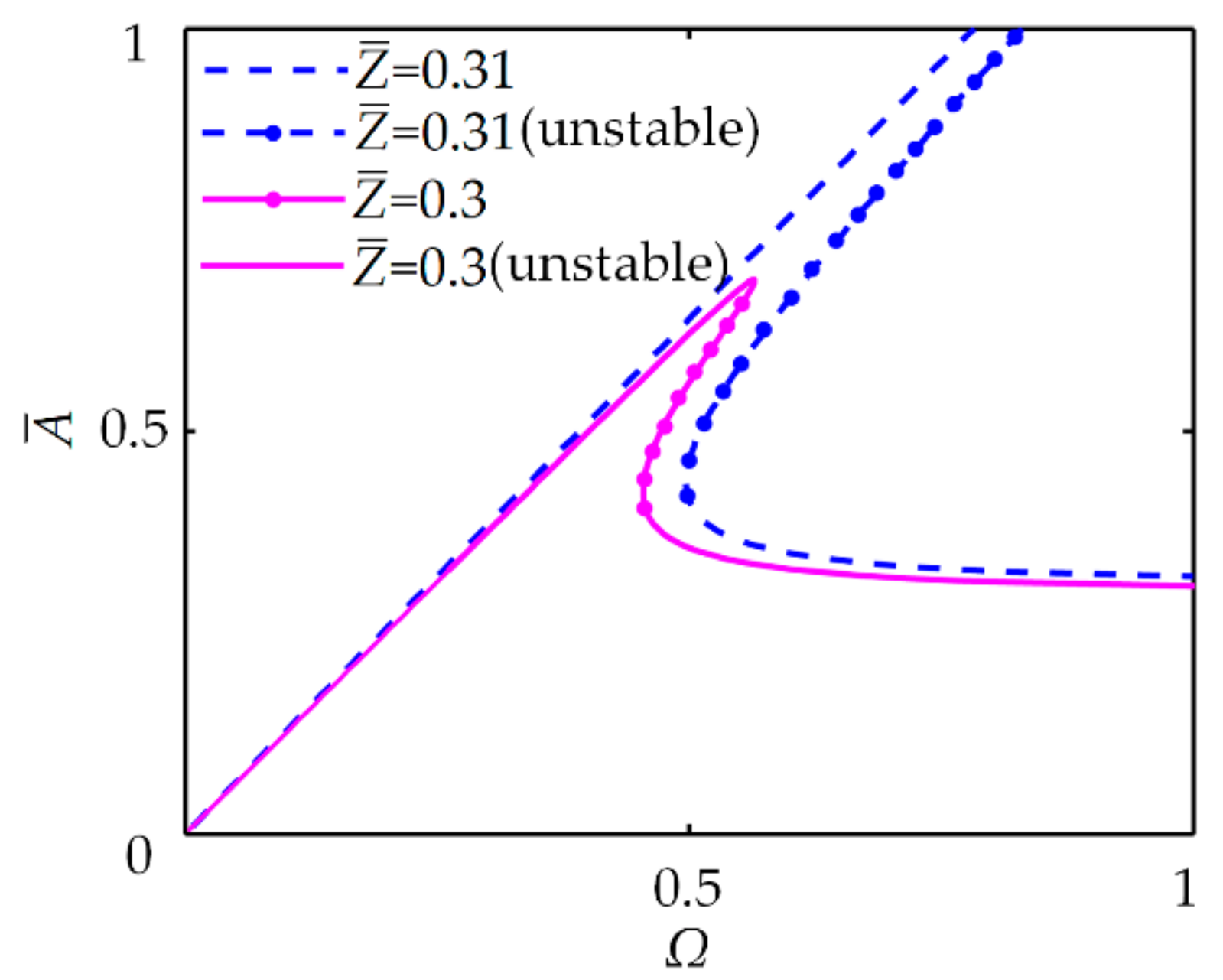
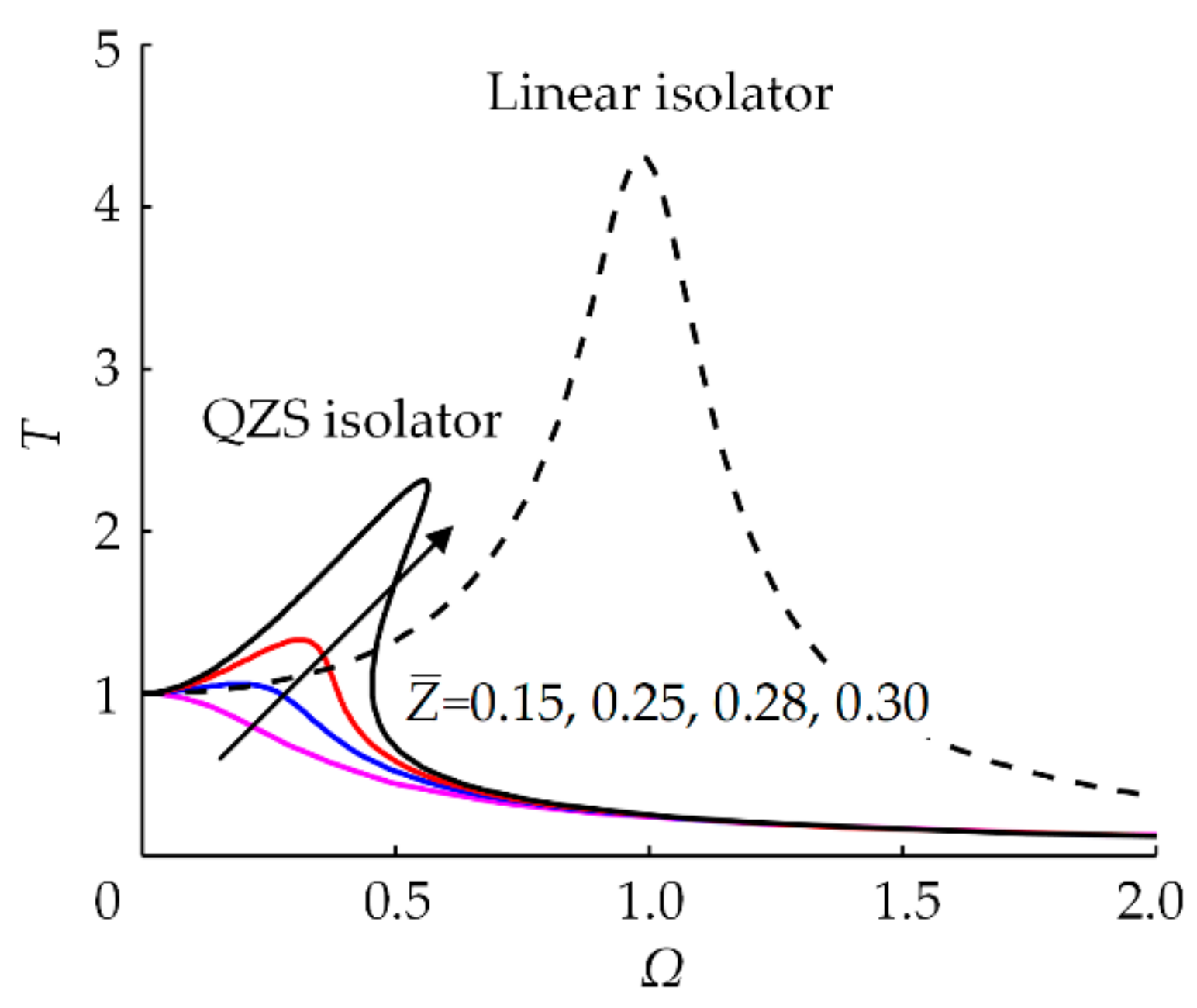
4.2. Frequency Response Characteristics and Stability
4.3. Advantage of QCRM in Calculation Accuracy
4.4. Vibration Isolation Performance under Different Excitations
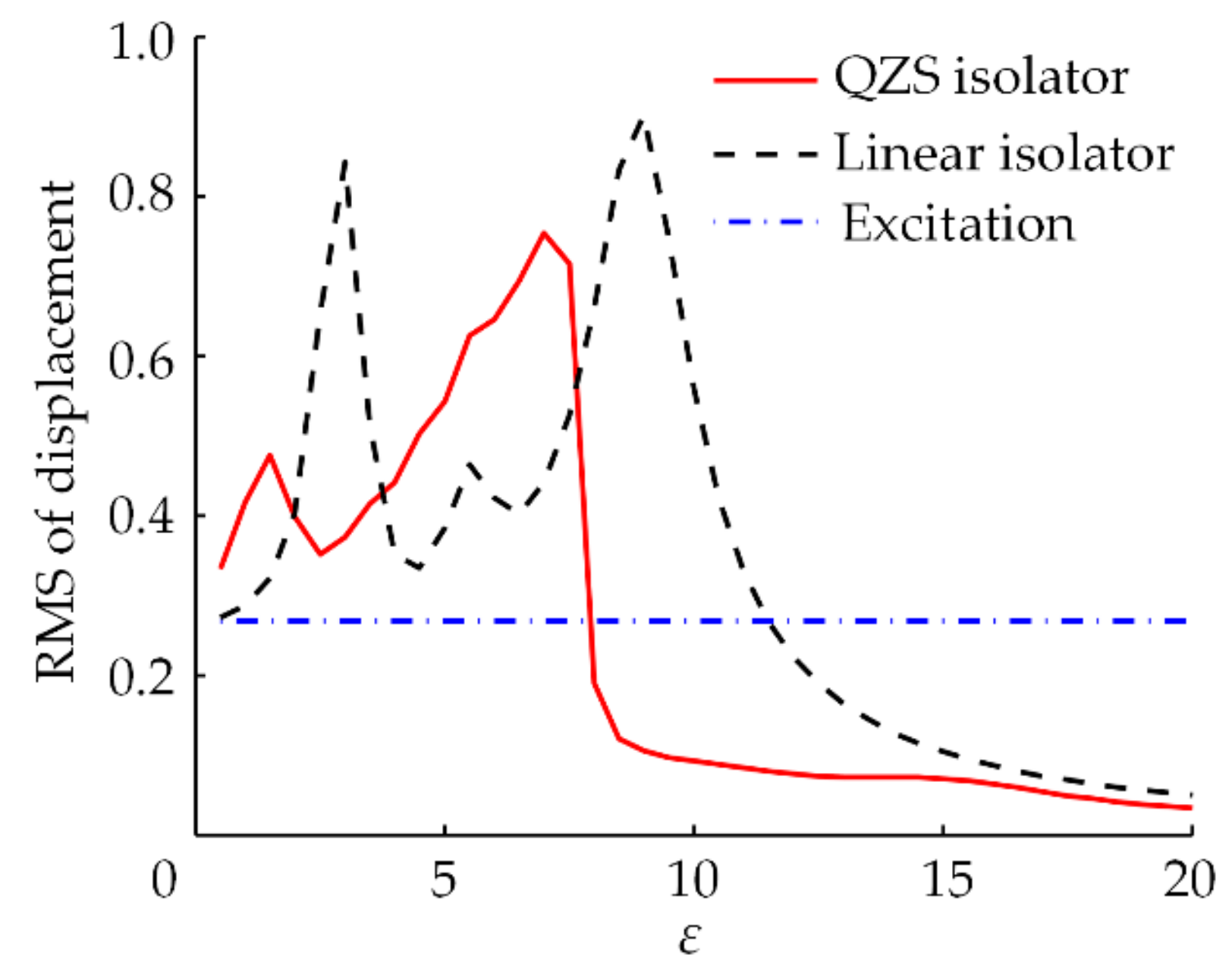
4.4.1. Displacement Transmissibility to Sinusoidal Excitation
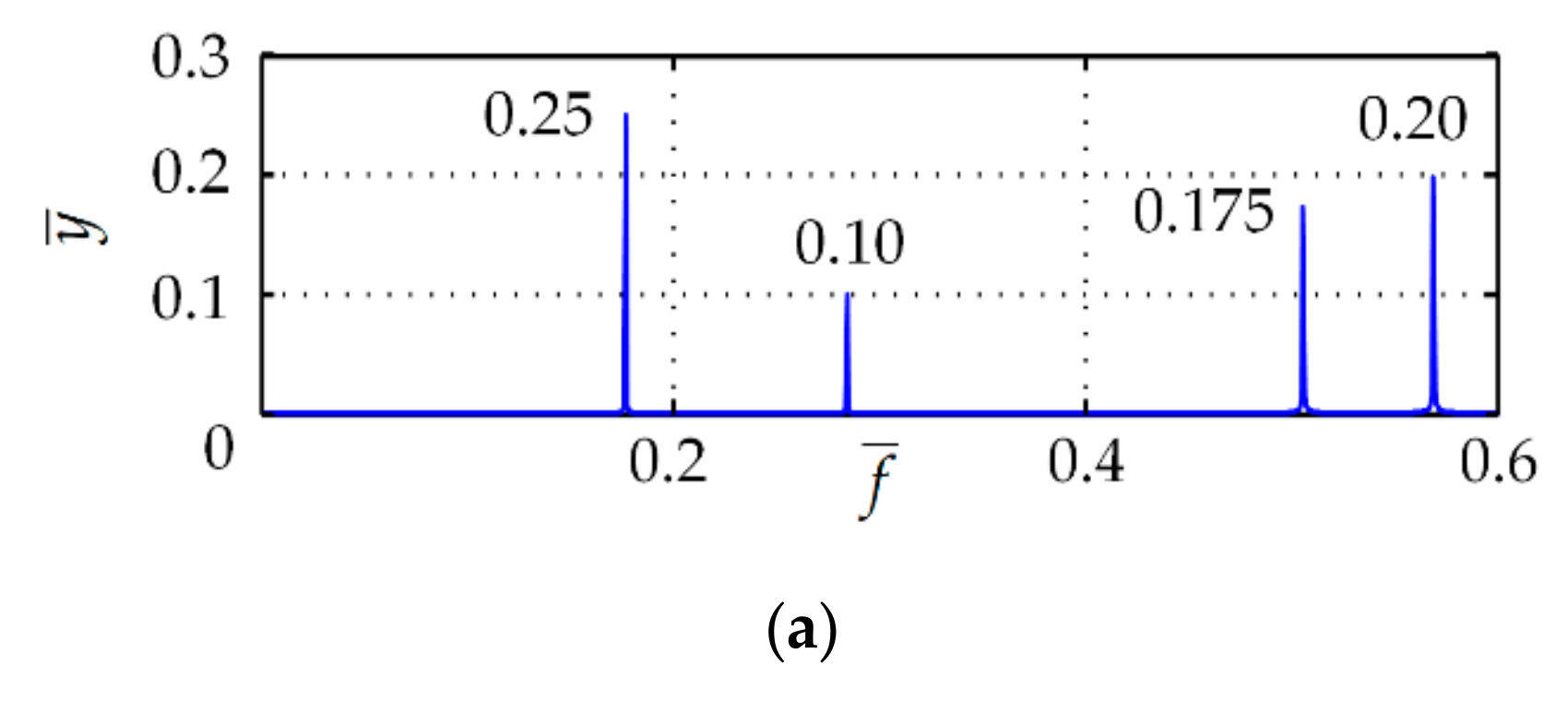
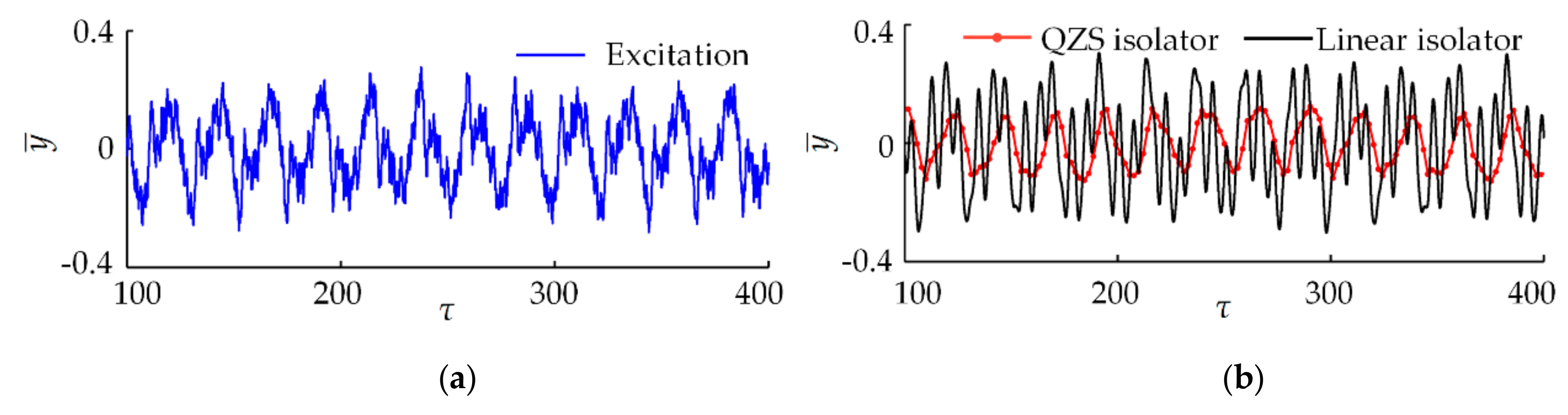
4.4.2. Vibration Isolation Performance under Multi-Frequency Wave Excitation
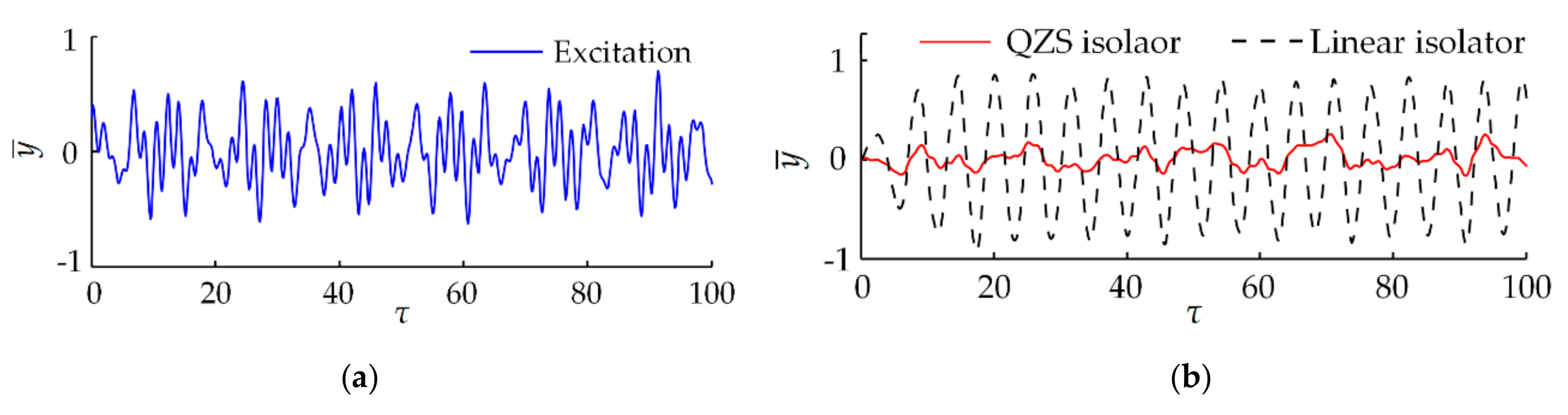
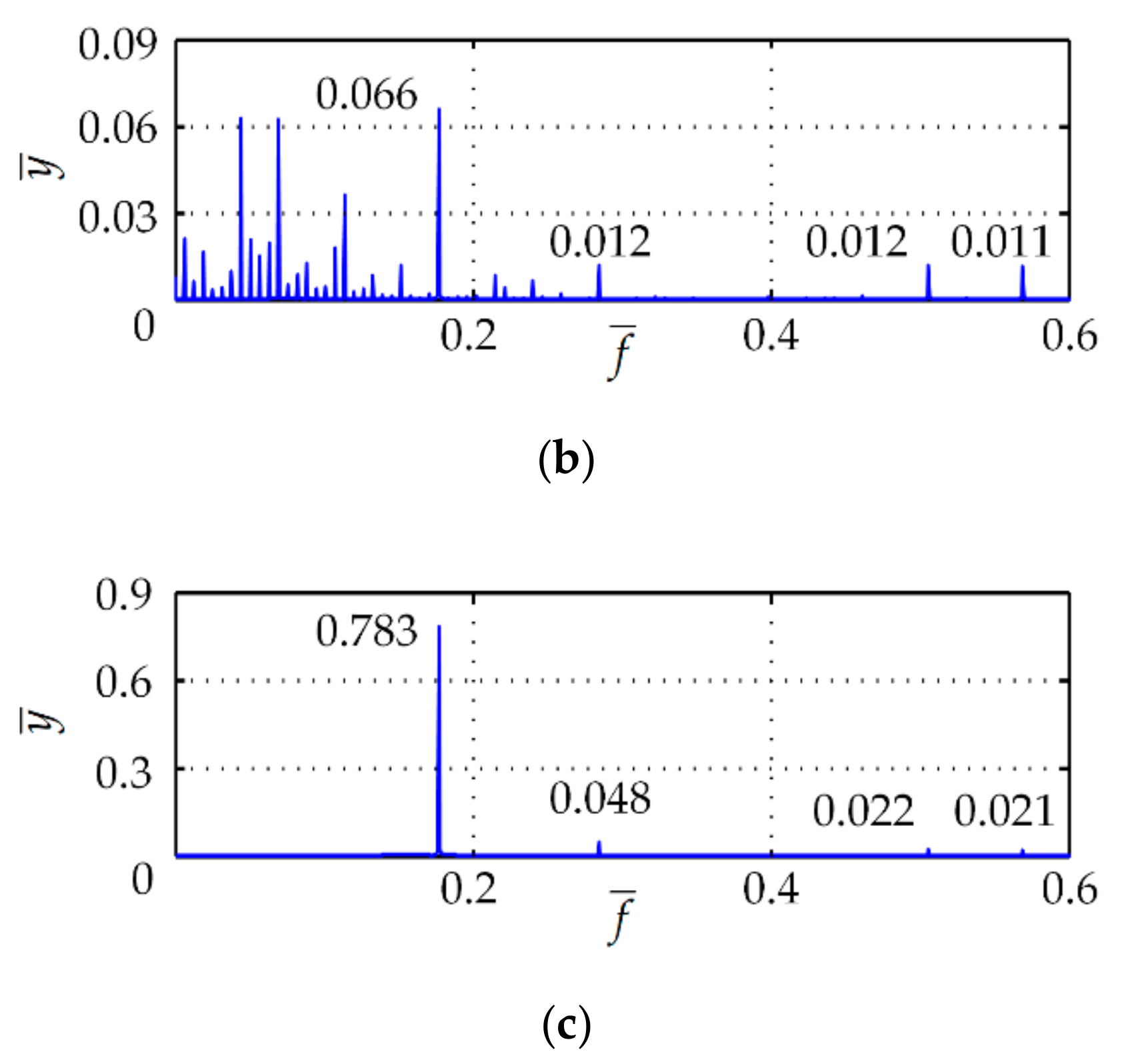
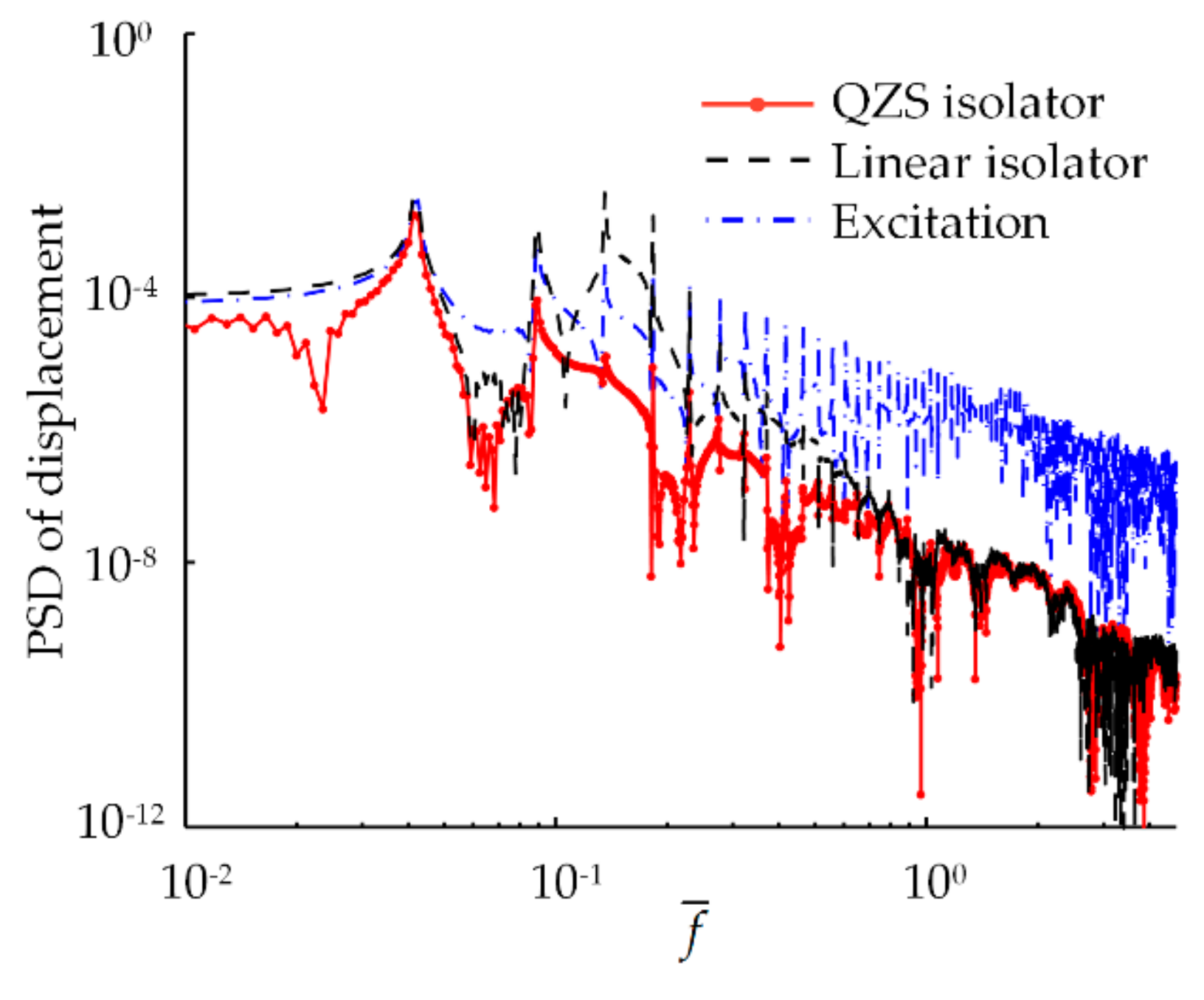
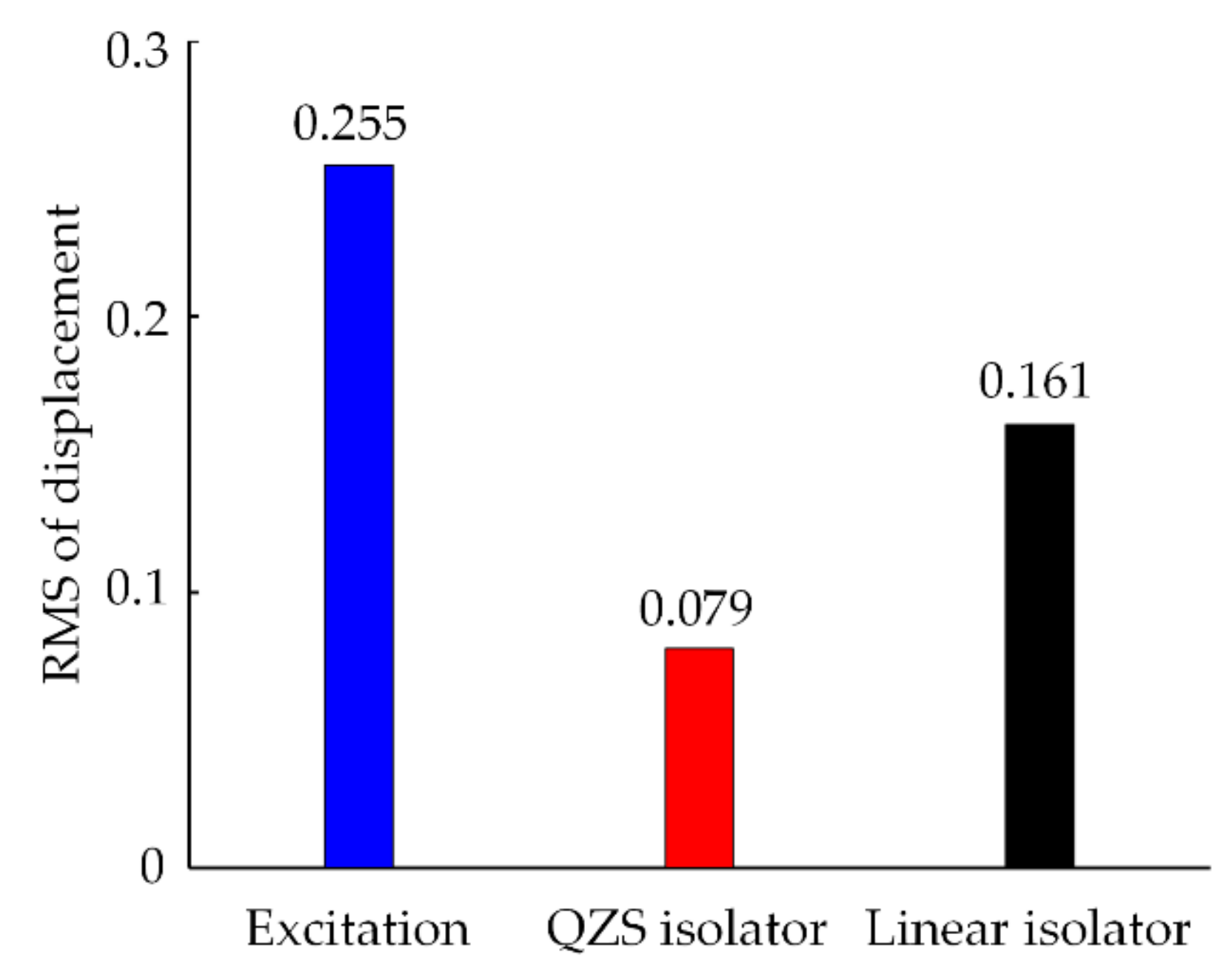
4.4.3. Vibration Isolation Performance under Random Excitation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Diez-Jimenez, E.; Rizzo, R.; Gómez-García, M.J.; Corral-Abad, E. Review of passive electromagnetic devices for vibration damping and isolation. Shock Vib. 2019, 2019, 1–16. [Google Scholar] [CrossRef]
- Lyratzakis, A.; Tsompanakis, Y.; Psarropoulos, P.N. Efficient mitigation of high-speed trains induced vibrations of railway embankments using expanded polystyrene blocks. Transp. Geotech. 2020, 22. [Google Scholar] [CrossRef]
- Dong, Z.X.; Sun, X.W.; Xu, F.S.; Liu, W.J. A low-rank and sparse decomposition-based method of improving the accuracy of sub-pixel grayscale centroid extraction for spot images. IEEE Sens. J. 2020, 20, 5845–5854. [Google Scholar] [CrossRef]
- Gangemi, P.J.; Kanapathipillai, S. Submarine structural and acoustic attenuation. J. Vib. Control. 2016, 22, 3135–3150. [Google Scholar] [CrossRef]
- Sun, M.N.; Song, G.Q.; Li, Y.M.; Huang, Z.L. Effect of negative stiffness mechanism in a vibration isolator with asymmetric and high-static-low-dynamic stiffness. Mech. Syst. Signal Pr. 2019, 124, 388–407. [Google Scholar] [CrossRef]
- Zeng, X.H.; Zhang, L.; Yu, Y.; Shi, M.; Zhou, J.F. The stiffness and damping characteristics of a dual-chamber air spring device applied to motion suppression of marine structures. Appl. Sci. 2016, 6, 74. [Google Scholar] [CrossRef] [Green Version]
- Tu, S.W.; Lu, X.F.; Zhu, X.L. Effect of structure parameters on Polycal wire rope isolator. Shock Vib. 2019, 2019, 1–10. [Google Scholar] [CrossRef]
- Feng, X.; Jing, X.J.; Xu, Z.D.; Guo, Y.Q. Bio-inspired anti-vibration with nonlinear inertia coupling. Mech. Syst. Signal Pr. 2019, 124, 562–595. [Google Scholar] [CrossRef]
- Sadeghi, S.; Li, S. Fluidic origami cellular structure with asymmetric quasi-zero stiffness for low-frequency vibration isolation. Smart Mater. Struct. 2019, 28, 065006. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P.; Lopes, V.J. Force and displacement transmissibility of a nonlinear isolator with high-static-low-dynamic-stiffness. Int. J. Mech. Sci. 2012, 55, 22–29. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P. Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic. J. Sound Vib. 2007, 31, 678–689. [Google Scholar] [CrossRef]
- Fulcher, B.A.; Shahan, D.W.; Haberman, M.R.; Seepersad, C.C.; Wilson, P.S. Analytical and experimental investigation of buckled beams as negative stiffness elements for passive vibration and shock isolation systems. J. Vib. Acoust. 2014, 136, 031009. [Google Scholar] [CrossRef]
- Virgin, L.N.; Davis, R.B. Vibration isolation using buckled struts. J. Sound Vib. 2003, 260, 965–973. [Google Scholar] [CrossRef]
- Zheng, Y.S.; Li, Q.P.; Luo, B.; Luo, Y.J.; Zhang, X.N. A Stewart isolator with high-static-low-dynamic stiffness struts based on negative stiffness magnetic springs. J. Sound Vib. 2018, 422, 390–408. [Google Scholar] [CrossRef]
- Debeau, D.A.; Seepersad, C.C.; Haberman, M.R. Impact behavior of negative stiffness honeycomb materials. J. Mater. Res. 2018, 33, 290–299. [Google Scholar] [CrossRef]
- Papaioannou, G.; Voutsinas, A.; Koulocheris, D.; Antoniadis, I. Dynamic performance analysis of vehicle seats with embedded negative stiffness elements. Veh. Syst. Dyn. 2020, 58, 307–337. [Google Scholar] [CrossRef]
- Yang, F.X.; Zhao, L.L.; Yu, Y.W.; Zhou, C.C. Matching, stability, and vibration analysis of nonlinear suspension system for truck cabs. Shock Vib. 2019, 2019, 1–10. [Google Scholar] [CrossRef]
- Li, Y.L.; Xu, D.L. Force transmissibility of floating raft system with quasi-zero-stiffness isolators. J. Vib. Control 2018, 24, 3608–3616. [Google Scholar]
- Zhou, J.X.; Wang, K.; Xu, D.L.; Ouyang, H.J.; Fu, Y.M. Vibration isolation in neonatal transport by using a quasi-zero-stiffness isolator. J. Vib. Control 2018, 24, 3278–3291. [Google Scholar] [CrossRef]
- Zhou, P.; Fang, Q.H. Match of negative stiffness and viscous damping in a passive damper for cable vibration control. Shock Vib. 2019, 2019, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Shaw, A.D.; Neild, A.; Wagg, D.J. Dynamic analysis of high static low dynamic stiffness vibration isolation mounts. J. Sound Vib. 2013, 332, 1437–1455. [Google Scholar] [CrossRef] [Green Version]
- Shaw, A.D.; Neild, A.; Friswell, M.I. Relieving the effect of static load errors in nonlinear vibration isolation mounts through stiffness asymmetries. J. Sound Vib. 2015, 339, 84–98. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.X.; Wang, X.L.; Xu, D.L.; Bishop, S. Nonlinear dynamic characteristics of a quasi-zero stiffness vibration isolator with cam-roller-spring mechanisms. J. Sound Vib. 2015, 346, 53–69. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Xu, L.L.; Song, C.F.; Gu, H.S.; Ji, W. Dynamic characteristics of a quasi-zero stiffness vibration isolator with nonlinear stiffness and damping. Arch. Appl. Mech. 2019, 89, 1743–1759. [Google Scholar] [CrossRef]
- Le, T.D.; Ahn, K.K. A vibration isolation system in low frequency excitation region using negative stiffness structure for vehicle seat. J. Sound Vib. 2011, 330, 6311–6335. [Google Scholar] [CrossRef]
- Ahn, H.J.; Lim, S.H.; Park, C.K. An integrated design of quasi-zero stiffness mechanism. J. Mech. Sci. Technol. 2016, 30, 1071–1075. [Google Scholar] [CrossRef]
- Cheng, C.; Li, S.M.; Wang, Y.; Jiang, X.X. Force and displacement transmissibility of a quasi-zero stiffness vibration isolator with geometric nonlinear damping. Nonlinear Dynam. 2017, 87, 2267–2279. [Google Scholar] [CrossRef]
- Calleja, A.; Fernández, A.; Rodríguez, A.; de Lacalle, L.N.L.; Lamikiz, A. Turn-milling of blades in turning centres and multitasking machines controlling tool tilt angle. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 1324–1336. [Google Scholar] [CrossRef]
- Durali, L.; Khajepour, A.; Jeon, S. Design and optimization of a cam-actuated electrohydraulic brake system. Proc. IMechE. Inst. Mech. Eng. Part D J. Automob. Eng. 2018, 232, 909–920. [Google Scholar] [CrossRef]
- Kaul, S. Attributes of a vibration isolator design with stiffness nonlinearities. Int. J. Acoust. Vib. 2018, 23, 208–216. [Google Scholar] [CrossRef]
- General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration of the People’s Republic of China. GB/T 7031-2005 Mechanical Vibration-Road Surface Profiles Reporting of Measured Data; China Quality & Standards Press: Beijing, China, 2005. [Google Scholar]
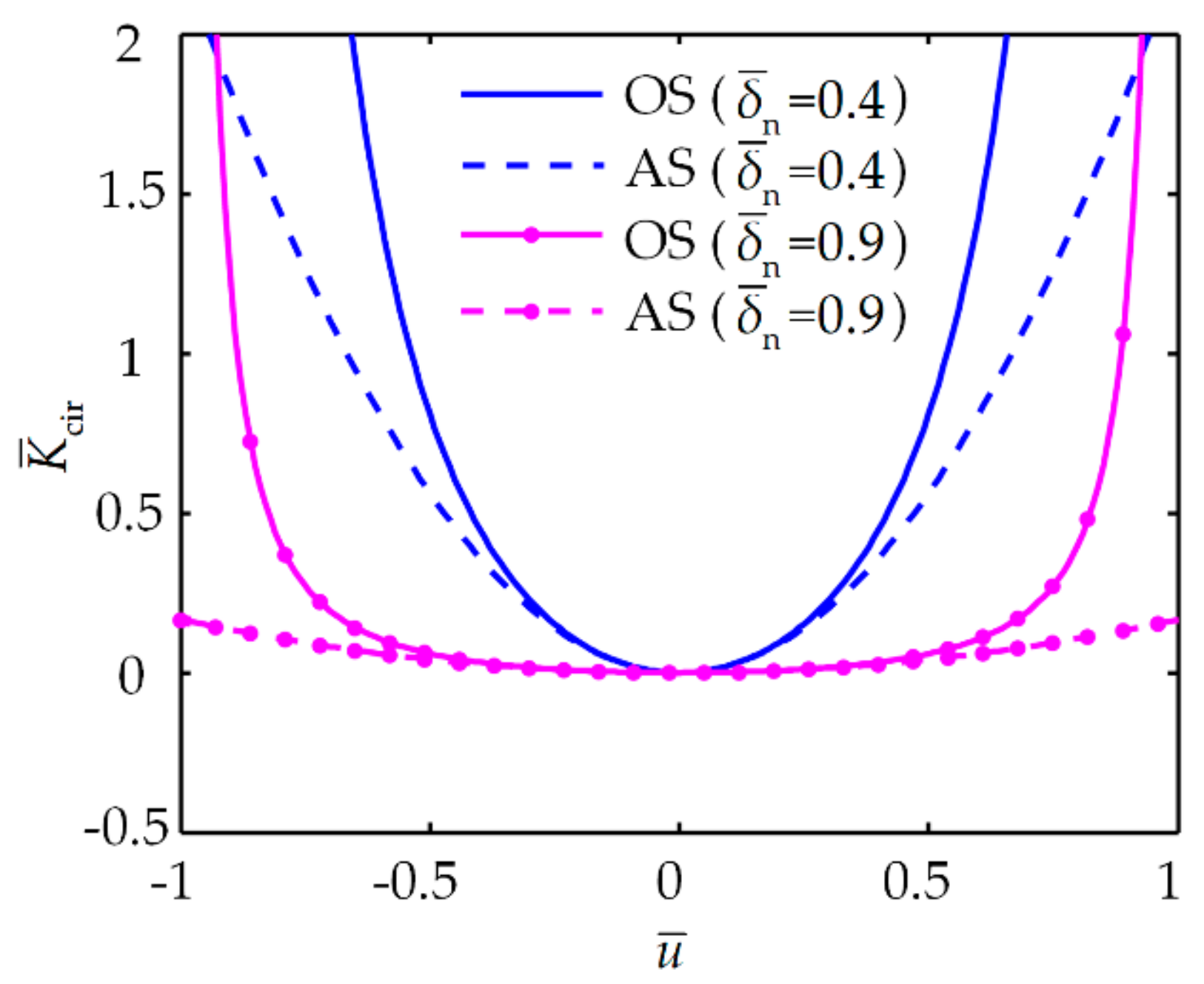
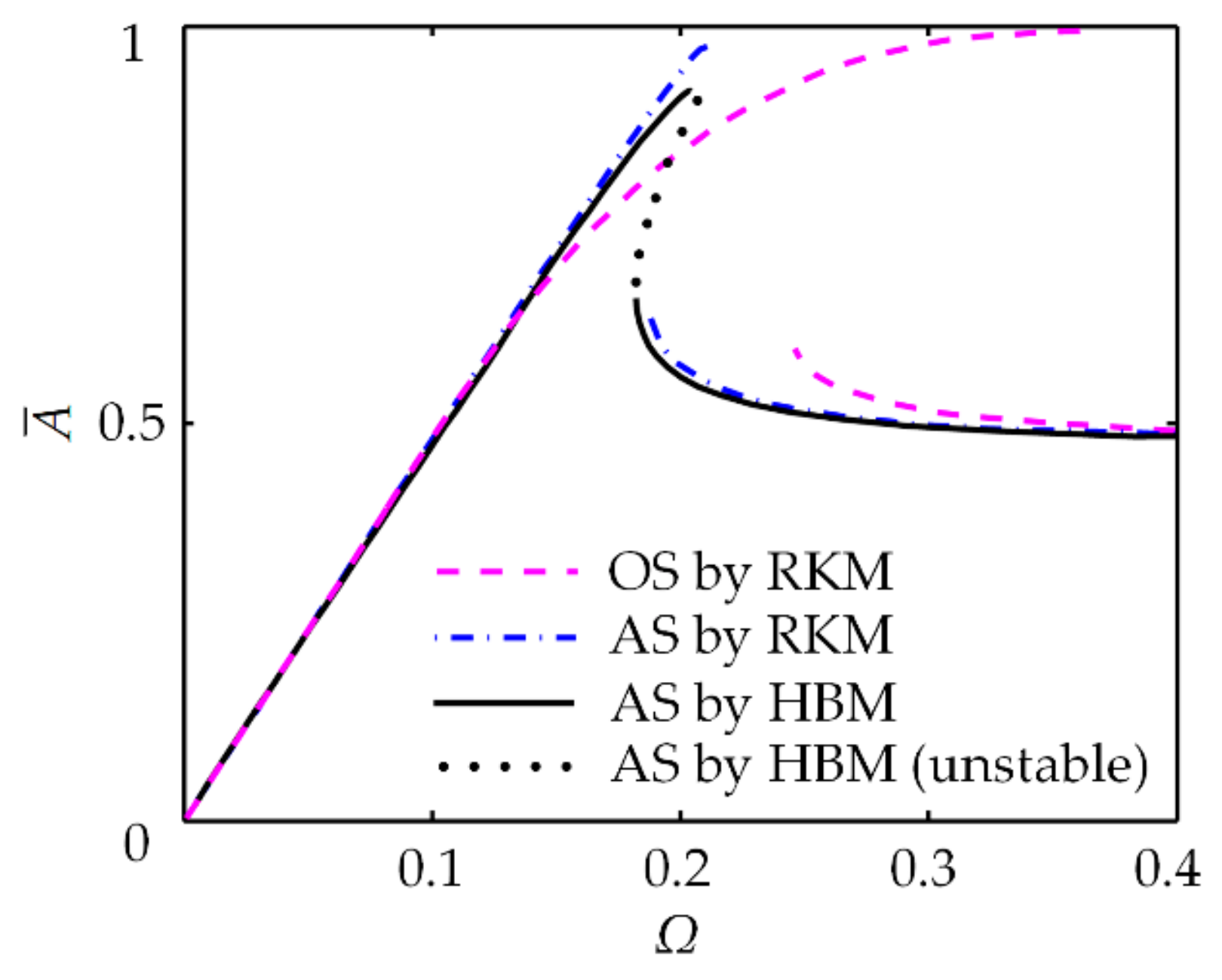
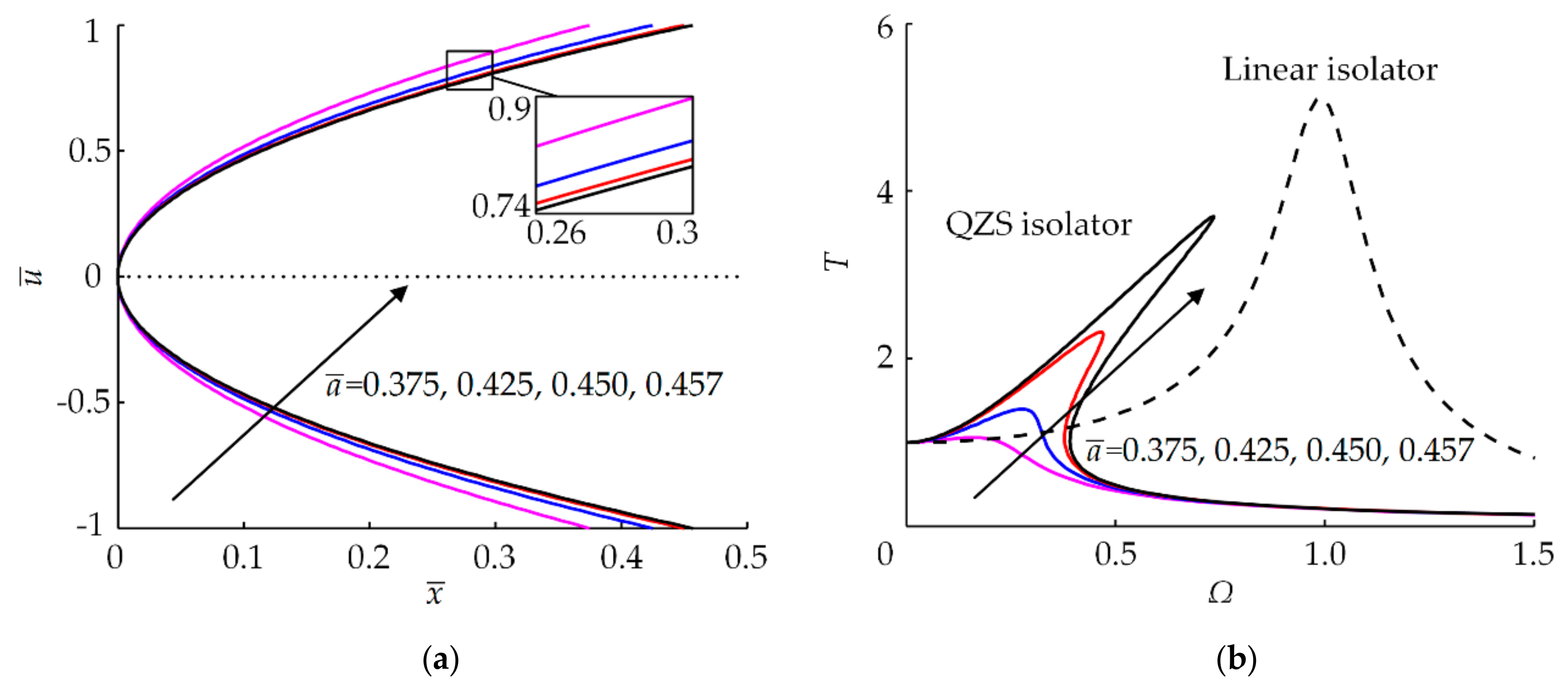
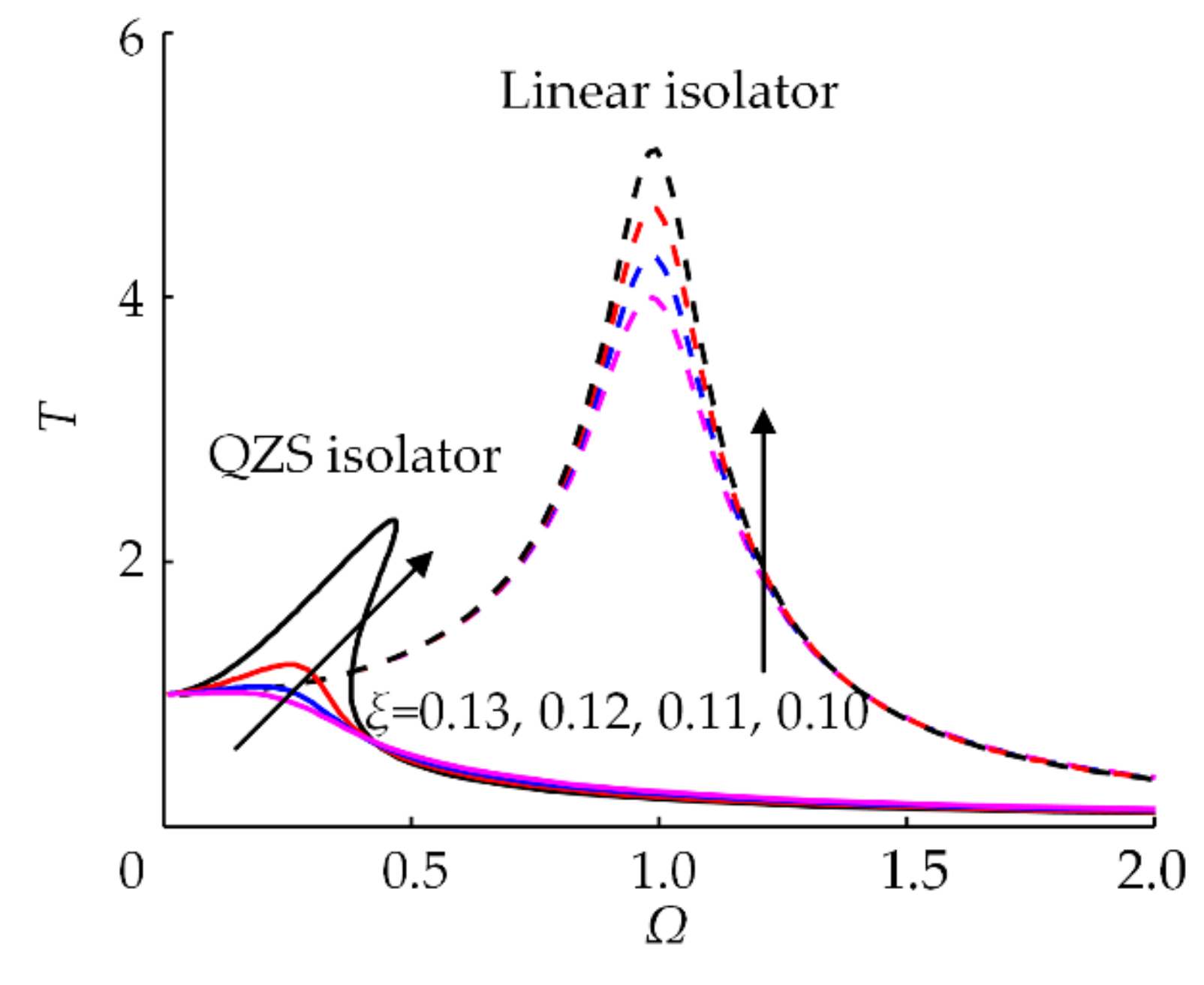
| Parameter | Value | |||
|---|---|---|---|---|
| 0.375 | 0.425 | 0.450 | 0.457 | |
| ξ | 0.10 | 0.11 | 0.12 | 0.13 |
| 0.15 | 0.25 | 0.28 | 0.30 | |
| r | 1 | 1 | 1 | 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, M.; Dong, Z.; Song, G.; Sun, X.; Liu, W. A Vibration Isolation System Using the Negative Stiffness Corrector Formed by Cam-Roller Mechanisms with Quadratic Polynomial Trajectory. Appl. Sci. 2020, 10, 3573. https://doi.org/10.3390/app10103573
Sun M, Dong Z, Song G, Sun X, Liu W. A Vibration Isolation System Using the Negative Stiffness Corrector Formed by Cam-Roller Mechanisms with Quadratic Polynomial Trajectory. Applied Sciences. 2020; 10(10):3573. https://doi.org/10.3390/app10103573
Chicago/Turabian StyleSun, Mengnan, Zhixu Dong, Guiqiu Song, Xingwei Sun, and Weijun Liu. 2020. "A Vibration Isolation System Using the Negative Stiffness Corrector Formed by Cam-Roller Mechanisms with Quadratic Polynomial Trajectory" Applied Sciences 10, no. 10: 3573. https://doi.org/10.3390/app10103573




