Model Reference Adaptive Control of Vehicle Slip Ratio Based on Speed Tracking
Abstract
1. Introduction
2. Problem Formulation
2.1. Vehicle Slip Ratio Model
2.2. Problem Formulations
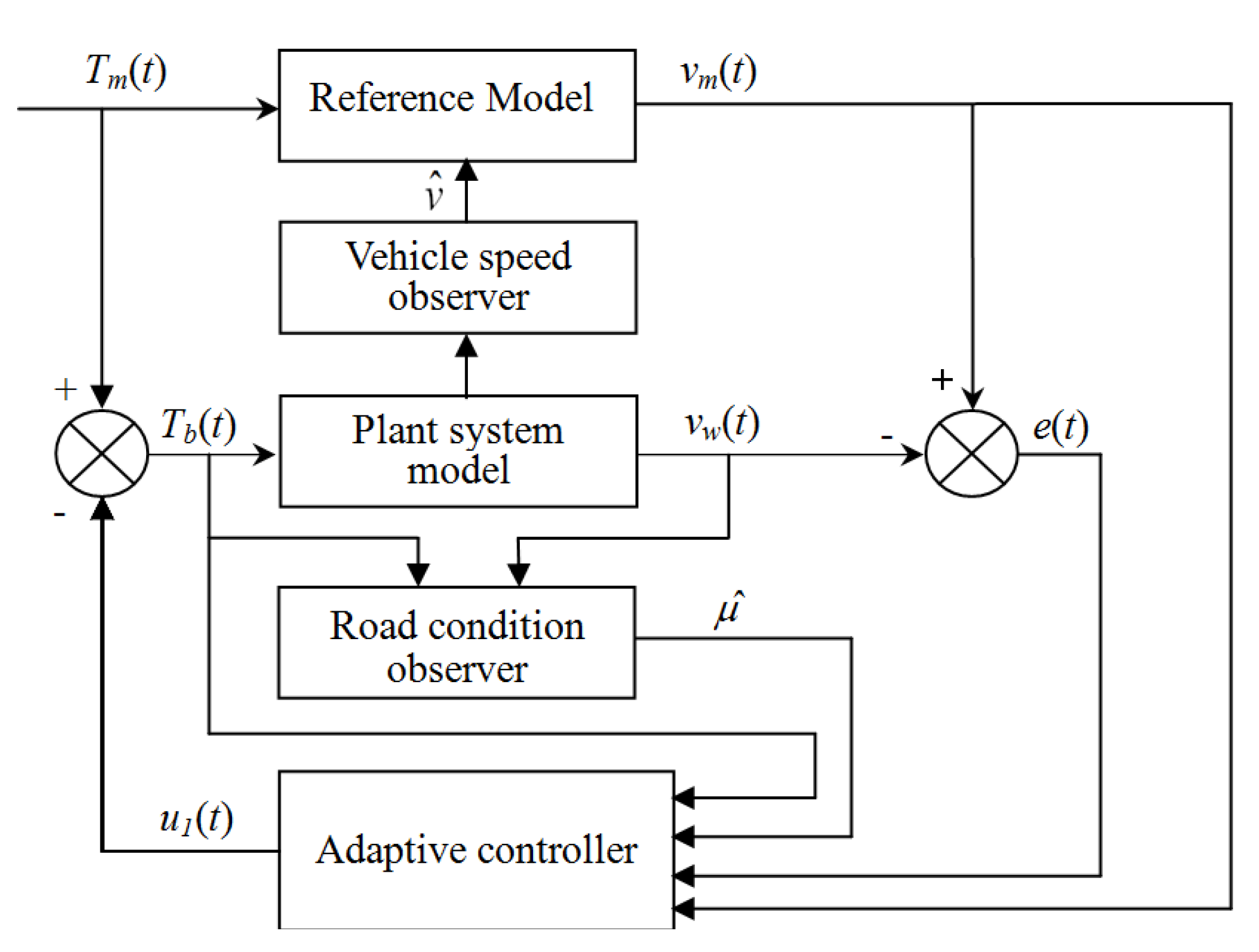
3. Model Reference Adaptive Control for Slip Ratio Control
3.1. Model Reference Adaptive Controller
3.2. Road Adhesion Coefficient Observer
3.3. Vehicle Speed Observer
4. Simulations Results and Analysis
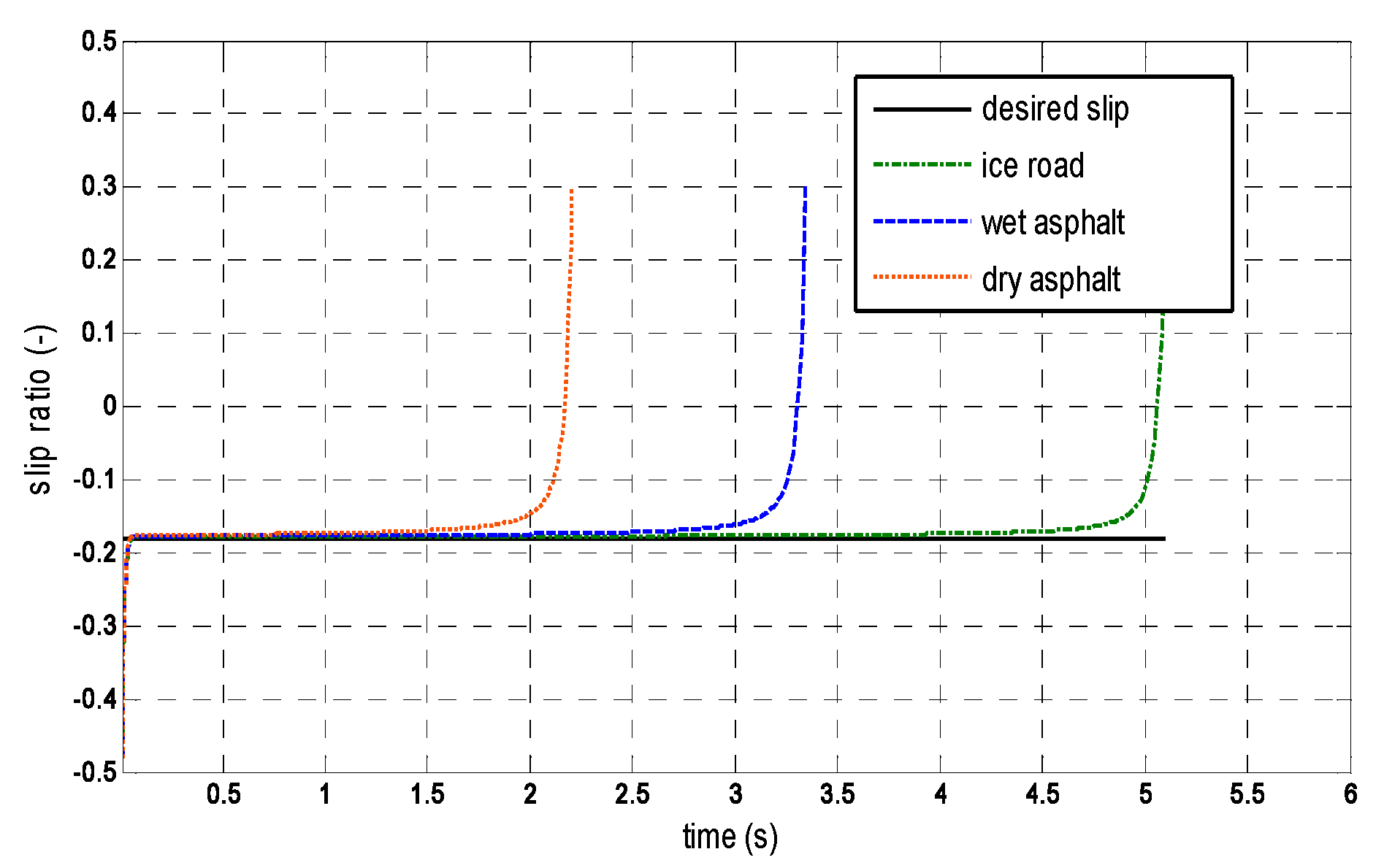
4.1. Simulation Research under Different Road Conditions
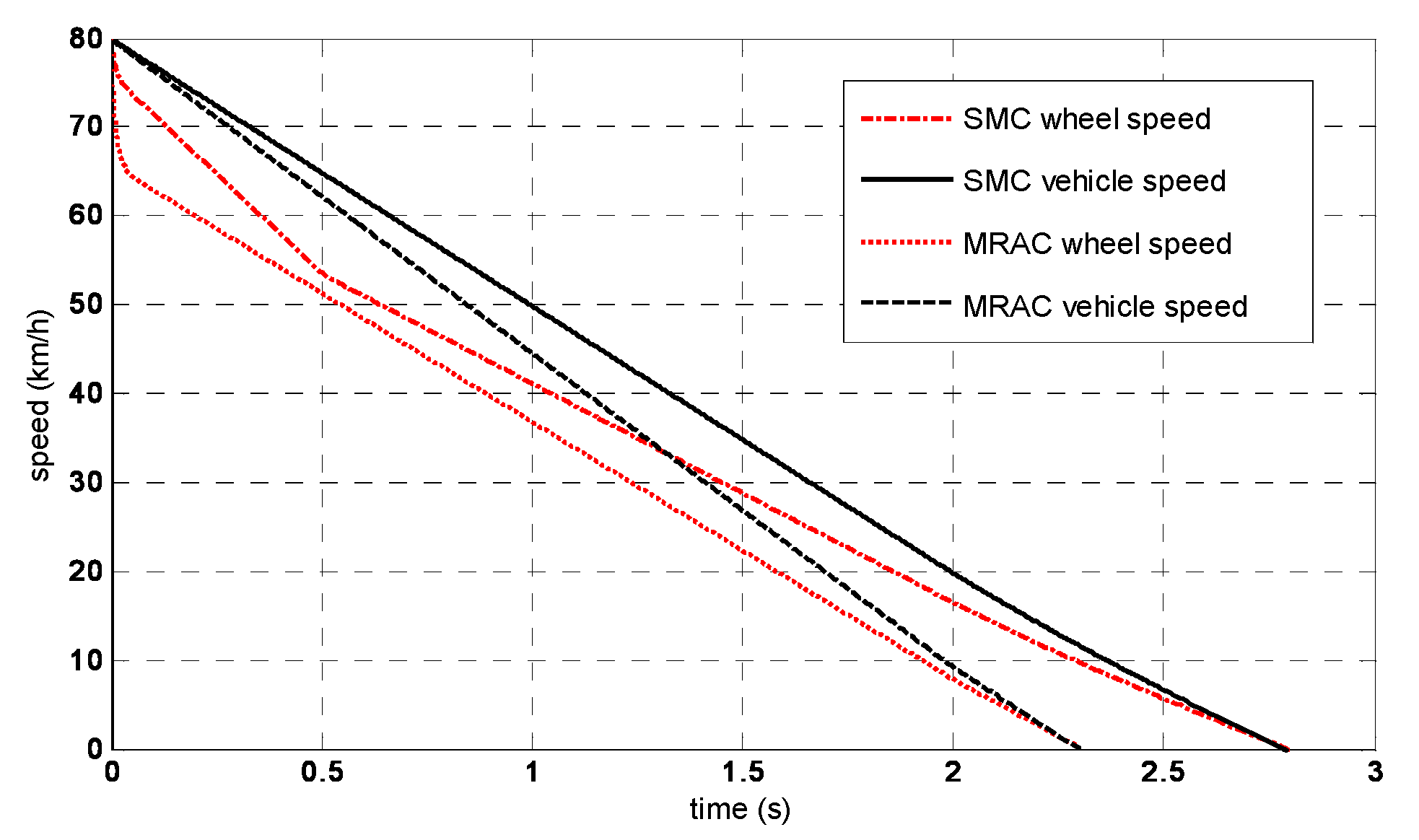
4.2. Simulation Comparison with SMC Method
4.3. Simulation Research with Uncertainties and Modeling Errors
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, W.; Guo, X.X. An ABS control strategy for commercial vehicle. IEEE Trans. Mech. 2015, 20, 384–392. [Google Scholar]
- Xu, G.Q.; Xu, K.; Zheng, C.H.; Zahid, T. Optimal operation point detection based on force transmitting behavior for wheel slip prevention of electric vehicles. IEEE Trans. Intell. Transp. Syst. 2016, 17, 481–490. [Google Scholar] [CrossRef]
- Castillo, J.J.; Cabrera, J.A.; Guerra, A.J.; Simón, A. A novel electrohydraulic brake system with tire-road friction estimation and continuous brake pressure control. Trans. Ind. Electron. 2016, 63, 1863–1875. [Google Scholar] [CrossRef]
- Sun, W.C.; Zhang, J.H.; Liu, Z.Y. Two-time-scale redesign for antilock braking systems of ground vehicles. IEEE Trans. Ind. Electron. 2019, 66, 4577–4586. [Google Scholar] [CrossRef]
- Reza, H.; Alireza, B.H. Efficient antilock braking by direct maximization of tire-road frictions. IEEE Trans. Ind. Electron. 2011, 58, 3593–3600. [Google Scholar]
- Castro, R.D.; Araújo, R.E.; Freitas, D. Wheel slip control of EVs based on sliding mode technique with conditional integrators. IEEE Trans. Ind. Electron. 2013, 60, 3256–3271. [Google Scholar] [CrossRef]
- Fazeli, A.; Zeinali, M.; Khajepour, A. Application of adaptive sliding mode control for regenerative braking torque control. IEEE Trans. Mech. 2012, 17, 745–755. [Google Scholar] [CrossRef]
- Amodeo, M.; Ferrara, A.; Terzaghi, R.; Vecchio, C. Wheel slip control via second-order sliding-mode generation. IEEE Trans. Intell. Transp. Syst. 2010, 11, 122–131. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, Y.; Han, M.; Lian, Q. Adaptive fuzzy fractional-order sliding mode controller design for antilock braking systems. J. Dyn. Syst. Meas. Control. 2016, 138, 122–130. [Google Scholar] [CrossRef]
- Lin, C.M.; Hsu, C.F. Self-Learning fuzzy sliding-mode control for antilock braking systems. IEEE Trans. Control Syst. Technol. 2003, 11, 273–278. [Google Scholar] [CrossRef]
- Mi, C.T.; Lin, H.; Zhang, Y. Iterative learning control of antilock braking of electric and hybrid vehicles. IEEE Trans. Veh. Technol. 2005, 54, 486–494. [Google Scholar] [CrossRef]
- Paul, D.; Velenis, E.; Cao, D.; Dobo, T. Optimal μ-estimation based regenerative braking strategy for an AWD HEV. IEEE Trans. Transp. Electr. 2017, 3, 249–258. [Google Scholar] [CrossRef]
- Johansen, T.; Petersen, I.; Kalkkuhl, J.; Lüdemann, J. Gain-scheduled wheel slip control in automotive brake systems. IEEE Trans. Control Syst. Technol. 2003, 11, 799–811. [Google Scholar] [CrossRef]
- Qiu, Y.; Liang, X.; Dai, Z. Backstepping dynamic surface control for an anti-skid braking system. Control Eng. Pract. 2015, 42, 140–152. [Google Scholar] [CrossRef]
- Rath, J.J.; Veluvolu, K.C.; Defoort, M. Simultaneous estimation of road profile and tire road friction for automotive vehicle. IEEE Trans. Veh. Technol. 2015, 64, 4461–4471. [Google Scholar] [CrossRef]
- Han, K.; Hwang, Y.; Lee, E.; Choi, S. Robust estimation of maximum tire-road friction coefficient considering road surface irregularity. Int. J. Automot. Technol. 2015, 17, 415–425. [Google Scholar] [CrossRef]
- Wu, J.; Huang, J.; Wang, Y.J.; Xing, K.X. Nonlinear disturbance observer-based dynamic surface control for trajectory tracking of pneumatic muscle system. IEEE Trans. Control Syst. Technol. 2014, 22, 440–455. [Google Scholar] [CrossRef]
- Mirkin, B.; Gutman, P.O. Robust adaptive output-feedback tracking for a class of nonlinear time-delayed plants. IEEE Trans. Automat. Contr. 2010, 55, 2418–2424. [Google Scholar] [CrossRef]
- Han, J.; Yu, S.; Yi, S. Adaptive control for robust air flow management in an automotive fuel cell system. Appl. Energy 2017, 190, 73–83. [Google Scholar] [CrossRef]
- Elzaghir, W.; Zhang, Y.; Natarajan, N.; Massey, F.; Mi, C. Model reference adaptive control for hybrid electric vehicle with dual clutch transmission configurations. IEEE Trans. Veh. Technol. 2018, 67, 991–999. [Google Scholar] [CrossRef]
- Subudhi, B.; Ge, S.S. Sliding-mode-observer-based adaptive slip ratio control for electric and hybrid vehicles. IEEE Trans. Intell. Transp. Syst. 2012, 13, 1617–1626. [Google Scholar] [CrossRef]
- Wang, B.; Huang, X.Y.; Wang, J.M. A robust wheel slip ratio control design combining hydraulic and regenerative braking systems for in-wheel-motors-driven electric Vehicles. J. Frankl. Inst. 2015, 352, 577–602. [Google Scholar] [CrossRef]
- Yin, G.; Jin, X.J. Cooperative control of regenerative braking and antilock braking for a hybrid electric vehicle. Math. Probl. Eng. 2013, 4, 1–9. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, J.; Zhang, L. Automotive ABS/DYC coordinated control under complex driving conditions. IEEE Access. 2018, 6, 32769–32779. [Google Scholar] [CrossRef]
- Pacejka, H.B.; Bakker, E. The Magic Formula tyre model. Veh. Sys. Dyn. 1992, 21, 1–18. [Google Scholar] [CrossRef]
- Burckhardt, M. Fahrwerktechnik Radschlupfregelsysteme; Vogel-verlag: München, Germnay, 1993. [Google Scholar]
- Canudas, D.W.C.; Olsson, H.; Aostrcom, K.J. A new model for control of systems with friction. IEEE Trans. Auto. Contr. 1995, 40, 419–425. [Google Scholar] [CrossRef]
- Bhandari, R.; Patil, S.; Singh, R.K. Surface prediction and control algorithms for anti-lock brake system. Transp. Res. Part C. 2012, 21, 181–195. [Google Scholar] [CrossRef]
- Harifi, A.; Aghagolzadeh, A.; Alizadeh, G.; Sadeghi, M. Designing a sliding mode controller for slip control of antilock brake systems. Transp. Res. Part C Emer. Technol. 2008, 16, 731–741. [Google Scholar] [CrossRef]
- Popov, V.M. Hyper-Stability of Control System; Springer: New York, NY, USA, 1973. [Google Scholar]
- Qu, Z.; Dawson, D.M.; Lim, S.Y.; Dorsey, J.F. A new class of robust control laws for tracking of robots. Int. J. Robot. Res. 1994, 13, 355–363. [Google Scholar]












| Symbol | Quantity | Value |
|---|---|---|
| m | ¼ Car vehicle mass | 350 kg |
| J | Inertia | 0.65 kg m2 |
| rw | Wheel radius | 0.31 m |
| cf | Friction coefficient | 0.4 |
| cv | Air resistance coefficient | 0.595 N/(m2 s2) |
| nw | Number of brake wheel | 4 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| k01 | 600 | k02 | 0.045 |
| k11 | 0.1 | k12 | 0.005 |
| g01 | 0.01 | g02 | 0.0005 |
| l01 | 1 | l02 | 0.002 |
| Road Conditions | Braking Distance (m) | Improved | |
| SMC | MRAC | ||
| Dry asphalt | 33.6 | 25.5 | 24% |
| Wet asphalt | 43.9 | 37.2 | 15% |
| Ice road | 85.6 | 60.8 | 22% |
| Road Conditions | Braking Time (s) | Improved | |
| SMC | MRAC | ||
| Dry asphalt | 2.8 | 2.3 | 19% |
| Wet asphalt | 3.9 | 3.5 | 19% |
| Ice road | 7.7 | 5.4 | 29% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Guo, G. Model Reference Adaptive Control of Vehicle Slip Ratio Based on Speed Tracking. Appl. Sci. 2020, 10, 3459. https://doi.org/10.3390/app10103459
Zhao X, Guo G. Model Reference Adaptive Control of Vehicle Slip Ratio Based on Speed Tracking. Applied Sciences. 2020; 10(10):3459. https://doi.org/10.3390/app10103459
Chicago/Turabian StyleZhao, Xiuchun, and Ge Guo. 2020. "Model Reference Adaptive Control of Vehicle Slip Ratio Based on Speed Tracking" Applied Sciences 10, no. 10: 3459. https://doi.org/10.3390/app10103459
APA StyleZhao, X., & Guo, G. (2020). Model Reference Adaptive Control of Vehicle Slip Ratio Based on Speed Tracking. Applied Sciences, 10(10), 3459. https://doi.org/10.3390/app10103459





