User–Topic Modeling for Online Community Analysis

Abstract

Analyzing user behavior in online spaces is an important task. This paper is dedicated to analyzing the online community in terms of topics. We present a user–topic model based on the latent Dirichlet allocation (LDA), as an application of topic modeling in a domain other than textual data. This model substitutes the concept of word occurrence in the original LDA method with user participation. The proposed method deals with many problems regarding topic modeling and user analysis, which include: inclusion of dynamic topics, visualization of user interaction networks, and event detection. We collected datasets from four online communities with different characteristics, and conducted experiments to demonstrate the effectiveness of our method by revealing interesting findings covering numerous aspects.

1. Motivation

The online community is an important virtual space where information spreads and users express their opinions and emotions. The efficiency and immediacy of online communication encourage users to be more active, and it becomes possible to overcome spatial and temporal restrictions, so that a large number of users can interact with each other at the same time and—albeit virtual—place. The high level of activity in online communities provides large amounts of information from various perspectives. Many commercial and social agencies, such as tourism [1], advertising [2], recruiting [3], and social security [4] have benefited by utilizing interaction data from these online spaces. On the other hand, this instant communication can cause serious problems, such as rapid propagation of fake news [5] and conflicts [6]. These side effects of web activity are not limited to the online space, rather they affect our lives profoundly. While attempting to resolve these social problems, it is important to analyze how users behave, how they communicate, and how they interact in this virtual space. Many researchers have focused on discovering the fundamental mechanism of a certain behavior, such as empathy [7] or conflict [6]. Some work concentrated on specific user types, such as contributors [8], anti-social users [9,10], and lurkers [11]. Others focused on changes in word usage [12,13], and the development of conventions [14].

This work is focused on analyzing user behavior from the perspective of topics. For this purpose, we utilize the latent Dirichlet allocation (LDA), originally developed for language processing tasks. LDA is one of the most successful language modeling methods, whose basic concept is that words appear according to their latent topics. It infers the latent topic of each word using a generative probabilistic model, which describes the concept. There have been many extensions to this method, adding more variables and dependencies reflecting a variety of features available in web communities [15,16,17]. These often involve substantial computation and a high degree of complexity in their implementation. Complex models have low flexibility, in that they tend to fail when part of a required data field is not available; for example, a model using rating scores cannot work for web communities that do not provide a user-rating system.

Instead of developing a complex probabilistic model for analyzing user behavior, we adopted the simple form of the topic modeling method to ensure flexibility, but we make an important and effective substitution. Specifically, we use the LDA technique, substituting the concept of “words” in the textual data with “users” in the online community. We also present a preprocessing method that should be considered when taking into account the exploitation of online community datasets, which enables the proposed method to capture both the temporal and thematic features of user behavior effectively. Although the concept itself has been introduced in our previous work [18], we provide extensive experimental results in this work especially focusing on demonstrating the capability of analyzing user behavior in web communities from many perspectives, which the previous work did not cover.

The contributions of this paper are as follows:

• We present an analysis method, using topic modeling, for user behavior in online communities, with applications.
• The proposed method is simple because it uses standard LDA with the small substitution of user participation for word occurrence. It is also flexible, because it does not use too many features, yet ensures sufficient functionality in many applications of user behavior analysis.
• We also demonstrate the effectiveness of our method by conducting experiments on various datasets and revealing interesting findings.

The remainder of the paper is organized as follows. After briefly reviewing related work in Section 2, we introduce the main concept of the proposed method, including the analogy between standard topic modeling and our work, with procedural details, in Section 3. In Section 4, we describe the datasets which will be used for the case studies, showing the application of the proposed method in Section 5. We present our conclusions in Section 6.

2. Related Work

Topic modeling is one of the most successful methods in computational linguistics. The latent Dirichlet allocation (LDA, [19]) was presented as a generative probabilistic model to estimate the latent topics from observable words. This method was shown to be effective in many tasks in natural language processing, and it has seen many improvements and extensions over the last two decades. As a direct application, LDA has been used to analyze textual content in terms of topics in many document types, such as research articles [20] and software requirement documents [21]. More complex tasks involving textual data, such as link prediction of authors based on the contents of their work [22] have also benefited from the topic modeling method.

Topic modeling has also been exploited in domains other than conventional text.

Table 1. Related work using analogies from latent Dirichlet allocation (LDA).

	Domain	Analogy		Main Goal
		Document	Word
[23]	Java Program Code	Source file	Token	Extracting source code concepts
[24]	Word Network	Word	Adjacent Word	Topic modeling with short texts
[25]	Phenome Information	Drug	Phenotype	Searching similar drugs
[26]	Web Browsing History	User	Visited URL	Analyzing mobile user preferences
[27]	Purchase List	User	Item	Item recommendation
[28]	Twitter Network	User	Follower/Followee	User (friend) recommendation
[29]	Twitter Network	User	Follower/Followee	User grouping and labeling
[30]	Researcher Network	Author	Co-author	Community detection

lists several related studies that exploit the topic modeling method in different domains using appropriate analogies, similar to our work presented in this paper. Target domains include program source code [23], word network [24], information of the side effects of medical drugs [25], web browsing history [26], and item purchase lists [27]. Especially, several studies applied the topic modeling to user analysis [28,29,30]. These methods exploit the topic modeling technique to analyze the user network. This user network can be obtained directly from the dataset such as Twitter [28,29], or is constructed from a user co-occurrence relationship [30]. However, this network-based exploitation of topic modeling is not quite effective for online community analysis. We discuss the differences from the proposed method in detail in the experimental section.

Several extensions have also been presented for application to user modeling and web data. Li et al. presented an extended LDA that uses tagging and resource information in a social bookmarking web service [15]. Nguyen and Shirai proposed a prediction model based on LDA combining stock prices and articles from a financial forum [31]. Pu et al. extended topic modeling, including item and sentiment to analyze user reviews, and demonstrated their model’s use on movie and restaurant review datasets [17]. Other applications have also been considered, such as link prediction [16] and rating prediction [32]. A major challenge has been dealing with the dynamic way that topics change over time. After Blei and Lafferty presented dynamic topic modeling [33], which adds temporal components to the standard topic modeling method, several variations have been presented [34]. Some researchers took dynamic topic modeling into account in their applications [35]. Several studies have proposed the development of the topic modeling itself by considering the characteristics of the target domain (for example [36]).

3. Topical User Modeling

In this section, we present our proposed method, which we name the user–topic model. First, we briefly present the analogy between standard topic modeling and our proposed method, which is the core concept of the method. Then we present the topic assignment procedure, which consists of three parts: (i) preliminaries, which introduces the notation used in the remainder of the paper, (ii) preprocessing, which involves data filtering, and (iii) implementation, which describes the utilization of Gibbs sampling for topic estimation.

3.1. Analogy

The underlying concept of the proposed method is that the users in an online community leave comments according to their own behavioral characteristics, affected by personal behavior such as interests and active time slots, and environmental factors such as social events and influential incidents. This is analogous to the concept of the classical topic-modeling method, in which words appear in documents according to their latent topics. We use this conceptual similarity between user behavior and text modeling to analyze user behavior in online communities by exploiting classical topic modeling methods. The analogies listed in

Table 2. Analogies used in user–topic modeling.

Classical Topic Modeling	User–Topic Modeling
Corpus	Community
Document	Article
Word	Comment Writer (User)
Topic	Behavioral Characteristic of Users

show the correspondence between the two models.

An online community is analogous to a corpus of textual documents. When an article (or post, thread) is uploaded to an online community, users read it and are involved by leaving comments to it. Although a comment has a textual content, we use its writer to represent it. Therefore, an article is represented as a sequence of users (comment writers), which is analogous to a document being represented as a sequence of words. Recalling the generative probabilistic model of standard topic modeling, we can describe the generative procedure of our probabilistic model as follows. Let K be a prespecified number of topics. For each article $a_i$, we randomly pick a K-dimensional multinomial distribution $P\left(\tau \right|a_i)$ from the Dirichlet distribution with a prespecified parameter. For each comment, we randomly sample its latent topic $\tau \in \{1,\cdots ,K\}$ from the multinomial distribution; let $\tau$ be the selected topic. Then a user is chosen from the distribution $P\left(x\right|\tau )$. We need to estimate two probability distributions, $P\left(\tau \right|a_i)$ and $P\left(x\right|\tau )$, from the observed user sequence.

3.2. Topic Assignment Procedure

This subsection describes the procedure for estimating the latent topic in user–topic modeling.

3.2.1. Preliminaries

We denote by $\mathcal{A}=\{a_1,\cdots ,a_n\}$ the set of n articles, each of which is represented as a sequence $a_i=\langle u_j^{\left(i\right)}\rangle$ of users where $u_j^{\left(i\right)}\in \mathcal{U}$ indicates the user who wrote the j-th comment on the i-th article. The user set $\mathcal{U}$ consists of m users, and a specific user is denoted by x. The time at which article $a_i$ is posted is denoted by $t\left(a_i\right)$.

Let K be the number of topics. In the topic assignment procedure, each individual user’s participation is labeled with one of the topics ${\tau }_1,\cdots ,{\tau }_K$. We denote this assigned label as a latent variable $\mathbf{z}=\langle z_j^{\left(i\right)}\rangle$, where $z_j^{\left(i\right)}\in \{1,\cdots ,K\}$ indicates the topic assigned to the user contributing to the j-th comment in the i-th article.

3.2.2. Preprocessing

In topic modeling on natural language data, the input textual data is preprocessed before it is used in the main process. This includes such procedures as removing tokenization, lemmatization, stop word removal, and insignificant word filtering. Likewise, we need to preprocess the user sequence data rather than using it in its raw form. Although we utilize the same method, there are differences in characteristics between the two domains. Focusing on these differences, we propose our own preprocessing technique before applying the topic modeling method to user participation data.

Similar to preprocessing linguistic data, where documents that are too short are filtered out, we exclude articles that only a small number of users have participated in. On the other hand, unlike natural language data, where there are some words like “a” and “the” that appear in every document, we do not observe an individual user leaving comments on every article in the online community. What matters more in web community data are users who have an exceedingly short lifetime. These users have participated in only a small number of articles, then quit the community. If we analyze user behavior without excluding these temporary users, latent topics would be dominated by the lifetime of their engaged users, so we may fall into a trap where only temporal behavior is taken into account. Therefore, we only include users whose lifetime spans almost the full timeline of the dataset.

Let $T\left(x\right)$ be the set of all timestamps of articles in which user x is involved:

$$T\left(x\right)=\{t\left(a_i\right):a_i\in \mathcal{A},u_j^{\left(i\right)}=x \mathrm{for} \mathrm{some} j\}$$

(1)

Then we define the lifetime $\lambda \left(x\right)$ of user x as the number of articles between the first and last participation of x as a fraction of the total number of articles:

$$\lambda \left(x\right)=\frac{\left|\right\{a_i\in \mathcal{A}:minT\left(x\right)\le t\left(a_i\right)\le maxT\left(x\right)\}}{\left|\mathcal{A}\right|}$$

(2)

Figure 1 shows a topic distribution over time and provides an example of how this lifetime filter works. Figure 1a shows the topic distribution without applying the lifetime filter, where the distribution is dominated by time; for example, articles posted at the beginning are most likely to have Topic 6 and those at the end of the timeline are most likely to have Topic 1, regardless of what they contain and how users have responded. In Figure 1b, when the lifetime filter is applied, this excessive temporal dominance is moderated while dynamic features in topic variations can still be detected.

We also filter out articles in which too small a number of users participated, and users who participated in too small a number of articles. Specifically, we remove articles in which less than ${\theta }_1$ users participated, and we also remove users who appeared in less than ${\theta }_2$ articles. We repeat this removal until all the remaining articles have at least ${\theta }_1$ users and all the remaining users participated in at least ${\theta }_2$ articles.

3.2.3. Topic Assignment with Gibbs Sampling

After preprocessing, we estimate the latent topic for each occurrence of a user using Gibbs sampling. First we assign random topics for each latent variable $\mathbf{z}=\langle z_j^{\left(i\right)}\rangle$, where $z_j^{\left(i\right)}$ indicates the latent topic of the user for the j-th comment in the i-th article. Subsequently, iterating each of indices i and j, we choose the latent topic $z_j^{\left(i\right)}$ by random sampling, regarding the distribution of topics in the remainder of the assignment after removing $z_j^{\left(i\right)}$, denoted by ${\widehat{\mathbf{z}}}_j^{\left(i\right)}$. We also denote by ${\mathbf{z}}_{-j}^{\left(i\right)}$ the partial assignment of ${\widehat{\mathbf{z}}}_j^{\left(i\right)}$ corresponding to the i-th article; i.e., the topic assignment for the user participating in comments in the i-th article except its j-th comment. The probability for sampling can be computed as follows:

$$\begin{array}{cc}\hfill P(z_j^{\left(i\right)}=k|{\widehat{\mathbf{z}}}_j^{\left(i\right)},\mathcal{A})& =P(z_j^{\left(i\right)}=k|{\widehat{\mathbf{z}}}_j^{\left(i\right)},u_j^{\left(i\right)})\hfill \\ \hfill & \propto P(z_j^{\left(i\right)}=k,u_j^{\left(i\right)}|{\widehat{\mathbf{z}}}_j^{\left(i\right)})\hfill \\ \hfill & \propto P\left(u_j^{\left(i\right)}\right|z_j^{\left(i\right)}=k,{\widehat{\mathbf{z}}}_j^{\left(i\right)})P(z_j^{\left(i\right)}=k|{\widehat{\mathbf{z}}}_j^{\left(i\right)})\hfill \\ \hfill & \propto P\left(u_j^{\left(i\right)}\right|z_j^{\left(i\right)}=k)P(z_j^{\left(i\right)}=k|{\mathbf{z}}_{-j}^{\left(i\right)})\hfill \end{array}$$

(3)

We define two matrices M and D where $M_{k,x}$ is the number of assignments of topic ${\tau }_k$ to user $x\in \{1,\cdots ,m\}$, and $D_{i,k}$ is the number of assignments of topic ${\tau }_k$ in article $a_i$. Then the first factor $P\left(u_j^{\left(i\right)}\right|z_j^{\left(i\right)}=k)$ can be computed from the k-th row of M, and the second factor $P(z_j^{\left(i\right)}=k|{\mathbf{z}}_{-j}^{\left(i\right)})$ can be computed from the i-th row of D. Thus, we can compute this probability as follows:

$$\begin{array}{cc}\hfill P(z_j^{\left(i\right)}=k|{\widehat{\mathbf{z}}}_j^{\left(i\right)},\mathcal{A})& \propto \frac{M_{k,x}}{{\sum }_{y=1}^m{M}_{k,y}}\frac{D_{i,k}}{{\sum }_{l=1}^K{D}_{i,l}}\hfill \\ \hfill & \propto \frac{D_{i,k}{M}_{k,x}}{{\sum }_{y=1}^m{M}_{k,y}}\hfill \end{array}$$

(4)

We also use Laplace smoothing for these matrices by adding $\alpha$ (and $\beta$) for every entry of matrix D (and M, respectively), in order to avoid dividing by zero. We used $\alpha =1$ and $\beta =0.1$ in this work.

4. Dataset Description

Before presenting our use of the proposed method in the analysis of online communities, we provide a detailed description of the datasets used. We collected articles with attached comments from three online communities (Reddit, Slashdot, and PGR21) as in

Table 3. Datasets used in this paper.

id	Community	Articles	Comments	Users	Period
R1	Reddit r/politics	56 K	4.1 M	209 K	Mar 2018–Jun 2018	(≈83 days)
R2	Reddit r/AskReddit	483 K	13.6 M	1.2 M	Mar 2018–Jun 2018	(≈91 days)
SD	Slashdot	22 K	3.5 M	33.7 K	Jan 2015–Dec 2017	(3 years)
PG	PGR21	17 K	975 K	9.1 K	Jan 2015–Dec 2017	(3 years)

.

Reddit is one of the largest online communities in the United States, and it consists of a number of subcommunities called subreddits, among which we selected two subreddits: r/politics and r/AskReddit. Our reason for selecting these is two-fold. They are both popular subreddits with a large number of active users. In subreddit r/politics, the main topic is political issues, as its name indicates, and on average more than 650 articles are posted per day. In the dataset we collected, more than 209 k users participated in the articles, leaving a total of 4.1 M comments. In r/AskReddit, questions across a variety of fields, ranging from “personal stuff” to serious social problems, are uploaded, and users answer and discuss the questions they are interested in. There are 5 k articles per day on average, in which 1.2 M users leave a total of more than 13 M comments. The users in these two subreddits display different behaviors. The user interaction in r/politics is observed to be more intensive than that in the AskRedit subreddit. The number of articles receiving more than 10 comments in r/politics is 63.8% of all articles, while only 40.4% of articles in r/AskReddit achieved this. About 7% of users leave at least 50 comments in r/politics, while the portion of such users in r/AskReddit is only 3.6%.

Slashdot is a discussion-centric community with a moderate scale. This community supports many functionalities, such as categorization and comment-rating systems, to encourage intensive and constructive discussion across a variety of topics. The average number of articles posted per day is about 20, which is considerably smaller than for the Reddit datasets. Due to this difference in scale, we collected articles over 3 years from Slashdot, while the duration of the Reddit dataset is about 3 months. However, this difference in article generation rates provides another perspective on community characteristics. User participation in Slashdot is more active as the exposure of each individual article lasts much longer, and almost all articles have at least 10 comments, while about 36% of the articles in r/politics have less than 10 comments.

PGR21 is another moderate-scale community in South Korea, which also has a relatively low article generation rate, less than 20 articles per day. We collected articles from PGR21 freeboard for 3 years. This community is not as dedicated to discussion as Slashdot is. Users can post articles on any topic, ranging from “mild” stories of everyday life to controversial political issues. However, some community rules (for example each article should contain a certain amount of personal opinion from the article uploader), and a relatively longer exposure of articles (about 2–3 days on the front page), encourage users to actively communicate with each other, which sometimes leads to intense discussion.

5. Case Study: Experimental Results

In this section, we present some experimental results obtained using our proposed user–topic model. For the preprocessing step, we used the parameters ${\theta }_1=25$, ${\theta }_2=50$, except for PGR21 where ${\theta }_1={\theta }_2=10$ is used, due to its relatively small scale. For the implementation of Gibbs-sampling for topic modeling, we used GibbsLDA++ [37]. We performed topic modeling with the number of topics ranging from 2 to 64. From these we selected some notable results, which show the variety of ways in which our method can be applied.

5.1. Thematic and Temporal Analysis

User–topic modeling can be used to analyze the behavioral characteristics of community users in terms of thematic and temporal factors. A temporal topic is one that users actively engage with over a certain time period. A temporal topic can be generated from a significant event, or it can develop naturally when some particular users are consistently active over a certain time period. An article with a thematic topic is consistently addressed over time, and involves users who are interested in this topic.

5.1.1. Temporal Topic Flow

The basic method of demonstrating the characteristics of topics is to depict how active they are over time. We define topic flow ${\phi }_k(d;w)$ of a topic ${\tau }_k$ starting at time d (in days), with time window size w, as the number of occurrences of ${\tau }_k$ in the topic assignment within the given time interval; e.g., ${\phi }_2(5;w=10)$ indicates the number of occurrences of topic ${\tau }_2$ within 10 days from the 5th day in the dataset.

$${\phi }_k(t;w)=\sum _{a_i\in {\mathcal{A}}_d^{d+w}}\left|\{j:z_j^{\left(i\right)}=k\}\right|$$

(5)

where ${\mathcal{A}}_d^{d+w}$ is the set of articles that are uploaded within the interval $[d,d+w]$:

$${\mathcal{A}}_d^{d+w}=\{a_i\in \mathcal{A}:d\le t_{\mathtt{day}}\left(a_i\right)<d+w\}$$

(6)

Figure 2 shows the topic flow for the SD dataset with the number of topics $K=4$ and $w=20$. We observe that Topic 1 occupies a large portion of the first half of the dataset, and the portion of Topic 3 gradually increases with time. Topics 2 and 4 are more evenly distributed over time than the other topics.

From the variation of a topic over time, we can distinguish temporal topics from thematic topics. Temporal topics are formed by users who actively participate in community activity over a certain time frame, therefore the temporal factor can be determined from the difference between the maximum and minimum degree of topic activation. We define the temporality of a topic ${\tau }_k$ as follows:

$$\mathtt{temporality}\left(k\right)=lg\frac{{max}_d{\phi }_k\left(d\right)}{{min}_d{\phi }_k\left(d\right)}$$

(7)

Note that temporal and thematic topic factors are not mutually exclusive, which means a topic can have both temporal and thematic factors. For example, if many users are involved in discussion of a political election, this user behavior can be detected as a topic that has political issues as a thematic factor, and the election period as a temporal factor.

Table 4. Qualitative assessment of topics in Figure 2.

Topic	Temporality	Class	Subjects
1	3.44	Temporal	Mixed
2	1.76	Thematic	Climate Change
3	2.44	Thematic + Temporal	Technology, Business
4	1.11	Thematic	OS Development

shows the temporality of each topic depicted in Figure 2. We also list the topic subjects, and their classification as temporal or thematic topics according to their temporalities. It is obvious that Topic 1 is a temporal topic, because it has gradually decreased over time, and its share has almost disappeared by the end of the dataset period. Topics 2 and 4 are classified as thematic topics due to low temporality measures. Their contents are climate change and OS development, respectively. Topic 3 is determined to be a combination of the two classes. Several articles regarding technology and business tend to have topics with this classification. Its portion gradually increases over time, but the change is not as great as that of Topic 1, which has shrunk almost to zero by the end of the period.

5.1.2. Qualitative Topic Assessment from Top Articles

We can qualitatively determine which thematic subjects belong to a topic by examining the articles whose engaged users mostly have the topic assigned to them. From the topic assignment we can easily compute the probability $P\left({\tau }_k\right|a_i)$, which indicates the portion of topic ${\tau }_k$ in article $a_i$.

Table 5. Top-5 articles per topic in Slashdot data ($K=4$).

Topic	Rank	Prob	Title
1	1	0.96	Sending Angry Emails Just Makes You Angrier
	2	0.95	Connected Gun Lets Anyone Watch What Or Who You Are Shooting
	3	0.95	Judge: Warrantless Airport Seizure of Laptop ‘Cannot Be Justified’
	4	0.94	Secret Service Plans New Fence, Full Scale White House Replica, But No Moat
	5	0.94	New Molecular 3D Printer Can Create Billions of Compounds
2	1	0.97	Top Democrats Request FBI Investigation of Trump Campaign Ties To Russia
	2	0.96	Scientists: What We’re Doing To The Earth Has No Parallel In 66 Million Years
	3	0.96	Climate Deal: US and China Join Paris Climate Accords
	4	0.95	Climate Change Is Altering Global Air Currents
	5	0.95	Ice Loss In West Antarctica Is Speeding Up
3	1	0.97	Michigan Lets Autonomous Cars On Roads Without Human Driver
	2	0.96	Virtual Zuck Fails To Connect
	3	0.96	DNA Testing For Jobs May Be On Its Way, Warns Gartner
	4	0.95	India’s Infosys To Hire 10,000 American Workers After Trump Criticism
	5	0.94	Let Consumers Sue Companies
4	1	0.98	Devuan’s Systemd-Free Linux Hits Beta 2
	2	0.97	Windows Switch To Git Almost Complete: 8500 Commits and 1760 Builds Each Day
	3	0.97	Mozilla Will Deprecate XUL Add-ons Before the End of 2017
	4	0.97	Debian 8 Jessie Released
	5	0.96	Ubuntu 15.04 Released, First Version To Feature systemd

shows the top-5 articles per topic in terms of probability $P\left({\tau }_k\right|a_i)$ from the Slashdot dataset (SR) with $K=4$. Even though we did not use any textual information in our modeling, we observe that the resulting topics show thematic consistency in their textual contents. This demonstrates our underlying assumption that users would behave according to the thematic subjects with their own interests. More specifically, Topics 2 and 4 clearly show their related thematic topics from the titles of the top engaged articles. The articles of Topic 2 deal with environmental issues such as climate change. Although its top article does not seem to show this topic in its title, some users opened the discussion on this topic with the election pledges and statements of the presidential election candidates. Topic 4 deals with subjects in software development, such as operating systems and related software. Meanwhile, articles on Topic 3 are observed to be related to technology, economics and business, which cover a broader area than Topics 2 and 4. Lastly, articles on Topic 1 have a variety of subjects and are likely to be affected by temporal factors, as shown in Figure 2, where the distribution of Topic-1 articles is biased towards the first half of the dataset.

5.1.3. Comparison with Textual Topic Modeling

We also compared our proposed modeling with classical text-based topic modeling. For this comparison, we exploited the topic modeling method, using the textual content of the articles. Figure 3 shows the results of both user-based and text-based topic modeling. We depicted the relative portion of topics in order to show the temporal variation of the distribution clearly.

In the text-based topic modeling, the topics are more evenly distributed along the time axis compared to the user–topic modeling. This shows that text-based topic modeling is not appropriate for representing temporal factors, which change dynamically over time, in tasks such as event detection. On the other hand, our user–topic model shows more variation with time. It deals with the dynamic nature of topics in a way which addresses the concerns raised in the literature [33]. While other researchers have tackled this dynamicity problem using more complex probabilistic models [33,34], our proposed method can be used for dynamic analysis without any further modification other than the substitution of words with users.

5.2. User Clustering

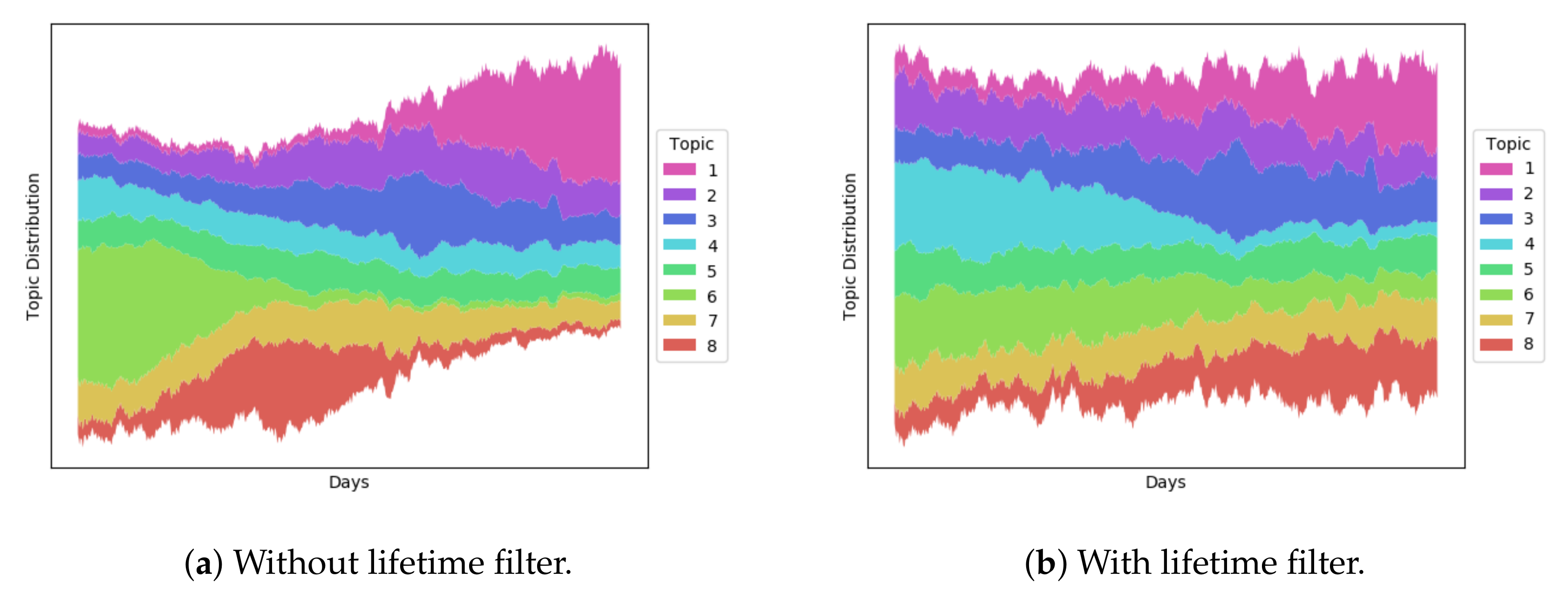
As user–topic modeling is based on the assumption that users with similar latent topics are likely to be engaged in the same article, the proposed method can also be used for clustering purposes. Each user can be represented as a vector of its topic distribution, which means we can use any clustering method based on vector spaces. In this subsection, we conduct two experiments using this approach, one of which is for the purpose of visualization of the user interaction network, while the other is for the assessment of its effectiveness.

5.2.1. Visual Analytics with User Replying Network

The user replying network (or user interaction network) is a graph representing the intensity of user interactions, where each vertex represents a user, and an edge established between two vertices has a weight, indicating how many times two users exchange comments. It is important to visualize the user replying network, so that we can use visual analytics to determine the characteristics of user interactions and the induced community structure.

To visualize this network effectively, we use two graphs: (i) the placement graph, and (ii) the interaction graph.

First, we organize the placement graph, in which edge weights are determined by the similarity of the corresponding user vectors of the two end vertices. We set the vertices, each of which indicates a user, and is associated with its topical distribution. We compute the cosine measure for each pair of users as the similarity. For each user, we establish edges to its 10 nearest users with the computed cosine similarities as the weights. Then we perform the force-based layout method on this graph, in order to place the vertices.

With this vertex placement, we construct the interaction graph for the final visualization. We label the vertices with their dominant topic, to make the relationship between topics visually clear. Then we remove all the edges computed by the topical similarity among users. We reestablish edges using the user replying network, which completes the user interaction graph. The weight of an edge between users is set to the number of articles in which the two users wrote comments to each other. We visualized the constructed graph using Gephi [38].

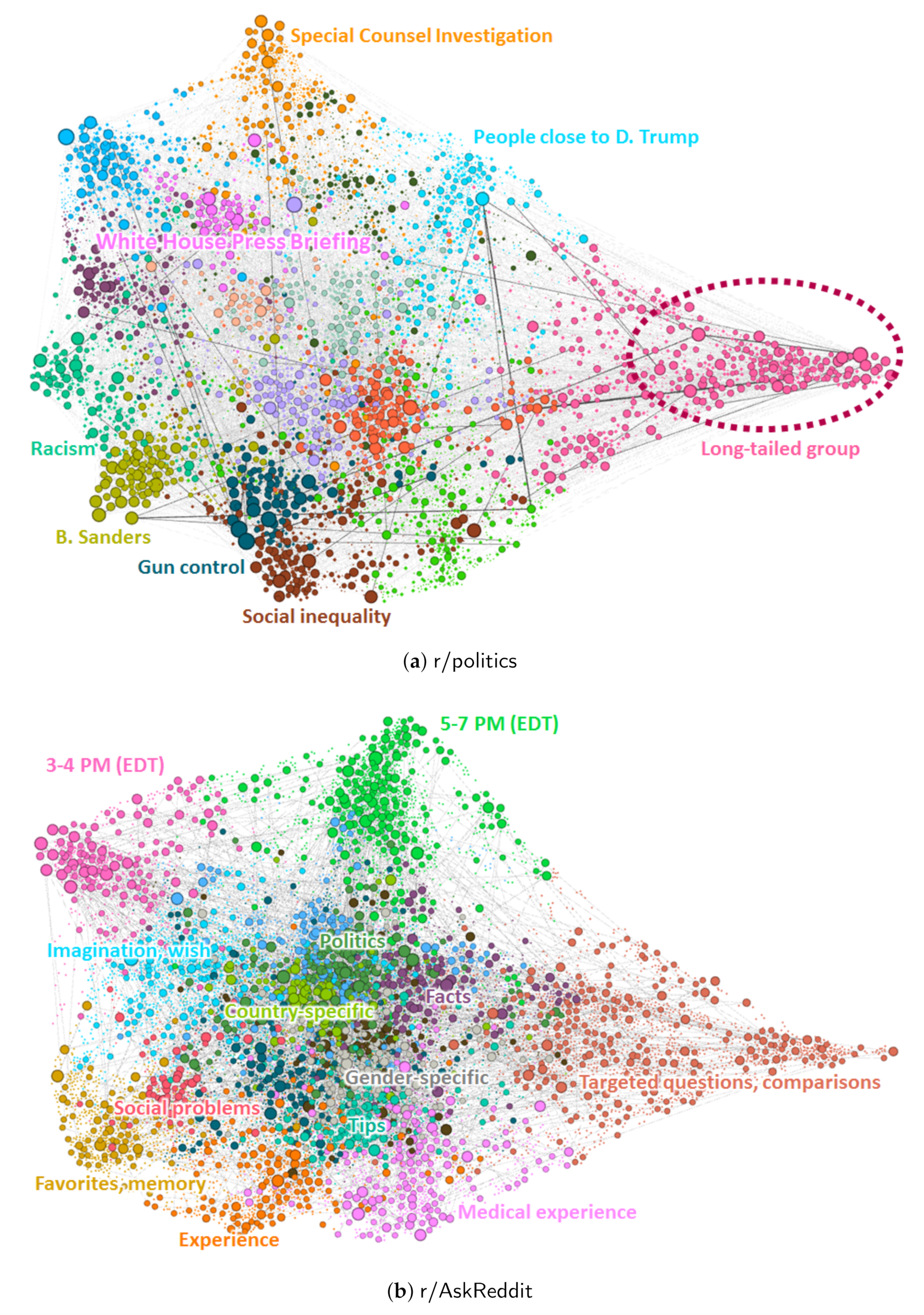
Figure 4 and Figure 5 show the visualized user replying networks obtained using the user–topic model. Vertices are placed according to the dominant topic of the corresponding users. The dominant topics of different users are indicated using different colors. As described, the thickness of an edge indicates weight, which measures how many times the two users interacted. We also assigned different sizes to vertices to represent their degrees (the numbers of neighbors in terms of user interaction).

We see individual characteristics in these visualizations. Comparing the two Reddit datasets depicted in Figure 4, we observe that users with different topics in r/politics are separated more clearly than those in r/AskReddit. There are more thick edges observed in r/politics, which indicates two users meet and debate in many articles, while two users in r/AskReddit rarely meet each other again. This low probability is due to the excessively large numbers of users and articles.

Long-tailed user groups are observed in both Reddit datasets, on the right sides of the figures. If there are a number of users with the same topic whose nearest neighbors are similar to them, edges are unlikely to be connected outside this topic group. This leads to a protrusion (“long tail”) during the force-based vertex placement, and indicates that some users in this topic have generally participated only in some particular articles. In r/politics, they may be avid supporters or critics of a certain political group, although we should investigate more closely to discover the cause of this phenomenon. In r/AskReddit, articles include questions targeting specific groups of people such as transgender people, girls wearing long claw-like nails, and people with face tattoos. These articles also include questions asking users for their personal tips, experiences or preferences, that others do not have. Perhaps these target-specific questions cause the users who participate in these articles to group together tightly.

We also observe that users with related thematic topics are placed close together. Recall that we place the user vertices according to the similarity of their topical distribution vectors. Thus, users close to each other on the graph are likely to share behavioral characteristics. For example in r/politics, users interested in the special counsel investigation are at the top of the graph. Users who like to discuss people close to the president are located close to them (below and right), and users who frequently reacted to the White House Press Briefing are located below and left. As another example, users who are interested in Bernie Sanders are located at the bottom-left corner of the graph. Close to this group, we find several groups of users who have actively participated in articles with content on racism, gun control, and social inequality, issues closely related to this politician.

In r/AskReddit, there are also groups of users who are active at specific times. At the top left and center of the graph in Figure 4b, we find two user groups who usually participated in articles posted around 3–4 p.m. and 5–7 p.m. EDT time, respectively. We also find separate groups of users who leave comments in the articles with their own topics, although the group clusters are not as clear as those in r/politics. Users with related topics tend to be located nearby. For example, users interested in political questions are located close to those who answer country-specific questions such as “What is better in Europe than America?” There are also questions about serious social problems, such as asking opinions on suicide rates in America. Users who discuss such topics are also located close to the country-specific topics. We believe this is because these questions naturally involve comparisons among different countries.

Compared to the Reddit datasets, we observe different distributions in vertex degrees in the two datasets in Figure 5, indicated by the vertex sizes. We observe that there are a small number of users who are excessively active, and interact with a large number of other users, especially for controversial topics. We also observe that these users are clustered according to their interests. For example, in Slashdot, users interested in energy issues such as nuclear power are close to users who are concerned about climate change, as we find them close together at the bottom-right corner of the graph. In PGR21, users interested in political issues are located close to one another, and a number of small groups have been formed. Among these small groups, users sensitive to gender issues are in the middle of the other groups, which means they are likely to simultaneously participate in the articles with political topics around them. Users with these political topics tend to have large degrees, meaning they interact with a large number of users across many articles.

5.2.2. Clustering Coefficient

In order to demonstrate that user–topic modeling can be used in clustering users on user replying networks, we evaluate the proposed method, which assigns users to clusters according to their dominant topics, and compare it with other baseline methods. We used two baseline methods: (i) spectral clustering and (ii) random assignment. Spectral clustering is a popular clustering method for graph data. Using the adjacency matrix of the input graph, it decomposes the vertices into several groups to separate them as much as possible. Random assignment is used for comparison, to show how well both the proposed method and spectral clustering performed the clustering task. As evaluation measure we used the modularity on the user interaction graph, where edges having a weight less than $\theta$ were removed. The modularity of cluster $C=\{C_i\subset V\left(G\right)\}$ on graph G is a measure of the probability of two vertices within the same cluster having an edge between them, compared to random chance, and is defined as follows:

$$\mathtt{modularity}(G,C)=\frac{1}{\left|E\right(G\left)\right|}\sum _{j=1}^k({\Psi }_C\left(j\right)-{\Delta }_C{\left(j\right)}^2)$$

(8)

where ${\Psi }_C\left(j\right)$ is the number of vertex pairs $(v,w)\in C_j\times C_j$ such that $(v,w)\in E\left(G\right)$, and ${\Delta }_C\left(j\right)$ is the sum of the degrees of vertices $v\in C_j$.

Table 6. Clustering performance in terms of modularity.

Dataset	Topics	$\mathit{\theta }=0$			$\mathit{\theta }=1$
		Proposed	Spectral	Random	Proposed	Spectral	Random
R1	2	0.066	0.034	0.001	0.106	0.000	0.000
	4	0.074	0.092	−0.001	0.114	0.000	−0.002
	8	0.060	0.093	0.000	0.094	0.000	0.001
	16	0.044	0.092	−0.001	0.070	0.001	0.001
	32	0.029	0.087	−0.001	0.049	0.002	−0.001
	64	0.018	0.074	0.000	0.032	0.180	-0.001
R2	2	0.035	0.000	0.000	0.062	0.000	0.001
	4	0.055	0.000	0.000	0.081	0.000	0.000
	8	0.046	0.000	0.001	0.068	0.000	−0.002
	16	0.033	0.034	0.000	0.051	0.001	0.000
	32	0.023	0.098	0.000	0.036	0.002	0.000
	64	0.016	0.067	0.000	0.026	0.006	−0.001
SD	2	0.038	0.048	0.000	0.052	0.000	0.000
	4	0.039	0.052	−0.001	0.053	0.000	−0.001
	8	0.032	0.043	−0.001	0.044	0.000	−0.001
	16	0.021	0.034	−0.001	0.030	0.001	0.000
	32	0.014	0.024	−0.001	0.019	0.068	−0.001
	64	0.007	0.000	−0.001	0.011	0.050	−0.002
PG	2	0.079	0.000	−0.001	0.102	0.000	0.002
	4	0.090	0.000	0.001	0.116	0.000	0.002
	8	0.072	0.000	0.000	0.093	0.001	0.001
	16	0.050	0.000	−0.001	0.072	0.002	−0.001
	32	0.033	0.038	−0.002	0.050	0.004	−0.002
	64	0.022	0.014	−0.001	0.036	0.019	−0.003

shows the modularity obtained using the above three methods. For a small number of topics the user–topic method tends to outperform the spectral clustering method. If we choose a higher “threshold” $\theta$, which makes the interaction graph more sparse, and each edge likely to represent more intense interaction, the difference in clustering quality becomes clearer, especially for a small number of topics.

Performing better for a small number of topics is an advantage in many qualitative assessments from which human analysts use the results. Clearly, interpreting results for more than 100 topics would be difficult compared to dealing with just 10 topics. We point out that the spectral clustering method is specialized for improving clustering measures, while our method is not dedicated to this particular task. Nevertheless, the user–topic method performs better than spectral clustering under certain conditions.

In addition, spectral clustering is not robust in some cases, while our method performs consistently. Spectral clustering sometimes fails, especially when the user interaction graph has very small clusters that are weakly connected to the remainder of the graph, resulting in a giant component and isolated small vertex groups after clustering.

5.3. User Behavior Analysis

As a result that users with similar behavior are likely to have the same topic in user–topic modeling, we can use this to analyze community characteristics from the behavioral perspective.

5.3.1. Temporal Behavior of Community Users

Users are active in different time slots; for example, some users connect to the community at night during weekdays, while others are online during working hours. This difference in active hours may affect user interactions. When a large number of articles are uploaded within a given time interval, it is difficult for users with different active hours to be involved in the same article, unless it is marked as a hot. article on the front page. On the other hand, if articles are exposed on the front page for several days due to a low article-upload rate, users are more likely to have a chance to participate in the same article, regardless of their active hours.

Figure 6 shows the active times of users in terms of hour and day of the week for two online communities (R1 and PG datasets). We performed topic modeling with $K=16$ for both datasets, but different scales are used in the figures. In r/politics, we find some groups of users have common active times. For example, users with Topics 2 and 10 are highly active at 18:00–22:00 GMT. Users with Topic 2 are inactive on the weekend, while those with Topic 10 are just less active then. Topic 11 is active during 00:00–05:00 on weekdays. We deduce that these users may live in a different time zone, because their active hours are shifted 3–4 h later than other topic users.

However, these differences in users’ active hours are not observed in the PGR21 dataset. In this community, there is not a sufficient number of articles to push recent articles onto the next page of the article list. Newly uploaded articles can be exposed on the front page for several days, sufficient time for all users to participate, according to their interests. Consequently, the active hours are less important in separating user interactions than in the case of Reddit.

5.3.2. Herd Behavior and Event Detection

We can also detect herd behavior of users affected by high-impact social events. Figure 7a shows the topic flow of the PGR21 dataset with $K=8$. We see peaks in Topic 2 during the second half of the timeline. At that time, a series of events occurred in South Korea concerning the impeachment of the president, and the election of a new president. Moreover, around this time, community rules forced articles on sport and entertainment to be uploaded to a separate bulletin board, which gave the remaining users fewer choices of topics. As a result, almost all users in the community show a shared interest in this topic, resulting in the single-topic peaks at that time. Figure 7b shows another visualization of this topic flow using the dominant topic of articles, instead of topic distribution in individual assignments. For example, if an article has a topic distribution $\langle 0.1,0.1,0.2,0.6\rangle$ with $K=4$, we simply count 1 for Topic 4 instead of summing the distribution vector itself. In this visualization, we can analyze the topic flow more focused on articles, while the original visualization places more emphasis on the user perspective. The peaks are observed much more significantly, which means the articles with this topic dominated the community. The time interval between two peaks of Topic 2 is the period between the impeachment judgment and the presidential election.

5.4. Comparison with Topic Models on User Network

In this subsection, we compare the proposed method with a topic modeling method based on user networks, which is the basic approach that was followed to apply the LDA technique to user analysis in many related studies [24,28,29,30]. Applying the topic modeling technique to user networks is probably effective for a certain type of data where a large user network, such as the Twitter network, is explicitly established, or in certain cases in which a small number of users are involved for an individual engagement; e.g., only a few authors contribute to a single research paper. However, in online community data, the number of users involved in an individual article is quite large; thus, we would not gain any advantage by constructing the user network over them. Furthermore, aggregating the user co-occurrences over articles would make each of the meaningful engagements indistinguishable. For example, we can suppose such a case in which user A and B have commonly participated in a politics-related article, B and C in a sports-related article, A and C in an art-related article. When we construct the user network here, these three users would form a triangle, which would render these users symmetric and indistinguishable. However, note that our proposed method would be able to distinguish the interests of each user in this case.

Figure 8 depicts the histogram of topic distributions of users by comparing the proposed method with the network-based method in which the user network is constructed using co-occurrences. For the purpose of illustration, we ran the topic modeling with two topics, thus each user has a probability distribution $(p,1-p)$; the histograms show the distribution of p over the users. In the proposed method, users are divided into two groups: those with $p\approx 0$ and other with $p\approx 1$, and the other users are almost evenly distributed. This means that users can successfully be clustered using the topic probability. In contrast, network-based topic modeling produced distributions centered at $p=0.5$. This prevents two topics from being distinguished clearly.

For the purpose of quantitative evaluation, we measured the standard deviation of topic distributions as listed in

Table 7. Standard deviation of topic probability distribution of users.

Dataset	#Topics	User-Wise		Topic-Wise
		Proposed	Network-Based	Proposed	Network-Based
R1	2	0.321	0.055	0.348	0.066
	4	0.274	0.078	0.280	0.072
	8	0.203	0.071	0.203	0.052
R2	2	0.323	0.045	0.344	0.056
	4	0.276	0.055	0.283	0.053
	8	0.195	0.040	0.195	0.037
SD	2	0.268	0.107	0.310	0.090
	4	0.256	0.092	0.267	0.092
	8	0.194	0.068	0.200	0.053
PG	2	0.350	0.149	0.366	0.160
	4	0.304	0.179	0.308	0.148
	8	0.227	0.097	0.225	0.089

. Considering a $M\times K$ matrix, where M is the number of users and K is the number of topics, let each row indicate the topic distribution of a user. We computed the standard deviation in both directions: row-wise (user-wise), and column-wise (topic-wise), after which we averaged the values. If the user-wise standard deviation is high, it means a small number of topics form a large portion while the other topics form a small portion; e.g., consider a user with the topic distribution (1,0,0,0). In other words, if this value is low, each topic forms a similar portion, thus they are insignificantly distinguishable; e.g., a user with the topic distribution (0.25,0.25,0.25,0.25) where the standard deviation is zero. On the other hand, the topic-wise standard deviation indicates user variation across a specific topic; e.g., if all users have 0.1 for Topic ${\tau }_1$, then the standard deviation would be 0 and it means ${\tau }_1$ is not meaningful for distinguishing users. The proposed method consistently outperforms network-based modeling as the proposed method has higher standard deviations.

The second drawback of applying network-based topic modeling to online community data is that a direct way to obtain article-level results does not exist, despite the use of the proposed article–user topic modeling, where one of the learnt parameters, i.e., the article–topic matrix, explicitly represents the topic distribution of an article. One may think of computing the topic distribution of an article for the network-based topic modeling method in such a way that aggregates the topic distribution of users involved in the target article. However, this method is not effective as shown in Figure 9. Despite the topic distributions derived from the proposed method, in which topics are distributes widely, the network-based modeling results in very narrow distributions around $p=0.5$, which means every article has a similar topic distribution.

6. Conclusions

Analyzing user behavior in online communities is an important task. We have presented the user–topic model, which utilizes user participation instead of word occurrence, to analyze online communities in terms of topics. The contributions of our work are summarized as follows:

• Textual coherence was observed in the measured topics, although the method is language-independent, as we did not use any textual data in the data processing. This showed that users’ behavior and interests are reflected in their interactions, especially in common engagement with related articles.
• The user–topic model can reflect dynamic features that change over time better than the topic model, which uses only textual data.
• Topic flow graphs and temporality measures were shown to be effective in distinguishing thematic and temporal factors in individual topics.
• The user–topic model can be used to cluster users, with their behavioral features, from various perspectives such as topical interests and active hours.
• The two-stage graph construction and visualization method presented here aids visual analysis of the user interaction network.
• Event detection can also be effectively performed with the user–topic model, by analyzing dynamic topic flow.

The work presented here is a macroscopic analysis method from the perspective of users and articles, which concerns how topics are distributed, how they change over time, and what significant tendencies we can observe. Future studies should consider a microscopic perspective of the user–topic model, performing behavioral analysis within an individual article. We also plan to extend the proposed method in various directions. One extension would be concerned with the weighting problem in constructing pseudo-documents. In this work, we use the sequence of comment writers, which are viewed as a set of users associated with weights, and the weight of a user is to be the number of comments written by the user in an article. We may apply different functions such as $logx$ and $x^2$ to this value and discover the different results that can be obtained with different weighting functions. In addition, many community-specific features exist other than user participation, such as rating, friend relationship, and replying structures. Furthermore, to extend the user–topic modeling method, we need a way to combine these additional features. As a result that one of the aspects we emphasized in this work was simplicity, we also plan to develop a simple method to combine multiple features rather than designing complicated probabilistic models specific to a particular domain.