Fingering Instability of a Gravity-Driven Thin Film Flowing Down a Vertical Tube with Wall Slippage
Abstract
1. Introduction
2. Mathematical Modeling
2.1. Governing Equations and Boundary Conditions
2.2. Scalings and Non-Dimensionalization
2.3. Two Dimensional Simulations
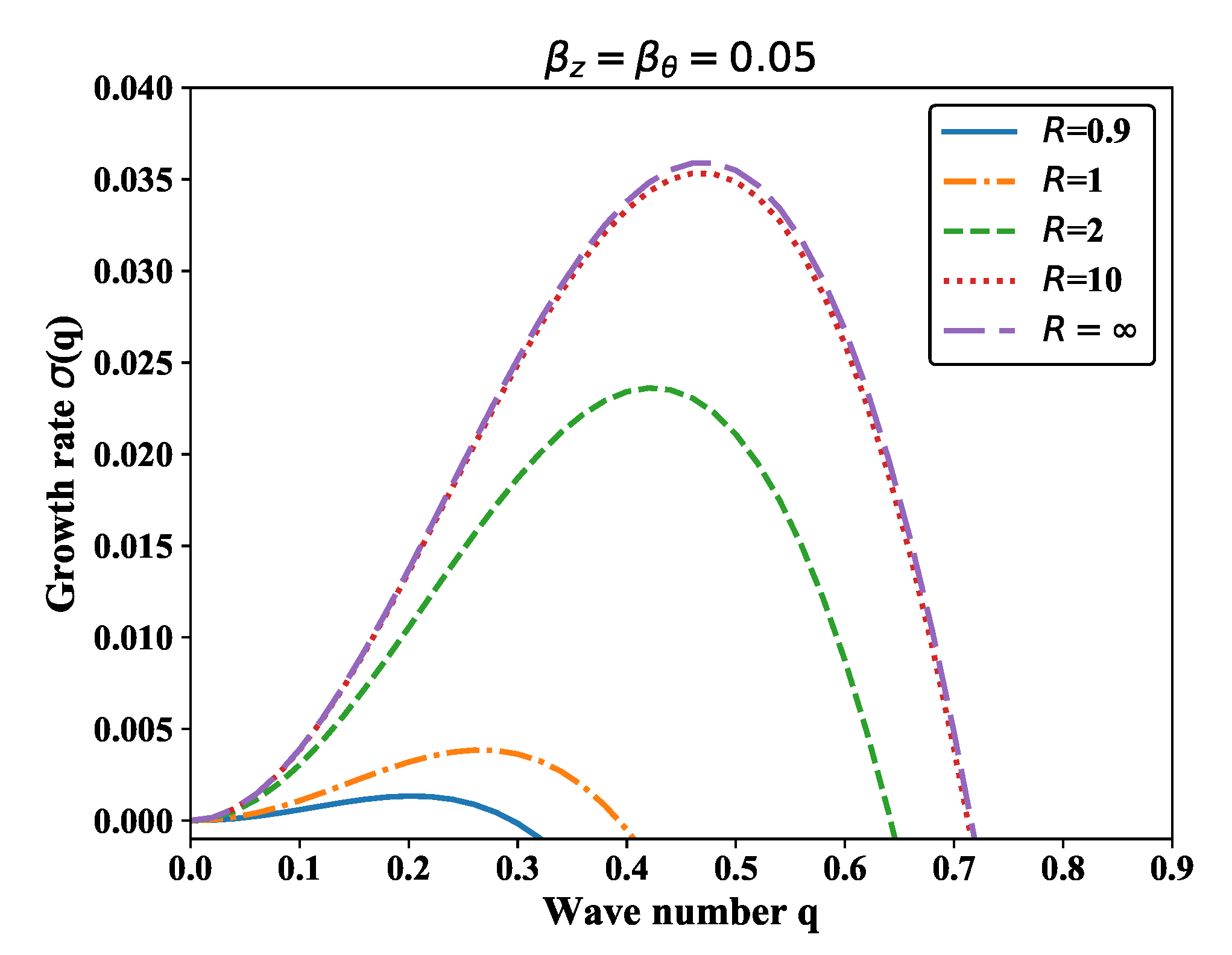
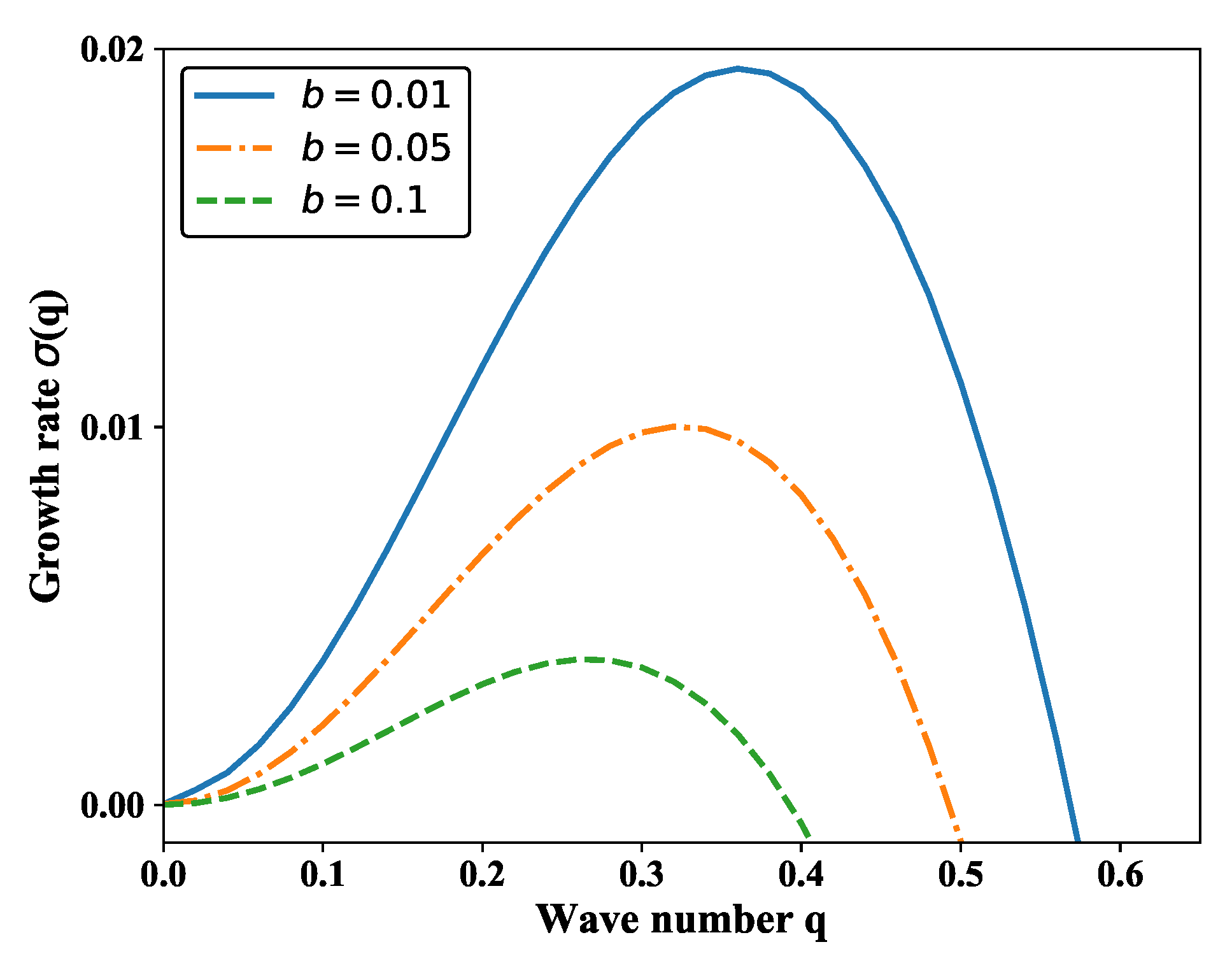
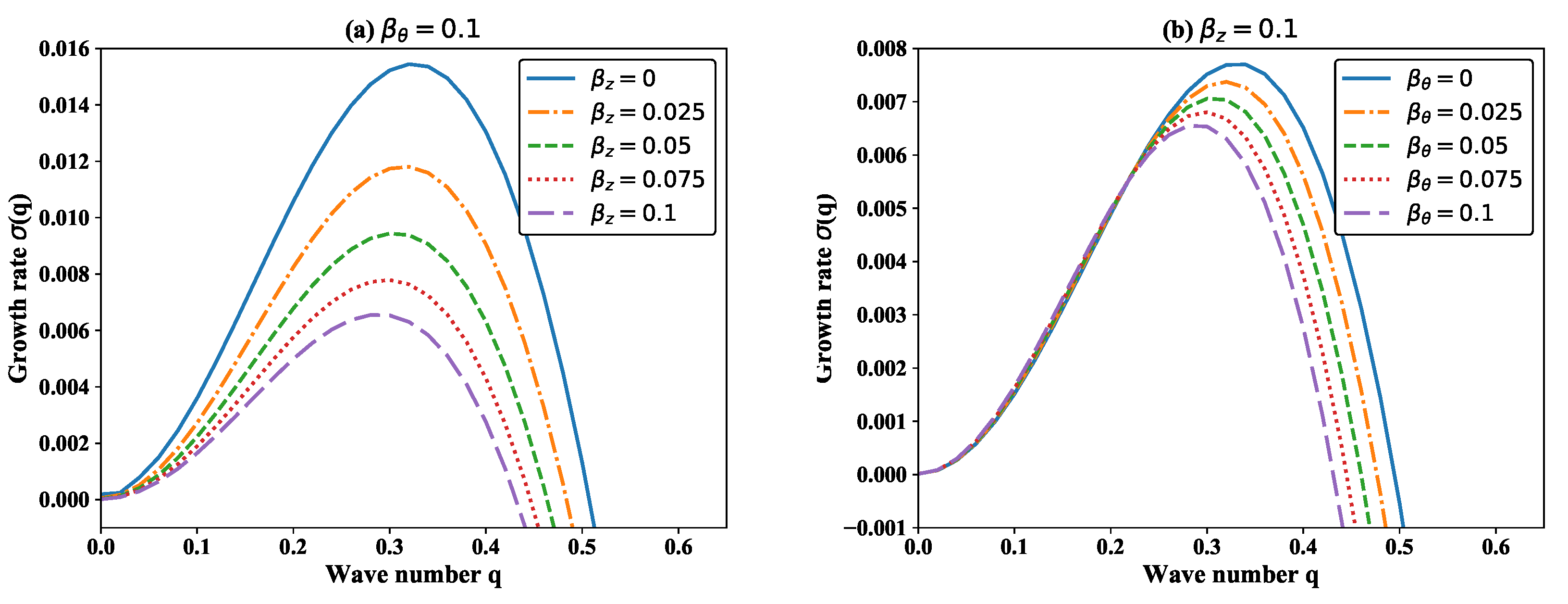
3. Linear Stability Analysis
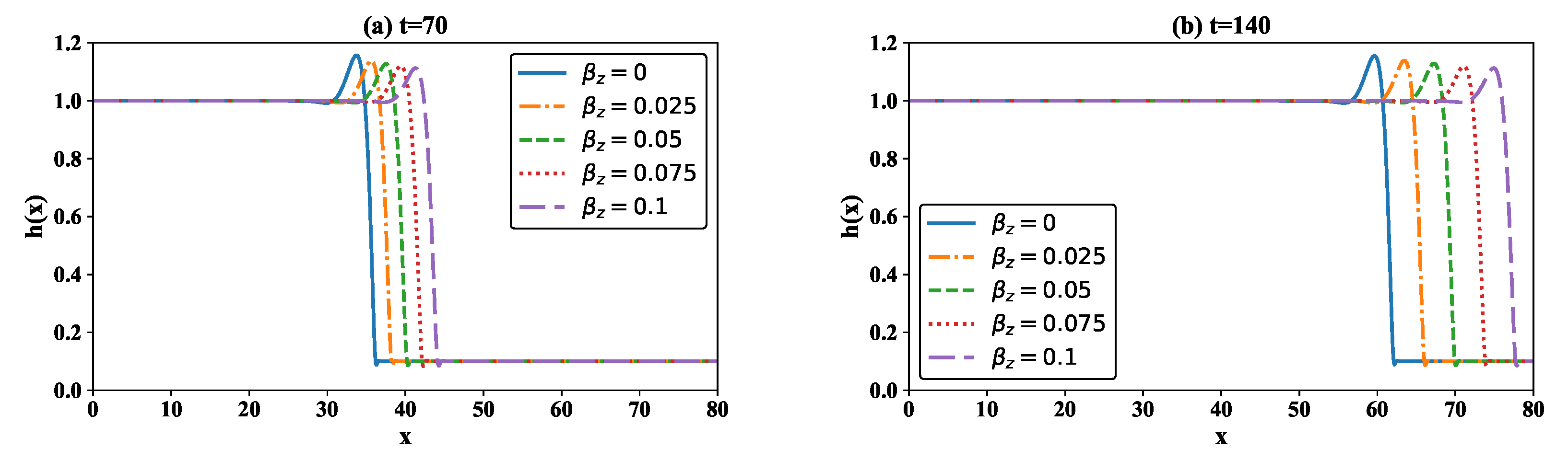
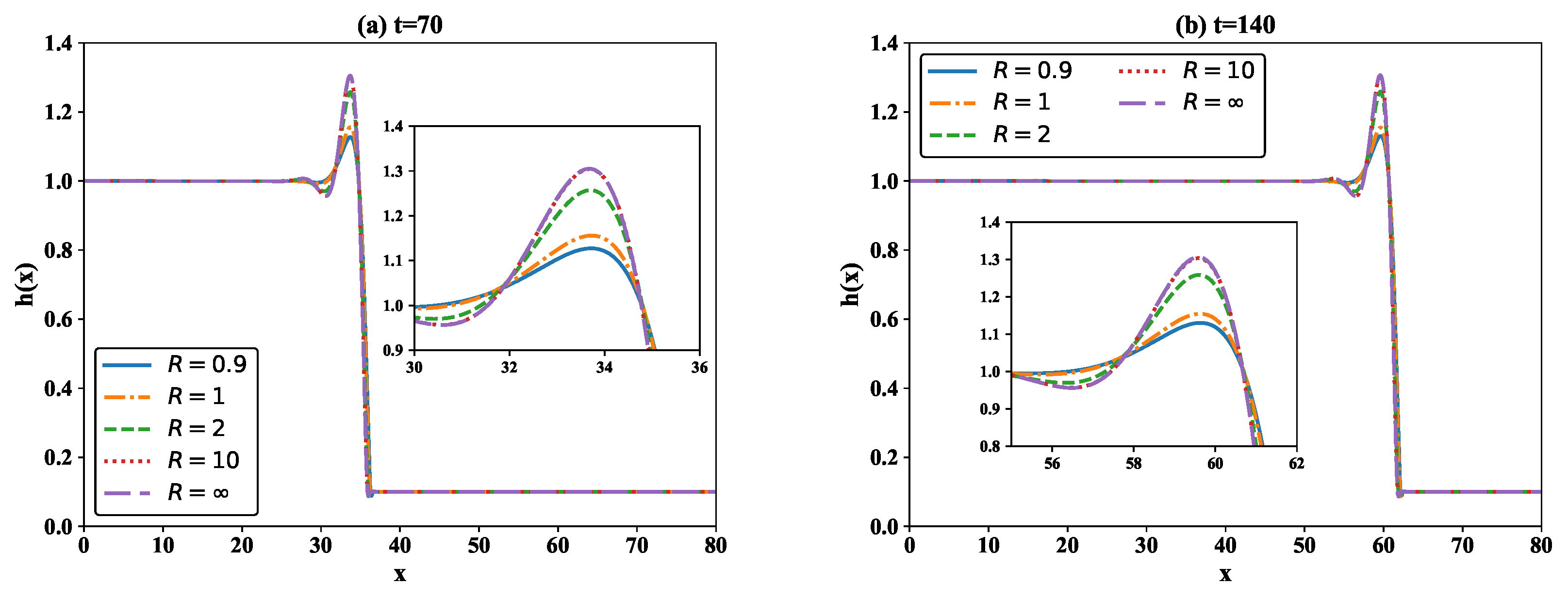
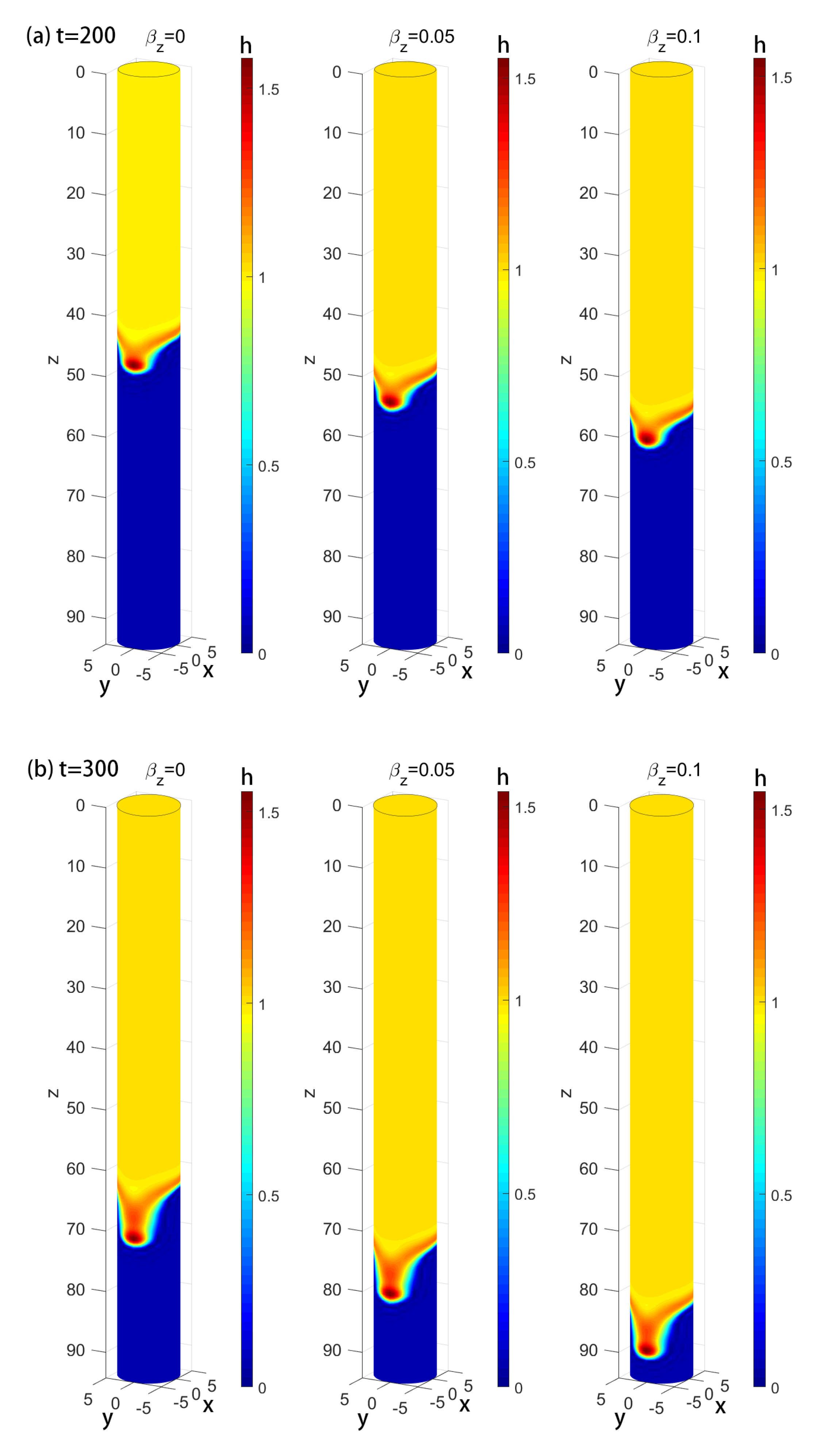
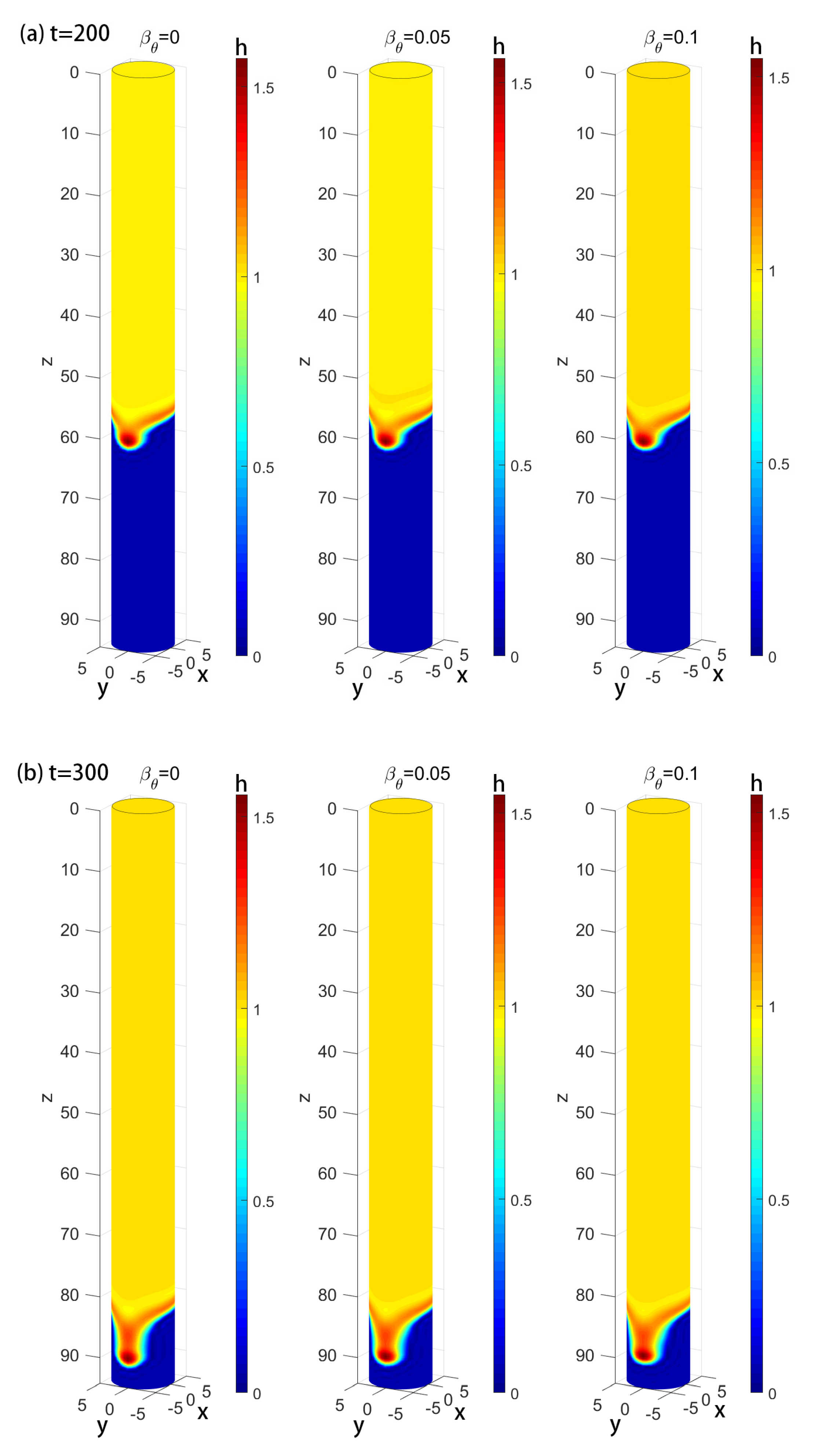
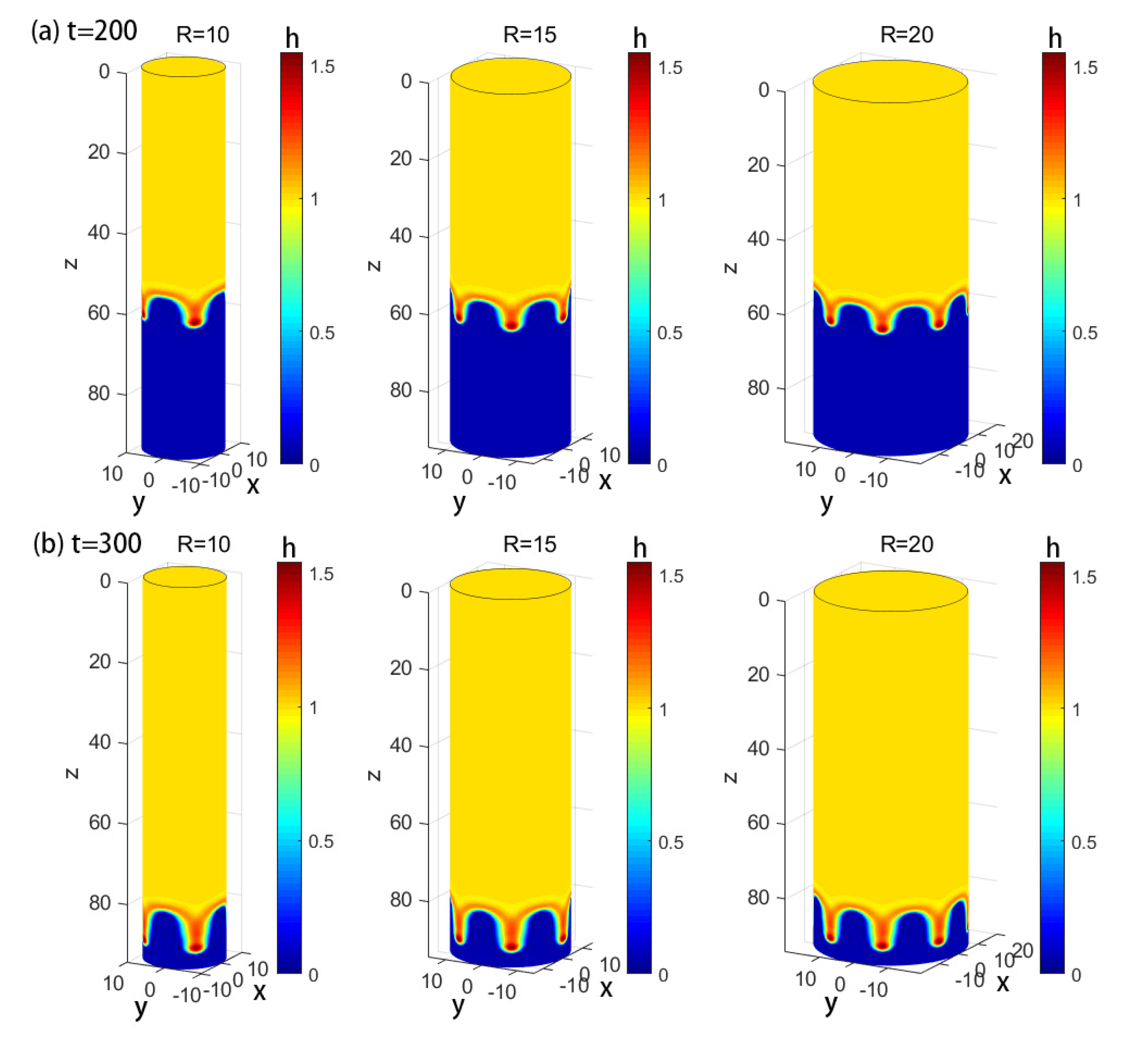
4. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huppert, H.E. Flow and instability of a viscous current down a slope. Nature 1982, 300, 427–429. [Google Scholar] [CrossRef]
- Schwartz, L.W. Viscous flows down an inclined plane: Instability and finger formation. Phys. Fluids A 1989, 1, 443–445. [Google Scholar] [CrossRef]
- Bertozzi, A.L.; Brenner, M.P. Linear stability and transient growth in driven contact lines. Phys. Fluids A 1997, 9, 530–539. [Google Scholar] [CrossRef]
- Oron, A.; Davis, S.H.; Bankoff, S.G. Long-scale evolution of thin liquid films. Rev. Mod. Phys. 1997, 69, 931–980. [Google Scholar] [CrossRef]
- Diez, J.A.; Kondic, L.; Bertozzi, A. Global models for moving contact lines. Phys. Rev. E 2000, 63, 011208. [Google Scholar] [CrossRef]
- Diez, J.A.; Kondic, L. Computing three-dimensional thin film flows including contact lines. J. Comput. Phys. 2002, 183, 274–306. [Google Scholar] [CrossRef]
- Matar, O.K.; Kumar, S. Dynamics and stability of flow down a flexible incline. J. Eng. Math. 2007, 57, 145–158. [Google Scholar] [CrossRef]
- Craster, R.V.; Matar, O.K. Dynamics and stability of thin liquid films. Rev. Mod. Phys. 2009, 81, 1131–1198. [Google Scholar] [CrossRef]
- Marshall, J.S.; Wang, S. Contact-line fingering and rivulet formation in the presence of surface contamination. Comput. Fluids 2005, 34, 664–683. [Google Scholar] [CrossRef]
- Craster, R.V.; Matar, O.K. Numerical simulations of fingering instabilities in surfactant-driven thin films. Phys. Fluids 2006, 18, 032103. [Google Scholar] [CrossRef]
- Kalliadasis, S. Nonlinear instability of a contact line driven by gravity. J. Fluid Mech. 2000, 413, 355–378. [Google Scholar] [CrossRef]
- Leizerson, I.; Lipson, S.G.; Lyushnin, A.V. Finger Instability in Wetting-Dewetting Phenomena. Langmuir 2004, 20, 291–294. [Google Scholar] [CrossRef]
- Kondic, L. Instabilities in gravity-driven flow of thin fluid films. Siam Rev. 2003, 45, 95–115. [Google Scholar] [CrossRef]
- Lin, T.S.; Kondic, L. Thin films flowing down inverted substrates: Two dimensional flow. Phys. Fluids 2010, 22, 052105. [Google Scholar] [CrossRef]
- Lin, T.S.; Kondic, L.; Filippov, A. Thin films flowing down inverted substrates: Three-dimensional flow. Phys. Fluids 2012, 24, 022105. [Google Scholar] [CrossRef]
- Mayo, L.C.; McCue, S.W.; Moroney, T.J. Gravity-driven fingering simulations for a thin liquid film flowing down the outside of a vertical cylinder. Phys. Rev. E 2013, 87, 053018. [Google Scholar] [CrossRef]
- Hu, B.; Kieweg, S.L. Contact line instability of gravity-driven flow of power-law fluids. J. Non-Newton. Fluid Mech. 2015, 225, 62–69. [Google Scholar] [CrossRef]
- Thiele, U.; Knobloch, E. Front and back instability of a liquid film on a slightly inclined plate. Phys. Fluids 2003, 15, 892–907. [Google Scholar] [CrossRef]
- Perazzo, C.A.; Gratton, J. Thin film of non-Newtonian fluid on an incline. Phys. Rev. E 2003, 67, 016307. [Google Scholar] [CrossRef]
- Kondic, L.; Diez, J. Pattern formation in the flow of thin films down an incline: Constant flux configuration. Phys. Fluids 2000, 13, 3168–3184. [Google Scholar] [CrossRef]
- Diez, J.A.; González, A.G.; Kondic, L. Instability of a transverse liquid rivulet on an inclined plane. Phys. Fluids 2012, 24, 032104. [Google Scholar] [CrossRef]
- Chao, Y.; Ding, Z. Thermocapillary thin-film flows on a compliant substrate. Phys. Rev. E 2019, 99, 043101. [Google Scholar] [CrossRef]
- Ding, Z.; Willis, A.P. Relative periodic solutions in conducting liquid films flowing down vertical fibres. J. Fluid Mech. 2019, 873, 835–855. [Google Scholar] [CrossRef]
- Ding, Z.; Liu, Z.; Liu, R.; Yang, C. Breakup of ultra-thin liquid films on vertical fiber enhanced by Marangoni effect. Chem. Eng. Sci. 2019, 199, 342–348. [Google Scholar] [CrossRef]
- Ma, C. Fingering instability analysis for thin gravity-driven films flowing down a uniformly heated/cooled cylinder. Int. J. Heat Mass Trans. 2019, 136, 719–729. [Google Scholar] [CrossRef]
- Ding, Z.; Wong, T.N.; Liu, R.; Liu, Q. Viscous liquid films on a porous vertical cylinder: Dynamics and stability. Phys. Fluids 2013, 25, 064101. [Google Scholar] [CrossRef]
- Liu, R.; Ding, Z. Stability of viscous film flow coating the interior of a vertical tube with a porous wall. Phys. Rev. E 2017, 95, 053101. [Google Scholar] [CrossRef]
- Liu, J.L.; Feng, X.Q.; Wang, G.F.; Yu, S.W. Mechanisms of superhydrophobicity on hydrophilic substrates. J. Phys.-Condens. Mat. 2007, 19, 356002. [Google Scholar] [CrossRef]
- Liu, J.L.; Feng, X.Q.; Yu, S.W. Morphology of liquid drops and thin films on a solid surface with sinusoidal microstructures. Acta Mech. Sin.-PRC 2006, 22, 315–322. [Google Scholar] [CrossRef]
- Liu, J.L.; Feng, X.Q. On elastocapillarity: A review. Acta Mech. Sin.-PRC 2012, 28, 928–940. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, L.; Wang, Y.; Bian, F.; Wang, Y.; Zhao, Y. Multibioinspired slippery surfaces with wettable bump arrays for droplets pumping. Proc. Natl. Acad. Sci. USA 2019, 116, 20863–20868. [Google Scholar] [CrossRef]
- Wong, T.S.; Kang, S.H.; Tang, S.K.; Smythe, E.J.; Hatton, B.D.; Grinthal, A.; Aizenberg, J. Bioinspired self-repairing slippery surfaces with pressure-stable omniphobicity. Nature 2011, 477, 443. [Google Scholar] [CrossRef]
- Kim, P.; Wong, T.S.; Alvarenga, J.; Kreder, M.J.; Adorno-Martinez, W.E.; Aizenberg, J. Liquid-infused nanostructured surfaces with extreme anti-ice and anti-frost performance. ACS Nano 2012, 6, 6569–6577. [Google Scholar] [CrossRef]
- Jiang, J.; Gao, J.; Zhang, H.; He, W.; Zhang, J.; Daniel, D.; Yao, X. Directional pumping of water and oil microdroplets on slippery surface. Proc. Natl. Acad. Sci. USA 2019, 116, 2482–2487. [Google Scholar] [CrossRef]
- Ding, Z.; Liu, Q. Stability of liquid films on a porous vertical cylinder. Phys. Rev. E 2011, 84, 046307. [Google Scholar] [CrossRef]
- Münch, A.; Wagner, B. Contact-line instability of dewetting thin films. Physica D 2005, 209, 178–190. [Google Scholar] [CrossRef]
- Samanta, A.; Ruyer-Quil, C.; Goyeau, B. A falling film down a slippery inclined plane. J. Fluid Mech. 2011, 684, 353–383. [Google Scholar] [CrossRef]
- Samanta, A.; Goyeau, B.; Ruyer-Quil, C. A falling film on a porous medium. J. Fluid Mech. 2013, 716, 414–444. [Google Scholar] [CrossRef]
- Ding, Z.; Wong, T.N. Falling liquid films on a slippery substrate with Marangoni effects. Int. J. Heat Mass Trans. 2015, 90, 689–701. [Google Scholar] [CrossRef]
- Chao, Y.; Ding, Z.; Liu, R. Dynamics of thin liquid films flowing down the uniformly heated/cooled cylinder with wall slippage. Chem. Eng. Sci. 2017, 175, 354–364. [Google Scholar] [CrossRef]
- Hecht, F.; Pironneau, O.; Le Hyaric, A.; Ohtsuka, K. FreeFem++ Manual; Laboratoire Jacques-Louis Lions, Université Pierre et Marie Curie: Paris, France, 2005. [Google Scholar]






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.; Hu, S.; Dong, G.; Li, B. Fingering Instability of a Gravity-Driven Thin Film Flowing Down a Vertical Tube with Wall Slippage. Appl. Sci. 2020, 10, 76. https://doi.org/10.3390/app10010076
Ma C, Hu S, Dong G, Li B. Fingering Instability of a Gravity-Driven Thin Film Flowing Down a Vertical Tube with Wall Slippage. Applied Sciences. 2020; 10(1):76. https://doi.org/10.3390/app10010076
Chicago/Turabian StyleMa, Chicheng, Shuaizhao Hu, Guangxu Dong, and Bo Li. 2020. "Fingering Instability of a Gravity-Driven Thin Film Flowing Down a Vertical Tube with Wall Slippage" Applied Sciences 10, no. 1: 76. https://doi.org/10.3390/app10010076
APA StyleMa, C., Hu, S., Dong, G., & Li, B. (2020). Fingering Instability of a Gravity-Driven Thin Film Flowing Down a Vertical Tube with Wall Slippage. Applied Sciences, 10(1), 76. https://doi.org/10.3390/app10010076




