Machine Learning in Football Betting: Prediction of Match Results Based on Player Characteristics
Abstract
1. Introduction
2. Related Work
2.1. Literature on Sports Betting
2.1.1. Financial Markets and Betting
2.1.2. Forecasting the Outcomes of Sporting Events
2.1.3. Forecasting Football League Match Results
- Reference [18] extracted time dependent skills of teams of the English Premier League as well as the Spanish Primera Division with a Bayesian dynamic generalized linear model. They employed an algorithm to find the parameters of their model and to predict the next football matches based on results of former matches. In total they examined 3892 football matches from 1993 to 1997 and yielded a final cumulative return of 40% (English Premier League) and 54% (Spanish Primera Division).
- Reference [19] predicted Premier League football games by incorporating Twitter Microposts in which users estiamated the outcome of a football match. Thus, these data were yielded from textual information by a parsing algorithm. For 200 matches in 2013/2014, they could realize a profit of about 30%.
- Reference [20] made predictions for match outcomes of the Dutch Eredivisie from 2000 to 2013. The data set uased included of the results of the former matches. Moreover, they added data about whether teams played in a lower leagues in the football season before, about whether a new coach was hired, and whether a top scorer of a team was injured. Different machine learning algorithms were analyzed based on these data regarding their prediction ability (e.g., Decision trees, Neural Networks, and Naive Bayes).
- References [21,22] predicted the football matche results extracting the characteristics of the corresponding teams. They exploited this information incorporating a risk-averse betting strategy. Based on in total 8082 football matches from 2013 to 2018, the authors could achieve economically as well as statistically significant returns.
2.2. Publications about Statistical Arbitrage
3. Simulation Study
3.1. Data Sources
3.1.1. Player Characteristics and Skills
3.1.2. Match Results
3.1.3. Betting Odds
3.2. Simulation Design
3.2.1. Formation Period
- Random forest (RAF): Random forest (In this context we use regression trees rather than classification trees.)combines several uncorrelated decision trees to output a weighted prediction of each tree. Most important, it can handle both, numeric and categorical input which makes it a good choice for a initial model. Overfitting to the formation period is avoided by correcting the habit of decision trees. For further details about this approach, see [30,31].
- Support vector machine (SVM): Support vector machine splits objects into categories, ensuring that no objects are located in the area around the estimated boundaries. As in most cases, we used the kernel trick in order to handle the case of non-linear separable data. References [34,35] explained the concept of SVM.
- Linear regression (LIR): Finally, we benchmarked the approsches with a classic linear regression. Consequently, statistical properties of this naive model can easily be shown. For further details about this approach, see [36].
3.2.2. Trading Period
- If , we forecast that the home team wins. In consequence, we invest 1 monetary unit () on the bet “home team wins”.
- If , we forecast that the away team wins. In consequence, we invest 1 monetary unit () on the bet “away team wins”.
- If , we forecast no clear victory of home team or away team. In consequence, no trading is conducted.
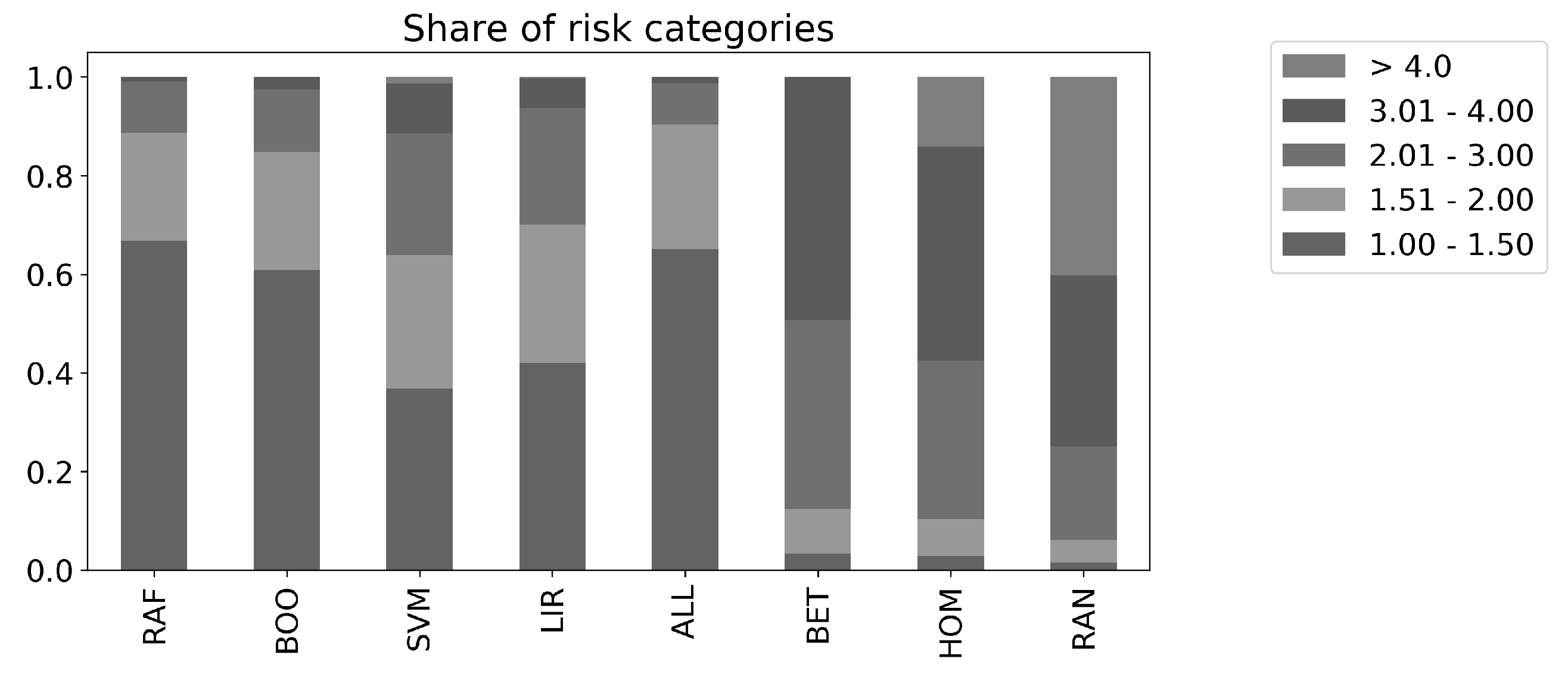
4. Results
4.1. Statistical Analysis
4.2. Financial Analysis
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gil, R.G.R.; Levitt, S.D. Testing the efficiency of markets in the 2002 World Cup. J. Predict. Mark. 2012, 1, 255–270. [Google Scholar]
- Croxson, K.; James Reade, J. Information and efficiency: Goal arrival in soccer betting. Econ. J. 2014, 124, 62–91. [Google Scholar] [CrossRef]
- Forrest, D.; Simmons, R. Sentiment in the betting market on Spanish football. Appl. Econ. 2008, 40, 119–126. [Google Scholar] [CrossRef]
- Franck, E.; Verbeek, E.; Nüesch, S. Prediction accuracy of different market structures - Bookmakers versus a betting exchange. Int. J. Forecast. 2010, 26, 448–459. [Google Scholar] [CrossRef]
- Franck, E.; Verbeek, E.; Nüesch, S. Inter–market arbitrage in betting. Economica 2013, 80, 300–325. [Google Scholar] [CrossRef]
- Spann, M.; Skiera, B. Sports forecasting: A comparison of the forecast accuracy of prediction markets, betting odds and tipsters. J. Forecast. 2009, 28, 55–72. [Google Scholar] [CrossRef]
- Stekler, H.O.; Sendor, D.; Verlander, R. Issues in sports forecasting. Int. J. Forecast. 2010, 26, 606–621. [Google Scholar] [CrossRef]
- Choi, D.; Hui, S.K. The role of surprise: Understanding overreaction and underreaction to unanticipated events using in-play soccer betting market. J. Econ. Behav. Organ. 2014, 107, 614–629. [Google Scholar] [CrossRef]
- Palomino, F.; Renneboog, L.; Zhang, C. Information salience, investor sentiment, and stock returns: The case of British soccer betting. J. Corp. Financ. 2009, 15, 368–387. [Google Scholar] [CrossRef]
- Levitt, S.D. Why are gambling markets organised so differently from financial markets? Econ. J. 2004, 114, 223–246. [Google Scholar] [CrossRef]
- Bernile, G.; Lyandres, E. Understanding investor sentiment: The case of soccer. Financ. Manag. 2011, 40, 357–380. [Google Scholar] [CrossRef]
- Stefani, R.T. Improved least squares football, basketball, and soccer predictions. IEEE Trans. Syst. Man Cybern. 1980, 10, 116–123. [Google Scholar]
- Archontakis, F.; Osborne, E. Playing it safe? A Fibonacci strategy for soccer betting. J. Sports Econ. 2007, 8, 295–308. [Google Scholar] [CrossRef]
- Luckner, S.; Schröder, J.; Slamka, C. On the forecast accuracy of sports prediction markets. In Negotiation, Auctions, and Market Engineering; Springer: Berlin/Heidelberg, Germany, 2008; pp. 227–234. [Google Scholar]
- Zeileis, A.; Leitner, C.; Hornik, K. Probabilistic Forecasts for the 2018 FIFA World Cup Based on the Bookmaker Consensus Model; EconStor: Kiel, Germany, 2018. [Google Scholar]
- Zeileis, A.; Leitner, C.; Hornik, K. Predictive Bookmaker Consensus Model for the UEFA Euro 2016; EconStor: Kiel, Germany, 2016. [Google Scholar]
- Lisi, F. Tennis betting: Can statistics beat bookmakers? Electron. J. Appl. Stat. Anal. 2017, 10, 790–808. [Google Scholar]
- Rue, H.; Salvesen, O. Prediction and retrospective analysis of soccer matches in a league. J. R. Stat. Soc. Ser. D (Stat.) 2000, 49, 399–418. [Google Scholar] [CrossRef]
- Godin, F.; Zuallaert, J.; Vandersmissen, B.; de Neve, W.; van de Walle, R. Beating the bookmakers: Leveraging statistics and Twitter microposts for predicting soccer results. In KDD Workshop on Large-Scale Sports Analytics; ACM: New York, NY, USA, 2014. [Google Scholar]
- Tax, N.; Joustra, Y. Predicting the Dutch football competition using public data: A machine learning approach. Trans. Knowl. Data Eng. 2015, 10, 1–13. [Google Scholar]
- Stübinger, J.; Knoll, J. Beat the bookmaker: Winning football bets with machine learning (best refereed application paper). In Artificial Intelligence XXXV; Springer: Cham, Switzerland, 2018; pp. 219–233. [Google Scholar]
- Knoll, J.; Stübinger, J. Machine-learning-based statistical arbitrage football betting. KI Künstliche Intelligenz 2019. forthcoming. [Google Scholar] [CrossRef]
- Gatev, E.; Goetzmann, W.N.; Rouwenhorst, K.G. Pairs trading: Performance of a relative-value arbitrage rule. Rev. Financ. Stud. 2006, 19, 797–827. [Google Scholar] [CrossRef]
- Avellaneda, M.; Lee, J.H. Statistical arbitrage in the US equities market. Quant. Financ. 2010, 10, 761–782. [Google Scholar] [CrossRef]
- Bertram, W.K. Analytic solutions for optimal statistical arbitrage trading. Phys. A Stat. Mech. Appl. 2010, 389, 2234–2243. [Google Scholar] [CrossRef]
- Do, B.; Faff, R. Does simple pairs trading still work? Financ. Anal. J. 2010, 66, 83–95. [Google Scholar] [CrossRef]
- Li, Y.; Wu, J.; Bu, H. When quantitative trading meets machine learning: A pilot survey. In Proceedings of the 13th International Conference on Service Systems and Service Management, Kunming, China, 24–26 June 2016; pp. 1–6. [Google Scholar]
- Liu, B.; Chang, L.B.; Geman, H. Intraday pairs trading strategies on high frequency data: The case of oil companies. Quant. Financ. 2017, 17, 87–100. [Google Scholar] [CrossRef]
- Stübinger, J.; Endres, S. Pairs trading with a mean-reverting jump-diffusion model on high-frequency data. Quant. Financ. 2018, 18, 1735–1751. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Boulesteix, A.L.; Janitza, S.; Kruppa, J.; König, I.R. Overview of random forest methodology and practical guidance with emphasis on computational biology and bioinformatics. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2012, 2, 493–507. [Google Scholar] [CrossRef]
- Ideker, T.; Dutkowski, J.; Hood, L. Boosting signal-to-noise in complex biology: Prior knowledge is power. Cell 2011, 144, 860–863. [Google Scholar] [CrossRef]
- Zhou, Z.H. Ensemble Methods: Foundations and Algorithms; Chapman and Hall: Boca Raton, FL, USA, 2012. [Google Scholar]
- Schölkopf, B.; Tsuda, K.; Vert, J.P. Support Vector Machine Applications in Computational Biology; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Steinwart, I.; Christmann, A. Support Vector Machines; Springer: New York, NY, USA, 2008. [Google Scholar]
- Mead, R. Statistical Methods in Agriculture and Experimental Biology; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Kotsiantis, S.B.; Zaharakis, I.; Pintelas, P. Supervised machine learning: A review of classification techniques. Emerg. Artif. Intell. Appl. Comput. Eng. 2007, 160, 3–24. [Google Scholar]
- Dietterich, T.G. Ensemble methods in machine learning. In Multiple Classifier Systems; Springer: Berlin/Heidelberg, Germany, 2000; pp. 1–15. [Google Scholar]
- Genre, V.; Kenny, G.; Meyler, A.; Timmermann, A. Combining expert forecasts: Can anything beat the simple average? Int. J. Forecast. 2013, 29, 108–121. [Google Scholar] [CrossRef]
- Bollinger, J. Bollinger on Bollinger Bands; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Stübinger, J.; Bredthauer, J. Statistical arbitrage pairs trading with high-frequency data. Int. J. Econ. Financ. Issues 2017, 7, 650–662. [Google Scholar]
- Rundo, F.; Trenta, F.; Di Stallo, A.; Battiato, S. Grid Trading System Robot (GTSbot): A novel mathematical algorithm for trading FX market. Appl. Sci. 2019, 9, 1796. [Google Scholar] [CrossRef]
- Rundo, F.; Trenta, F.; Di Stallo, A.; Battiato, S. Advanced Markov-based machine learning framework for making adaptive trading system. Computation 2019, 7, 4. [Google Scholar] [CrossRef]
- Kizys, R.; Juan, A.; Sawik, B.; Calvet, L. A biased-randomized iterated local search algorithm for rich portfolio optimization. Appl. Sci. 2019, 9, 3509. [Google Scholar] [CrossRef]
- Knoll, J.; Stübinger, J.; Grottke, M. Exploiting social media with higher-order factorization machines: Statistical arbitrage on high-frequency data of the S&P 500. Quant. Financ. 2019, 19, 571–585. [Google Scholar]
- Stübinger, J. Statistical arbitrage with optimal causal paths on high-frequency data of the S&P 500. Quant. Financ. 2019, 19, 921–935. [Google Scholar]
- Stübinger, J.; Mangold, B.; Krauss, C. Statistical arbitrage with vine copulas. Quant. Financ. 2018, 18, 1831–1849. [Google Scholar] [CrossRef]
- Li, B.; Zhao, P.; Hoi, S.C.H.; Gopalkrishnan, V. PAMR: Passive aggressive mean reversion strategy for portfolio selection. Mach. Learn. 2012, 87, 221–258. [Google Scholar] [CrossRef]
- Endres, S.; Stübinger, J. Optimal trading strategies for Lévy-driven Ornstein-Uhlenbeck processes. Appl. Econ. 2019, 51, 3153–3169. [Google Scholar] [CrossRef]
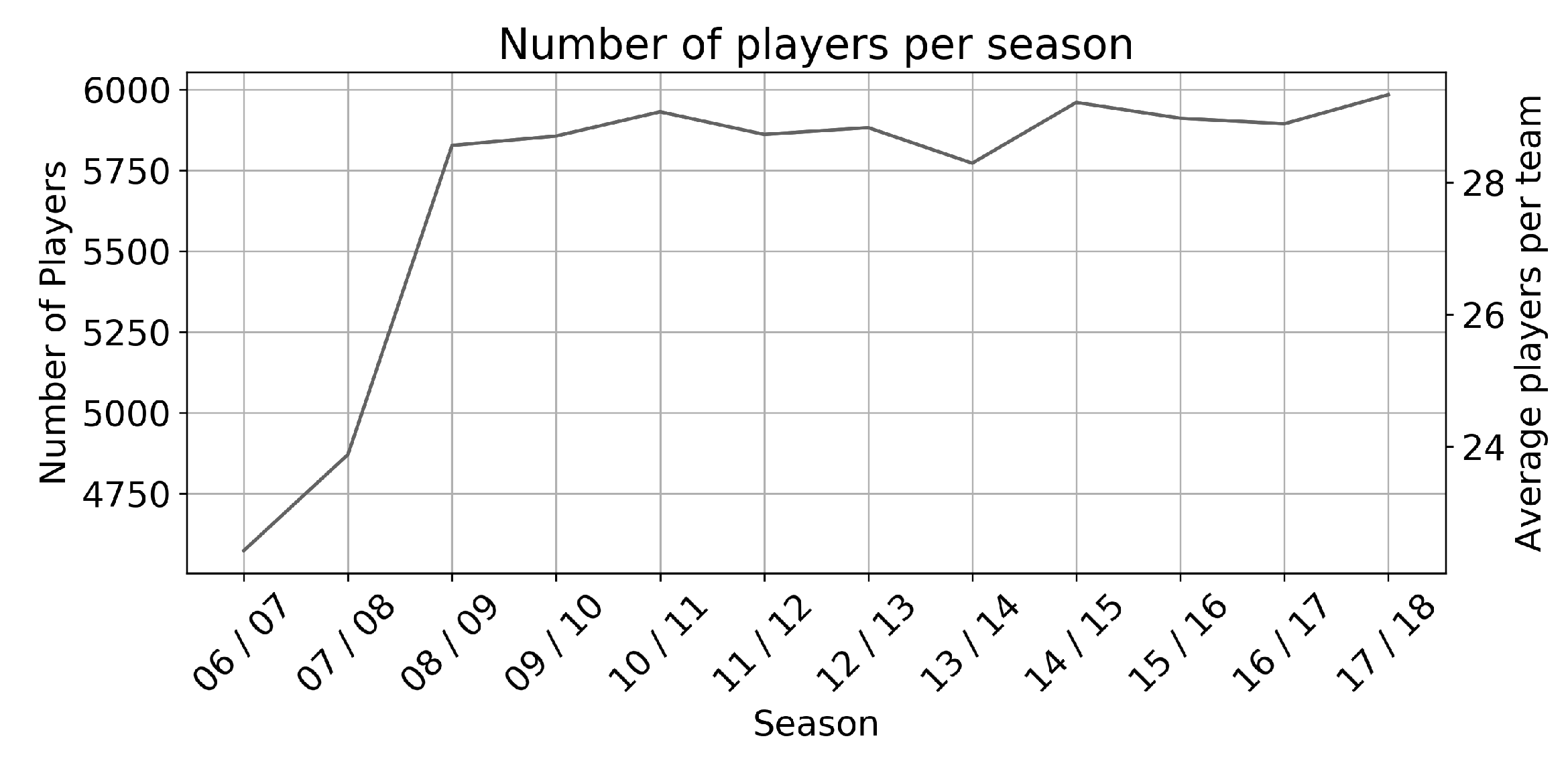
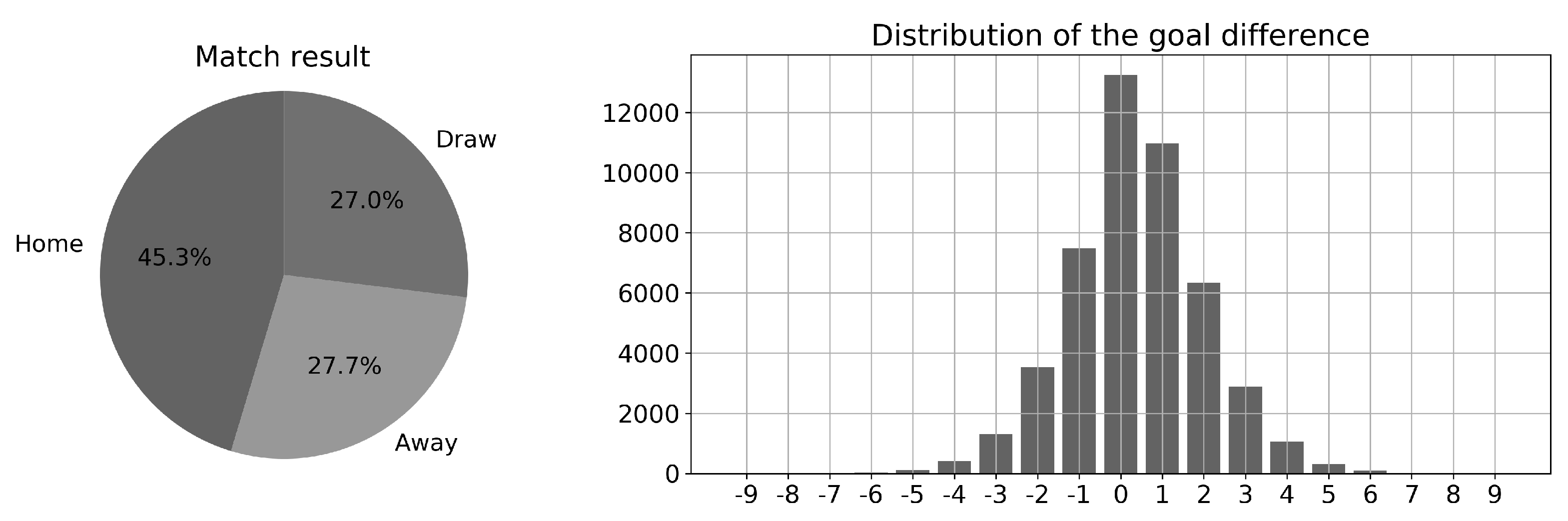

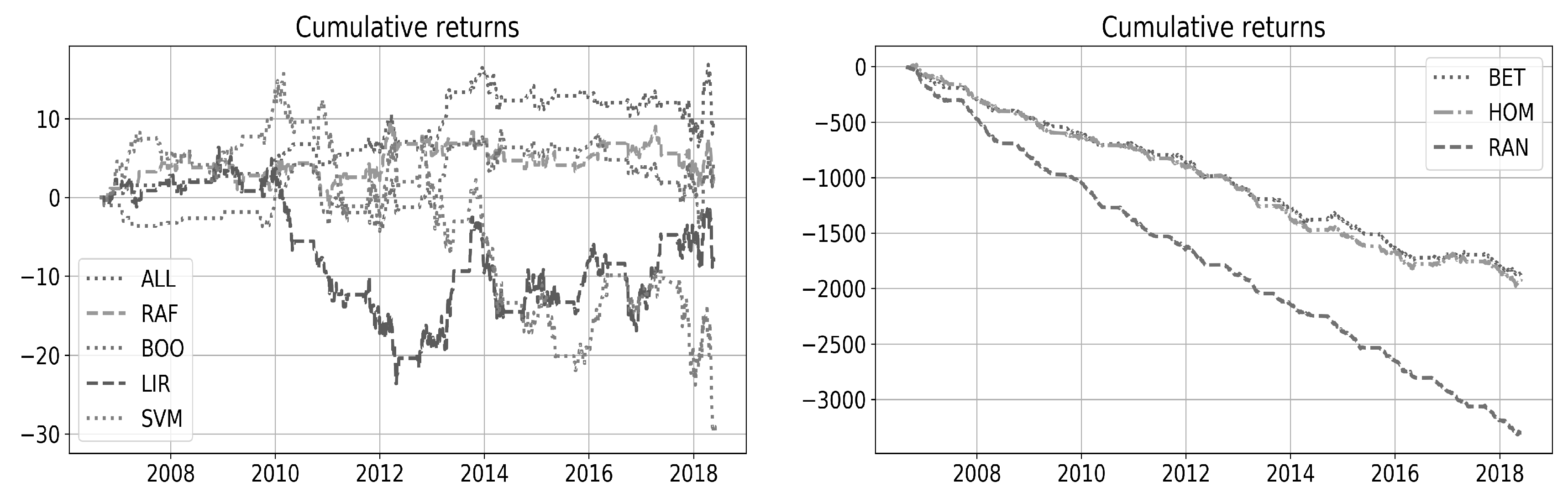
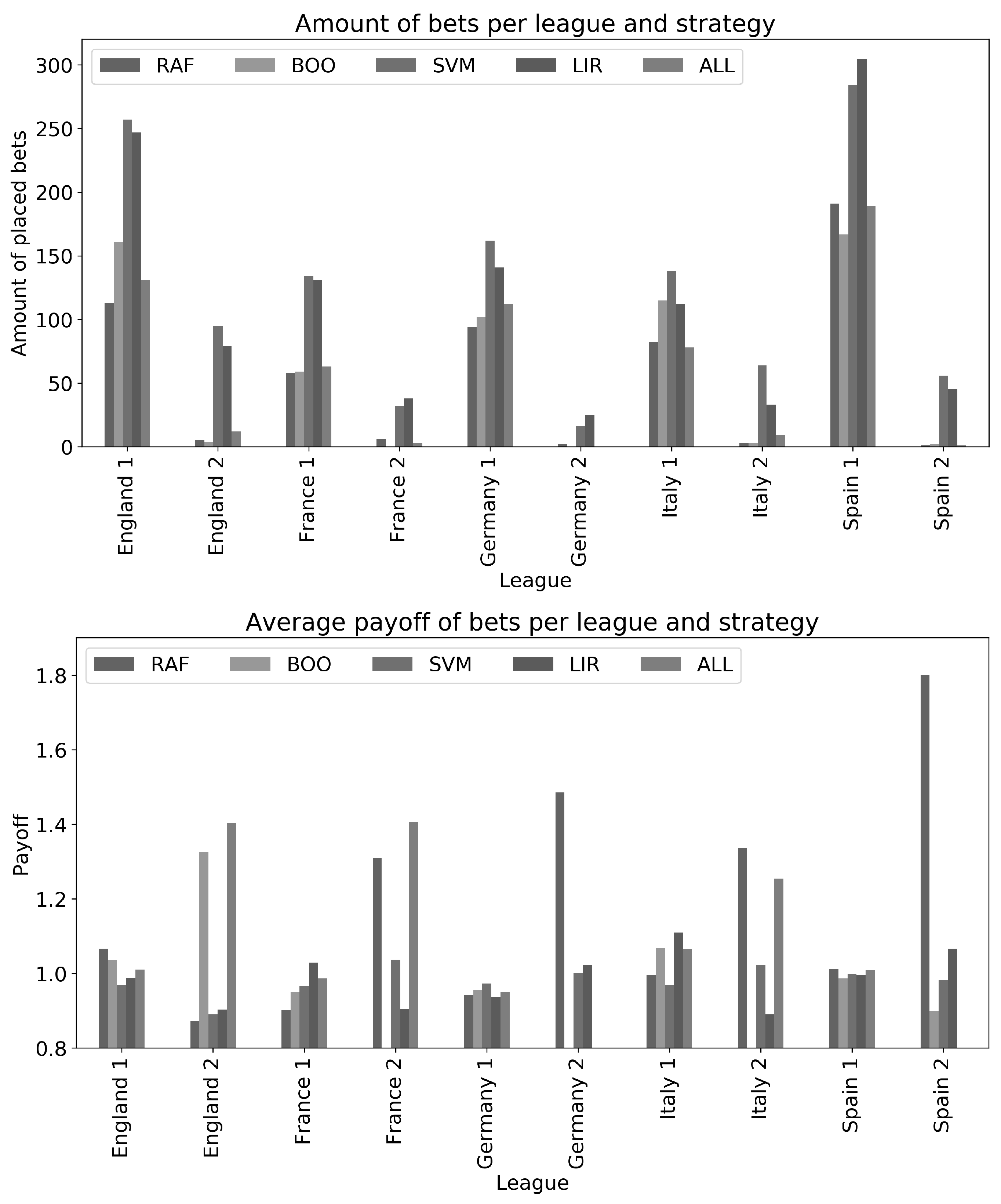
| Min. | Quart. 1 | Median | Quart. 3 | Max. | Mean | |
|---|---|---|---|---|---|---|
| 1. General | ||||||
| Age | 15 | 21 | 25 | 28 | 46 | 25.20 |
| Height | 150 | 178 | 182 | 186 | 204 | 181.68 |
| Weight | 50 | 71 | 75 | 80 | 110 | 75.74 |
| 2. Ball Skills | ||||||
| Ball Control | 5 | 54 | 64 | 72 | 97 | 60.18 |
| Dribbling | 1 | 44 | 60 | 69 | 97 | 55.16 |
| 3. Passing | ||||||
| Crossing | 1 | 40 | 56 | 66 | 95 | 52.18 |
| Short Pass | 1 | 53 | 63 | 71 | 97 | 59.63 |
| Long Pass | 3 | 45 | 57 | 66 | 97 | 54.66 |
| 4. Shooting | ||||||
| Heading | 1 | 47 | 58 | 68 | 95 | 55.31 |
| Shot Power | 2 | 48 | 61 | 71 | 97 | 57.95 |
| Finishing | 1 | 30 | 48 | 63 | 97 | 46.89 |
| Long Shots | 1 | 35 | 53 | 64 | 96 | 49.55 |
| Curve | 1 | 36 | 52 | 64 | 93 | 49.67 |
| Free Kick Accuracy | 1 | 34 | 48 | 61 | 97 | 47.04 |
| Penalties | 3 | 41 | 52 | 63 | 96 | 51.00 |
| Volleys | 1 | 31 | 47 | 60 | 93 | 45.51 |
| 5. Defence | ||||||
| Marking | 1 | 25 | 49 | 65 | 96 | 45.95 |
| Slide Tackle | 2 | 25 | 52 | 66 | 95 | 46.83 |
| Stand Tackle | 1 | 26 | 55 | 69 | 94 | 49.08 |
| Tackling | 1 | 28 | 53 | 68 | 95 | 49.77 |
| 6. Physical | ||||||
| Acceleration | 13 | 59 | 68 | 75 | 97 | 66.08 |
| Stamina | 9 | 58 | 68 | 75 | 96 | 65.22 |
| Strength | 3 | 59 | 67 | 75 | 96 | 65.88 |
| Balance | 15 | 56 | 65 | 73 | 96 | 63.96 |
| Sprint Speed | 14 | 60 | 68 | 75 | 97 | 66.52 |
| Agility | 15 | 56 | 65 | 74 | 96 | 63.99 |
| Jumping | 14 | 59 | 67 | 73 | 96 | 65.85 |
| 7. Mental | ||||||
| Aggression | 2 | 49 | 62 | 72 | 97 | 59.21 |
| Reactions | 11 | 58 | 65 | 71 | 96 | 64.20 |
| Att. Position | 2 | 37 | 55 | 66 | 96 | 50.98 |
| Interceptions | 4 | 28 | 52 | 66 | 94 | 48.64 |
| Vision | 1 | 44 | 56 | 66 | 97 | 54.27 |
| Composure | 3 | 51 | 61 | 69 | 96 | 59.37 |
| 8. Goalkeeper (GK) | ||||||
| GK Positioning | 1 | 9 | 13 | 21 | 96 | 18.58 |
| GK Diving | 1 | 7 | 10 | 13 | 93 | 15.23 |
| GK Handling | 1 | 8 | 11 | 14 | 91 | 16.18 |
| GK Kicking | 1 | 8 | 11 | 14 | 95 | 15.92 |
| GK Reflexes | 1 | 7 | 10 | 13 | 94 | 13.36 |
| Reflexes | 1 | 20 | 21 | 23 | 96 | 24.31 |
| Handling | 1 | 20 | 21 | 23 | 93 | 23.93 |
| Minimum | Median | Maximum | Mean | |
|---|---|---|---|---|
| Home | 1.02 | 2.10 | 26.00 | 2.42 |
| Draw | 1.29 | 3.30 | 17.00 | 3.53 |
| Away | 1.08 | 3.50 | 51.00 | 4.27 |
| RAF | BOO | SVM | LIR | ALL | BET | HOM | RAN | |
|---|---|---|---|---|---|---|---|---|
| Prediction Quality | ||||||||
| Accuracy | 0.8126 | 0.7912 | 0.6971 | 0.7292 | 0.8177 | 0.4991 | 0.4544 | 0.3605 |
| RMSE | 1.8717 | 1.9606 | 2.0827 | 2.0210 | 1.9079 | 9.5602 | 9.7600 | 10.1493 |
| MAD | 1.4736 | 1.5417 | 1.6939 | 1.6346 | 1.4945 | 9.4253 | 9.6190 | 10.0065 |
| Betting details | ||||||||
| Average Payoff | 1.0043 | 1.0072 | 0.9757 | 0.9932 | 1.0158 | 0.9547 | 0.9540 | 0.9183 |
| Placed bets | 555 | 613 | 1238 | 1156 | 598 | 41077 | 41681 | 41681 |
| Home team bet | 0.8595 | 0.8173 | 0.8102 | 0.8183 | 0.8428 | 0.7907 | 1.0000 | 0.4981 |
| Away team bet | 0.1405 | 0.1827 | 0.1898 | 0.1817 | 0.1572 | 0.2093 | 0.0000 | 0.5019 |
| Predicted Values | ||||||||
| Maximum | 4.8715 | 5.1226 | 5.8372 | 5.9047 | 5.2657 | - | - | - |
| Minimum | −2.8546 | −2.6029 | −3.9798 | −4.5213 | −2.9441 | - | - | - |
| RAF | BOO | SVM | LIR | ALL | BET | HOM | RAN | |
|---|---|---|---|---|---|---|---|---|
| Mean | 0.0043 | 0.0072 | −0.0243 | −0.0068 | 0.0158 | −0.0453 | −0.0460 | −0.0817 |
| p-value of Wilcoxon-Test | 0.0000 | 0.0000 | 0.3924 | 0.0029 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Minimum | −1.0000 | −1.0000 | −1.0000 | −1.0000 | −1.0000 | −1.0000 | −1.0000 | −1.0000 |
| Quartile 1 | 0.0650 | 0.0600 | −1.0000 | −1.0000 | 0.0700 | −1.0000 | −1.0000 | −1.0000 |
| Median | 0.1600 | 0.1700 | 0.1800 | 0.1800 | 0.1700 | −1.0000 | −1.0000 | −1.0000 |
| Quartile 3 | 0.2500 | 0.2800 | 0.4000 | 0.3900 | 0.2500 | 0.9100 | 0.9100 | 0.8500 |
| Maximum | 1.7500 | 1.8800 | 3.0000 | 2.1000 | 1.7500 | 1.8000 | 16.0000 | 25.0000 |
| Standard deviation | 0.5131 | 0.5620 | 0.7046 | 0.6533 | 0.5132 | 0.9962 | 1.1802 | 1.4538 |
| Skewness | −1.0569 | −0.7224 | −0.1647 | −0.4736 | −1.0397 | 0.2267 | 1.3737 | 2.2716 |
| Kurtosis | 3.3994 | 3.1293 | 2.5016 | 2.2271 | 3.5229 | 1.3018 | 8.2053 | 14.4552 |
| Share with return > 0 | 0.8126 | 0.7912 | 0.6971 | 0.7292 | 0.8177 | 0.4991 | 0.4544 | 0.3605 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stübinger, J.; Mangold, B.; Knoll, J. Machine Learning in Football Betting: Prediction of Match Results Based on Player Characteristics. Appl. Sci. 2020, 10, 46. https://doi.org/10.3390/app10010046
Stübinger J, Mangold B, Knoll J. Machine Learning in Football Betting: Prediction of Match Results Based on Player Characteristics. Applied Sciences. 2020; 10(1):46. https://doi.org/10.3390/app10010046
Chicago/Turabian StyleStübinger, Johannes, Benedikt Mangold, and Julian Knoll. 2020. "Machine Learning in Football Betting: Prediction of Match Results Based on Player Characteristics" Applied Sciences 10, no. 1: 46. https://doi.org/10.3390/app10010046
APA StyleStübinger, J., Mangold, B., & Knoll, J. (2020). Machine Learning in Football Betting: Prediction of Match Results Based on Player Characteristics. Applied Sciences, 10(1), 46. https://doi.org/10.3390/app10010046





