A Novel Optimization Layout Method for Clamps in a Pipeline System
Abstract
1. Introduction
- Active control of the pipe directly to reduce the vibration;
- Use damping materials between the hydraulic pipeline and the foundation to suppress the vibration transmission;
- Control the fluid pulsation in the pipeline to reduce the vibration of the excitation source;
- Adjust the number, position and layout of the supports in the system to change the dynamic characteristics of the system.
2. Materials and Methods
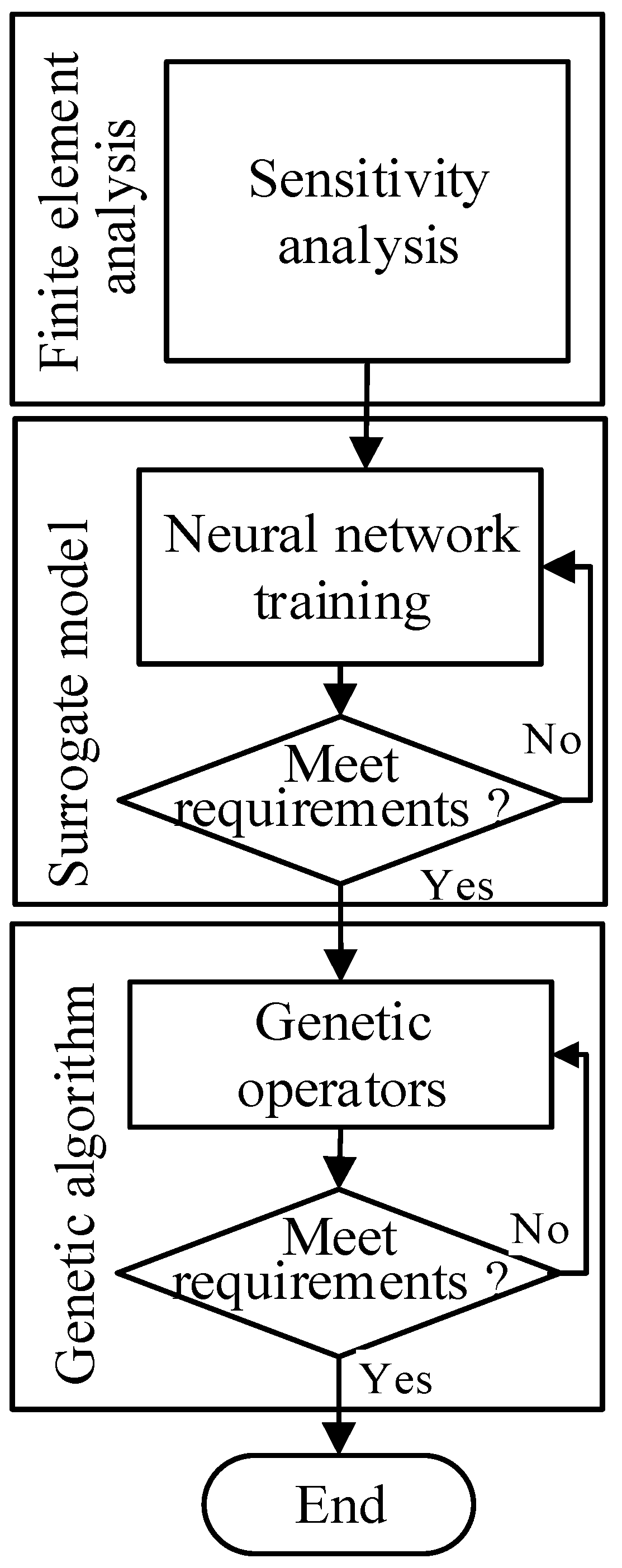
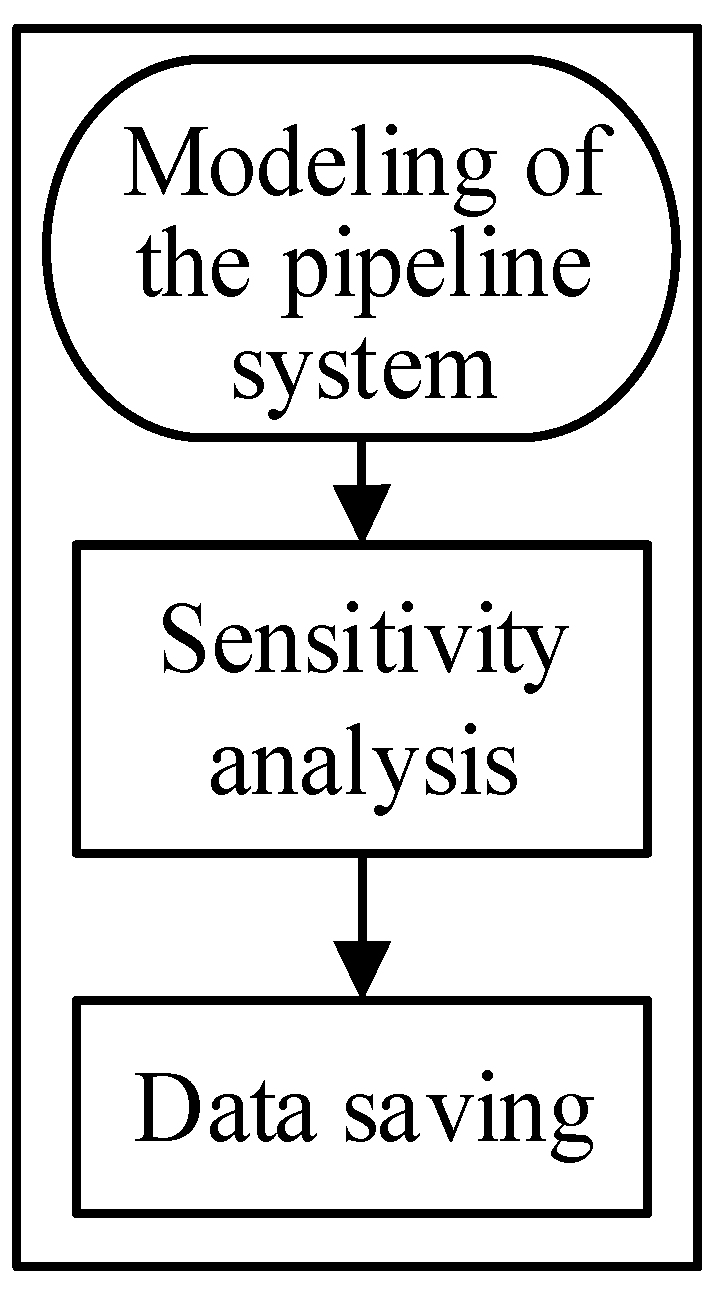
2.1. Process of the Optimization
2.1.1. Global Sensitivity Analysis Based on Sobol Method
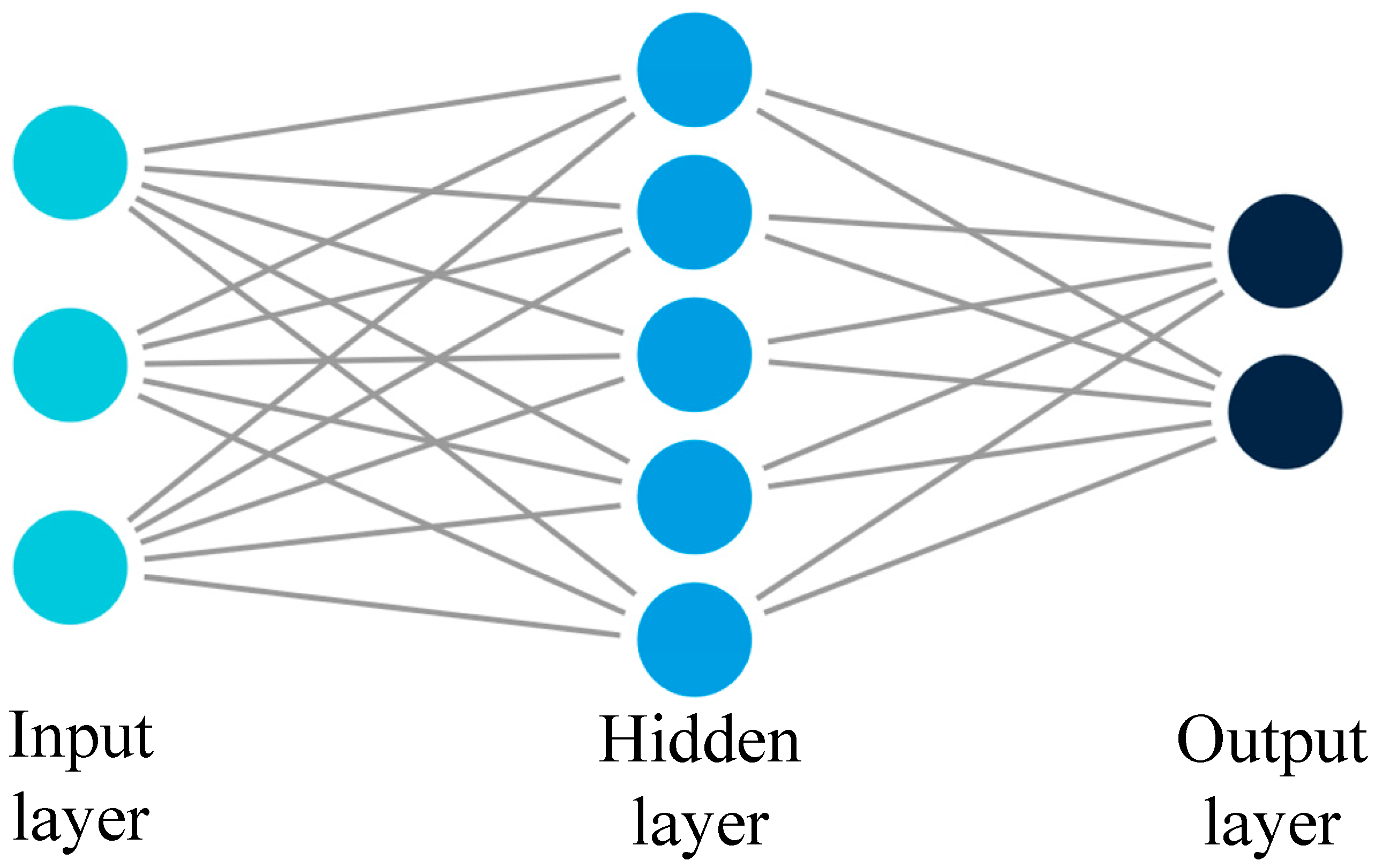
2.1.2. Prediction by Neural Network
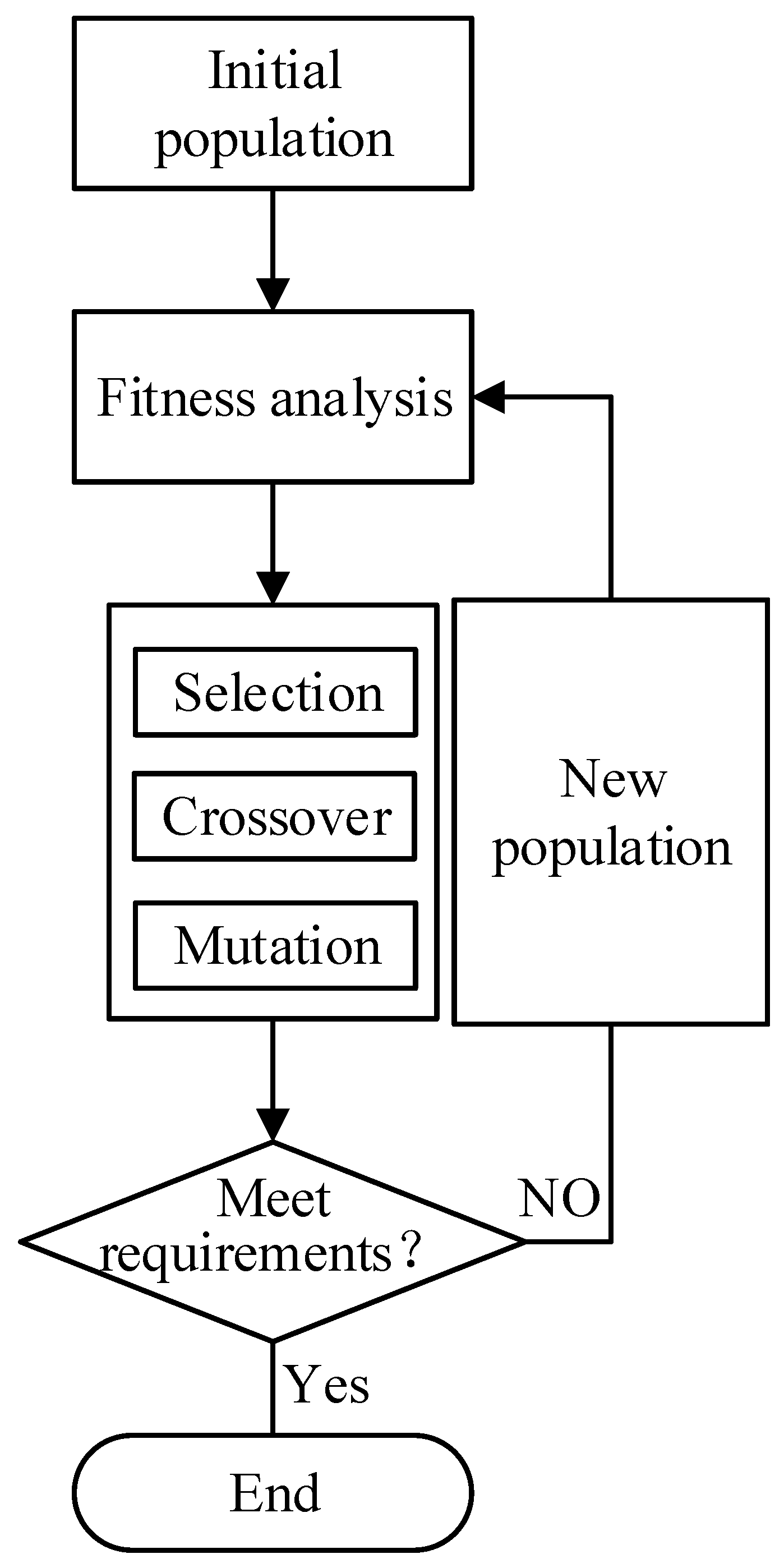
2.1.3. Optimization by Genetic Algorithm
- Set the population size and initialize all involved variables;
- Select the initial group S according to the group isolation;
- Calculate the fitness of the population, searching for individuals with higher fitness;
- Selection, crossover, and mutation in the group and generate a transitional group ST;
- Replace the individuals with lower fitness in S by the one with higher fitness in ST to generate a new group SN;
- Check if the condition is met; if so, the loop is ended, and the individual with optimal fitness is outputted as the optimal solution; Otherwise, the process will return to Step 3 and continue until the termination condition is met.
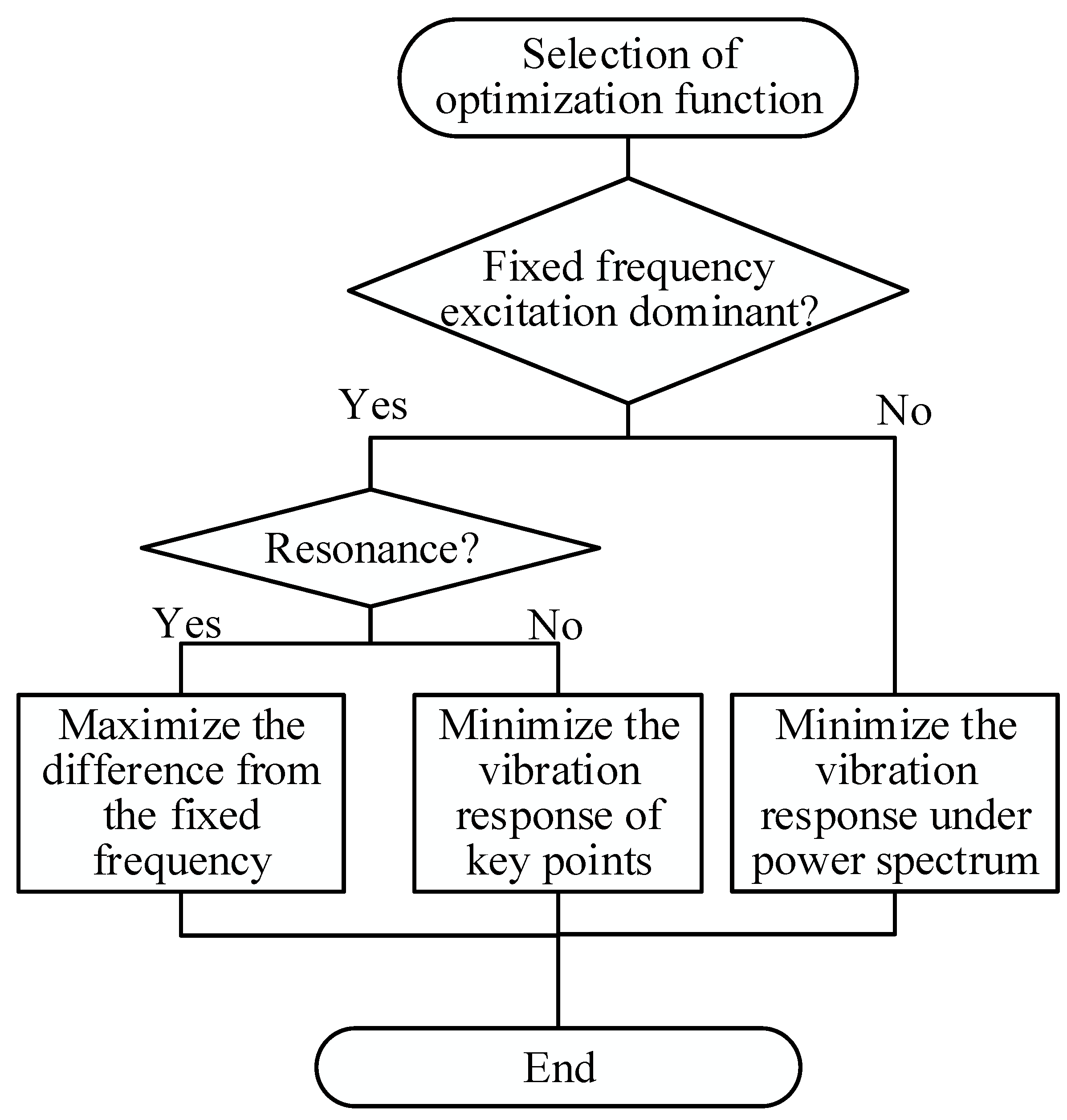
2.2. Optimization Function
2.3. Optimization Parameters
2.4. Constraints
3. Results and Discussion
3.1. Sensitivity Analysis of the Input Variables
3.2. Prediction by Neural Network
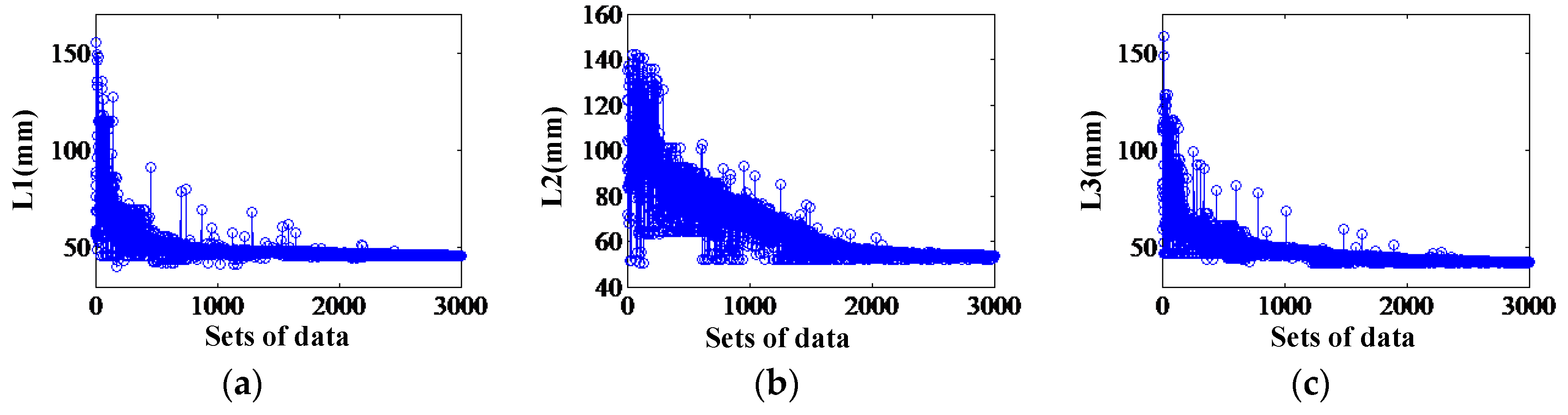
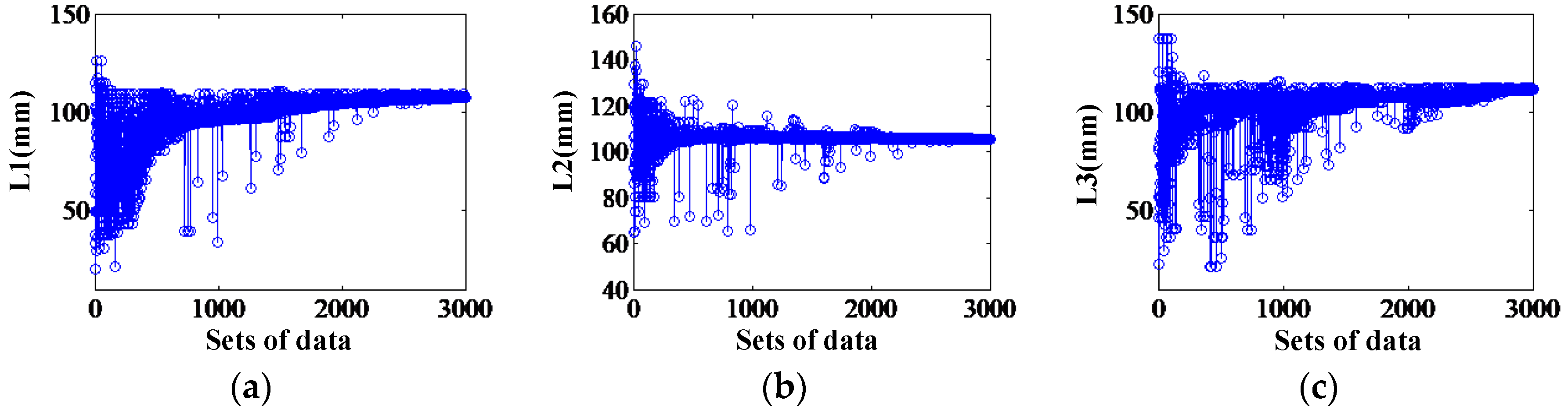
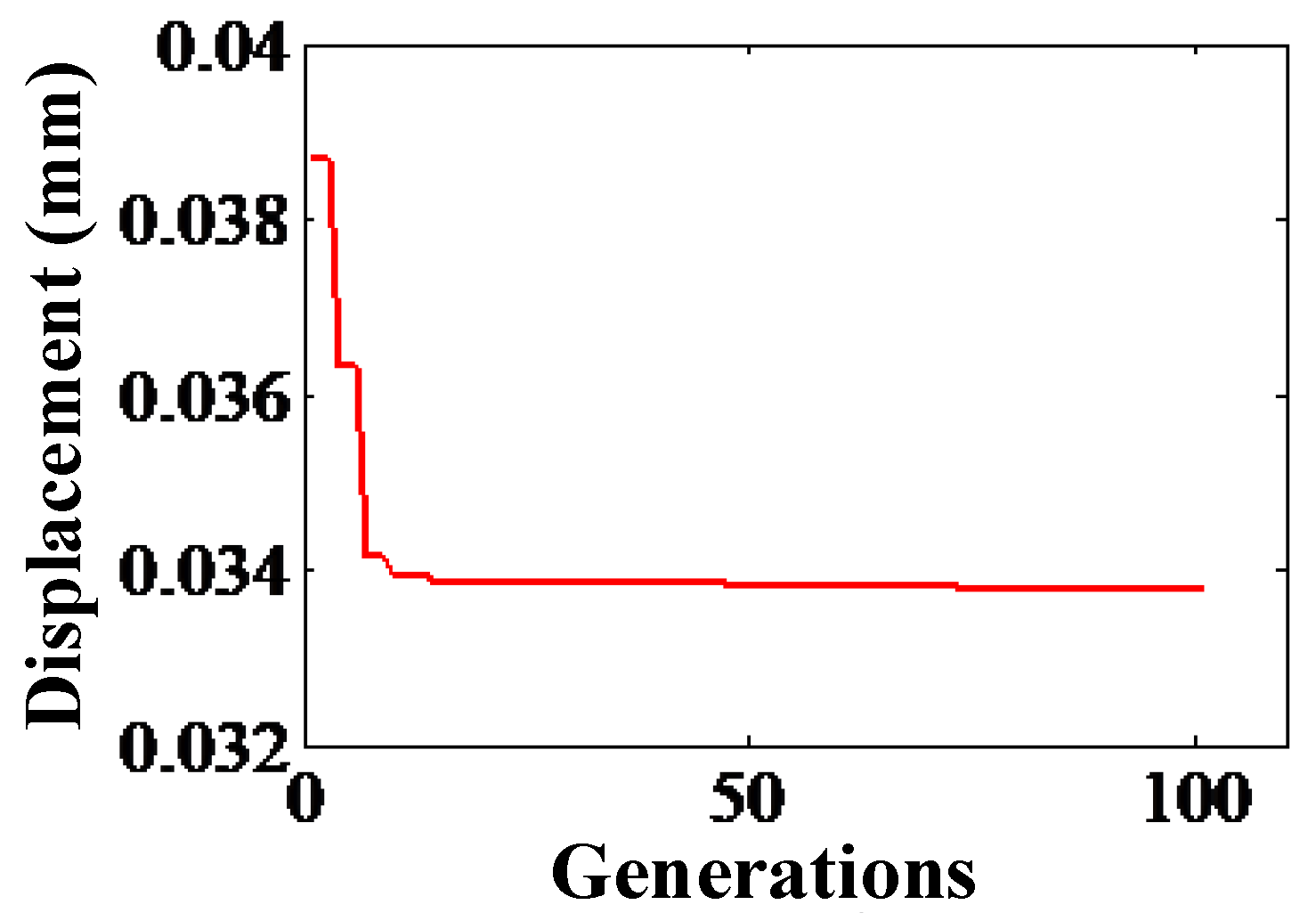
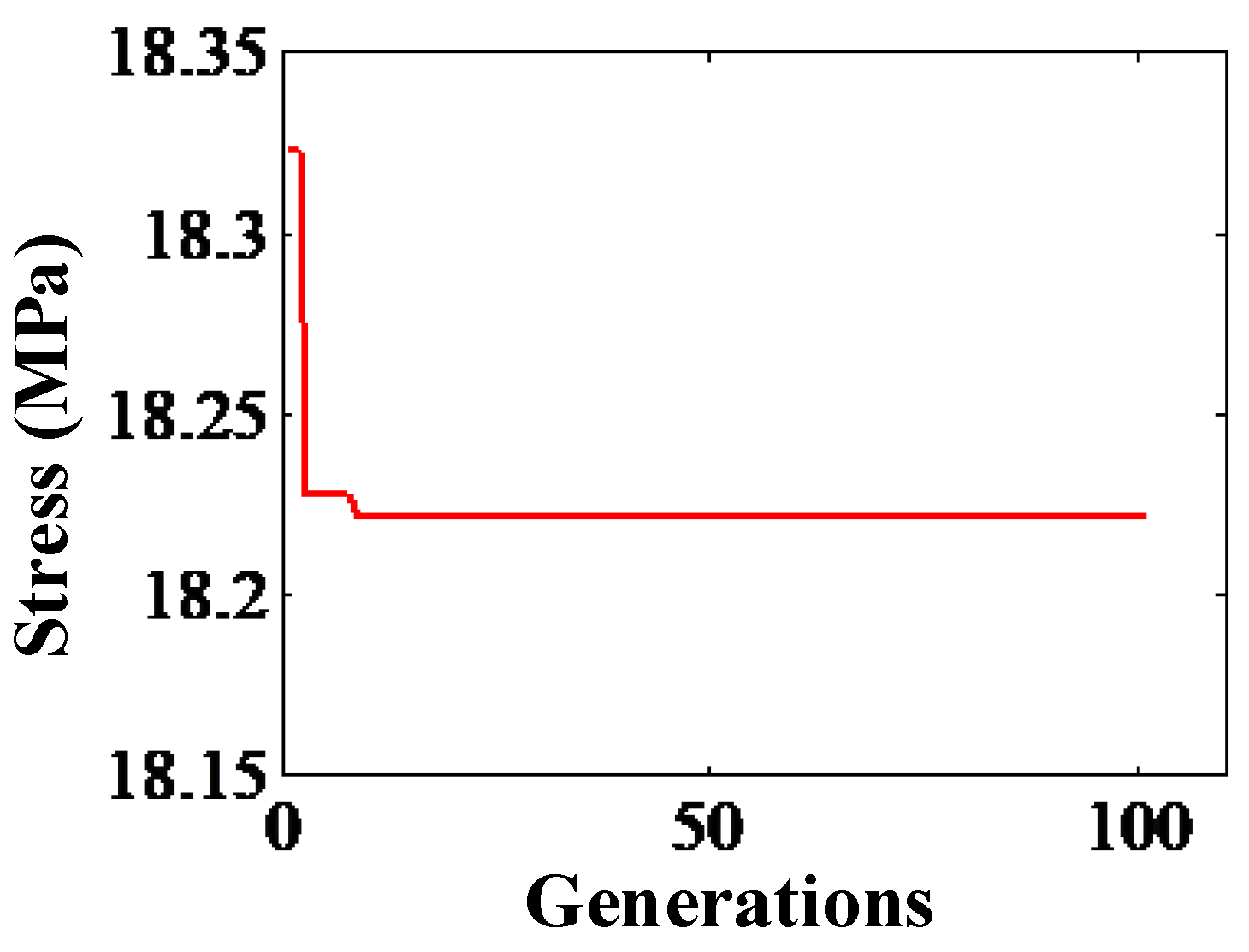
3.3. Optimization by Genetic Algorithm
3.4. Validation of the Optimization
4. Conclusions and Prospects
Author Contributions
Funding
Conflicts of Interest
References
- Ray, M.C.; Reddy, J.N. Active damping of laminated cylindrical shells conveying fluid using 1–3 piezoelectric composites. Compos. Struct. 2013, 98, 261–271. [Google Scholar] [CrossRef]
- Herold, S.; Mayer, D. Adaptive Piezoelectric Absorber for Active Vibration Control. Actuators 2016, 5, 7. [Google Scholar] [CrossRef]
- Tan, J.; Ho, S.M.; Zhang, P.; Jiang, J. Experimental Study on Vibration Control of Suspended Piping System by Single-Sided Pounding Tuned Mass Damper. Appl. Sci. 2019, 9, 285. [Google Scholar] [CrossRef]
- Sorokin, S.; Holst-Jensen, O. On Power Flow Suppression in Straight Elastic Pipes by Use of Equally Spaced Eccentric Inertial Attachments. J. Vib. Acoust. 2012, 134, 041003. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, L.; Cui, Y.; Li, Y.; Ye, L. Experimental and theoretical study on a novel dual-functional replaceable stiffening angle steel component. Soil Dyn. Earthq. Eng. 2018, 114, 378–391. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Farajpour, A. Pulsatile vibrations of viscoelastic microtubes conveying fluid. Microsyst. Technol. 2019, 25, 3609. [Google Scholar] [CrossRef]
- Zhang, Y.; He, L.; Yang, J.; Wan, F.; Gao, J. Vibration Control of an Unbalanced Single-Side Cantilevered Rotor System with a Novel Integral Squeeze Film Bearing Damper. Appl. Sci. 2019, 9, 4371. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; The University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Yu, F.; Xu, X. A short-term load forecasting model of natural gas based on optimized genetic algorithm and improved BP neural network. Appl. Energy 2014, 134, 102–113. [Google Scholar] [CrossRef]
- Konak, A.; Coit, D.W.; Smith, A.E. Multi-objective optimization using genetic algorithms: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- Zhihui, L.; Wang, M.Y.; Kedian, W.; Xuesong, M. Fixture performance Improv. by an accelerated integral method of fixture layout and clamping force plan. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2013, 227, 1819–1829. [Google Scholar] [CrossRef]
- Zhang, X.P.; Yang, W.Y.; Li, M. Fixture Layout and Clamping Force Optimization for Large-Scale Workpiece Using Augmented Lagrangian Method. Appl. Mech. Mater. 2010, 29–32, 560–565. [Google Scholar] [CrossRef]
- Chen, W.; Ni, L.; Xue, J. Deformation control through fixture layout design and clamping force optimization. Int. J. Adv. Manuf. Technol. 2008, 38, 860–867. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Mcclelland, J.L. Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Foundations; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Zheng, Y.; Zhong, H.; Fang, Y.; Zhang, W.; Liu, K.; Fang, J. Rockburst Prediction Model Based on Entropy Weight Integrated with Grey Relational BP Neural Network. Adv. Civ. Eng. 2019, 2019, 8. [Google Scholar] [CrossRef]
- Ren, C.; An, N.; Wang, J.; Li, L.; Hu, B.; Shang, D. Optimal parameters selection for BP neural network based on particle swarm optimization: A case study of wind speed forecasting. Knowl. Based Syst. 2014, 56, 226–239. [Google Scholar] [CrossRef]
- Wang, D.; Luo, H.; Grunder, O.; Lin, Y.; Guo, H. Multi-step ahead electricity price forecasting using a hybrid model based on two-layer decomposition technique and BP neural network optimized by firefly algorithm. Appl. Energy 2017, 190, 390–407. [Google Scholar] [CrossRef]
- Cui, K.; Qin, X. Virtual reality research of the dynamic characteristics of soft soil under metro vibration loads based on BP neural networks. Neural Comput. Appl. 2018, 29, 1233–1242. [Google Scholar] [CrossRef]
- Pronzato, L. Sensitivity analysis via Karhunen–Loève expansion of a random field model: Estimation of Sobol’ indices and experimental design. Reliab. Eng. Syst. Saf. 2019, 187, 93–109. [Google Scholar] [CrossRef]
- Roostaie, T.; Farsi, M.; Rahimpour, M.R. Dehydration of crude oil by cellulose-based demulsifiers: Statistical modeling sensitivity analysis and optimization. Pet. Sci. Technol. 2019, 37, 2134–2141. [Google Scholar] [CrossRef]
- Jaxa-Rozen, M.; Kwakkel, J. Tree-based ensemble methods for sensitivity analysis of environmental models: A performance comparison with Sobol and Morris techniques. Environ. Model. Softw. 2018, 107, 245–266. [Google Scholar] [CrossRef]
- Nossent, J.; Elsen, P.; Bauwens, W. Sobol’ sensitivity analysis of a complex environmental model. Environ. Model. Softw. 2011, 26, 1515–1525. [Google Scholar] [CrossRef]
- Tripathy, R.K.; Bilionis, I. Deep UQ: Learning deep neural network surrogate models for high dimensional uncertainty quantification. J. Comput. Phys. 2018, 375, 565–588. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, H.; Li, Y. Effective design space exploration of gradient nanostructured materials using active learning based surrogate models. Mater. Des. 2019, 183, 108085. [Google Scholar] [CrossRef]
- Meng, D.; Yang, S.; Zhang, Y.; Zhu, S.P. Structural reliability analysis and uncertainties-based collaborative design and optimization of turbine blades using surrogate model. Fatigue Fract. Eng. Mater. 2019, 42, 1219–1227. [Google Scholar] [CrossRef]
- Hecht-Nielsen, R. Kolmogorov’s Mapping Neural Network Existence Theorem. In Proceedings of the International Conference on Neural Networks, San Diego, CA, USA, 21–24 June 1987; Volume 3, pp. 11–13. [Google Scholar]
- Ansari, H.R.; Zarei, M.J.; Sabbaghi, S.; Keshavarz, P. A new comprehensive model for relative viscosity of various nanofluids using feed-forward back-propagation MLP neural networks. Int. Commun. Heat Mass 2018, 91, 158–164. [Google Scholar] [CrossRef]









| Optimization Goal | L1 (mm) | L2 (mm) | L3 (mm) | Frequency Difference (Hz) | Displacement (mm) | Stress (MPa) |
|---|---|---|---|---|---|---|
| Before Optimization | 50 | 100 | 50 | 50.42 | 0.0502 | 29.56 |
| Maximizing the frequency difference | 40.3 | 50.7 | 41.7 | 68.41 | 0.0374 | 37.54 |
| Minimizing the displacement | 111.3 | 100.8 | 110.7 | 37.54 | 0.0338 | 20.75 |
| Minimizing the stress | 128.3 | 85.7 | 122.7 | 37.24 | 0.0849 | 18.22 |
| Characteristics | Methods | Direction | before Optimization | after Optimization |
|---|---|---|---|---|
| Frequency (Hz) | Experiment | / | 48.4 | 70.2 |
| Simulation | / | 50.42 | 68.41 | |
| Stress (MPa) | Experiment | Horizontal | 9.82 | 5.54 |
| Vertical | 6.46 | 4.13 | ||
| Simulation | / | 29.56 | 18.022 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, P.; Li, J.; Zhai, J.; Tao, Y.; Han, Q. A Novel Optimization Layout Method for Clamps in a Pipeline System. Appl. Sci. 2020, 10, 390. https://doi.org/10.3390/app10010390
Gao P, Li J, Zhai J, Tao Y, Han Q. A Novel Optimization Layout Method for Clamps in a Pipeline System. Applied Sciences. 2020; 10(1):390. https://doi.org/10.3390/app10010390
Chicago/Turabian StyleGao, Peixin, Jiwu Li, Jingyu Zhai, Yang Tao, and Qingkai Han. 2020. "A Novel Optimization Layout Method for Clamps in a Pipeline System" Applied Sciences 10, no. 1: 390. https://doi.org/10.3390/app10010390
APA StyleGao, P., Li, J., Zhai, J., Tao, Y., & Han, Q. (2020). A Novel Optimization Layout Method for Clamps in a Pipeline System. Applied Sciences, 10(1), 390. https://doi.org/10.3390/app10010390





