Abstract
The main purpose of the present analysis is to report the numerical solution of the thermal radiations and magnetohydrodynamic (MHD) effect on the flow of micropolar nanofluid. Further, the effect of Brownian motion and thermophoresis on the flow field are also elucidated. The combined phenomenon of heat and mass transfer is considered. Compatible similarities are implemented for the conversion of nonlinear ordinary differential equations from nonlinear partial differential equations. The numerical solution of the governing differential equations is obtained via the implicit Keller box technique. This is an efficient scheme based on the finite difference method. Findings demonstrate that the heat and mass exchange reduce with growth of the Brinkman parameter, whereas the wall shear stress enhances with improving the magnitude of the Brinkman factor. The temperature contour enhances when the radiation parameter reaches its peak, which is useful for industrial processes. The heat and mass flow rates decrease against higher magnitudes of inclination.
1. Introduction
Numerous investigators have elucidated the MHD impacts in several energy-related flows made by stretching sheet. Stretching sheets have received much consideration due to their significant applications in engineering and practical fields such as MHD power producers, hyperthermia cancer cure, brain tumor treatment, and solar energy devices. The physical effects in MHD offer influential situations in heat flow problems. Lenz’s law indicates that the electric current is induced on a moving conductor under the magnetic field impact that comprises its own magnetic field. The motion of fluid modifies when conducting fluid moves under the impact of the magnetic field, and the magnetic nanoparticles interact with Lorentz forces. MHD fluids control system performance by means of electrically conducting fluids. For brief information, one can see investigators’ efforts on MHD effects in references [1,2,3,4,5,6,7].
With the introduction of nanoscience, nanofluids have transformed into a main point of concern in the research of the flow of nanofluids with mixtures of nanoparticles. Nanofluids are prepared by dissipating nanometer-sized materials, for example, nanofibers, nanoparticles, droplets, nanotubes, etc., in fluids. Actually, nanofluids are the mixture of concise nanometer-sized materials with nanoscale shattered suspensions. Nanofluids must be employed to enhance the thermal conductivity of the liquids due to Brownian motion and thermophoresis involvement. Nano science is employed to discover the suitable working fluid to recover convective heat exchange improvement. Nanofluids are utilized in nanotechnology, hyperthermia cancer cure, microelectronics, medical procedures, and hybrid power devices. Usman et al. [8] studied the flow Casson nanofluid towards an inclined stretching cylinder. Khan et al. [9] examined the flow of Jeffery nanofluid towards an inclined stretching surface. Ghadikolaei et al. [10] investigated the flow of Casson nanofluid towards a porous inclined surface. Recently, Rafique et al. [11] investigated the flow of Casson nanofluid towards an inclined surface. For details, see references [12,13,14,15,16,17,18,19,20].
Over the last few decades, scholars have paid prodigious attention to the boundary layer flows towards stretching inclined surfaces. The primary reasons behind such substantial thought is their mechanisms and uses. This commitment to the investigation of boundary layer flows is due to their vast utilization in industries, technology, and engineering such as the extrusion of plastic sheets, glass fiber production, crystal growing, hot rolling, wire drawing, metal and polymer extrusion, and metal spinning. Ramesh et al. [21] examined the boundary layer flow towards a slanted sheet. Abo-Eldahab et al. [22] studied the energy transport towards an extending slanted sheet. Rehman et al. [23] investigated the heat and mass exchange flow through an inclined surface. The flow of Powell–Erying fluid towards an inclined surface by incorporating the radiation impact was examined by Hayat et al. [24]. Recently, Tlili [25] studied the flow of Jeffrey fluid towards a slanted sheet by incorporating the heat generation effect.
In the modern age, the investigation of non-Newtonian fluid towards stretching-inclined surfaces has increased the consideration of researchers because of the extensive range of practical uses in numerous industries, for example, ground water pollution, food procedures, the production of plastic materials, the manufacturing of electronic chips, the cooling of nuclear apparatuses, etc. Micropolar fluid is one of the most important non-Newtonian fluids to have gained a great deal of attention among the new age investigators, because Newtonian fluids have failed to describe the features of fluids with suspended particles accurately. The basic theory about the micropolar fluid was introduced by Eringen [26] in his pioneering paper. Beg et al. [27] studied the flow of microplar fluid towards an inclined surface numerically. The flow of convective micropolar fluid towards an inclined surface has been discussed by Rahaman et al. [28]. Shah et al. [29] discussed the flow of micropolar fluid between two plates. Rafique et al. [30] investigated the flow of micropolar nanofluid towards an inclined surface numerically. For further detail about the flow of micropolar fluid towards an inclined surface with different impacts, see [31,32,33,34]. However, there is a lack of academic literature regarding heat and mass exchange of Brinkman-type micropolar nanofluid flow towards an inclined stretching sheet. Furthermore, there is always a need to develop an updated methodological approach that aims to assist heat transportation because of its importance in industry, in engineering, and in building envelopes. Therefore, in this paper we consider the Brownian motion and thermophoretic effects on the flow field, instead of alternative heat transfer techniques (see [35,36,37]).
The abovementioned literature and its uses in engineering is the basis of the inspiration to probe the effect of thermal radiations and inclination on the Brinkman-type micropolar nanofluid flow past an inclined stretching surface. It is also clear from the available literature that the inclination effect along with thermal radiation on the flow of Brinkman-type micropolar nanofluid towards an inclined stretching surface has not been yet investigated. Therefore, the core purpose of this paper is to fill this gap. More exactly, the reason behind this motivation is the growing application of non-Newtonian nanofluids in industrial and engineering fields. Heat and mass transfer phenomena are also considered. Suitable similarities are utilized to recover ordinary differential equations. The attained system of equations is then solved via the Keller box scheme [38]. A comparison of the reduced Nusselt number and reduced Sherwood number is made with available literature outcomes, and good settlement is noted.
2. Mathematical Formulation
The flow of microploar nanofluid is generated due to a linear stretching inclined surface in the presence of thermal radiations, Brinkman parameter, and an inclination factor . The inclined surface is stretched with the velocity of , where is a constant. Brownian motion and thermophoretic impacts are considered. The momentum boundary layer develops over the surface when fluid flows on it; the thermal boundary develops if the surface temperature differs from the bulk temperature, and, above the surfaces of species, the concentration boundary layer develops in the flow regime.
The governing equations for the study are as follows:
Here, the Rosseland estimation (for radiation flux) is characterized as
where the Stefan-Boltzmann coefficient is given by and mean absorption constant represented by , whereas the temperature changes between local temperature and free steam is very small, since it ignores higher-order terms in the expansion of in Taylor succession about for
By using Equations (5) and (6), the Equation (3) converted into
where in the directions and the velocity constituents are and , individually, is the gravitational acceleration, strength of magnetic field is defined by , is the electrical conductivity, viscosity is given by , density of conventional fluid is given by , density of the nanoparticle is given by , is the Brinkman parameter, thermal expansion factor is denoted by , concentration expansion constant is given by , denotes the Brownian dissemination factor, represents the thermophoresis dispersion factor, the thermal conductivity given by , the heat capacity of the nanoparticles symbolically is given as , heat capacity of the conventional liquid is given by , denotes thermal diffusivity parameter, and the symbolic representation of the relation among current heat capacity of the nanoparticle and the liquid is .
The subjected boundary conditions are
Here, the stream function Ψ = Ψ (x, y) is demarcated as
where Equation of continuity in Equation (1) is fulfilled. The similarity transformations are defined as
On substituting Equation (8), system of Equations (2)–(5) converted to
where
Here, primes denotes the differentiation with respect to , denotes the magnetic factor called Hartmann number, denotes the kinematic viscosity of the liquid, denotes the Prandtl number, signifies the dimension less Brinkman parameter, Lewis number is denoted by , and the material parameter denoted by .
The corresponding boundary settings are changed to
It is found that by eliminating the vertex viscosity, i.e., = 0, it agrees to a nanofluid model deprived of micropolar effects. The skin friction, Sherwood number, and Nusselt number for the current study are defined as
The related expressions for the skin-friction coefficient , the reduced Sherwood number , and the reduced Nusselt number are demarcated as
where is the local Reynolds number.
3. Results and Discussion
A series of numerical calculations has been accomplished by employing a useful numerical technique called the Keller-box method on system of Equations (12)–(15) with their appropriate boundary settings (15) to achieve insight into the physical situation of flow configuration. These computations are attained for various values of Brownian motion factor , thermophoresis assumed by , magnetic factor , buoyancy factor , solutal buoyancy constraint , inclination factor , Prandtl number , Lewis number , radiation effect Brinkman parameter , suction or injection parameter , and material factor which are presented in different tables and figures. The flow pattern of the current study is presented in Figure 1 using the curves, showing the profiles of velocity, temperature and concentration.
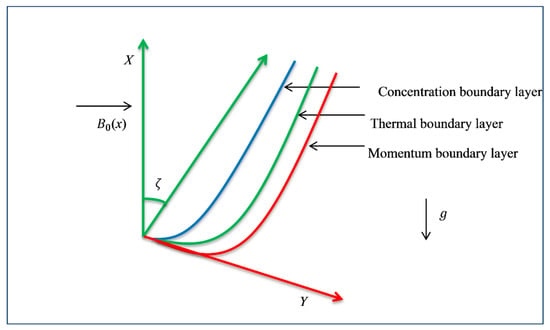
Figure 1.
Physical geometry with coordinate system.
In order to certify the algorithm established in MATLAB software (The MathWorks Inc., Natick, MA, USA) for the current method, the numerical results for the reduced Nusselt number and reduced Sherwood number are compared with the results of Khan and Pop [39] and prepared the Table 1, in the absence of , , , , and taking factors with = 90°. The current results display agreement, which verifies accuracy of studied problem. The effects on and against altered values of involved physical parameters , , , , , , , , and are displayed in Table 2.

Table 1.
Comparison of the reduced Nusselt number and the reduced Sherwood number when M, , S, , , , = 0, Pr = Le =10, and = 90°.

Table 2.
Values of , , and . The bold data shows the variation in that parameter while others are kept constant
Table 2 shows and with the altered magnitudes of the under concern parameters. It is clear from Table 2 that the heat and mass exchange rate decrease with growth of the Brinkman factor. On the other hand, wall shear stress improves for cumulative impact of Brinkman factor. A similar effect can be seen in the case of inclination change as the heat and mass flux flow reduce. In addition, the energy exchange rate decreases for the higher values of thermophoretic effect whereas an opposite impact is seen in the case of mass exchange rate. It is observed that the skin friction along with heat and mass exchange rate reduce for the growing values of thermal radiation effect. Moreover, the skin friction enhances for improved values of inclination. The energy flux rate and mass flux rate decline with growing magnitude of Brownian motion effect. Moreover, the skin friction increases by increasing the Brownian motion effect.
3.1. Velocity Profile
Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 are depicted to show the physical behavior of , , , , and on velocity profile. The variations of on the velocity is exhibited in the Figure 2. As expected, the velocity of the fluid flow become lower with the strengthening of the magnetic field. It is an agreement with the fact that growth in causes Lorentz force that creates resistance to the flow, due to which the momentum boundary layer thins across the boundary. A similar effect is shown in Figure 3, contradicting the variation in . The angular velocity shows inverse relation with the magnetic field strength. The variations in material parameter show the velocity profile upturn (see Figure 4). The variation in angular velocity contradicts the material parameter portrayed in Figure 5. Clearly, increases with growing magnitudes of on matching with the Newtonian case (); additionally, the boundary layer thickness reduces with growth of . The relation between and the velocity field is depicted in Figure 6. Here, presents the characteristics of the buoyancy forces, which offer a direct relation with the velocity field. Physically, the growing magnitude of the buoyancy forces causes a decline in the viscous force, which improves the fluid flow, which causes faster motion. Moreover, the relationship between the solutal buoyancy forces and velocity field is shown in Figure 7. Physically, the length, concentration difference, and kinematic viscosity of the fluid affect parameter . On the other hand, there is an inverse relationship between the viscosity and velocity of the fluid. Therefore, the viscosity of the fluid declines once it has increased the magnitude of (which as a result causes faster the motion), and the concentration upsurges directly, due to which the velocity field rises. Finally, a direct relationship between factor and the velocity outline is shown. Figure 8 presents the inclination variation in the velocity field. It can be observed that there is an inverse relation between and . This can be ascribed to the fact that the maximum gravitational force acts on flow when the inclination factor because in this state the sheet will be vertical. However, for the sheet will be horizontal, which causes the reduction in the velocity profile as the strength of the bouncy forces decline. The variation in Brinkman factor causes a decline in the velocity profile (see Figure 9). Parameter is the ratio between the drag force and density; therefore, by increasing the drag force improves and the fluid velocity reduces [40].
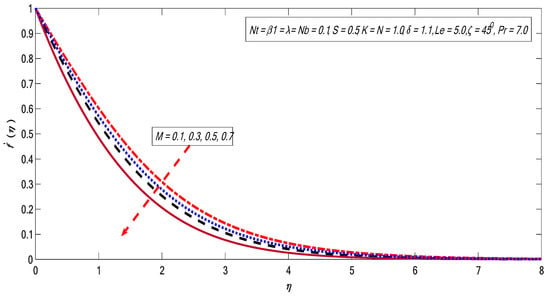
Figure 2.
Variations in velocity profile for several values of .
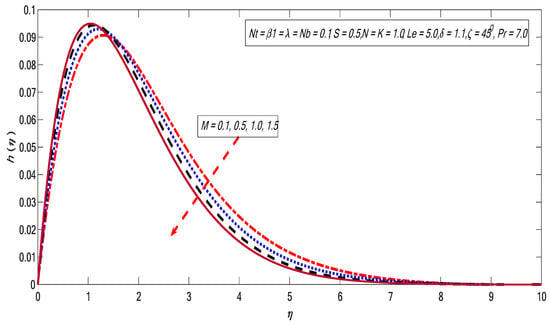
Figure 3.
Variations in angular velocity for several values of .
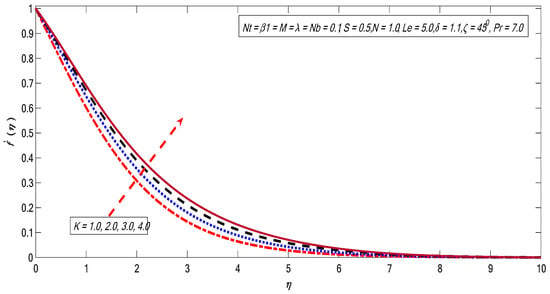
Figure 4.
Variations in velocity profile for several values of .
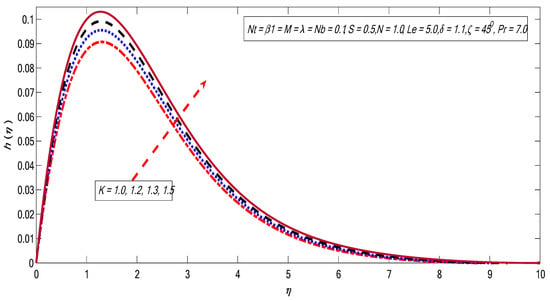
Figure 5.
Variations in angular velocity profile for several values of .
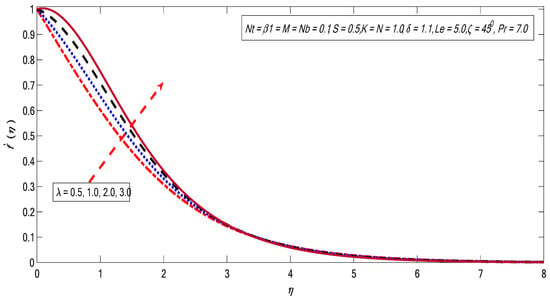
Figure 6.
Variations in velocity profile for several values of .
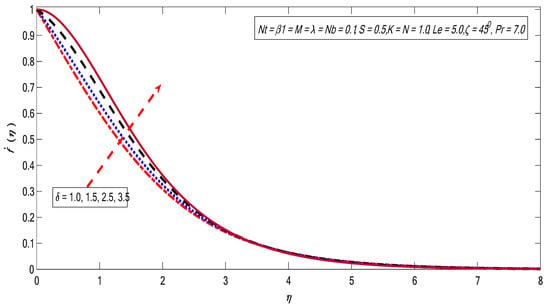
Figure 7.
Variations in velocity profile for several values of .
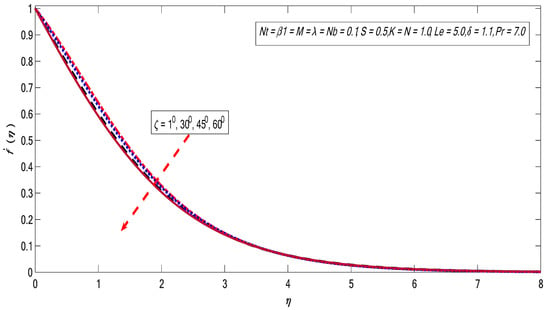
Figure 8.
Variations in velocity profile for several value of .
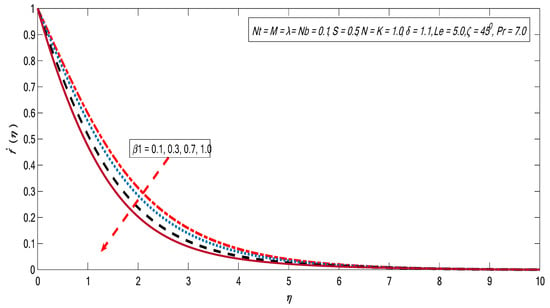
Figure 9.
Variations in velocity profile for several value of .
3.2. Temperature Profile
Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 are plotted to get insight into the variations of and on the temperature profile. The magnetic field strength shows favorable behavior for the temperature profile in Figure 10. Here, hydromagnetic case is stronger than the hydrodynamic case (). It can be observed that the thickness of the thermal boundary layer thickness improves with growth in [41]. Figure 11 illustrates the behavior of temperature profile against the variations in the Brownian motion factor. Brownian motion is an irregular movement of the fluid particles which produces collisions among the particles. Therefore, the heat of the fluid increases with growing the Brownian motion impact. Consequently, free surface nanoparticle volume fraction reduces. The variations in increase the temperature profile (see Figure 12). The restrictions on the thermophoresis favor the rise of the surface temperature. The irregular movement (Brownian motion) produces kinetic energy because of nano suspended particles that cause an enhancement in the temperature; consequently, thermopheretic force develops. Due to the intensity generated by this force, the fluid starts in the reverse direction of the extending sheet. Finally, an enhancement in causes an improvement in temperature; as a result, the surface temperature also increases. The effect of Prandtl number on temperature profile is presented in Figure 13. The ratio of momentum diffusivity to thermal diffusivity is termed the Prandtl number. It is a well-known fact that higher thermal conductivities are linked with lower Prandtl fluids; therefore, heat diffuses rapidly from the surface compared to higher Prandtl fluids. Thus, Pr can be employed to control the rate of cooling in conducting flows [42]. Finally, the temperature profile decreases with the growth of Prandtl number. Figure 14 shows that the favorable behavior corresponds to the radiation effect. The higher surface heat flux rate corresponds to the higher radiation impact, causing the fluid to be warmer.
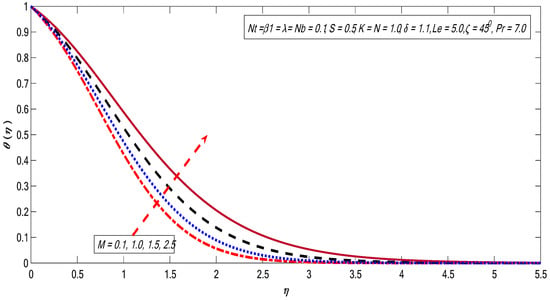
Figure 10.
Variations in temperature profile for several values of .
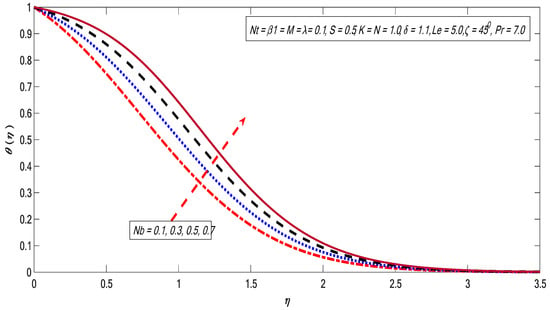
Figure 11.
Variations in temperature profile for several values of .
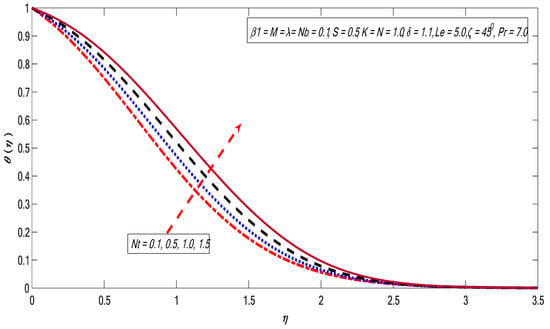
Figure 12.
Variations in temperature profile for several values of .
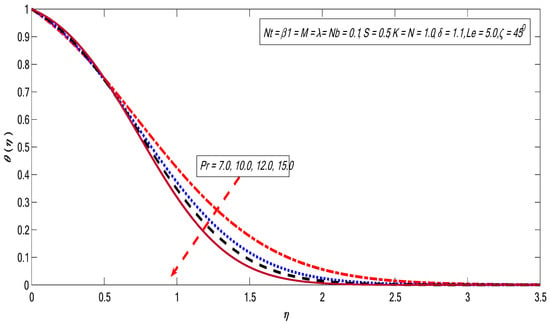
Figure 13.
Variations in temperature profile for several values of .
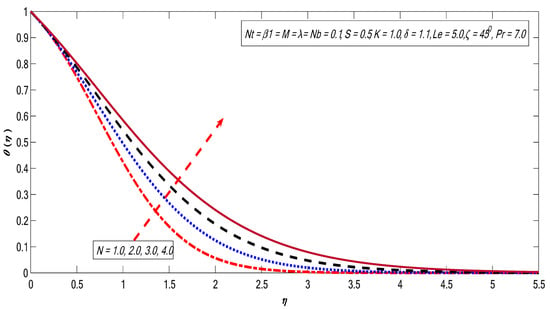
Figure 14.
Variations in temperature profile for several values of .
3.3. Concentration Profile
Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19 represent the variations of and on the concentration profile. The magnetic field strength plays a favorable role for the concentration profile (see Figure 15). As discussed earlier in the case of velocity profile, the magnet field produces the Lorentz force, thus creating resistance, which causes improvement in the thermal and concentration boundary layer thicknesses. Figure 16 exhibits the Brownian motion effect on the concentration profile. It is noticed that the concentration outline decreases with the growing magnitude of the Brownian motion impact. The boundary layer thickness is moderated by the enhancement in Brownian movement, which is the reason for the reduction of concentration profile. The thermophoretic effect boosts the concentration field (see Figure 17). This is due to the fact that the molecular kinetic energy of the fluid particles is enhanced by enhancing the thermophoretic impact. The variation in radiation impact causes the reduction in the concentration field (see Figure 18). The effect of Lewis number is demonstrated in Figure 19. It is noticeable that the concentration profile falls with the improvement of the Lewis number. The boundary layer viscosity decreases when the values of Lewis number are improved.
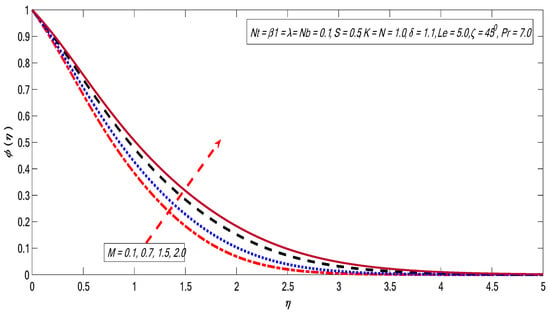
Figure 15.
Variations in concentration profile for several values of .
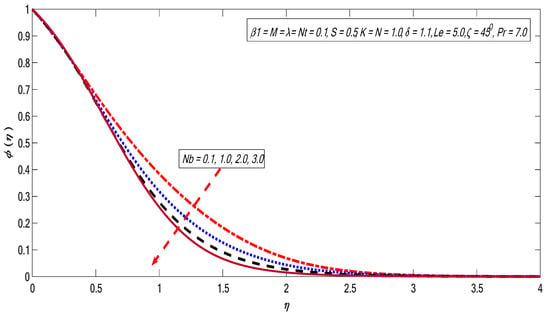
Figure 16.
Variations in concentration profile for several values of .
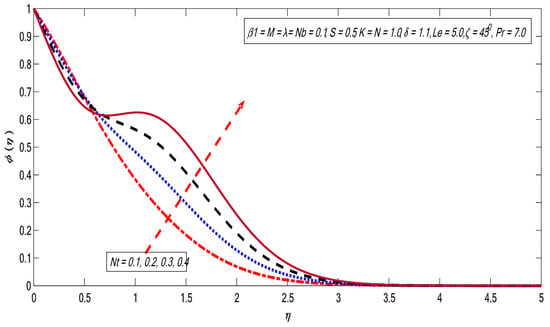
Figure 17.
Variations in concentration profile for several values of .
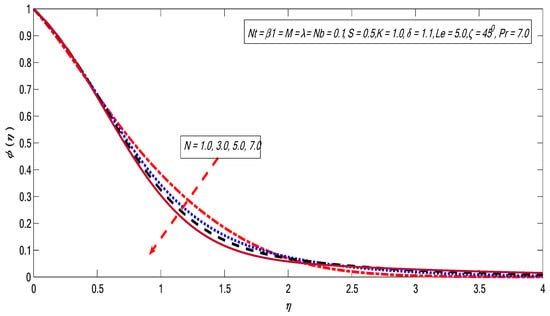
Figure 18.
Variations in concentration profile for several values of .
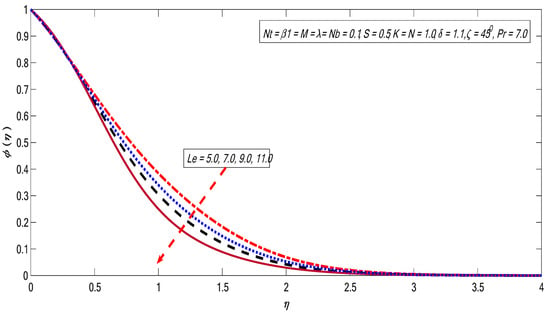
Figure 19.
Variations in concentration profile for several value of .
3.4. Heat and Mass Exchange
Behaviors of heat and mass exchange rates along with skin friction are presented in Figure 20, Figure 21, Figure 22, Figure 23, Figure 24 and Figure 25 for altered values of and . Figure 20 and Figure 21 demonstrate that the heat and mass exchange rates are reduced with growth of inclination and Brownian motion impact. On the other hand, the skin friction improves when the Brownian motion and inclination effect portrayed in Figure 22 are increased. Similarly, the heat and mass exchange fluxes fall against the growing magnitudes of thermophorectic and inclination parameters (see Figure 23 and Figure 24). Moreover, wall shear stress is enhanced with the growth of inclination and thermophoretic impacts (see Figure 25).
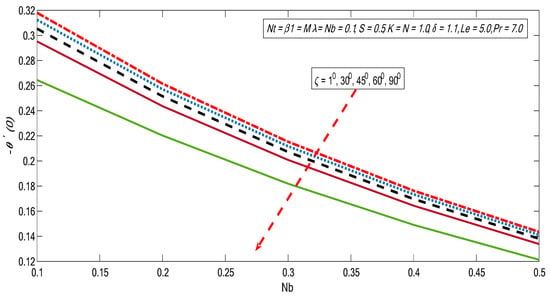
Figure 20.
Variations of reduced Nusselt number with for different values of .
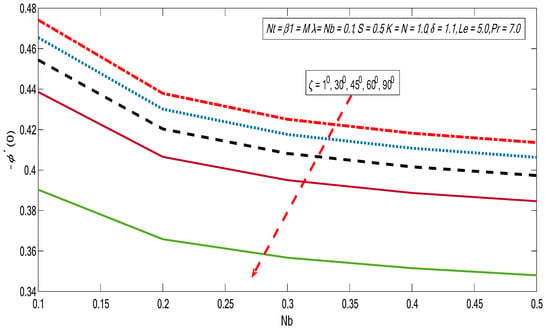
Figure 21.
Variations of reduced Sherwood number with for different values of .
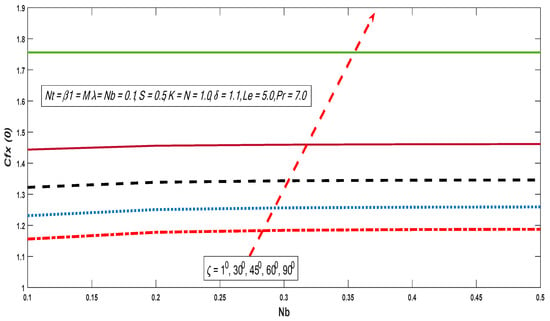
Figure 22.
Variations skin friction with for different values of .
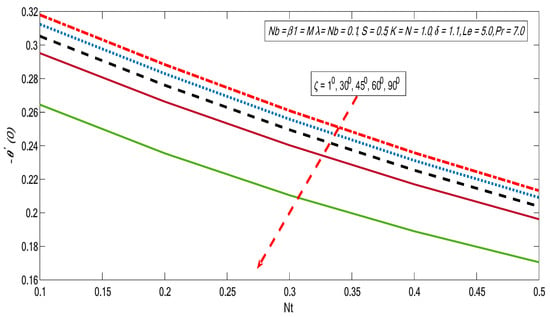
Figure 23.
Variations of reduced Nusselt number with for different values of .
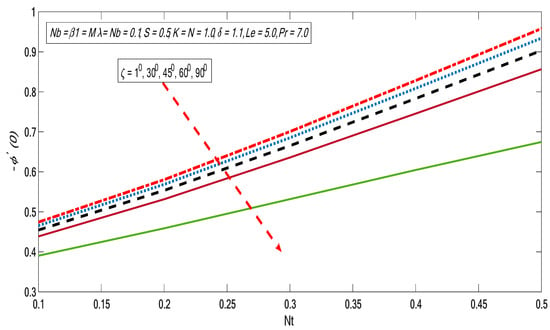
Figure 24.
Variations of reduced Sherwood number with for different values of .
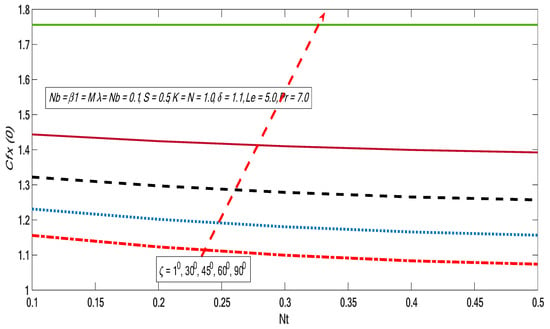
Figure 25.
Variations skin friction with for different values of .
4. Conclusions
In the numerical analysis of the present study, the effect Brinkman parameter with thermal radiations on the micropolar nanofluid flow on an inclined surface was investigated. For numerical results, the Keller-box method was applied. This method is based on finite difference discretization. Table 1 shows the comparison of the current outcomes with already published results, and shows a good settlement. The main key conclusions drawn from the study under concern are as follows:
- The Brinkman effect reduces the velocity profile for the higher magnitudes;
- The heat and mass exchange rate reduce with growth of the Brinkman factor;
- The skin friction enhances by increasing the Brinkman parameter;
- The growing variations in the thermal radiations improve the temperature field;
- The skin friction increases with the increase in inclination parameter;
- The buoyancy forces impact improves the velocity profile for large values;
- The heat and mass exchange rate decline with enhancing the Brownian movement.
Author Contributions
K.R. and E.-S.M.S. formulated the problem; M.I.A. and M.M. performed the numerical simulations, K.R. and I.K. plotted the results. All the authors equally contributed in manuscript writing. All authors have read and agreed to the published version of the manuscript.
Funding
Researchers Supporting Project number (RSP-2019/33), King Saud University, Riyadh, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Noor, N.F.M.; Abbasbandy, S.; Hashim, I. Heat and mass transfer of thermophoretic MHD flow over an inclined radiate isothermal permeable surface in the presence of heat source/sink. Int. J. Heat Mass Transf. 2012, 55, 2122–2128. [Google Scholar] [CrossRef]
- Das, K. Slip effects on heat and mass transfer in MHD micropolar fluid flow over an inclined plate with thermal radiation and chemical reaction. Int. J. Numer. Methods Fluids 2012, 70, 96–113. [Google Scholar] [CrossRef]
- Ali, F.; Khan, I.; Shafie, S. Conjugate effects of heat and mass transfer on mhd free convection flow over an inclined plate embedded in a porous medium. PLoS ONE 2013, 8, e65223. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Khan, I.; Ali, F.; Shafie, S. Effects of wall shear stress on MHD conjugate flow over an inclined plate in a porous medium with ramped wall temperature. Math. Probl. Eng. 2014, 2014, 15. [Google Scholar] [CrossRef]
- Das, S.; Jana, R.N.; Makinde, O.D. Magnetohydrodynamic mixed convective slip flow over an inclined porous plate with viscous dissipation and Joule heating. Alex. Eng. J. 2015, 54, 251–261. [Google Scholar] [CrossRef]
- Gupta, S.; Kumar, D.; Singh, J. MHD mixed convective stagnation point flow and heat transfer of an incompressible nanofluid over an inclined stretching sheet with chemical reaction and radiation. Int. J. Heat Mass Transf. 2018, 118, 378–387. [Google Scholar] [CrossRef]
- Shamshuddin, M.D.; Mishra, S.R.; Bég, O.A.; Kadir, A. Unsteady reactive magnetic radiative micropolar flow, heat and mass transfer from an inclined plate with joule heating: A model for magnetic polymer processing. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 1246–1261. [Google Scholar] [CrossRef]
- Usman, M.; Soomro, F.A.; Haq, R.U.; Wang, W.; Defterli, O. Thermal and velocity slip effects on Casson nanofluid flow over an inclined permeable stretching cylinder via collocation method. Int. J. Heat Mass Transf. 2018, 122, 1255–1263. [Google Scholar] [CrossRef]
- Khan, M.; Shahid, A.; Malik, M.Y.; Salahuddin, T. Thermal and concentration diffusion in Jeffery nanofluid flow over an inclined stretching sheet: A generalized Fourier’s and Fick’s perspective. J. Mol. Liq. 2018, 251, 7–14. [Google Scholar] [CrossRef]
- Ghadikolaei, S.S.; Hosseinzadeh, K.; Ganji, D.D.; Jafari, B. Nonlinear thermal radiation effect on magneto Casson nanofluid flow with Joule heating effect over an inclined porous stretching sheet. Case Stud. Therm. Eng. 2018, 12, 176–187. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M. Keller-box study on casson nano fluid flow over a slanted permeable surface with chemical reaction. Asian Res. J. Math. 2019. [Google Scholar] [CrossRef][Green Version]
- Rana, P.; Bhargava, R.; Bég, O.A. Numerical solution for mixed convection boundary layer flow of a nanofluid along an inclined plate embedded in a porous medium. Comput. Math. Appl. 2012, 64, 2816–2832. [Google Scholar] [CrossRef]
- Ullah, A.; Shah, Z.; Kumam, P.; Ayaz, M.; Islam, S.; Jameel, M. Viscoelastic MHD Nanofluid Thin Film Flow over an Unsteady Vertical Stretching Sheet with Entropy Generation. Processes 2019, 7, 262. [Google Scholar] [CrossRef]
- Maleki, H.; Alsarraf, J.; Moghanizadeh, A.; Hajabdollahi, H.; Safaei, M.R. Heat transfer and nanofluid flow over a porous plate with radiation and slip boundary conditions. J. Cent. South Univ. 2019, 26, 1099–1115. [Google Scholar] [CrossRef]
- Elgazery, N.S. Nanofluids flow over a permeable unsteady stretching surface with non-uniform heat source/sink in the presence of inclined magnetic field. J. Egypt. Math. Soc. 2019, 27, 9. [Google Scholar]
- Saidulu, N.; Gangaiah, T.; Lakshmi, A.V. Radiation effect on mhd flow of a tangent hyperbolic nanofluid over an inclined exponentially stretching sheet. Int. J. Fluid Mech. Res. 2019, 46, 277–293. [Google Scholar] [CrossRef]
- Murthy, P.V.S.N.; Sutradhar, A.; RamReddy, C. Double-diffusive free convection flow past an inclined plate embedded in a non-Darcy porous medium saturated with a nanofluid. Transp. Porous Media 2013, 98, 553–564. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, S.; Alsaedi, A.; Shafiq, A. Inclined magnetic field and heat source/sink aspects in flow of nanofluid with nonlinear thermal radiation. Int. J. Heat Mass Transf. 2016, 103, 99–107. [Google Scholar] [CrossRef]
- Kolsi, L.; Alrashed, A.A.; Al-Salem, K.; Oztop, H.F.; Borjini, M.N. Control of natural convection via inclined plate of CNT-water nanofluid in an open sided cubical enclosure under magnetic field. Int. J. Heat Mass Transf. 2017, 111, 1007–1018. [Google Scholar] [CrossRef]
- Rashad, A.M. Unsteady nanofluid flow over an inclined stretching surface with convective boundary condition and anisotropic slip impact. Int. J. Heat Technol. 2017, 35, 82–90. [Google Scholar] [CrossRef]
- Ramesh, G.K.; Gireesha, B.J.; Bagewadi, C.S. Heat transfer in MHD dusty boundary layer flow over an inclined stretching sheet with non-uniform heat source/sink. Adv. Math. Phys. 2012, 2012, 13. [Google Scholar] [CrossRef]
- Abo-Eldahab, E.M.; El Aziz, M.A. Blowing/suction effect on hydromagnetic heat transfer by mixed convection from an inclined continuously stretching surface with internal heat generation/absorption. Int. J. Therm. Sci. 2004, 43, 709–719. [Google Scholar] [CrossRef]
- Rahman, M.M.; Salahuddin, K.M. Study of hydromagnetic heat and mass transfer flow over an inclined heated surface with variable viscosity and electric conductivity. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2073–2085. [Google Scholar] [CrossRef]
- Hayat, T.; Asad, S.; Mustafa, M.; Alsaedi, A. Radiation effects on the flow of Powell-Eyring fluid past an unsteady inclined stretching sheet with non-uniform heat source/sink. PLoS ONE 2014, 9, e103214. [Google Scholar] [CrossRef] [PubMed]
- Tlili, I. Effects MHD and Heat Generation on Mixed Convection Flow of Jeffrey Fluid in Microgravity Environment over an Inclined Stretching Sheet. Symmetry 2019, 11, 438. [Google Scholar] [CrossRef]
- Eringen, A.C. Simple microfluids. Int. J. Eng. Sci. 1964, 2, 205–217. [Google Scholar] [CrossRef]
- Bég, O.A.; Zueco, J.; Chang, T.B. Numerical analysis of hydromagnetic gravity-driven thin film micropolar flow along an inclined plane. Chem. Eng. Commun. 2010, 198, 312–331. [Google Scholar] [CrossRef]
- Rahman, M.M.; Uddin, M.J.; Aziz, A. Effects of variable electric conductivity and non-uniform heat source (or sink) on convective micropolar fluid flow along an inclined flat plate with surfaceheat flux. Int. J. Therm. Sci. 2009, 48, 2331–2340. [Google Scholar] [CrossRef]
- Shah, Z.; Islam, S.; Gul, T.; Bonyah, E.; Khan, M.A. The electrical MHD and hall current impact on micropolar nanofluid flow between rotating parallel plates. Results Phys. 2018, 9, 1201–1214. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M. Numerical Study on Micropolar Nanofluid Flow over an Inclined Surface by Means of Keller-Box. Asian J. Probab. Stat. 2019. [Google Scholar] [CrossRef]
- Kasim, A.R.M.; Mohammad, N.F.; Shafie, S. Unsteady MHD mixed convection flow of a micropolar fluid along an inclined stretching plate. Heat Transf. Asian Res. 2013, 42, 89–99. [Google Scholar]
- Srinivasacharya, D.; Bindu, K.H. Entropy generation in a micropolar fluid flow through an inclined channel. Alex. Eng. J. 2016, 55, 973–982. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; RamReddy, C.; Naveen, P. Double dispersion effect on nonlinear convective flow over an inclined plate in a micropolar fluid saturated non-Darcy porous medium. Eng. Sci. Technol. Int. J. 2018, 21, 984–995. [Google Scholar] [CrossRef]
- Shamshuddin, M.D.; Thumma, T. Numerical study of a dissipative micropolar fluid flow past an inclined porous plate with heat source/sink. Propuls. Power Res. 2019, 8, 56–68. [Google Scholar]
- Mavromatidis, L.E. Study of coupled transient radiation-natural convection heat transfer across rectangular cavities in the vicinity of low emissivity thin films for innovative building envelope applications. Energy Build. 2016, 120, 114–134. [Google Scholar] [CrossRef]
- Mavromatidis, L. Coupling architectural synthesis to applied thermal engineering, constructal thermodynamics and fractal analysis: An original pedagogic method to incorporate “sustainability” into architectural education during the initial conceptual stages. Sustain. Cities Soc. 2018, 39, 689–707. [Google Scholar] [CrossRef]
- Mavromatidis, L. Constructal Macroscale Thermodynamic Model of Spherical Urban Greenhouse Form with Double Thermal Envelope within Heat Currents. Sustainability 2019, 11, 3897. [Google Scholar] [CrossRef]
- Anwar, M.I.; Shafie, S.; Hayat, T.; Shehzad, S.A.; Salleh, M.Z. Numerical study for MHD stagnation-point flow of a micropolar nanofluid towards a stretching sheet. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 89–100. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Ali, F.; Aamina, B.; Khan, I.; Sheikh, N.A.; Saqib, M. Magnetohydrodynamic flow of brinkman-type engine oil based MoS2-nanofluid in a rotating disk with hall effect. Int. J. Heat Technol. 2017, 4, 893–902. [Google Scholar]
- Gnaneswara Reddy, M.; Reddy, S.; Rama, G. Micropolar fluid flow over a nonlinear stretching convectively heated vertical surface in the presence of Cattaneo-Christov heat flux and viscous dissipation. Front. Heat Mass Transf. 2017, 8. [Google Scholar] [CrossRef]
- Ullah, I.; Abdullah Alkanhal, T.; Shafie, S.; Nisar, K.S.; Khan, I.; Makinde, O.D. MHD Slip Flow of Casson Fluid along a Nonlinear Permeable Stretching Cylinder Saturated in a Porous Medium with Chemical Reaction, Viscous Dissipation, and Heat Generation/Absorption. Symmetry 2019, 11, 531. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).