Abstract
The compensation of an electrical system from passive compensators mainly focuses on linear systems where the consumption of charges does not vary significantly over time. In three-phase three-wire systems, when the network voltages are unbalanced, negative-sequence voltages and currents appear, which can significantly increase the total apparent power supplied by the network. This also increases the network losses. This paper presents a method for calculating the compensation of the positive-sequence reactive power and unbalanced powers caused by the negative-sequence line currents using reactive elements (coils and/or capacitors). The compensation is applied to three-phase three-wire linear systems with unbalanced voltages and loads, which are connected to an infinite power network. The method is independent of the load characteristics, where only the line-to-line voltages and line currents, at the point where compensation is desired, need to be known in advance. The solution obtained is optimal, and the system observed from the network behaves as one that only consumes the active power required by a load with a fully balanced current system. To understand the proposed method and demonstrate its validity, a case study of a three-phase three-wire linear system connected to an infinite power network with unbalanced voltages and currents is conducted.
1. Introduction
At present, it is practically impossible to achieve balanced low-voltage distribution systems as these systems, to a greater or lesser degree, are unbalanced. These imbalances are caused by the asymmetry of voltages and use of unbalanced loads. In both cases, unbalanced powers are generated, which degrade the system efficiency. Note that when the electrical systems are high voltage, these unbalanced powers are very small, which make the system inefficient [1,2,3,4], in turn causing increases in line losses and malfunction of equipment, such as motors, generators, transformers, and protective equipment. Therefore, the apparent power of the system is considerably increased [5,6,7,8], and thus, it is necessary to calculate these unbalanced powers to design compensation devices. In this study, a passive compensator formed of coils and capacitors is used.
At present, there is no theory agreed by the scientific community that allows to assess this type of phenomenon [9]. Most of the previous studies followed the expressions proposed in IEEE Std. 1459–2010 [10] and Buchholz [11], which use the RMS values of voltage and current, which are expressed in symmetric or phase components [12]. The use of these values does not allow us to assess these inefficient powers. According to [13,14], imbalances at one point in the system can help offset some of the imbalances at another point. Such situations cannot be analyzed if only the modules of voltages and currents are known.
The application of electronics, in the compensation of electrical systems, indicates that most industries today mainly focus on the use of active compensators. The advantages of these compensators or filters cannot be denied, especially for the compensation of non-linear systems. As compared to passive compensators, the active compensators are more expensive, less robust, and consume more energy. In certain situations, for linear systems, where the load does not vary with time, the use of passive compensators is a good alternative. They are configured from reactive elements (coils and/or capacitors). In this study, passive compensators are used to compensate for the reactive and unbalanced power resulting from the negative-sequence current of any three-wire system.
The concept of compensation of an electrical system by passive compensators is not new. Steinmetz [15] developed a passive compensator to obtain a system of balanced line currents. He used a single-phase load with known data, and compensated it with a coil and capacitor and we believe that the voltages in the study were balanced. This study has been extended by many authors [16,17,18,19,20,21,22,23,24].
Gyugyi et al. [25] studied compensation through passive compensators for a three-wire linear system with unbalanced load and balanced voltages. For this purpose, they categorised the line currents into symmetric component values, and proposed two delta-connected compensators: one for compensating the imaginary part of the positive-sequence current and the other for compensating the negative-sequence current. Finally, these two compensators were unified by associating them in parallel. However, for the formulation of their expressions, the values and characteristics of the load were required.
Czarnecki [26] applied the decomposition of the currents, proposed previously [27], to a non-linear three-wire circuit with unbalanced loads. He focused on linear systems with balanced voltages, and broke down the original load into several equivalent circuits: a resistive circuit, representing active power; an inductive circuit, representing reactive power; and a circuit from the current sources to represent its unbalanced current. For each equivalent circuit, a passive compensator was proposed.
Willems [28] proposed a matrix of suceptances to compensate for the reactive and unbalanced power resulting from negative-sequence currents using passive elements. During the development, the voltages were considered balanced. The method presented infinite solutions for a three-phase three-wire system.
Origa et al. [29] applied a previous study [25] to three-phase four-wire systems to compensate for the reactive and unbalanced power consumed by an unbalanced load through passive elements. Similar to [28], the solution presented infinite possibilities. As highlighted in previous studies, the voltages were balanced. In addition, as starting data, the values and characteristics of the load were required.
Jeon and Willems [30], based on [28], presented a procedure to compensate for only the reactive power through passive compensating circuits, both in star and delta connections. This system applied three wires and multi-phase to unbalanced three-phase systems.
León and Montañana [31], based on [32], broke down an unbalanced load into several equivalent circuits, which represented active, reactive, and unbalanced power. Except for active power, all other equivalent circuits were configured from reactive elements (coils and/or capacitors). They used the circuits opposite to the equivalents obtained as compensators of the unbalanced power and positive-sequence reactive power. They considered the voltages to be balanced, and the charges to be known.
Finally, Czarnecki and Haley [33] extended the previous studies [26,27] to four-wire systems and showed that the unbalanced power, in these systems, is formed by a negative- and a zero-sequence current. To compensate for the two currents, it is necessary to use at least two compensators. This conclusion was also considered in [31] and shared by us as well. As in most previous studies, it applies to systems with balanced voltages.
Besides the advantages and disadvantages of the studies analyzed above, they all have something in common: they are only applicable to systems with balanced voltages. With unbalanced voltages, their behaviour is not adequate, especially in electrical systems of infinite power, where the network imposes voltages.
This paper proposes a new procedure for calculating the compensation of a three-phase three-wire linear system connected to an infinite power network. For non-infinite power networks, the procedure is perfectly valid. Through two passive star-connected compensators, configured only with reactive elements (coils and capacitors), the positive-sequence reactive power and unbalanced power, resulting from the negative-sequence current, are compensated. Using star-delta transformations, these phenomena are unified into a single delta-connected compensator. A significant advantage of the proposed method is its application to systems with unbalanced voltages, and that it is not necessary to know the load values. It simply requires the use of line-to-line voltages and line currents that can be easily measured on the bus. The proposed method is valid for any voltage level. However, in this work, we have considered low voltage networks where imbalances are most important.
For this purpose, in Section 2, the balance of powers involved in such systems is identified, and its effects are analyzed. The expression of Buchholz apparent power, expressed in values of symmetric voltage and current components, is used. This relation between powers and their expressions of calculation form the basis of our method. In Section 3, through application to a three-phase three-wire system with unbalanced loads and balanced line-to-line voltages, the new method of calculating the compensators is proposed. Separating the two compensation lines, one compensator is used to compensate for the positive-sequence reactive power and another for the unbalanced power resulting from the negative-sequence current, both in star connection. In Section 4, the design of both compensators is adapted to three-phase three-wire systems with unbalanced voltages that are connected to an infinite power network, whose voltages are imposed by the network itself. Its design analyses the interactions occurring in these compensators when connected to a system with these characteristics. In Section 5, the two compensators are unified into one with a delta connection. In Section 6, a three-phase three-wire system connected to an infinite power network with unbalanced loads and voltages is used to facilitate and verify the proposed method. Finally, Section 7 presents the conclusions of this study.
2. Unbalanced Power Analysis in a Three-Phase Linear System
Figure 1 displays a linear unbalanced load connected to a three-phase system with three-wire unbalanced line-to-line voltages.
Figure 1.
Three-phase three-wire system with an unbalanced load.
The instantaneous power p of the system is determined by (1), where , and are the line-to-line voltages on the bus, and , and are the line currents.
For example, considering the first equality of Equation (1) and expressing these values in complex form, we can determine the active power , reactive power , and apparent power of the system using Equations (2)–(4), respectively.
Using the Fortescue transformation matrix, the line-to-line voltages and line currents in terms of symmetric components are expressed in Equations (5) and (6). As it is a three-wire system, the zero-sequence line-to-line voltage and line current are zero.
Given that and , the positive-sequence line-to-neutral voltage and negative-sequence line-to-line voltage are determined by Equations (7) and (8), respectively, where and are the angles referred to Phase A of both line-to-line voltages and , where is complex phasor rotation operator.
At the measuring point (PCC or bus) and under these conditions, the total apparent power of Buchholz is determined by Equation (9). In balanced systems, has the same value as , while in unbalanced systems, does not reflect the real apparent power of the system, and has a different value than .
Developing Equation (9), we obtain Equation (10).
Here
- indicates the positive-sequence apparent power resulting from the positive-sequence voltage and current.
- indicates the negative-sequence apparent power resulting from the negative-sequence voltage and current.
- indicates the apparent power resulting from the positive-sequence voltage and negative-sequence current.
- indicates the apparent power resulting from the negative-sequence voltage and positive-sequence current.
and are related to the apparent power of Equation (4) by Equation (11).
Substituting Equation (11) into Equation (10) and considering Equation (4), we obtain Equation (12).
3. Compensation in Three-Phase Three-Wire Systems with Balanced Voltages
Figure 2 shows an unbalanced three-phase linear load connected to a three-phase three-wire system with infinite power. As the voltages are balanced, the powers , and included in (12) are zero. Therefore, the total apparent power is determined by Equation (13), and includes the following powers: active power , which with balanced voltages is equal to ; reactive power , which with balanced voltages is equal to ; and the unbalanced apparent power .
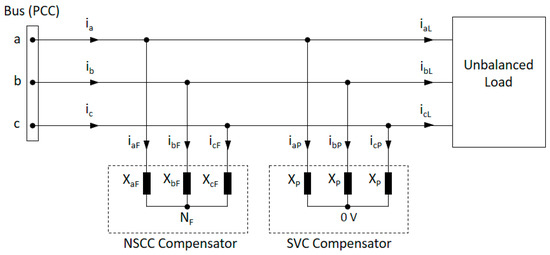
Figure 2.
Compensation of a system with an unbalanced load. NSCC: negative-sequence current compensator; SVC: static VAR compensator.
and are powers whose average value is zero, and therefore, they can be compensated from reactive elements (coils and/or capacitors). With this objective, we incorporate two compensators: static VAR compensator (SVC), to compensate , and negative-sequence current compensator (NSCC), to compensate . As the voltages are balanced, both compensators are independent, that is, the design of one compensator does not affect those of the others. However, this statement is not valid when the voltages are unbalanced.
3.1. Reactive Power Compensator
The use of reactive power compensators (SVC) has been extensively studied. The two methods, frequently used to calculate the reactance values, are sinusoidal and balanced current (SBC) and minimum line loss (MLL). We use the SBC method in this study. In the SBC method, the values of reactance in each phase are identical and determined from the positive-sequence voltages and currents according to (14). with a positive value represents a coil, while a negative value represents a capacitor. Normally, this compensator is capacitive in nature, as the charges are usually inductive. The only positive sequence reactive power to compensate for the balanced voltages is that of the load; therefore, is equal to .
Here
- is the reactance value of SVC compensator.
- is the positive-sequence line-to neutral voltage.
- is the total positive-sequence reactive power to compensate.
- is the total positive-sequence reactive power of the load.
3.2. Negative-Sequence Current Compensator
As Figure 2 shows, to compensate for the unbalanced apparent power , we use the NSCC compensator from reactive elements (coils and/or capacitors). In this case, the compensator reactance values (, and ) are different in each phase, because the positive-sequence voltage and negative-sequence current have different sequences.
In our case, the objective is to compensate for the unbalanced powers due to the negative-sequence currents of the load (, and ). Therefore, the currents consumed by the SVC compensator are equal to , and , but in opposite directions, according to Equation (15).
Considering reference point “0” for all voltages, and applying Kirchhoff’s second law to the compensator, the Equations (16)–(18) are obtained. The positive-sequence voltages are used because they are balanced. On the other hand, the powers in each phase consumed by the NSCC compensator at the balanced voltages are due to voltages and currents of different sequences; therefore, the sum of the values of all phases is null, complying with Equation (19).
Equations (16)–(19) form a system of four equations with complex numbers, where , , and are unknown. Solving the system of equations would directly provide the values of the reactors of the NSCC compensator. We use another approach to solve the system, to obtain simpler and quicker expressions.
Considering that Equation (16) refers to Phase A, and decomposing this expression into real and imaginary parts, Equations (20) and (21) are obtained. The angle of is when it is a coil, and when it is a capacitor. We consider that the load is inductive, and therefore, the reactance of the compensator, , is capacitive and its angle is .
Squaring Equations (20) and (21), adding both equations, and regrouping the terms, we obtain (22). To simplify, we consider that .
Developing the same procedure for Phase B from Equation (17) and for Phase C from Equations (18), (23) and (24) are obtained.
To include the condition defined in Equation (19), we graphically analyse different case studies, where we vary the characteristics of the loads as well as the line-to-line voltages. Figure 3 shows the relation between the difference in the modules (for ), and the sum of the compensator reactances , and . It is observed that regardless of the characteristics of the load and the voltages, the sum of the reactances is null when the difference in the modules . This implies that Equation (19) is true when the modules of and are equal. Considering this condition in Equations (22)–(24), and generalizing for , Equation (25) is obtained.
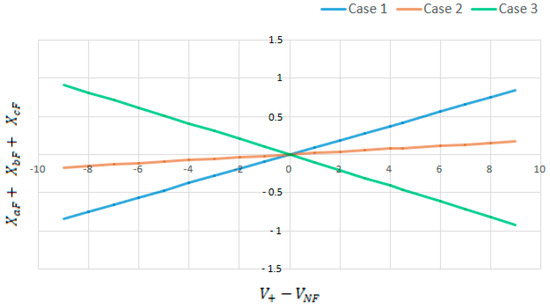
Figure 3.
Graph of the relation between and the sum of reactances of the compensator.
Solving Equation (25), the reactance values , , and are obtained from Equation (26).
Considering that , we obtain:
Multiplying both terms of (27) by the square of , and using (15), we obtain:
On the other hand, it is known that:
where is the reactive power consumed by the NSCC compensator in all phases, and is the reactive power caused by the positive-sequence voltage and negative-sequence current for any phase of the load. Substituting Equations (29) and (30) into (28), Equation (31) is obtained. It is observed that the power consumed by the compensator in one phase is equal to twice the reactive power caused by the negative-sequence current in the load in any phase with opposite sign. The change in sign identifies that the power of the load and compensator, in any phase, are of a different nature (inductive and capacitive).
According to Equation (15), ; therefore, the reactance value in each phase of the NSCC compensator is determined by Equation (32). We consider that the power in the load is inductive; therefore, is a capacitor when its value is negative and coil when it is positive.
With these values, a system of negative-sequence currents is obtained, but in the opposite direction to that of the load. This compensates for the unbalanced powers generated because of the product of the positive-sequence line-to-neutral voltage and negative-sequence current consumed by the load, without any modification to the active power supplied by the network.
4. Compensation with Unbalanced Voltages
Let us consider that the line-to-line voltages of the system shown in Figure 2 are unbalanced. Under these conditions, the apparent power includes all terms of powers defined in Equation (12). As an infinite power system is considered, the values of the line-to-line voltages on the bus do not change, therefore, we obtain a negative-sequence line-to-line voltage with constant value. As a result, the apparent power cannot be compensated, as the bus imposes the negative-sequence line-to-line voltage. The value of once connected with the SVC and NSCC compensators is modified based on the new value of the positive-sequence current on the bus, which is delivered by the network, and is lower than its initial value.
In contrast to systems with balanced voltages, the behaviour of the SVC and NSCC compensators are not independent. There is an interaction between both compensators, so that the design of one of them affects the other, and vice versa. The reason for this is evident, when the voltages are unbalanced, the SVC compensator consumes a positive-sequence and negative-sequence current. This negative-sequence current must be considered in the design of the NSCC compensator. The NSCC compensator reaction is similar at unbalanced voltages, it consumes a positive-sequence and negative-sequence current. This positive-sequence current must be considered in the SVC compensator design. This dependence of one compensator on another makes the iteration necessary, to determine the reactance values of both compensators. The number of iterations required to converge on the optimal solution depends on the degree of unbalance of the voltages. The proposed calculation method allows us to obtain the optimal solution without having to iterate. For this purpose, we analyse the system and behaviour of the SVC and NSCC compensators at unbalanced voltages, from which the following considerations are deduced:
- In a three-wire system with unbalanced voltages, the total active power consumed by the system is determined by the sum of the active positive- and negative-sequence powers, that is: . This power is unidirectional, and the SVC and NSCC compensators can only compensate powers with a null average value because they are configured from reactive elements (coils and/or capacitors). For this reason, the value of must be constant and continue to be supplied by the network or generator. The NSCC compensator is responsible for maintaining a constant . This compensator consumes a positive-sequence active power in each phase of the same value as that of the negative-sequence active power consumed by load and a negative-sequence active power in each phase in the opposite direction, that is, . Therefore, will compensate and . The SVC compensator consumes neither positive-sequence nor negative-sequence active power, because the voltages and currents of the same sequence are out of phase, , because the SVC compensator reactances have the same value. The sign depends on the inductive or capacitive nature of the system to be compensated and will be the same for the values of each sequence.
- The total reactive power consumed by the system is determined by the sum of the positive-sequence reactive power and the negative-sequence reactive power ; therefore, . At unbalanced voltages, both compensators consume positive- and negative-sequence reactive powers. The optimal solution is one whose result cancels the reactive powers and ; therefore, . It is observed, from analysing both compensators to obtain the optimal solution, that in the SVC compensator, the relation (33) is fulfilled, and in the NSCC compensator, the Equation (34) is fulfilled, where .
Next, to calculate the values of reactances of the SVC and NSCC compensators with unbalanced voltages, we first consider the calculation of the SVC compensator, and then that of the NSCC compensator.
4.1. Calculation of SVC Compensator Reactances with Unbalanced Voltages
Consider the system shown in Figure 2 at unbalanced voltages. It is known that the reactive power consumed by the load, , is determined by Equation (35), and that consumed by the SVC compensator, , is determined by Equation (36).
On the other hand, the reactive power , consumed by the NSCC compensator, is determined by Equation (37).
If we consider that the balance of powers is met:
Substituting condition (34), defined for the NSCC compensator, into Equations (38) and (39), Equation (40) is obtained.
Considering the condition Equation (33) defined for the SVC compensator in Equation (40), Equation (41) is obtained.
Equation (41) indicates that the reactive power consumed by the SVC compensator in each phase, , at unbalanced voltages is equal, and its value is determined by Equation (42). Considering the values of in (14) for each phase, Equation (43) is obtained, which allows us to determine the values of the SVC compensator reactances (, and ). with a positive value represents a coil, and that with a negative value represents a capacitor. Obviously, .
With balanced voltages, Equations (14) and (43) are identical, as and .
4.2. Calculation of the NSCC Compensator Reactances with Unbalanced Voltages
According to Equation (32), to determine the values of reactances , y , it is necessary to determine the negative-sequence current consumed by the NSCC compensator. From the values of and , we will determine the reactive power .
is given by Equation (44), where is the negative-sequence current that consumes the load, and is the negative-sequence current consumed by the SVC compensator. As the reactances in each phase of the SVC compensator are equal, the value of is obtained from Equation (45).
Considering the value in each phase obtained from Equation (44), the reactive power is determined from Equation (46).
Substituting the values of Equations (44) and (46) into Equation (32), the values of reactances , and are calculated from (47). For negative values of we use capacitors, and for positive values, we use coils.
With balanced voltages, Equations (32) and (47) are identical as it is true that and .
5. Joint Compensator “SVC + NSCC” in Delta Connection
The SVC and NSCC compensators used in previous sections are star-connected. As the reactances of the NSCC compensator are not equal, point of the NSCC compensator and point “0” of the SVC compensator are not at the same potential, therefore, it is impossible to associate them in parallel. To join both compensators in a single compensator, it is necessary to convert them to a delta connection using the Kennelly–Rosen transformation (refer to Figure 4 for system compensation using the joint compensator “SVC + NSCC”).
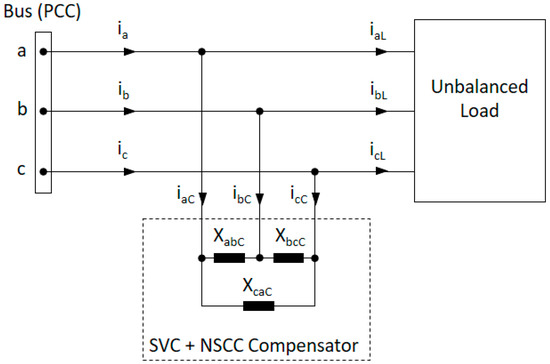
Figure 4.
Joint compensation “SVC + NSCC” in delta connection.
As the values of the SVC compensator reactances in star connection are identical, those of the reactances in delta connection can be obtained from (48). Here, .
Applying the transformation of star-delta connection of Kennelly–Rosen in the NSCC compensator, the reactance values are obtained from Equations (49)–(51).
Therefore, the reactances , , and of the compensator “SVC + NSCC” shown in Figure 4 are obtained from Equation (52).
6. Practical Application
In this section, a practical case study to verify all concepts discussed in the previous sections is conducted. Figure 5 shows an unbalanced three-phase linear three-wire system connected to an infinite power network with unbalanced voltages. An equivalent unbalanced load representing the entire network downstream of the bus is considered. The characteristics of the entire network from the bus are unknown. The following values of the line-to-line voltages and line currents have been measured on the bus (PCC):
Figure 5.
Unbalanced three-wire three-phase linear system connected to an infinite power network with unbalanced voltages.
Considering the values of line-to-line voltages and line currents measured on the bus, Table 1 and Table 2 show these values in symmetric components.

Table 1.
Positive-sequence line-to-line voltages and negative-sequence line-to-line voltages in the bus.

Table 2.
Positive- and negative-sequence line currents in the bus.
Table 3 shows the values of the line-to-neutral voltages in symmetric components according to Equations (7) and (8). These values are calculated from Table 1.

Table 3.
Positive- and negative-sequence line-to-neutral voltages in the bus.
Next, we proceed to determine the reactance values in each phase of the SVC and NSCC compensators according to the scheme shown in Figure 2.
6.1. Calculation of the Star Connected SVC Compensator
The positive-sequence reactive power consumed by the equivalent load is determined by the following expression:
where substituting the values in Table 2 and Table 3, we obtain:
On the other hand, the negative-sequence reactive power consumed by the equivalent load is determined by the following expression:
where substituting the values in Table 2 and Table 3, we obtain:
The positive-sequence reactive power, consumed by the SVC compensator, is determined by (42), and its value is obtained as follows:
Considering in (43), the reactances that the SVC compensator must have are determined by:
As the value is negative, is a capacitor.
To calculate the reactances of the NSCC compensator, it is necessary to determine the negative-sequence currents consumed by the SVC compensator. Considering Equation (45), the values of these currents are as follows:
6.2. Calculation of NSCC Star-Connected Compensator
The negative-sequence currents of the NSCC compensator are determined from Equation (44). The values of have been obtained in the previous section, and those of are listed in Table 2. Therefore, the values of are as follows:
Considering Equation (46), the imbalance powers caused by the positive-sequence voltages and negative-sequence currents are as follows:
Substituting the values of and in (47), the values of reactances in the NSCC compensator are obtained as:
From its sign, is a capacitor, is a coil, and is a capacitor.
6.3. Calculation of the Set Compensator “NSCC + SVC” Connected in Delta
Considering Figure 4 and applying the star-delta transformations according to Equations (50)–(52), the values of the compensator reactances “NSCC + SVC” are obtained as follows:
From its sign, is a coil, is a capacitor, and is a capacitor.
6.4. Analysis of Line Currents and Powers before and after Compensation
Table 4 shows the line currents supplied by the network on the bus, before and after compensation. Note that the line currents after compensation are fully balanced.

Table 4.
Values of line currents.
Table 5 displays the total active power , total reactive power , total positive-sequence active power , total positive-sequence reactive power , total negative-sequence active power and total negative-sequence reactive power supplied to the network on the bus, before and after compensation. The apparent power is determined by (4). As described above, it is noted that:

Table 5.
Powers caused by voltages and currents of the same sequence.
- is constant and equal to the initial one (before compensating). after compensating has been increased to maintain a constant .
- Except after compensation, the remaining powers supplied by the network are zero. Therefore, the total apparent power decreases with respect to the initial one.
Table 6 shows the powers caused by voltages and currents of different sequences in each phase that supplies the network to the bus. Here, the powers caused by the negative-sequence currents are cancelled after compensation. This does not occur with the powers caused by the negative-sequence voltages, as an infinite power network has been considered.

Table 6.
Powers caused by voltages and currents of different sequence.
Table 7 displays the values of the powers caused by the voltages and currents in sequence, as well as (total apparent power of Buchholz). As expected, and are zero as the negative-sequence currents are compensated by NSCC. has reduced value due to the compensation of by the SVC compensator. This power compensation reduces the value of , which is delivered by the network to the bus.

Table 7.
Apparent powers in symmetric components and apparent power of Buchholz.
7. Conclusions
This paper proposes a procedure for compensation by passive compensators formed by reactive elements (coils and/or capacitors), to compensate for the positive-sequence reactive power, and the unbalanced powers caused by the negative-sequence currents. Unlike most other methods, the proposed method is valid for systems that are fed with unbalanced voltages, and does not require the characteristics and values of the loads connected to the bus or measurement point. It is enough to know the line-to-line voltages and line currents to design the compensators that compensate for these inefficient powers. Although it has been assumed that the network is of infinite power, it can be observed that the compensator adapts to the fixed voltages on the bus. These voltages and currents at the measuring point can be measured with any traditional measuring device. It has been confirmed that when the system is fed with balanced voltages, the positive-sequence reactive and unbalanced powers represent two different phenomena that occur in the transfer of energy from the network to the bus load. These phenomena can be compensated with two independent compensators. It has also been shown that when the voltages are unbalanced, the compensators are not independent of each other, and the two phenomena indicated are compensated between the two compensators. These compensators can be connected in star or delta. They can also be unified into a single compensator that compensates for both phenomena, coupling them into a single delta connection. The equations that have been presented are simple, and their application is immediate.
Therefore, the objective of this study is fulfilled, that is, the efficiency in the transfer of electrical energy from the network to the charges through the bus should be as efficient as possible, by eliminating negative-sequence currents and positive-sequence reactive currents. With this, the streams of lines delivered by the network to the system form a symmetrical system of positive sequence. To facilitate the application of the method, a case study was analyzed based on a three-phase unbalanced three-wire linear system connected to an infinite power network with unbalanced voltages.
Author Contributions
Conceptualization, P.A.B., R.M. and J.M.D.; Methodology, P.A.B., R.M.-M., J.M.D. and R.M.; Validation, P.A.B., R.M.-M. and R.M.; Formal Analysis, P.A.B. and R.M.-M.; Investigation, P.A.B., R.M.-M., J.M.D. and R.M.; Resources, P.A.B. and R.M.-M.; Data Curation, P.A.B. and R.M.-M.; Writing-Original Draft Preparation, J.M.D. and R.M.; Writing-Review & Editing, R.M.-M., J.M.D. and R.M.; Visualization, P.A.B. and R.M.-M.; Supervision, J.M.D., R.M. and M.J.R.; Project Administration, J.M.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Spanish Ministry of Science, Innovation and Universities (MICINN) and the European Regional Development Fund (ERDF) under Grant RTI2018-100732-B-C21.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Emanuel, A.E. On the definition of power factor and apparent power in unbalanced polyphase circuits with sinusoidal voltage and currents. IEEE Trans. Power Deliv. 1993, 8, 841–852. [Google Scholar] [CrossRef]
- Willems, J.L. Reflections on apparent power and power factor in non-sinusoidal and polyphase situations. IEEE Trans. Power Deliv. 2004, 19, 835–840. [Google Scholar] [CrossRef]
- Emanuel, A.E. Apparent power definitions for three-phase systems. IEEE Trans. Power Deliv. 1999, 14, 767–772. [Google Scholar] [CrossRef]
- Czarnecki, J.L. Misinterpretation of some power properties of circuits. IEEE Trans. Power Deliv. 1994, 9, 1760–1764. [Google Scholar] [CrossRef]
- Kerting, W.H. Causes and effects of unbalanced voltages serving an induction motors. IEEE Trans. Ind. Appl. 2001, 37, 165–170. [Google Scholar] [CrossRef]
- Pillay, P.; Manyage, M. Loss of life in induction machines operating with unbalanced supplies. IEEE Trans. Energy Convers. 2006, 21, 813–822. [Google Scholar] [CrossRef]
- Angarita, M.L.; Ramos, G.A. Power calculations in nonlinear and unbalanced conditions according to IEEE Std 1459–2010. In Proceedings of the 2013 Workshop on Power Electronics and Power Quality Applications (PEPQA), Bogota, Colombia, 6–7 July 2013; pp. 1–7. [Google Scholar] [CrossRef]
- Langella, R.; Testa, A.; Emanuel, A.E. Unbalance definition for electrical power systems in the presence of harmonics and interharmonics. IEEE Trans. Instrum. Meas. 2012, 61, 2622–2631. [Google Scholar] [CrossRef]
- Kukačka, L.; Kraus, J.; Kolář, M.; Dupuis, P.; Zissis, G. Review of AC power theories under stationary and non-stationary, clean and distorted conditions. IET Gener. Transm. Distrib. 2016, 10, 221–231. [Google Scholar] [CrossRef]
- IEEE Standards Association. IEEE Standard Definittion for the Measurement of Electric Power Quantities under Sinusoidal, Nonsinusoidal, Balanced, or Unbalanced Conditions. IEEE Std. 1459–2010; IEEE Standards Association: New York, NY, USA, 2010; pp. 1–50. [Google Scholar]
- Buchholz, F. Die drehstrom-scheinleistung bei ungleichmassiger belastung der drei zweige. Licht und Kraft 1922, 2, 9–11. [Google Scholar]
- Fortescue, C.L. Method of symmetrical coordinates applied to the solution of poly-phase networks. In Proceedings of the 34th Convention on American Institute of Electrical Engineers, Atlantic City, NJ, USA, 28 June 1918. [Google Scholar]
- Chicco, G.; Postolache, P.; Toader, C. Analysis of three-phase systems with neutral under distorted and unbalanced conditions in symmetrical component-based framework. IEEE Trans. Power Deliv. 2007, 22, 674–683. [Google Scholar] [CrossRef]
- Paap, G.C. Symmetrical components in the time domain and their application to power network calculations. IEEE Trans. Power Syst. 2000, 15, 522–528. [Google Scholar] [CrossRef]
- Steinmetz, C.P. Theory and Calculation of Electrical Apparatur; McGraw-Hill: New York, NY, USA, 1917. [Google Scholar]
- Grandpierr, M.; Trannoy, B. A static power device to rebalance and compensate reactive power in three-phase network. In Conference Record, IAS Annual Meeting 1977: IEEE Industry Applications Society, Papers Presented at the Twelfth Annual Meeting, Marriott Hotel, Los Angeles, California, 2–6 October 1977; IEEE: Piscataway Township, NJ, USA; pp. 127–135.
- Klinger, G. LC Kompensation und symmetirung fur Mehrphasensysteme mit belibigen Spanungdverlauf. ETZ Arch. 1979, 2, 57–61. [Google Scholar]
- Miller, J.E. Reactive Power Control in Electric Systems; Wiley-Interscience: NewYork, NY, USA, 1982. [Google Scholar]
- Czarnecki, L.S. Minimization of unbalanced currents in three-phase asymmetrical circuits with nonsinusoidal voltage. IEE Proc. B 1992, 139, 347–354. [Google Scholar] [CrossRef]
- Lee, S.Y.; Wu, C.J. On-line reactive power compensation schemes for unbalanced three-phase four wire distribution feeders. IEEE Trans. Power Deliv. 1993, 8, 1958–1965. [Google Scholar] [CrossRef]
- Czarnecki, L.S. Supply and loading quality improvement in sinusoidal power systems with unbalanced loads supplied with asymmetrical voltage. Archiv für Elektrotechnik 1994, 77, 169–177. [Google Scholar] [CrossRef]
- Sainz, L.; Caro, M.; Caro, E. Analytical study of series resonance in power systems with the Steinmetz circuit. IEEE Trans. Power Deliv. 2009, 24, 2090–2099. [Google Scholar] [CrossRef]
- Mayer, D.; Kropik, P. New approach to symmetrization of three phase networks. Int. J. Electr. Eng. 2005, 56, 156–161. [Google Scholar]
- Arendse, C.; Atkinson-Hope, G. Design of Steinmetz symmetrizer and application in unbalanced network. In Proceedings of the 45th International Universities Power Engineering Conference UPEC2010, Cardiff, Wales, UK, 31 August–3 September 2010. [Google Scholar]
- Gyugyi, L.; Otto, R.A.; Putman, T.H. Principles and applications of static, thyristor-controlled shunt compensators. IEEE Trans. Power Deliv. 1978, 5, 1935–1945. [Google Scholar] [CrossRef]
- Czarnecki, L.S. Reactive and unbalanced currents compensation in three-phase asymmetrical circuits under nonsinusoidal conditions. IEEE Trans. Instrum. Meas. 1989, 38, 754–759. [Google Scholar] [CrossRef]
- Czarnecki, L.S. Orthogonal decomposition of the currents in a 3-phase nonlinear asymetrical circuit with a nonsinusoidal voltage source. IEEE Trans. Instrum. Meas. 1988, 37, 30–34. [Google Scholar] [CrossRef]
- Willems, J.L. Currents compensation in three-phase power systems. Eur. Trans. Electr. Power 1993, 3, 61–66. [Google Scholar] [CrossRef]
- De Oliveira, L.C.O.; Neto, M.C.B.; De Souza, J.B. Load compensation in four-wire electrical power systems. In Proceedings of the 2000 International Conference on Power System Technology (Cat. No.00EX409), Perth, Australia, 4–7 December 2000; pp. 1575–1580. [Google Scholar] [CrossRef]
- Jeon, S.J.; Willems, J.L. Reactive power compensation in a multi-line system under sinusoidal unbalanced conditions. Inst. J. Circ. Theory Appl. 2011, 39, 211–224. [Google Scholar] [CrossRef]
- León-Martinez, V.; Montañana-Romeu, J. Representation of load imbalances through reactances. Application to working standards. In Proceedings of the 2014 16th International Conference on Harmonics and Quality of Power (ICHQP), Bucharest, Romania, 25–28 May 2014; pp. 307–311. [Google Scholar] [CrossRef]
- León-Martinez, V.; Giner-García, J.; Montañana-Romeu, J.; Cazorla-Navarro, A. Inefficiencies in the Power Systems: Effects, Quantification an Efficiency Improvement Devices; Editorial UPV: Valencia, Spain, 2001. [Google Scholar]
- Czarnecki, L.S.; Haley, P.M. Unbalanced power in four-wire systems and its reactive compensation. IEEE Trans. Power Deliv. 2015, 30, 53–63. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).