Preliminary Study on Mini-Modus Device Designed to Oxygenate Bottom Anoxic Waters without Perturbing Polluted Sediments
Abstract
1. Introduction
2. Materials and Methods
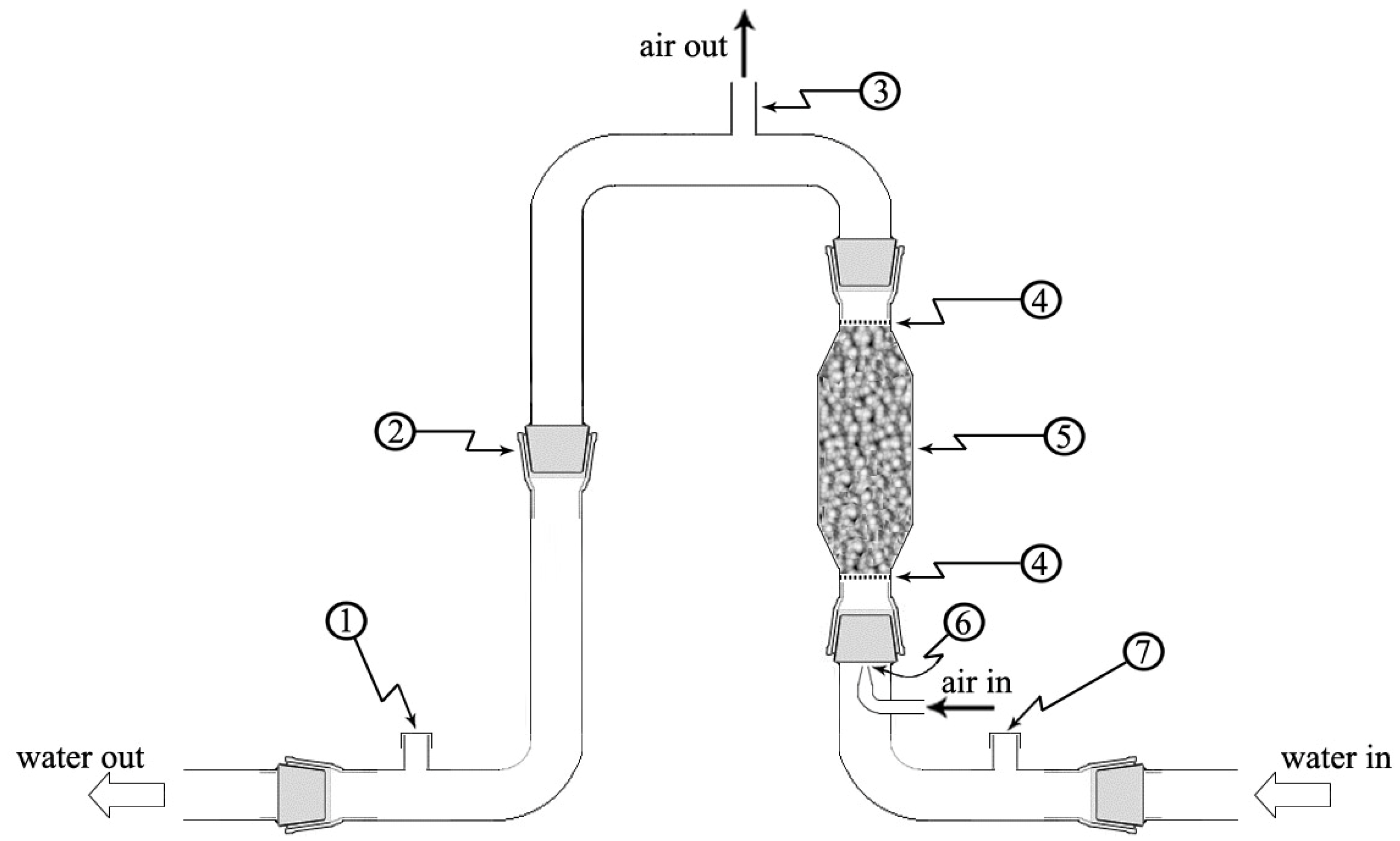
2.1. Equipment Description
2.2. Sampling, Analysis, and Data Elaboration
3. Results
3.1. Turbulence Tests (Sediment Resuspension Tests)
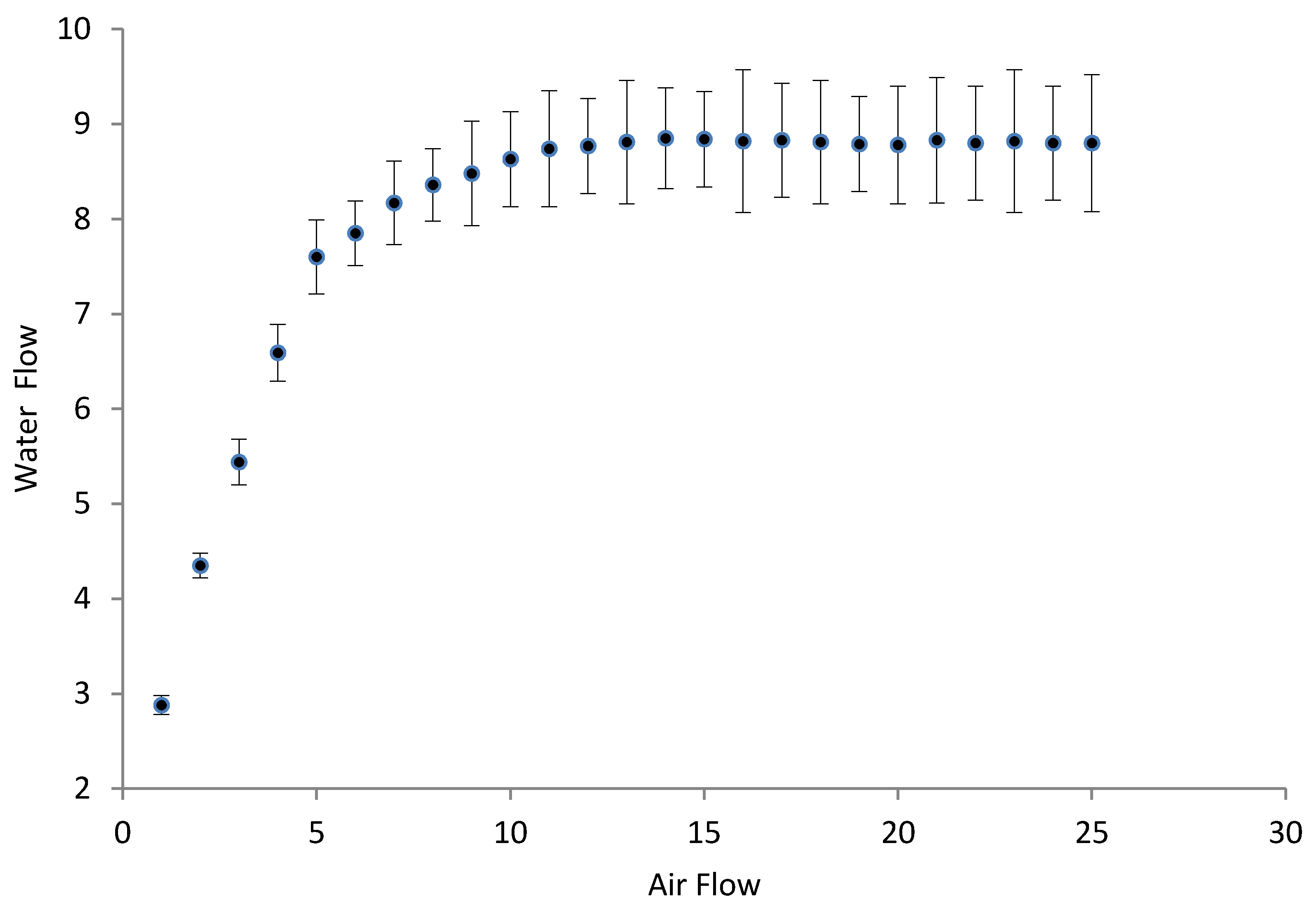
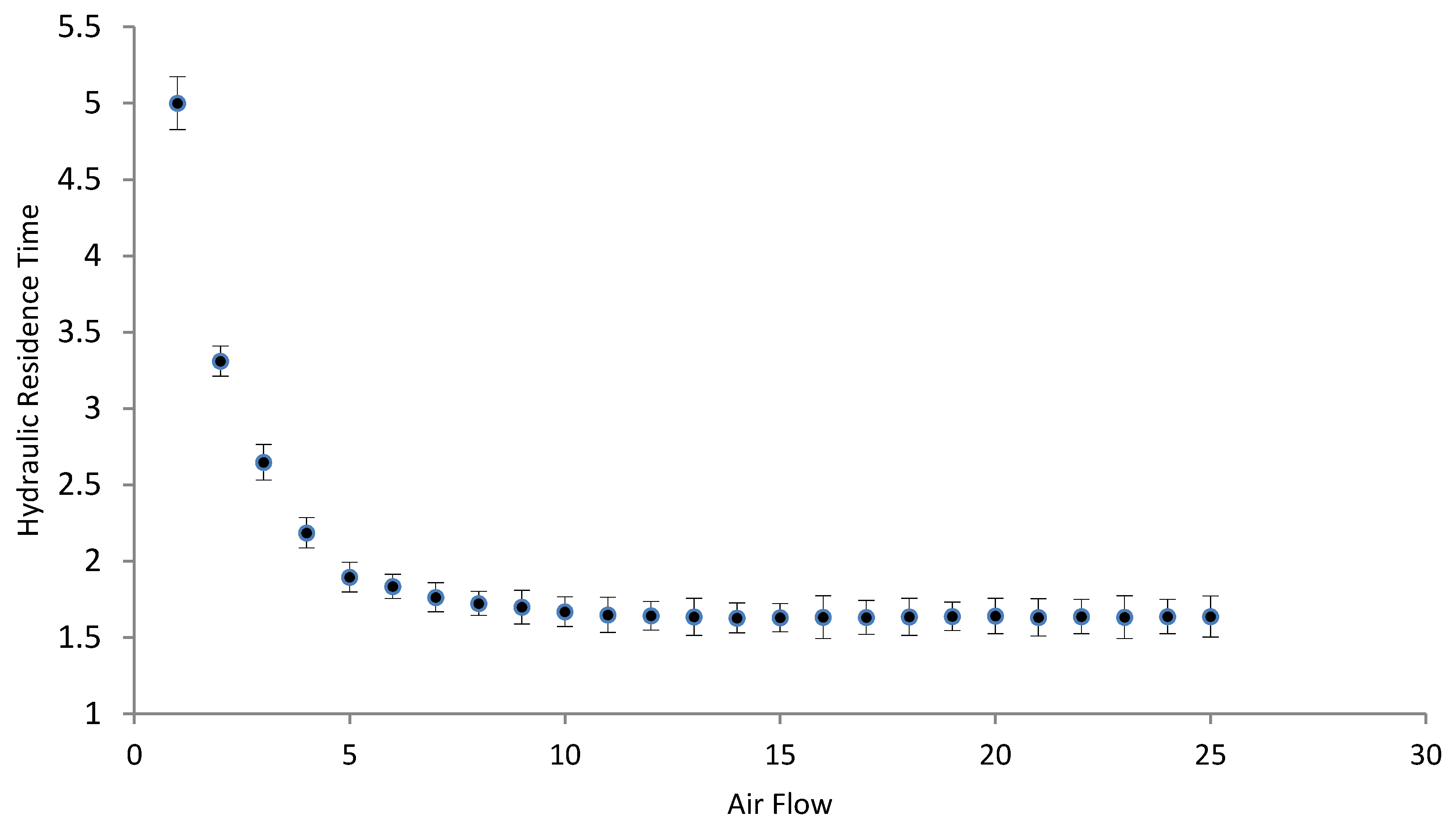
3.2. Hydrodynamic Tests
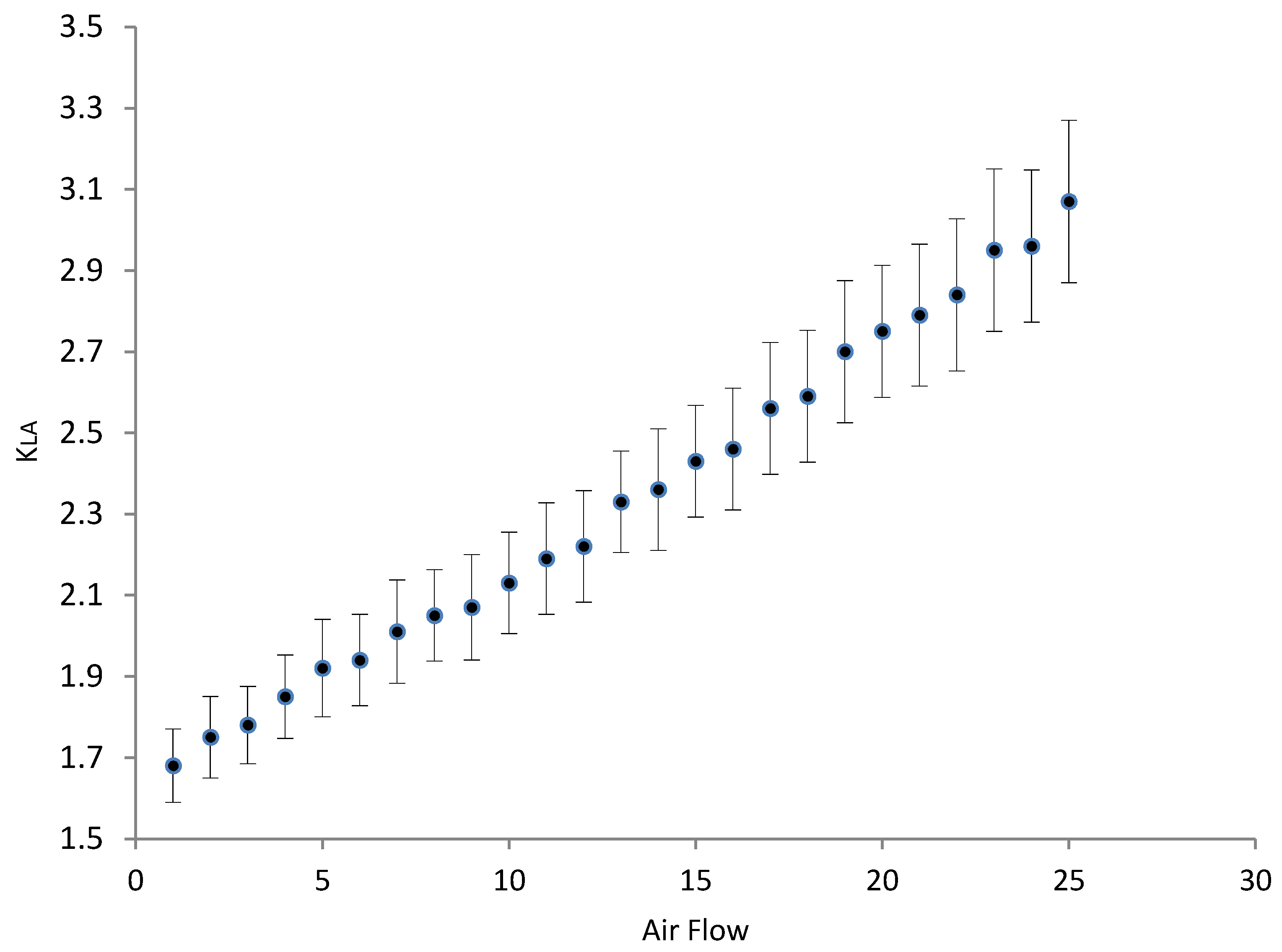
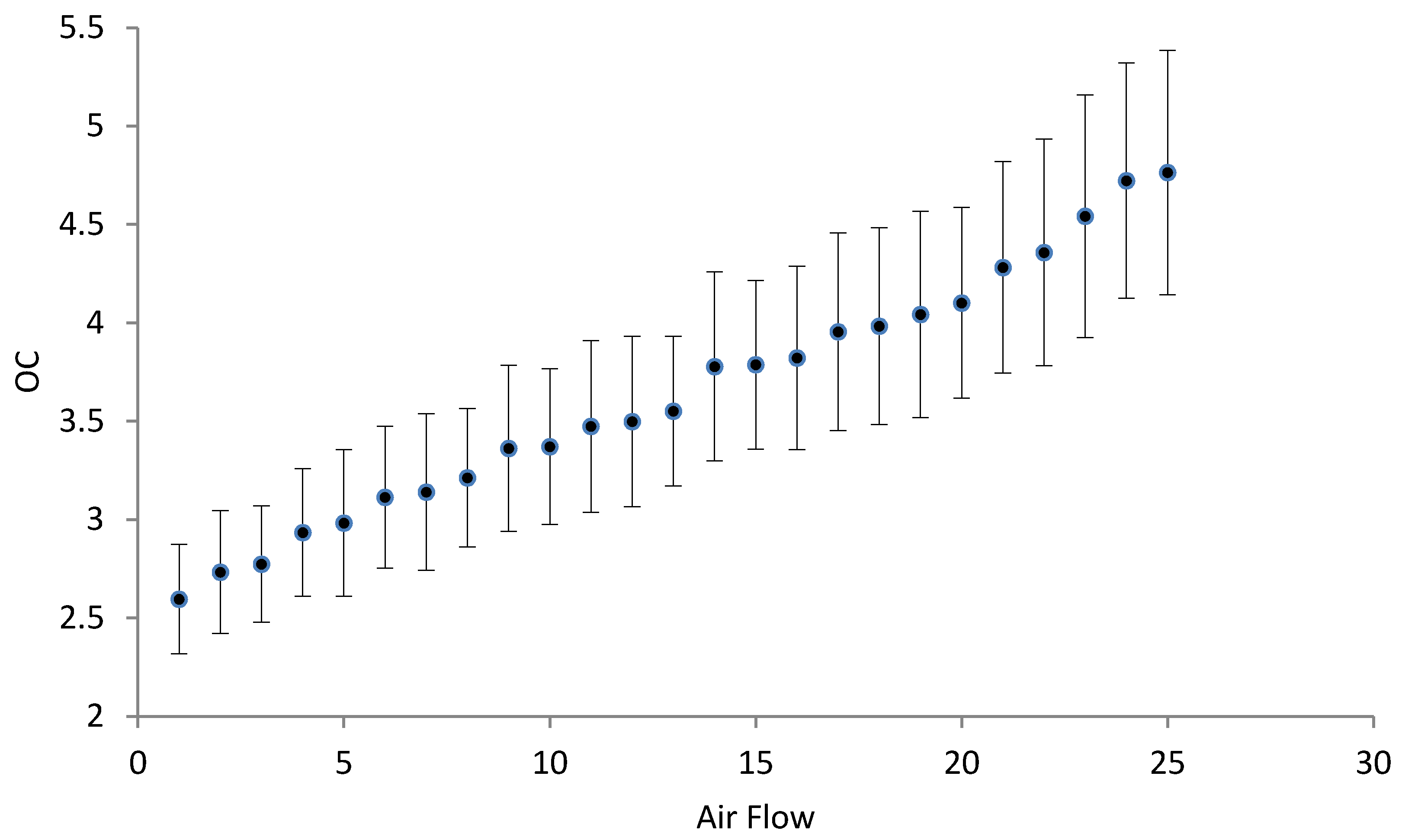
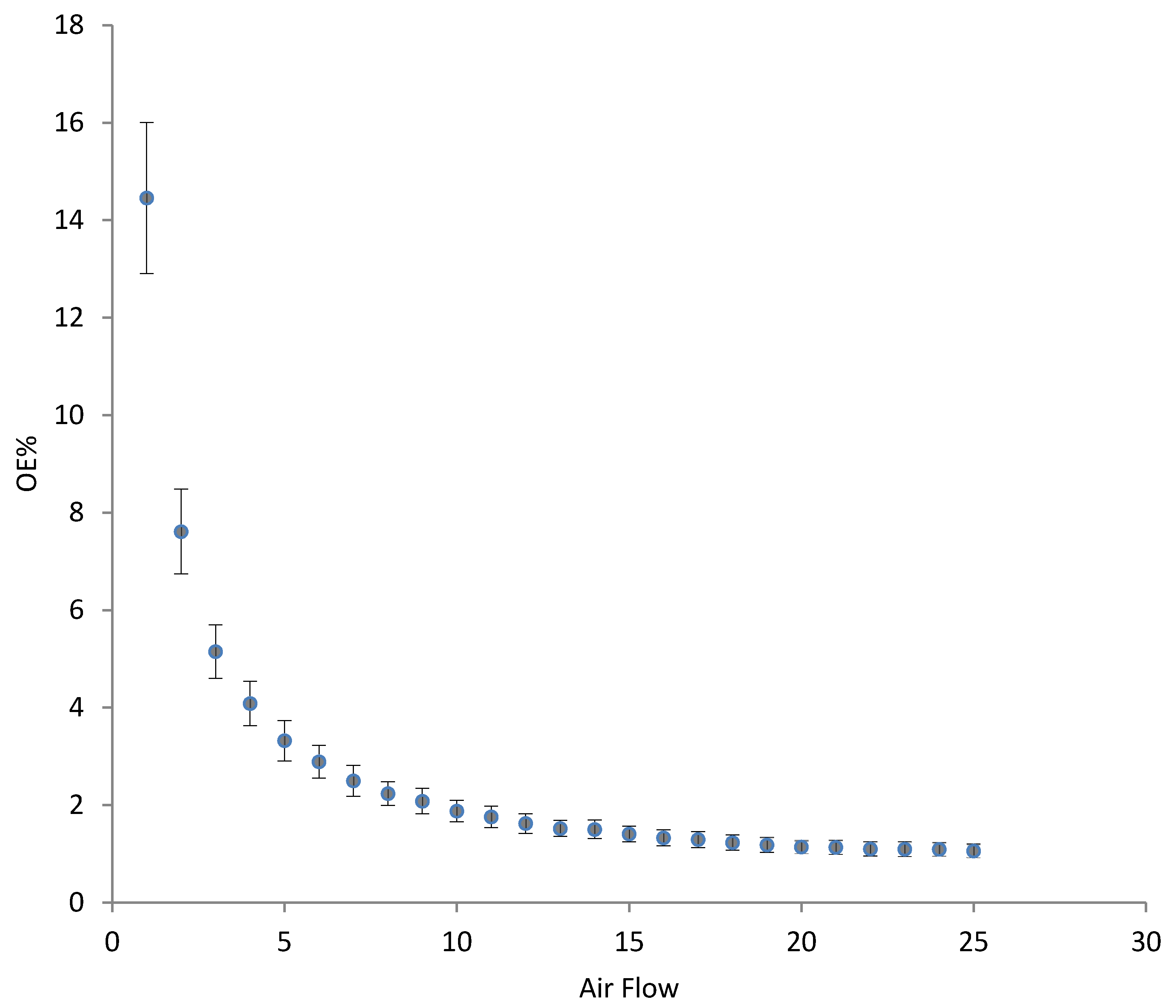
3.3. Oxygenation/Aeration Tests
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huang, J.-C.; Shi, T.-L.; Wen, G.; Liu, F.; Qiu, X.-P.; Wang, B.-S. The Variation Characteristic of Sulfides and VOSc in a Source Water Reservoir and Its Control Using a Water-Lifting Aerator. Int. J. Environ. Res. Public Health 2016, 13, 427. [Google Scholar]
- Chern, J.M.; Yu, C.F. Volatile organic compound emission from diffused aeration systems: Experiment and modeling. Ind. Eng. Chem. Res. 1999, 38, 2156–2159. [Google Scholar] [CrossRef]
- Loyless, J.C.; Malone, R.F. Evaluation of air-lift pump capabilities for water delivery, aeration and degasification for application to recirculating aquaculture systems. Aquac. Eng. 1998, 18, 117–133. [Google Scholar] [CrossRef]
- Soltero, R.A.; Sexton, L.M.; Ashley, K.I.; McKee, K.O. Partial and full lift hypolimnetic aeration of medical Lake, WA to improve water quality. Water Res. 1994, 28, 2297–2308. [Google Scholar] [CrossRef]
- Shimizu, K.; Takada, S.; Minekawa, K.; Kawase, Y. Phenomenological model for bubble column reactors prediction of gas hold-ups and volumetric mass transfer coefficients. Chem. Eng. J. 2000, 78, 21–28. [Google Scholar] [CrossRef]
- Nakamura, Y.; Inoue, T. A theoretical study on operational condition of hypolimnetic aerators. Water Sci. Technol. 1996, 34, 211–218. [Google Scholar] [CrossRef]
- Vickie, L.; Singleton, J.; Little, C. Designing Hypolimnetic Aeration and Oxygenation Systems—A Review. Environ. Sci. Technol. 2006, 4024, 7512–7520. [Google Scholar]
- Shuklaa, B.K.; Goel, A. Study on oxygen transfer by solid jet aerator with multiple openings. Eng. Sci. Technol. 2018, 21, 255–260. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, S.; Yang, C.; Chen, F.; Lu, S. Bioreactor consisting of pressurized aeration and dissolved air flotation for domestic wastewaters. Sep. Purif. Technol. 2014, 138, 186–190. [Google Scholar] [CrossRef]
- Research and Development Office Science and Technology Program. Top-Down Water Storage Mixing Systems Scoping Report, Final Report No. ST-2016-6415-01. 2016. Available online: https://www.google.com.sg/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&cad=rja&uact=8&ved=2ahUKEwi46LC58ajoAhUCCqYKHV0DCRMQFjAAegQIBRAB&url=https%3A%2F%2Fwww.usbr.gov%2Fresearch%2Fprojects%2Fdownload_product.cfm%3Fid%3D2495&usg=AOvVaw2diCkUCDLU-Rw2vEkCrmHy (accessed on 13 November 2019).
- Punnett, R.E. Design and Operation of Axial Flow Pumps for Reservoir Destratification; US Army Corps of Engineers: Washington, DC, USA, 1991.
- Khalil, M.F.; Elshorbagy, K.A.; Kassab, S.Z.; Fahmy, R.I. Effect of air injection method on the performance of an air lift pump. Int. J. Heat Fluid Flow 1999, 20, 598–604. [Google Scholar] [CrossRef]
- Couvert, A.; Roustan, M.; Chatellier, P. Two-phase hydrodynamic study of a rectangular air-lift loop reactor with an internal baffle. Chem. Eng. Sci. 1999, 54, 5245–5252. [Google Scholar] [CrossRef]
- Couvert, A.; Bastoul, D.; Roustan, M.; Line, A.; Chatellier, P. Prediction of liquid velocity and gas hold-up in rectangular air-lift reactors of different scales. Chem. Eng. Process. 2001, 40, 113–119. [Google Scholar] [CrossRef]
- Camarasa, E.; Meleiro, L.A.C.; Carvalho, E.; Domingues, A.; Maciel Filho, R.; Wild, G.; Poncin, S.; Midoux, N.; Bouillard, J. A Complete model for oxidation air-lift reactors. Computers and Chemical Engineering 2001, 25, 577–584. [Google Scholar] [CrossRef]
- Bekassy–Molnar, E.; Majeed, J.G.; Vatai, G. Overall volumetric oxygen transfer coefficient and optimal geometry of airlift tube reactor. Chem. Eng. J. 1997, 68, 29–33. [Google Scholar] [CrossRef]
- Dudley, J. Mass transfer in bubble columns: A comparison of correlations. Water Res. 1995, 29, 1129–1138. [Google Scholar] [CrossRef]
- Drandev, S.; Penev, K.I.; Karamanev, D. Study of the hydrodynamics and mass transfer in a rectangular air-lift bioreactor. Chem. Eng. Sci. 2016, 146, 180–188. [Google Scholar] [CrossRef]
- Parkhill, K.L.; Gulliver, J.S. Indirect measurement of oxygen solubility. Water Res. 1997, 31, 2564–2572. [Google Scholar] [CrossRef]
- Chern, J.M.; Yu, C.F. Oxygen transfer modeling of diffused aeration systems. Ind. Eng. Chem. Res. 1997, 36, 5447–5453. [Google Scholar] [CrossRef]
- Oliveira, M.E.C.; Franca, A.S. Simulation of oxygen transfer in aeration systems. Int. Commun. Heat Mass Transf. 1998, 25, 853–862. [Google Scholar] [CrossRef]
- Lee, J. Development of a model to determine mass transfer. Heliyon 2017, 3, e00248. [Google Scholar] [CrossRef]
- Gillot, S.; Heduit, A. Effect of air flow rate on oxygen transfer in an oxidation ditch equipped with fine bubble diffusers and slow speed mixers. Water Res. 2000, 34, 1756–1762. [Google Scholar] [CrossRef]
- Morchain, J.; Maranges, C.; Fonade, C. CFD modelling of two-phase jet aerator under influence of a crossflow. Water Res. 2000, 34, 3460–3472. [Google Scholar] [CrossRef]
- Moraveji, M.K.; Fakhari, M.E.; Mohsenzadeh, E.; Davarnejad, R. Hydrodynamics and oxygen mass transfer in a packed bed split-cylinder airlift reactor containing dilute alcoholic solutions. Heat Mass Transf. 2013, 49, 11–19. [Google Scholar] [CrossRef]
- Chisti, Y.; Jauregui-Haza, U.J. Oxygen transfer and mixing in mechanically agitated airlift bioreactors. Biochem. Eng. J. 2002, 10, 143–153. [Google Scholar] [CrossRef]
- Camarasa, E.; Carvalho, E.; Meleiro, L.A.C.; Maciel Filho, R.; Domingues, A.; Wild, G.; Poncin, S.; Midoux, N.; Bouillard, J. A hydrodynamic model for air-lift reactors. Chem. Eng. Process. 2001, 40, 121–128. [Google Scholar] [CrossRef]
- Camarasa, E.; Carvalho, E.; Meleiro, L.A.C.; Maciel Filho, R.; Domingues, A.; Wild, G.; Poncin, S.; Midoux, N.; Bouillard, J. Development of a complete model for an air-lift reactor. Chem. Eng. Sci. 2001, 56, 493–502. [Google Scholar] [CrossRef]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perin, G.; Romagnoli, F.; Perin, F.; Giacometti, A. Preliminary Study on Mini-Modus Device Designed to Oxygenate Bottom Anoxic Waters without Perturbing Polluted Sediments. Environments 2020, 7, 23. https://doi.org/10.3390/environments7030023
Perin G, Romagnoli F, Perin F, Giacometti A. Preliminary Study on Mini-Modus Device Designed to Oxygenate Bottom Anoxic Waters without Perturbing Polluted Sediments. Environments. 2020; 7(3):23. https://doi.org/10.3390/environments7030023
Chicago/Turabian StylePerin, Guido, Francesco Romagnoli, Fabrizio Perin, and Andrea Giacometti. 2020. "Preliminary Study on Mini-Modus Device Designed to Oxygenate Bottom Anoxic Waters without Perturbing Polluted Sediments" Environments 7, no. 3: 23. https://doi.org/10.3390/environments7030023
APA StylePerin, G., Romagnoli, F., Perin, F., & Giacometti, A. (2020). Preliminary Study on Mini-Modus Device Designed to Oxygenate Bottom Anoxic Waters without Perturbing Polluted Sediments. Environments, 7(3), 23. https://doi.org/10.3390/environments7030023



