1. Introduction
Urban growth is considered a complex phenomenon due to the strong interactions between different economic, social, environmental, cultural, and institutional components. A deeper understanding of how, why, and where these interactions occur is required in order to be able to plan the territory and create better futures for a constantly growing population. Thus, urban planning is fundamental, as is the need to comprehend and anticipate territorial changes. Modeling offers an alternative means to achieve this due to its capacity to create different possible future scenarios and depict the consequences of urban growth [
1,
2,
3].
Recent decades have witnessed exponential growth in the use of exploratory models based on different techniques (e.g., stochastic, artificial intelligence, and fuzzy tolerance) in the field of simulation. Although cellular automata (CA) predominate [
2], agent-based models (ABM) open new perspectives. Both were originally developed in the field of artificial intelligence with the aim of reproducing the knowledge and reasoning of several heterogeneous agents with the capacity for autonomous action in a specific environment, who at the same time need to coordinate to jointly solve planning problems [
4].
However, the use of modeling as a tool to support urban planning has remained limited due to historical skepticism about modeling designed for this purpose [
5,
6,
7]. Nevertheless, although few ABMs have been employed to address urban issues, other cellular models such as CA have gained more widespread acceptance [
8,
9,
10,
11]. This is confirmed in a review of urban simulation modeling techniques by Triantakonstantis and Mountrakis [
2], who found that more than 80% of the publications analyzed had used a CA, whereas ABM only accounted for less than 10%. These statistics must be placed in context, since CAs have a long history of being used for spatial modeling, whereas ABM are comparatively new in this field. Nevertheless, CAs pose some problems, for example when considering long distance interactions [
3], thus paving the way for the use of ABM in the urban modeling arena.
ABM techniques are particularly suitable in this field to gain a better understanding of the urban development process because they allow individual simulation of each agents’ behavior and show how, in conjunction, their behavior produces changes in the territory in the form of urban growth. Hence, ABM provides a good laboratory for developing new models of cities, since they elucidate how different city elements interact and thus enable planners to better understand what might happen in the future [
3,
12,
13].
Another important issue to consider is the geographical scope of urban ABM, which varies according to purpose and encompasses multiple spatial scales, although always considering individual behavior. Thus, the literature contains models aimed at exploring local issues such as residential mobility [
14] or emergency situations [
3,
15], and others with a broader, regional scope, for example those aimed at determining urban segregation or informal settlement formation [
16,
17,
18,
19]. Most have been designed to simulate housing and land market dynamics [
20,
21,
22,
23,
24,
25,
26,
27]. Consequently, the application of ABM has proved very versatile at different scales, including the sub-regional scale, here understood as the geographical level between the municipal and regional scale.
The sub-regional scale is particularly suitable for urban planning, since urban growth and its impacts can be better controlled at this level. This is especially useful in Spain, where planning is legally proposed at municipal level, with few examples at regional scale [
28]; however, it is at this latter level where not only urban growth phenomena but also their territorial, environmental, and other associated impacts could be managed more efficiently. The lack of legal instruments at sub-regional scale has created serious problems, especially during the recent real estate boom [
29,
30,
31].
Besides scale, a further advantage of ABM when simulating urban growth processes is their capacity to reproduce the behavior, actions, and interactions of the multiple agents involved, who may present diverse profiles (e.g., social, political, and economic). Urban planners and developers are unquestionably among the most important agents in urban growth, since they decide the amount of land to be converted to urban uses, as well as where development should first take place. The population represents another important agent in this process, since the population’s behavior is responsible for the demand for new housing, in this case occupying the available dwellings generated by the two abovementioned agents.
Implementing an ABM that simultaneously considers both policy-making and the residential development process poses an enormous challenge in modeling due to the large number of variables to consider (accounting for both internal status and externalities), the spatial (sub-regional) and temporal scale (behavior may occur at different time intervals), and above all, the combination of top-down and bottom-up approaches. With respect to the spatial and temporal scale, it is assumed that these are strictly linked to the kind of data used. Many models developed to study changes observed at the urban level consider stylized data in a hypothetical world. Artificial cities and rules are constantly being created in order to test these models and their underlying theories [
21,
22,
26,
32].
Although some independent allocation models have been used to simultaneously simulate both levels of the planning process (policy-making by urban planners and residential expansion by developers), only a few ABMs have been aimed at considering both when simulating urban growth at the sub-regional scale [
33,
34,
35]. Some of these have considered the environment or urban planners as agents, albeit not with the same goal [
18,
20,
36,
37]. In contrast, many urban ABMs consider developers as agents, mostly focusing on land market dynamics [
21,
22,
23,
32]. Similar models have accounted for both agents [
36,
37,
38,
39], although neither coincided with the purpose of modeling, which is to test and explore the urban process or the system itself. The closest example would be the study by Ligmann-Zielinska et al. [
27], who developed a model using these three agents, although an independent deterministic model rather than an ABM was developed separately in order to simulate the typical top-down process of planning.
In line with these precedents, the objective of the present study was to create a model (AMEBA) in order to address the abovementioned gaps by simulating the urban development process at the sub-regional scale considering urban planners, developers, and the population, while simultaneously addressing the challenge of acting at heterogeneous intervals. This paper discusses the first and second submodels of the prototype, which adopt a more deterministic rather than stochastic approach, and were thus based on an urban land allocation model. The population submodel represents a parallel stage of this research and takes a stochastic approach to the occupation of newly developed areas, rather than the territorial expansion presented here. Since this latter forms part of the final integrated model, it is briefly introduced in the explanation of the model structure, but is not discussed further.
AMEBA has been developed as a prototype with three submodels developed independently on the same ABM platform, endowing it with sufficient flexibility to be adapted to other study areas and reproduce different future urban growth contexts. The submodels and the final prototype were created, fed, and tested using empirical data on a specific area in Spain, the Corredor del Henares. The sub-regional profile of the study area presents substantial socioeconomic and urban development diversity, and thus represents a suitable area to test the model.
Following this introduction,
Section 2 gives a conceptual overview of the prototype (with three integrated submodels), and describes the study area, model structure, and other technical issues (platform and database).
Section 3 reports on the implementation of the submodels that address territorial expansion (individually and in conjunction), the simulation experiments, and the validation process.
Section 4 concludes the paper with a discussion of the submodels’ capabilities and limitations, and directions for future research.
2. Testing Area, Conceptual Model, and Data
As previously mentioned, ABM are suitable for studying complex issues, and therefore could serve as a valuable tool to support urban planning processes. This section presents the conceptual model of the prototype (AMEBA), describing its structure, platform, and database, as well as the variables used to test the model in the study area.
2.1. Testing Area
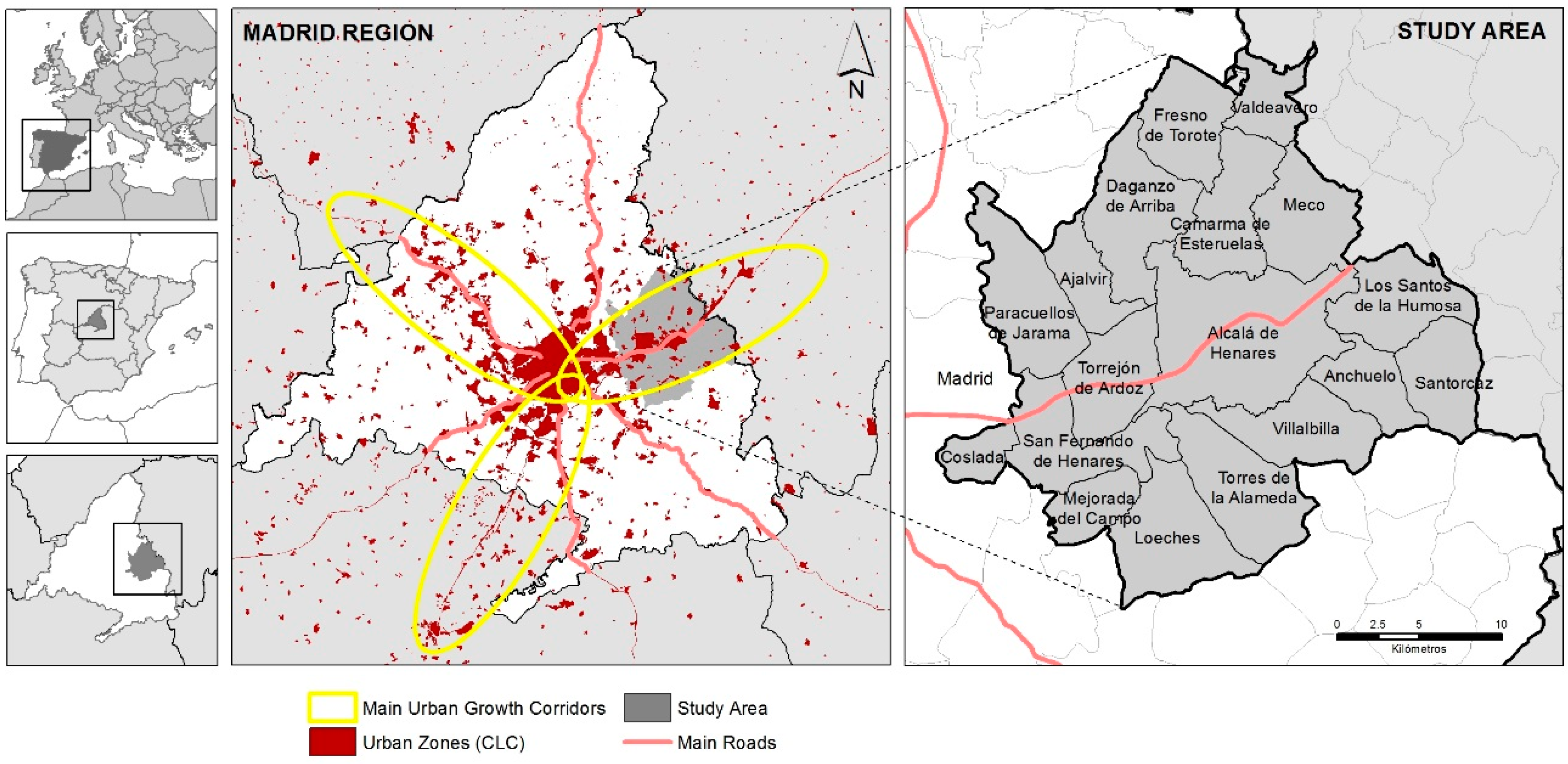
The metropolitan area of Madrid has become one of the most dynamic areas of urban growth in the Iberian Peninsula and Europe [
40]. It has three main urban growth corridors, each with their own defining characteristics (
Figure 1). The study area encompassed 18 municipalities in the Region of Madrid selected from the northeast corridor, known as the
Corredor del Henares, which runs from Madrid to Guadalajara (the capital of the neighboring region). This area is home to almost 600,000 inhabitants [
41], covers 624 km
2, and is strongly influenced by its proximity to the city of Madrid. In addition, it is a particularly dynamic area in urban and demographic terms, with substantial internal sociodemographic and urban development differences. This complexity is further increased by the lack of regulation aimed at solving territorial problems at the regional level, rendering it an ideal laboratory to test the prototype reported here.
The general urban growth trends identified in the main Spanish cities in the period of economic wealth (1997–2007) indicate rapid and chaotic urban development. This coincided with the housing bubble, subsequently followed by a stable period of consolidation [
42,
43,
44]. Such trends have been witnessed in many other European urban areas in countries, such as Italy, Croatia, and France, mainly associated with their principal cities and coastal zones [
45,
46].
2.2. Prototype Structure, Platform and Database
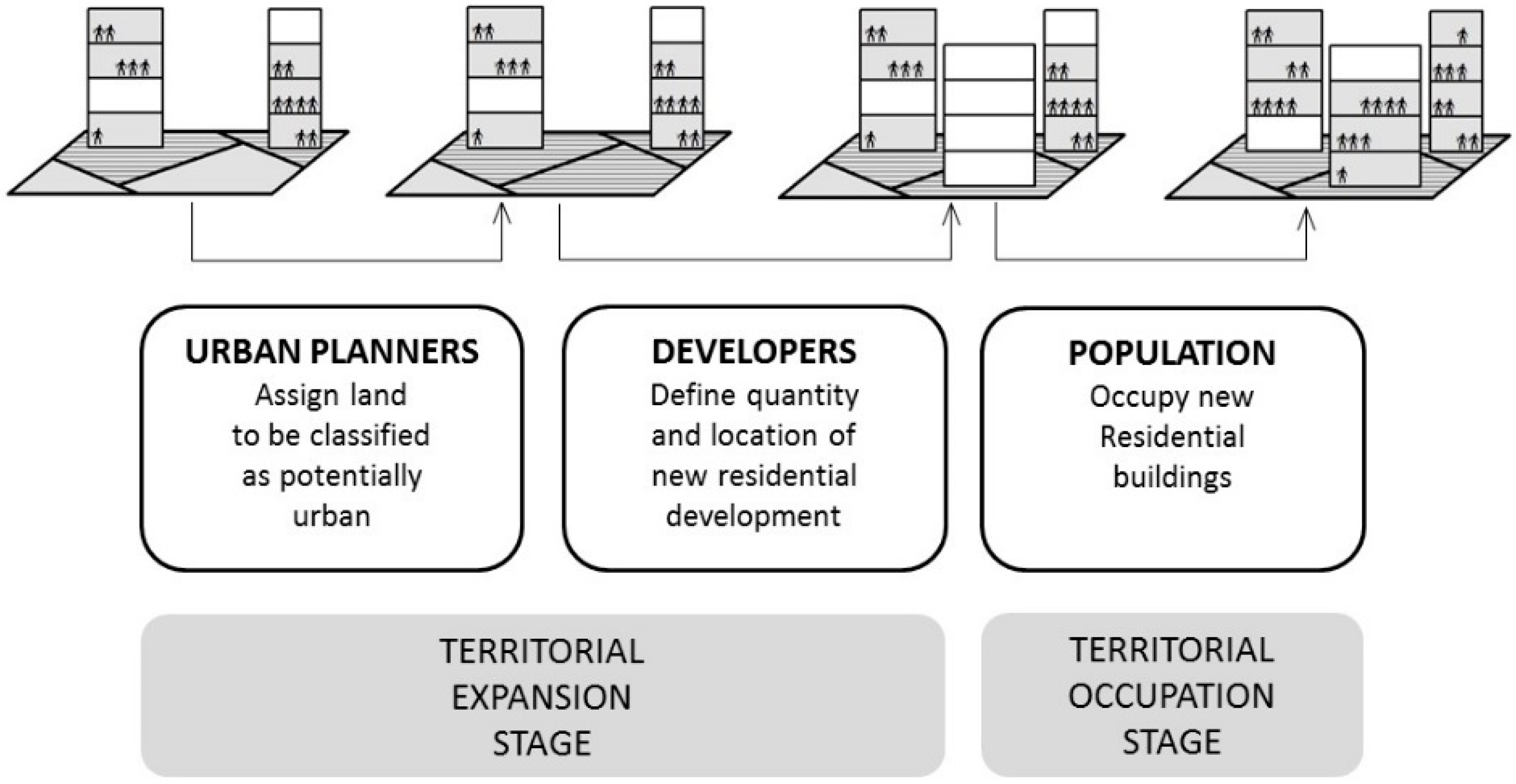
The urban growth process at the regional scale could be theoretically and logically described as a three-stage process involving three types of agent: urban planners, developers, and the population [
47]. The first two are responsible for the territorial expansion itself, while the latter represents the occupation of the territory, and all three converge to shape a complex urban system. The urban growth process starts with the identification of new potential urban areas by urban planners in line with national, regional, and local policies. In the second stage, developers choose where to promote new residential developments. Finally, the population selects where to live based on their individual preferences and according to their income possibilities. Although other elements may also be involved in the urban development process (such as infrastructure expansion or political guidelines), these would have been difficult to include in our model, so we decided to limit our agents to these three. Each of them is considered in an independent submodel with different characteristics. The first represents the typical deterministic, top-down process, while the second may be considered a transition between deterministic and stochastic approaches, and the third could be considered the closest representation of an ABM as we understand it (using a bottom-up approach), where complex interactions between agents are represented stochastically. The three of them are coordinated separately before subsequent integration in a final model, where outputs and inputs feed each other continuously. It is worth mentioning that the model is explicitly spatial, so all variables are spatially distributed.
The prototype is intended to be as useful as possible, and therefore it was constructed using an adaptable structure of submodels, each covering a critical variable in the urban growth process. This approach was adopted in response to the low impact that urban growth simulations have had on real-life planning processes, due to their closed architecture and the high amount of data needed to run them, not commonly available in many regions or countries [
2].
As presented in Cantergiani et al. [
48] the submodels are described below:
The first submodel (urban planner) simulates the urban planner´s decision-making process, which consists of selecting new areas for urban development according to physical restrictions (e.g., protected areas, high slopes, or proximity to water bodies), distance to elements of interest (e.g., roads or consolidated urban areas), and the amount of growth required to meet existing demand. These criteria are set as parameters and can be modified at initialization to generate different scenarios.
The second submodel (developer) focuses on the developer’s decision-making process regarding new residential developments. As part of their behavior, developers must decide where to build new housing, how many new developments must be built, their capacity, and their target economic group. This process takes into account the legal status of the territory (defined by urban planners in the first submodel), as well as the areas that will optimize their profits.
The third submodel (population) simulates the process of residential location choice and occupation by the population. In this case, different agents look for the best place to move according to their purchasing power and location preferences, which may include distance to the public transport network, education facilities, and other factors.
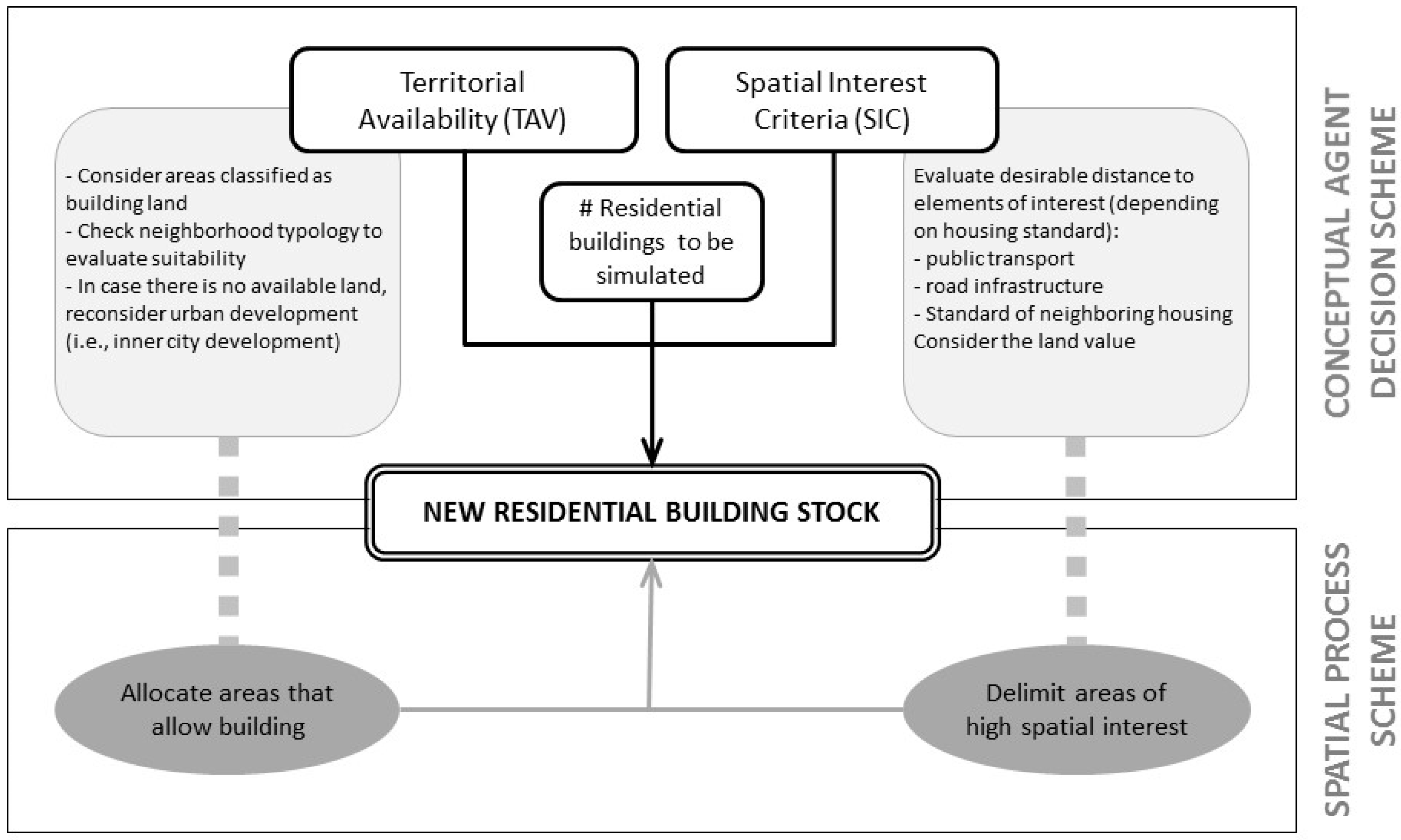
The flowchart in
Figure 2 shows how the submodels are integrated and where the result of each submodel feeds into the next in a chain-like process.
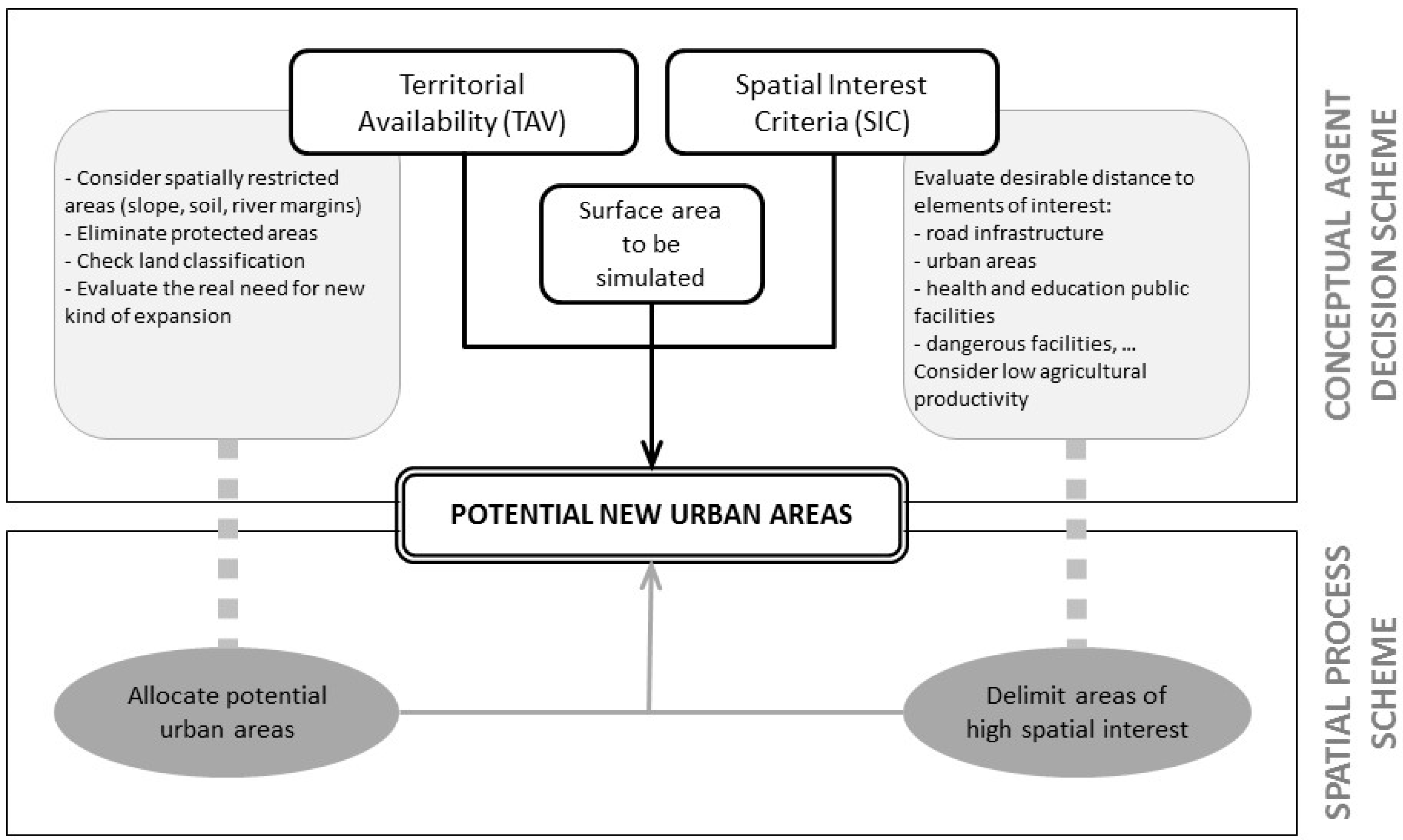
The conceptual model considers two components for the three agents: territorial availability (TA) and spatial interest criteria (SIC). The first (TA) indicates potential areas taking into account spatial restrictions. For urban planners, it considers the limits imposed by legal regulations (e.g., master plans, law on protected areas) and physical urban development restrictions (e.g., along rivers, steep slopes) to spatially delineate potential areas for development. For developers, TA restricts the area to those classified as potentially urban. The second component (SIC) represents attractiveness, which indicates the preferences of each agent regarding the distance to given spatial elements. For urban planners, these include roads, public facilities, hazardous areas, agricultural productivity, and existing urban fabric, while for developers they include roads, public transport stops, existing urban fabric, and status of the existing residential stock. Due to the flexibility of each submodel of the prototype, several variables can be selected to represent these components and run the model [
47], although here we only report those tested in the study area.
The platform used to develop the prototype was NetLogo v.5.3.1 (Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston-IL, IL, USA) [
49], which met the technical requirements and presents many advantages. To name a few, it has an intuitive and simple interface, it is widely used for similar applications, it is user-friendly, and it is open source. Moreover, it enables simple connection with geographical databases through a Geographic Information System (GIS) extension, fundamental for spatial analysis. For instance, this connection facilitates the flexibility required for adaptation to other study areas, with different input data in terms of extension or resolution.
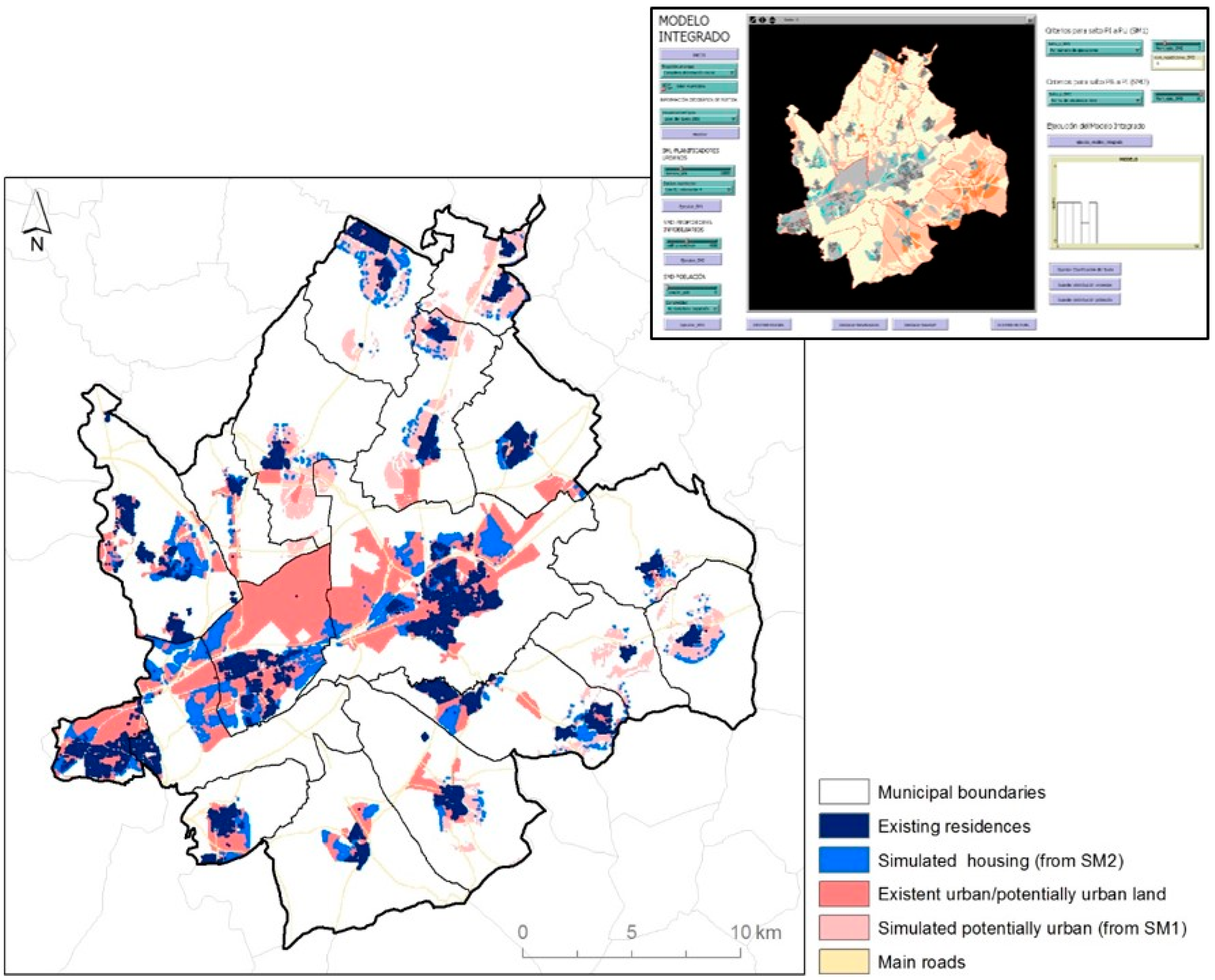
The submodel interface consists of three sections: (i) an input box where geographical information is called up and spatially represented in a visualization panel; (ii) an area where the user sets the initial parameters that will define the scenarios to simulate; and finally (iii) a third area where the results are represented in the form of graphs, spatial distribution, and an external matrix containing statistical references (
Figure 3).
All submodels have a similar interface, differing only in the number and kind of external parameters to be set, and obviously in the expected outputs. Since a set of parameters can be freely modeled, users can adapt the model to their specific context and generate different future urban growth scenarios.
Bearing in mind the regional scale and main drivers of urban growth in the context cited and other similar contexts, a considerable effort was made to compile the most appropriate alphanumerical and geographical information, always considering the territorial component. Although they might form part of the process, statistical components were only incorporated into the model when they could be spatially represented (such as price and income distribution). Other variables, such as traffic flows, global climate change, mobility, and time variation, were not included at this stage for the abovementioned reasons, although we recognize they must play a partial role in the evolution of the phenomenon studied.
The input data used to implement the submodels were selected to reflect the drivers of urban growth, empirical knowledge of urban growth trends in the study area [
47,
48,
50,
51], and the most commonly used variables in other studies [
8,
33]. These latter included the municipal boundaries (surface), zoning status (surface), and housing distribution (pixel) used by agents to assess specific environments and conditions, as well as the other spatial information indicated in
Table 1 below. These were represented by pixels measuring 50 × 50 m. Once data had been collected, they were transformed into determinants for subsequent use in the model.
3. Implementation of the Territorial Expansion Simulation
3.1. Urban Planner Submodel
The urban planner submodel simulates regional urban growth and represents the most general scale of the three submodels, indicating areas where it is legally permissible to construct new residential buildings. This submodel presents a simple and deterministic structure, since the behavior of urban planners generally reflects a top-down approach whereby decisions are made within a general plan by an institutional agent rather than by individuals (or by an individual representing an institution). Nonetheless, the allocation model was developed in NetLogo in order to facilitate integration into future submodels that might simulate agents’ behavior using the bottom-up approach.
The expected result is useful for any urban planner, and represents a laboratory that allows the selection of new areas for reclassification as potentially urban (
Figure 4), generated from their decision regarding the most suitable areas according to criteria that may differ depending on the agent’s profile. Rather than testing the model with different types of urban planner, we only considered one type presenting different profiles that in turn could generate numerous scenarios.
Besides defining the amount of land for potential reclassification as urban, the interface allows the user to set initial conditions that characterize each profile (
Figure 5). Hence, the interface settings allow the user to establish weights for variables such as distance to urban areas, locally unwanted land uses (e.g., hazardous waste dumps, prisons, and trash disposal plants), road infrastructures, and health/education services, and to define priority areas for potential reclassification as urban according to their agricultural productivity.
The agent must convert the amount of land specified by the user in the interface, and the simulation outcomes should show where these changes will take place. The model mechanism works as follows: from among the non-restricted surface areas—limited according to user selection from among the three available options—urban planners first analyze those areas with the highest values of interest. These values are graduated using the average of the weights indicated on the sliders at the interface for each pixel (
Figure 5). Then, the last coefficient (agricultural productivity) is set, and the model assumes that the proposed percentage is homogeneously distributed spatially and randomly throughout each area according to its agricultural productivity, defined as high (forest and natural areas), medium (agricultural areas), or low (all other categories) based on a reclassification of the CORINE Land Cover land use categories considered artificial [
52]. The final selection is then taken as the best option.
Having described and implemented the conceptual model in NetLogo, the simulation experiments conducted to test the prototype are reported below. Several authors have suggested that the validation process should consist of different components: verification, validation, and a sensitivity analysis [
12,
53,
54,
55,
56,
57,
58]. However, since this paper presents a prototype of an ABM, it focuses less on predicting the future and more on understanding and exploring the behavior of the urban system and reproducing specific scenarios. Consequently, only verification of correct model construction and validation by comparing the results with real data will be discussed further. Verification (also known as internal validation) refers to the correctness of the internal structure, ensuring that the model has been developed in a formally correct manner (e.g., system diagrams, units of measurement, and equations) in accordance with a specified methodology [
58]. This implies corroborating that the implemented model conforms to the specifications by running it after changing some initial parameters, as done by other modelers [
33]. Statistical validation, or just validation, refers to determining if the model is correct by checking whether it achieves the expected level of accuracy in its predictions. This involves analyzing whether the structure of the model is appropriate for its intended purpose from a conceptual and operational point of view by comparing results to real data.
The goal of these procedures was twofold: on the one hand, to confirm that the results of specific scenarios could help determine whether the model had been correctly constructed, and on the other, to confirm that the model has the capacity to generate the expected simulation, given the scale, available data, and initial set of conditions.
For verification, three different contexts were set for each model by varying some of the initial parameters (e.g., adopting a sustainable, economically conservative, or speculative approach), so that they were sufficiently diverse to generate different outputs. It is important to note that throughout this paper, the term “scenarios” is used to refer to different future contexts, rather than according to the definition of scenario in the strict sense of the term. Moreover, all of the prototype submodels represent tools in the form of open possibilities that can reproduce different urban development scenarios (as reported here) and generate a sequence of products that could be used for a validation process such as a sensitivity analysis, employed by many scientists for this purpose [
16,
18,
36]. We propose to conduct such an analysis on the final model once all three submodels have been integrated.
Hence, although very different results could arise from minor changes in these initial conditions, the usefulness of the simulations resides in the fact that they were not aimed at identifying or analyzing specific urban growth shapes or statistics for the Corredor del Henares, but at determining whether the model was correctly constructed. If this latter were to be demonstrated, it would support the notion that ABM constitute a powerful tool for use in real situations and would confirm that the prototype achieves the proposed goal. The flexibility and high number of setting options increase the possibility of employing this tool in different contexts and using real data on other areas.
For the validation process, we compared the results of the different simulations (of the two submodels once integrated) with the corresponding urban land data available for the study area, and obtained the percentage of coincidence.
With these goals in mind, we simulated the expansion of potential development areas using three different urban planner profiles defined by the tendency to employ: (i) a sustainable approach, (ii) an economically conservative approach (typical behavior in a crisis situation), or (iii) a speculative approach (corresponding to a business-as-usual scenario), in accordance with the storyline and scenarios described in Plata Rocha et al. [
50]. In order to run the three simulations, the same initial conditions were used, but different parameters were set to characterize each profile (
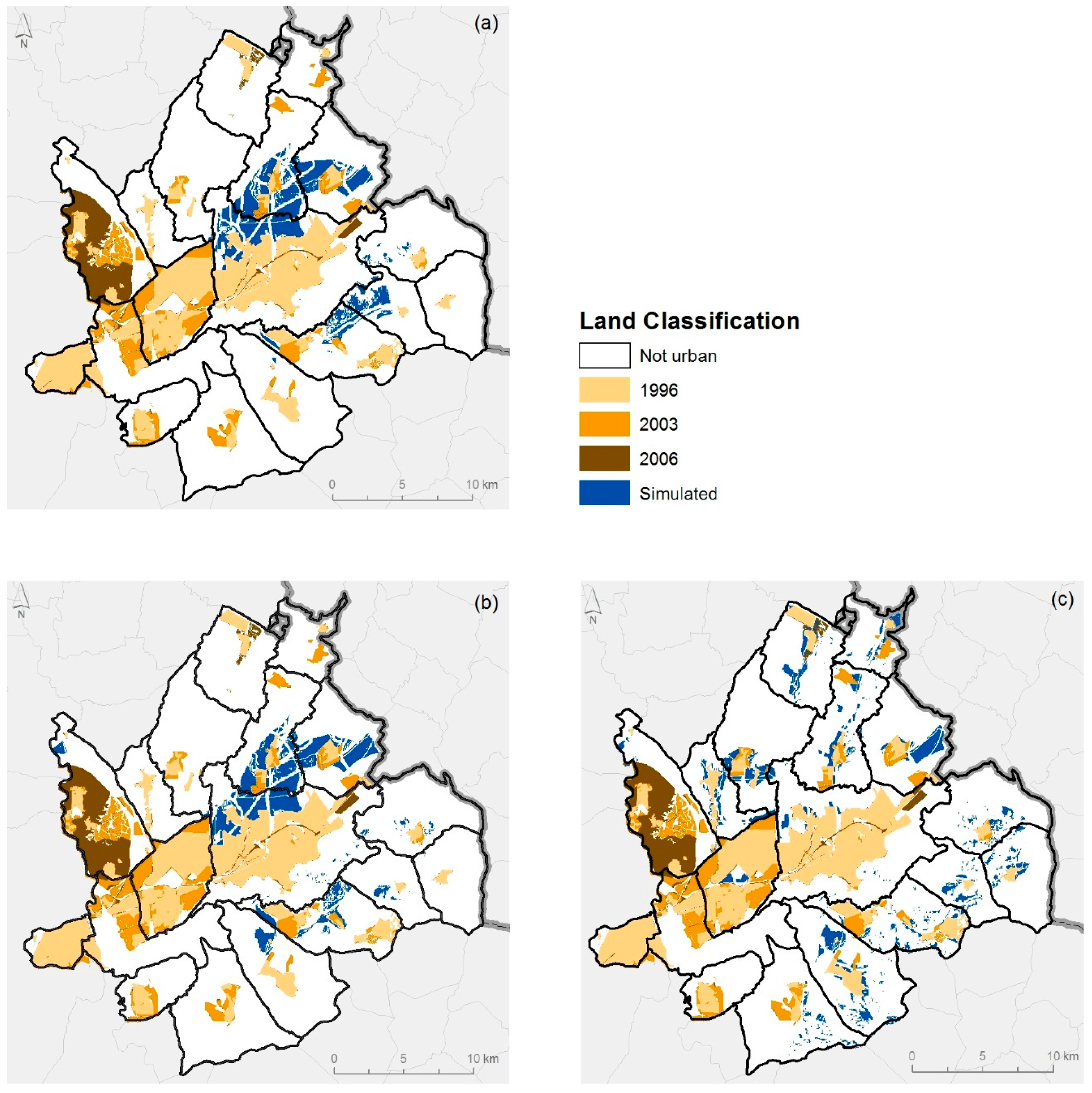
Table 2), based on the work cited. As expected, the simulations yielded some notable differences for the three urban planner profiles, all of them with growth concentrated close to the most dynamic existing urban areas, but distributed differently throughout the territory. Other future contexts could be easily defined by changing values for each parameter.
Therefore, the simulation results are acceptable since they are spatially and conceptually coherent. An aggregated visualization of real data on the evolution of past and recent urban plans (the municipalities in the study area have relatively old plans and many updates are under discussion) and simulation with a five-year horizon for the three planner profiles (
Figure 6) indicate alternative distributions that could be used as a reference for urban planning decision-making.
3.2. Developer Submodel
The developer submodel considers a bottom-up rather than a top-down approach [
27], assuming a more spatially-restricted knowledge of the territory (in the urban planner submodel, agents are assumed to be familiar with the entire territory in order to make a decision). Simulation of their behavior is expected to yield a new distribution of low, medium, and high standard residential buildings.
In the first instance, the only restrictions (TA) considered referred to regulations; thus, only already-designated areas were candidates for new residential development. As regards attractiveness (SIC), the preferred distance to elements of spatial interest was defined according to the standard of the building for which expansion was to be simulated. In this model, land value and neighborhood characteristics were the two main elements that strongly affected the decision to assign a new area for development (
Figure 7).
As in the previous case, agents in this submodel present a unique type of behavior regarding the variables considered, although users may change some of the parameters depending on whether they aim to simulate the construction of high-, medium-, or low-standard housing. In addition, the interface again allows the user to establish the initial conditions by changing parameters such as the quantification of new buildings, specification of respective percentage of each type, and calibration of available coefficients for each standard (distance to roads, urban areas, and public transport). The user can also define the maximum search area that developers should take into account, considering the elements necessary to identify a suitable location (where no ideal location is identified within the area defined, the model allows the user to redefine the search area). The combination of these parameters defines the future scenario.
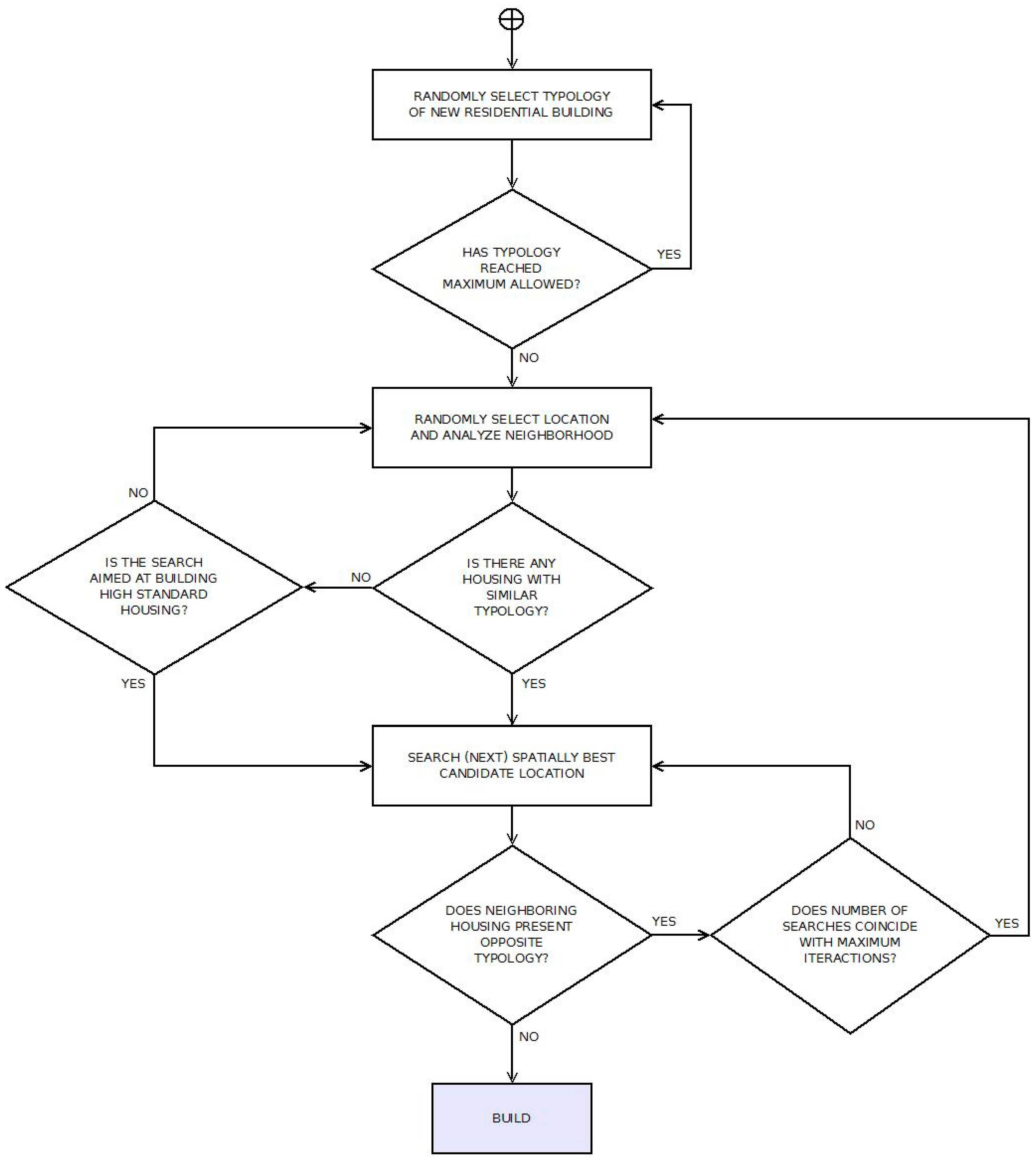
The decision flow chart (
Figure 8) leads to the final location where new housing should be built.
Unlike the urban planner submodel, the developer submodel starts with the selection of the typology of building proposed, i.e., whether the agent will seek free land to build high, medium, or low standard housing. This information is vital to confirm the area of interest, which is different for each case, and later it will also be useful to define the number of dwellings assigned to each new building typology. This choice must respect the maximum allowed for each typology. In the next step, the model focuses on a random point that must obey the restrictions and analyzes the neighborhood, considering an extension which is also indicated in the interface by the user. The preference criteria include the degree of similarity with nearby buildings (attraction for similar, or in some cases, rejection for different) and the spatial interest defined as in the previous submodel. Whenever there is an option that complies with these criteria, and the maximum number of runs has not yet been reached, the new building is assigned to the corresponding pixel. The number of dwellings assigned will depend on building typology, going from high density (low standard) to low density (high standard).
As in the previous case, in order to confirm prototype flexibility and correct construction, scenarios were defined according to the external environment rather than the agent’s profile (as in submodel 1). In this case, two parameters could be modified: the residential growth predicted for each housing standard and the maximum search area. In order to test the model, different settings were defined for these parameters in order to simulate the real estate market under three different situations: (i) sustainable (environmental protection approach), (ii) crisis (conservative approach) and (iii) speculative (business as usual). Each scenario reflects different building dynamics, housing typology distribution balance, and urban growth shape, all defined by adjusting the values for the initial submodel conditions (
Table 3).
The last column in
Table 3 presents a short description of the results, indicating satisfactory agreement between the proposal and the expected and simulated results, mainly considering the spatial response for the three situations (
Figure 9). Furthermore, the final distribution shows the actual and projected housing together, indicating the lack of development in restricted areas (non-building areas or roads, for example). The spatial results for the developed area were generated from pixel distribution over the surface designated for that purpose (urban and developable land). We did not consider illegal settlement dynamics at this stage of the model.
3.3. Integration of the Urban Planner and Developer Submodels
Although we only integrated two of three prototype submodels, this still presented a challenge due to the problem of how to combine two different submodels in one, which must also be clear and robust. Below, we describe how this difficulty was solved and the two submodels combined to represent the territorial expansion process:
The submodels were combined through continuous feedback of inputs and outputs. Thus, the developer submodel uses the output of the urban planner submodel (land classification) as one of the inputs; hence, depending on the established criteria, an updated layer is periodically obtained showing areas classified as potential building land. As developers behave according to these legal restrictions, the results of the independent submodels and integrated model should differ.
Temporal resolution also presents a challenge because the two submodels use different time intervals to reflect the fact that developers build housing in a shorter period of time than urban planners take to develop new planning proposals. By law in Spain, urban plans must be revised at least every ten years with some periodical, partial reviews; thus, five years was the interval considered for the urban planner submodel, although it could easily be modified according to where the prototype is being employed. For the developer submodel, we considered an interval of one year to reflect the time taken to construct new residential housing, although we are aware that this is often a continuous process.
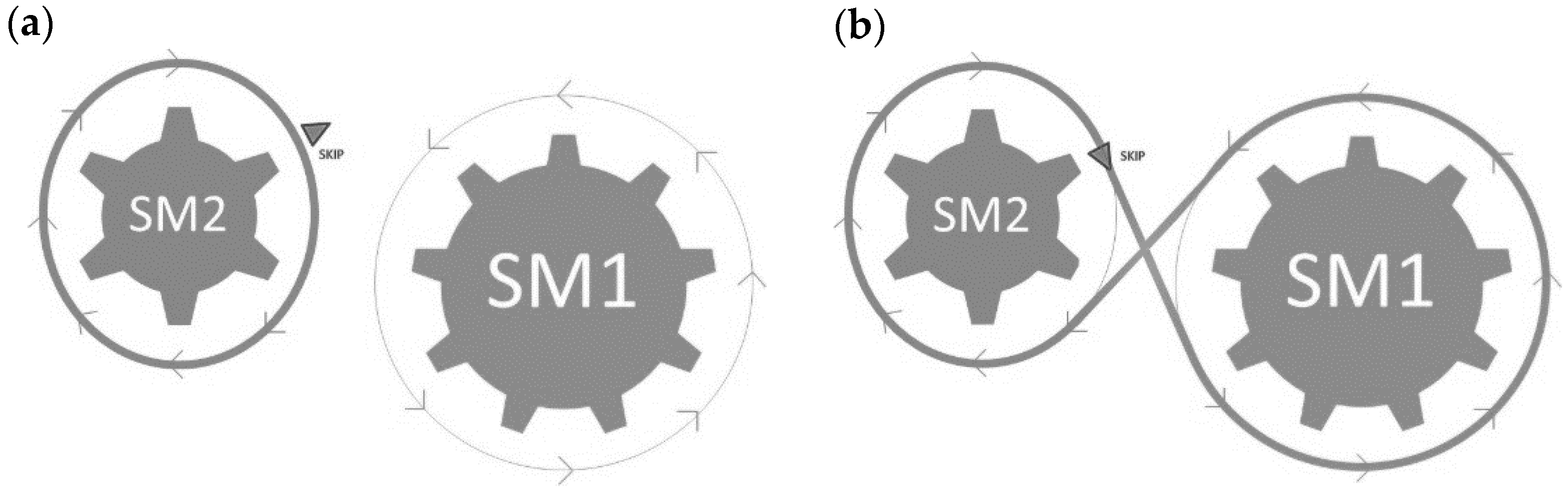
Successful integration of the two submodels depended not only on which inputs/outputs were considered, but also on when and how they were interchanged, since the submodels employ different time intervals. The rate is determined by compliance with criteria that interrupt the running of one submodel to start that of the other. In order to obtain the first results, to skip from the developer to the urban planner submodel, either (i) the free area suitable for development should not exceed a defined percentage of the total, or (ii) one of the submodels should reach a given number of runs (
Figure 10).
In summary, the model starts with a territory classified into urban, potentially urban, and other, and also with a fixed distribution of buildings. The prototype internally calculates the percentage of potentially urban areas occupied by residential buildings and the number of runs for each (starting from zero). If the result exceeds the amount defined by the user (meaning that new areas are in demand), then the urban planner submodel is launched. Otherwise, the developer submodel is run continuously until that percentage is reached. Both submodels run in accordance with the independent procedures described previously. In this case, the NetLogo platform was selected in order to better integrate both of these with each other and with the third population submodel in an ABM context, since other techniques such as CA or multi-criteria models might not be able to solve integration.
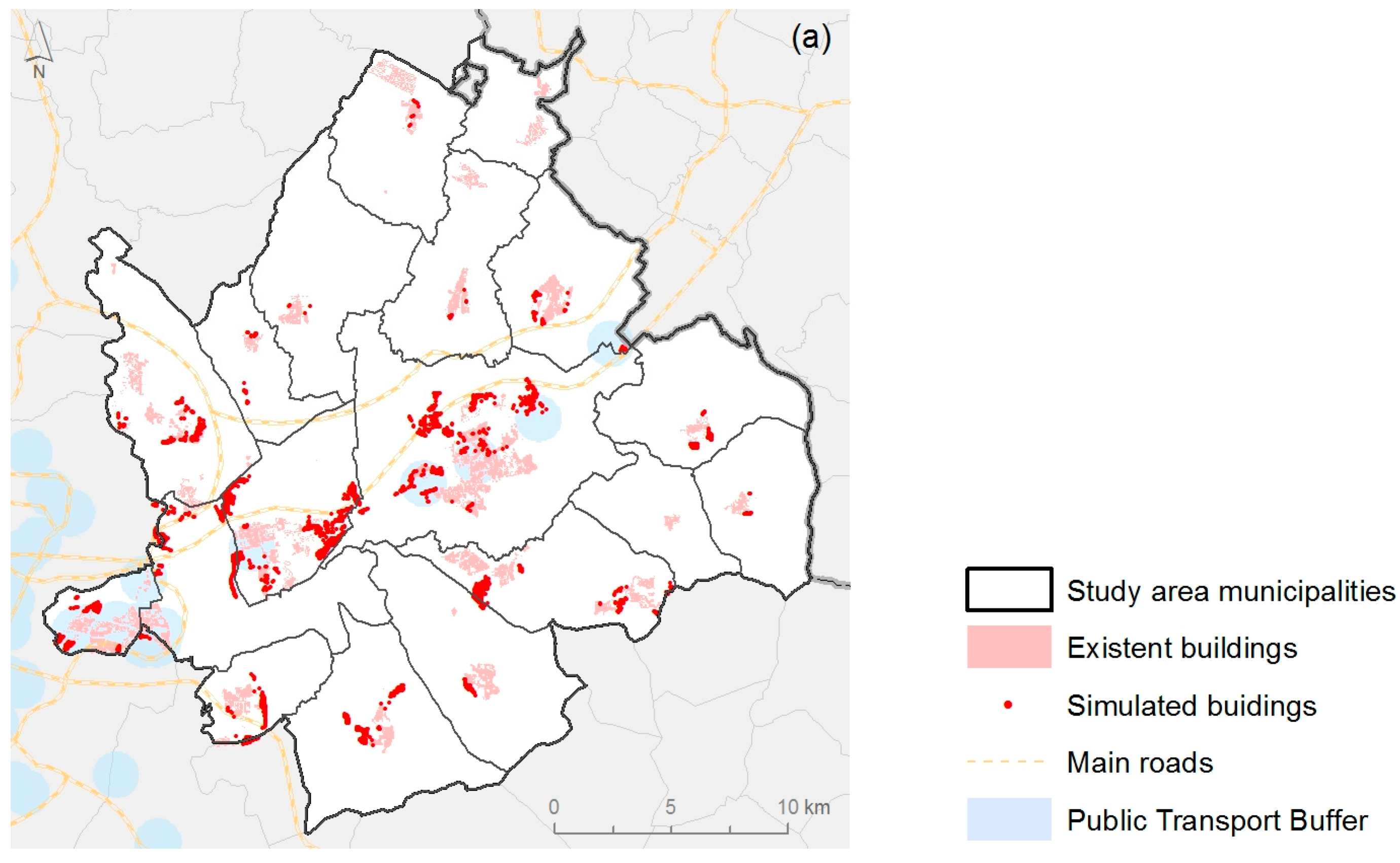
In order to conduct initial integration of the submodels, we considered a fixed sustainable scenario for both. In the first instance, this should represent the ideal approach to urban development, taking into consideration legal and strategic factors. Although this variable would depend entirely on the user’s interests, for this simulation experiment we set the urban planner submodel to run once for each three runs of the developer submodel, with the latter running at one-year intervals. As expected, the results of this integrated simulation indicated urban growth along roads and around existing developments: potential urban land expansion occurred close to residential buildings in the smaller municipalities, and mainly in the central ones (
Figure 11).
The tests performed on these models represent the only verification that it was possible to conduct at this time, according to the existing data and structure described for these two submodels. Verification therefore consisted of testing model reliability by running it with different future scenarios in order to confirm that the results complied with the established rules and expected operation. This would demonstrate that the model generates acceptable simulations according to the available established parameters, and was thus considered sufficient verification for a prototype. Many partial modifications were performed throughout the construction of both submodels and the integrated model; for each procedure, additional queries were hosted in the programming to verify correct operation at different stages. An iterations routine was also introduced, and the test results achieved a mean of 90% coincidence after 10 sequential runs. This high level of coincidence is explained by the fact that the structure of both models was based on a deterministic approach.
Before reporting the validation process, it is important to note that the combined outputs of the two submodels comprise a partial result, indicating the proposed developable surface, with which there is no available real data for comparison (a comparison between different scenario outputs is given in
Figure 6), and the new distribution of individual built-up pixels in those areas. With this in mind, a validation step was performed comparing the new simulated buildings with real land use data. To this end, we used the only updated data available: the Spanish Land Cover and Use Information System (Spanish initials: SIOSE) produced by the National Geographic Institute of Spain (Spanish initials: IGN), available for 2011 with a reference scale of 1:25,000. This includes the basic land use categories, such as artificial zones, crops, grassland, woodland, scrub, and land without vegetation [
59]. Although the model result represents built-up areas in pixels, while the only available data on observed spatial urban growth for the same year refer to surfaces, the intersection of these shows the level of correspondence between model products and reality.
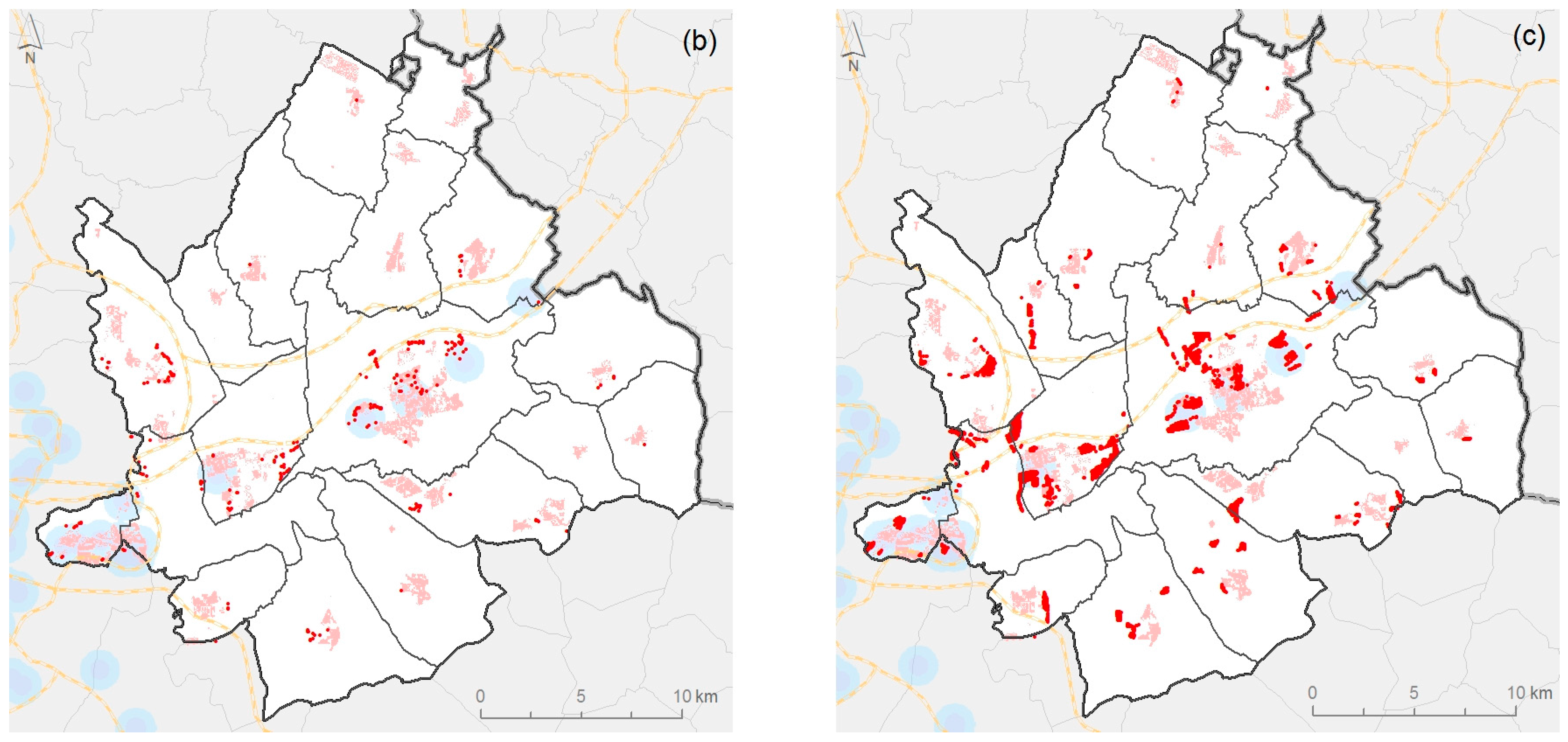
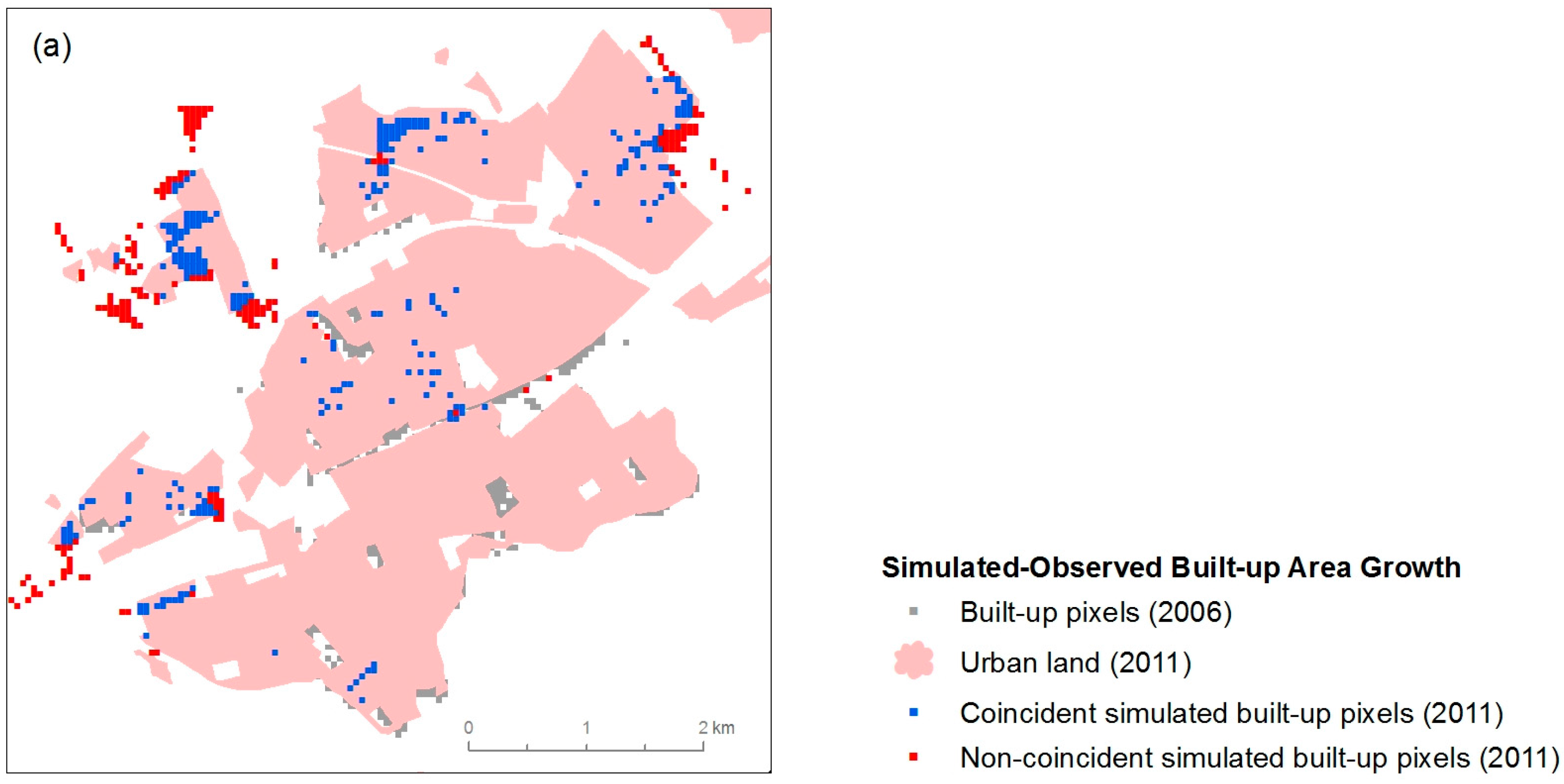
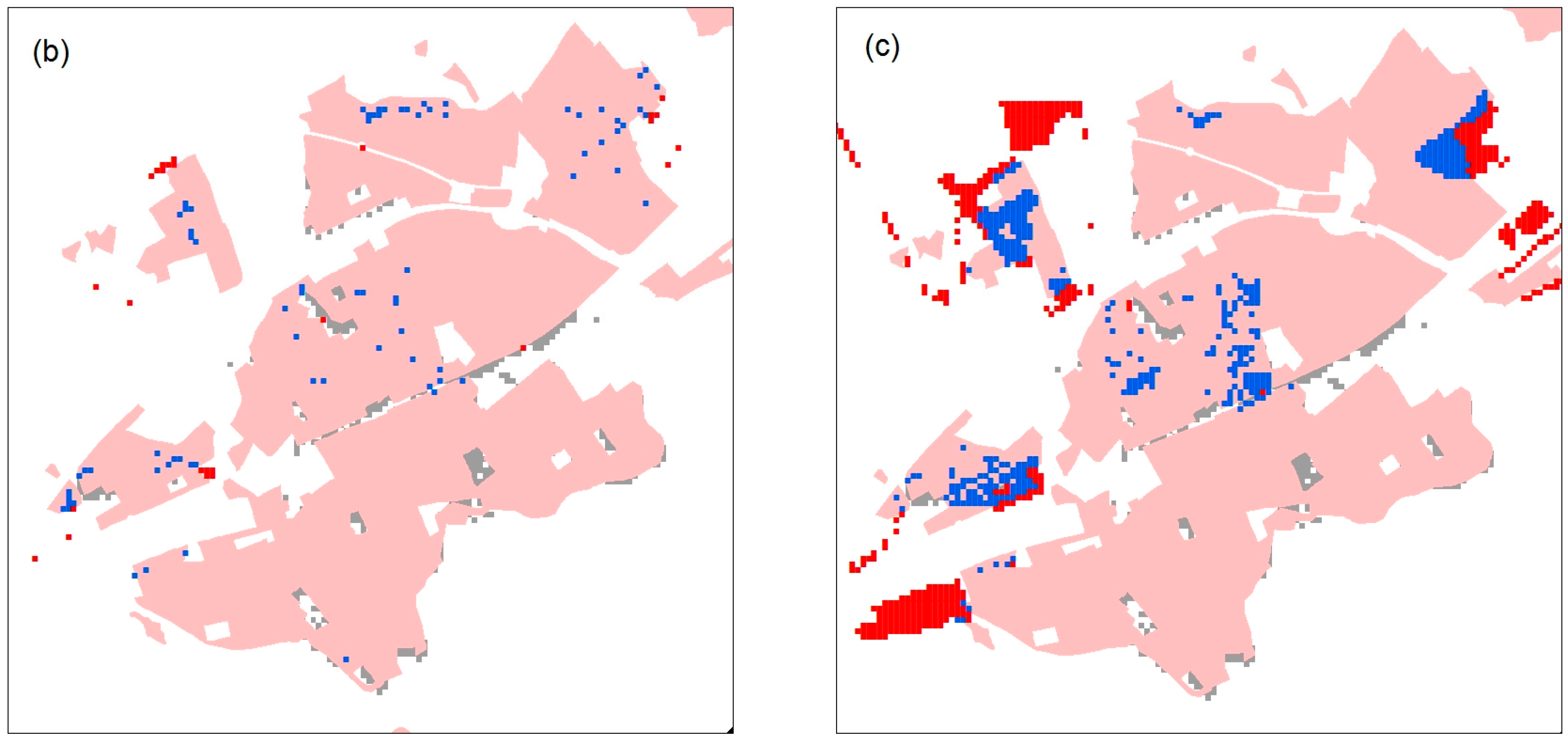
This comparison (
Figure 12) revealed an acceptable level of coincidence, bearing in mind that the difference in data shape (pixel and surface) limited coincidence. In terms of percentages of correspondence, our results show that the model closely reflected the real situation in the study area tested, obtaining the highest percentage for the crisis scenario (62.3%), which mirrored the profound real estate crisis that hit Spain during the simulation period. Furthermore, the results for the speculation scenario (39.9%) and the sustainable scenario (48.8%) were coherent, because the former represents the scenario furthest from reality in the study area, while the sustainable scenario indicates more conservative growth, closer to the crisis scenario (see the parameter established for each scenario in
Table 2 and
Table 3).
4. Discussion
It was a challenge to design a model that simulated the urban system considering its territorial expansion process, since it was necessary to integrate two agents that act at different scales and with different goals, although their products and behaviors are closely related. A larger number of examples of application at similar scales would be required to discuss its possibilities further; nonetheless, the existing ones serve as references, to which we have added empirical knowledge about the region and the urban process in Spain, enabling us to create, run, and test both submodels and the integrated model.
The structure of the agent-based model described here consists of three agents, constructed independently for subsequent integration. When analyzed separately, the territorial expansion reported here is more deterministic, while the stochastic element is given by the third submodel (population) and the integration of the first two (as presented here) or all three submodels. The novelty of this model resides in its capacity to simulate the urban growth decision-making process in an ABM context, and to integrate the submodels, which would be problematic if using other urban growth simulation techniques such as CA or multicriteria evaluation.
It is worth mentioning that the decision to work with separate submodels, running them individually first, endowed us with more control at each step in the entire process, and in some cases it also enabled us to forestall errors. Unlike other authors, who have considered similar agents and goals [
27], we used three submodels—urban planner, developer, and population—to represent the main agents when modeling the urban development process. In this paper, we have reported the first two, which together show the spatial distribution of urban growth. These agents´ decisions are based on a set of criteria and weighted preferences that together with other interaction elements would be difficult to simulate using urban growth models based on multicriteria evaluation, cellular automata, or other techniques. A further innovation is the interaction of the submodels using input and output feedback in the same framework, generating a continuous process of land reclassification and residential building expansion focusing on the influence of one behavior on another. The ABM architecture facilitates the representation of agent interactions, which will be completed by integrating the population submodel, designed to represent occupation of the available residences generated by the developers.
We believe that this model, which is sufficiently flexible to combine the top-down approach of urban planners and the bottom-up approach of developers, could serve as a useful tool to stimulate lively discussion about planning support modeling at the intermediate scale. In addition, it could also serve to further analyze the impact of land use changes or their relationship to transport system evolution using this bottom-up perspective.
As indicated throughout this paper, this structure enabled us to combine agents’ behavior and transform it into mathematical rules that could be entered independently into the urban planner and developer submodels and then transferred to the integrated model. NetLogo was the best platform for this, since its simple interface and GIS extension made it possible to obtain a user-friendly model. This capacity to connect an ABM with GIS represents an important advance for urban simulation, since there are usually clear limitations on cartographic representation in an ABM. Furthermore, the processing power of NetLogo, which may sometimes be considered a limitation for more demanding models [
60,
61], was sufficient in this case.
In all stages, our model works with territorial information, and thus is explicitly spatial as regards not only input but also output data. Even if the best mechanisms were available to develop an ABM, the data would represent a significant constraint if they were poor quality or did not comply with geographical and scale needs. One of the submodels’ outstanding properties is their flexibility in terms of the amount and kind of data that can be used, since this allows the user to easily adapt the prototype to other similar study areas.
An analysis of the physical distribution of housing and potential urban land or a thematic analysis of the results were not among the goals of this study, although some such analyses were performed in order to confirm that the model was correctly constructed and generated accurate products. ABM validation is a controversial issue [
12,
53,
54,
56,
62,
63,
64], and will continue to be so until more research is conducted in this field. Nevertheless, we performed a verification procedure by means of programming tests, empirical reviews, and comparison of results, simulating growth under different contexts (setting different initial parameter values and constituting future scenarios). Furthermore, we performed a validation by comparing the simulated results to real world data, which confirmed our expectations. This step was considered sufficient since, our goal at this stage was simply to test the submodels, considering that further validation will be required in the future when the model (AMEBA) is complete, i.e., once the population submodel has been integrated.