Measuring State and Trait Anxiety: An Application of Multidimensional Item Response Theory
Abstract
1. Introduction
2. Materials and Method
2.1. Participants
2.2. Measures
2.3. Statistical Analysis
Models Tested
3. Results
3.1. Sample Characteristics
3.2. Item Response Theory Assumptions
3.3. Models-Data Fit and Comparison
3.4. Comparison of Item Fit and Parameters
3.5. Comparison of TIFs and Marginal Reliability
3.6. Multidimensional Item Diagnostic
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
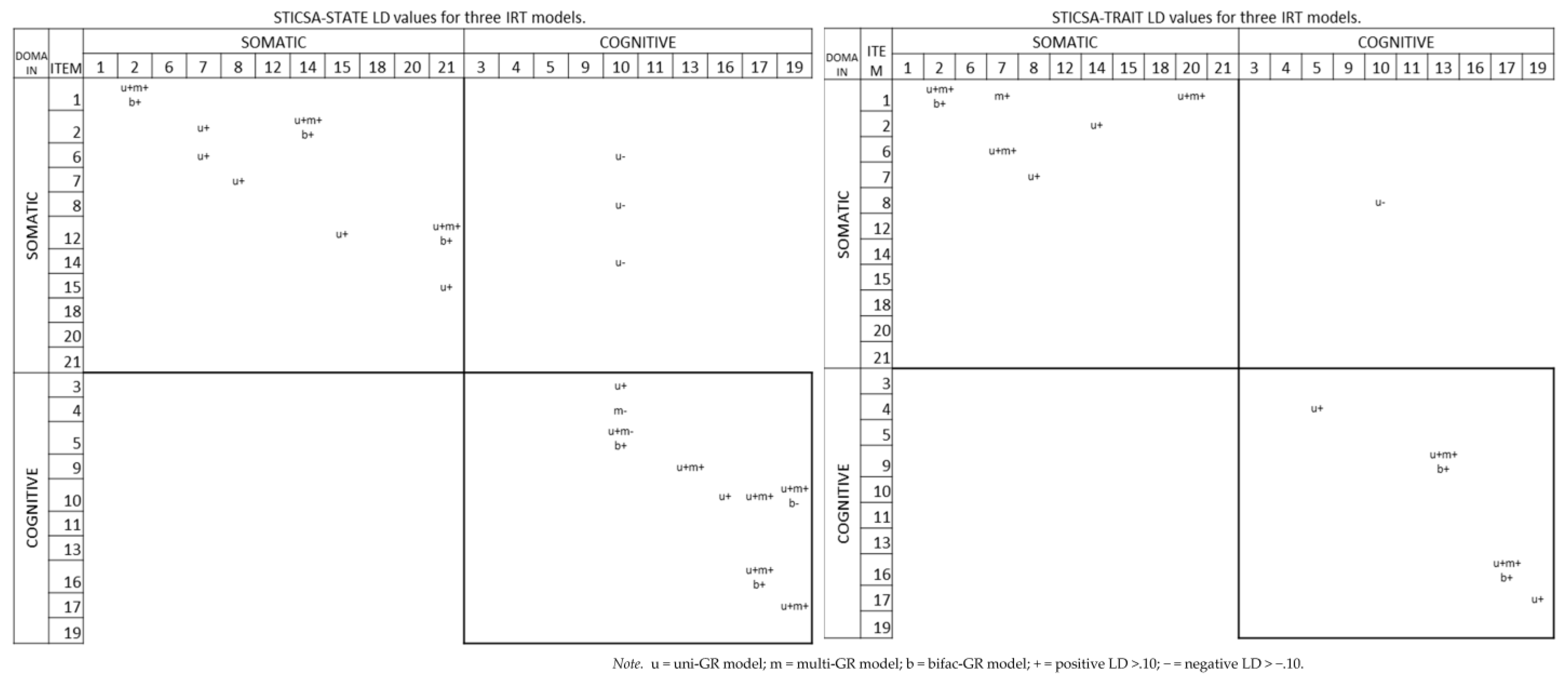
Appendix B
| Item | Uni-GR | Bifac-GR Conditional | Bifac-GR Marginal | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| c1 | c2 | c3 | a | c1 | c2 | c3 | ag | aS1 | aS2 | c1 | c2 | c3 | a*g | a*S1 | a*S2 | |
| STIC_S_1 | −0.339 | −1.839 | −3.855 | 1.196 | −0.369 | −1.971 | −4.072 | 1.017 | 0.979 | −0.363 | −1.938 | −4.004 | 0.881 | 0.840 | ||
| STIC_S_2 | −0.314 | −2.337 | −4.020 | 1.528 | −0.365 | −2.695 | −4.543 | 1.365 | 1.415 | −0.267 | −1.974 | −3.328 | 1.049 | 1.103 | ||
| STIC_S_6 | −1.517 | −3.181 | −4.715 | 1.649 | −1.774 | −3.704 | −5.407 | 1.442 | 1.574 | −1.230 | −2.569 | −3.750 | 1.058 | 1.200 | ||
| STIC_S_7 | −0.924 | −2.791 | −4.698 | 1.799 | −1.084 | −3.274 | −5.445 | 1.659 | 1.636 | −0.653 | −1.973 | −3.282 | 1.195 | 1.171 | ||
| STIC_S_8 | −2.497 | −4.307 | −6.115 | 2.516 | −2.910 | −5.060 | −7.136 | 2.389 | 1.993 | −1.218 | −2.118 | −2.987 | 1.550 | 1.156 | ||
| STIC_S_12 | −0.942 | −2.550 | −4.291 | 1.339 | −1.013 | −2.735 | −4.556 | 1.143 | 1.063 | −0.886 | −2.393 | −3.986 | 0.969 | 0.882 | ||
| STIC_S_14 | −1.442 | −3.405 | −5.131 | 2.012 | −1.773 | −4.170 | −6.191 | 1.910 | 1.928 | −0.928 | −2.183 | −3.241 | 1.263 | 1.282 | ||
| STIC_S_15 | −0.824 | −2.566 | −4.022 | 1.280 | −0.881 | −2.732 | −4.254 | 1.074 | 1.018 | −0.820 | −2.544 | −3.961 | 0.921 | 0.861 | ||
| STIC_S_18 | −1.530 | −3.229 | −5.039 | 1.817 | −1.612 | −3.409 | −5.289 | 1.597 | 1.177 | −1.009 | −2.135 | −3.312 | 1.313 | 0.858 | ||
| STIC_S_20 | −1.168 | −2.239 | −3.398 | 1.055 | −1.181 | −2.265 | −3.432 | 0.914 | 0.591 | −1.292 | −2.478 | −3.755 | 0.863 | 0.521 | ||
| STIC_S_21 | −0.656 | −1.985 | −3.180 | 0.920 | −0.691 | −2.075 | −3.299 | 0.736 | 0.773 | −0.939 | −2.819 | −4.482 | 0.670 | 0.709 | ||
| STIC_S_3 | 0.477 | −1.958 | −3.549 | 1.980 | 0.512 | −2.091 | −3.799 | 2.207 | 0.148 | 0.232 | −0.947 | −1.721 | 2.207 | 0.090 | ||
| STIC_S_4 | −0.815 | −2.660 | −4.337 | 1.715 | −0.842 | −2.741 | −4.457 | 1.816 | −0.146 | −0.464 | −1.509 | −2.454 | 1.816 | −0.100 | ||
| STIC_S_5 | −0.093 | −2.153 | −3.653 | 1.551 | −0.088 | −2.217 | −3.775 | 1.646 | 0.314 | −0.053 | −1.347 | −2.293 | 1.646 | 0.228 | ||
| STIC_S_9 | −0.824 | −2.660 | −4.519 | 1.897 | −1.162 | −3.689 | −6.136 | 2.882 | −1.023 | −0.403 | −1.280 | −2.129 | 2.882 | −0.546 | ||
| STIC_S_10 | 0.701 | −1.102 | −2.407 | 1.534 | 0.806 | −1.278 | −2.789 | 1.933 | 0.601 | 0.417 | −0.661 | −1.443 | 1.933 | 0.408 | ||
| STIC_S_11 | −0.054 | −1.999 | −3.664 | 1.298 | −0.045 | −1.933 | −3.566 | 1.191 | 0.143 | −0.038 | −1.623 | −2.994 | 1.191 | 0.117 | ||
| STIC_S_13 | −1.492 | −3.428 | −5.117 | 2.256 | −2.414 | −5.521 | −8.163 | 3.932 | −1.549 | −0.614 | −1.404 | −2.076 | 3.932 | −0.659 | ||
| STIC_S_16 | 0.052 | −1.733 | −3.247 | 1.643 | 0.055 | −1.907 | −3.546 | 1.883 | 0.555 | 0.029 | −1.013 | −1.883 | 1.883 | 0.381 | ||
| STIC_S_17 | −0.051 | −2.320 | −4.177 | 2.063 | −0.085 | −3.067 | −5.507 | 2.909 | 1.146 | −0.029 | −1.054 | −1.893 | 2.909 | 0.615 | ||
| STIC_S_19 | −0.275 | −2.475 | −4.163 | 2.108 | −0.337 | −2.912 | −4.893 | 2.597 | 0.820 | −0.130 | −1.121 | −1.884 | 2.597 | 0.466 | ||
| Item | Uni-GR | Bifac-GR Conditional | Bifac-GR Marginal | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| c1 | c2 | c3 | a | c1 | c2 | c3 | ag | aS1 | aS2 | c1 | c2 | c3 | a*g | a*S1 | a*S2 | |
| STIC_T_1 | 1.377 | −0.721 | −3.059 | 1.020 | 1.483 | −0.787 | −3.264 | 1.205 | −0.392 | 1.231 | −0.653 | −2.709 | 1.174 | −0.320 | ||
| STIC_T_2 | 1.230 | −1.044 | −3.202 | 1.264 | 1.288 | −1.096 | −3.324 | 1.402 | −0.078 | 0.919 | −0.782 | −2.371 | 1.401 | −0.060 | ||
| STIC_T_6 | −0.267 | −2.154 | −3.997 | 1.485 | −0.314 | −2.483 | −4.564 | 1.859 | 0.608 | −0.169 | −1.336 | −2.455 | 1.750 | 0.410 | ||
| STIC_T_7 | 0.185 | −2.107 | −4.112 | 1.577 | 0.266 | −3.127 | −5.972 | 2.543 | 1.501 | 0.105 | −1.230 | −2.348 | 1.906 | 0.834 | ||
| STIC_T_8 | −1.162 | −3.211 | −4.927 | 1.991 | −1.409 | −3.874 | −5.923 | 2.565 | 0.746 | −0.549 | −1.510 | −2.309 | 2.349 | 0.412 | ||
| STIC_T_12 | −0.281 | −2.088 | −3.909 | 1.285 | −0.310 | −2.241 | −4.149 | 1.514 | −0.100 | −0.205 | −1.480 | −2.740 | 1.511 | −0.075 | ||
| STIC_T_14 | −0.961 | −2.969 | −4.892 | 1.801 | −1.064 | −3.264 | −5.338 | 2.118 | 0.154 | −0.502 | −1.541 | −2.520 | 2.109 | 0.096 | ||
| STIC_T_15 | −0.399 | −2.496 | −4.260 | 1.406 | −0.440 | −2.699 | −4.574 | 1.659 | −0.162 | −0.265 | −1.627 | −2.757 | 1.652 | −0.116 | ||
| STIC_T_18 | −0.694 | −2.780 | −4.702 | 1.723 | −0.785 | −3.091 | −5.169 | 2.025 | −0.390 | −0.388 | −1.526 | −2.553 | 1.974 | −0.251 | ||
| STIC_T_20 | −0.147 | −1.589 | −3.112 | 0.897 | −0.165 | −1.745 | −3.365 | 1.056 | −0.571 | −0.156 | −1.652 | −3.187 | 1.001 | −0.485 | ||
| STIC_T_21 | −0.367 | −1.924 | −3.278 | 0.922 | −0.413 | −2.116 | −3.553 | 1.131 | −0.528 | −0.365 | −1.871 | −3.141 | 1.080 | −0.440 | ||
| STIC_T_3 | 1.553 | −1.003 | −3.123 | 1.691 | 1.685 | −1.092 | −3.387 | 1.443 | 1.332 | 1.168 | −0.757 | −2.347 | 1.443 | 1.266 | ||
| STIC_T_4 | 0.004 | −2.006 | −3.928 | 1.409 | 0.006 | −2.097 | −4.081 | 1.173 | 1.026 | 0.005 | −1.788 | −3.479 | 1.173 | 0.973 | ||
| STIC_T_5 | 0.447 | −1.503 | −3.320 | 1.307 | 0.476 | −1.577 | −3.478 | 1.066 | 1.023 | 0.447 | −1.479 | −3.263 | 1.066 | 1.007 | ||
| STIC_T_9 | 0.094 | −1.883 | −3.802 | 1.669 | 0.097 | −2.019 | −4.066 | 1.431 | 1.253 | 0.068 | −1.411 | −2.841 | 1.431 | 1.161 | ||
| STIC_T_10 | 1.659 | −0.365 | −2.105 | 1.426 | 1.811 | −0.403 | −2.305 | 1.182 | 1.242 | 1.532 | −0.341 | −1.950 | 1.182 | 1.274 | ||
| STIC_T_11 | 0.492 | −1.463 | −3.082 | 1.030 | 0.493 | −1.459 | −3.076 | 0.965 | 0.335 | 0.511 | −1.512 | −3.188 | 0.965 | 0.296 | ||
| STIC_T_13 | −0.630 | −2.761 | −4.466 | 1.919 | −0.678 | −2.953 | −4.764 | 1.671 | 1.360 | −0.406 | −1.767 | −2.851 | 1.671 | 1.181 | ||
| STIC_T_16 | 0.740 | −1.064 | −2.849 | 1.352 | 0.763 | −1.103 | −2.935 | 1.127 | 0.914 | 0.677 | −0.979 | −2.604 | 1.127 | 0.852 | ||
| STIC_T_17 | 0.705 | −1.650 | −3.856 | 1.900 | 0.762 | −1.785 | −4.157 | 1.651 | 1.411 | 0.462 | −1.081 | −2.518 | 1.651 | 1.260 | ||
| STIC_T_19 | 0.314 | −1.886 | −3.806 | 1.964 | 0.341 | −2.022 | −4.074 | 1.722 | 1.387 | 0.198 | −1.174 | −2.366 | 1.722 | 1.189 | ||
References
- Shear, M.K.; Bjelland, I.; Beesdo, K.; Gloster, A.T.; Wittchen, H.U. Supplementary dimensional assessment in anxiety disorders. Int. J. Methods Psychiatr. Res. 2007, 16, S52–S64. [Google Scholar] [CrossRef]
- Lebeau, R.T.; Glenn, D.E.; Hanover, L.N.; Beesdo-Baum, K.; Wittchen, H.U.; Craske, M.G. A dimensional approach to measuring anxiety for DSM-5. Int. J. Methods Psychiatr. Res. 2012, 21, 258–272. [Google Scholar] [CrossRef]
- Martens, R.; Vealey, R.S.; Burton, D. Competitive Anxiety in Sport; Human Kinetics: Champaign, IL, USA, 1990. [Google Scholar]
- Stein, D.J.; Craske, M.G.; Rothbaum, B.O.; Chamberlain, S.R.; Fineberg, N.A.; Choi, K.W.; Jonge, P.; Baldwin, D.S.; Maj, M. The clinical characterization of the adult patient with an anxiety or related disorder aimed at personalization of management. World Psychiatry 2021, 20, 336–356. [Google Scholar] [CrossRef]
- Pacheco-Unguetti, A.P.; Acosta, A.; Callejas, A.; Lupiáñez, J. Attention and Anxiety. Psychol. Sci. 2010, 21, 298–304. [Google Scholar] [CrossRef]
- Spielberg, C.D. Assessment of State and Trait Anxiety: Conceptual and Methodological Issues. South. Psychol. 1985, 2, 6–16. [Google Scholar]
- Heeren, A.; Jones, P.J.; McNally, R.J. Mapping network connectivity among symptoms of social anxiety and comorbid depression in people with social anxiety disorder. J. Affect. Disord. 2018, 228, 75–82. [Google Scholar] [CrossRef] [PubMed]
- Tellegen, A. Structures of Mood and Personality and Their Relevance to Assessing Anxiety, with an Emphasis on Self-Report. In Anxiety and the Anxiety Disorders; Routledge: London, UK, 1985; pp. 681–706. [Google Scholar]
- Ashton, M.C.; Lee, K.; Goldberg, L.R. A Hierarchical Analysis of 1,710 English Personality-Descriptive Adjectives. J. Personal. Soc. Psychol. 2004, 87, 707–721. [Google Scholar] [CrossRef]
- Goldberg, L.R. The development of markers for the Big-Five factor structure. Psychol. Assess. 1992, 4, 26–42. [Google Scholar] [CrossRef]
- Weems, C.F.; Costa, N.M.; Watts, S.E.; Taylor, L.K.; Cannon, M.F. Cognitive Errors, Anxiety Sensitivity, and Anxiety Control Beliefs. Behav. Modif. 2007, 31, 174–201. [Google Scholar] [CrossRef] [PubMed]
- Lilienfeld, S.O.; Turner, S.M.; Jacob, R.G. Anxiety sensitivity: An examination of theoretical and methodological issues. Adv. Behav. Res. Ther. 1993, 15, 147–183. [Google Scholar] [CrossRef]
- Cox, R. Sports Psychology: Concepts and Applications, 4th ed.; McGraw-Hill: New York, NY, USA, 2007; Volume 45, pp. 124–154. [Google Scholar]
- Allen, B.P.; Potkay, C.R. On the arbitrary distinction between states and traits. J. Personal. Soc. Psychol. 1981, 41, 916–928. [Google Scholar] [CrossRef]
- Luthans, F.; Avolio, B.J.; Avey, J.B.; Norman, S.M. Positive Psychological Capital: Measurement and Relationship with Performance and Satisfaction. Pers. Psychol. 2007, 60, 541–572. [Google Scholar] [CrossRef]
- Steptoe, A.; Kearsley, N. Cognitive and somatic anxiety. Behav. Res. Ther. 1990, 28, 75–81. [Google Scholar] [CrossRef] [PubMed]
- Ree, M.J.; French, D.; MacLeod, C.; Locke, V. Distinguishing Cognitive and Somatic Dimensions of State and Trait Anxiety: Development and Validation of the State-Trait Inventory for Cognitive and Somatic Anxiety (STICSA). Behav. Cogn. Psychother. 2008, 36, 313–332. [Google Scholar] [CrossRef]
- Bryant, C. Anxiety and depression in old age: Challenges in recognition and diagnosis. Int. Psychogeriatr. 2010, 22, 511–513. [Google Scholar] [CrossRef]
- Flint, A.J. Generalised Anxiety Disorder in Elderly Patients. Drugs Aging 2005, 22, 101–114. [Google Scholar] [CrossRef]
- Wetherell, J.L.; Gatz, M.; Pedersen, N.L. A longitudinal analysis of anxiety and depressive symptoms. Psychol. Aging 2001, 16, 187–195. [Google Scholar] [CrossRef]
- Clark, L.A.; Watson, D. Tripartite model of anxiety and depression: Psychometric evidence and taxonomic implications. J. Abnorm. Psychol. 1991, 100, 316–336. [Google Scholar] [CrossRef]
- Watson, D.; Clark, L.A.; Weber, K.; Assenheimer, J.S.; Strauss, M.E.; McCormick, R.A. Testing a tripartite model: II. Exploring the symptom structure of anxiety and depression in student, adult, and patient samples. J. Abnorm. Psychol. 1995, 104, 15–25. [Google Scholar] [CrossRef]
- Therrien, Z.; Hunsley, J. Assessment of anxiety in older adults: A systematic review of commonly used measures. Aging Ment. Health 2012, 16, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Balsamo, M.; Romanelli, R.; Innamorati, M.; Ciccarese, G.; Carlucci, L.; Saggino, A. The State-Trait Anxiety Inventory: Shadows and Lights on its Construct Validity. J. Psychopathol. Behav. Assess. 2013, 35, 475–486. [Google Scholar] [CrossRef]
- Grös, D.F.; Antony, M.M.; Simms, L.J.; McCabe, R.E. Psychometric properties of the State-Trait Inventory for Cognitive and Somatic Anxiety (STICSA): Comparison to the State-Trait Anxiety Inventory (STAI). Psychol. Assess. 2007, 19, 369–381. [Google Scholar] [CrossRef]
- Roberts, K.E.; Hart, T.A.; Eastwood, J.D. Factor structure and validity of the State-Trait Inventory for Cognitive and Somatic Anxiety. Psychol. Assess. 2016, 28, 134–146. [Google Scholar] [CrossRef] [PubMed]
- Carlucci, L.; Watkins, M.W.; Sergi, M.R.; Cataldi, F.; Saggino, A.; Balsamo, M. Dimensions of Anxiety, Age, and Gender: Assessing Dimensionality and Measurement Invariance of the State-Trait for Cognitive and Somatic Anxiety (STICSA) in an Italian Sample. Front. Psychol. 2018, 9, 2345. [Google Scholar] [CrossRef] [PubMed]
- Saggino, A.; Balsamo, M.; Carlucci, L.; Cavalletti, V.; Sergi, M.R.; da Fermo, G.; Dèttore, D.; Marsigli, N.; Petruccelli, I.; Pizzo, S.; et al. Psychometric Properties of the Italian Version of the Young Schema Questionnaire L-3: Preliminary Results. Front. Psychol. 2018, 9, 312. [Google Scholar] [CrossRef] [PubMed]
- Saggino, A.; Carlucci, L.; Sergi, M.R.; D’Ambrosio, I.; Fairfield, B.; Cera, N.; Balsamo, M. A Validation Study of the Psychometric Properties of the Other As Shamer Scale–2. SAGE Open 2017, 7, 215824401770424. [Google Scholar] [CrossRef]
- Carlucci, L.; D’Ambrosio, I.; Innamorati, M.; Saggino, A.; Balsamo, M. Co-rumination, anxiety, and maladaptive cognitive schemas: When friendship can hurt. Psychol. Res. Behav. Manag. 2018, 11, 133–144. [Google Scholar] [CrossRef]
- Balsamo, M.; Carlucci, L.; Sergi, M.R.; Romanelli, R.; D’Ambrosio, I.; Fairfield, B.; Ree, M.J.; Saggino, A. A new measure for trait and state anxiety: The State Trait Inventory of Cognitive and Somatic Anxiety (STICSA). Standardization in an Italian population. Psicoter. Cogn. Comport. 2016, 22, 229–232. [Google Scholar]
- Balsamo, M.; Innamorati, M.; Van Dam, N.T.; Carlucci, L.; Saggino, A. Measuring anxiety in the elderly: Psychometric properties of the state trait inventory of cognitive and somatic anxiety (STICSA) in an elderly Italian sample. Int. Psychogeriatr. 2015, 27, 999–1008. [Google Scholar] [CrossRef]
- Styck, K.M.; Rodriguez, M.C.; Yi, E.H. Dimensionality of the State–Trait Inventory of Cognitive and Somatic Anxiety. Assessment 2022, 29, 103–127. [Google Scholar] [CrossRef]
- Barros, F.; Figueiredo, C.; Brás, S.; Carvalho, J.M.; Soares, S.C. Multidimensional assessment of anxiety through the State-Trait Inventory for Cognitive and Somatic Anxiety (STICSA): From dimensionality to response prediction across emotional contexts. PLoS ONE 2022, 17, e0262960. [Google Scholar] [CrossRef]
- Kline, R.B. Principles and Practice of Structural Equation Modeling; Guilford Publications: New York, NY, USA, 2023. [Google Scholar]
- Hinkin, T.R. A brief tutorial on the development of measures for use in survey questionnaires. Organ. Res. Methods 1998, 1, 104–121. [Google Scholar] [CrossRef]
- Bentler, P.M.; Bonett, D.G. Significance tests and goodness of fit in the analysis of covariance structures. Psychol. Bull. 1980, 88, 588–606. [Google Scholar] [CrossRef]
- Bentler, P.M.; Satorra, A. Testing model nesting and equivalence. Psychol. Methods 2010, 15, 111–123. [Google Scholar] [CrossRef]
- Preacher, K.J. Quantifying Parsimony in Structural Equation Modeling. Multivar. Behav. Res. 2006, 41, 227–259. [Google Scholar] [CrossRef] [PubMed]
- Howard, M.C. A review of exploratory factor analysis decisions and overview of current practices: What we are doing and how can we improve? Int. J. Hum.-Comput. Interact. 2016, 32, 51–62. [Google Scholar] [CrossRef]
- Schmitt, T.A. Current methodological considerations in exploratory and confirmatory factor analysis. J. Psychoeduc. Assess. 2011, 29, 304–321. [Google Scholar] [CrossRef]
- Tindall, I.K.; Curtis, G.J.; Locke, V. Dimensionality and Measurement Invariance of the State-Trait Inventory for Cognitive and Somatic Anxiety (STICSA) and Validity Comparison with Measures of Negative Emotionality. Front. Psychol. 2021, 12, 644889. [Google Scholar] [CrossRef]
- Jabrayilov, R.; Emons, W.H.; Sijtsma, K. Comparison of classical test theory and item response theory in individual change assessment. Appl. Psychol. Meas. 2016, 40, 559–572. [Google Scholar] [CrossRef]
- Horton, M.C.; Marais, I.; Christensen, K.B. Dimensionality. In Rasch Models in Health, 1st ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2013; pp. 137–162. [Google Scholar]
- Thomas, M.L. The Value of Item Response Theory in Clinical Assessment: A Review. Assessment 2011, 18, 291–307. [Google Scholar] [CrossRef]
- van der Linden, W.J.; Hambleton, R.K. Item Response Theory: Brief History, Common Models, and Extensions. In Handbook of Modern Item Response Theory; Springer: New York, NY, USA, 1997; pp. 1–28. [Google Scholar] [CrossRef]
- Wicherts, J.M. Psychometric problems with the method of correlated vectors applied to item scores (including some nonsensical results). Intelligence 2017, 60, 26–38. [Google Scholar] [CrossRef]
- Reckase, M.D. Multidimensional Item Response Theory Models. In Multidimensional Item Response Theory; Springer: New York, NY, USA, 2009; pp. 79–112. [Google Scholar] [CrossRef]
- Baker, F.B. The Basics of Item Response Theory, 2nd ed.; Office of Educational Research and Improvement (ED): Washington, DC, USA, 2001. [Google Scholar]
- Stucky, B.D.; Edelen, M.O. Using hierarchical IRT models to create unidimensional measures from multidimensional data. In Handbook of Item Response Theory Modeling; Routledge: London, UK, 2014; pp. 201–224. [Google Scholar]
- Balsamo, M.; Carlucci, L.; Innamorati, M.; Lester, D.; Pompili, M. Further insights into the beck hopelessness scale (BHS): Unidimensionality among psychiatric inpatients. Front. Psychiatry 2020, 11, 727. [Google Scholar] [CrossRef] [PubMed]
- Balsamo, M.; Saggino, A.; Carlucci, L. Tailored Screening for Late-Life Depression: A Short Version of the Teate Depression Inventory (TDI-E). Front. Psychol. 2019, 10, 2693. [Google Scholar] [CrossRef] [PubMed]
- Chalmers, R.P. mirt: A Multidimensional Item Response Theory Package for the R Environment. J. Stat. Softw. 2012, 48, 1–29. [Google Scholar] [CrossRef]
- Mokken, R.J. A Theory and Procedure of Scale Analysis; De Gruyter: Berlin, Germany, 1971. [Google Scholar]
- Sijtsma, K.; Molenaar, I.W. Introduction to Noparametric Item Response Theory; Sage: Newcastle upon Tyne, UK, 2002; Volume 5. [Google Scholar]
- Chen, W.-H.; Thissen, D. Local Dependence Indexes for Item Pairs Using Item Response Theory. J. Educ. Behav. Stat. 1997, 22, 265–289. [Google Scholar] [CrossRef]
- Muraki, E.; Carlson, J.E. Full-Information Factor Analysis for Polytomous Item Responses. Appl. Psychol. Meas. 1995, 19, 73–90. [Google Scholar] [CrossRef]
- Cai, L.; Monroe, S. A New Statistic for Evaluating Item Response Theory Models for Ordinal Data; CRESST Report 839; University of California: Los Angeles, CA, USA, 2014. [Google Scholar]
- Schermelleh-Engel, K.; Moosbrugger, H.; Müller, H. Evaluating the fit of structural equation models: Tests of significance and descriptive goodness-of-fit measures. Methods Psychol. Res. Online 2003, 8, 23–74. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Orlando, M.; Thissen, D. Likelihood-Based Item-Fit Indices for Dichotomous Item Response Theory Models. Appl. Psychol. Meas. 2000, 24, 50–64. [Google Scholar] [CrossRef]
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Toland, M.D. Practical Guide to Conducting an Item Response Theory Analysis. J. Early Adolesc. 2014, 34, 120–151. [Google Scholar] [CrossRef]
- Hasmy, A. Compare Unidimensional & Multidimensional Rasch Model for Test with Multidimensional Construct and Items Local Dependence. J. Educ. Learn. 2014, 8, 187–194. [Google Scholar] [CrossRef]
- Gros, D.F.; Simms, L.J.; Antony, M.M. Psychometric properties of the State-Trait Inventory for Cognitive and Somatic Anxiety (STICSA) in friendship dyads. Behav. Ther. 2010, 41, 277–284. [Google Scholar] [CrossRef] [PubMed]
- Reise, S.P.; Morizot, J.; Hays, R.D. The role of the bifactor model in resolving dimensionality issues in health outcomes measures. Qual. Life Res. 2007, 16, 19–31. [Google Scholar] [CrossRef]
- Sireci, S.G.; Thissen, D.; Wainer, H. On the Reliability of Testlet-Based Tests. J. Educ. Meas. 1991, 28, 237–247. [Google Scholar] [CrossRef]
- Stucky, B.D.; Thissen, D.; Orlando Edelen, M. Using Logistic Approximations of Marginal Trace Lines to Develop Short Assessments. Appl. Psychol. Meas. 2013, 37, 41–57. [Google Scholar] [CrossRef]
- Woods, C.M.; Thissen, D. Item Response Theory with Estimation of the Latent Population Distribution Using Spline-Based Densities. Psychometrika 2006, 71, 281–301. [Google Scholar] [CrossRef]
- Tuerlinckx, F.; De Boeck, P. Modeling Local Item Dependencies in Item Response Theory. Psychol. Belg. 1998, 38, 61. [Google Scholar] [CrossRef]
- Anderson, D.R. Model Based Inference in the Life Sciences: A Primer on Evidence; Springer: New York, NY, USA, 2008; Volume 31. [Google Scholar]
- Calvo, M.G.; Avero, P.; Castillo, M.D.; Miguel-Tobal, J.J. Multidimensional Anxiety and Content-specificity Effects in Preferential Processing of Threat. Eur. Psychol. 2003, 8, 252–265. [Google Scholar] [CrossRef]
- Endler, N.S.; Kocovski, N.L. State and trait anxiety revisited. J. Anxiety Disord. 2001, 15, 231–245. [Google Scholar] [CrossRef]
- Allen, L.; Choate, M. Toward a unified treatment for emotional disorder. Behav. Ther. 2004, 35, 205–230. [Google Scholar]
- Carlucci, L.; Saggino, A.; Balsamo, M. On the efficacy of the unified protocol for transdiagnostic treatment of emotional disorders: A systematic review and meta-analysis. Clin. Psychol. Rev. 2021, 87, 101999. [Google Scholar] [CrossRef]
- Bock, R.D.; Aitkin, M. Marginal maximum likelihood estimation of item parameters: Application of an EM algorithm. Psychometrika 1981, 46, 443–459. [Google Scholar] [CrossRef]
- Chernyshenko, O.S.; Stark, S.; Chan, K.-Y.; Drasgow, F.; Williams, B. Fitting item response theory models to two personality inventories: Issues and insights. Multivar. Behav. Res. 2001, 36, 523–562. [Google Scholar] [CrossRef]
- Krueger, R.F.; Nichol, P.E.; Hicks, B.M.; Markon, K.E.; Patrick, C.J.; lacono, W.G.; McGue, M. Using Latent Trait Modeling to Conceptualize an Alcohol Problems Continuum. Psychol. Assess. 2004, 16, 107–119. [Google Scholar] [CrossRef]
- Pitt, M.A.; Myung, I.J.; Zhang, S. Toward a method of selecting among computational models of cognition. Psychol. Rev. 2002, 109, 472–491. [Google Scholar] [CrossRef] [PubMed]
- Bornovalova, M.A.; Choate, A.M.; Fatimah, H.; Petersen, K.J.; Wiernik, B.M. Appropriate Use of Bifactor Analysis in Psychopathology Research: Appreciating Benefits and Limitations. Biol. Psychiatry 2020, 88, 18–27. [Google Scholar] [CrossRef] [PubMed]
- Balsamo, M.; Imperatori, C.; Sergi, M.R.; Belvederi Murri, M.; Continisio, M.; Tamburello, A.; Innamorati, M.; Saggino, A. Cognitive Vulnerabilities and Depression in Young Adults: An ROC Curves Analysis. Depress. Res. Treat. 2013, 2013, 407602. [Google Scholar] [CrossRef] [PubMed]
- Innamorati, M.; Tamburello, S.; Contardi, A.; Imperatori, C.; Tamburello, A.; Saggino, A.; Balsamo, M. Psychometric Properties of the Attitudes toward Self-Revised in Italian Young Adults. Depress. Res. Treat. 2013, 2013, 209216. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.-C.; Chen, P.-H.; Cheng, Y.-Y. Improving Measurement Precision of Test Batteries Using Multidimensional Item Response Models. Psychol. Methods 2004, 9, 116–136. [Google Scholar] [CrossRef] [PubMed]
- McCracken, L.M.; Gross, R.T.; Aikens, J.; Carnrike, C.L.M. The assessment of anxiety and fear in persons with chronic pain: A comparison of instruments. Behav. Res. Ther. 1996, 34, 927–933. [Google Scholar] [CrossRef] [PubMed]
- Buckelew, S.P.; Hannay, H.J. Relationships among Anxiety, Defensiveness, Sex, Task Difficulty, and Performance on Various Neuropsychological Tasks. Percept. Mot. Ski. 1986, 63, 711–718. [Google Scholar] [CrossRef]
- Koksal, F.; Power, K.G. Four Systems Anxiety Questionnaire (FSAQ): A Self-Report Measure of Somatic, Cognitive, Behavioral, and Feeling Components. J. Personal. Assess. 1990, 54, 534–545. [Google Scholar] [CrossRef] [PubMed]
- Sijtsma, K.; Junker, B.W. Item Response Theory: Past Performance, Present Developments, and Future Expectations. Behaviormetrika 2006, 33, 75–102. [Google Scholar] [CrossRef]
- Reise, S.P.; Waller, N.G. Item Response Theory and Clinical Measurement. Annu. Rev. Clin. Psychol. 2009, 5, 27–48. [Google Scholar] [CrossRef]
- Balsamo, M. Personality and depression: Evidence of a possible mediating role for anger trait in the relationship between cooperativeness and depression. Compr. Psychiatry 2013, 54, 46–52. [Google Scholar] [CrossRef]
- Balsamo, M. Anger and depression: Evidence of a possible mediating role for rumination. Psychol. Rep. 2010, 106, 3–12. [Google Scholar] [CrossRef]
- Barlow, D.H.; Farchione, T.J.; Bullis, J.R.; Gallagher, M.W.; Murray-Latin, H.; Sauer-Zavala, S.; Bentley, K.H.; Thompson-Hollands, J.; Conklin, L.R.; Boswell, J.F.; et al. The Unified Protocol for Transdiagnostic Treatment of Emotional Disorders Compared With Diagnosis-Specific Protocols for Anxiety Disorders. JAMA Psychiatry 2017, 74, 875. [Google Scholar] [CrossRef]
- Colledani, D.; Anselmi, P.; Robusto, E. Using multidimensional item response theory to develop an abbreviated form of the Italian version of Eysenck’s IVE questionnaire. Personal. Individ. Differ. 2019, 142, 45–52. [Google Scholar] [CrossRef]
- Finch, H. Item Parameter Estimation for the MIRT Model. Appl. Psychol. Meas. 2010, 34, 10–26. [Google Scholar] [CrossRef]
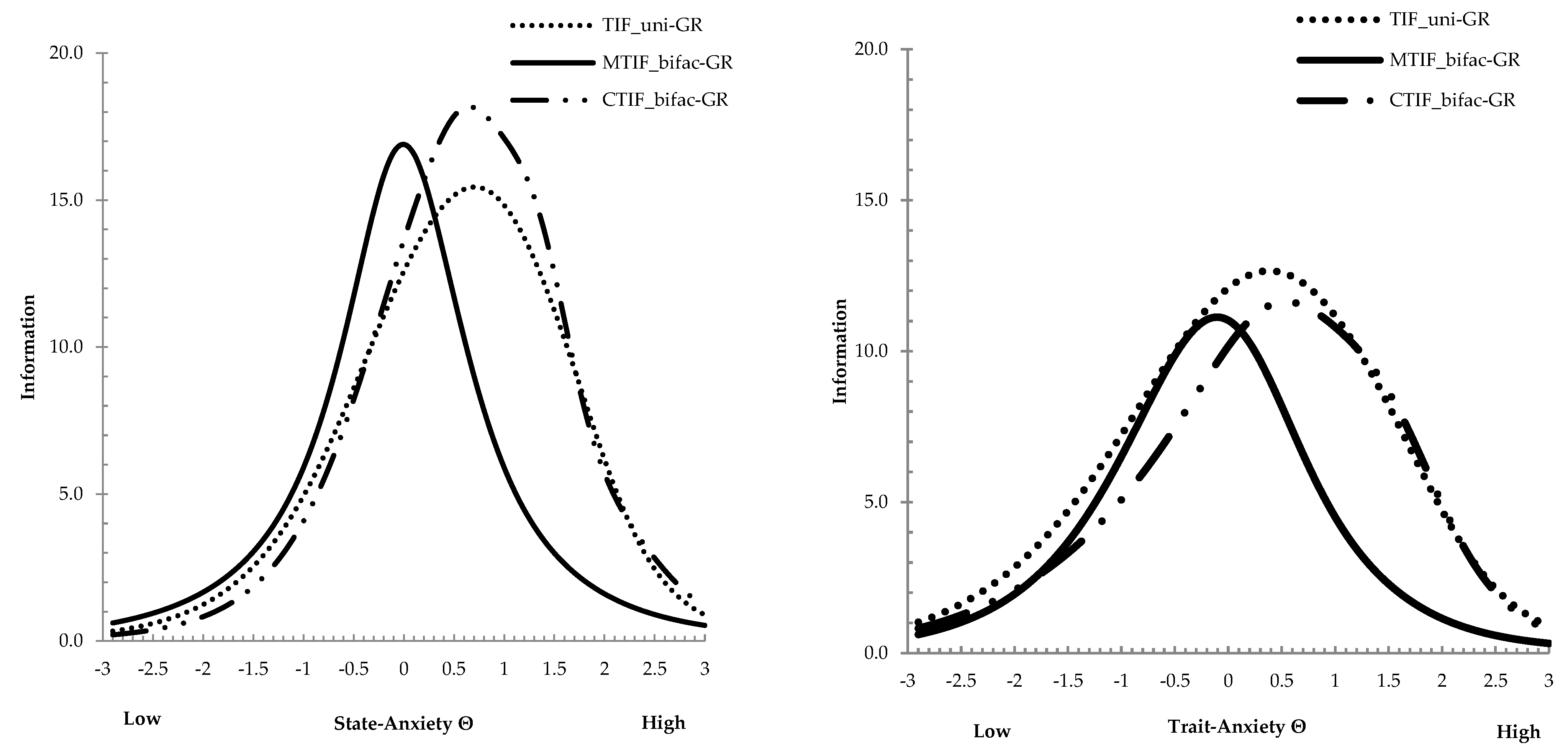
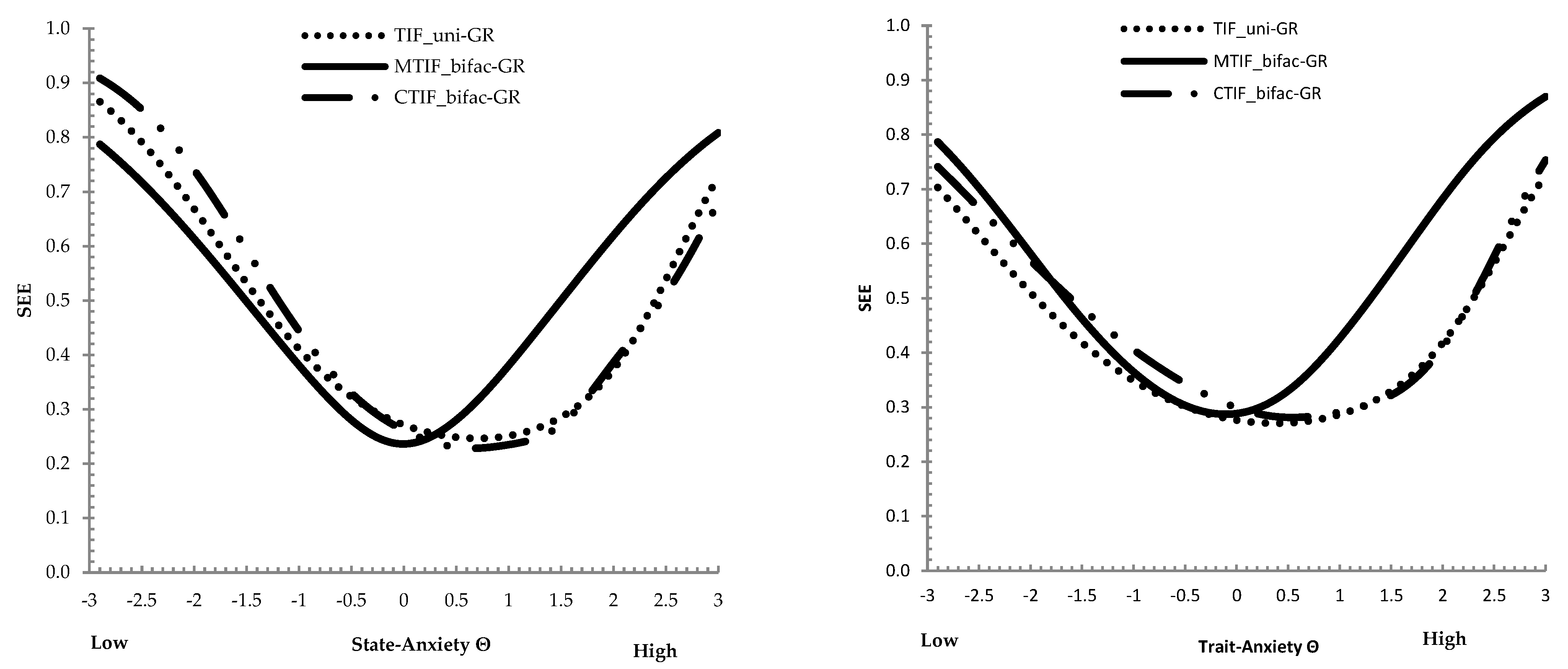
| (a) | |||
| Uni-GR | Multi-GR | Bifac-GR | |
| # of positive LD pairs flagged | 16 | 8 | 4 |
| # of negative LD pairs flagged | 3 | 2 | 2 |
| # of parameters | 84 | 85 | 105 |
| −2LL | −60,047.66 | −58,793.31 | −58,477.48 |
| BIC | 120,776.5 | 118,275.9 | 117,806.4 |
| AIC | 120,263.3 | 117,756.6 | 117,165 |
| C2 (df) | 6505.643 (189) *** | 2499.159 (188) *** | 1858.838 (168) *** |
| RMSEA | 0.100 | 0.061 | 0.055 |
| TLI | 0.916 | 0.969 | 0.974 |
| CFI | 0.984 | 0.972 | 0.979 |
| SRMSR | 0.074 | 0.047 | 0.043 |
| Precision (marginal reliability) [θ −3;3] | 0.89 | 0.86–0.88 | 0.087–0.62–0.42 |
| (b) | |||
| Uni-GR | Multi-GR | Bifac-GR | |
| # of positive LD pairs flagged | 9 | 6 | 3 |
| # of negative LD pairs flagged | 1 | 0 | 0 |
| # of parameters | 84 | 85 | 105 |
| −2LL | −69,934.32 | −69,002.42 | −68,742.61 |
| BIC | 140,549.8 | 138,694.1 | 138,336.7 |
| AIC | 140,036.6 | 138,174.8 | 137,695.2 |
| C2 (df) | 5253.537(189) *** | 2673.871(188) *** | 2033.147(168) *** |
| RMSEA | 0.090 | 0.063 | 0.058 |
| TLI | 0.919 | 0.960 | 0.966 |
| CFI | 0.927 | 0.964 | 0.973 |
| SRMR | 0.065 | 0.047 | 0.041 |
| Precision (marginal reliability) [θ −3;3] | 0.90 | 0.86–0.88 | 0.86–0.40–0.65 |
| STICSA—State | STICSA—Trait | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Item | Uni-GR | Bifac-GR Conditional | Bifac-GR Marginal | Item | Uni-GR | Bifac-GR Conditional | Bifac-GR Marginal | ||||||||
| a | ag | aS1 | aS2 | a*g | a*S1 | a*S2 | a | ag | aS1 | aS2 | a*g | a*S1 | a*S2 | ||
| STIC_S_1 | 1.196 | 1.017 | 0.979 | 0.881 | 0.840 | STIC_T_1 | 1.020 | 1.205 | −0.392 | 1.174 | −0.320 | ||||
| STIC_S_2 | 1.528 | 1.365 | 1.415 | 1.049 | 1.103 | STIC_T_2 | 1.264 | 1.402 | −0.078 | 1.401 | −0.060 | ||||
| STIC_S_6 | 1.649 | 1.442 | 1.574 | 1.058 | 1.200 | STIC_T_6 | 1.485 | 1.859 | 0.608 | 1.750 | 0.410 | ||||
| STIC_S_7 | 1.799 | 1.659 | 1.636 | 1.195 | 1.171 | STIC_T_7 | 1.577 | 2.543 | 1.501 | 1.906 | 0.834 | ||||
| STIC_S_8 | 2.516 | 2.389 | 1.993 | 1.550 | 1.156 | STIC_T_8 | 1.991 | 2.565 | 0.746 | 2.349 | 0.412 | ||||
| STIC_S_12 | 1.339 | 1.143 | 1.063 | 0.969 | 0.882 | STIC_T_12 | 1.285 | 1.514 | −0.100 | 1.511 | −0.075 | ||||
| STIC_S_14 | 2.012 | 1.910 | 1.928 | 1.263 | 1.282 | STIC_T_14 | 1.801 | 2.118 | 0.154 | 2.109 | 0.096 | ||||
| STIC_S_15 | 1.280 | 1.074 | 1.018 | 0.921 | 0.861 | STIC_T_15 | 1.406 | 1.659 | −0.162 | 1.652 | −0.116 | ||||
| STIC_S_18 | 1.817 | 1.597 | 1.177 | 1.313 | 0.858 | STIC_T_18 | 1.723 | 2.025 | −0.390 | 1.974 | −0.251 | ||||
| STIC_S_20 | 1.055 | .914 | 0.591 | 0.863 | 0.521 | STIC_T_20 | 0.897 | 1.056 | −0.571 | 1.001 | −0.485 | ||||
| STIC_S_21 | 0.920 | 0.736 | 0.773 | 0.670 | 0.709 | STIC_T_21 | 0.922 | 1.131 | −0.528 | 1.080 | −0.440 | ||||
| STIC_S_3 | 1.980 | 2.207 | 0.148 | 2.207 | 0.090 | STIC_T_3 | 1.691 | 1.443 | 1.332 | 1.443 | 1.266 | ||||
| STIC_S_4 | 1.715 | 1.816 | −0.146 | 1.816 | −0.100 | STIC_T_4 | 1.409 | 1.173 | 1.026 | 1.173 | 0.973 | ||||
| STIC_S_5 | 1.551 | 1.646 | 0.314 | 1.646 | 0.228 | STIC_T_5 | 1.307 | 1.066 | 1.023 | 1.066 | 1.007 | ||||
| STIC_S_9 | 1.897 | 2.882 | −1.023 | 2.882 | −0.546 | STIC_T_9 | 1.669 | 1.431 | 1.253 | 1.431 | 1.161 | ||||
| STIC_S_10 | 1.534 | 1.933 | 0.601 | 1.933 | 0.408 | STIC_T_10 | 1.426 | 1.182 | 1.242 | 1.182 | 1.274 | ||||
| STIC_S_11 | 1.298 | 1.191 | 0.143 | 1.191 | 0.117 | STIC_T_11 | 1.030 | 0.965 | 0.335 | 0.965 | 0.296 | ||||
| STIC_S_13 | 2.256 | 3.932 | −1.549 | 3.932 | −0.659 | STIC_T_13 | 1.919 | 1.671 | 1.360 | 1.671 | 1.181 | ||||
| STIC_S_16 | 1.643 | 1.883 | 0.555 | 1.883 | 0.381 | STIC_T_16 | 1.352 | 1.127 | 0.914 | 1.127 | 0.852 | ||||
| STIC_S_17 | 2.063 | 2.909 | 1.146 | 2.909 | 0.615 | STIC_T_17 | 1.900 | 1.651 | 1.411 | 1.651 | 1.260 | ||||
| STIC_S_19 | 2.108 | 2.597 | 0.820 | 2.597 | 0.466 | STIC_T_19 | 1.964 | 1.722 | 1.387 | 1.722 | 1.189 | ||||
| (a) | |||||||||||
| STICSA—State | |||||||||||
| Bifac-GR | Multi-GR | ||||||||||
| MDISC | MDIFF1 | MDIFF2 | MDIFF3 | Itemfit p (fdr) | MDISC | MDIFF1 | MDIFF2 | MDIFF3 | Itemfit p (fdr) | ||
| STIC_S_1 | 1.412 | 0.261 | 1.396 | 2.885 | 0.504 | STIC_S_1 | 1.413 | 0.268 | 1.403 | 2.891 | 0.573 |
| STIC_S_2 | 1.966 | 0.186 | 1.371 | 2.311 | 0.599 | STIC_S_2 | 1.924 | 0.194 | 1.390 | 2.342 | 0.546 |
| STIC_S_6 | 2.135 | 0.831 | 1.735 | 2.533 | 0.614 | STIC_S_6 | 2.084 | 0.843 | 1.757 | 2.567 | 0.609 |
| STIC_S_7 | 2.330 | 0.465 | 1.405 | 2.337 | 0.145 | STIC_S_7 | 2.293 | 0.474 | 1.420 | 2.360 | 0.128 |
| STIC_S_8 | 3.112 | 0.935 | 1.626 | 2.293 | 0.599 | STIC_S_8 | 3.145 | 0.941 | 1.632 | 2.300 | 0.701 |
| STIC_S_12 | 1.561 | 0.649 | 1.752 | 2.919 | 0.467 | STIC_S_12 | 1.565 | 0.655 | 1.758 | 2.924 | 0.389 |
| STIC_S_14 | 2.713 | 0.654 | 1.537 | 2.282 | 0.321 | STIC_S_14 | 2.658 | 0.663 | 1.554 | 2.306 | 0.128 |
| STIC_S_15 | 1.480 | 0.596 | 1.847 | 2.875 | 0.374 | STIC_S_15 | 1.484 | 0.601 | 1.852 | 2.878 | 0.268 |
| STIC_S_18 | 1.984 | 0.813 | 1.719 | 2.666 | 0.609 | STIC_S_18 | 2.008 | 0.817 | 1.719 | 2.662 | 0.633 |
| STIC_S_20 | 1.088 | 1.086 | 2.082 | 3.154 | 0.488 | STIC_S_20 | 1.095 | 1.089 | 2.083 | 3.150 | 0.526 |
| STIC_S_21 | 1.067 | 0.648 | 1.945 | 3.091 | 0.145 | STIC_S_21 | 1.069 | 0.653 | 1.948 | 3.094 | 0.128 |
| STIC_S_3 | 2.211 | −0.232 | 0.945 | 1.718 | 0.145 | STIC_S_3 | 2.272 | −0.222 | 0.944 | 1.708 | 0.144 |
| STIC_S_4 | 1.822 | 0.462 | 1.505 | 2.446 | 0.488 | STIC_S_4 | 1.822 | 0.469 | 1.510 | 2.455 | 0.473 |
| STIC_S_5 | 1.676 | 0.052 | 1.323 | 2.253 | 0.145 | STIC_S_5 | 1.696 | 0.059 | 1.324 | 2.248 | 0.114 |
| STIC_S_9 | 3.058 | 0.380 | 1.206 | 2.006 | 0.145 | STIC_S_9 | 2.161 | 0.421 | 1.336 | 2.258 | 0.131 |
| STIC_S_10 | 2.024 | −0.398 | 0.631 | 1.378 | 0.145 | STIC_S_10 | 1.898 | −0.403 | 0.658 | 1.426 | 0.114 |
| STIC_S_11 | 1.200 | 0.037 | 1.611 | 2.972 | 0.145 | STIC_S_11 | 1.217 | 0.044 | 1.604 | 2.952 | 0.114 |
| STIC_S_13 | 4.226 | 0.571 | 1.306 | 1.931 | 0.567 | STIC_S_13 | 2.467 | 0.648 | 1.471 | 2.200 | 0.796 |
| STIC_S_16 | 1.964 | −0.028 | 0.971 | 1.806 | 0.145 | STIC_S_16 | 1.870 | −0.024 | 0.998 | 1.854 | 0.114 |
| STIC_S_17 | 3.127 | 0.027 | 0.981 | 1.761 | 0.479 | STIC_S_17 | 2.526 | 0.031 | 1.049 | 1.881 | 0.268 |
| STIC_S_19 | 2.723 | 0.124 | 1.070 | 1.797 | 0.437 | STIC_S_19 | 2.456 | 0.131 | 1.117 | 1.872 | 0.276 |
| (b) | |||||||||||
| STICSA—Trait | |||||||||||
| Bifac-GR | Multi-GR | ||||||||||
| MDISC | MDIFF1 | MDIFF2 | MDIFF3 | itemfit p (fdr) | MDISC | MDIFF1 | MDIFF2 | MDIFF3 | itemfit p (fdr) | ||
| STIC_T_1 | 1.267 | −1.171 | 0.621 | 2.577 | 0.074 | STIC_T_1 | 1.151 | −1.239 | 0.664 | 2.757 | 0.055 |
| STIC_T_2 | 1.405 | −0.917 | 0.781 | 2.367 | 0.074 | STIC_T_2 | 1.409 | −0.910 | 0.785 | 2.369 | 0.055 |
| STIC_T_6 | 1.956 | 0.160 | 1.270 | 2.334 | 0.999 | STIC_T_6 | 1.802 | 0.174 | 1.325 | 2.433 | 0.968 |
| STIC_T_7 | 2.953 | −0.090 | 1.059 | 2.023 | 0.100 | STIC_T_7 | 1.917 | −0.097 | 1.227 | 2.365 | 0.042 |
| STIC_T_8 | 2.672 | 0.528 | 1.450 | 2.217 | 0.044 | STIC_T_8 | 2.444 | 0.550 | 1.499 | 2.288 | 0.016 |
| STIC_T_12 | 1.517 | 0.204 | 1.477 | 2.735 | 0.999 | STIC_T_12 | 1.490 | 0.211 | 1.498 | 2.772 | 1.000 |
| STIC_T_14 | 2.123 | 0.501 | 1.537 | 2.514 | 0.004 | STIC_T_14 | 2.154 | 0.504 | 1.534 | 2.508 | 0.003 |
| STIC_T_15 | 1.667 | 0.264 | 1.619 | 2.744 | 0.102 | STIC_T_15 | 1.631 | 0.271 | 1.641 | 2.786 | 0.117 |
| STIC_T_18 | 2.062 | 0.381 | 1.499 | 2.506 | 0.796 | STIC_T_18 | 1.891 | 0.397 | 1.558 | 2.623 | 0.770 |
| STIC_T_20 | 1.200 | 0.138 | 1.453 | 2.803 | 0.044 | STIC_T_20 | 0.950 | 0.168 | 1.713 | 3.332 | 0.037 |
| STIC_T_21 | 1.249 | 0.331 | 1.695 | 2.846 | 0.696 | STIC_T_21 | 1.024 | 0.380 | 1.943 | 3.286 | 0.630 |
| STIC_T_3 | 1.964 | −0.858 | 0.556 | 1.724 | 0.837 | STIC_T_3 | 1.936 | −0.858 | 0.565 | 1.741 | 0.691 |
| STIC_T_4 | 1.558 | −0.004 | 1.346 | 2.619 | 0.587 | STIC_T_4 | 1.552 | 0.002 | 1.356 | 2.633 | 0.591 |
| STIC_T_5 | 1.478 | −0.322 | 1.067 | 2.353 | 0.308 | STIC_T_5 | 1.464 | −0.317 | 1.080 | 2.373 | 0.204 |
| STIC_T_9 | 1.902 | −0.051 | 1.061 | 2.138 | 0.074 | STIC_T_9 | 1.898 | −0.046 | 1.069 | 2.147 | 0.063 |
| STIC_T_10 | 1.714 | −1.056 | 0.235 | 1.345 | 0.117 | STIC_T_10 | 1.646 | −1.072 | 0.245 | 1.376 | 0.055 |
| STIC_T_11 | 1.021 | −0.482 | 1.429 | 3.012 | 0.187 | STIC_T_11 | 0.974 | −0.495 | 1.482 | 3.128 | 0.195 |
| STIC_T_13 | 2.155 | 0.315 | 1.370 | 2.211 | 0.074 | STIC_T_13 | 2.170 | 0.319 | 1.374 | 2.212 | 0.055 |
| STIC_T_16 | 1.451 | −0.526 | 0.760 | 2.023 | 0.074 | STIC_T_16 | 1.448 | −0.522 | 0.767 | 2.032 | 0.055 |
| STIC_T_17 | 2.172 | −0.351 | 0.822 | 1.914 | 0.074 | STIC_T_17 | 2.179 | −0.345 | 0.827 | 1.918 | 0.055 |
| STIC_T_19 | 2.211 | −0.154 | 0.914 | 1.842 | 0.385 | STIC_T_19 | 2.215 | −0.150 | 0.920 | 1.849 | 0.411 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carlucci, L.; Innamorati, M.; Ree, M.; D’Ignazio, G.; Balsamo, M. Measuring State and Trait Anxiety: An Application of Multidimensional Item Response Theory. Behav. Sci. 2023, 13, 628. https://doi.org/10.3390/bs13080628
Carlucci L, Innamorati M, Ree M, D’Ignazio G, Balsamo M. Measuring State and Trait Anxiety: An Application of Multidimensional Item Response Theory. Behavioral Sciences. 2023; 13(8):628. https://doi.org/10.3390/bs13080628
Chicago/Turabian StyleCarlucci, Leonardo, Marco Innamorati, Melissa Ree, Giorgia D’Ignazio, and Michela Balsamo. 2023. "Measuring State and Trait Anxiety: An Application of Multidimensional Item Response Theory" Behavioral Sciences 13, no. 8: 628. https://doi.org/10.3390/bs13080628
APA StyleCarlucci, L., Innamorati, M., Ree, M., D’Ignazio, G., & Balsamo, M. (2023). Measuring State and Trait Anxiety: An Application of Multidimensional Item Response Theory. Behavioral Sciences, 13(8), 628. https://doi.org/10.3390/bs13080628








