A Compartmental Mathematical Model to Assess the Impact of Vaccination, Isolation, and Key Epidemiological Parameters on Mpox Control
Abstract
1. Introduction
2. Materials and Methods
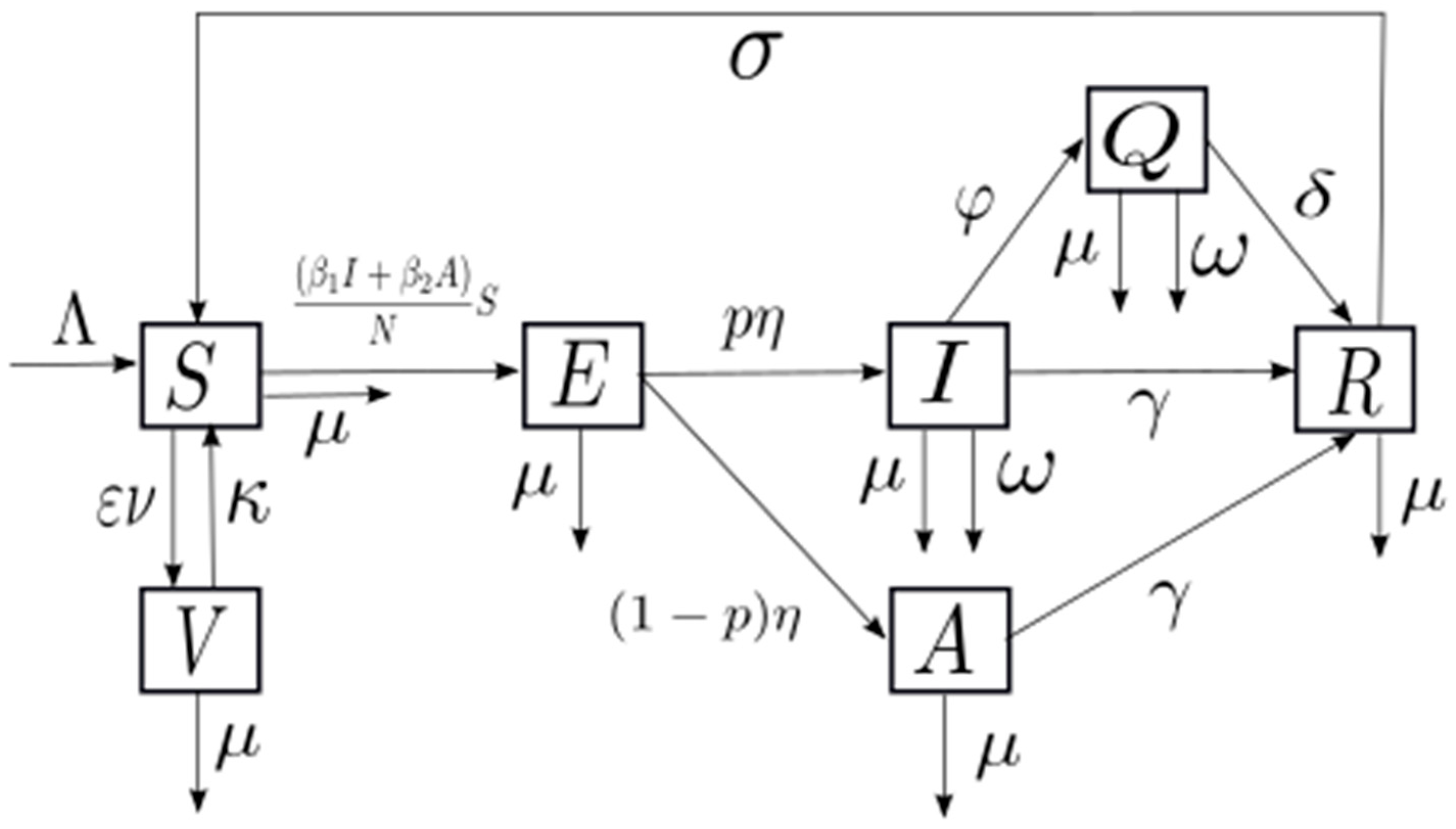
2.1. Model Building
2.2. Simulations and Sensitivity Analysis
2.2.1. Simulations
2.2.2. Sensitivity Analysis
2.3. Case Study of the Epidemiological Mpox Outbreak of 2022
2.3.1. Parameter Estimation and Model Fitting
2.3.2. Potential Impact of Vaccination
3. Results
3.1. Model Building
3.1.1. Positivity
3.1.2. Boundedness
3.1.3. Existence of the Equilibrium Points
Disease-Free Equilibrium Point
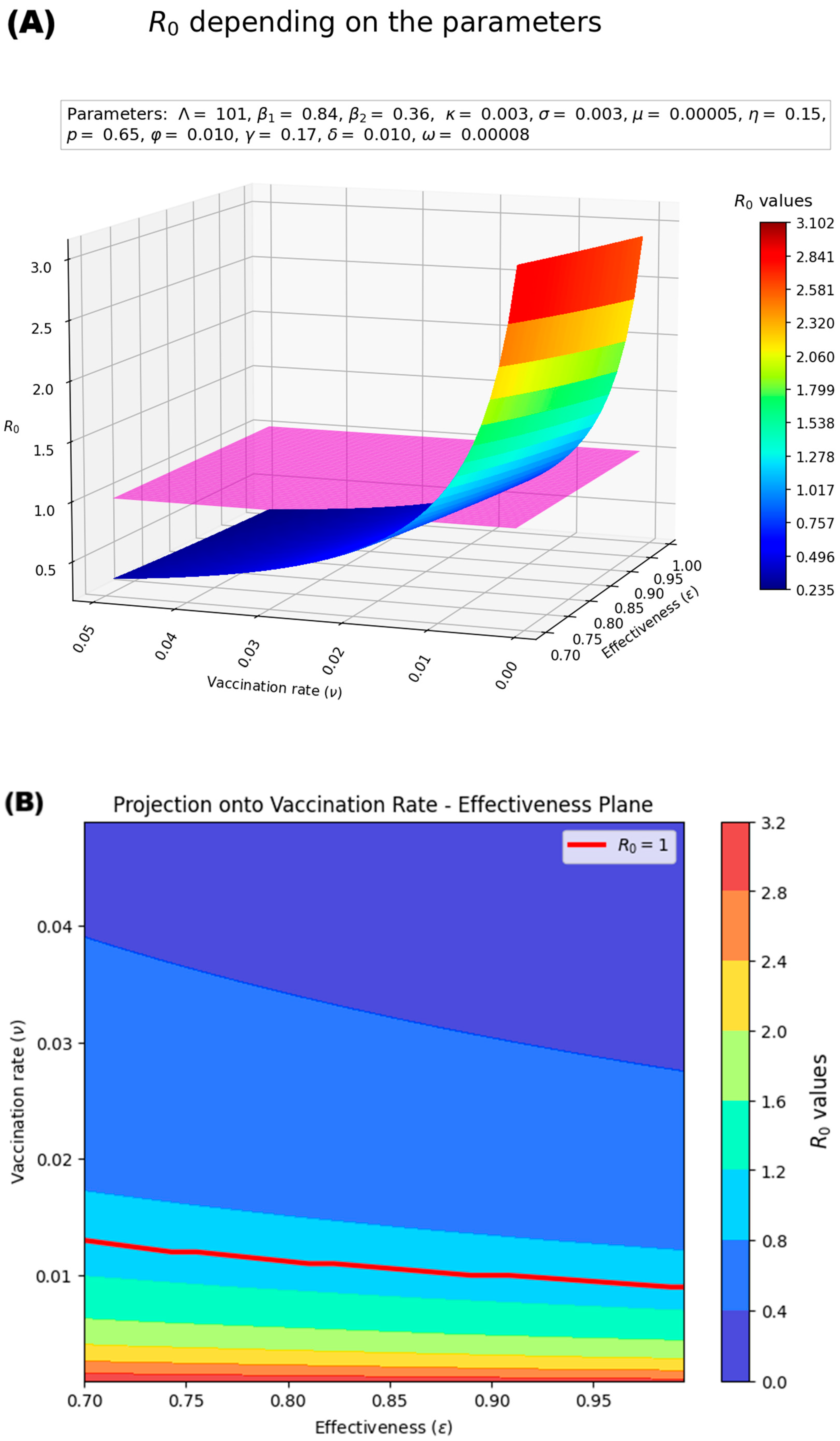
Estimation of the Basic Reproduction Number (R0)
Endemic Equilibrium Point
3.1.4. Local Stability Analysis
Disease-Free Equilibrium Point
Endemic Equilibrium Point
3.2. Simulations and Sensitivity Analysis of the Model
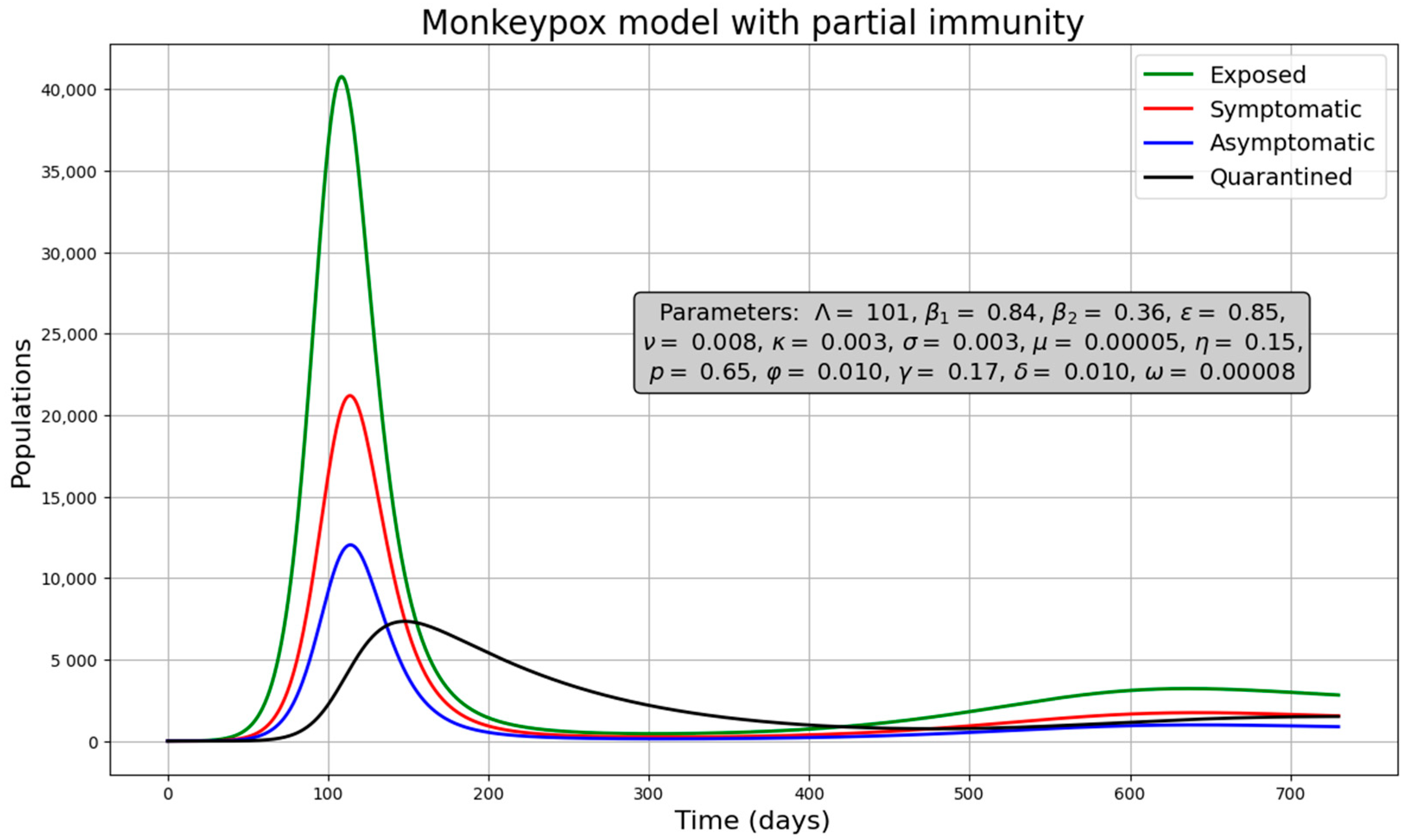
3.2.1. Simulations
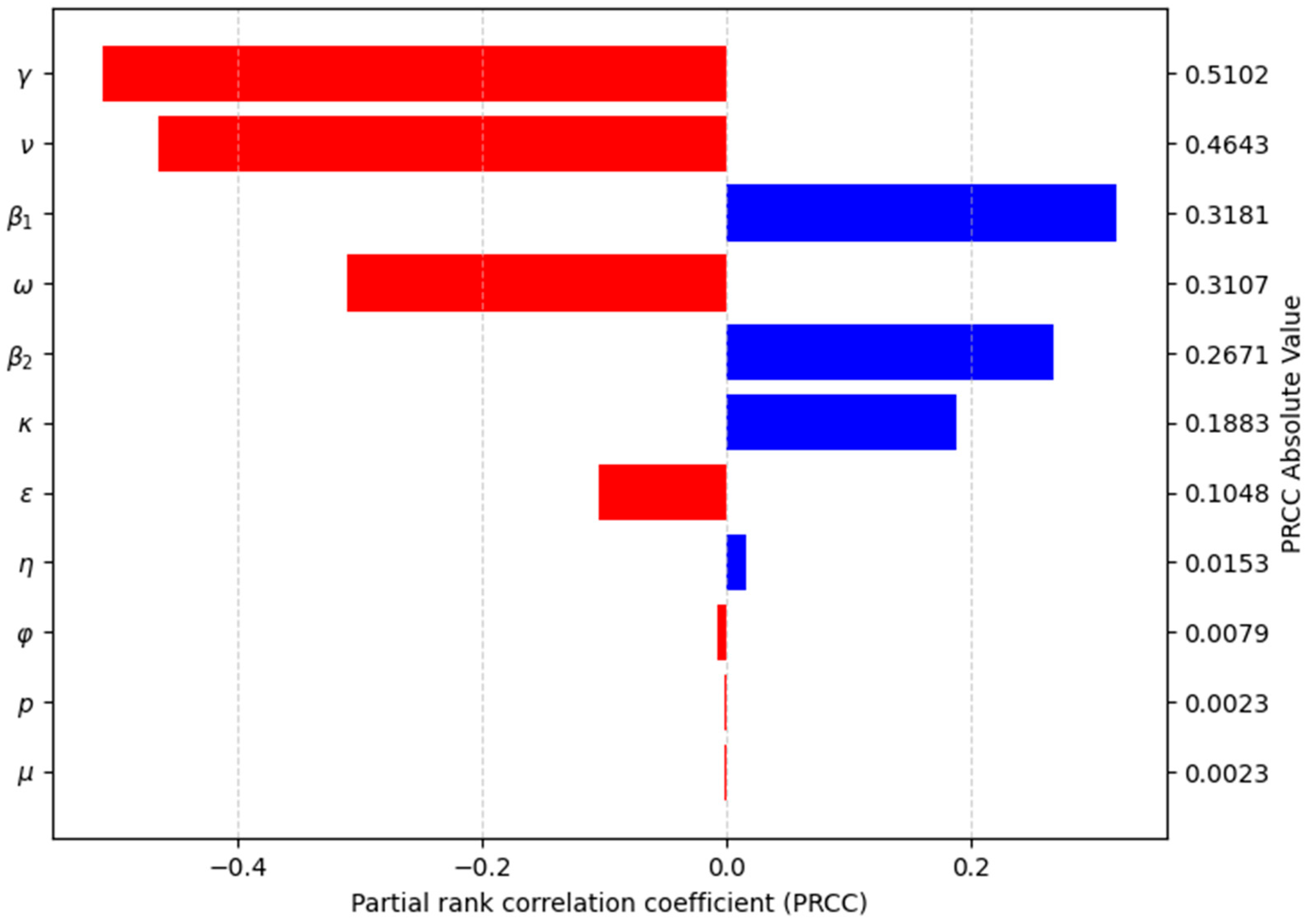
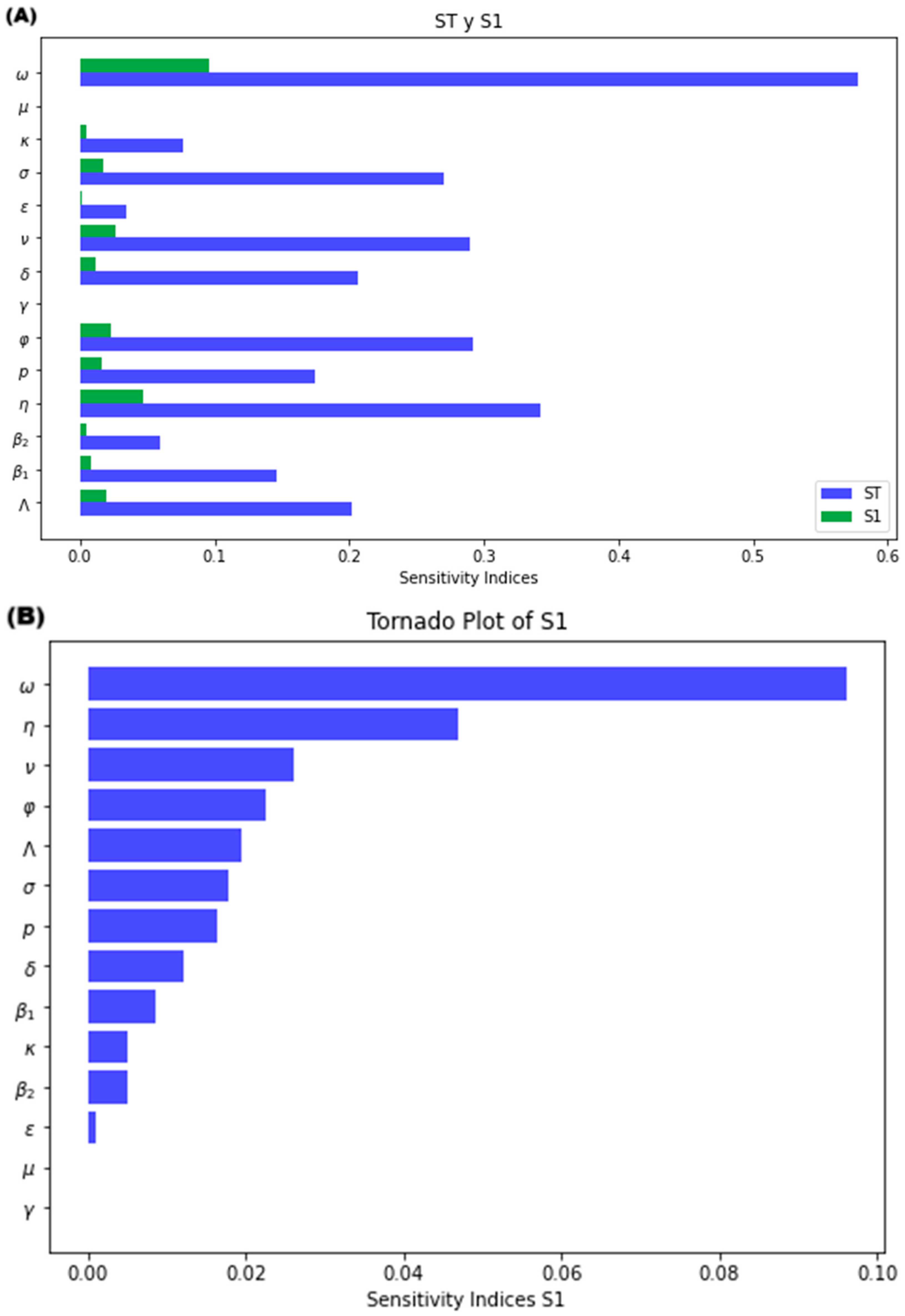
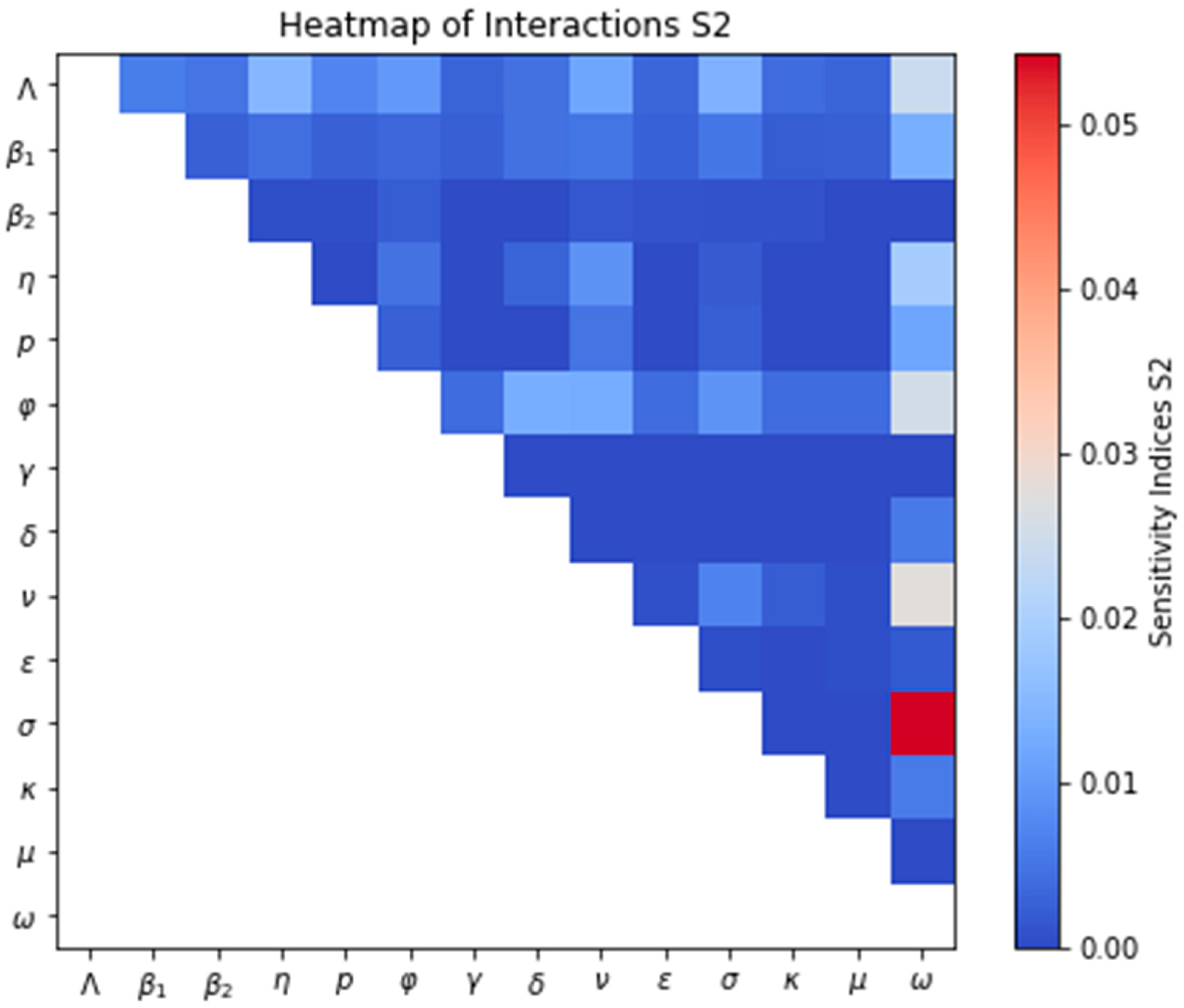
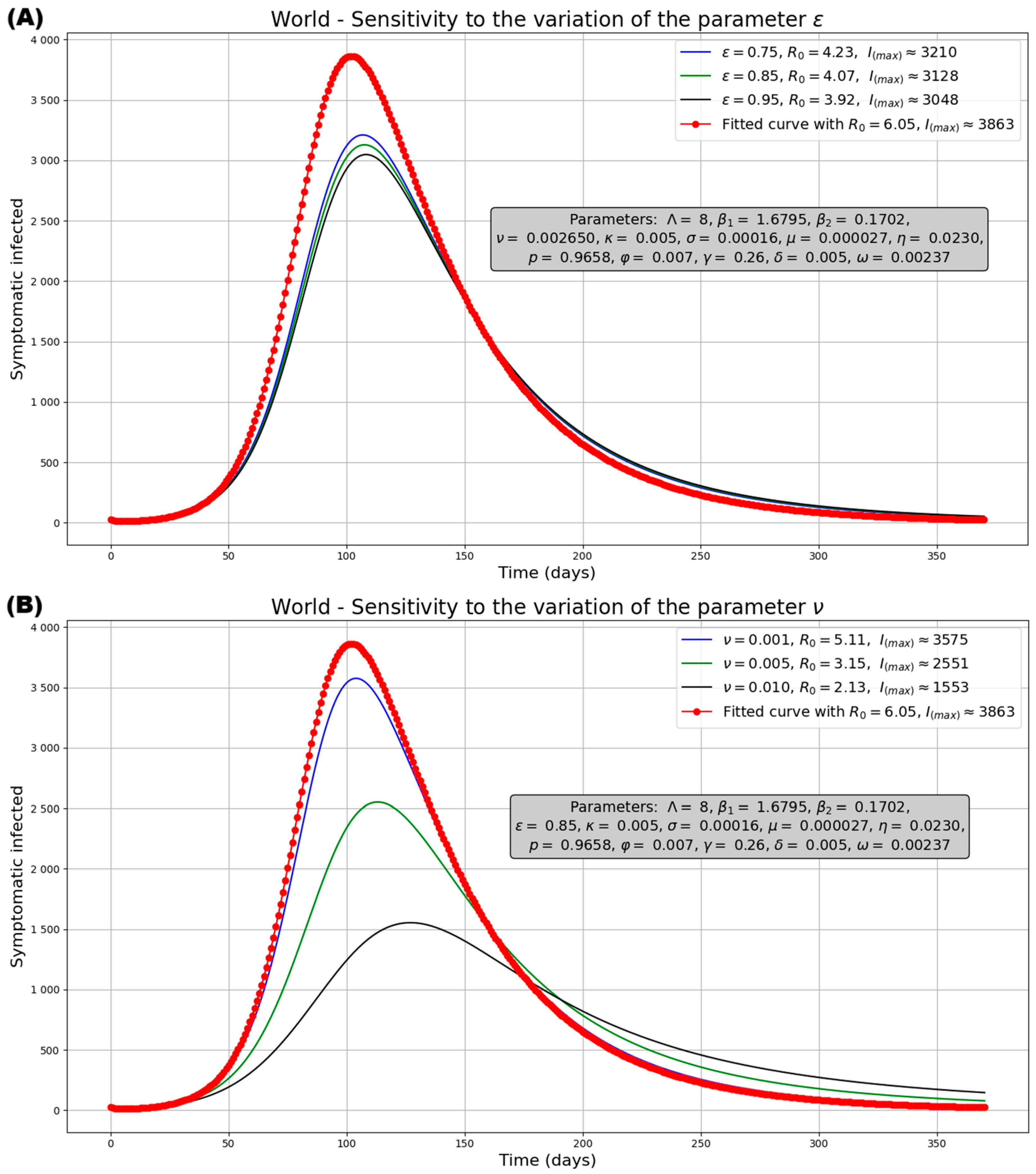
3.2.2. Sensitivity Analysis of the Model
Sensitivity Analysis for R0
Sensitivity Analysis for the Model
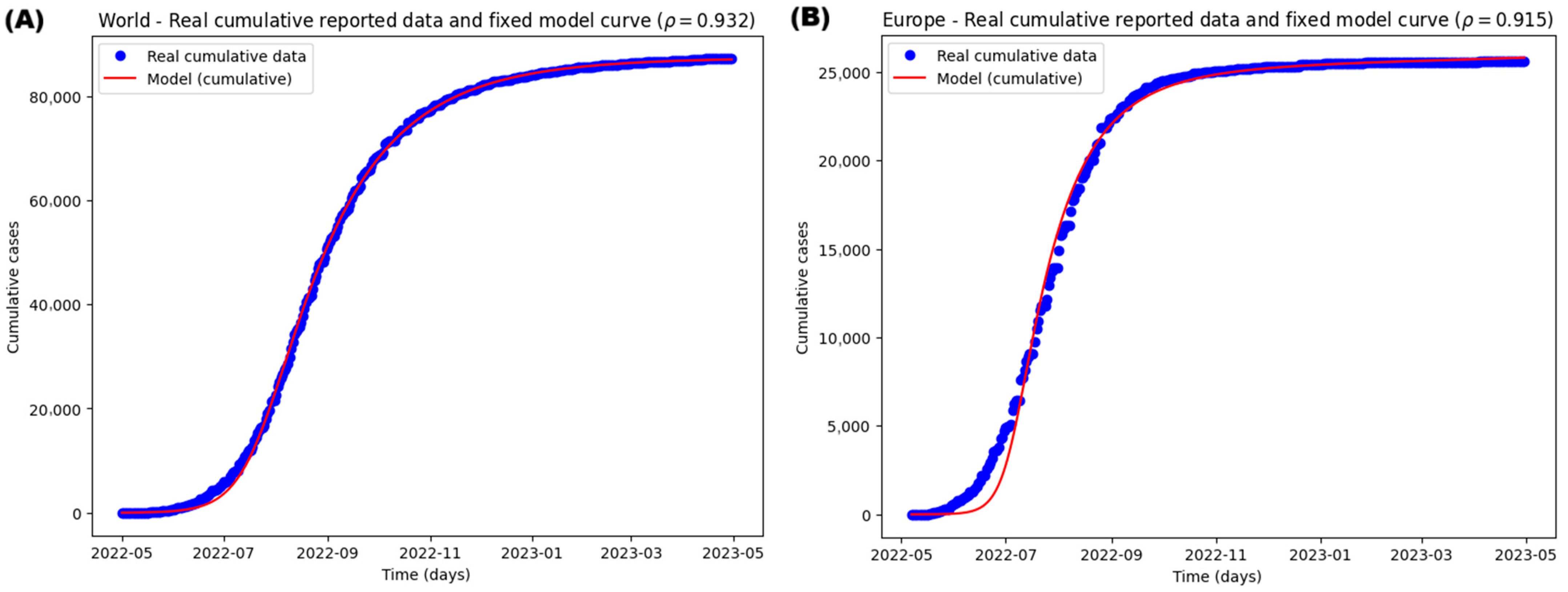
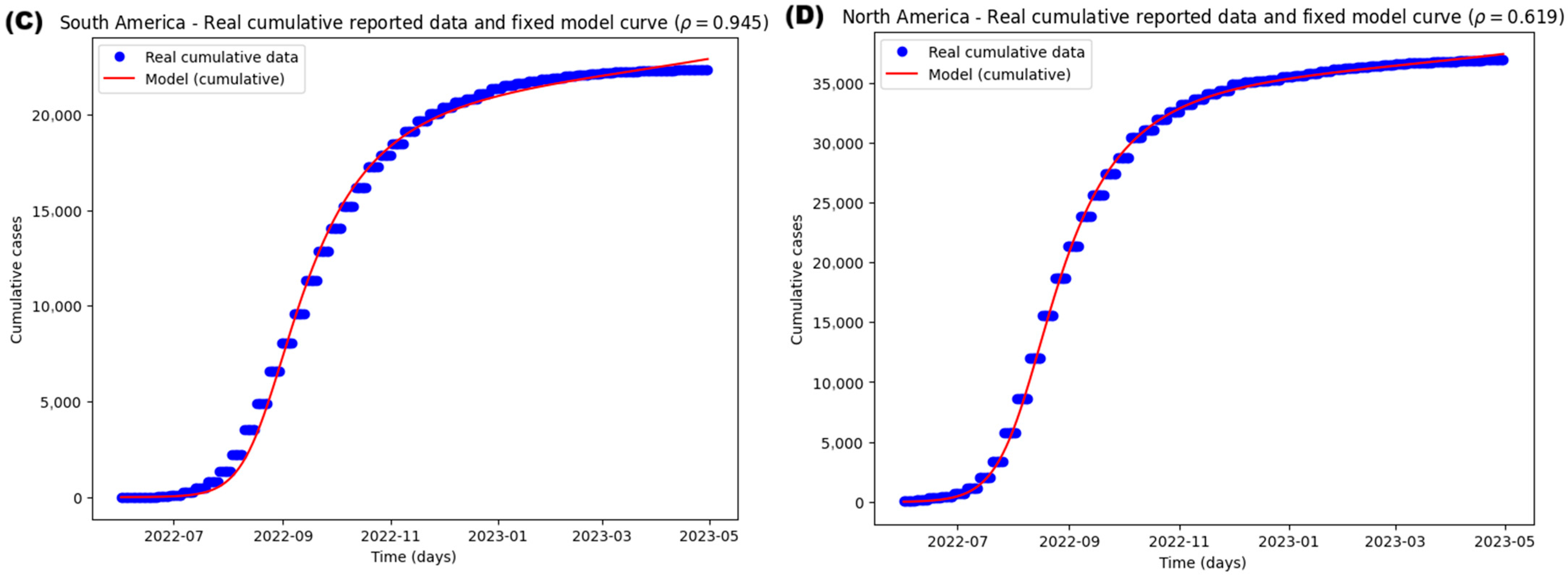
3.3. Case Study of the Epidemiological Mpox Outbreak of 2022
3.3.1. Parameter Estimation and Model Fitting
- If cases are interpreted as the onset of symptoms, the relevant flow is:
- If, alternatively, the data corresponds to reported cases, the correct flow is:
3.3.2. Potential Impact of Vaccination
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- McCollum, A.M.; Damon, I.K. Human Monkeypox. Clin. Infect. Dis. 2014, 58, 260–267. [Google Scholar] [CrossRef]
- World Health Organization (WHO). Multi-Country Monkeypox Outbreak in Non-Endemic Countries. Available online: https://www.who.int/emergencies/disease-outbreak-news/item/2022-DON385 (accessed on 4 June 2025).
- Thornhill, J.P.; Barkati, S.; Walmsley, S.; Rockstroh, J.; Antinori, A.; Harrison, L.B.; Palich, R.; Nori, A.; Reeves, I.; Habibi, M.S.; et al. Monkeypox Virus Infection in Humans across 16 Countries—April–June 2022. N. Engl. J. Med. 2022, 387, 679–691. [Google Scholar] [CrossRef]
- Mathieu, E.; Spooner, F.; Dattani, S.; Ritchie, H.; Roser, M. Mpox. Our World in Data. 2022. Available online: https://ourworldindata.org/mpox (accessed on 4 June 2025).
- Jiang, L.; Xu, A.; Guan, L.; Tang, Y.; Chai, G.; Feng, J.; Wu, Y.; Li, M.; Zhang, C.; Liu, X.; et al. A Review of Mpox: Biological Characteristics, Epidemiology, Clinical Features, Diagnosis, Treatment, and Prevention Strategies. Exploration 2025, 5, 20230112. [Google Scholar] [CrossRef]
- Happi, C.; Adetifa, I.; Mbala, P.; Njouom, R.; Nakoune, E.; Happi, A.; Ndodo, N.; Ayansola, O.; Mboowa, G.; Bedford, T.; et al. Urgent Need for a Non-Discriminatory and Non-Stigmatizing Nomenclature for Monkeypox Virus. PLoS Biol. 2022, 20, e3001769. [Google Scholar] [CrossRef]
- Luna, N.; Ramírez, A.L.; Muñoz, M.; Ballesteros, N.; Patiño, L.H.; Castañeda, S.A.; Bonilla-Aldana, D.K.; Paniz-Mondolfi, A.; Ramírez, J.D. Phylogenomic Analysis of the Monkeypox Virus (MPXV) 2022 Outbreak: Emergence of a Novel Viral Lineage? Travel. Med. Infect. Dis. 2022, 49, 102402. [Google Scholar] [CrossRef]
- Gigante, C.M.; Korber, B.; Seabolt, M.H.; Wilkins, K.; Davidson, W.; Rao, A.K.; Zhao, H.; Smith, T.G.; Hughes, C.M.; Minhaj, F.; et al. Multiple Lineages of Monkeypox Virus Detected in the United States, 2021–2022. Science 2022, 378, 560–565. [Google Scholar] [CrossRef]
- Naga, N.G.; Nawar, E.A.; Mobarak, A.A.; Faramawy, A.G.; Al-Kordy, H.M.H. Monkeypox: A Re-Emergent Virus with Global Health Implications—A Comprehensive Review. Trop. Dis. Travel. Med. Vaccines 2025, 11, 2. [Google Scholar] [CrossRef] [PubMed]
- Brüssow, H. Monkeypox Virus: WHO’s Second Public Health Emergency of International Concern Within 2 Years. Microb. Biotechnol. 2025, 18, e70142. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Wen, T.-H.; Shih, W.-L.; Vermund, S.H.; Fang, C.-T. Impact of Vaccination and High-Risk Group Awareness on the Mpox Epidemic in the United States, 2022-2023: A Modelling Study. eClinicalMedicine 2024, 68, 102407. [Google Scholar] [CrossRef]
- Taha, A.M.; Mahmoud, A.M.; Abouelmagd, K.; Saed, S.A.A.; Khalefa, B.B.; Shah, S.; Satapathy, P.; Shamim, M.A.; Sah, S.; Serhan, H.A.; et al. Effectiveness of a Single Dose of JYNNEOS Vaccine in Real World: A Systematic Review and Meta-Analysis. Health Sci. Rep. 2024, 7, e70069. [Google Scholar] [CrossRef] [PubMed]
- Endo, A.; Murayama, H.; Abbott, S.; Ratnayake, R.; Pearson, C.A.B.; Edmunds, W.J.; Fearon, E.; Funk, S. Heavy-Tailed Sexual Contact Networks and Monkeypox Epidemiology in the Global Outbreak, 2022. Science 2022, 378, 90–94. [Google Scholar] [CrossRef] [PubMed]
- Brainard, J.; Lake, I.; Hunter, P.R. Evaluation of Three Control Strategies to Limit Mpox Outbreaks in an Agent Based Model. medRxiv 2024, 1–24. [Google Scholar] [CrossRef]
- Mummah, R.O.; Hoff, N.A.; Rimoin, A.W.; Lloyd-Smith, J.O. Controlling Emerging Zoonoses at the Animal-Human Interface. One Health Outlook 2020, 2, 17. [Google Scholar] [CrossRef]
- Koenig, K.L.; Beÿ, C.K.; Marty, A.M. Monkeypox 2022 Identify-Isolate-Inform: A 3I Tool for Frontline Clinicians for a Zoonosis with Escalating Human Community Transmission. One Health 2022, 15, 100410. [Google Scholar] [CrossRef]
- Peter, O.J.; Kumar, S.; Kumari, N.; Oguntolu, F.A.; Oshinubi, K.; Musa, R. Transmission Dynamics of Monkeypox Virus: A Mathematical Modelling Approach. Model. Earth Syst. Environ. 2022, 8, 3423–3434. [Google Scholar] [CrossRef] [PubMed]
- Al-Shomrani, M.M.; Musa, S.S.; Yusuf, A. Unfolding the Transmission Dynamics of Monkeypox Virus: An Epidemiological Modelling Analysis. Mathematics 2023, 11, 1121. [Google Scholar] [CrossRef]
- Frank, T.D. Mathematical Analysis of Four Fundamental Epidemiological Models for Monkeypox Disease Outbreaks: On the Pivotal Role of Human–Animal Order Parameters—In Memory of Hermann Haken. Mathematics 2024, 12, 3215. [Google Scholar] [CrossRef]
- Adepoju, O.A.; Ibrahim, H.O. An Optimal Control Model for Monkeypox Transmission Dynamics with Vaccination and Immunity Loss Following Recovery. Healthc. Anal. 2024, 6, 100355. [Google Scholar] [CrossRef]
- Marín-Machuca, O.; Chacón, R.D.; Alvarez-Lovera, N.; Pesantes-Grados, P.; Pérez-Timaná, L.; Marín-Sánchez, O. Mathematical Modeling of COVID-19 Cases and Deaths and the Impact of Vaccinations during Three Years of the Pandemic in Peru. Vaccines 2023, 11, 1648. [Google Scholar] [CrossRef]
- Molla, J.; Sekkak, I.; Mundo Ortiz, A.; Moyles, I.; Nasri, B. Mathematical Modeling of Mpox: A Scoping Review. One Health 2023, 16, 100540. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array Programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Iwanaga, T.; Usher, W.; Herman, J. Toward SALib 2.0: Advancing the Accessibility and Interpretability of Global Sensitivity Analyses. Socio-Environ. Syst. Model. 2022, 4, 18155. [Google Scholar] [CrossRef]
- Herman, J.; Usher, W. SALib: An Open-Source Python Library for Sensitivity Analysis. J. Open Source Softw. 2017, 2, 97. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Yuan, S.; Jiang, S.-C.; Zhang, Z.-W.; Fu, Y.-F.; Yang, X.-Y.; Li, Z.-L.; Hu, J. How and When Does Monkeypox (Mpox) Transmit: Implications for Prevention and Treatments. Front. Pharmacol. 2022, 13, 1109928. [Google Scholar] [CrossRef]
- Vogel, L. Making Sense of Monkeypox Death Rates. CMAJ 2022, 194, E1097. [Google Scholar] [CrossRef] [PubMed]
- World Bank: United Nations Population Division. World Population Prospects: 2024 Revision. Birth Rate, Crude (Per 1000 People). Available online: https://data.worldbank.org/indicator/SP.DYN.CBRT.IN?end=2021&name_desc=false&start=2007 (accessed on 4 June 2025).
- World Bank: United Nations Population Division. World Population Prospects: 2024 Revision. Population, Total. Available online: https://data.worldbank.org/indicator/SP.POP.TOTL (accessed on 4 June 2025).
- World Bank: United Nations Population Division. World Population Prospects: 2024 Revision. Death Rate, Crude (Per 1,000 People). Available online: https://data.worldbank.org/indicator/SP.DYN.CDRT.IN?end=2021&name_desc=false&start=1997 (accessed on 4 June 2025).
- Brand, S.P.C.; Cavallaro, M.; Cumming, F.; Turner, C.; Florence, I.; Blomquist, P.; Hilton, J.; Guzman-Rincon, L.M.; House, T.; Nokes, D.J.; et al. The Role of Vaccination and Public Awareness in Forecasts of Mpox Incidence in the United Kingdom. Nat. Commun. 2023, 14, 4100. [Google Scholar] [CrossRef]
- Leandry, L.; Mureithi, E.W. An Investigation on the Monkeypox Virus Dynamics in Human and Rodent Populations for a Deterministic Mathematical Model. Inform. Med. Unlocked 2023, 41, 101325. [Google Scholar] [CrossRef]
- Ngungu, M.; Addai, E.; Adeniji, A.; Adam, U.M.; Oshinubi, K. Mathematical Epidemiological Modeling and Analysis of Monkeypox Dynamism with Non-Pharmaceutical Intervention Using Real Data from United Kingdom. Front. Public Health 2023, 11, 1101436. [Google Scholar] [CrossRef]
- Yang, S.; Guo, X.; Zhao, Z.; Abudunaibi, B.; Zhao, Y.; Rui, J.; Wang, Y.; Song, W.; Wei, H.; Chen, T. Possibility of Mpox Viral Transmission and Control from High-Risk to the General Population: A Modeling Study. BMC Infect. Dis. 2023, 23, 119. [Google Scholar] [CrossRef]
- Hazra, A.; Zucker, J.; Bell, E.; Flores, J.; Gordon, L.; Mitjà, O.; Suñer, C.; Lemaignen, A.; Jamard, S.; Nozza, S.; et al. Mpox in People with Past Infection or a Complete Vaccination Course: A Global Case Series. Lancet Infect. Dis. 2024, 24, 57–64. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.-S.; Mandal, S.; Mohammed, H.; Turner, C.; Florence, I.; Walker, J.; Niyomsri, S.; Amirthalingam, G.; Ramsay, M.; Charlett, A.; et al. Transmission Dynamics and Effect of Control Measures on the 2022 Outbreak of Mpox among Gay, Bisexual, and Other Men Who Have Sex with Men in England: A Mathematical Modelling Study. Lancet Infect. Dis. 2024, 24, 65–74. [Google Scholar] [CrossRef] [PubMed]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A Methodology for Performing Global Uncertainty and Sensitivity Analysis in Systems Biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef] [PubMed]
- Sobol’, I.M. On Sensitivity Estimation for Nonlinear Mathematical Models. Mat. Model. 1990, 2, 112–118. [Google Scholar]
- Sobol’, I.M. Global Sensitivity Indices for Nonlinear Mathematical Models and Their Monte Carlo Estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- López-Cruz, I.L.; Salazar-Moreno, R.; Rojano-Aguilar, A.; Ruiz-García, A. Global Sensitivity Analysis of a Greenhouse Lettuce (Lactuca sativa L.) Crop Model. Agrociencia 2012, 46, 383–397. [Google Scholar]
- Balesdent, M.; Brevaul, L.; Lacaze, S.; Missoum, S.; Morio, J. Methods for High-Dimensional and Computationally Intensive Models. In Estimation of Rare Event Probabilities in Complex Aerospace and Other Systems; Elsevier Inc.: Cambridge, UK, 2016; pp. 109–136. ISBN 978-0-08-100091-5. [Google Scholar]
- Newville, M.; Stensitzki, T.; Allen, D.B.; Ingargiola, A. LMFIT: Non-Linear Least-Square Minimization and Curve-Fitting for Python. 2014. Available online: https://zenodo.org/records/11813 (accessed on 4 June 2025).
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A Limited Memory Algorithm for Bound Constrained Optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Zhu, C.; Byrd, R.H.; Lu, P.; Nocedal, J. Algorithm 778: L-BFGS-B: Fortran Subroutines for Large-Scale Bound-Constrained Optimization. ACM Trans. Math. Softw. 1997, 23, 550–560. [Google Scholar] [CrossRef]
- Chowell, G.; Viboud, C.; Simonsen, L.; Moghadas, S.M. Characterizing the Reproduction Number of Epidemics with Early Subexponential Growth Dynamics. J. R. Soc. Interface 2016, 13, 20160659. [Google Scholar] [CrossRef]
- Gostic, K.M.; McGough, L.; Baskerville, E.B.; Abbott, S.; Joshi, K.; Tedijanto, C.; Kahn, R.; Niehus, R.; Hay, J.A.; De Salazar, P.M.; et al. Practical Considerations for Measuring the Effective Reproductive Number, Rt. PLoS Comput. Biol. 2020, 16, e1008409. [Google Scholar] [CrossRef]
- Frank, T.D. COVID-19 Epidemiology and Virus Dynamics, 1st ed.; Springer: Cham, Switzerland, 2022; pp. 1–355. [Google Scholar]
- van den Driessche, P.; Watmough, J. Reproduction Numbers and Sub-Threshold Endemic Equilibria for Compartmental Models of Disease Transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef] [PubMed]
- Diekmann, O.; Heesterbeek, J.A.P.; Roberts, M.G. The Construction of Next-Generation Matrices for Compartmental Epidemic Models. J. R. Soc. Interface 2010, 7, 873–885. [Google Scholar] [CrossRef]
- Wiggers, S.L.; Pedersen, P. Structural Stability and Vibration; Springer Tracts in Mechanical Engineering; Springer International Publishing: Cham, Switzerland, 2018; ISBN 978-3-319-72720-2. [Google Scholar]
- Keeling, M.J.; Rohani, P. Modeling Infectious Diseases in Humans and Animals, 1st ed.; Princeton University Press: Princeton, NJ, USA, 2008; pp. 1–366. [Google Scholar]
- Diekmann, O.; Heesterbeek, H.; Britton, T. Mathematical Tools for Understanding Infectious Disease Dynamics, 1st ed.; Princeton University Press: Princeton, NJ, USA, 2013; pp. 1–520. [Google Scholar]
- Arenas, A.; Cota, W.; Gómez-Gardeñes, J.; Gómez, S.; Granell, C.; Matamalas, J.T.; Soriano-Paños, D.; Steinegger, B. Derivation of the Effective Reproduction Number for COVID-19 in Relation to Mobility Restrictions and Confinement. medRxiv 2020, 1–24. [Google Scholar] [CrossRef]
- Giordano, G.; Blanchini, F.; Bruno, R.; Colaneri, P.; Di Filippo, A.; Di Matteo, A.; Colaneri, M. Modelling the COVID-19 Epidemic and Implementation of Population-Wide Interventions in Italy. Nat. Med. 2020, 26, 855–860. [Google Scholar] [CrossRef]
- Marín-Sánchez, O.; Pesantes-Grados, P.; Pérez-Timaná, L.; Marín-Machuca, O.; Sánchez-Llatas, C.J.; Chacón, R.D. Comparative Epidemiological Assessment of Monkeypox Infections on a Global and Continental Scale Using Logistic and Gompertz Mathematical Models. Vaccines 2023, 11, 1765. [Google Scholar] [CrossRef] [PubMed]
- Singh, V.; Khan, S.A.; Yadav, S.K.; Akhter, Y. Modeling Global Monkeypox Infection Spread Data: A Comparative Study of Time Series Regression and Machine Learning Models. Curr. Microbiol. 2023, 81, 15. [Google Scholar] [CrossRef]
- Khan, A.; Sabbar, Y.; Din, A. Stochastic Modeling of the Monkeypox 2022 Epidemic with Cross-Infection Hypothesis in a Highly Disturbed Environment. Math. Biosci. Eng. 2022, 19, 13560–13581. [Google Scholar] [CrossRef] [PubMed]
- Jezek, Z.; Grab, B.; Dixon, H. Stochastic Model for Interhuman Spread of Monkeypox. Am. J. Epidemiol. 1987, 126, 1082–1092. [Google Scholar] [CrossRef]
- Brainard, J.; Hunter, P.R. Misinformation Making a Disease Outbreak Worse: Outcomes Compared for Influenza, Monkeypox, and Norovirus. Simulation 2020, 96, 365–374. [Google Scholar] [CrossRef]
- Van Dijck, C.; Hens, N.; Kenyon, C.; Tsoumanis, A. The Roles of Unrecognized Mpox Cases, Contact Isolation and Vaccination in Determining Epidemic Size in Belgium: A Modeling Study. Clin. Infect. Dis. 2023, 76, e1421–e1423. [Google Scholar] [CrossRef]
- Liu, B.; Farid, S.; Ullah, S.; Altanji, M.; Nawaz, R.; Wondimagegnhu Teklu, S. Mathematical Assessment of Monkeypox Disease with the Impact of Vaccination Using a Fractional Epidemiological Modeling Approach. Sci. Rep. 2023, 13, 13550. [Google Scholar] [CrossRef]
- Okyere, S.; Ackora-Prah, J. Modeling and Analysis of Monkeypox Disease Using Fractional Derivatives. Results Eng. 2023, 17, 100786. [Google Scholar] [CrossRef]
- Li, S.; Samreen; Ullah, S.; AlQahtani, S.A.; Tag, S.M.; Akgül, A. Mathematical Assessment of Monkeypox with Asymptomatic Infection: Prediction and Optimal Control Analysis with Real Data Application. Results Phys. 2023, 51, 106726. [Google Scholar] [CrossRef]
- Chaturvedi, M.; Rodiah, I.; Kretzschmar, M.; Scholz, S.; Lange, B.; Karch, A.; Jaeger, V.K. Estimating the Relative Importance of Epidemiological and Behavioural Parameters for Epidemic Mpox Transmission: A Modelling Study. BMC Med. 2024, 22, 297. [Google Scholar] [CrossRef]
- Mizushima, D.; Shintani, Y.; Takano, M.; Shiojiri, D.; Ando, N.; Aoki, T.; Watanabe, K.; Nakamoto, T.; Gatanaga, H.; Oka, S. Prevalence of Asymptomatic Mpox among Men Who Have Sex with Men, Japan, January-March 2023. Emerg. Infect. Dis. 2023, 29, 1872–1876. [Google Scholar] [CrossRef] [PubMed]
- Reda, A.; El-Qushayri, A.E.; Shah, J. Asymptomatic Monkeypox Infection: A Call for Greater Control of Infection and Transmission. Lancet Microbe 2023, 4, e15–e16. [Google Scholar] [CrossRef]
- Karem, K.L.; Reynolds, M.; Hughes, C.; Braden, Z.; Nigam, P.; Crotty, S.; Glidewell, J.; Ahmed, R.; Amara, R.; Damon, I.K. Monkeypox-Induced Immunity and Failure of Childhood Smallpox Vaccination to Provide Complete Protection. Clin. Vaccine Immunol. 2007, 14, 1318–1327. [Google Scholar] [CrossRef] [PubMed]
- Clay, P.A.; Asher, J.M.; Carnes, N.; Copen, C.E.; Delaney, K.P.; Payne, D.C.; Pollock, E.D.; Mermin, J.; Nakazawa, Y.; Still, W.; et al. Modelling the Impact of Vaccination and Sexual Behaviour Adaptations on Mpox Cases in the USA during the 2022 Outbreak. Sex. Transm. Infect. 2024, 100, 70–76. [Google Scholar] [CrossRef] [PubMed]
- Xiridou, M.; Miura, F.; Adam, P.; Op de Coul, E.; de Wit, J.; Wallinga, J. The Fading of the Mpox Outbreak Among Men Who Have Sex With Men: A Mathematical Modelling Study. J. Infect. Dis. 2024, 230, e121–e130. [Google Scholar] [CrossRef]
- Augsburger, I.B.; Galanthay, G.K.; Tarosky, J.H.; Rychtář, J.; Taylor, D. Voluntary Vaccination May Not Stop Monkeypox Outbreak: A Game-Theoretic Model. PLoS Negl. Trop. Dis. 2022, 16, e0010970. [Google Scholar] [CrossRef]
- Das, H.K. Exploring the Dynamics of Monkeypox Transmission with Data-Driven Methods and a Deterministic Model. Front. Epidemiol. 2024, 4, 1334964. [Google Scholar] [CrossRef]
- Alshahrani, A.M. Cost-Benefit Analysis of Interventions to Mitigate the Monkeypox Virus. Int. J. Environ. Res. Public Health 2022, 19, 13789. [Google Scholar] [CrossRef]
- Bankuru, S.V.; Kossol, S.; Hou, W.; Mahmoudi, P.; Rychtář, J.; Taylor, D. A Game-Theoretic Model of Monkeypox to Assess Vaccination Strategies. PeerJ 2020, 8, e9272. [Google Scholar] [CrossRef]
- Reynolds, M.G.; Damon, I.K. Outbreaks of Human Monkeypox after Cessation of Smallpox Vaccination. Trends Microbiol. 2012, 20, 80–87. [Google Scholar] [CrossRef]
- Mungmunpuntipantip, R.; Wiwanitkit, V. Wanning Smallpox Vaccination, Decreased Population Immunity Rate and Increased Incidence of Monkeypox: Reappraisal on West African Situation. Int. J. Prev. Med. 2024, 14, 130. [Google Scholar] [CrossRef]
- Hébert-Dufresne, L.; Althouse, B.M.; Scarpino, S.V.; Allard, A. Beyond R0: Heterogeneity in Secondary Infections and Probabilistic Epidemic Forecasting. J. R. Soc. Interface 2020, 17, 20200393. [Google Scholar] [CrossRef] [PubMed]
- Rochman, N.; Wolf, Y.I.; Koonin, E.V. Evolution of Human Respiratory Virus Epidemics. F1000Research 2021, 10, 447. [Google Scholar] [CrossRef] [PubMed]
- Blanquart, F.; Grabowski, M.K.; Herbeck, J.; Nalugoda, F.; Serwadda, D.; Eller, M.A.; Robb, M.L.; Gray, R.; Kigozi, G.; Laeyendecker, O.; et al. A Transmission-Virulence Evolutionary Trade-off Explains Attenuation of HIV-1 in Uganda. eLife 2016, 5, e20492. [Google Scholar] [CrossRef] [PubMed]
- Kawashima, K.; Matsumoto, T.; Akashi, H. Disease Outbreaks: Critical Biological Factors and Control Strategies. In Urban Resilience; Springer: Cham, Switzerland, 2016; pp. 173–204. [Google Scholar] [CrossRef]
- Crenshaw, E.G.; Onnela, J.-P. Modeling the 2022 Mpox Outbreak with a Mechanistic Network Model. arXiv 2025, arXiv:2505.05534. [Google Scholar] [CrossRef]


| Parameter | Description | Range (Unit) | Reference |
|---|---|---|---|
| Recruitment rate | [30,31,32] | ||
| Transmission rate for symptomatic infected | [38]. Assumed | ||
| Transmission rate for asymptomatic infected | Assumed | ||
| Incubation rate | [28,33,36,38] | ||
| Probability to develop symptoms | Assumed | ||
| Isolation rate | Assumed | ||
| Recovery rate for symptomatic and asymptomatic | [36,38] | ||
| Recovery rate for isolated | Assumed | ||
| Vaccination rate | Assumed | ||
| Effectiveness | [36] | ||
| Rate of loss of natural immunity | [37] | ||
| Rate of loss of immunity from vaccination | [37] | ||
| Mortality rate | [32] | ||
| Lethality rate | [29,34,35] |
| Parameter Estimation | Geographic Region | ||||
|---|---|---|---|---|---|
| Parameter or Initial Condition | Range | World | Europe | South America | North America |
| Fitted Value (Initial Guess) | Fitted Value (Initial Guess) | Fitted Value (Initial Guess) | Fitted Value (Initial Guess) | ||
| 94,854.1383 (160,000) | 26,132.5978 (25,000) | 16,330.4531 (25,000) | 103,602.999 (25,000) | ||
| - | 27 (27) | 1 (1) | 2 (2) | 103 (103) | |
| 7.73970439 (34) | 22.6202113 (30) | 54.2253827 (30) | 189.385924 (15) | ||
| 1.67953368 (1.2) | 2.04177890 (1.2) | 1.76850088 (1.2) | 0.91634522 (0.9) | ||
| 0.17020184 (0.8) | 0.39950298 (0.8) | 0.37955379 (0.8) | 0.66563355 (0.8) | ||
| 0.02295726 (0.08) | 0.04005441 (0.08) | 0.04000883 (0.08) | 0.04191390 (0.05) | ||
| 0.96584613 (0.46) | 0.94874630 (0.46) | 0.94346047 (0.46) | 0.44090917 (0.46) | ||
| 0.00717407 (0.006) | 0.04094240 (0.03) | 0.04788072 (0.03) | 0.00466125 (0.006) | ||
| 0.25943508 (0.06) | 0.21399404 (0.06) | 0.33142887 (0.06) | 0.14785275 (0.06) | ||
| 0.00494816 (0.005) | 0.00469751 (0.005) | 0.00455631 (0.005) | 0.00494974 (0.005) | ||
| (0.003) | (0.003) | (0.003) | (0.003) | ||
| (0.00002) | (0.000005) | (0.000005) | ) | ||
| 0.00237251 (0.00004) | (0.00004) | ) | |||
| 0.93219423 (0.7) | 0.91519545 (0.6) | 0.94531585 (0.6) | 0.61892306 (0.6) | ||
| Geographic Region | R2 | A.I.C. | B.I.C. |
|---|---|---|---|
| World | 0.9996 | 4824.20197 | 4894.40013 |
| Europe | 0.9952 | 4666.83938 | 4736.73918 |
| South America | 0.9973 | 4118.41144 | 4187.01198 |
| North America | 0.9989 | 4110.58893 | 4179.18947 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pesantes-Grados, P.; Escalante-Ccoyllo, N.; Marín-Machuca, O.; Zambrano-Cabanillas, A.W.; Ango-Aguilar, H.; Marín-Sánchez, O.; Chacón, R.D. A Compartmental Mathematical Model to Assess the Impact of Vaccination, Isolation, and Key Epidemiological Parameters on Mpox Control. Med. Sci. 2025, 13, 226. https://doi.org/10.3390/medsci13040226
Pesantes-Grados P, Escalante-Ccoyllo N, Marín-Machuca O, Zambrano-Cabanillas AW, Ango-Aguilar H, Marín-Sánchez O, Chacón RD. A Compartmental Mathematical Model to Assess the Impact of Vaccination, Isolation, and Key Epidemiological Parameters on Mpox Control. Medical Sciences. 2025; 13(4):226. https://doi.org/10.3390/medsci13040226
Chicago/Turabian StylePesantes-Grados, Pedro, Nahía Escalante-Ccoyllo, Olegario Marín-Machuca, Abel Walter Zambrano-Cabanillas, Homero Ango-Aguilar, Obert Marín-Sánchez, and Ruy D. Chacón. 2025. "A Compartmental Mathematical Model to Assess the Impact of Vaccination, Isolation, and Key Epidemiological Parameters on Mpox Control" Medical Sciences 13, no. 4: 226. https://doi.org/10.3390/medsci13040226
APA StylePesantes-Grados, P., Escalante-Ccoyllo, N., Marín-Machuca, O., Zambrano-Cabanillas, A. W., Ango-Aguilar, H., Marín-Sánchez, O., & Chacón, R. D. (2025). A Compartmental Mathematical Model to Assess the Impact of Vaccination, Isolation, and Key Epidemiological Parameters on Mpox Control. Medical Sciences, 13(4), 226. https://doi.org/10.3390/medsci13040226









