An Evaluation of Catchment Transit Time Model Parameters: A Comparative Study between Two Stable Isotopes of Water
Abstract
1. Introduction
- To evaluate the distribution of δ18O- and δ2H-based behavioral parameters from which the MTT was extracted.
- To determine how early in the model time-step δ18O- and δ2H-based behavioral solutions are achieved.
- To assess the agreement (or lack thereof) of the absolute MTT values as retrieved from the δ18O and δ2H model kernels and to infer if they lead to similar conclusions about the nested catchment system.
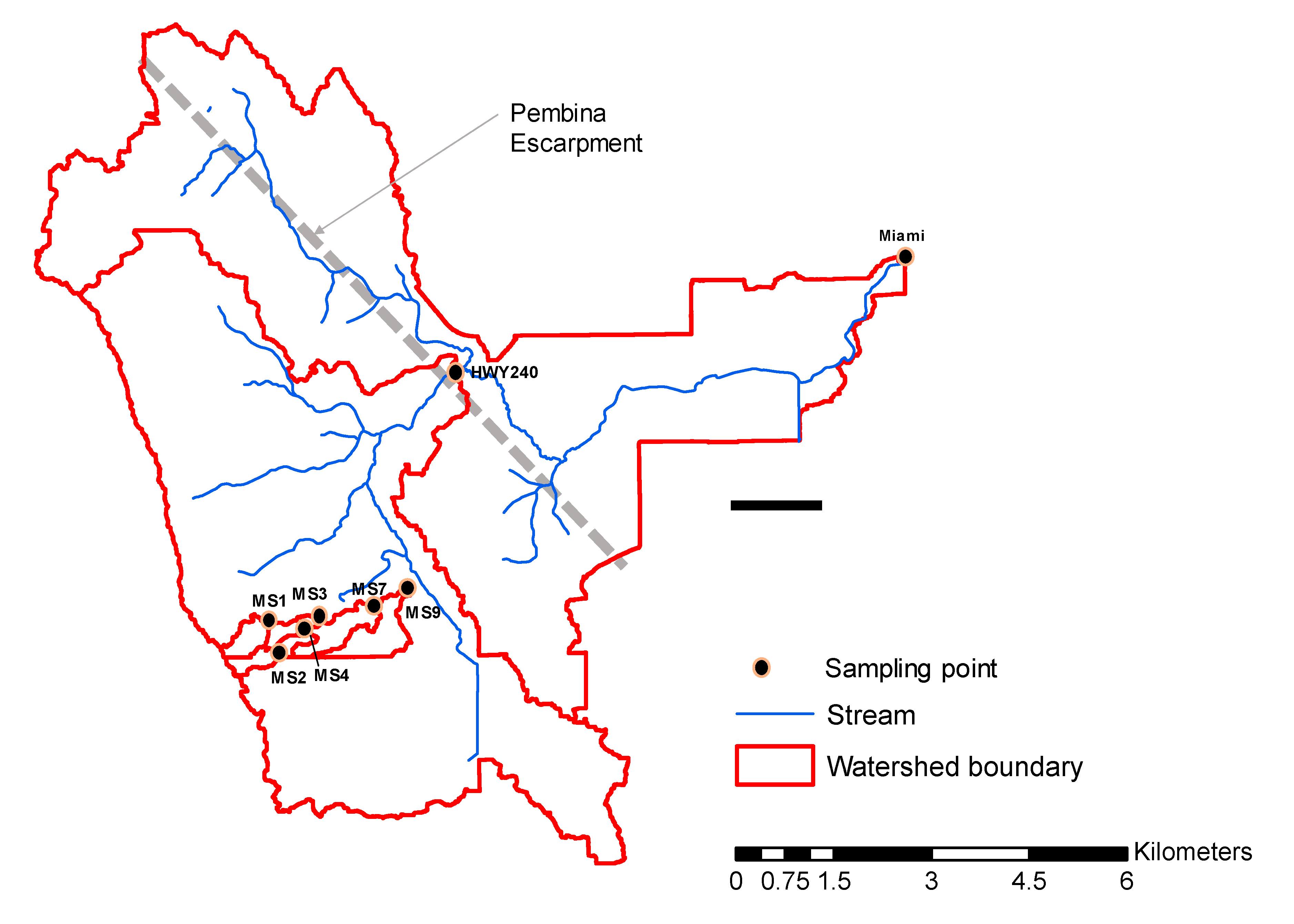
2. Materials and Methods
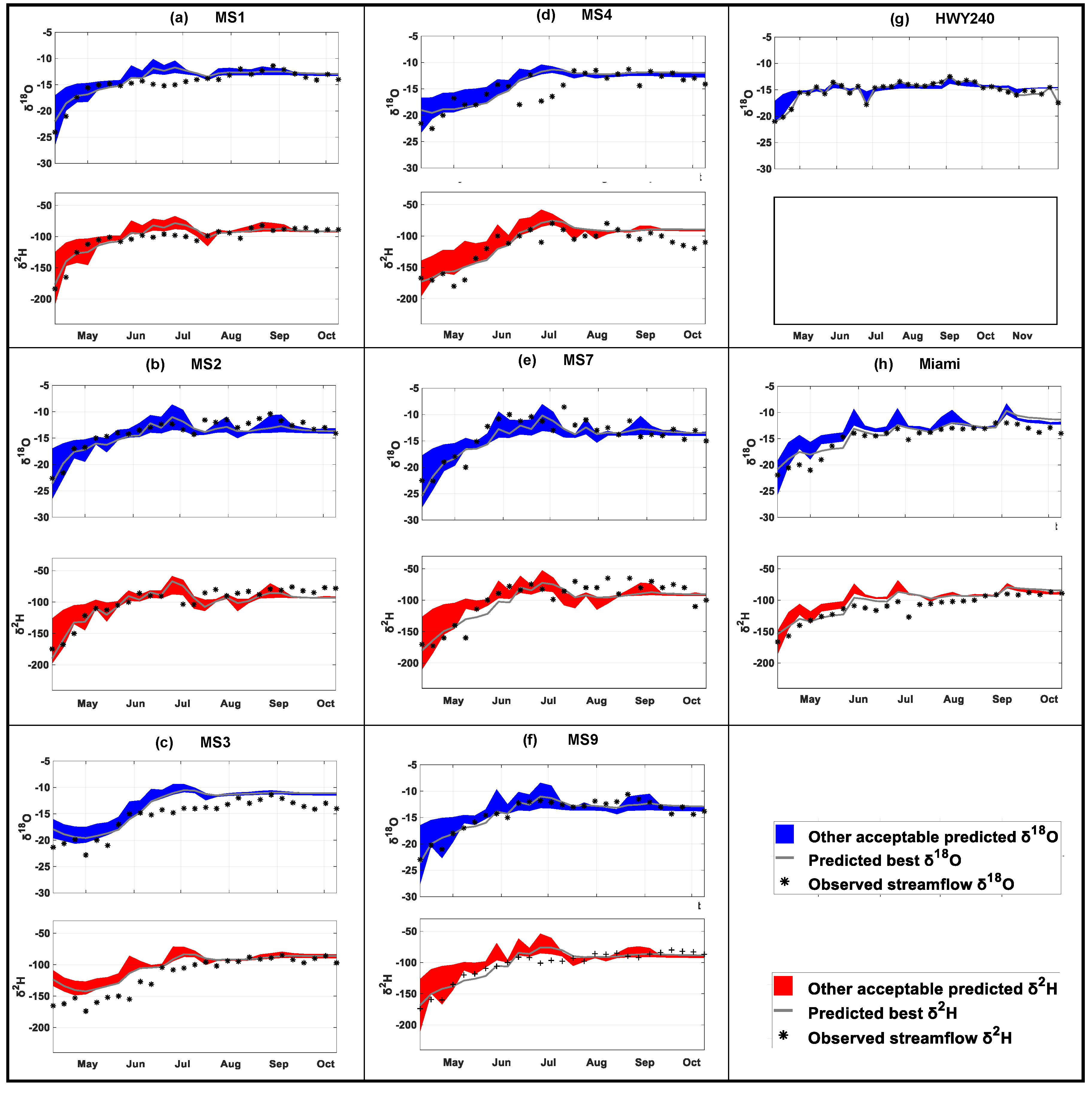
3. Results
4. Discussion and Implications
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McDonnell, J.J.; McGuire, K.; Aggarwal, P.; Beven, K.J.; Biondi, D.; Destouni, G.; Dunn, S.; James, A.; Kirchner, J.; Kraft, P.; et al. How old is streamwater? Open questions in catchment transit time conceptualization, modelling and analysis. Hydrol. Process. 2010, 24, 1745–1754. [Google Scholar] [CrossRef]
- Wolock, D.M.; Fan, J.; Lawrence, G.B. Effects of basin size on low-flow stream chemistry and subsurface contact time in the Neversink River Watershed, New York. Hydrol. Process. 1997, 11, 1273–1286. [Google Scholar] [CrossRef]
- Kendall, C.; McDonnell, J.J. Isotope Tracers in Catchment Hydrology; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- McGuire, K.J.; McDonnell, J.J. A review and evaluation of catchment transit time modeling. J. Hydrol. 2006, 330, 543–563. [Google Scholar] [CrossRef]
- Pacheco, F.A.L.; Van der Weijden, C.H. Integrating topography, hydrology and rock structure in weathering rate models of spring watersheds. J. Hydrol. 2012, 428, 32–50. [Google Scholar] [CrossRef]
- Frisbee, M.D.; Wilson, J.L.; Gomez-Velez, J.D.; Phillips, F.M.; Campbell, A.R. Are we missing the tail (and the tale) of residence time distributions in watersheds? Geophys. Res. Lett. 2013, 40, 4633–4637. [Google Scholar] [CrossRef]
- Rademacher, L.K.; Clark, J.F.; Clow, D.W.; Hudson, G.B. Old groundwater influence on stream hydrochemistry and catchment response times in a small Sierra Nevada catchment: Sagehen Creek, California. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Singleton, M.J.; Moran, J.E. Dissolved noble gas and isotopic tracers reveal vulnerability of groundwater in a small, high-elevation catchment to predicted climate changes. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Manning, A.H.; Clark, J.F.; Diaz, S.H.; Rademacher, L.K.; Earman, S.; Plummer, L.N. Evolution of groundwater age in a mountain watershed over a period of thirteen years. J. Hydrol. 2012, 460, 13–28. [Google Scholar] [CrossRef]
- Kirchner, J.W.; Feng, X.H.; Neal, C. Fractal stream chemistry and its implications for contaminant transport in catchments. Nature 2000, 403, 524–527. [Google Scholar] [CrossRef]
- Jasechko, S.; Wassenaar, L.I.; Mayer, B. Isotopic evidence for widespread cold-season-biased groundwater recharge and young streamflow across central Canada. Hydrol. Process. 2017, 31, 2196–2209. [Google Scholar] [CrossRef]
- Benettin, P.; Rinaldo, A.; Botter, G. Tracking residence times in hydrological systems: Forward and backward formulations. Hydrol. Process. 2015, 29, 5203–5213. [Google Scholar] [CrossRef]
- Harman, C.J. Time-variable transit time distributions and transport: Theory and application to storage-dependent transport of chloride in a watershed. Water Resour. Res. 2015, 51, 1–30. [Google Scholar] [CrossRef]
- Brooks, J.R.; Barnard, H.R.; Coulombe, R.; McDonnell, J.J. Ecohydrologic separation of water between trees and streams in a Mediterranean climate. Nat. Geosci. 2010, 3, 100–104. [Google Scholar] [CrossRef]
- Klaus, J.; McDonnell, J.J. Hydrograph separation using stable isotopes: Review and evaluation. J. Hydrol. 2013, 505, 47–64. [Google Scholar] [CrossRef]
- Pinder, G.F.; Jones, J.F. Determination of the groundwater component of peak discharge from the chemistry of total runoff. J. Water Resour. Res. 1969, 5, 438–445. [Google Scholar] [CrossRef]
- Kennedy, V.C. Silica variation in stream water with time and discharge. In Non-Equilibrium Systems in Natural Water Chemistry; Advances in Chemistry Series, Volume 106; Hem, J.D., Ed.; American Chemical Society: Washington, DC, USA, 1971; pp. 106–130. [Google Scholar]
- Kirchner, J.W.; Tetzlaff, D.; Soulsby, C. Comparing chloride and water isotopes as hydrological tracers in two Scottish catchments. Hydrol. Process. 2010, 24, 1631–1645. [Google Scholar] [CrossRef]
- Svensson, T.; Lovett, G.M.; Likens, G.E. Is chloride a conservative ion in forest ecosystems? Biogeochemistry 2012, 107, 125–134. [Google Scholar] [CrossRef]
- Jenkins, A.; Ferrier, R.C.; Harriman, R.; Ogunkkoya, Y.O. A case study in catchment hydrochemistry: Conflicting interpretations from hydrological and chemical observations. J. Hydrol. Process. 1994, 8, 335–349. [Google Scholar] [CrossRef]
- Iqbal, M.Z. Application of environmental isotopes in storm discharge analysis of two contrasting stream channels in a Watershed. J. Water Resour. 1998, 32, 2959–2968. [Google Scholar] [CrossRef]
- Brown, V.A.; McDonnell, J.J.; Burns, D.A.; Kendall, C. The role of event water, a rapid shallow flow component, and catchment size in summer stormflow. J. Hydrol. 1999, 217, 171–190. [Google Scholar] [CrossRef]
- Maloszewski, P.; Rauert, W.; Stichler, W.; Herrmann, A. Application of flow models in an alpine catchment-area using tritium and deuterium data. J. Hydrol. 1983, 66, 319–330. [Google Scholar] [CrossRef]
- Stockinger, M.P.; Bogena, H.R.; Lucke, A.; Diekkruger, B.; Weiler, M.; Vereecken, H. Seasonal soil moisture patterns: Controlling transit time distributions in a forested headwater catchment. Water Resour. Res. 2014, 50, 5270–5289. [Google Scholar] [CrossRef]
- Timbe, E.; Windhorst, D.; Crespo, P.; Frede, H.G.; Feyen, J.; Breuer, L. Understanding uncertainties when inferring mean transit times of water trough tracer-based lumped-parameter models in Andean tropical montane cloud forest catchments. Hydrol. Earth Syst. Sci. 2014, 18, 1503–1523. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models I: A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Tiessen, K.H.D.; Elliott, J.A.; Yarotski, J.; Lobb, D.A.; Flaten, D.N.; Glozier, N.E. Conventional and Conservation Tillage: Influence on Seasonal Runoff, Sediment, and Nutrient Losses in the Canadian Prairies. J. Environ. Qual. 2010, 39, 964–980. [Google Scholar] [CrossRef] [PubMed]
- Environment Canada. Canadian Climate Normals 1981–2014 Station Data. 2014. Available online: http://climate.weather.gc.ca/climate_normals/results_1981_2010_e.html?searchType=stnProv&lstProvince=MB&txtCentralLatMin=0&txtCentralLatSec=0&txtCentralLongMin=0&txtCentralLongSec=0&stnID=3582&dispBack=0 (accessed on 7 March 2019).
- Craig, H. Standard for reporting concentrations of deuterium and oxygen-18 in natural waters. Science 1961, 133. [Google Scholar] [CrossRef] [PubMed]
- Hrachowitz, M.; Soulsby, C.; Tetzlaff, D.; Malcolm, I.A.; Schoups, G. Gamma distribution models for transit time estimation in catchments: Physical interpretation of parameters and implications for time-variant transit time assessment. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- McGuire, K.J.; DeWalle, D.R.; Gburek, W.J. Evaluation of mean residence time in subsurface waters using oxygen-18 fluctuations during drought conditions in the mid-Appalachians. J. Hydrol. 2002, 261, 132–149. [Google Scholar] [CrossRef]
- Rodgers, P.; Soulsby, C.; Waldron, S.; Tetzlaff, D. Using stable isotope tracers to assess hydrological flow paths, residence times and landscape influences in a nested mesoscale catchment. Hydrol. Earth Syst. Sci. 2005, 9, 139–155. [Google Scholar] [CrossRef]
- Hrachowitz, M.; Soulsby, C.; Tetzlaff, D.; Malcolm, I.A. Sensitivity of mean transit time estimates to model conditioning and data availability. Hydrol. Process. 2011, 25, 980–990. [Google Scholar] [CrossRef]
- Beven, K.; Freer, J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology. J. Hydrol. 2001, 249, 11–29. [Google Scholar] [CrossRef]
- Bansah, S.; Ali, G. Streamwater ages in nested, seasonally cold Canadian watersheds. Hydrol. Process. 2019, 33, 495–511. [Google Scholar] [CrossRef]
- Cappa, D.C.; Hendricks, B.M.; DePaolo, D.J.; Cohen, R.C. Isotope fractionation of water during evaporation. Geophys. Res. 2003, 108, D16. [Google Scholar] [CrossRef]
- Bansah, S.; Ali, G. Evaluating the effects of tracer choice and end-member definitions on hydrograph separation results across nested seasonally cold watersheds. Water Resour. Res. 2017, 53, 8851–8871. [Google Scholar] [CrossRef]
- Fang, X.; Minke, A.; Pomeroy, J.; Brown, T.; Westbrook, C.; Guo, X.; Guangul, S. A Review of Canadian Priaire Hydrology: Principles, Modelling and Response to Land Use and Drainage Change; Center for Hydrology Report #2, Version2; University of Saskatchewan: Saskatoon, SK, Canada, 2007. [Google Scholar]
- Bansah, S.; Ali, G.; Tang, W. Validation of dominant flow processes in a Canadian prairie watershed using hydrometric and isotopic approaches. Manuscript in preparation.
- McDonnell, J.J.; Beven, K. Debates—The future of hydrological sciences: A (common) path forward? A call to action aimed at understanding velocities, celerities, and residence time distributions of the headwater hydrograph. Water Resour. Res. 2014, 50, 5342–5350. [Google Scholar] [CrossRef]
- Dansgaard, W. Stable isotopes in precipitation. Tellus 1964, 16, 436–468. [Google Scholar] [CrossRef]
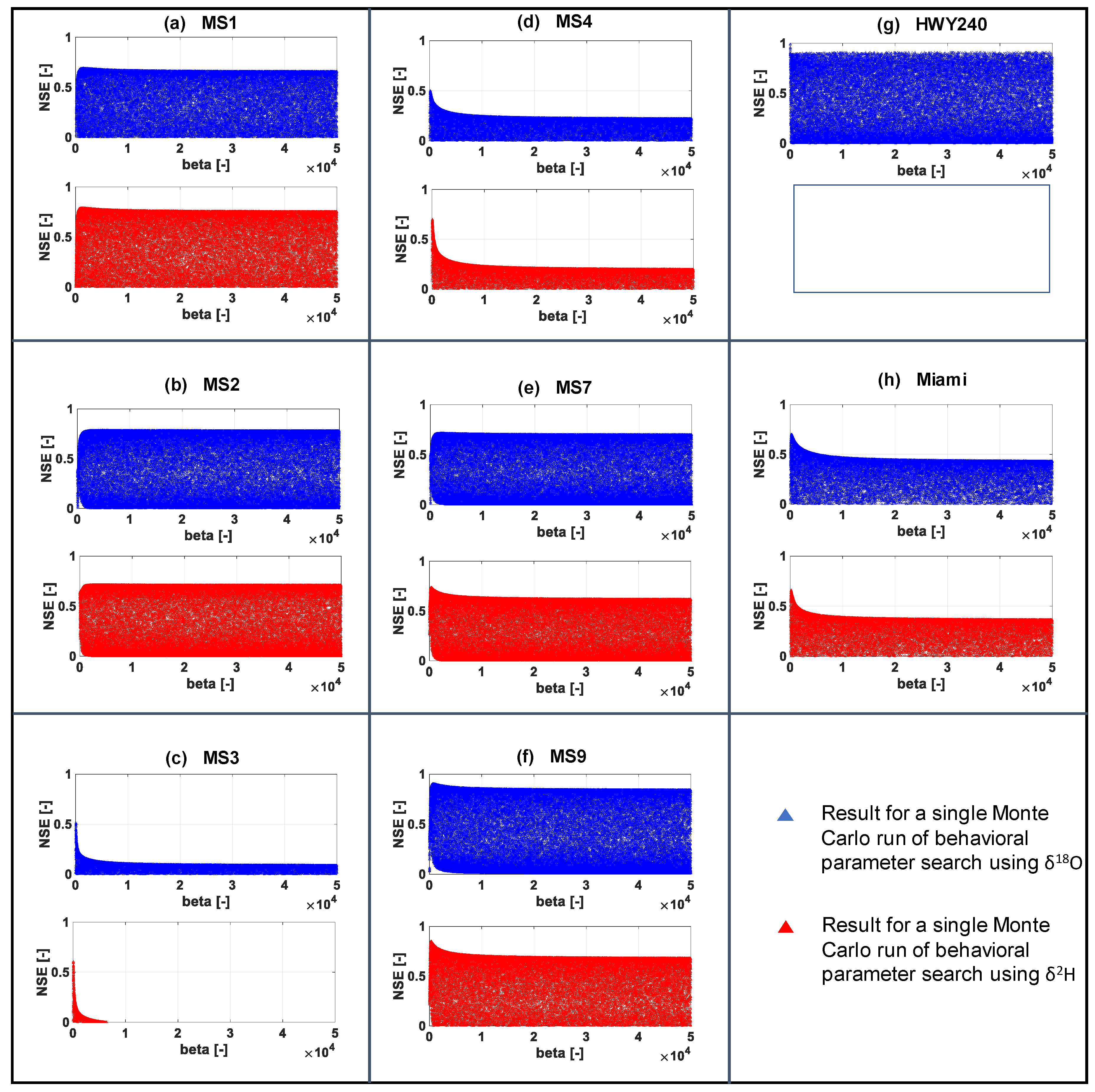
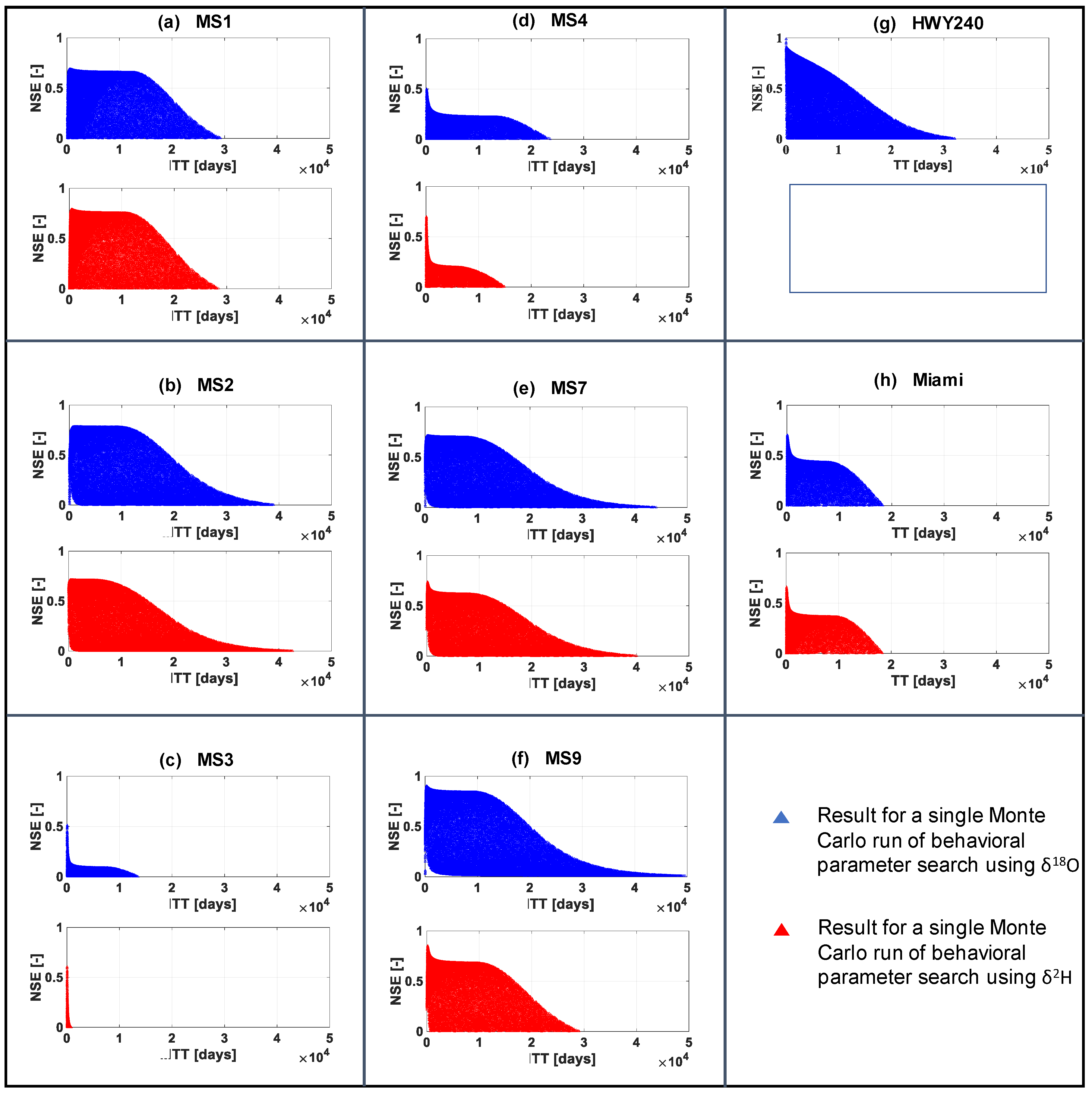
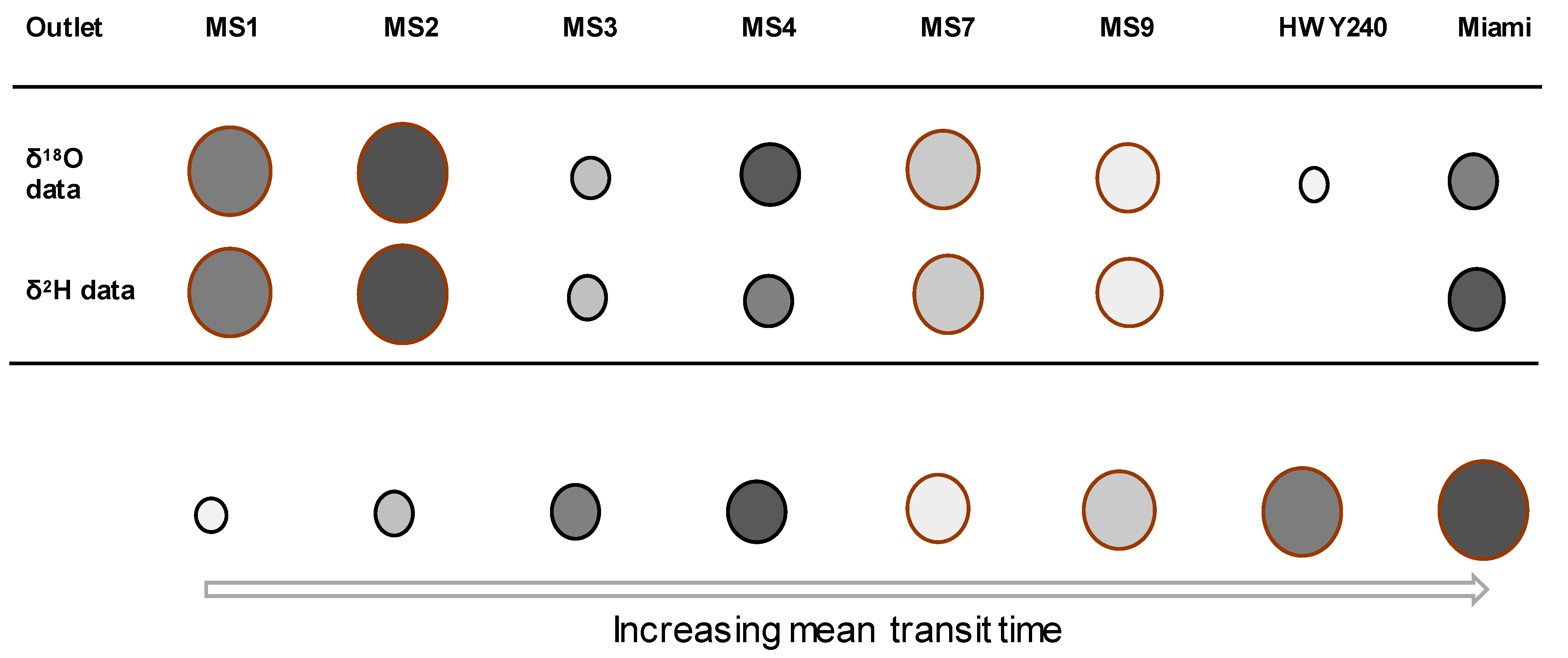
| Variable | Tracer | MS1 | MS2 | MS3 | MS4 | MS7 | MS9 | HWY240 | Miami |
|---|---|---|---|---|---|---|---|---|---|
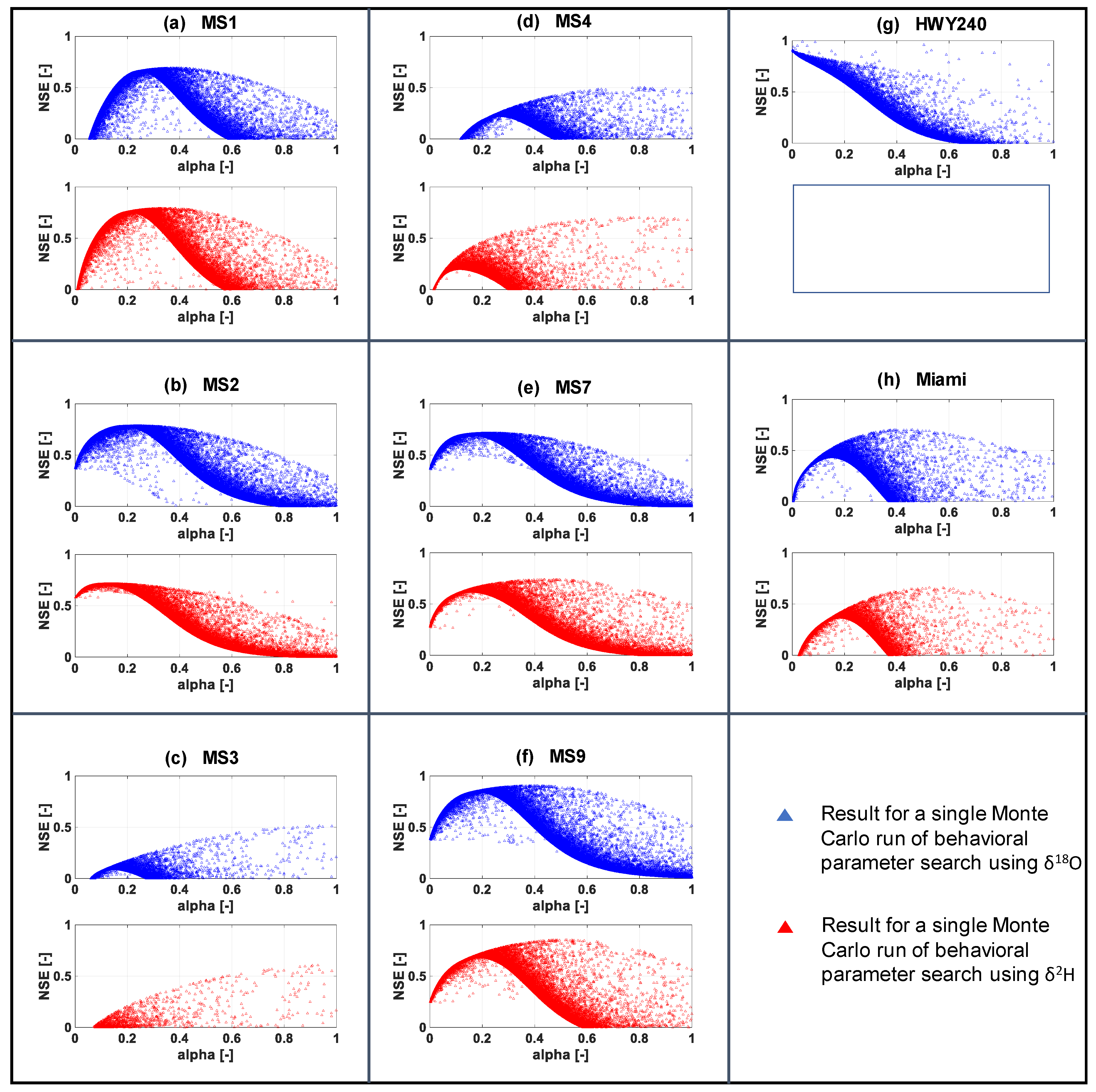
| Total number of behavioral outcomes | δ18O-based | 17,467 | 24,796 | 99 | 515 | 23,267 | 26,199 | 18,515 | 12,210 |
| δ2H-based | 20,618 | 21,696 | 96 | 755 | 22,221 | 21,992 | 0 | 8497 | |
| Percentage of behavioral outcomes | δ18O-based | 35 | 50 | <1 | 1 | 47 | 52 | 37 | 24 |
| δ2H-based | 41 | 43 | <1 | 2 | 44 | 44 | 0 | 17 | |
| Best NSE score (-) | δ18O-based | 0.69 | 0.79 | 0.51 | 0.50 | 0.72 | 0.90 | 0.99 | 0.70 |
| δ2H-based | 0.79 | 0.71 | 0.61 | 0.70 | 0.74 | 0.85 | NB | 0.66 | |
| Alpha value corresponding to the best NSE score (-) | δ18O-based | 0.39 | 0.23 | 0.93 | 0.82 | 0.24 | 0.39 | 0.04 | 0.46 |
| δ2H-based | 0.32 | 0.14 | 0.93 | 0.78 | 0.44 | 0.52 | NB | 0.52 | |
| Count of Monte Carlo run where alpha best was observed | δ18O-based | 43,310 | 19,915 | 47,134 | 43,865 | 30,875 | 23,107 | 33,308 | 40,627 |
| δ2H-based | 30,307 | 48,520 | 47,220 | 49,490 | 17,550 | 15,369 | NB | 37,956 | |
| Beta value corresponding to the best NSE score (-) | δ18O-based | 1409 | 4747 | 66 | 140 | 2163 | 745 | 2 | 207 |
| δ2H-based | 1477 | 3701 | 50 | 75 | 363 | 300 | NB | 182 | |
| Time-step of Monte Carlo run where beta best was observed | δ18O-based | 43,310 | 19,915 | 47,134 | 43,865 | 30,875 | 23,107 | 33,308 | 40,627 |
| δ2H-based | 30,307 | 48,520 | 47,220 | 49,490 | 17,550 | 15,369 | NB | 37,956 | |
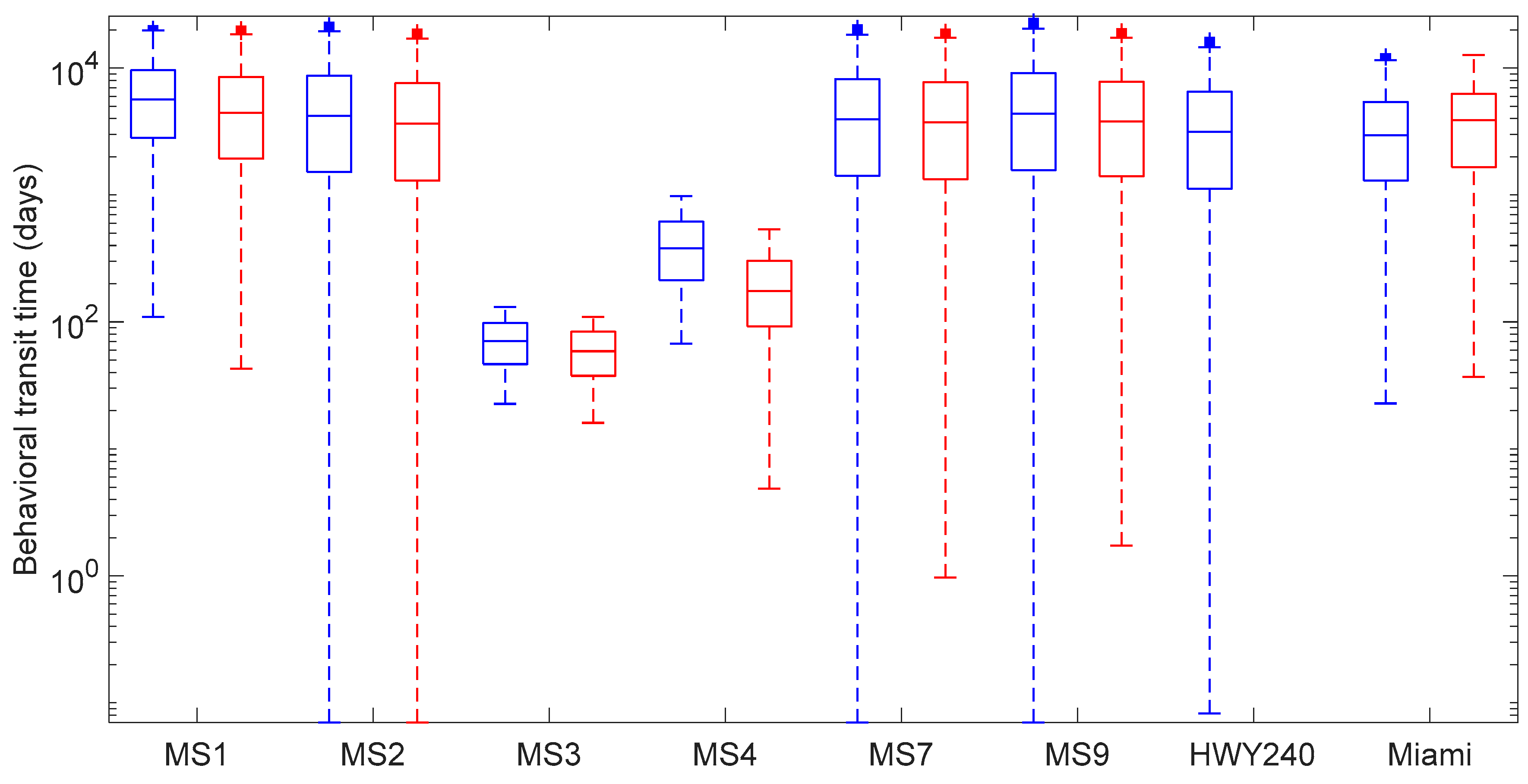
| Mean transit time (days) | δ18O-based | 549 [± 63] | 1155 [± 18] | 62 [± 3] | 115 [± 3] | 509 [± 34] | 287 [± 10] | <1 [± 0.1] | 95 [± 7] |
| δ2H-based | 482 [± 53] | 507 [± 33] | 47 [± 1] | 58 [± 1] | 158 [± 2] | 157 [± 15] | NB | 95 [± 4] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bansah, S.; Andam-Akorful, S.A.; Quaye-Ballard, J.; Wilson, M.C.; Gidigasu, S.S.; Anornu, G.K. An Evaluation of Catchment Transit Time Model Parameters: A Comparative Study between Two Stable Isotopes of Water. Geosciences 2019, 9, 318. https://doi.org/10.3390/geosciences9070318
Bansah S, Andam-Akorful SA, Quaye-Ballard J, Wilson MC, Gidigasu SS, Anornu GK. An Evaluation of Catchment Transit Time Model Parameters: A Comparative Study between Two Stable Isotopes of Water. Geosciences. 2019; 9(7):318. https://doi.org/10.3390/geosciences9070318
Chicago/Turabian StyleBansah, Samuel, Samuel Ato Andam-Akorful, Jonathan Quaye-Ballard, Matthew Coffie Wilson, Solomon Senyo Gidigasu, and Geophrey K. Anornu. 2019. "An Evaluation of Catchment Transit Time Model Parameters: A Comparative Study between Two Stable Isotopes of Water" Geosciences 9, no. 7: 318. https://doi.org/10.3390/geosciences9070318
APA StyleBansah, S., Andam-Akorful, S. A., Quaye-Ballard, J., Wilson, M. C., Gidigasu, S. S., & Anornu, G. K. (2019). An Evaluation of Catchment Transit Time Model Parameters: A Comparative Study between Two Stable Isotopes of Water. Geosciences, 9(7), 318. https://doi.org/10.3390/geosciences9070318





