Earthquake-Induced Landslide Risk Assessment: An Example from Sakhalin Island, Russia
Abstract
1. Introduction
2. Materials and Methods
2.1. Fully Probabilistic Risk Assessment Technique
2.2. Causative Factors of Studied Area
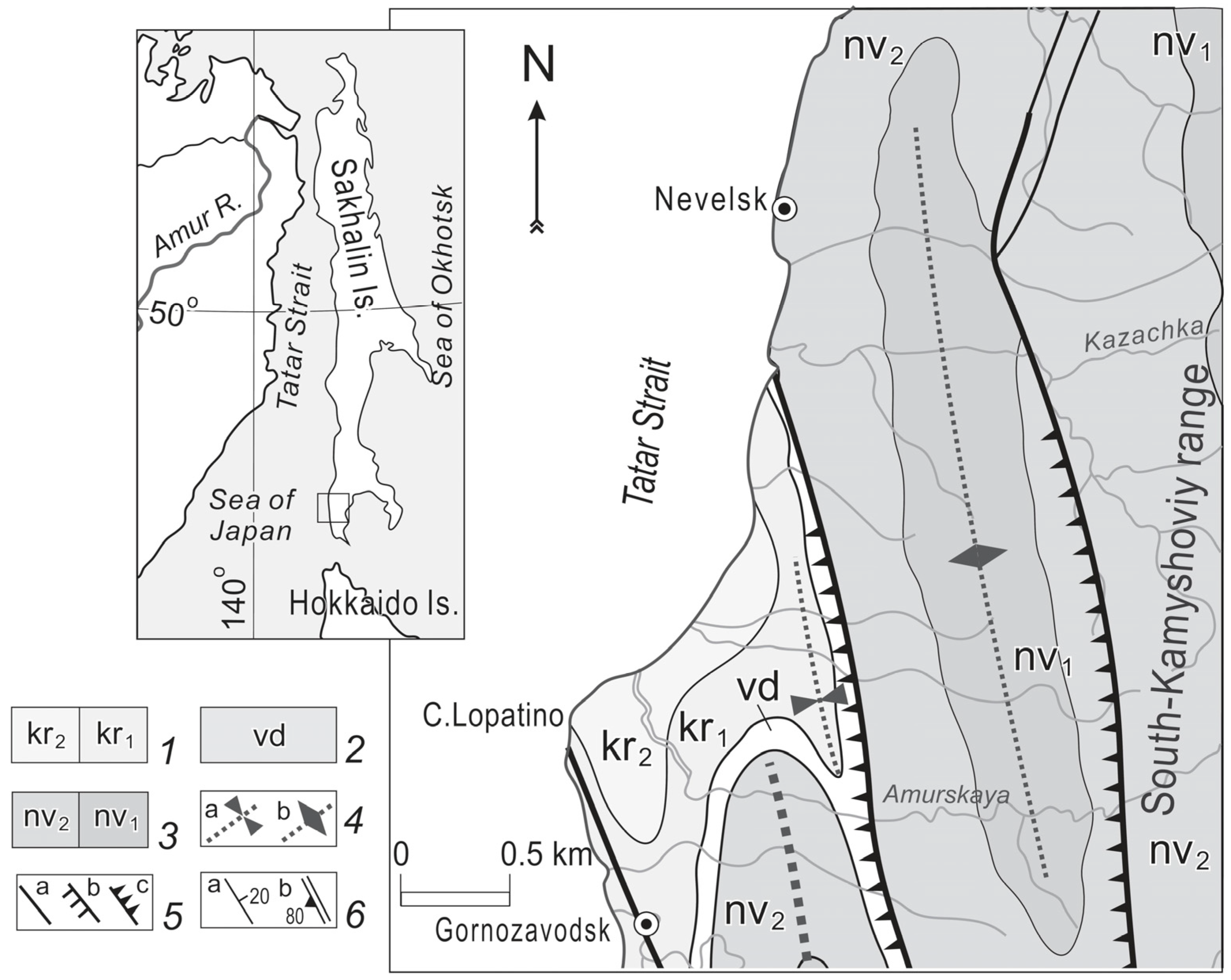
2.2.1. Geology
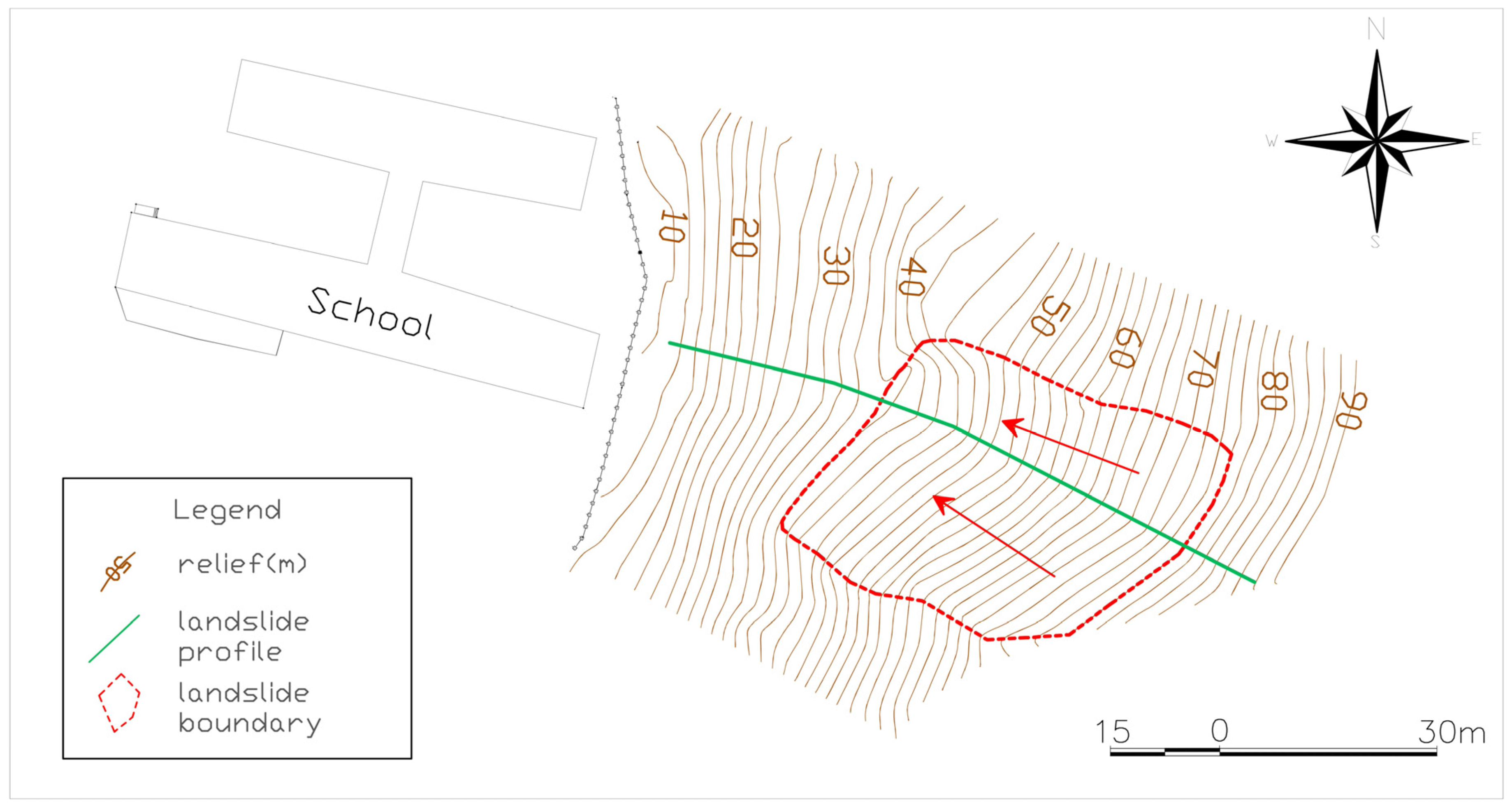
2.2.2. Geomorphology
2.2.3. Climatic Settings
2.2.4. Soil Moisture Conditions
- Slightly wet—Shallow invasion of the water into the soil mass. Dry soil conditions are typical for drought periods and for periods with stable snow cover. The overall period duration is about five months;
- Moist—Invasion of the water into the soil mass to a 1 m depth. The overall period duration is three months;
- Water saturated—Soil mass is waterlogged to a ~2 m depth. This model is typical for the rain precipitation and rapid snow melting coincidence period and for cyclone/typhoon occurrences. The overall period duration is about four months.
2.3. Materials
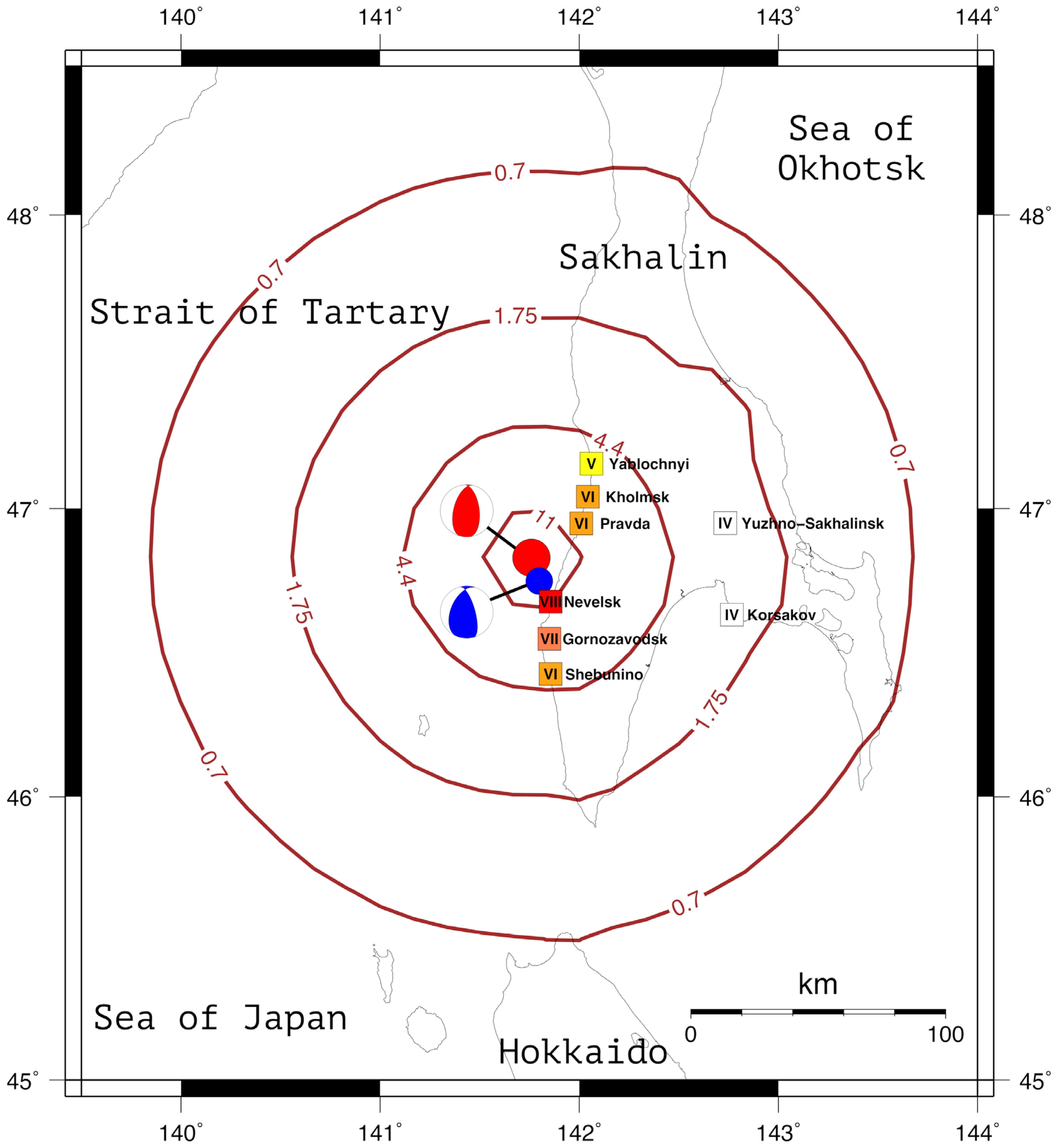
2.3.1. Ground Motion Scenarios
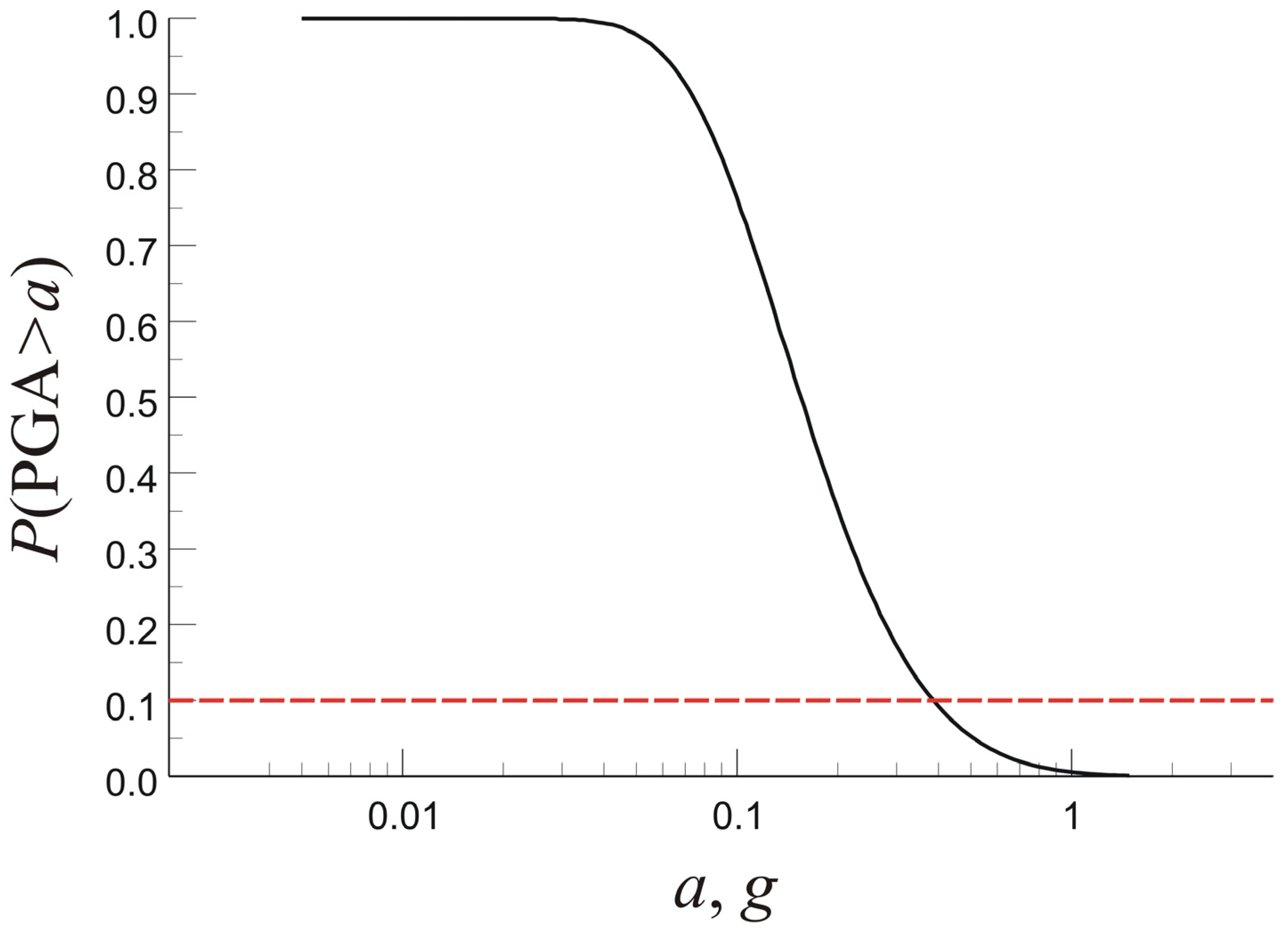
2.3.2. Probability of Landslide Triggering
2.3.3. Geomechanical Slope Models and Logic Tree
2.3.4. Vulnerability Assessment
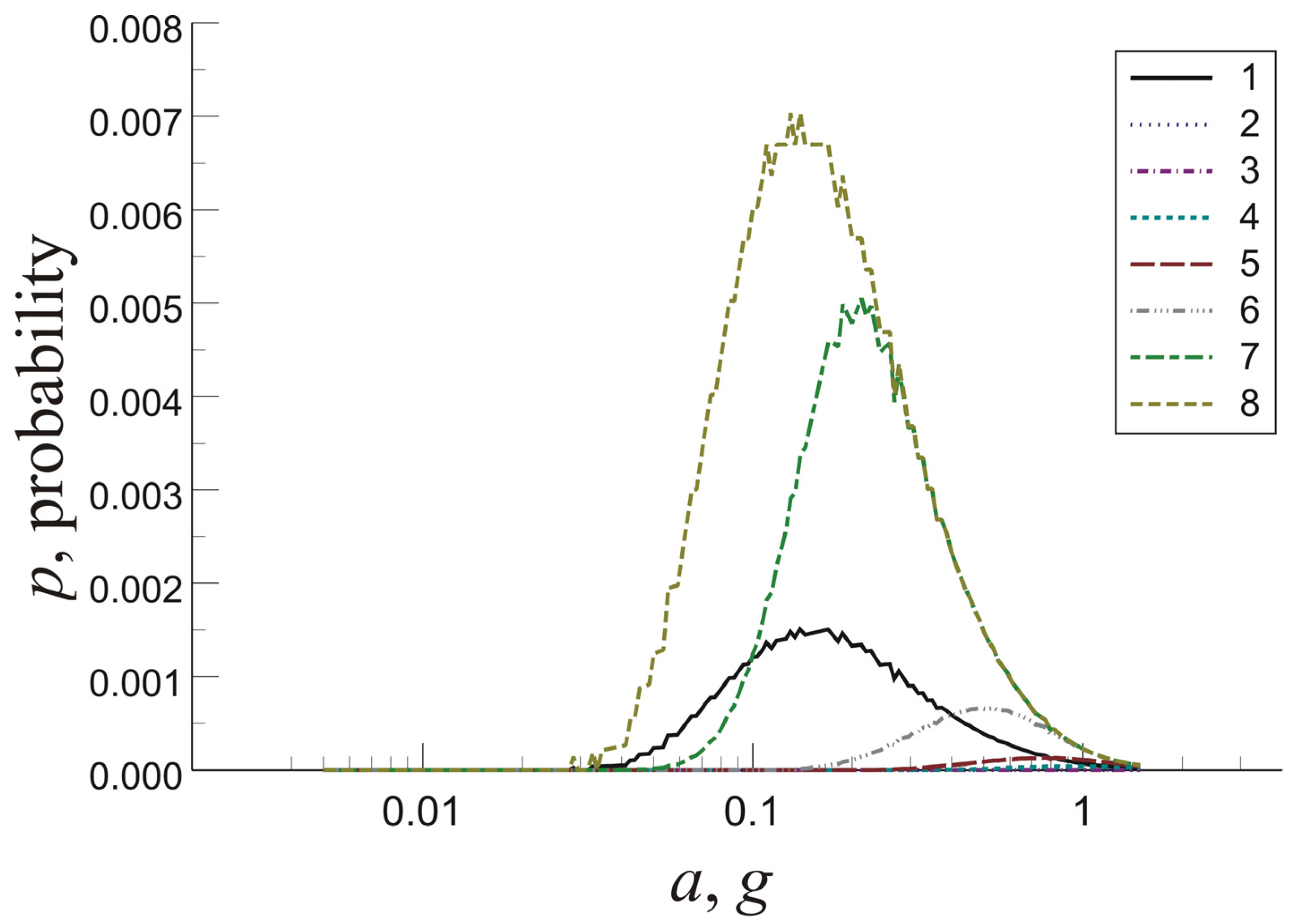
3. Results and Discussion
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Mohammad, E.; Babak, O.; Mahdi, M.; Mohammad, A.N.; Ali, A.A. Sensitivity analysis in seismic loss estimation of urban infrastructures. Geomat. Nat. Hazards Risk 2018, 9, 624–644. [Google Scholar]
- Martino, S.; Battaglia, S.; Delgado, J.; Esposito, C.; Martini, G.; Missori, C. Probabilistic Approach to Provide Scenarios of Earthquake-Induced Slope Failures (PARSIFAL) Applied to the Alcoy Basin (South Spain). Geosciences 2018, 8, 57. [Google Scholar] [CrossRef]
- Forte, G.; Fabbrocino, S.; de Magistris, F.S.; Silvestri, F.; Fabbrocino, G. Earthquake Triggered Landslides: The Case Study of a Roadway Network in Molise Region (Italy). In Engineering Geology for Society and Territory; Springer: Cham, Switzerland, 2015; Volume 2, pp. 765–768. [Google Scholar]
- Keefer, D.K. Statistical analysis of an earthquake-induced landslide distribution—The 1989 Loma Prieta, California event. Eng. Geol. 2000, 58, 231–249. [Google Scholar] [CrossRef]
- Xu, C.; Xu, X.; Yao, X.; Dai, F. Three (nearly) complete inventories of landslides triggered by the May 12, 2008 Wenchuan Mw 7.9 earthquake of China and their spatial distribution statistical analysis. Landslides 2014, 11, 441–461. [Google Scholar] [CrossRef]
- Esposito, E.; Guerrieri, L.; Porfido, S.; Vittori, E.; Blumetti, A.M.; Comerci, V.; Michetti, A.M.; Serva, L. Landslides induced by historical and recent earthquakes in Central-Southern Apennines (Italy): A tool for intensity assessment and seismic hazard. Landslide Sci. Pract. 2013, 295–303. [Google Scholar]
- Porfido, S.; Esposito, E.; Spiga, E.; Sacchi, M.; Molisso, F.; Mazzola, S. Impact of ground effects for an appropriate mitigation strategy in seismic area: The example of Guatemala 1976 earthquake. In Engineering Geology for Society and Territory; Springer: Cham, Switzerland, 2015; Volume 2, pp. 703–708. [Google Scholar]
- Lobkina, V.A.; Kazakova, E.N.; Zhiruev, S.P.; Kazakov, N.A. Methods of landslide risk assessment for territory of settlements of Sakhalin Region (Makarov city, Sakhalin). Russ. J. Pac. Geol. 2013, 32, 100–109. (In Russian) [Google Scholar]
- Ulomov, V.I.; Bogdanov, M.I. Explanatory note on the GSZ-2016 maps set of general seismic zoning of the Russian Federation territory. Eng. Surv. 2016, 7, 49–122. (In Russian) [Google Scholar]
- Konovalov, A.V.; Nagornykh, T.V.; Safonov, D.A.; Lomtev, V.L. Nevelsk earthquakes of August 2, 2007 and seismic setting in the southeastern margin of Sakhalin Island. Russ. J. Pac. Geol. 2015, 9, 451–466. [Google Scholar] [CrossRef]
- Reliable Prognosis. Available online: https://rp5.ru/%D0%90%D1%80%D1%85%D0%B8%D0%B2_%D0%BF%D0%BE%D0%B3%D0%BE%D0%B4%D1%8B_%D0%B2_%D0%9D%D0%B5%D0%B2%D0%B5%D0%BB%D1%8C%D1%81%D0%BA%D0%B5 (accessed on 10 April 2019).
- Jibson, R.W.; Harp, E.L.; Michael, J.A. A method for producing digital probabilistic seismic landslide hazard maps. Eng. Geol. 2000, 58, 271–289. [Google Scholar] [CrossRef]
- Lee, C.T. Statistical seismic landslide hazard analysis: An example from Taiwan. Eng. Geol. 2014, 182, 201–212. [Google Scholar] [CrossRef]
- Jibson, R.W. Mapping seismic landslide hazards in Anchorage, Alaska. In Proceedings of the 10th National Conference in Earthquake Engineering, Earthquake Engineering Research Institute, Anchorage, AK, USA, 21–25 July 2014. [Google Scholar]
- Martino, S.; Battaglia, S.; D’Alessandro, F.; Della Seta, M.; Esposito, C.; Martini, G.; Pallone, F.; Troiani, F. Earthquake-induced landslide scenarios for seismic microzonation: Application to the Accumoli area (Rieti, Italy). Bull. Earthq. Eng. 2019, 1–19. [Google Scholar] [CrossRef]
- Del Gaudio, V.; Wasowski, J.; Pierri, P. An Approach to Time-Probabilistic Evaluation of Seismically Induced Landslide Hazard. Bull. Seismol. Soc. Am. 2003, 93, 557–569. [Google Scholar] [CrossRef]
- Galli, M.; Guzzetti, F. Landslide vulnerability criteria: A case study from Umbria, Central Italy. Environ. Manag. 2007, 40, 649–664. [Google Scholar] [CrossRef] [PubMed]
- Jaiswal, P.; van Westen, C.J.; Jetten, V. Quantitative estimation of landslide risk from rapid debris slides on natural slopes in the Nilgiri hills, India. Nat. Hazards Earth Syst. Sci. 2011, 11, 1723–1743. [Google Scholar] [CrossRef]
- Guillard-Gonçalves, C.; Zêzere, J.L.; Pereira, S.; Garcia, R.A.C. Assessment of physical vulnerability of buildings and analysis of landslide risk at the municipal scale: Application to the Loures municipality, Portugal. Nat. Hazards Earth Syst. Sci. 2016, 16, 311–331. [Google Scholar] [CrossRef]
- Golozubov, V.V.; Kasatkin, S.A.; Grannik, V.M.; Nechayuk, A.E. Deformation of the Upper Cretaceous and Cenozoic complexes of the West Sakhalin terrane. Geotectonics 2012, 46, 333–351. [Google Scholar] [CrossRef]
- Atlas of the Sakhalin Region; Komsomolskiy, G.V., Siryk, I.M., Eds.; GUGK Sovmin USSR: Moscow, Russia, 1967; 137p. (In Russian) [Google Scholar]
- Handbook of Climate of the USSR; Pilnikova, Z.N., Ed.; Sakhalin Region, Gidrometeoizdat: Saint Petersburg, Russia, 1990; pp. 48–64. (In Russian) [Google Scholar]
- Cornell, C.А. Engineering seismic risk analysis. Bull. Seismol. Soc. Am. 1968, 58, 1583–1606. [Google Scholar]
- Aguilar-Meléndez, A.; Ordaz Schroeder, M.G.; De la Puente, J.; Gonzalez Rocha, S.N.; Rodrigez Lozoya, H.E.; Cordova Ceballos, A.; Garcia Elias, A.; Calderon Ramon, C.M.; Escalante Martinez, J.E.; Laguna Camacho, J.R.; et al. Development and Validation of Software CRISIS to Perform Probabilistic Seismic Hazard Assessment with Emphasis on the Recent CRISIS2015. Computacion y Sistemas 2017, 21, 67–90. [Google Scholar] [CrossRef]
- Konovalov, A.V.; Sychov, A.S.; Manaychev, K.A.; Stepnov, A.A.; Gavrilov, A.V. Testing of a New GMPE Model in Probabilistic Seismic Hazard Analysis for the Sakhalin Region. Seismic Instr. 2019, 55, 283–290. [Google Scholar] [CrossRef]
- Newmark, N.M. Effects of earthquakes on dams and embankments. Geotechnique 1965, 15, 139–159. [Google Scholar] [CrossRef]
- Fabbrocino, S.; Paduano, P.; Lanzano, G.; Forte, G.; de Magistris, F.S.; Fabbrocino, G. Engineering Geology Model for Seismic Vulnerability Assessment of Critical Infrastructures; Engineering Geology Special Publications; Geological Society: London, UK, 2016. [Google Scholar]
- Rossetto, T.; Elnashai, A. Derivation of vulnerability functions for European-type RC structures based on observational data. Eng. Struct. 2003, 25, 1241–1263. [Google Scholar] [CrossRef]
- Ciurean, R.L.; Schröter, D.; Glade, T. Conceptual Frameworks of Vulnerability Assessments for Natural Disasters Reduction. In Approaches to Disaster Management—Examining the Implications of Hazards, Emergencies and Disasters; Tiefenbacher, J., Ed.; InTech: Rijeka, Croatia, 2013; pp. 3–32. [Google Scholar]
- Sorokin, A.A.; Makogonov, S.I.; Korolev, S.P. The Information Infrastructure for Collective Scientific Work in the Far East of Russia. Sci. Tech. Inf. Process. 2017, 44, 302–304. [Google Scholar] [CrossRef]



| Soil Type | , Kpa | , deg. | , kN/m3 | , kN/m3 | , deg. |
|---|---|---|---|---|---|
| Tuffaceous sandstone | 24 | 40 | 26.8 | 9.8 | 30 |
| Thickness of Sliding Mass, m | Estimated Landslide Volume, m3 | Landslide Intensity Class | Vulnerability According to [11] | Vulnerability According to [8] |
|---|---|---|---|---|
| 1 | <1000 | M-I | 0.05 ± 0.05 | 0.25 ± 0.16 |
| 2 | 2824 | M-II | 0.30 ± 0.10 | 0.31 ± 0.19 |
| 4 | 9340 | M-II | 0.30 ± 0.10 | 0.54 ± 0.19 |
| 8 | 18,680 | M-III | 0.80 ± 0.20 | 0.72 ± 0.20 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konovalov, A.; Gensiorovskiy, Y.; Lobkina, V.; Muzychenko, A.; Stepnova, Y.; Muzychenko, L.; Stepnov, A.; Mikhalyov, M. Earthquake-Induced Landslide Risk Assessment: An Example from Sakhalin Island, Russia. Geosciences 2019, 9, 305. https://doi.org/10.3390/geosciences9070305
Konovalov A, Gensiorovskiy Y, Lobkina V, Muzychenko A, Stepnova Y, Muzychenko L, Stepnov A, Mikhalyov M. Earthquake-Induced Landslide Risk Assessment: An Example from Sakhalin Island, Russia. Geosciences. 2019; 9(7):305. https://doi.org/10.3390/geosciences9070305
Chicago/Turabian StyleKonovalov, Alexey, Yuriy Gensiorovskiy, Valentina Lobkina, Alexandra Muzychenko, Yuliya Stepnova, Leonid Muzychenko, Andrey Stepnov, and Mikhail Mikhalyov. 2019. "Earthquake-Induced Landslide Risk Assessment: An Example from Sakhalin Island, Russia" Geosciences 9, no. 7: 305. https://doi.org/10.3390/geosciences9070305
APA StyleKonovalov, A., Gensiorovskiy, Y., Lobkina, V., Muzychenko, A., Stepnova, Y., Muzychenko, L., Stepnov, A., & Mikhalyov, M. (2019). Earthquake-Induced Landslide Risk Assessment: An Example from Sakhalin Island, Russia. Geosciences, 9(7), 305. https://doi.org/10.3390/geosciences9070305





