Abstract
The goals of the study were: (i) To describe the distribution of summer near-surface water temperatures in lakes of the coterminous United States and southern Canada (ii) to determine the geographic, meteorological and limnological factors related to summer water temperatures and (iii) to develop and test predictive models for summer near-surface water temperatures. We used data from the United States National Lakes Assessments of 2007 and 2012 as well as data collected from several different studies of Canadian lakes. Using multiple regressions, we quantified the general observations that summer water temperatures decreased when going from south to north, from east to west, and from lower elevations to higher elevations. Our empirical model using 8-day average air temperatures, latitude, longitude, elevations and month was able to predict water temperatures in individual lakes on individual summer days with a standard deviation of 1.7 °C for United States lakes and 2.3 °C for lakes in the southern regions of Canada.
1. Introduction
Summer near-surface lake water temperatures in lakes are highly important to physical, chemical and biological properties of lakes, including lake stratification [1], likelihood of algal blooms [2,3] and distribution of aquatic plants and animals [4]. Near-surface summer water temperatures are warming in lakes worldwide, with over 90% of observed lakes exhibiting warming trends [5,6,7,8]. For example, warmer near-surface water temperatures in north temperate lakes are contributing to the northward range expansion of warmwater fishes, such as the smallmouth bass [9,10]. Concurrently, coolwater and coldwater fishes, such as walleye and lake trout, are declining in abundance owing to the loss of suitable thermal habitat and novel competitive interactions with smallmouth bass [11,12,13].
The mechanistic drivers of near-surface water temperatures are well established [14,15,16]. For example, Hondzo and Stefan [17] used mean daily values for six meteorological variables, specifically solar radiation, air temperature, dew point temperature, wind speed, wind direction and precipitation to estimate near-surface water temperatures for Minnesota lakes. Empirical studies have suggested that air temperatures are the most important factor explaining water temperatures, such that water temperatures tend to be higher in lakes found in warmer regions [14,18,19,20]. Latitudinal and altitudinal gradients in air temperature and solar radiation reflect the importance of lake geography in explaining near-surface water temperatures [6,15]. It is generally understood that lakes in southern latitudes are warmer than those in the north, and that those lakes located at higher elevations are cooler than those at lower elevations.
Lake morphometry and water chemistry have also been shown to be important determinants of summer near-surface water temperatures within a lake [8,20,21,22]. For example, smaller and shallower lakes are expected to have higher epilimnion water temperatures than larger and deeper lakes [8,21]. Water chemistry, particularly those indicators related to water clarity, including Secchi depth, dissolved organic carbon and turbidity have been shown to be significant predictors of epilimnion water temperatures at local and regional scales, whereby clearer lakes tend to be warmer [20,21].
In recent years many models have been developed to simulate water temperatures for individual lakes [16,23,24,25] that are based on the physics of heat balances in lake waters. For example, Piccolroaz et al. [24] developed a hybrid model called air2water that can reproduce lake water temperatures at different depths in a study lake for any day of the year and has applied it to Lake Tahoe [26] and Lake Superior [16]. For each lake there is a calibration period of several years where lake data is gathered on air and water temperatures as well. The results of this model produce comparisons of predicted and measured water temperatures with an RMSE of about 0.59 °C. Other models have similar requirements for multi-year calibration periods to develop a simulation model for an individual lake.
Our study started with a serendipitous discovery of correlations between summer surface water temperatures and latitude, longitude and elevation above sea level for a large sample of lakes in the United States collected in the months of June, July, August and September of 2007 and 2012. We followed up on this with a multiple regression and found that we could predict the summer surface water temperatures in these lakes with an RMSE of about 2.7 °C using inputs of latitude, longitude and elevation alone. This was a surprising result, so we expanded on these results by adding data on air temperatures above the study lakes and by extending our sample to include lakes in southern portion of Canada.
The overall goal of our study was to develop a widely applicable model to calculate near-surface water temperatures on any summer day for lakes in the coterminous United States and Canada. Specifically, our objectives were three-fold to: (i) Describe the distribution of summer near-surface water temperatures in Canadian and United States lakes; (ii) identify some of the geographic, meteorological and limnological factors related to summer near-surface water temperatures and (iii) develop and validate empirical models for summer near-surface water temperatures for lakes in the United States and Canada. Although empirical models exist at local [16,27], regional [19,22] and national scales [20], to our knowledge, this is the first study to develop empirical models using readily available lake information, including geography and climate for inland lakes at the continental scale across Canada and the United States.
2. Materials and Methods
2.1. United States Lakes
We used the water temperature data for United States lakes sampled by the United States Environmental Protection Agency (USEPA) as a part of their programs of National Lake Assessment (NLA) of 2007 and 2012 [28,29]. They used lakes identified in the National Hydrography Dataset [30] as a basis and selected the sample lakes with a stratified random sampling technique [31]. The lakes were located in the 48 coterminous states (Figure 1). The same equipment and protocols were used to sample each lake, and a large amount of metadata is also available on geographic locations and limnological characteristics of the sampled lakes. The sampling program was designed to yield a representative picture of lakes in the coterminous United States. The sample included both natural and manmade lakes but excluded the Laurentian Great Lakes. Candidate lakes in 2007 were greater than 4 ha in surface area, at least 1 m deep and with at least 0.1 ha of open water. The 2012 survey used a minimum size of 1 ha in surface area. The majority of the samples were taken in the months of June, July, August and September. We did not include the small number of samples collected in May and October. In addition to the randomly selected lakes we also included data from a smaller number of lakes selected by USEPA as reference lakes. We, however, did not use the proportionality weighting factors, so each lake sample had an equal weight in our calculations. Some of the lakes were sampled in both years, and some lakes were sampled twice in the same year, but we only used the data collected for the first visit in each year. For each lake a temperature profile was obtained at the deepest point in the lake. From the profiles we recorded the measured water temperatures at 1 m. For each lake we also used NLA information on latitude, longitude, elevation, surface area, maximum depth, turbidity, Secchi depth and water color. We had 1905 United States lakes in our final sample.
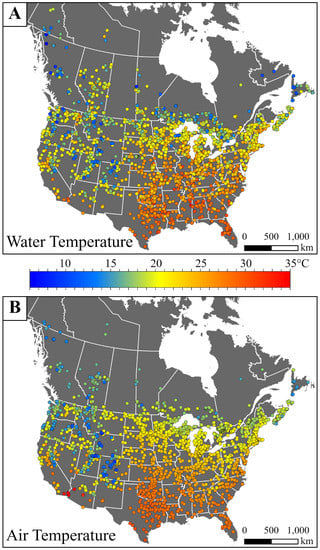
Figure 1.
(A) Water temperatures measured at 1 m in in depth in lakes at some time in the months of June, July, August and September. (B) Average July air temperatures in the period 1981–2010 at stations near lakes with water temperature data.
For each lake we extracted data for the mean air temperatures for the day of sampling and for each of the preceding nine days. These were obtained from the PRISM Climate group, Oregon State University http://prism.oregonstate.edu, created 12 May 2018. Their website allows one to obtain mean daily air temperatures and other meteorological data based on a grid of 30-arcseconds of latitude and longitude. The cells are about 900 m × 700 m in size [32].
2.2. Canadian Lakes
Since there has been no survey of lakes in Canada comparable to the NLA, we used data collected by different studies during the period 1943 through 2011 (Figure 1). We obtained water temperatures at 1 m, latitudes, longitudes and elevations for 10,831 lakes [20]. We compared the latitudes and longitudes of each of the sample lakes with the latitudes and longitudes of 1011 weather stations in the Environment Canada data base (https://data.edmonton.ca/Environmental-Services/Weather-Station-Locations-Environment-Canada/q8e4-6g4e) to identify lakes within 25 km of a weather station. We searched for lakes having air temperature data at the time of lake sampling and for the previous nine days. We also removed lakes north of 67° N, because there was a dearth of information and only a few lakes. We noted that lakes in the provinces of Ontario and Nova Scotia were greatly overrepresented in our sample of Canadian lakes, so we randomly selected 12% of the lakes from each of those two provinces, an amount about equal to the number of lakes from other provinces, resulting in us having 750 Canadian lakes in our final sample.
2.3. Data Analyses
We combined the data from the Canadian and United States lakes into a single dataset with 2655 lakes. This includes 750 Canadian lakes plus 1219 individual lakes in the United States plus data from 686 United States lakes sampled in both 2007 and 2012. We calculated average air temperatures for periods of one through ten days prior to and including the day of sampling for each lake. We used these data in regression analyses between measured lake water temperatures and each of the 10 average air temperatures to identify which number of days (eight days) to use in our predictive equations. We also used simple regression analyses with the entire data set to identify relationships between lake temperatures, latitude, longitude and elevation and average air temperatures at each lake. Since the United States lakes had data on several additional limnological variables, we used that data set in a forward stepwise multiple regression of water temperatures as the dependent variable and air temperatures, latitude, longitude, lake origin (natural or man-made), elevation, surface area, maximum depth, turbidity, Secchi depth and water color as independent variables. For the Canadian lakes we added the year of sampling as an additional variable since about 98% of the samples were collected from 1967 to 2010. When each variable was added to the regression, we recorded the probability that the variable was statistically significant, the coefficient of determination (R2), the root-mean-squared-error (RMSE) and the Akaike information criterion (AIC). In our final equations we only included variables that were statistically significant (p < 0.05), reduced the AIC when they were added to the equation and whose inclusion resulted in a substantial decrease in the root-mean-squared-error (RMSE) of the predicted water temperature. We used the JMP software, v7.0 (SAS Institute Inc., Cary, NC, USA) [33] for all of our statistical summaries and analyses.
Subsequently, we used a random process to divide the United States and Canadian datasets, so that 50% of the lakes from each country were placed in a training dataset and 50% were in a testing dataset. The combined training data were used to construct a multiple regression model to identify relationships between lake water temperatures and 8-day average air temperatures leading up to and including the lake sampling day, latitude, longitude, elevation and month (numbered 6 through 9) for the combination of Canadian and United States lakes. We used the testing dataset to test how well the resulting model predicted water temperatures. We ran a regression of the measured water temperatures against the predicted temperatures and evaluated the R2 and RMSE of the regression. This was done for the combination of lakes from Canada and the United States and also for lakes from the two countries separately but using the same predictive equation.
We also were interested in determining if better predictive equations could be obtained for the lakes in the two countries separately. We used the training datasets for each of the countries to run multiple regression analyses of water temperatures versus 8-day average air temperatures leading up to and including the lake sampling day, latitude, longitude and elevation, and separately for measurements made in the months of June, July, August and September. The predicted values were then evaluated with the testing dataset with regressions of measured versus predicted temperatures as we had done with the common equations.
Since air temperatures were very important in determining water temperatures, we were interested in learning if the geographic distribution of average air temperatures were related to the distribution of the summer water temperatures. As an example, for each lake we chose the average air temperatures in the month of July for the 30-year period 1981 to 2010. For the 1905 United States lakes these data were available from the same PRISM website we used to find daily air temperatures. For the Canadian lakes we again used the Environment Canada website to find the 30-year monthly averages for July from weather stations within 25 km of the sample lakes. We could not find 30-year average July air temperature for all of the Canadian lakes in our study.
3. Results
Summer temperatures at 1 m in lakes of the coterminous United States and Canada varied with latitude, longitude and elevation (Figure 2a–c). Water temperatures tended to increase moving from west to east and also in going from north to south. They tended to be greatest at low elevations and decreased with increasing elevations. We noted the elevations of the lakes tended to be highest in the western parts of the United States and Canada reflecting the location of the western mountains (Figure 2d). The measures of longitude, latitude and elevation are all related to each other and were included in the predictive equations (Table 1). The basic data used in this study are presented in Table S1.
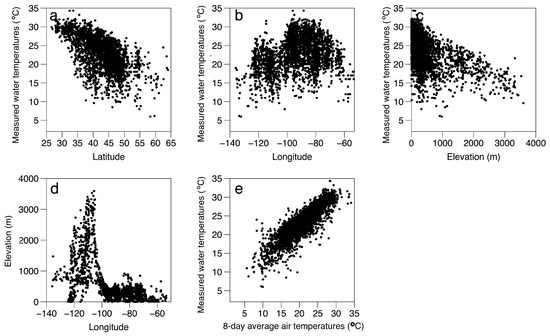
Figure 2.
Measured water temperatures at 1 m for lakes in Canada and the United States sampled in the months of June, July, August and September plotted against each lake’s (a) latitude, (b) longitude and (c) elevation. (d) The elevations of the lakes in the sample are plotted against longitude. (e) The water temperatures are plotted against the 8-day average air temperatures for each lake.

Table 1.
Pearson correlation coefficients for relationships between summer water temperatures at 1-m in depth in United States lakes and lake latitudes, longitudes and elevations. All relationships were statistically significant (p < 0.01).
Confirming the results of others [16,23,24,25,26,34,35,36,37,38], air temperatures were related to water temperatures (Figure 2e). The R2 values of the regressions of water temperatures on averaged air temperatures increased going from averages of 1 day to 7 days and then remained constant at an R2 of 0.75 for averages of 7 to 10 days (Table 2). Thus, we used the 8-day average of air temperatures leading up to and including the lake sampling day in all of our models.

Table 2.
Relationship between measured water temperatures and air temperatures averaged over different number of days based on regressions using both Canadian and United States lakes.
When we used the United States lake data and the stepwise multiple regression to look for factors related to water temperatures, we found that after accounting for 8-day average air temperatures leading up to and including the lake sampling day, latitude, longitude and elevation the addition of surface area, maximum depth, turbidity, Secchi depth, lake origin or water color produced only very limited improvements in the predicted temperatures, so we did not use those limnological factors in our models (Table 3). Sharma et al. [20] also found that lake morphometry did not play a substantial role in predicting lake temperatures at broad spatial scales. As others have noted, the lack of a depth effect may be due to the fact that during summer stratification the thermal inertia is small [23,26,37,38,39]. For the Canadian lakes we found that once we had accounted for the 8-day air temperature, latitude, longitude, elevation and month the addition of the year of sampling did not significantly reduce the AIC or the RMSE (Table 4). Seemingly our Canadian equation is valid for the period of about 1967 through 2010.

Table 3.
Results of a stepwise forward multiple regression for the United States lakes. The variables are listed in the order of their selection for the model and for each variable we have listed the probability that it is statistically significant, the coefficient of determination (R2), the root-mean-squared-error (RMSE) and the Akaike information criterion (AIC).

Table 4.
Results of a stepwise forward multiple regression for the Canadian lakes. The variables are listed in the order of their selection for the model and for each variable we have listed the probability that it is statistically significant, the coefficient of determination (R2), the root-mean-squared-error (RMSE) and the Akaike information criterion (AIC).
The common predictive equation (Equation (1), Table 5) for both United States and Canadian lakes could be used to estimate the water temperatures at 1 m of our sample lakes for any day in the months of June, July, August and September. For the United States lakes this common equation was easy to apply for the years of 1981 to the present due to the air temperature data for individual lakes at the PRISM website. For Canadian lakes use of the equation would depend on the availability of air temperature records from a nearby weather station.

Table 5.
Empirical relationships with lake water temperatures at 1 m depth for lakes in Canada and the United States sampled in the months of June–September where T (°C) is a measured water temperature at 1-m, Long is the longitude of the lake, Lat is the latitude of the lake, Elev is the elevation above sea level (m) of the lake, Air is the 8-day average air temperature (°C) at the lake ending on the day of sampling and Mon are the summer months (6, 7, 8 and 9) listed in order. Equation numbers are in parentheses.
When the measured water temperatures in lakes from both the United States and Canada were regressed on the predicted water temperatures obtained using the common equation and the testing data set (N = 1327) the R2 was 0.81 and the RMSE was 1.9 °C indicating a good fit (Table 6 Figure 3). Applying the same equation to the United States lakes alone yielded a better fit (R2 = 0.83, RMSE = 1.7 °C) than when the common equation was applied to the Canadian lakes alone (R2 = 0.58, RMSE = 2.3 °C; Table 6, Figure 3).

Table 6.
Strength of relationships between predicted water temperatures (°C) at 1-m in United States and Canadian lakes based on regressions of measured water temperatures on predicted temperatures using the testing data sets. The common equation was first applied to the Canadian and United States lakes combined and the same equation was then applied to the Canadian and United States lakes separately. Separate equations were developed by month for the Canadian lakes and the results are presented for all months combined and for the four summer months separately. The same was done for the United States lakes.
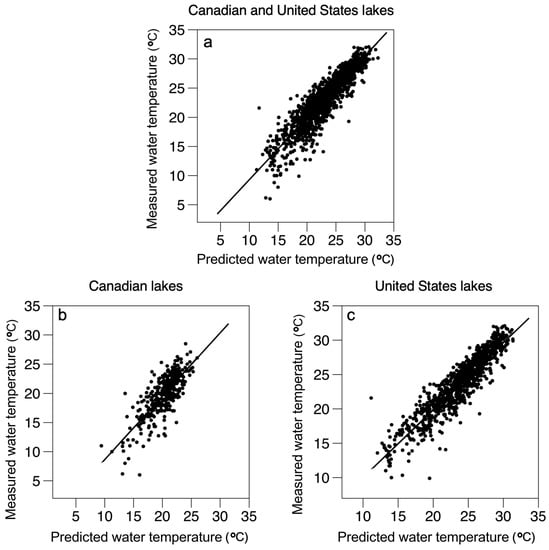
Figure 3.
(a) Plots of measured water temperatures at 1 m in Canadian and United States lakes versus predicted water temperatures based on a common equation for lakes in both countries using information on latitude, longitude, elevation, 8-day average air temperatures and month. (b) Same plot for Canadian lakes alone using the same common equation. (c) Same plot for United States lakes alone using the same common equation. Lines represent fitted regression lines.
As an alternative to a single equation for lakes in both countries including all four months, separate equations were developed for the lakes in each country for each of the four summer months. For the United States lakes, the variables for 8-day average air temperatures leading up to and including the lake sampling day, latitude, longitude and elevation were significant for June, July and August, but longitude was not important for the September data (Table 5). For the Canadian lakes the only significant independent variable for June and September was the for 8-day average air temperature. For July the air temperatures, latitude and elevation were significant and for August only air temperatures and latitude were significant (Table 5). For the lakes in both countries the separate equations gave slightly better fits between the measured water temperatures and those calculated from the multiple regression equations (Table 6). As was the case for the common equation, the fits were better for the United States lakes (R2 = 0.84, RMSE = 1.7 °C) than for the Canadian lakes (R2 = 0.60, RMSE = 2.2 °C) when the results for all four months are combined (Table 6, Figure 4).
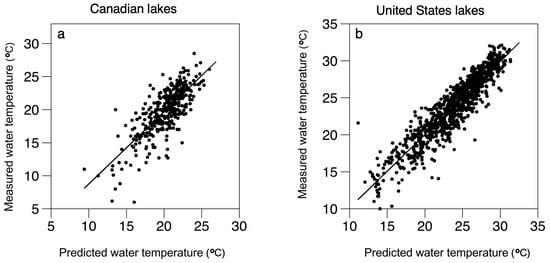
Figure 4.
Plots of measured water temperatures at 1 m in Canadian (a) and United States (b) lakes versus predicted water temperatures based on equations developed for the lakes in the months of June, July, August and September for each country separately. Lines represent fitted regression lines.
4. Discussion
Our study provided a picture of the distribution of summer water temperatures at 1 m depth for lakes in the coterminous United States and in the southern part of Canada. We quantified well-known ideas that lakes in the north were colder than those in the south, lakes at higher elevations were colder than those at lower elevations and that lakes in the western states and provinces tended to be cooler than those in the East, most likely because they were located in regions with higher elevations.
We developed an empirical equation (#1, Table 5) that could be used to hindcast water temperatures at 1 m using information on the average air temperatures for 8-days including the day of interest plus the latitude, longitude, elevation above sea level and the month of sampling. When testing the equation with a data set of lakes from both the United States and Canada not used to develop the equation, the RMSE for a calculated water temperature was 1.9 °C (Table 6). Applying the equation to just the Canadian lakes gave a RMSE of 2.3 °C, while applying the equation to United States lakes alone yielded a RMSE of 1.9 °C. Slightly better results were obtained when separate equations were developed for the lakes in each country and for each of the months of June, July, August and September (Table 5). In these cases the RMSE values for the Canadian lakes were 2.2 °C and for the United States lakes 1.7 °C (Table 6). For comparison, in a study of maximum summer water temperatures in a large sample of Canadian lakes Sharma et al. [20] developed multiple regressions using 4, 9, 10 and 17 predictive variables and found RMSE values of 2.7 °C, 2.4 °C, 2.3 °C and 2.4 °C respectively.
The plots of our calculated temperatures versus measured temperatures (Figure 3 and Figure 4) were relatively tight with RMSE values from 1.7 to 2.3 °C (Table 6) considering all of the factors involved in lake heating and cooling and the fact that the field measurements of lake temperatures could be taken at different times of day. It is noted that the equations used here are for predictions of daily water temperatures for lakes distributed over a very large geographic area. Others have developed predictive equations for single lakes or small groups of lakes in the same region with greater precision than our models [40].
The differences in precision for the calculated water temperatures between the United States and Canadian lakes that were present both when the same equation was used for both sets of lakes and when separate equations were developed for each country (Table 6) might reflect the fact that the United States lakes were sampled only in the summers of 2007 and 2012 by one organization with the same methods and equipment, while many different investigators collected the Canadian lake data over many different years with no standardized methodology. Further the lakes in the United States were mostly selected using a randomized process ensuring good geographic coverage of United States lakes. The Canadian lakes were not randomly selected and tended to be concentrated in the southern part of the country. There were also few Canadian lakes at elevations above 1000 m, resulting in elevation not being a significant factor for three of the four summer months (Table 5). A more complete data set might produce a more precise equation for these lakes.
One of the goals of this study was to develop predictive equations for hindcasting lake water temperature at 1 m for any day in the months of June, July, August and September for lakes in the coterminous United States and the southern portions of Canada. We found that the mean air temperatures at a lake of from seven to 10 days prior to and including the sampling day gave the best correlations between water and air temperatures (Table 2). Many other investigators have also found relationships between air and water temperatures for annual [18], monthly [41] and daily [15,19,42] periods and peak summer temperatures [43]. Others have used longer time periods in their averages when working with one or a smaller group of lakes. We also found that the precision of the predicted value was improved when the geographic variables of latitude, longitude and elevation above sea level were included with the air temperatures in a multiple regression. Others [42] have quantified the effect of increasing elevations on decreases in lake water temperatures. We also noted that as longitude progressed westward, the lake elevation increased as well, which probably explained the longitudinal effect. Latitude would be related to gradients in incident solar radiation [44]. We also noted that the distribution of mean air temperatures in July for the period 1981–2010 mirrors the general distribution of near-surface water temperatures for our study lakes in the summer months (Figure 1).
It should be noted that we are dealing with an empirical relationship and not a direct cause and effect relationship between lake-water and air temperatures. For lakes the main heat exchange processes across the air–water interface are the absorption of direct and diffuse short-wave solar radiation, the absorption of long-wave atmospheric radiation, the emission of long-wave radiation from the lake surface, the exchange of latent heat of evaporation and condensation and the conductive exchange of sensible heat [14,24]. Kettle et al. [15] points out that air temperatures are causally involved in all these heat exchange processes except the absorption of solar radiation and the emission of long-wave radiation from the lake surface. Further, air temperatures are often correlated with relative humidity and cloud cover.
Others have found that lake morphometry and water chemistry are also important determinants of summer near surface temperatures within a lake [8,16,20,21,22,23,35]. For example, smaller and shallower lakes are expected to have higher near-surface water temperatures than larger and deeper lakes [8,21]. Water chemistry, particularly those indicators related to water clarity, including Secchi depth, dissolved organic carbon and turbidity have been shown to be significant predictors of near-surface water temperatures at local and regional scales, whereby clearer lakes tend to be warmer [20,22]. For our data set we did not find that these factors were important once we had accounted for air temperature, latitude, longitude and elevation. The difference most likely is due to the scale of our study that covers a major portion of the North American continent. Studies of smaller groupings of lakes in more restricted areas may show the effects of these other variables.
The United Sates lakes examined in this study included both natural and manmade lakes and both kinds of lakes followed the same predictive equation. The exception would be artificial lakes that had large water inflows relative to their volume. We found such an example in Gorge Lake, Washington (Lat. 48.69, Long. −121.01) where the predicted temperature was 21.7 °C but the measured temperature in July was 9.9 °C, the largest difference in our data set. Gorge Lake is the last of a series of three hydroelectric impoundments on the Skagit River (Personal Communication, Ed Connor). The upstream reservoir is called Ross Lake (Lat. 48.82 Long. −121.04) and is fed by streams originating in glaciers and snowfields in the Cascade Mountains. It is large and deep (160 m) with a water residence time of over six months and has an extensive hypolimnion that is around 7 °C year-round. Water is released from Ross Lake from a depth of about 56 m and flows into Diablo Lake (Lat. 48.71 Long. −121.11), which has a residence time of about 11 days, so there is little opportunity for the water to warm before it flows into Gorge Lake with a residence time of less than one day. In this case the water temperatures in Gorge Lake are determined more by the temperatures in the inflowing water than ambient air temperatures.
The ability to estimate the summer near-surface water temperatures over a large geographic area is an addition to the toolbox of the quantitative limnologist and helps them to understand differences among lakes. Our equations should be of value in determining the distribution of species of fish and other aquatic organisms that are limited to a certain temperatures range. The equations may also be of utility in analyzing past records of fish populations over time and in testing hypotheses about the effects of temperature on growth and reproduction.
We would emphasize that we are using a different approach for estimating near-surface water temperatures from those used in many other studies that directly involve several physical processes involved in determining water temperatures and also involve a multi-year calibration period for each lake to be investigated [23,24,26,34]. Most of those models have a better agreement between predicted and measured water temperatures and can be used with several depths and for all days of the year. In contrast our method is empirical, works only for the months of June, July, August and September and has a larger error in the predicted values. Its advantage is that it can be used in lakes for which there are no calibration data. As such it can give a broad picture of the distribution of summer near-surface water temperatures, which should be useful in studies on the distributions of aquatic organisms.
Others have used models to look at the effects of climate change. Hondzo and Stefan [45] used lake models based on climatic factors to predict the effects of climate change on the thermal properties of lakes in the north central United States. Robertson and Ragotzkie [46] used both mechanistic and empirical models to estimate changes in the thermal structure of moderate to large sized lakes in the United States and Canada while Minns et al. [43] developed empirical models to forecast the impact of climate changes on the magnitude and time of occurrence of annual peak surface water temperatures of large lakes in Canada. This is important because others have indicated that lake surface summer water temperatures are warming worldwide over the past 25 years, with over 90% of observed lakes exhibiting warming trends since 1985 [5,6]. For example, warming water temperatures in north temperate lakes are contributing to the northward range expansion of warmwater fishes, such as the smallmouth bass [9,10]. Concurrently, coolwater and coldwater fishes, such as walleye and lake trout, are declining in abundance owing to the loss of suitable thermal habitat and novel competitive interactions with smallmouth bass [11,12,13].
Piccolroaz et al. [16] caution about the use of air-water regression models for future predictions of water temperatures when applied with air temperature ranges beyond the limits of the times series used for model calibration. In our case the model for Canadian lakes was calibrated with 98% of the water temperature data collected in the period 1967 through 2010. While this might have contributed to the errors of prediction, we did not find that the year of sampling had a significant effect on the predictions once we had accounted for air temperatures, latitude, longitude, elevation and month. The Canadian models should be valid for hindcasting water temperatures in the period 1967–2010. The models for the United States lakes were based on data collected in 2007 and 2012, so it is unknown how well they would perform for hindcasting water temperatures outside of that time period.
Supplementary Materials
The following is available online at https://www.mdpi.com/2076-3263/9/7/296/s1, Table S1: Data used for the statistical analyses in this study.
Author Contributions
Conceptualization, R.W.B., S.S. and D.E.C.J.; Data curation, R.W.B. and S.S.; Formal analysis, R.W.B. and D.E.C.J.; Methodology, R.W.B. and D.E.C.J.; Visualization, V.L.; Writing–original draft, R.W.B., S.S. and D.E.C.J.; Writing–review & editing, R.W.B., S.S., D.E.C.J. and V.L.
Funding
The Early Researcher Award from the Ontario Ministry of Innovation provided partial funding for Sapna Sharma. There was no other external funding.
Acknowledgments
Christopher Daly guided us through the process of obtaining air temperature data for our study lakes through the PRISM website. Ed Connor of Seattle Light provided us with information on the hydrologic properties of Gorge Lake, WA and the associated upstream reservoirs that determine its water temperatures. Kevin Blagrave assisted us by extracting the air temperature data from Environment Canada, and Mya Sharma assisted in organizing the Canadian temperature data. Three anonymous reviewers provided valuable comments and literature references that helped us to improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kraemer, B.M.; Anneville, O.; Chandra, S.; Dix, M.; Kuusisto, E.; Livingstone, D.M.; Rimmer, A.; Schladow, S.G.; Silow, E.; Sitoki, L.M.; et al. Morphometry and average temperature affect lake stratification responses to climate change. Geophys. Res. Lett. 2015, 42, 4981–4988. [Google Scholar] [CrossRef]
- Brookes, J.D.; Carey, C.C. Resilience to blooms. Science 2011, 334, 46–47. [Google Scholar] [CrossRef] [PubMed]
- Rigosi, A.; Hanson, P.; Hamilton, D.P.; Hipsey, M.; Rusak, J.A.; Bois, J.; Sparber, K.; Chorus, I.; Watkinson, A.J.; Qin, B.; et al. Determining the probability of cyanobacterial blooms: The application of Bayesian networks in multiple lake systems. Ecol. Appl. 2015, 25, 186–199. [Google Scholar] [CrossRef] [PubMed]
- Jackson, D.A.; Peres-Neto, P.R.; Olden, J.D. What controls who is where in freshwater fish communities—The roles of biotic, abiotic, and spatial factors. Can. J. Fish. Aquat. Sci. 2001, 58, 157–170. [Google Scholar]
- Schneider, P.; Hook, S.J. Space observations of inland water bodies show rapid surface warming since 1985. Geophys. Res. Lett. 2010, 37, 22. [Google Scholar] [CrossRef]
- O’Reilly, C.M.; Sharma, S.; Gray, D.K.; Hampton, S.E.; Read, J.S.; Rowley, R.J.; Schneider, P.; Lenters, J.D.; McIntyre, P.B.; Kraemer, B.M.; et al. Rapid and highly variable warming of lake surface waters around the globe. Geophys. Res. Lett. 2015, 42, 10–773. [Google Scholar]
- Richardson, D.C.; Melles, S.J.; Pilla, R.M.; Hetherington, A.L.; Knoll, L.; Williamson, C.E.; Kraemer, B.M.; Jackson, J.R.; Long, E.C.; Moore, K.; et al. Transparency, geomorphology, and mixing regime explain variability in trends in lake temperature and stratification across northeastern North America (1975–2012). Water 2017, 9, 442. [Google Scholar] [CrossRef]
- Woolway, R.I.; Jones, I.D.; Maberly, S.C.; French, J.R.; Livingstone, D.M.; Monteith, D.T.; Simpson, G.L.; Thackeray, S.J.; Andersen, M.R.; Battarbee, R.W.; et al. Diel surface temperature range scales with lake size. PLoS ONE 2016, 11, e0152466. [Google Scholar] [CrossRef]
- Sharma, S.; Jackson, D.A.; Minns, C.K.; Shuter, B.J. Will northern fish populations be in hot water because of climate change? Glob. Chang. Biol. 2007, 13, 2052–2064. [Google Scholar] [CrossRef]
- Alofs, K.M.; Jackson, D.A.; Lester, N.P. Ontario freshwater fishes demonstrate differing range-boundary shifts in a warming climate. Divers. Distrib. 2014, 20, 123–136. [Google Scholar] [CrossRef]
- Vander Zanden, J.M.; Casselman, J.M.; Rasmussen, J.B. Stable isotope evidence for the food web consequences of species invasions in lakes. Nature 1999, 401, 464–467. [Google Scholar] [CrossRef]
- Hansen, G.J.A.; Read, J.S.; Hansen, J.F.; Winslow, L.A. Projected shifts in fish species dominance in Wisconsin lakes under climate change. Glob. Chang. Biol. 2016, 23, 1463–1476. [Google Scholar] [CrossRef] [PubMed]
- Van Zuiden, T.M.; Chen, M.; Stefanoff, S.; Lopez, L.; Sharma, S. Projected impacts of climate change on three freshwater fishes and potential novel competitive interactions. Divers. Distrib. 2016, 22, 603–614. [Google Scholar] [CrossRef]
- Edinger, J.E.; Duttweiler, D.W.; Geyer, J.C. The response of water temperatures to meteorological conditions. Water Resour. Res. 1968, 4, 1137–1143. [Google Scholar] [CrossRef]
- Kettle, H.; Thompson, R.; Anderson, N.J.; Livingstone, D.M. Empirical modeling of summer lake surface temperatures in southwest Greenland. Limnol. Oceanogr. 2004, 49, 271–282. [Google Scholar] [CrossRef]
- Piccolroaz, S.; Healey, N.C.; Lenters, J.D.; Schladow, S.G.; Hook, S.J.; Sahoo, G.B.; Toffolon, M. On the predictability of lake surface temperature using air temperature in a changing climate: A case study for Lake Tahoe (USA). Limnol. Oceanogr. 2018, 63, 243–261. [Google Scholar] [CrossRef]
- Hondzo, M.; Stefan, H.G. Lake water temperature simulation model. J. Hydraul. Eng. 1993, 119, 1251–1273. [Google Scholar] [CrossRef]
- Shuter, B.J.; Schlesinger, D.A.; Zimmerman, A.P. Empirical predictors of annual surface water temperature cycles in North American lakes. Can. J. Fish. Aquat. Sci. 1983, 40, 1838–1845. [Google Scholar] [CrossRef]
- Livingstone, D.M.; Lotter, A.F. The relationship between air and water temperatures in lakes of the Swiss Plateau: A case study with paleolimnological implications. J. Paleolimnol. 1998, 19, 191–198. [Google Scholar] [CrossRef]
- Sharma, S.; Walker, S.C.; Jackson, D.A. Empirical modelling of lake water-temperature relationships: A comparison of approaches. Freshw. Biol. 2008, 53, 897–911. [Google Scholar] [CrossRef]
- Schmid, M.; Hunziker, S.; Wüest, A. Lake surface temperatures in a changing climate: A global sensitivity analysis. Clim. Chang. 2014, 124, 301–315. [Google Scholar] [CrossRef]
- Rose, K.C.; Winslow, L.A.; Read, J.S.; Hanson, G.J.A. Climate-induced warming of lakes can be either amplified or suppressed by trends in water clarity. Limnol. Oceanogr. Lett. 2016, 1, 44–53. [Google Scholar] [CrossRef]
- Magee, M.R.; Wu, C.H. Response of water temperatures and stratification to changing climate in three lakes with different morphometry. Hydrol. Earth Syst. Sci. 2017, 21, 6253–6274. [Google Scholar] [CrossRef]
- Piccolroaz, S.; Toffolon, M.; Majone, B.A. A simple lumped model to convert air temperature into surface water temperature in lakes. Hydrol. Earth Syst. Sci. 2013, 17, 3323–3338. [Google Scholar] [CrossRef]
- Toffolon, M.; Piccolroaz, S.; Majone, B.; Soja, A.M.; Peeters, F.; Schmid, M.; Wüest, A. Prediction of surface temperature in lakes with different morphology using air temperature. Limnol. Oceanogr. 2014, 59, 2185–2202. [Google Scholar] [CrossRef]
- Piccolroaz, S.; Toffolon, M.; Majone, B. The role of stratification on lakes’ thermal response: The case of Lake Superior. Water Resour. Res. 2015, 51, 7878–7894. [Google Scholar] [CrossRef]
- Livingstone, D.M.; Dokulil, M.T. Eighty years of spatially coherent Austrian lake surface temperatures and their relationship to regional air temperature and the North Atlantic Oscillation. Limnol. Oceanogr. 2001, 46, 1220–1227. [Google Scholar] [CrossRef]
- USEPA. National Lakes Assessment 2007: A Collaborative Survey of Lakes in the United States; EPA 841-R-16-009; United States Environmental Protection Agency: Washington DC, USA, 2009.
- USEPA. National Lakes Assessment 2012: A Collaborative Survey of Lakes in the United States; EPA 841-R-16-113; United States Environmental Protection Agency: Washington DC, USA, 2016.
- Dewald, T.G. Applications of the NHD at the US Environmental Protection Agency. Water Res. Impact. 2006, 8, 5–7. [Google Scholar]
- Peck, D.V.; Olsen, A.R.; Weber, M.H.; Paulsen, S.G.; Peterson, C.; Holdsworth, S.M. Survey design and extent estimates for the National Lakes Assessment. Freshw. Sci. 2013, 32, 1231–1245. [Google Scholar] [CrossRef]
- Daly, C.; Halbleib, M.; Smith, J.I.; Gibson, W.P.; Doggett, M.K.; Taylor, G.H.; Curtis, J.; Pasteris, P.A. Physiographically-sensitive mapping of temperature and precipitation across the conterminous United States. Int. J. Climatol. 2008, 28, 2031–2064. [Google Scholar] [CrossRef]
- SAS Institute Inc. Statistical Analysis System, Cary. In JMP Statistics and Graphics Guide, Version 7; SAS Institute Inc.: Cary, NC, USA, 2007. [Google Scholar]
- Carmack, E.C.; Vagle, S.; Morrison, J.; Laval, B.E. Space-for-time proxy for climate change in deep lakes in the Canadian cordillera: Seasonality along a latitudinal climate gradient. J. Great Lakes Res. 2014, 40, 608–617. [Google Scholar] [CrossRef]
- Ptak, M.; Sojka, M.; Choiński, A.; Nowak, B. Effect of Environmental Conditions and Morphometric Parameters on Surface Water Temperature in Polish Lakes. Water 2018, 10, 580. [Google Scholar] [CrossRef]
- Winslow, L.A.; Hansen, G.J.; Read, J.S.; Notaro, M. Large-scale modeled contemporary and future water temperature estimates for 10774 Midwestern US Lakes. Sci. Data 2017, 4, 170053. [Google Scholar] [CrossRef] [PubMed]
- Woolway, R.I.; Merchant, C.J. Amplified surface temperature response of cold, deep lakes to Inter-annual air temperature variability. Sci. Rep. 2017, 7, 4130. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y.; Notaro, M.; Vavrus, S.J.; Foster, M.J. Recent accelerated warming of the Laurentian Great Lakes: Physical drivers. Limnol. Oceanogr. 2016, 61, 1762–1786. [Google Scholar] [CrossRef]
- Zhong, Y.; Notaro, M.; Vavrus, S.J. Spatially variable warming of the Laurentian Great Lakes: An interaction of bathymetry and climate. Clim. Dynam. 2018, 52, 5833–5848. [Google Scholar] [CrossRef]
- Matuszek, J.E.; Shuter, B.J. An empirical method for the prediction of daily water temperatures in the littoral zone of temperate lakes. Trans. Am. Fish. Soc. 1996, 125, 622–627. [Google Scholar] [CrossRef]
- McCombie, A.M. Some relations between air temperatures and the surface water temperatures of lakes. Limnol. Oceanogr. 1959, 4, 252–258. [Google Scholar] [CrossRef]
- Livingstone, D.M.; Lotter, A.F.; Walkery, I.R. The decrease in summer surface water temperature with altitude in Swiss Alpine lakes: A comparison with air temperature lapse rates. Artct. Anarct. Alp. Res. 1999, 31, 341–352. [Google Scholar] [CrossRef]
- Minns, C.K.; Shuter, B.J.; Davidson, A.; Wang, S. Factors influencing peak summer surface water temperature in Canada’s large lakes. Can. J. Fish. Aquat. Sci. 2017, 75, 1005–1018. [Google Scholar] [CrossRef]
- Yin, X. Reconstructing monthly global solar radiation from air temperature and precipitation records: A general algorithm for Canada. Ecol. Model. 2011, 334, 46–47. [Google Scholar] [CrossRef]
- Hondzo, M.; Stefan, H.G. Regional water temperature characteristics of lakes subjected to climate change. Clim. Chang. 1993, 24, 187–211. [Google Scholar] [CrossRef]
- Robertson, D.M.; Ragotzkie, R.A. Changes in the thermal structure of moderate to large sized lakes in response to changes in air temperature. Aquat. Sci. 1990, 52, 360–380. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).