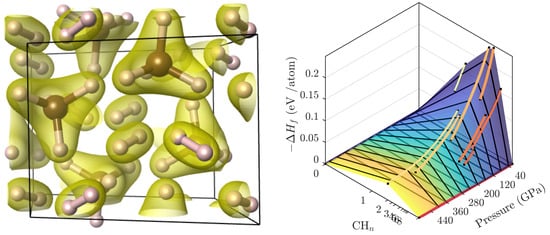
High Pressure Hydrocarbons Revisited: From van der Waals Compounds to Diamond
Abstract
1. Introduction
2. Materials and Methods
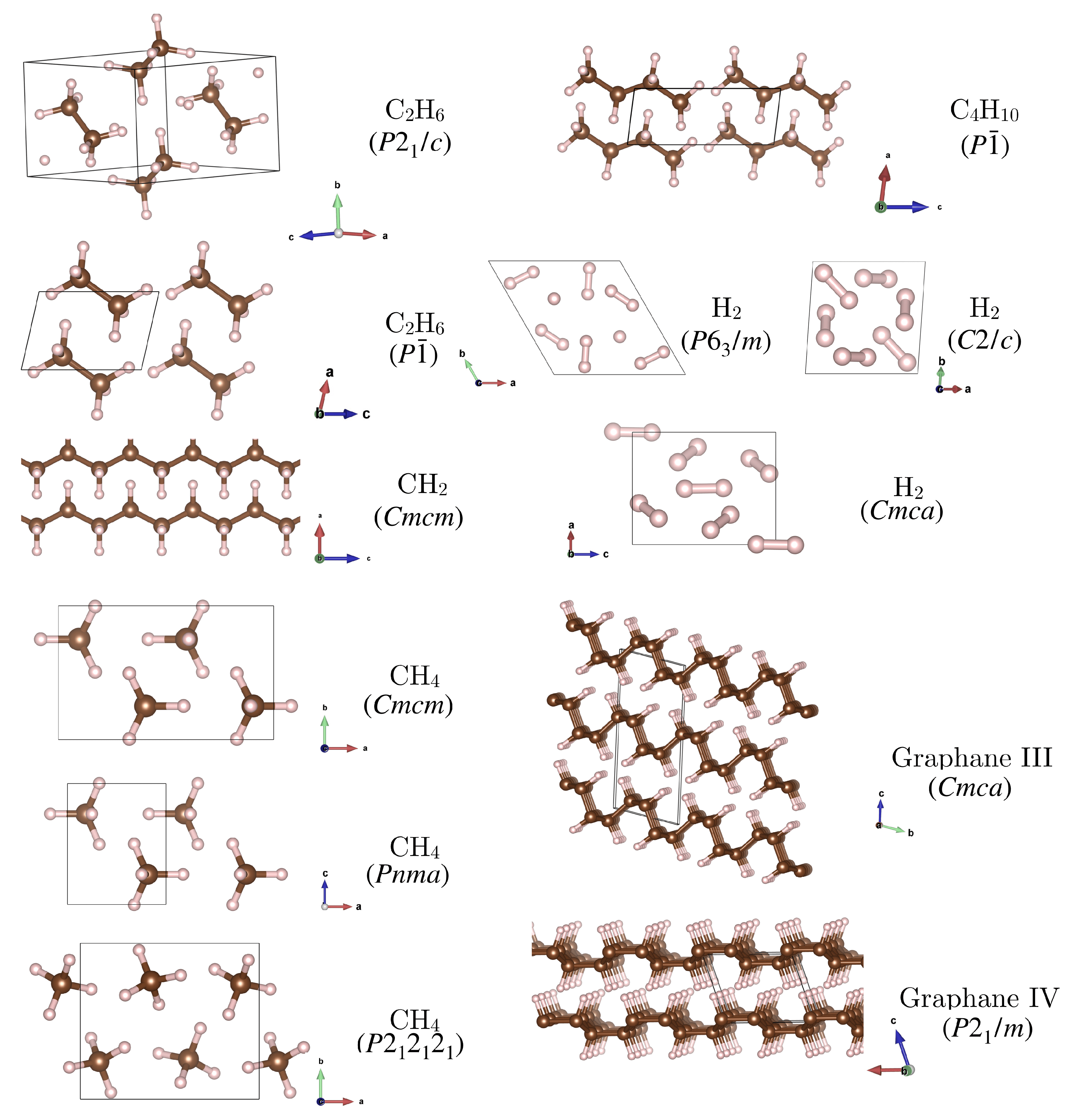
- For methane, CH, we included the three high pressure phases reported by Gao et al. [18]: a phase which was reported to be stable up to 78 GPa, where it is succeeded by a phase, and a phase stable above 90 GPa. The latter two are very similar: has two of the CH molecules flipped compared to , such that it has two molecules in the unit cell.
- For butane, CH, we considered a triclinic phase with molecules in the unit cell [18].
- For the stoichiometry CH the arrangement in graphane sheets is more favourable at high pressure than, e.g., formation of a molecular benzene crystal [50]. We consider two of the most stable high-pressure structures, graphane III () and IV (), with a transition III → IV predicted to occur at 220 GPa [50]. These structures feature distinct layers with graphane III consisting of ‘chair’ shaped sheets and graphane IV consisting of ‘boat’ shaped sheets.
3. Results
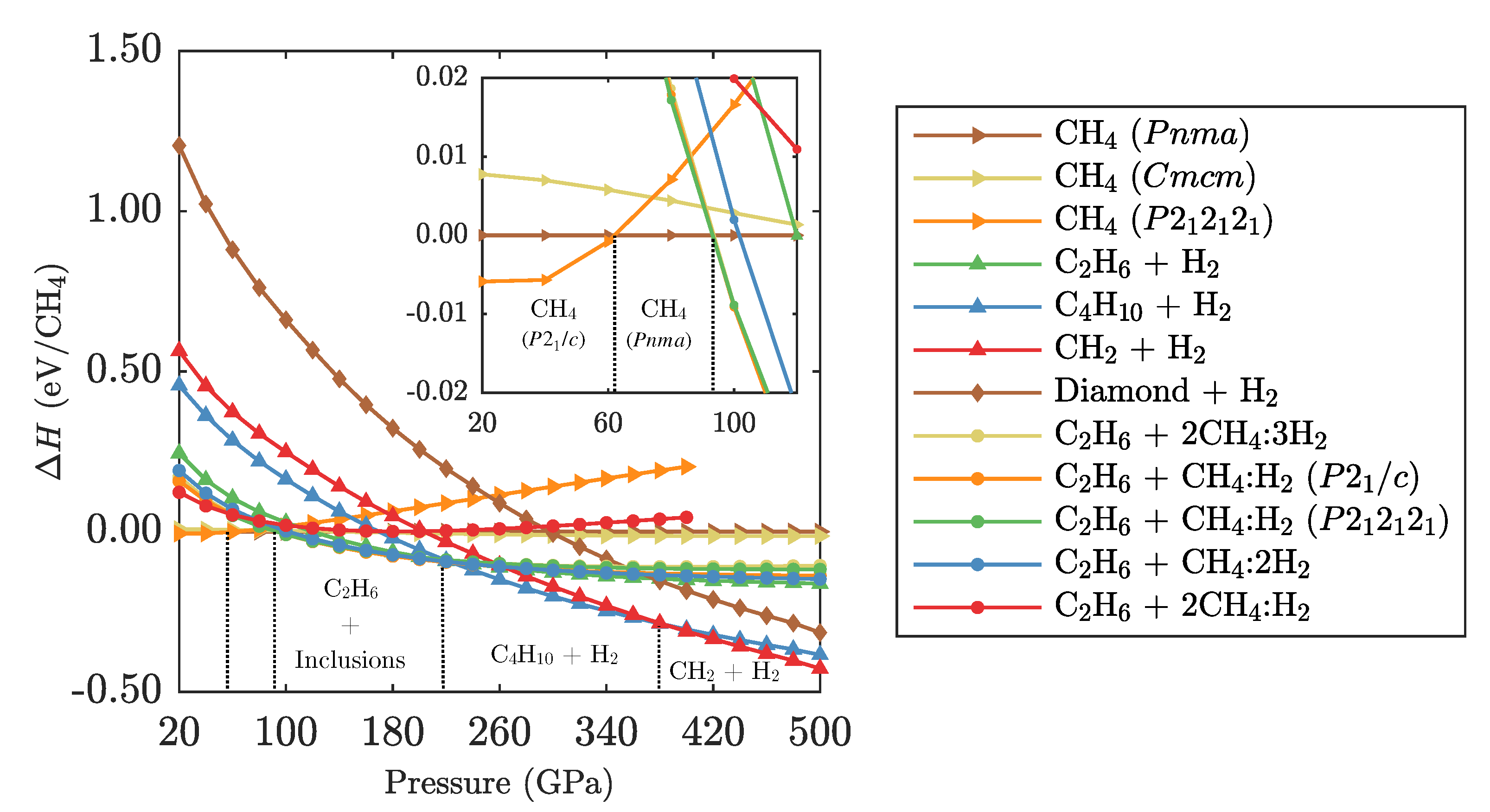
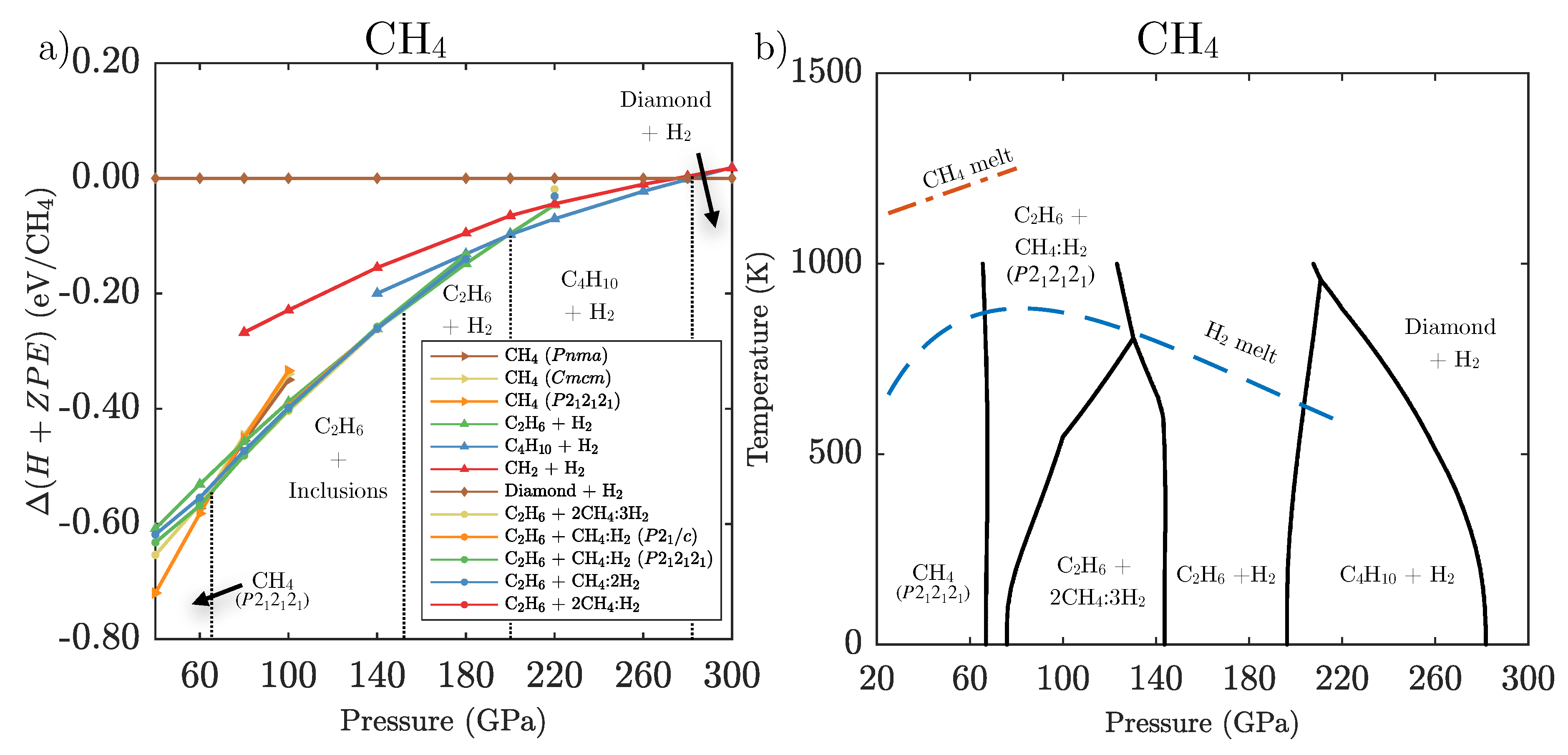
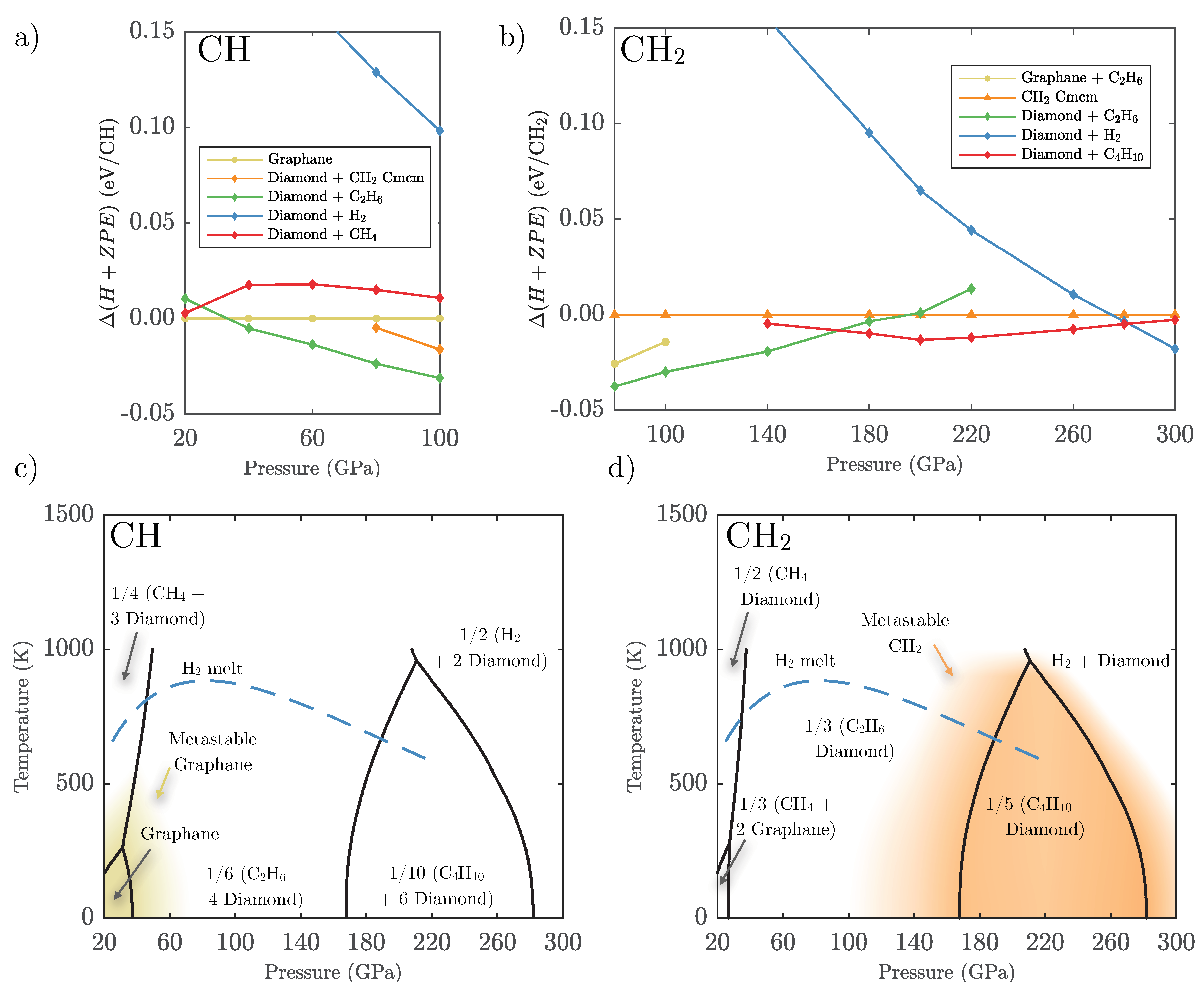
3.1. Ground State Phase Evolution of CH
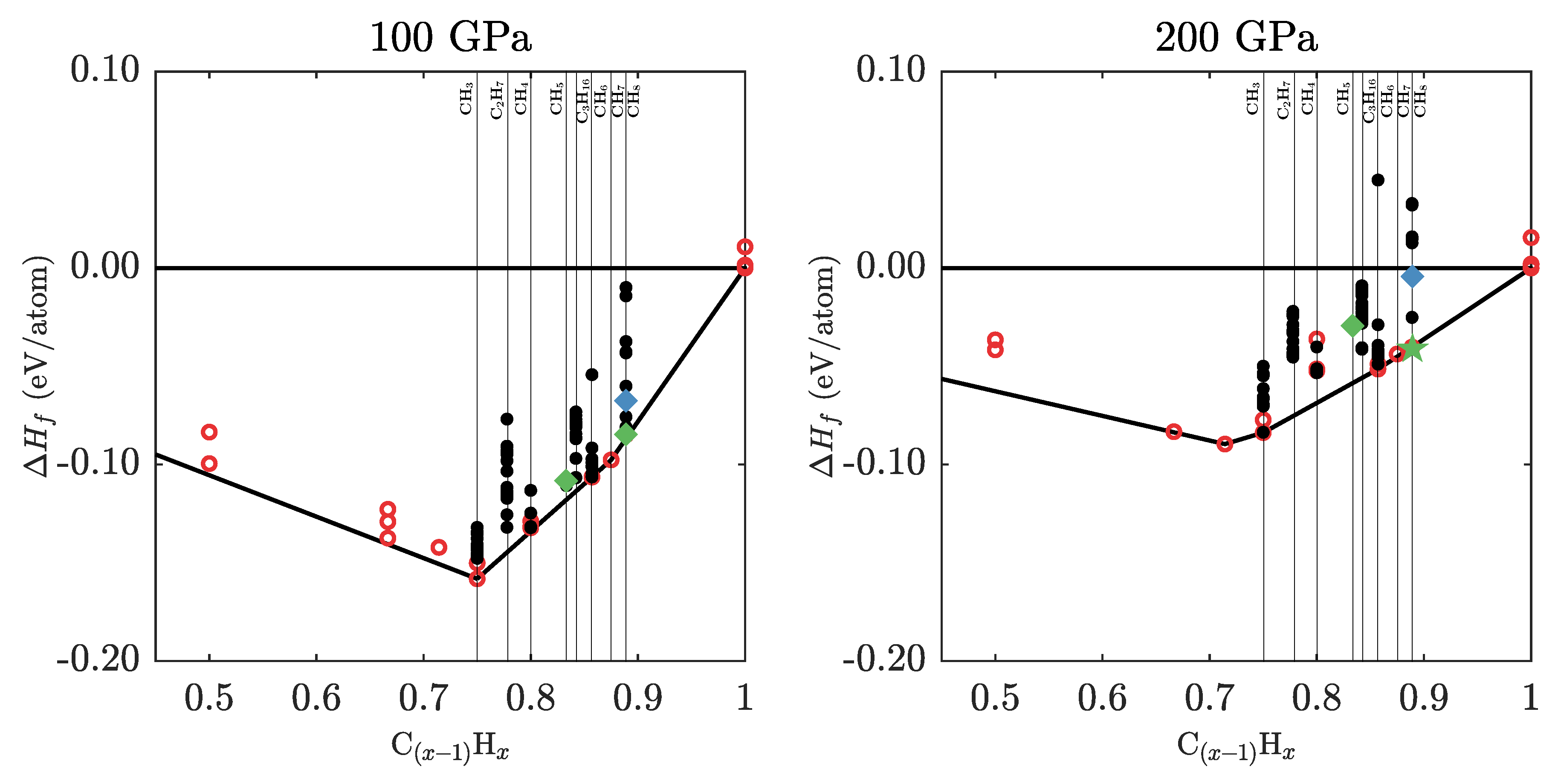
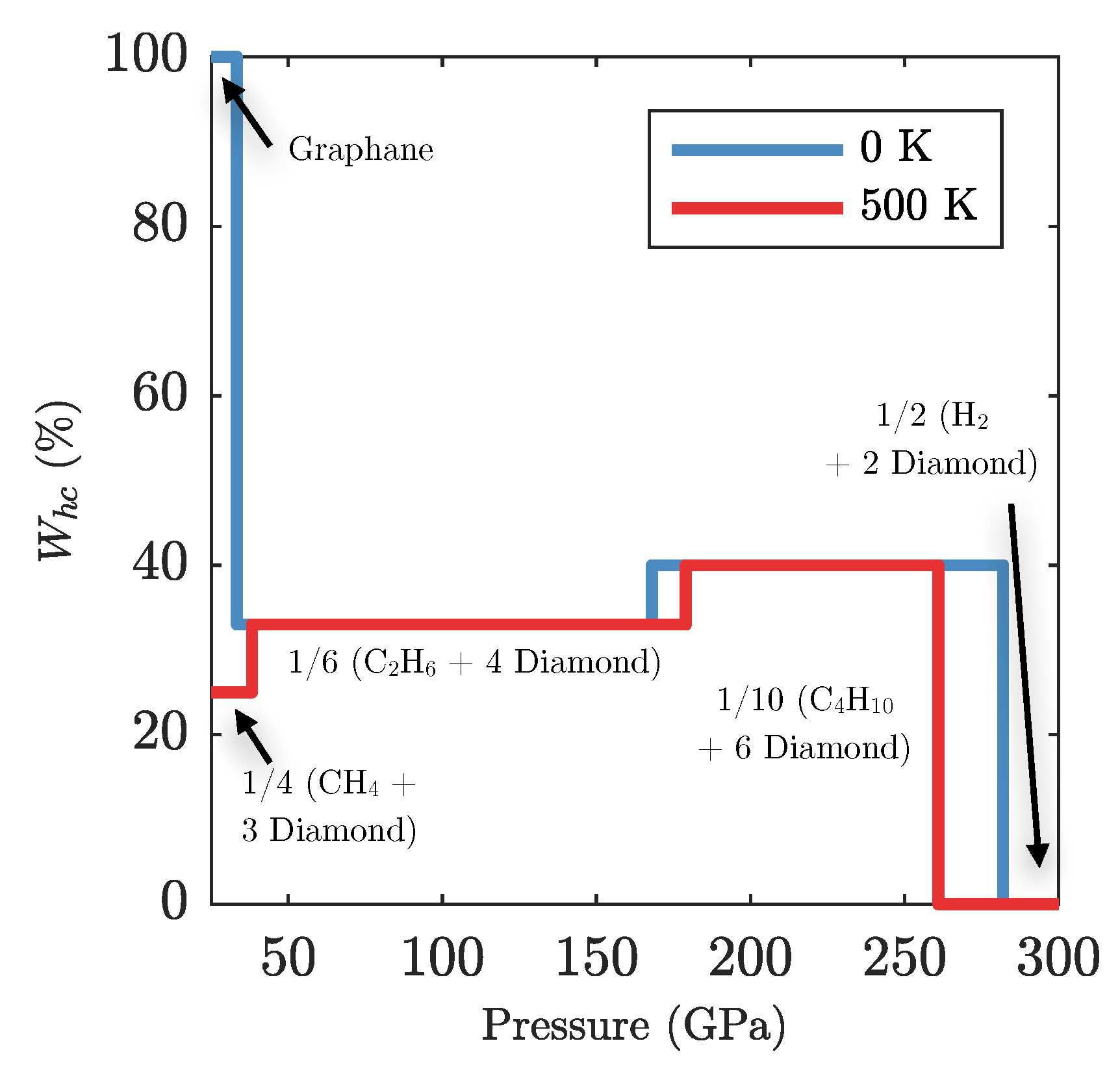
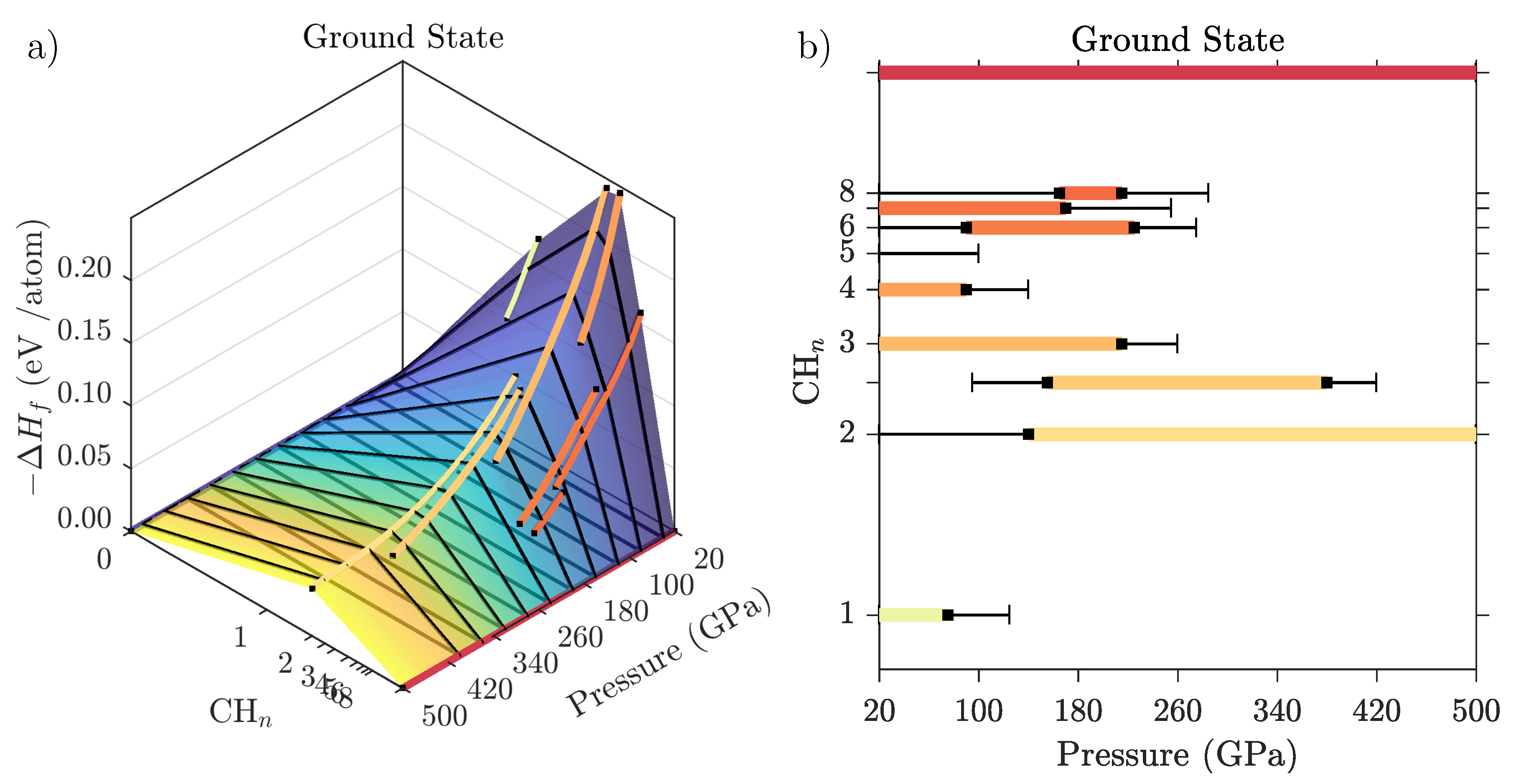
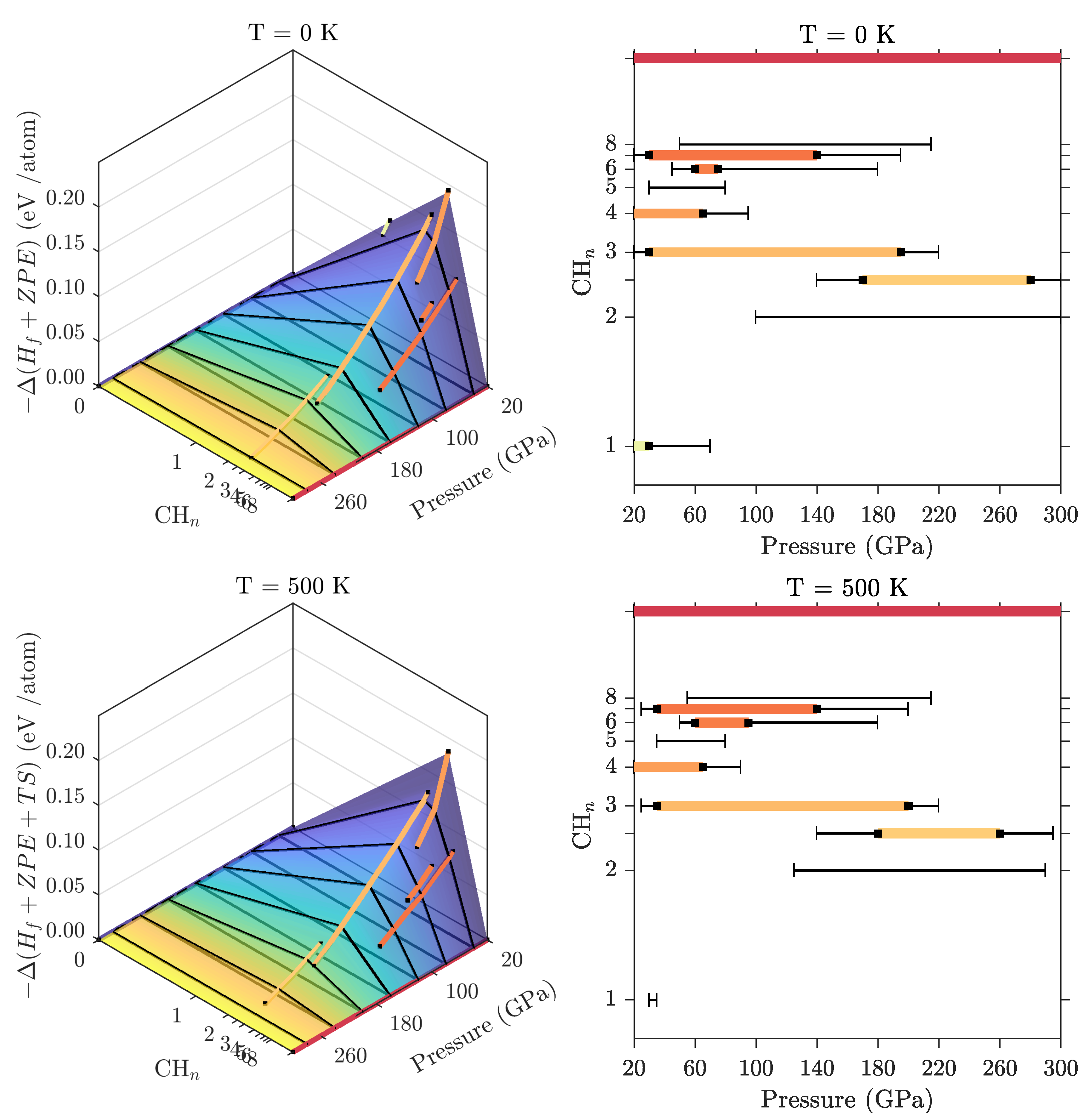
3.2. Ground State Hydrocarbon Phase Diagram
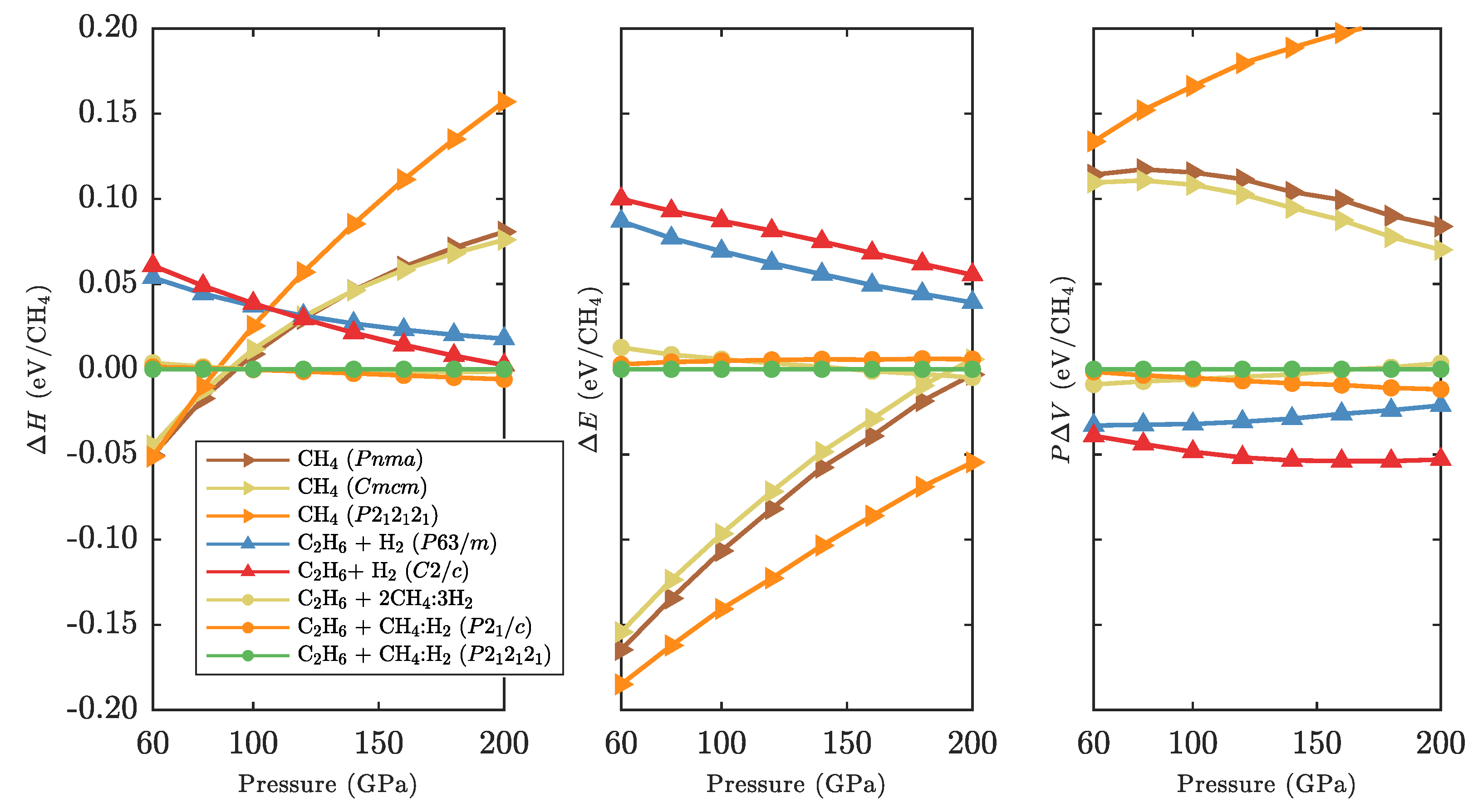
3.3. Zero-Point and Finite Temperature Effects
3.4. Polystyrene and Polyethylene under Pressure
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
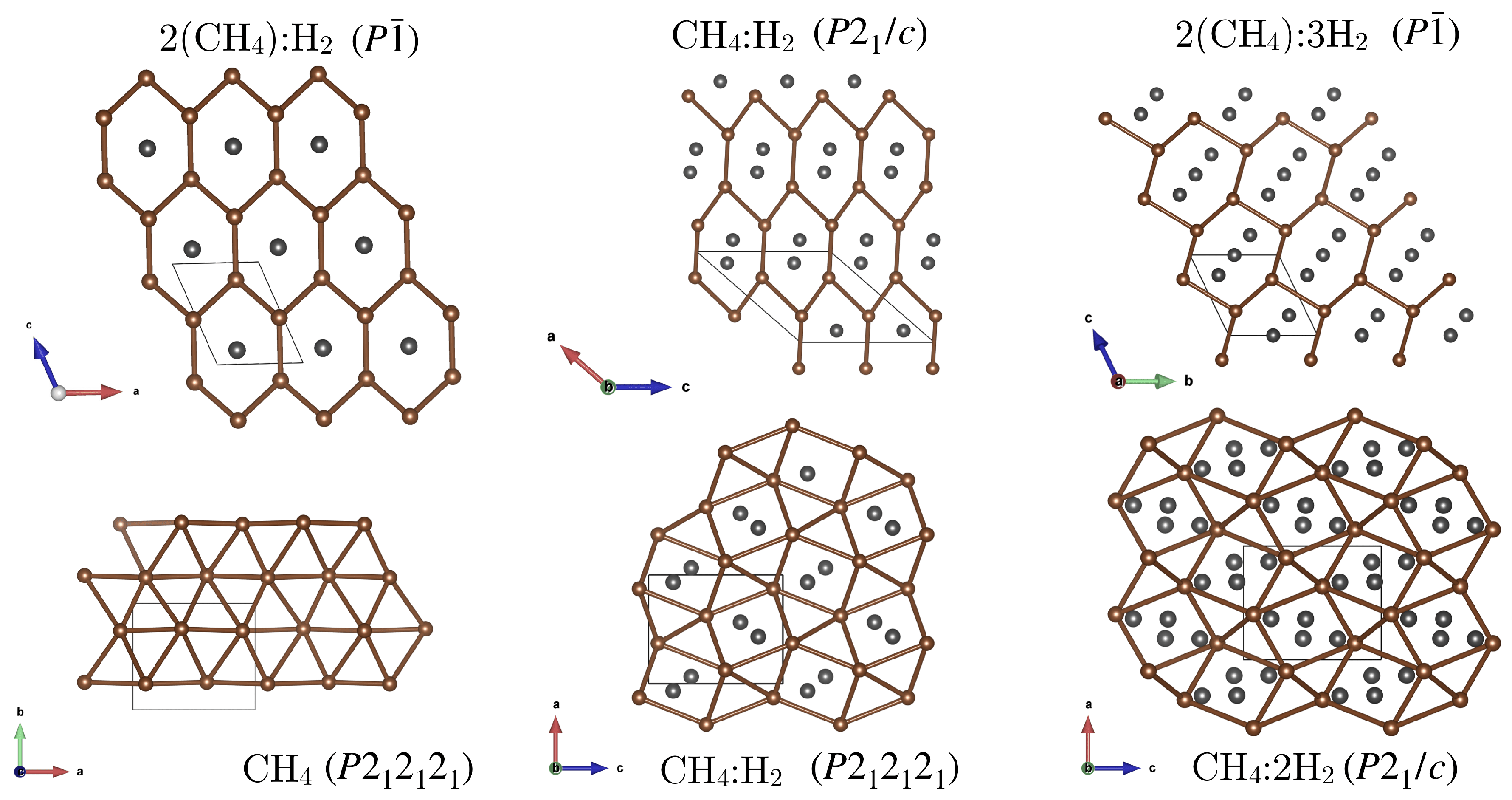
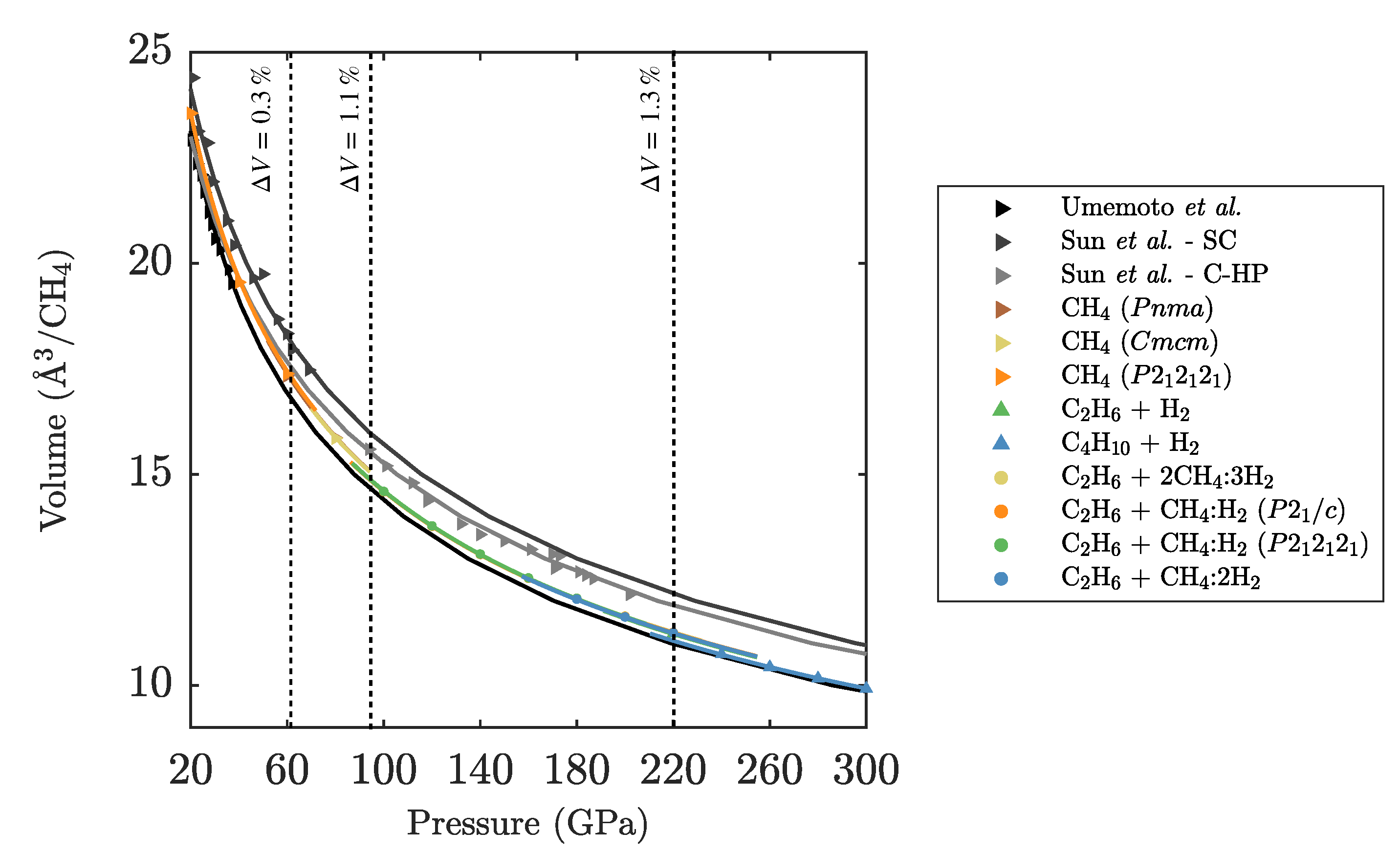
Appendix A. Structure Search Results
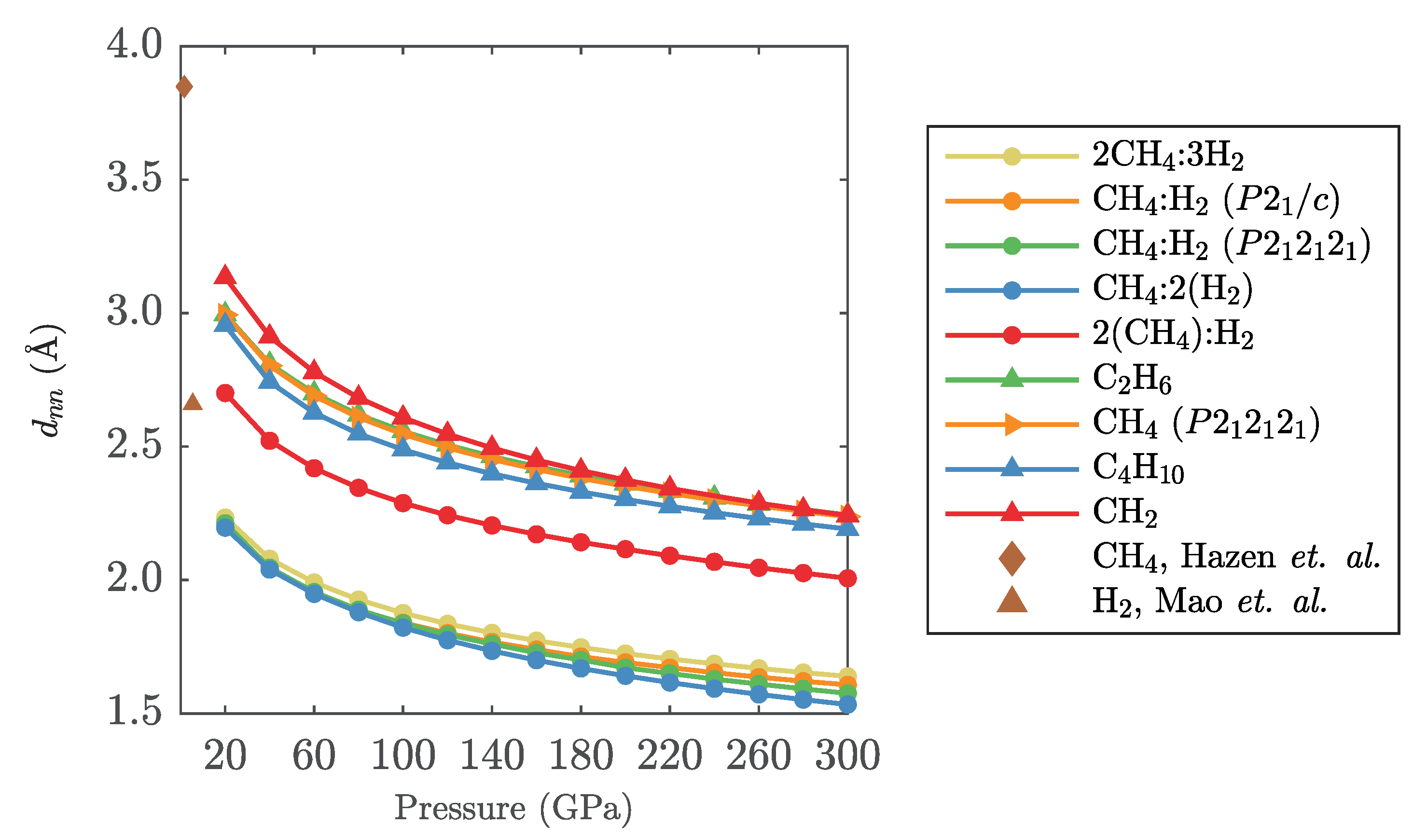
Appendix B. Intermolecular Distances
Appendix C. Equation of State Parameters
| Structure | ||
|---|---|---|
| Umemoto et al. CH [12] | ||
| Sun et al. CH SC [21] | ||
| Sun et al. CH C-HP [21] | ||
| CH () | ||
| CH () | ||
| CH () | ||
| CH + H | ||
| CH + 2CH:3H | ||
| CH + CH:H () | ||
| CH + CH:H () | ||
| CH + CH:2H | ||
| CH + H | ||
| Diamond + H |
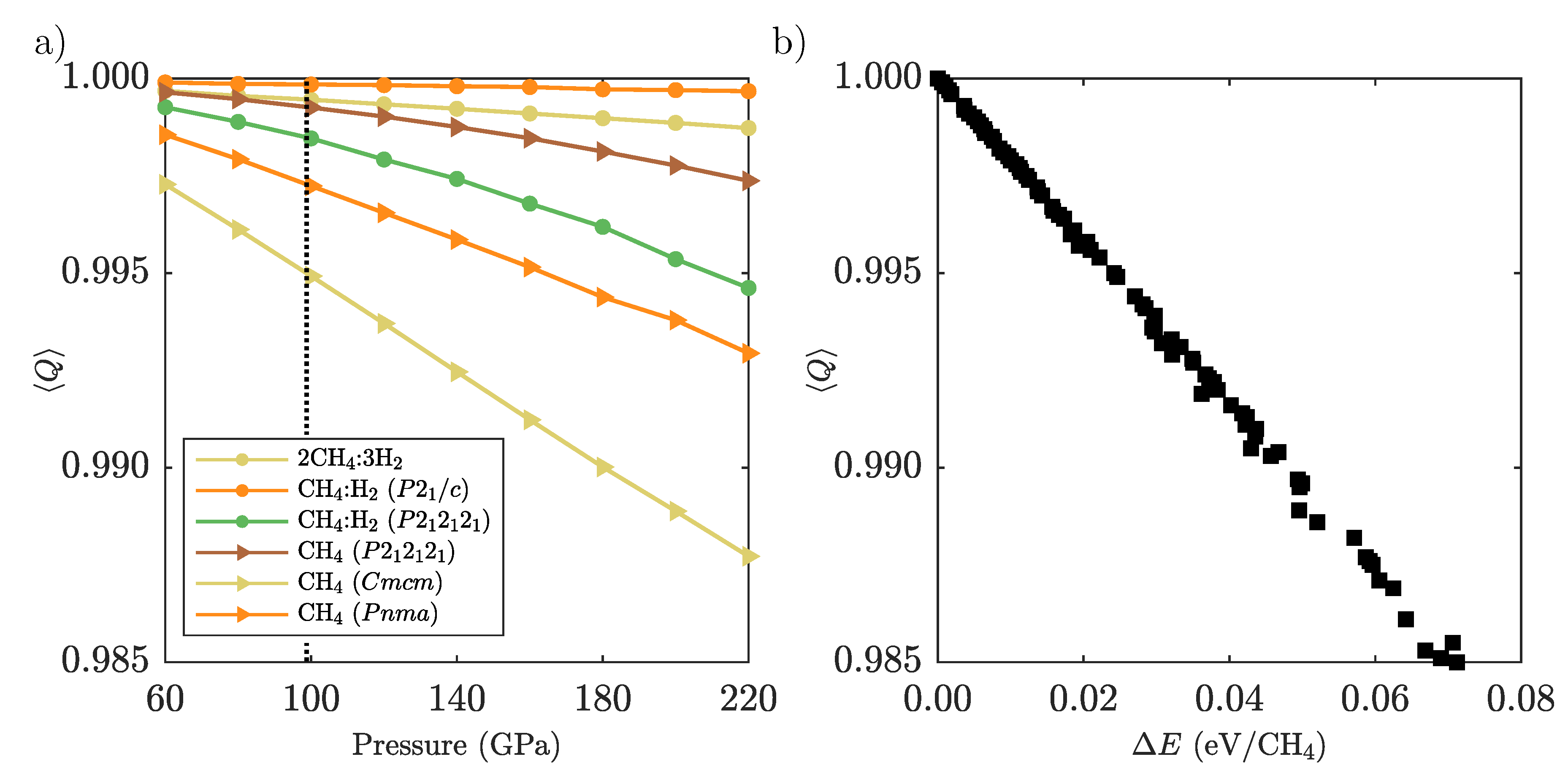
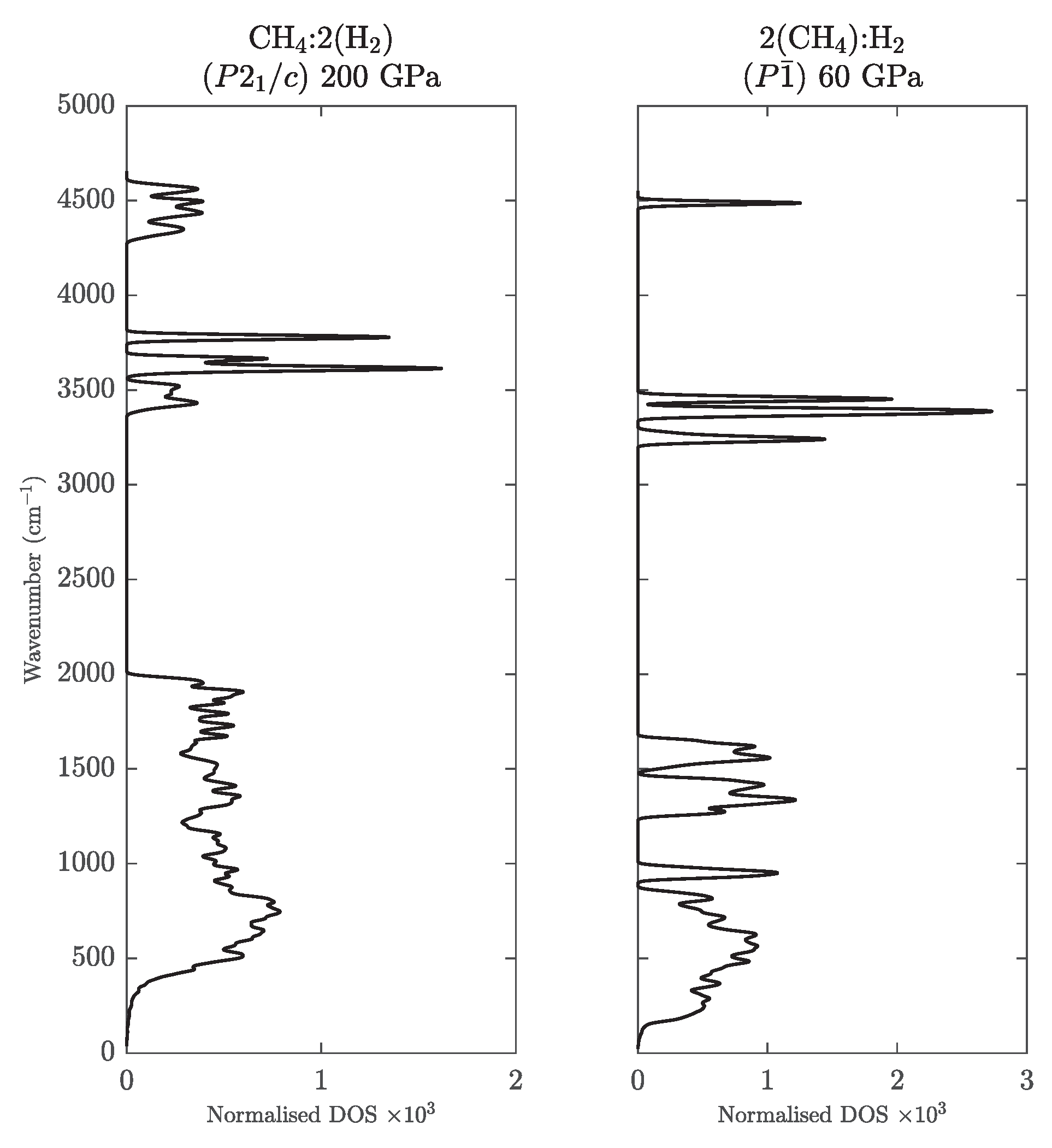
Appendix D. Methane Molecular Distortion
Appendix E. New van der Waals Compounds
| Phase | CH(H) | Atom | Wyckoff Position | x | y | z |
| Space Group | H1 | 4 e | 0.19196 | 0.10868 | −0.06364 | |
| Pressure | 200 GPa | H2 | 4 e | 0.44939 | 0.16238 | 0.39952 |
| Lattice Parameters | H3 | 4 e | 0.27257 | 0.12932 | 0.65204 | |
| a | 3.96446 | H4 | 4 e | 0.87835 | 0.54359 | 0.31216 |
| b | 3.94406 | H5 | 4 e | 0.09105 | 0.78918 | 0.46179 |
| c | 5.108100 | H6 | 4 e | 0.67736 | 0.25401 | 0.18750 |
| 90.000 | H7 | 4 e | 0.63765 | −0.05446 | −0.04190 | |
| 111.2178 | H8 | 4 e | 0.06088 | 0.37230 | 0.78998 | |
| 90.000 | C1 | 4 e | 0.69085 | 0.37449 | 0.86797 | |
| Phase | (CH)H | Atom | Wyckoff Position | x | y | z |
| Space Group | H1 | 2 i | 0.50567 | 0.12379 | 0.22215 | |
| Pressure | 100 GPa | H2 | 2 i | 0.15009 | 0.20191 | 0.58464 |
| Lattice Parameters | H3 | 2 i | 0.51137 | 0.33990 | 0.76335 | |
| a | 2.84033 | H4 | 2 i | −0.01370 | 0.40669 | 0.20115 |
| b | 3.19376 | H5 | 2 i | −0.09011 | −0.01841 | −0.04194 |
| c | 4.24946. | C1 | 2 i | 0.28534 | 0.34724 | 0.30943 |
| 68.11570 | ||||||
| 74.64800 | ||||||
| 89.75400 |
Appendix F. Diamond Reservoirs in Polystyrene
References
- Hubbard, W.B.; Nellis, W.J.; Mitchell, A.C.; Holmes, N.C.; Limaye, S.S.; McCandless, P.C. Interior Structure of Neptune: Comparison with Uranus. Science 1991, 253, 648–651. [Google Scholar] [CrossRef]
- Cavazzoni, C.; Chiarotti, L.; Scandolo, S.; Tosatti, E.; Bernasconi, M.; Parrinello, M. Superionic and Metallic States of Water and Ammonia at Giant Planet Conditions. Science 1999, 283, 44–46. [Google Scholar] [CrossRef]
- Pickard, C.J.; Needs, R.J. Highly compressed ammonia forms an ionic crystal. Nat. Mater. 2008, 7, 775–779. [Google Scholar] [CrossRef]
- Ninet, S.; Datchi, F.; Saitta, A.M. Proton disorder and superionicity in hot dense ammonia ice. Phys. Rev. Lett. 2012. [Google Scholar] [CrossRef]
- Hermann, A.; Ashcroft, N.W.; Hoffmann, R. High pressure ices. Proc. Natl. Acad. Sci. USA 2012, 109, 745–750. [Google Scholar] [CrossRef] [PubMed]
- Palasyuk, T.; Troyan, I.; Eremets, M.; Drozd, V.; Medvedev, S.; Zaleski-Ejgierd, P.; Magos-Palasyuk, E.; Wang, H.; Bonev, S.A.; Dudenko, D.; et al. Ammonia as a case study for the spontaneous ionization of a simple hydrogen-bonded compound. Nat. Commun. 2014, 5. [Google Scholar] [CrossRef] [PubMed]
- Ninet, S.; Datchi, F.; Dumas, P.; Mezouar, M.; Garbarino, G.; Mafety, A.; Pickard, C.J.; Needs, R.J.; Saitta, A.M. Experimental and theoretical evidence for an ionic crystal of ammonia at high pressure. Phys. Rev. B Condens. Matter Mater. Phys. 2014, 89, 174103. [Google Scholar] [CrossRef]
- Naden Robinson, V.; Wang, Y.; Ma, Y.; Hermann, A. Stabilization of ammonia-rich hydrate inside icy planets. Proc. Natl. Acad. Sci. USA 2017, 114, 201706244. [Google Scholar] [CrossRef]
- Naden Robinson, V.; Marqués, M.; Wang, Y.; Ma, Y.; Hermann, A. Novel phases in ammonia-water mixtures under pressure. J. Chem. Phys. 2018, 149, 234501. [Google Scholar] [CrossRef] [PubMed]
- Neumann, M.A.; Press, W.; Nöldeke, C.; Asmussen, B.; Prager, M.; Ibberson, R.M. The crystal structure of methane phase III. J. Chem. Phys. 2003, 119, 1586–1589. [Google Scholar] [CrossRef]
- Press, W. Structure and Phase Transitions of Solid Heavy Methane (CD4). J. Chem. Phys. 1972, 56, 2597–2609. [Google Scholar] [CrossRef]
- Umemoto, S.; Yoshii, T.; Akahama, Y.; Kawamura, H. X-ray diffraction measurements for solid methane at high pressures. J. Phys. Condens. Matter 2002, 14, 10675–10678. [Google Scholar] [CrossRef]
- Bini, R.; Pratesi, G. High-pressure infrared study of solid methane: Phase diagram up to 30 GPa. Phys. Rev. B 1997, 55, 14800–14809. [Google Scholar] [CrossRef]
- Maynard-Casely, H.E.; Bull, C.L.; Guthrie, M.; Loa, I.; McMahon, M.I.; Gregoryanz, E.; Nelmes, R.J.; Loveday, J.S. The distorted close-packed crystal structure of methane A. J. Chem. Phys. 2010, 133, 064504. [Google Scholar] [CrossRef]
- Maynard-Casely, H.E.; Lundegaard, L.F.; Loa, I.; McMahon, M.I.; Gregoryanz, E.; Nelmes, R.J.; Loveday, J.S. The crystal structure of methane B at 8 GPa-An alpha-Mn arrangement of molecules. J. Chem. Phys. 2014, 141, 234313. [Google Scholar] [CrossRef] [PubMed]
- Ross, M. The ice layer in Uranus and Neptune—Diamonds in the sky? Nature 1981, 292, 435–436. [Google Scholar] [CrossRef]
- Ancilotto, F.; Chiarotti, G.L.; Scandolo, S.; Tosatti, E. Dissociation of Methane into Hydrocarbons at Extreme (Planetary) Pressure and Temperature. Science 1997, 275, 1288–1290. [Google Scholar] [CrossRef] [PubMed]
- Gao, G.; Oganov, A.R.; Ma, Y.; Wang, H.; Li, P.; Li, Y.; Iitaka, T.; Zou, G. Dissociation of methane under high pressure. J. Chem. Phys. 2010, 133, 144508. [Google Scholar] [CrossRef]
- Bézard, B.; Romani, P.N.; Conrath, B.J.; Maguire, W.C. Hydrocarbons in Neptune’s stratosphere from Voyager infrared observations. J. Geophys. Res. 1991, 96, 18961. [Google Scholar] [CrossRef]
- Sun, L.; Ruoff, A.L.; Zha, C.S.; Stupian, G. Optical properties of methane to 288 GPa at 300 K. J. Phys. Chem. Solids 2006, 67, 2603–2608. [Google Scholar] [CrossRef]
- Sun, L.; Yi, W.; Wang, L.; Shu, J.; Sinogeikin, S.; Meng, Y.; Shen, G.; Bai, L.; Li, Y.; Liu, J.; et al. X-ray diffraction studies and equation of state of methane at 202GPa. Chem. Phys. Lett. 2009, 473, 72–74. [Google Scholar] [CrossRef]
- Proctor, J.E.; Maynard-Casely, H.E.; Hakeem, M.A.; Cantiah, D. Raman spectroscopy of methane (CH4) to 165 GPa: Effect of structural changes on Raman spectra. J. Raman Spectrosc. 2017, 48, 1777–1782. [Google Scholar] [CrossRef]
- Hirai, H.; Konagai, K.; Kawamura, T.; Yamamoto, Y.; Yagi, T. Polymerization and diamond formation from melting methane and their implications in ice layer of giant planets. Phys. Earth Planet. Inter. 2009. [Google Scholar] [CrossRef]
- Benedetti, L.R.; Nguyen, J.H.; Caldwell, W.A.; Liu, H.; Kruger, M.; Jeanloz, R. Dissociation of CH4 at High Pressures and Temperatures: Diamond Formation in Giant Planet Interiors? Science 2000, 286, 100–102. [Google Scholar] [CrossRef]
- Hazen, R.M.; Mao, H.K.; Finger, L.W.; Bell, P.M. Structure and compression of crystalline methane at high pressure and room temperature. Appl. Phys. Lett. 1980, 37, 288–289. [Google Scholar] [CrossRef]
- Chyba, C.; Sagan, C. Endogenous production, exogenous delivery and impact-shock synthesis of organic molecules: An inventory for the origins of life. Nature 1992, 355, 125–132. [Google Scholar] [CrossRef]
- Furukawa, Y.; Sekine, T.; Oba, M.; Kakegawa, T.; Nakazawa, H. Biomolecule formation by oceanic impacts on early Earth. Nat. Geosci. 2009, 2, 62–66. [Google Scholar] [CrossRef]
- Goldman, N.; Reed, E.J.; Fried, L.E.; William Kuo, I.F.; Maiti, A. Synthesis of glycine-containing complexes in impacts of comets on early Earth. Nat. Chem. 2010, 2, 949–954. [Google Scholar] [CrossRef] [PubMed]
- Martins, Z.; Price, M.C.; Goldman, N.; Sephton, M.A.; Burchell, M.J. Shock synthesis of amino acids from impacting cometary and icy planet surface analogues. Nat. Geosci. 2013, 6, 1045–1049. [Google Scholar] [CrossRef]
- Fitzgibbons, T.C.; Guthrie, M.; Xu, E.S.; Crespi, V.H.; Davidowski, S.K.; Cody, G.D.; Alem, N.; Badding, J.V. Benzene-derived carbon nanothreads. Nat. Mater. 2015, 14, 43–47. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Hoffmann, R.; Ashcroft, N.W.; Badding, J.; Xu, E.; Crespi, V. Linearly Polymerized Benzene Arrays As Intermediates, Tracing Pathways to Carbon Nanothreads. J. Am. Chem. Soc. 2015, 137, 14373–14386. [Google Scholar] [CrossRef]
- Zhan, H.; Zhang, G.; Tan, V.B.C.; Gu, Y. The best features of diamond nanothread for nanofibre applications. Nat. Commun. 2017, 8, 14863. [Google Scholar] [CrossRef] [PubMed]
- Nellis, W.J.; Ree, F.H.; Trainor, R.J.; Mitchell, A.C.; Boslough, M.B. Equation of state and optical luminosity of benzene, polybutene, and polyethylene shocked to 210 GPa (2.1 Mbar). J. Chem. Phys. 1984, 80, 2789–2799. [Google Scholar] [CrossRef]
- Cauble, R.; Da Silva, L.B.; Perry, T.S.; Bach, D.R.; Budil, K.S.; Celliers, P.; Collins, G.W.; Ng, A.; Barbee, T.W., Jr.; Hammel, B.A.; et al. Absolute measurements of the equations of state of low-Z materials in the multi-Mbar regime using laser-driven shocks. Phys. Plasmas 1997, 4, 1857–1861. [Google Scholar] [CrossRef]
- Barrios, M.A.; Hicks, D.G.; Boehly, T.R.; Fratanduono, D.E.; Eggert, J.H.; Celliers, P.M.; Collins, G.W.; Meyerhofer, D.D. High-precision measurements of the equation of state of hydrocarbons at 1–10 Mbar using laser-driven shock waves. Phys. Plasmas 2010, 17, 056307. [Google Scholar] [CrossRef]
- Kraus, D.; Chapman, D.A.; Kritcher, A.L.; Baggott, R.A.; Bachmann, B.; Collins, G.W.; Glenzer, S.H.; Hawreliak, J.A.; Kalantar, D.H.; Landen, O.L.; et al. X-ray scattering measurements on imploding CH spheres at the National Ignition Facility. Phys. Rev. E 2016, 94, 011202. [Google Scholar] [CrossRef] [PubMed]
- Kraus, D.; Vorberger, J.; Pak, A.; Hartley, N.J.; Fletcher, L.B.; Frydrych, S.; Galtier, E.; Gamboa, E.J.; Gericke, D.O.; Glenzer, S.H.; et al. Formation of diamonds in laser-compressed hydrocarbons at planetary interior conditions. Nat. Astron. 2017, 1, 606–611. [Google Scholar] [CrossRef]
- Kraus, D.; Hartley, N.J.; Frydrych, S.; Schuster, A.K.; Rohatsch, K.; Rödel, M.; Cowan, T.E.; Brown, S.; Cunningham, E.; Van Driel, T.; et al. High-pressure chemistry of hydrocarbons relevant to planetary interiors and inertial confinement fusion. Phys. Plasmas 2018, 25. [Google Scholar] [CrossRef]
- Hartley, N.J.; Vorberger, J.; Döppner, T.; Cowan, T.; Falcone, R.W.; Fletcher, L.B.; Frydrych, S.; Galtier, E.; Gamboa, E.J.; Gericke, D.O.; et al. Liquid Structure of Shock-Compressed Hydrocarbons at Megabar Pressures. Phys. Rev. Lett. 2018, 121, 245501. [Google Scholar] [CrossRef]
- Hartley, N.J.; Brown, S.; Cowan, T.E.; Cunningham, E.; Döppner, T.; Falcone, R.W.; Fletcher, L.B.; Frydrych, S.; Galtier, E.; Gamboa, E.J.; et al. Evidence for Crystalline Structure in Dynamically-Compressed Polyethylene up to 200 GPa. Sci. Rep. 2019, 9, 4196. [Google Scholar] [CrossRef]
- Mattsson, T.R.; Lane, J.M.D.; Cochrane, K.R.; Desjarlais, M.P.; Thompson, A.P.; Pierce, F.; Grest, G.S. First-principles and classical molecular dynamics simulation of shocked polymers. Phys. Rev. B 2010, 81, 054103. [Google Scholar] [CrossRef]
- Hu, S.X.; Collins, L.A.; Goncharov, V.N.; Kress, J.D.; McCrory, R.L.; Skupsky, S. First-principles equation of state of polystyrene and its effect on inertial confinement fusion implosions. Phys. Rev. E 2015, 92, 043104. [Google Scholar] [CrossRef]
- Hu, S.X.; Collins, L.A.; Goncharov, V.N.; Kress, J.D.; McCrory, R.L.; Skupsky, S. First-principles investigations on ionization and thermal conductivity of polystyrene for inertial confinement fusion applications. Phys. Plasmas 2016, 23, 042704. [Google Scholar] [CrossRef]
- Colin-Lalu, P.; Recoules, V.; Salin, G.; Plisson, T.; Brambrink, E.; Vinci, T.; Bolis, R.; Huser, G. Dissociation along the principal Hugoniot of the Laser Mégajoule ablator material. Phys. Rev. E 2016, 94, 023204. [Google Scholar] [CrossRef]
- Zhang, S.; Driver, K.P.; Soubiran, F.; Militzer, B. First-principles equation of state and shock compression predictions of warm dense hydrocarbons. Phys. Rev. E 2017, 96, 013204. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Militzer, B.; Benedict, L.X.; Soubiran, F.; Sterne, P.A.; Driver, K.P. Path integral Monte Carlo simulations of dense carbon-hydrogen plasmas. J. Chem. Phys. 2018, 148, 102318. [Google Scholar] [CrossRef]
- Liu, H.; Naumov, I.I.; Hemley, R.J. Dense Hydrocarbon Structures at Megabar Pressures. J. Phys. Chem. Lett. 2016, 7, 4218–4222. [Google Scholar] [CrossRef]
- Liu, Y.; Duan, D.; Tian, F.; Huang, X.; Li, D.; Zhao, Z.; Sha, X.; Chu, B.; Zhang, H.; Liu, B.; et al. Crystal structures and properties of the CH4H2compound under high pressure. RSC Adv. 2014, 4, 37569–37574. [Google Scholar] [CrossRef]
- Saleh, G.; Oganov, A.R. Novel Stable Compounds in the C-H-O Ternary System at High Pressure. Sci. Rep. 2016, 6, 32486. [Google Scholar] [CrossRef]
- Wen, X.D.; Hand, L.; Labet, V.; Yang, T.; Hoffmann, R.; Ashcroft, N.W.; Oganov, A.R.; Lyakhov, A.O. Graphane sheets and crystals under pressure. Proc. Natl. Acad. Sci. USA 2011, 108, 6833–6837. [Google Scholar] [CrossRef]
- Ji, C.; Goncharov, A.F.; Shukla, V.; Jena, N.K.; Popov, D.; Li, B.; Wang, J.; Meng, Y.; Prakapenka, V.B.; Smith, J.S.; et al. Stability of Ar(H2)2 to 358 GPa. Proc. Natl. Acad. Sci. USA 2017, 114, 3596–3600. [Google Scholar] [CrossRef] [PubMed]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Krist. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Pickard, C.J.; Needs, R.J. Structure of phase III of solid hydrogen. Nat. Phys. 2007, 3, 473–476. [Google Scholar] [CrossRef]
- Fontana, L.; Vinh, D.Q.; Santoro, M.; Scandolo, S.; Gorelli, F.A.; Bini, R.; Hanfland, M. High-pressure crystalline polyethylene studied by x-ray diffraction and ab initio simulations. Phys. Rev. B Condens. Matter Mater. Phys. 2007, 75, 174112. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Frank, W.; Elsässer, C.; Fähnle, M. Ab initio force-constant method for phonon dispersions in alkali metals. Phys. Rev. Lett. 1995, 74, 1791–1794. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 2012, 183, 2063–2070. [Google Scholar] [CrossRef]
- Teeratchanan, P.; Hermann, A. Computational phase diagrams of noble gas hydrates under pressure. J. Chem. Phys. 2015, 143. [Google Scholar] [CrossRef] [PubMed]
- Košata, J.; Merkl, P.; Teeratchanan, P.; Hermann, A. Stability of Hydrogen Hydrates from Second-Order Møller–Plesset Perturbation Theory. J. Phys. Chem. Lett. 2018, 9, 5624–5629. [Google Scholar] [CrossRef]
- Bonev, S.A.; Schwegler, E.; Ogitsu, T.; Galli, G. A quantum fluid of metallic hydrogen suggested by first-principles calculations. Nature 2004, 431, 669–672. [Google Scholar] [CrossRef]
- Pickard, C.J.; Martinez-Canales, M.; Needs, R.J. Decomposition and Terapascal Phases of Water Ice. Phys. Rev. Lett. 2013, 110, 245701. [Google Scholar] [CrossRef]
- Howie, R.T.; Guillaume, C.L.; Scheler, T.; Goncharov, A.F.; Gregoryanz, E. Mixed Molecular and Atomic Phase of Dense Hydrogen. Phys. Rev. Lett. 2012, 108, 125501. [Google Scholar] [CrossRef] [PubMed]
- Qian, G.R.; Hu, C.H.; Oganov, A.R.; Zeng, Q.; Zhou, H.Y.; Niu, H.; Hu, C.H.; Oganov, A.R.; Zeng, Q.; Zhou, H.Y. Diverse Chemistry of Stable Hydronitrogens, and Implications for Planetary and Materials Sciences. Sci. Rep. 2016, 6, 25947. [Google Scholar] [CrossRef] [PubMed]
- Reilly, A.M.; Cooper, R.I.; Adjiman, C.S.; Bhattacharya, S.; Boese, A.D.; Brandenburg, J.G.; Bygrave, P.J.; Bylsma, R.; Campbell, J.E.; Car, R.; et al. Report on the sixth blind test of organic crystal structure prediction methods. Acta Crystallogr. Sect. B 2016, 72, 439–459. [Google Scholar] [CrossRef] [PubMed]
- Bini, R.; Ceppatelli, M.; Citroni, M.; Schettino, V. From simple to complex and backwards. Chemical reactions under very high pressure. Chem. Phys. 2012, 398, 262–268. [Google Scholar] [CrossRef]
- Ghiringhelli, L.M.; Valeriani, C.; Meijer, E.J.; Frenkel, D. Local structure of liquid carbon controls diamond nucleation. Phys. Rev. Lett. 2007, 99, 055702. [Google Scholar] [CrossRef]
- Mao, H.K.; Jephcoat, A.P.; Hemley, R.J.; Finger, L.W.; Zha, C.S.; Hazen, R.M.; Cox, D.E. Synchrotron X-ray Diffraction Measurements of Single-Crystal Hydrogen to 26.5 Gigapascals. Science 1988, 239, 1131–1134. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Conway, L.J.; Hermann, A. High Pressure Hydrocarbons Revisited: From van der Waals Compounds to Diamond. Geosciences 2019, 9, 227. https://doi.org/10.3390/geosciences9050227
Conway LJ, Hermann A. High Pressure Hydrocarbons Revisited: From van der Waals Compounds to Diamond. Geosciences. 2019; 9(5):227. https://doi.org/10.3390/geosciences9050227
Chicago/Turabian StyleConway, Lewis J., and Andreas Hermann. 2019. "High Pressure Hydrocarbons Revisited: From van der Waals Compounds to Diamond" Geosciences 9, no. 5: 227. https://doi.org/10.3390/geosciences9050227
APA StyleConway, L. J., & Hermann, A. (2019). High Pressure Hydrocarbons Revisited: From van der Waals Compounds to Diamond. Geosciences, 9(5), 227. https://doi.org/10.3390/geosciences9050227