Finite Element Modelling of Coupled Fluid-Flow and Geomechanical Aspects for the Sustainable Exploitation of Reservoirs: The Case Study of the Cavone Reservoir
Abstract
1. Introduction
2. Basic Statements and Problem Setting
3. Preliminary Assessment of the Pressure at the Cavone Oilfield
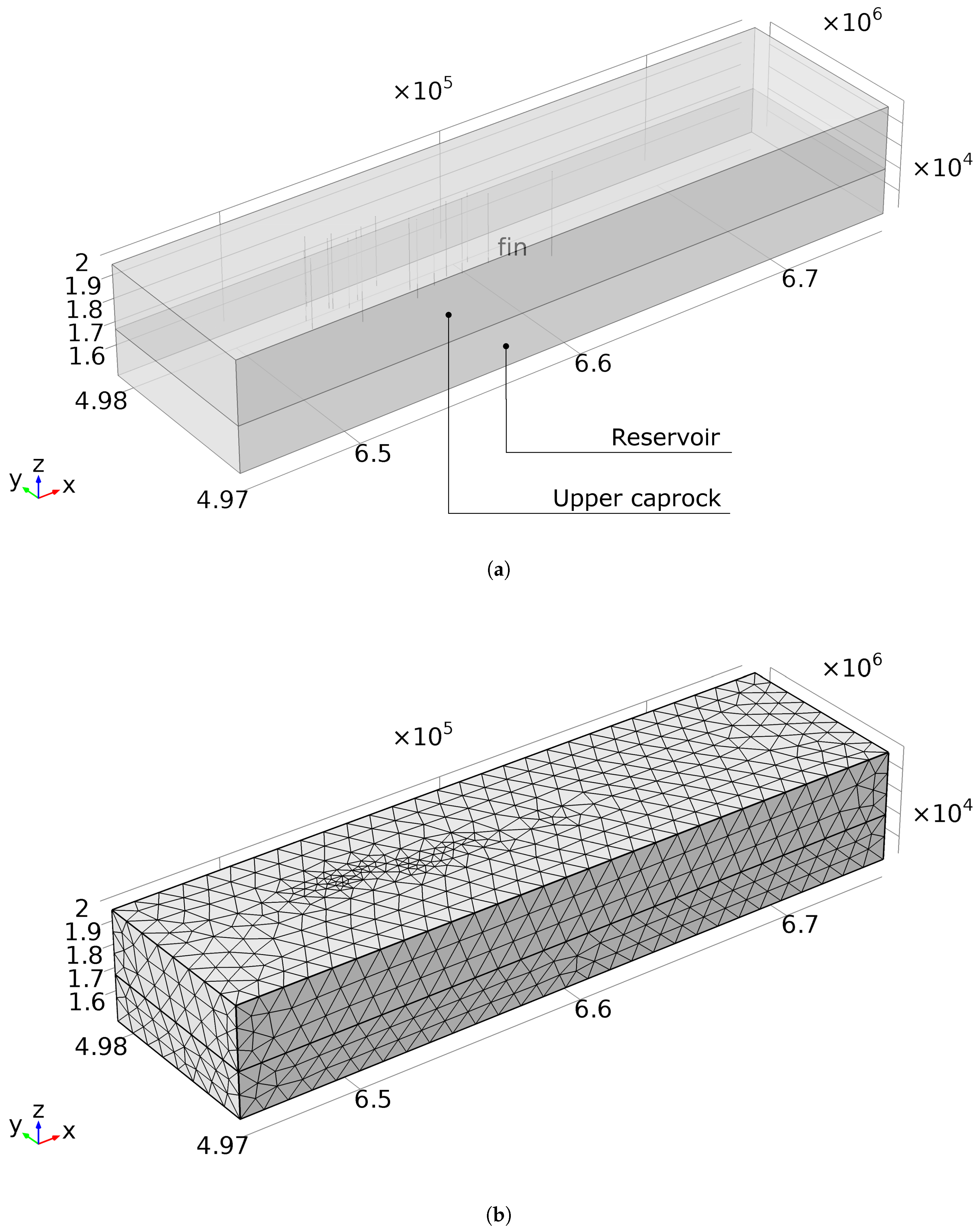
3.1. Finite Element Model of the Reservoir
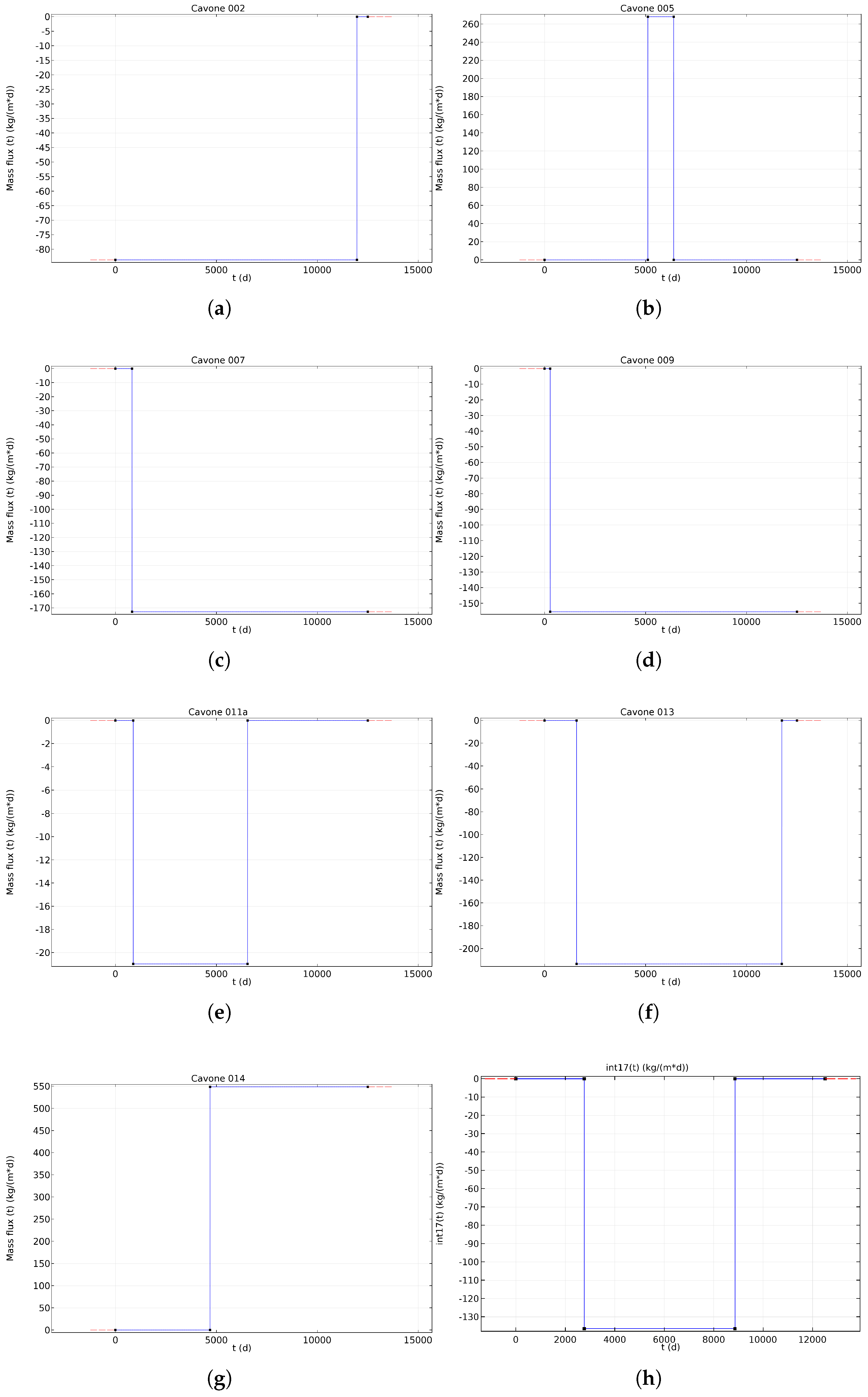
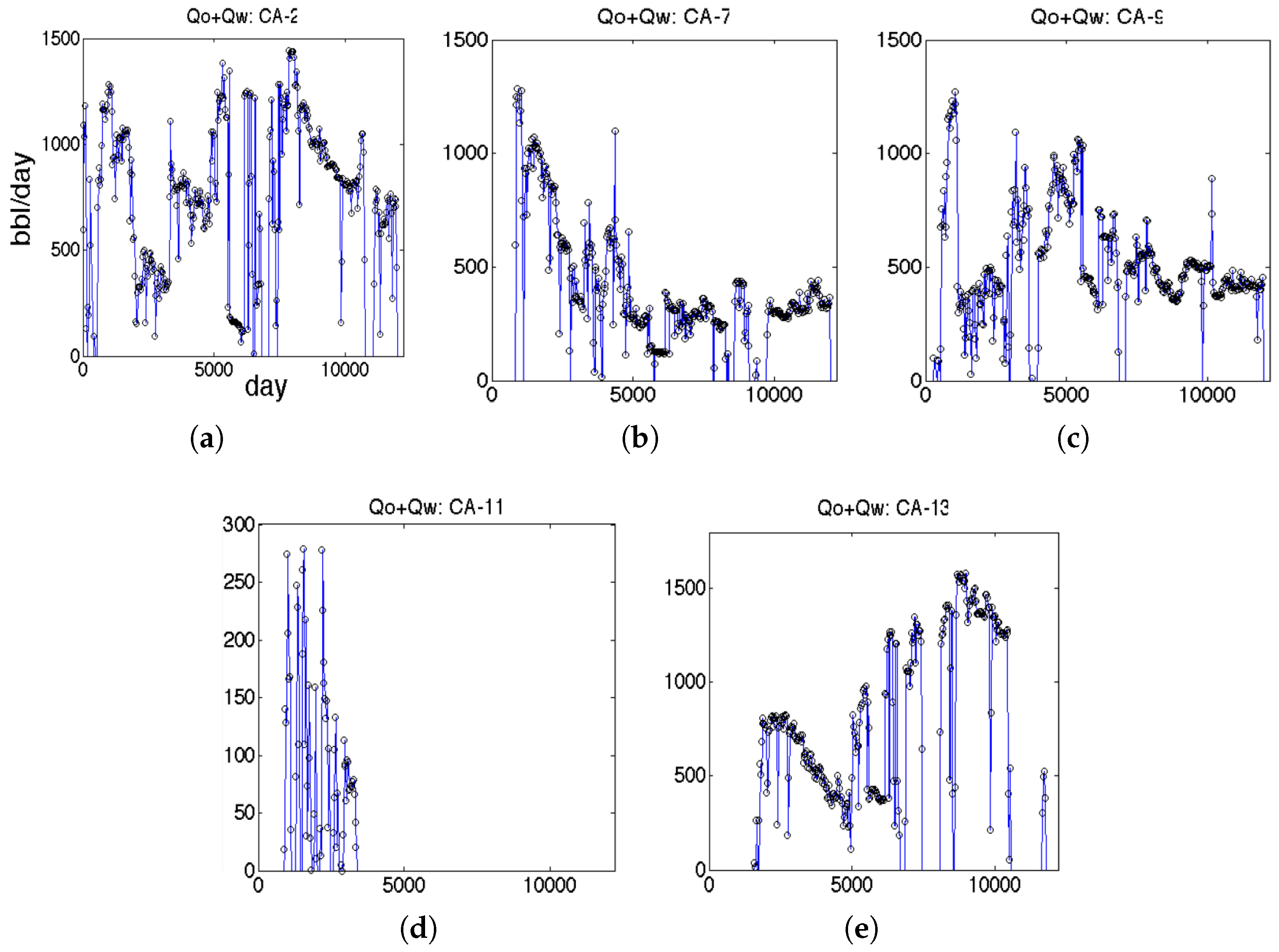
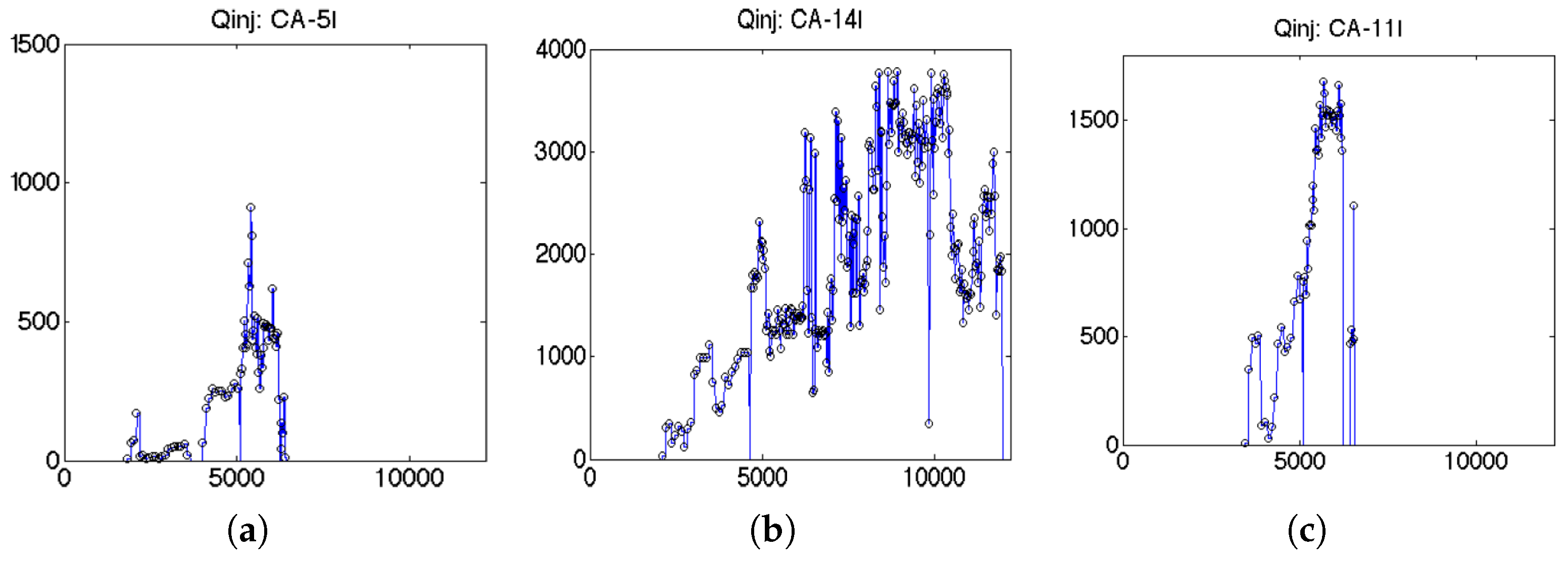
3.2. Production Activity
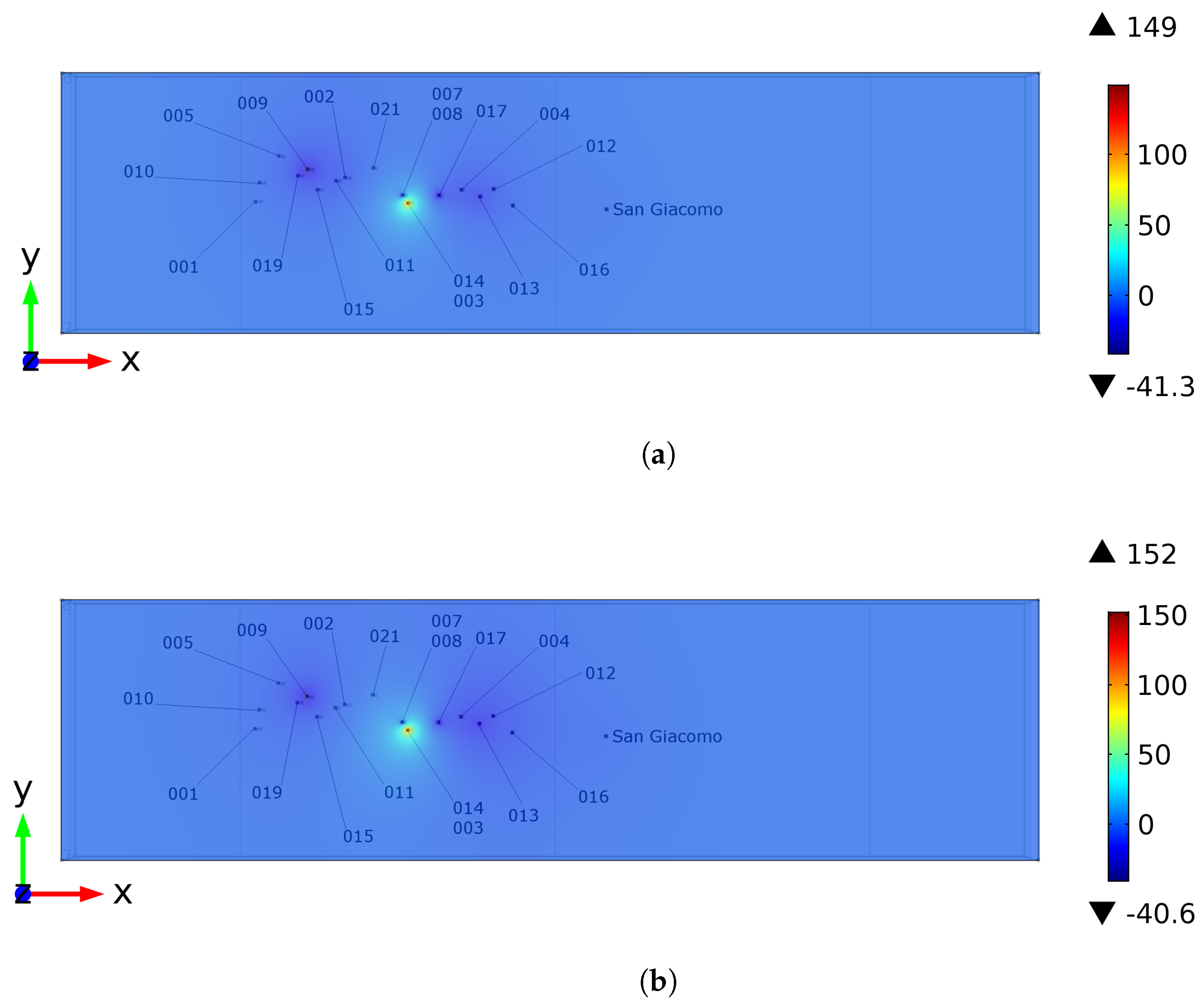
3.3. Results
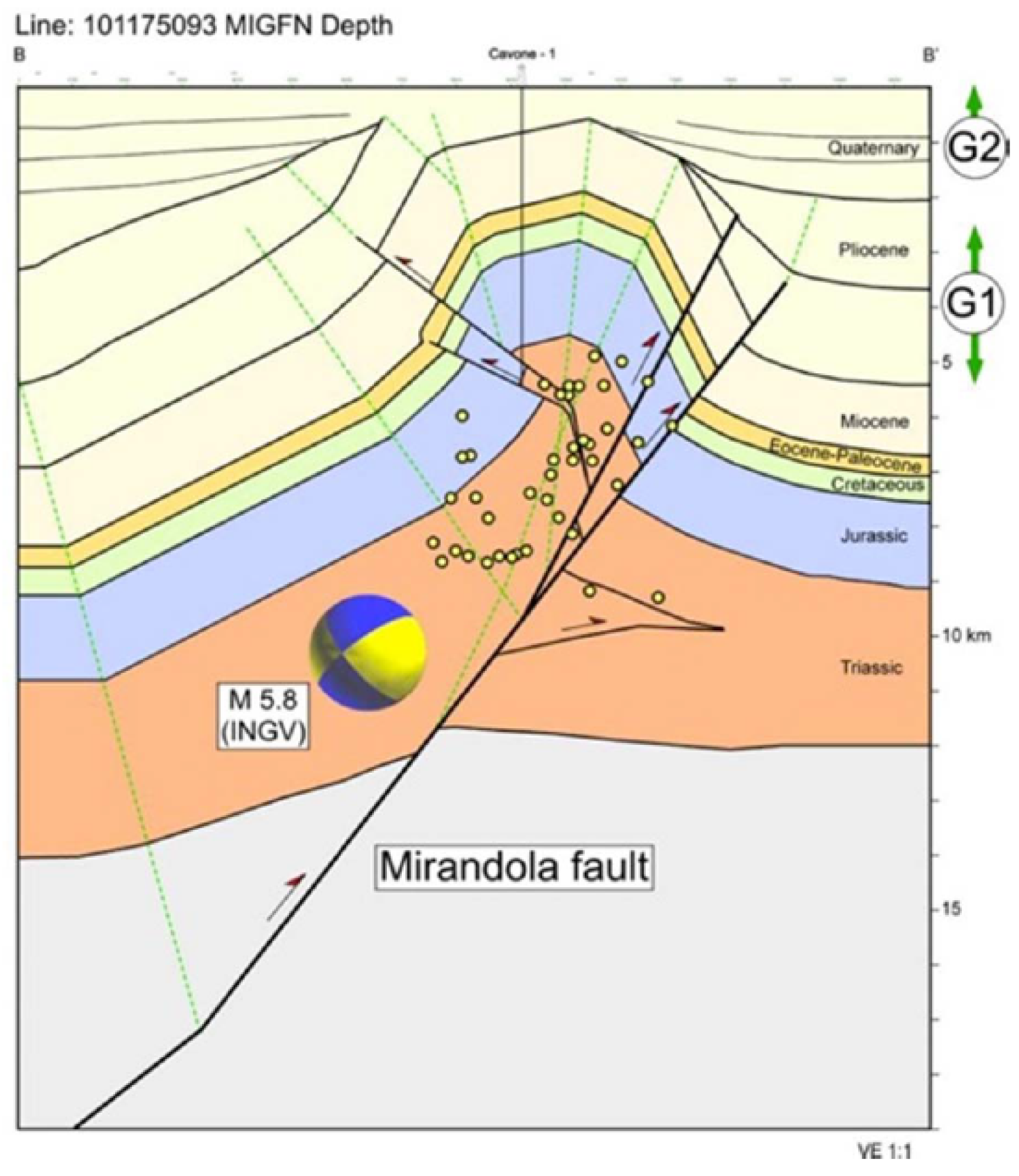
4. Modeling the Mirandola Fault and the Cavone Oilfield
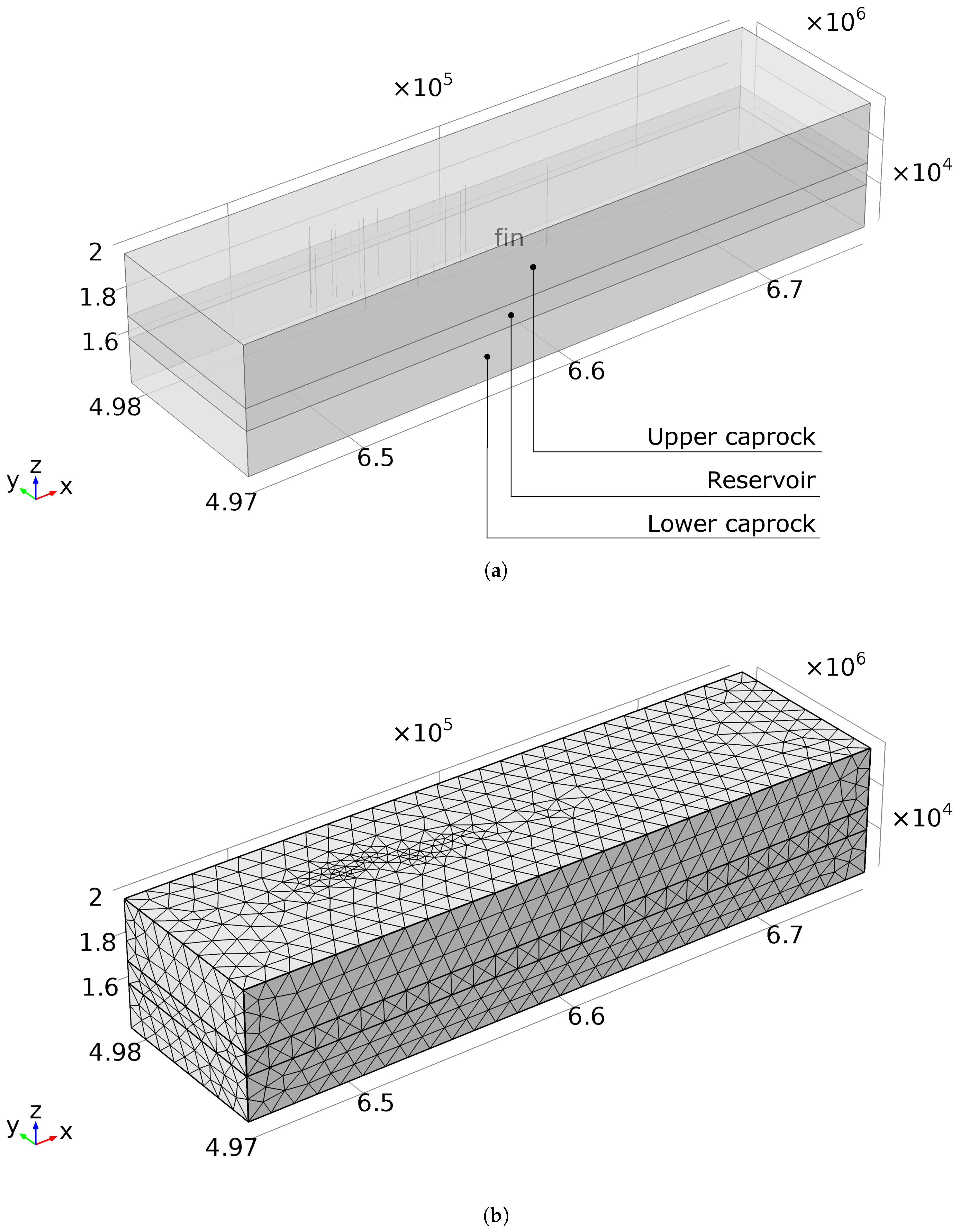
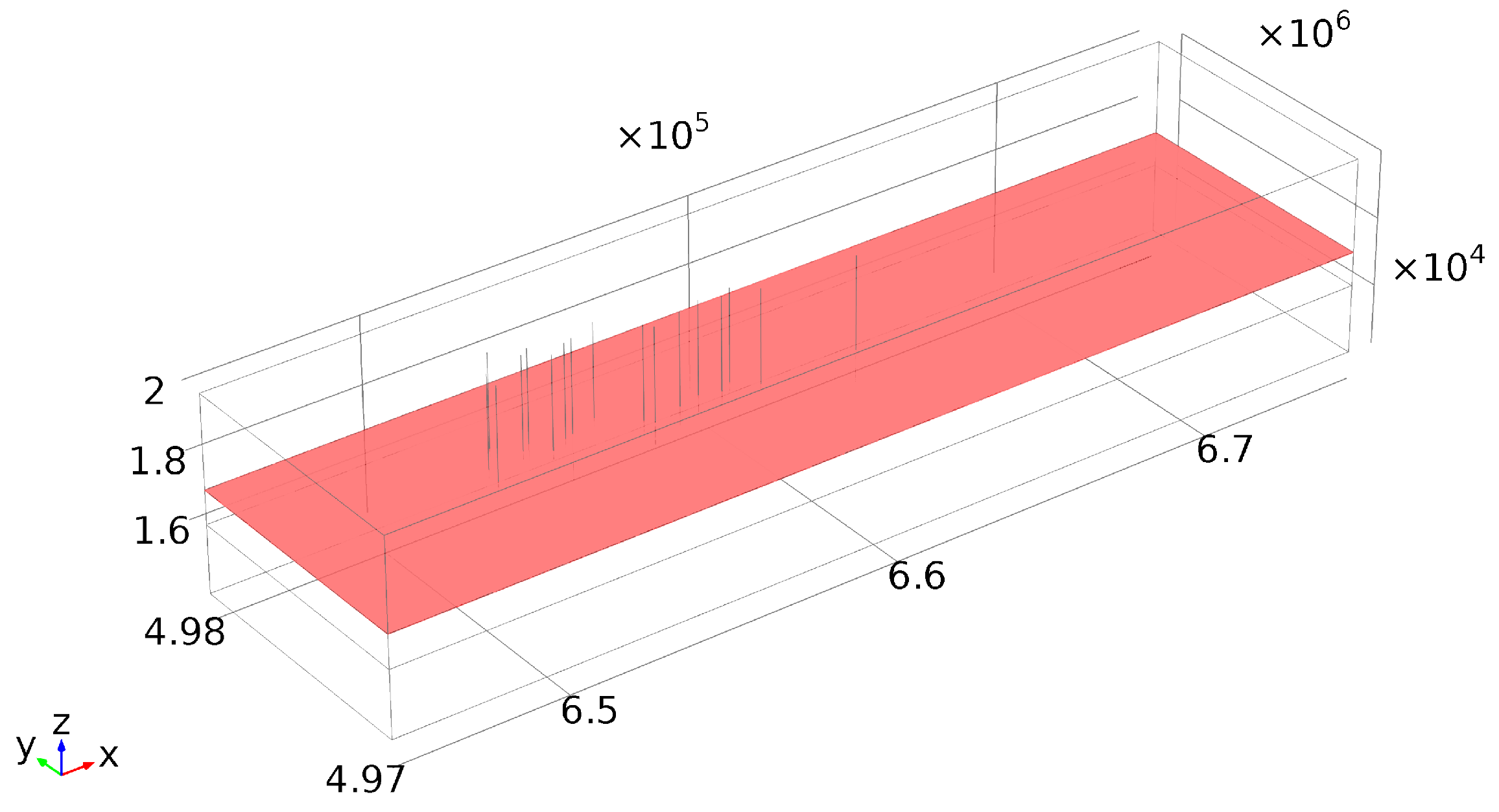
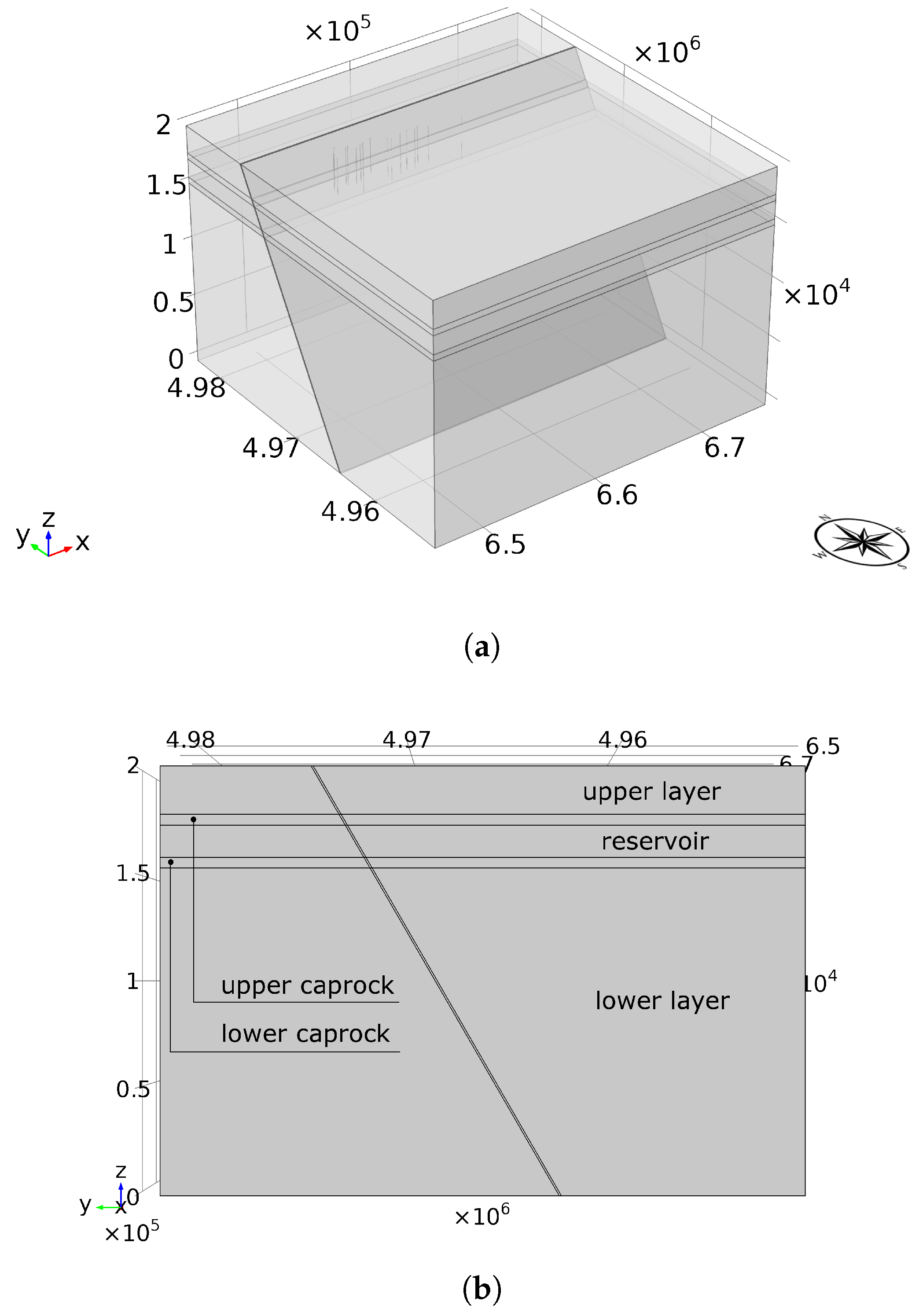
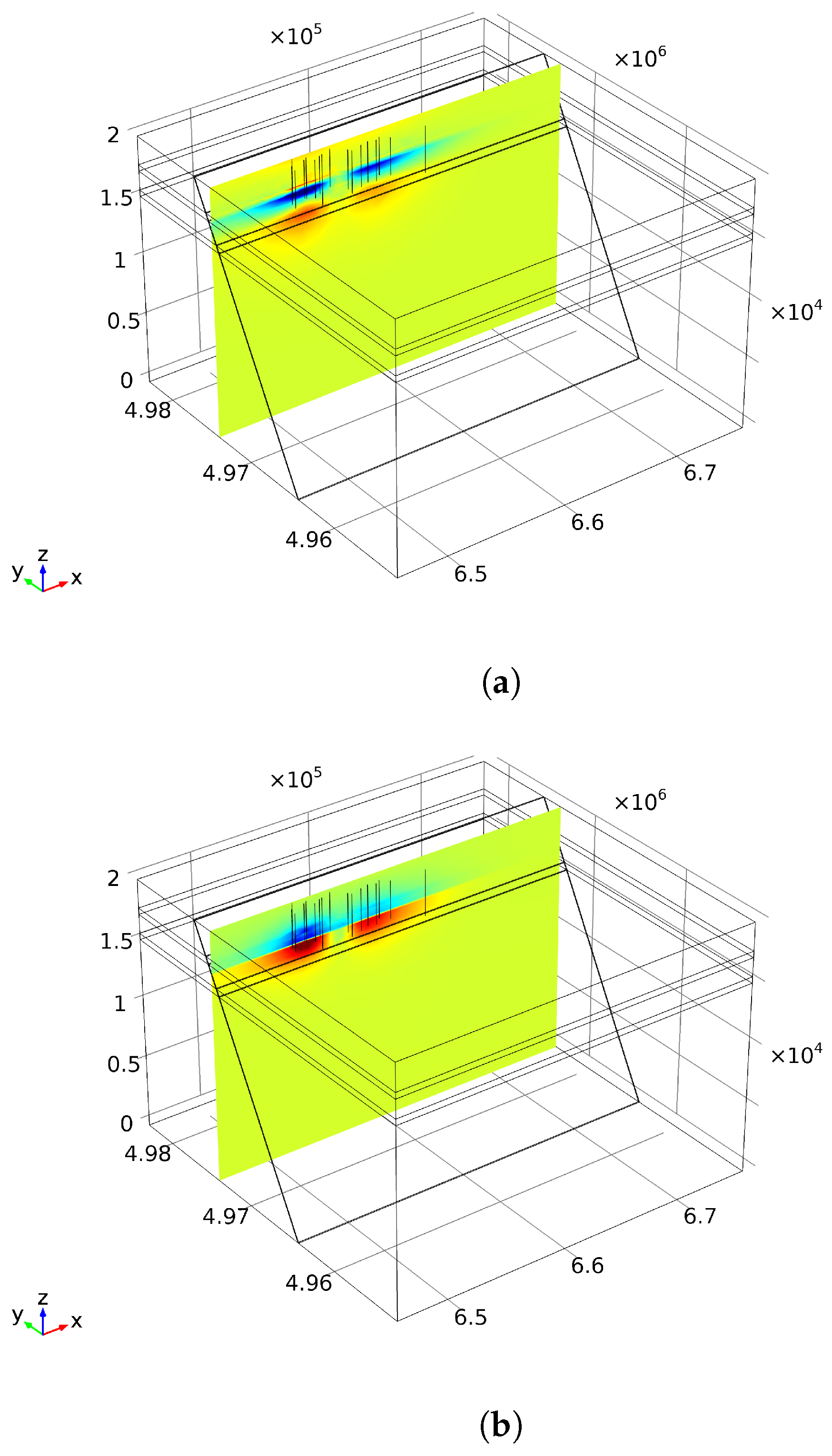
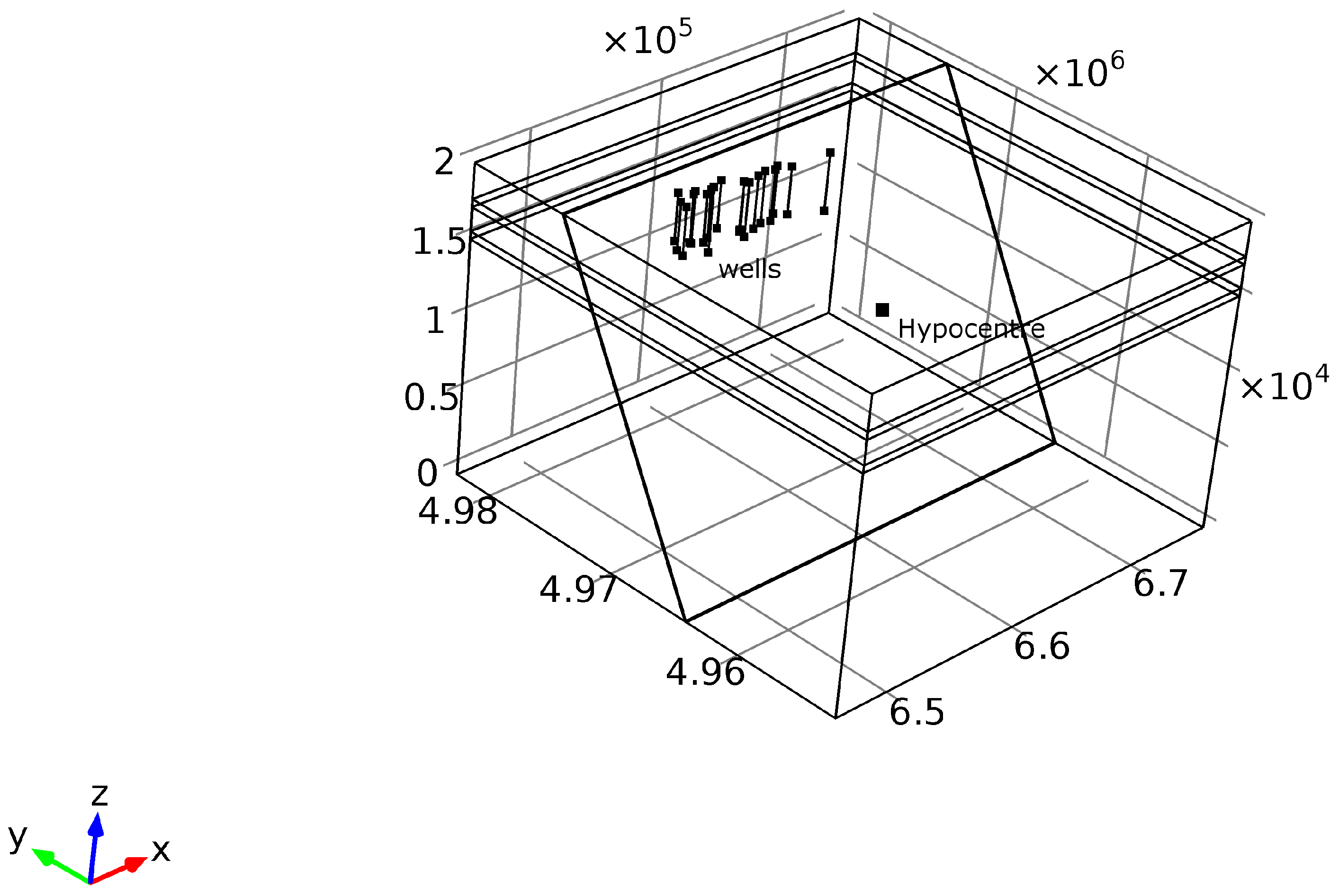
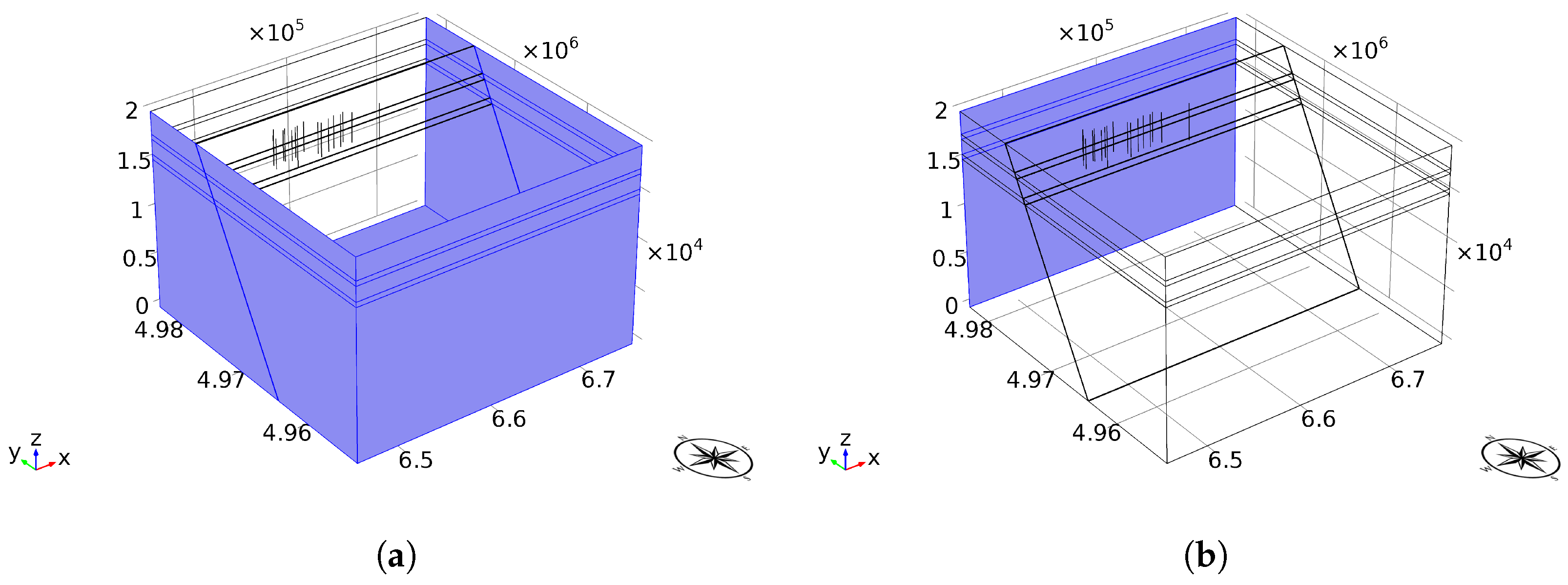
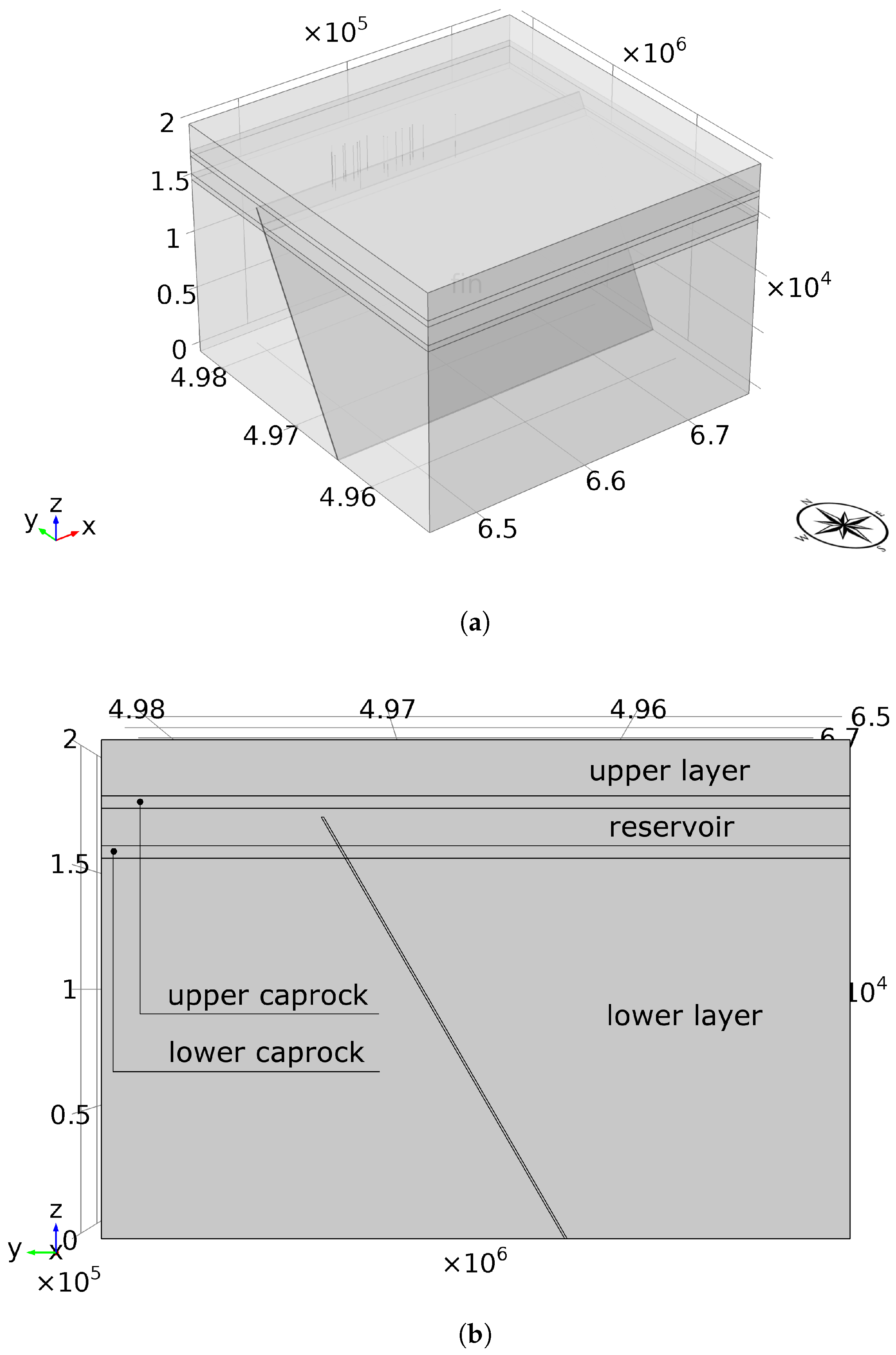
4.1. Model Geometry
4.2. Production Activities
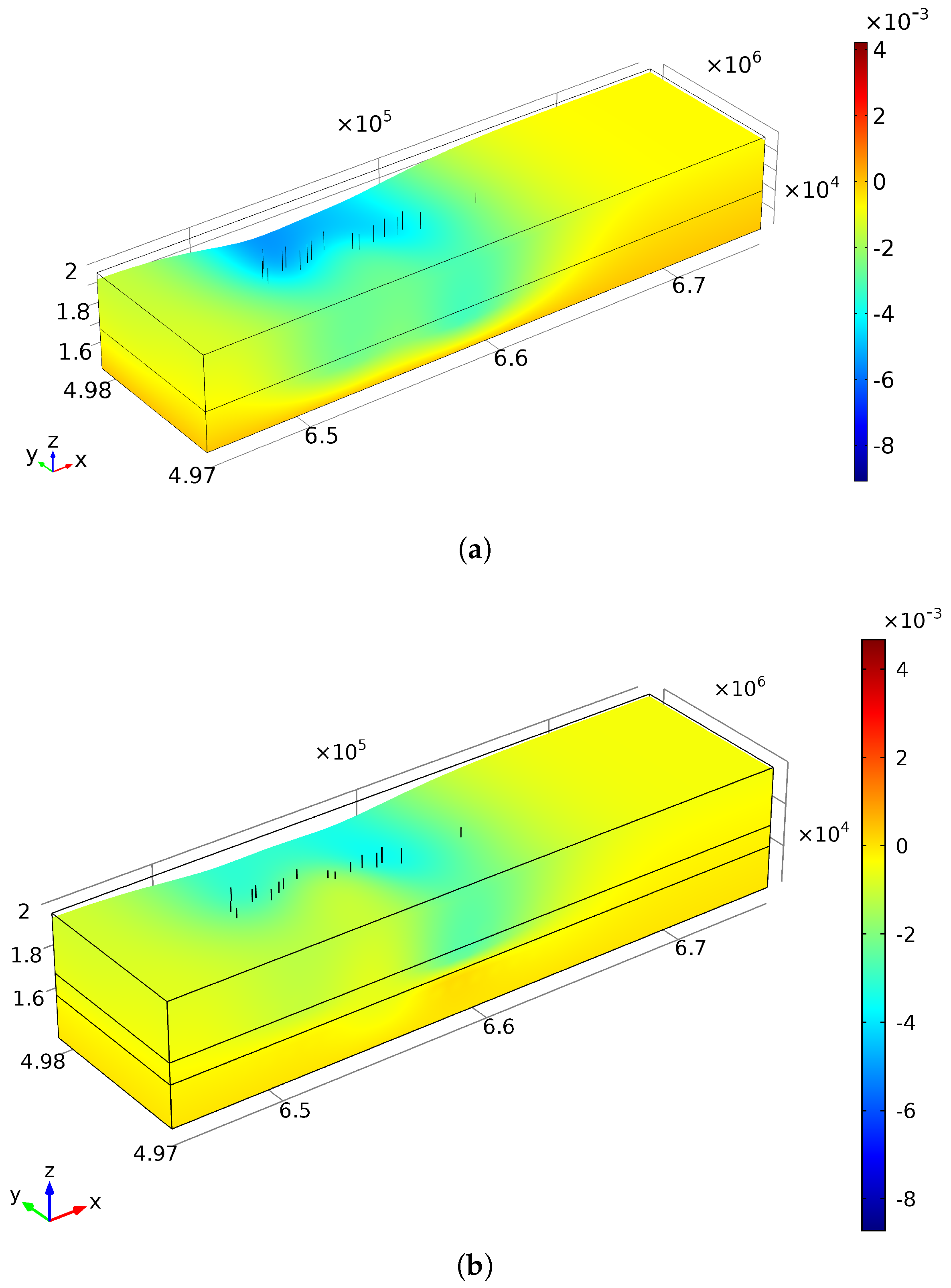
4.3. Mirandola Fault and Cavone Oilfield without In Situ Stress
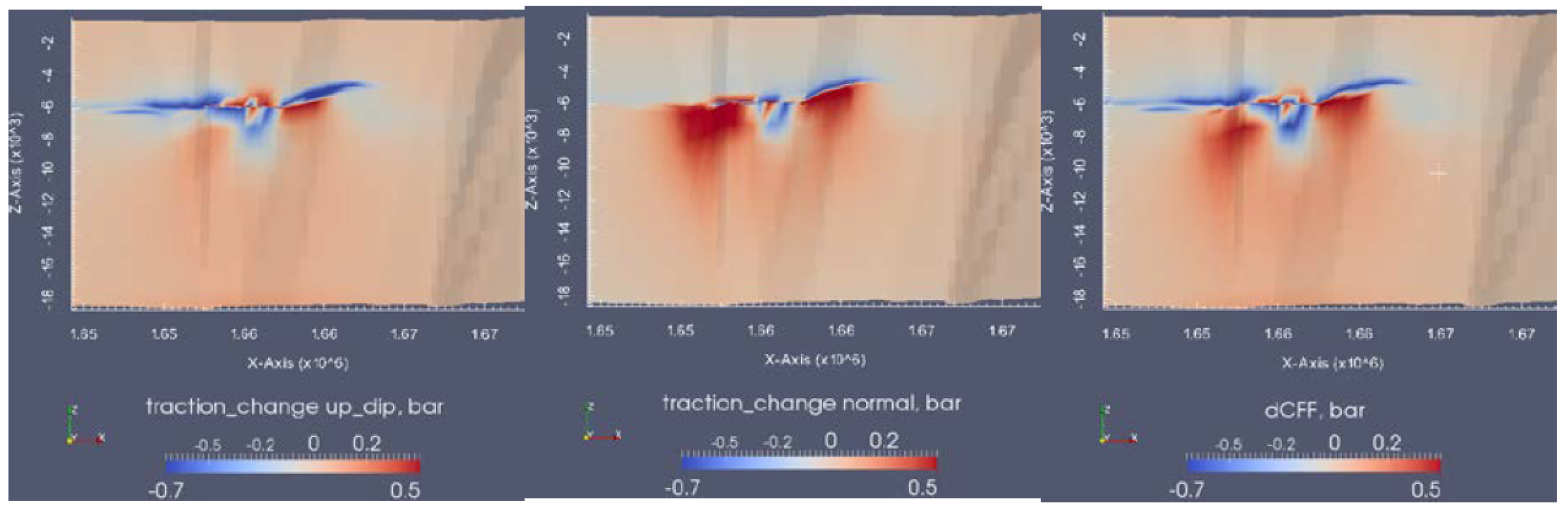
5. Coulomb Stress Changes
5.1. In Situ Stress Field
5.2. Variable Lower Caprock Permeability
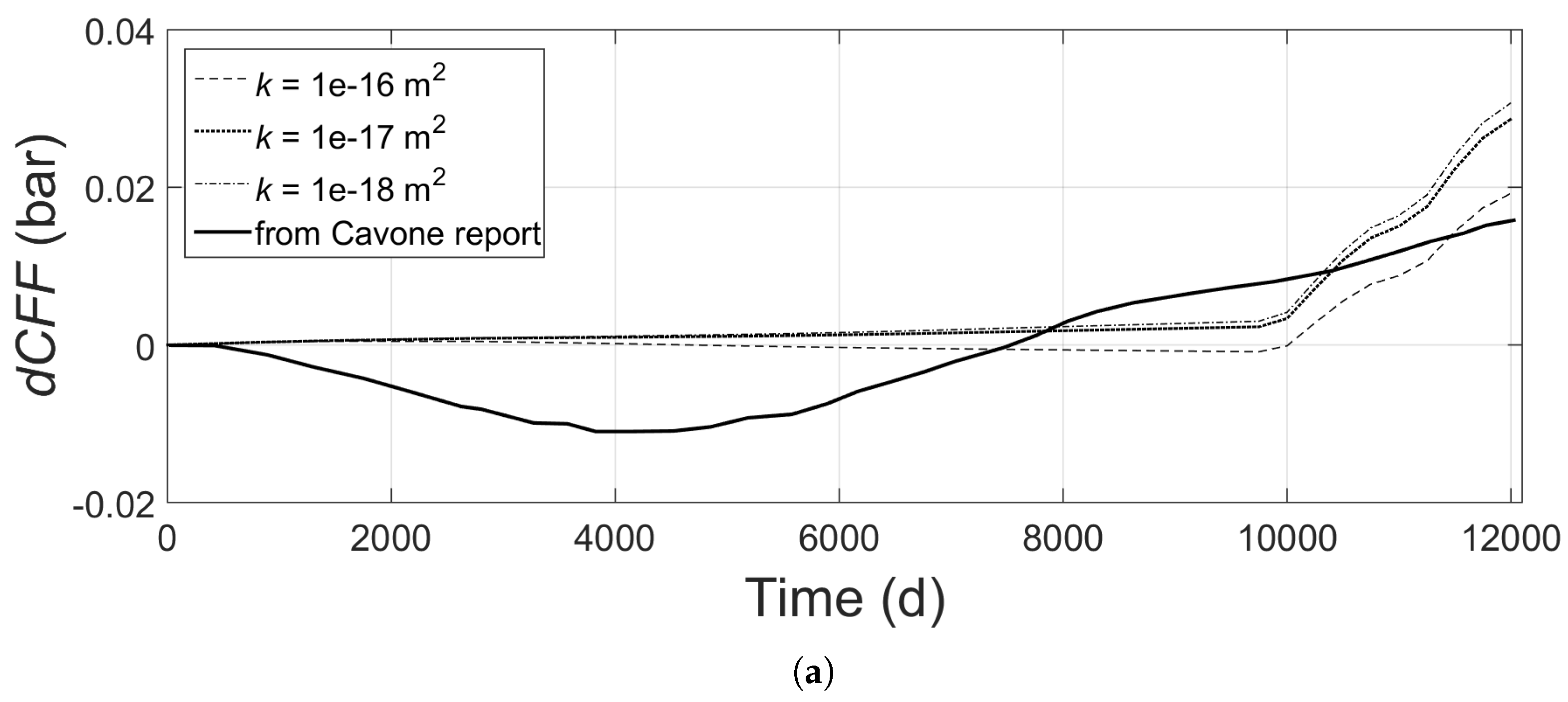
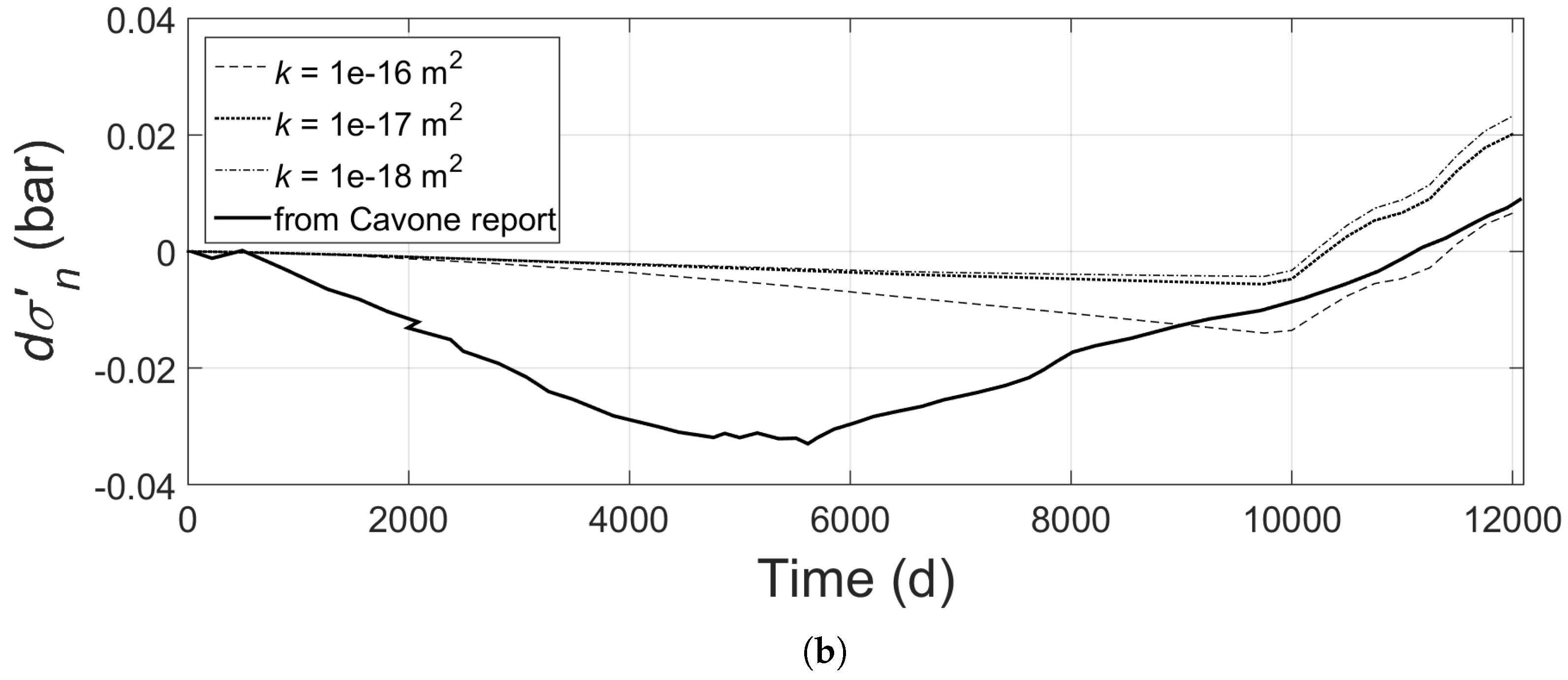
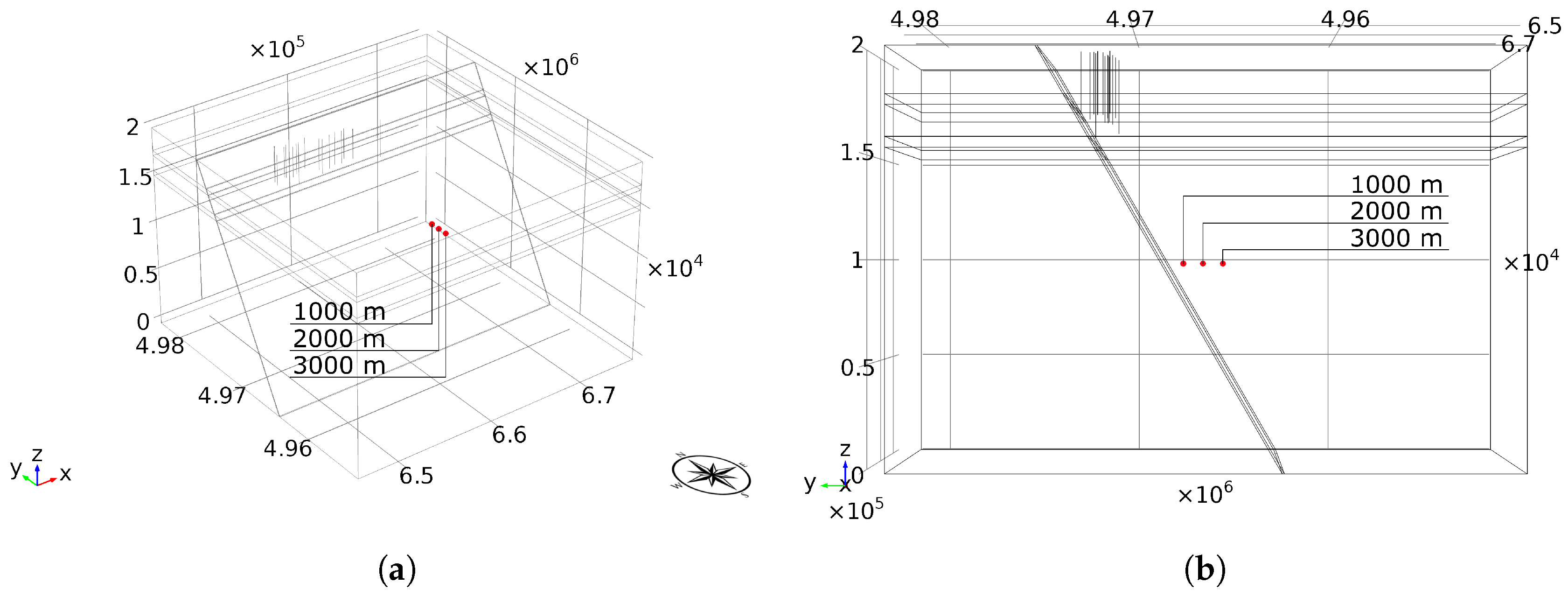
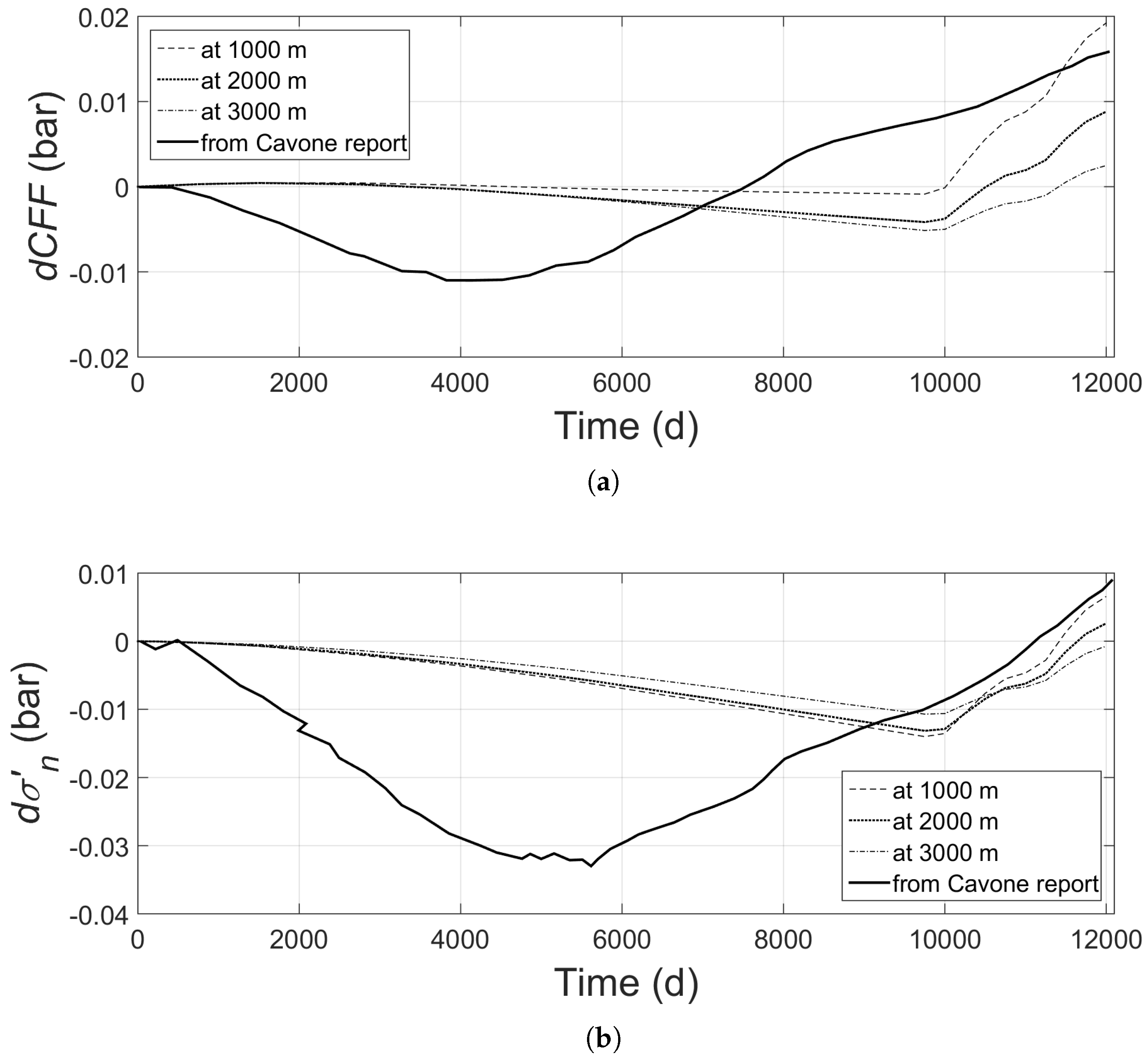
5.3. Results at Different Distances from the Hypocentre
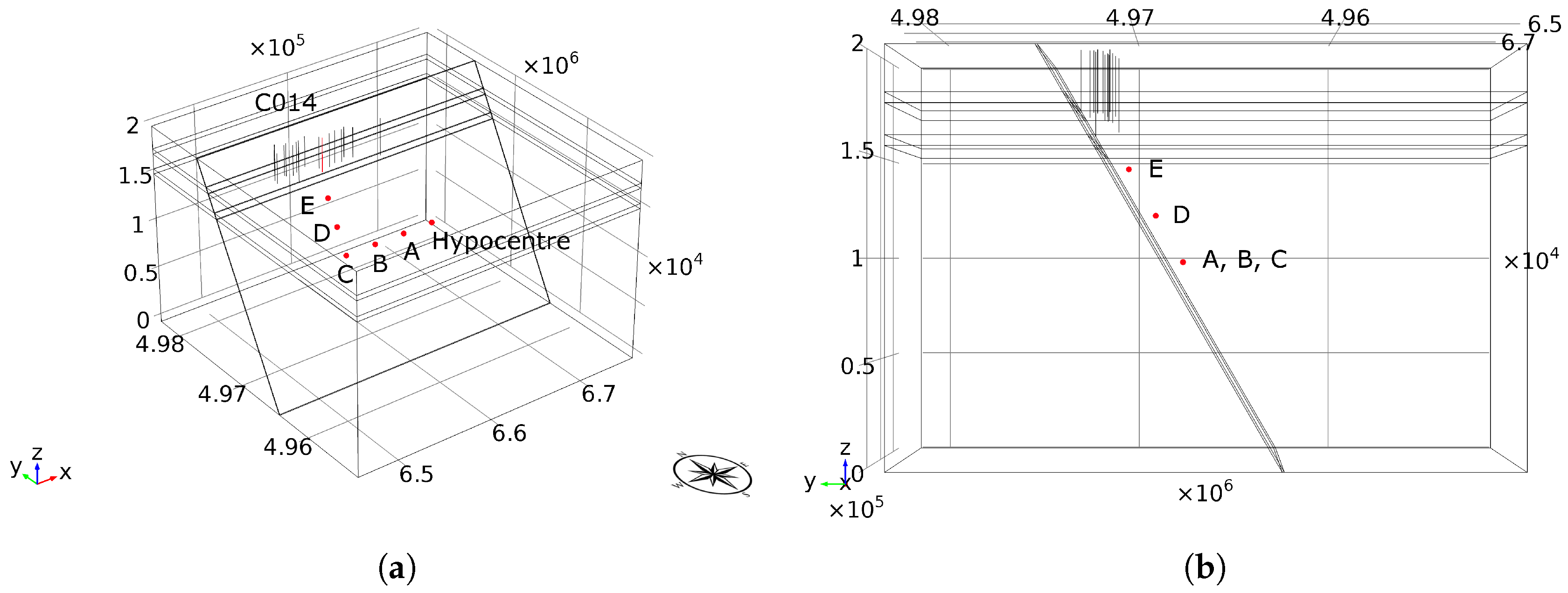
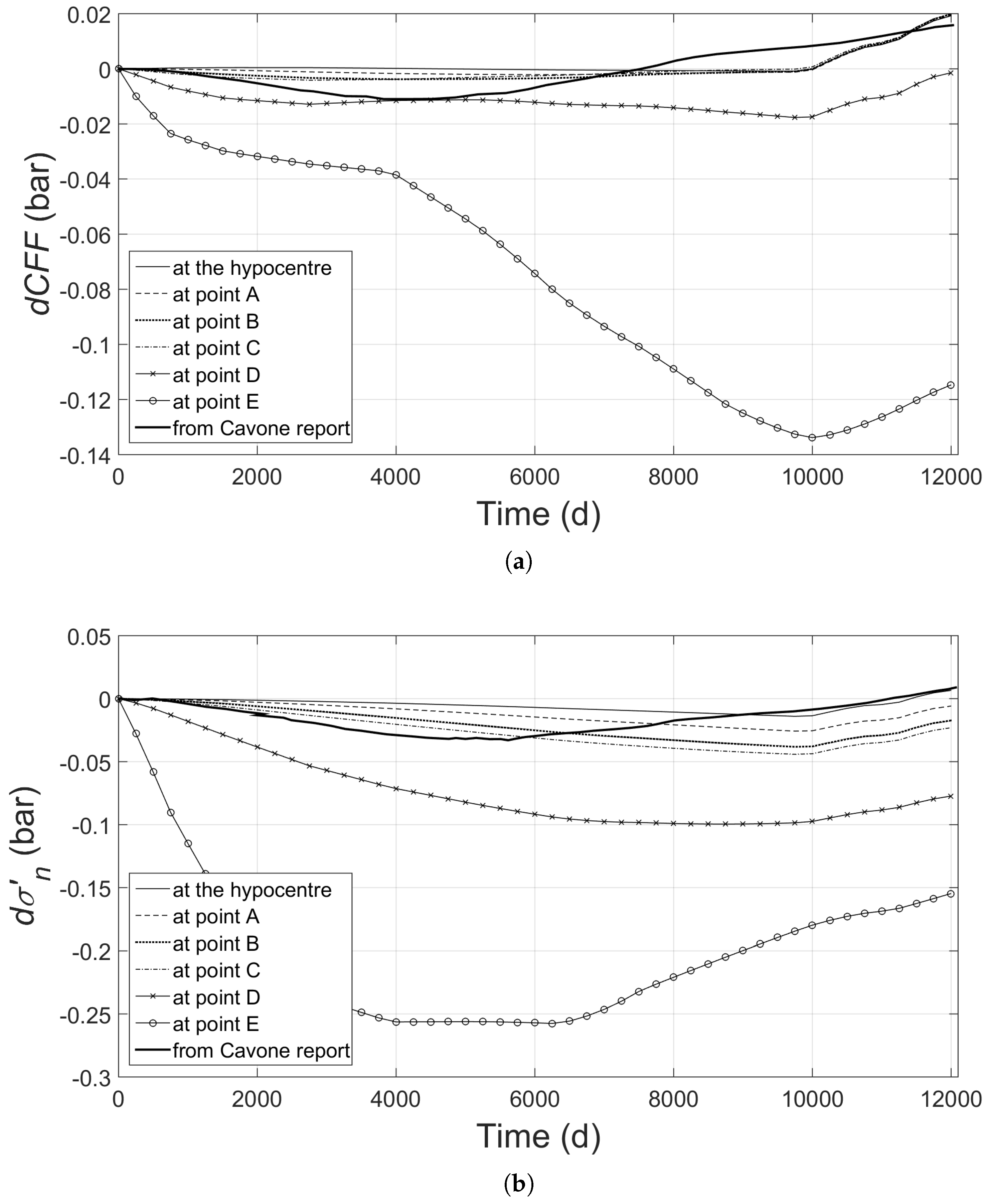
5.4. Blind Fault: Results at the Hypocentre for Variable Lower-Caprock’s Permeability
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- McGarr, A. Maximum magnitude earthquakes induced by fluid injection. J. Geophys. Res. Solid Earth 2014, 119. [Google Scholar] [CrossRef]
- Grigoli, F.; Cesca, S.; Rinaldi, A.; Manconi, A.; López-Comino, J.A.; Clinton, J.; Westaway, R.; Cauzzi, C.; Dahm, T.; Wiemer, S. The November 2017 Mw 5.5 Pohang earthquake: A possible case of induced seismicity in South Korea. Science 2018, 360. [Google Scholar] [CrossRef] [PubMed]
- Dempsey, D.; Suckale, J. Physics-based forecasting of induced seismicity at Groningen gas field, the Netherlands. Geophys. Res. Lett. 2017, 44. [Google Scholar] [CrossRef]
- Convertito, V.; Catalli, F.; Emolo, A. Combining stress transfer and source directivity: The case of the 2012 Emilia seismic sequence. Sci. Rep. 2013, 3, 3114. [Google Scholar] [CrossRef]
- King, G.; Stein, R.; Lin, J. Static stress changes and the triggering of earthquakes. Bull. Seismol. Soc. Am. 1994, 84, 935–953. [Google Scholar]
- Cappa, F.; Rutqvist, J. Modeling of coupled deformation and permeability evolution during fault reactivation induced by deep underground injection of CO2. Int. J. Greenh. Gas Control. 2011, 5, 336–346. [Google Scholar] [CrossRef]
- Astiz, L.; Dieterich, J.; Frohlich, C.; Hager, B.; Juanes, R.; Shaw, J. On the Potential for Induced Seismicity at the Cavone Oilfield: Analysis of Geological and Geophysical Data, and Geomechanical Modeling. Technical Report. 2014. Available online: http://labcavone.it/documenti/32/allegatrapporto-studiogiacimento.pdf (accessed on 1 July 2014).
- Juanes, R.; Jha, B.; Hager, B.; Shaw, J.; Plesch, A.; Astiz, L.; Dieterich, J.; Frohlich, C. Were the May 2012 Emilia-Romagna earthquakes induced? A coupled flow-geomechanics modeling assessment. Geophys. Res. Lett. 2016, 43, 6891–6897. [Google Scholar] [CrossRef]
- Albano, M.; Barba, S.; Tarabusi, G.; Saroli, M.; Stramondo, S. Discriminating between natural and anthropogenic earthquakes: Insights from the Emilia Romagna (Italy) 2012 seismic sequence. Sci. Rep. 2017, 7, 282. [Google Scholar] [CrossRef]
- Minkoff, S.; Stone, C.; Bryant, S.; Peszynska, M.; Wheeler, M. Coupled fluid flow and geomechanical deformation modeling. J. Pet. Sci. Eng. 2003, 38, 37–56. [Google Scholar] [CrossRef]
- Dean, R.; Gai, X.; Stone, C.; Minkoff, S. A comparison of techniques for coupling porous flow and geomechanics. Soc. Pet. Eng. J. 2006, 11, 132–140. [Google Scholar] [CrossRef]
- Rutqvist, J.; Birkholzer, J.; Tsang, C.F. Coupled reservoir–geomechanical analysis of the potential for tensile and shear failure associated with CO2 injection in multilayered reservoir–caprock systems. Int. J. Rock Mech. Min. Sci. 2008, 45, 132–143. [Google Scholar] [CrossRef]
- Rinaldi, A.P.; Rutqvist, J.; Cappa, F. Geomechanical effects on CO2 leakage through fault zones during large-scale underground injection. Int. J. Greenh. Gas Control. 2014, 20, 117–131. [Google Scholar] [CrossRef]
- Pruess, K.; Oldenburg, C.; Moridis, G. TOUGH2 User’S Guide Version 2; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 1999.
- Itasca. FLAC3D, Fast Lagrangian Analysis of Continua in 3 Dimensions, version 2.0; Itasca Consulting Group, Inc.: Itasca, MS, USA, 2006. [Google Scholar]
- Cao, H. Development of Techniques for General Purpose Simulators. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2002. [Google Scholar]
- Pan, H.; Cao, H. User Manual for General Purpose Research Simulator; Stanford University Petroleum Research Institute: Stanford, CA, USA, 2010. [Google Scholar]
- Aagaard, B.; Kientz, S.; Knepley, M.; Somala, S.; Strand, L.; Williams, C. PyLith User Manual, version 1.7. 1; Computational Infrastructure for Geodynamics: Davis, CA, USA, 2012. [Google Scholar]
- Aagaard, B.T.; Knepley, M.G.; Williams, C.A. A domain decomposition approach to implementing fault slip in finite-element models of quasi-static and dynamic crustal deformation. J. Geophys. Res. Solid Earth 2013, 118, 3059–3079. [Google Scholar] [CrossRef]
- Jha, B. Flow through Porous Media: From Mixing of Fluids to Triggering of Earthquakes. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2014. [Google Scholar]
- Jha, B.; Juanes, R. Coupled multiphase flow and poromechanics: A computational model of pore pressure effects on fault slip and earthquake triggering. Water Resour. Res. 2014, 50, 3776–3808. [Google Scholar] [CrossRef]
- Juanes, R.; Samper, J.; Molinero, J. A general and efficient formulation of fractures and boundary conditions in the finite element method. Int. J. Numer. Methods Eng. 2002, 54, 1751–1774. [Google Scholar] [CrossRef]
- Indelman, P.; Dagan, G. A note on well boundary condition for flow through heterogeneous formations. Water Resour. Res. 2004, 40, 1–7. [Google Scholar] [CrossRef]
- Cocco, M.; Rice, J. Pore pressure and poroelasticity effects in Coulomb stress analysis of earthquake interactions. J. Geophys. Res. Solid Earth 2002, 107, 2–17. [Google Scholar] [CrossRef]
- Biot, M. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Rice, J.; Cleary, M. Some basic stress-diffusion solutions for fluid-saturated elastic porous media with compressible constituents. Rev. Geophys. Space Phys. 1976, 14, 227–241. [Google Scholar] [CrossRef]
- Detournay, E.; Cheng, A.D. Fundamentals of poroelasticity. In Comprehensive Rock Engineering: Principles, Practice and Projects; Pergamon Press: Oxford, UK, 1993; Volume II, Chapter 5; pp. 113–171. [Google Scholar]
- Assomineraria. Rapporto ambientale 2015—Attività Oil&Gas; Technical Report; Associazione Mineraria Italiana per l’industria Mineraria e Petrolifera: Roma, Italy, 2015. [Google Scholar]
- Thiem, G. Hydrologische Methoden; J. M. Gebhardt: Leipzig, Germany, 1906. [Google Scholar]
- Styles, P.; Gasparini, P.; Huenges, E.; Scandone, P.; Lasocki, S.; Terlizzese, F. Report on the Hydrocarbon Exploration and Seismicity in Emilia Region; Technical Report; International Commission on Hydrocarbon Exploration and Seismicity in the Emilia Region (ICHESE), Regione Emilia Romagna: Bologna, Italy, 2014. [Google Scholar]
- Fan, Z.; Eichhubl, P.; Gale, J. Geomechanical analysis of fluid injection and seismic fault slip for the Mw4. 8 Timpson, Texas, earthquake sequence. J. Geophys. Res. Solid Earth 2016, 121, 2798–2812. [Google Scholar] [CrossRef]
- Byerlee, J. Friction of rocks. Pure Appl. Geophys. 1978, 116, 615–626. [Google Scholar] [CrossRef]
- Hardebeck, J.; Nazareth, J.; Hauksson, E. The static stress change triggering model: Constraints from two southern California aftershock sequences. J. Geophys. Res. Solid Earth 1998, 103, 24427–24437. [Google Scholar] [CrossRef]
- Pezzo, G.; Boncori, J.; Tolomei, C.; Salvi, S.; Atzori, S.; Antonioli, A.; Trasatti, E.; Novali, F.; Serpelloni, E.; Candela, L.; et al. Coseismic deformation and source modeling of the May 2012 Emilia (Northern Italy) earthquakes. Seismol. Res. Lett. 2013, 84, 645–655. [Google Scholar] [CrossRef]
- Bader, A.; Fisher, Q.; Harris, S. The importance of incorporating the multi-phase flow properties of fault rocks into production simulation models. Mar. Pet. Geol. 2005, 22, 365–374. [Google Scholar]



| E | 55 | [GPa] | Young’s modulus |
| 0.28 | [-] | Poisson’s ratio | |
| 2600 | [kg/m] | Rock density | |
| 0.1 | [-] | Porosity | |
| 0.3–1 | [mD] | Reservoir layer’s permeability | |
| 0.001 | [mD] | Upper and lower caprock-layers permeability in the model of Section 3 | |
| 1.013 | [mD] | Upper caprock layer’s permeability | |
| 0.1–0.001 | [mD] | Lower caprock layer’s permeability | |
| 1.013 | [mD] | Fault permeability | |
| 0.8 | [-] | Biot’s coefficient | |
| 0.6 | [-] | Friction coefficient |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benvenuti, E.; Maurillo, G. Finite Element Modelling of Coupled Fluid-Flow and Geomechanical Aspects for the Sustainable Exploitation of Reservoirs: The Case Study of the Cavone Reservoir. Geosciences 2019, 9, 213. https://doi.org/10.3390/geosciences9050213
Benvenuti E, Maurillo G. Finite Element Modelling of Coupled Fluid-Flow and Geomechanical Aspects for the Sustainable Exploitation of Reservoirs: The Case Study of the Cavone Reservoir. Geosciences. 2019; 9(5):213. https://doi.org/10.3390/geosciences9050213
Chicago/Turabian StyleBenvenuti, Elena, and Giulia Maurillo. 2019. "Finite Element Modelling of Coupled Fluid-Flow and Geomechanical Aspects for the Sustainable Exploitation of Reservoirs: The Case Study of the Cavone Reservoir" Geosciences 9, no. 5: 213. https://doi.org/10.3390/geosciences9050213
APA StyleBenvenuti, E., & Maurillo, G. (2019). Finite Element Modelling of Coupled Fluid-Flow and Geomechanical Aspects for the Sustainable Exploitation of Reservoirs: The Case Study of the Cavone Reservoir. Geosciences, 9(5), 213. https://doi.org/10.3390/geosciences9050213






