Edge Detectors as Structural Imaging Tools Using Aeromagnetic Data: A Case Study of Sohag Area, Egypt
Abstract
:1. Introduction
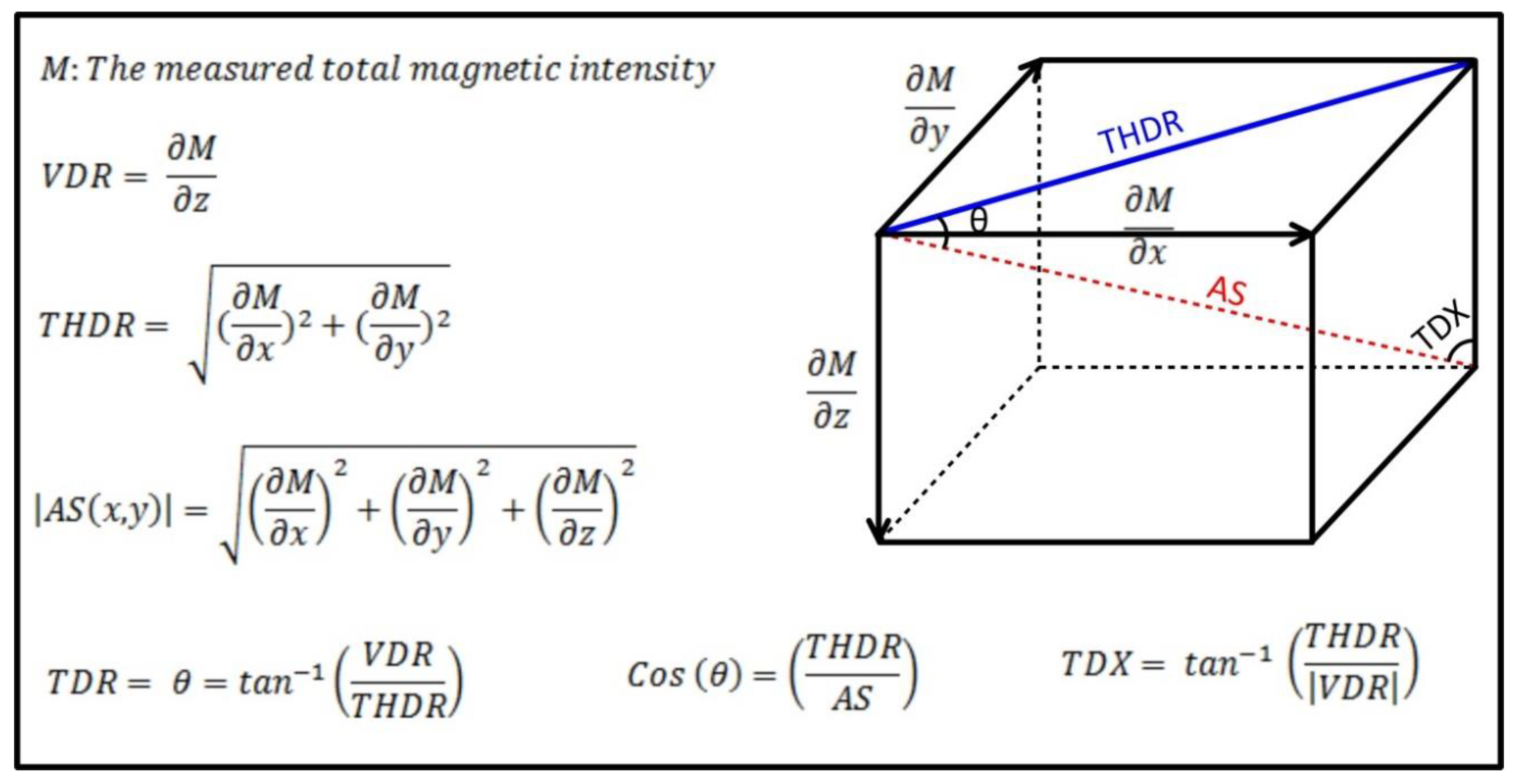
2. Background and Methodology
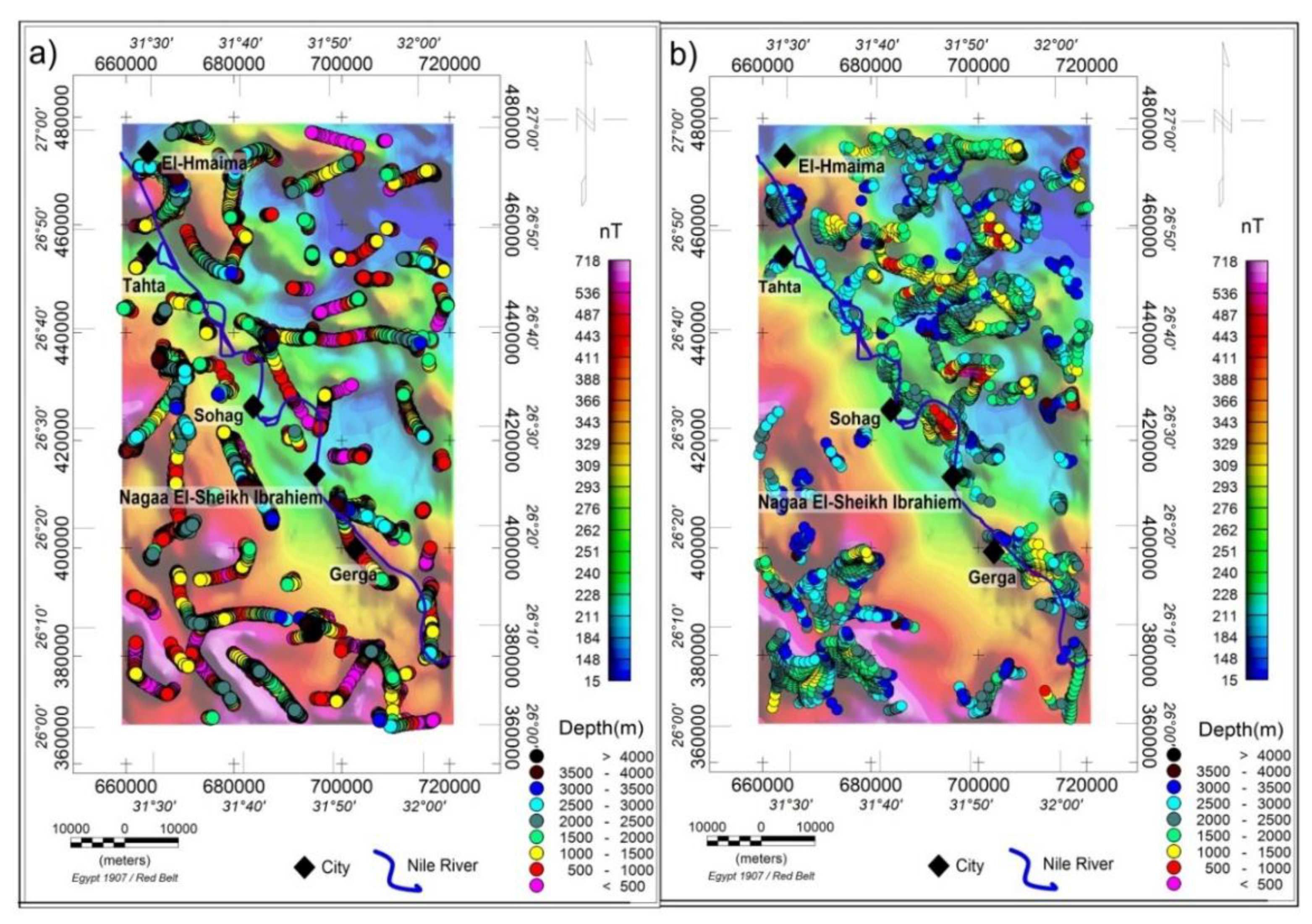
3. Application to the Aeromagnetic Data of the Sohag Area, Egypt
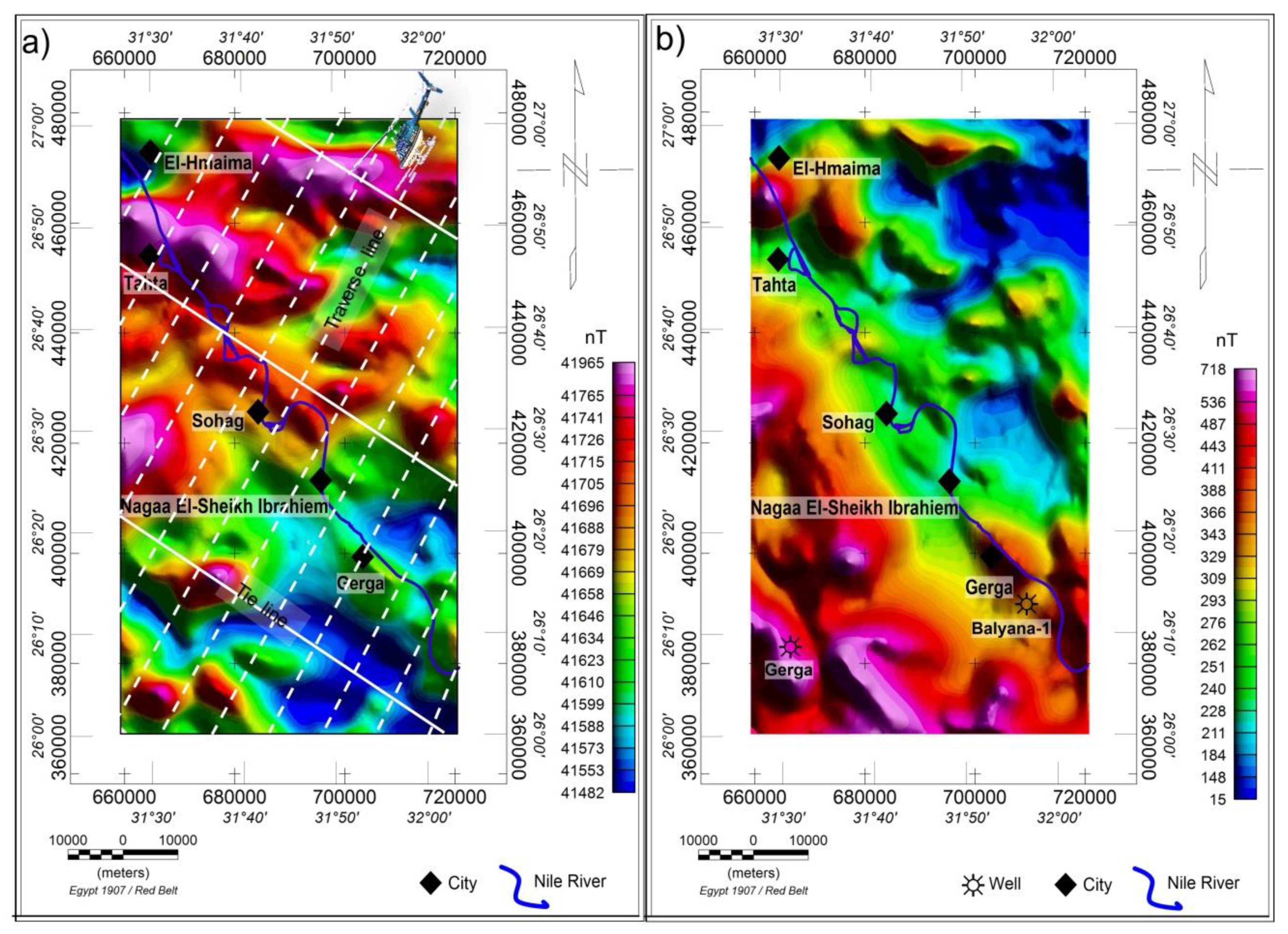
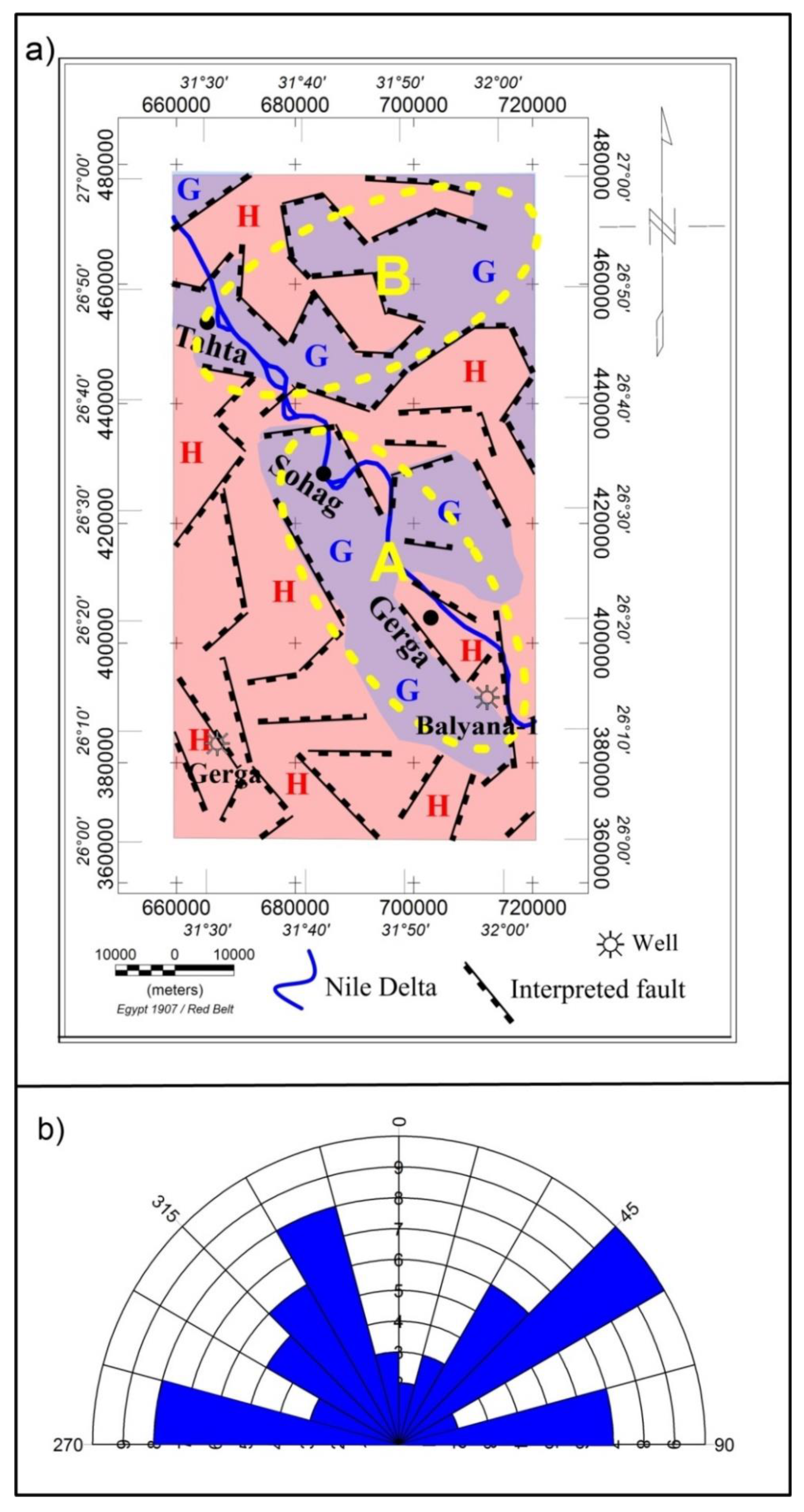
3.1. Location, Geology, and Structure of the Study Area
3.2. Airborne Geophysical Magnetic Data
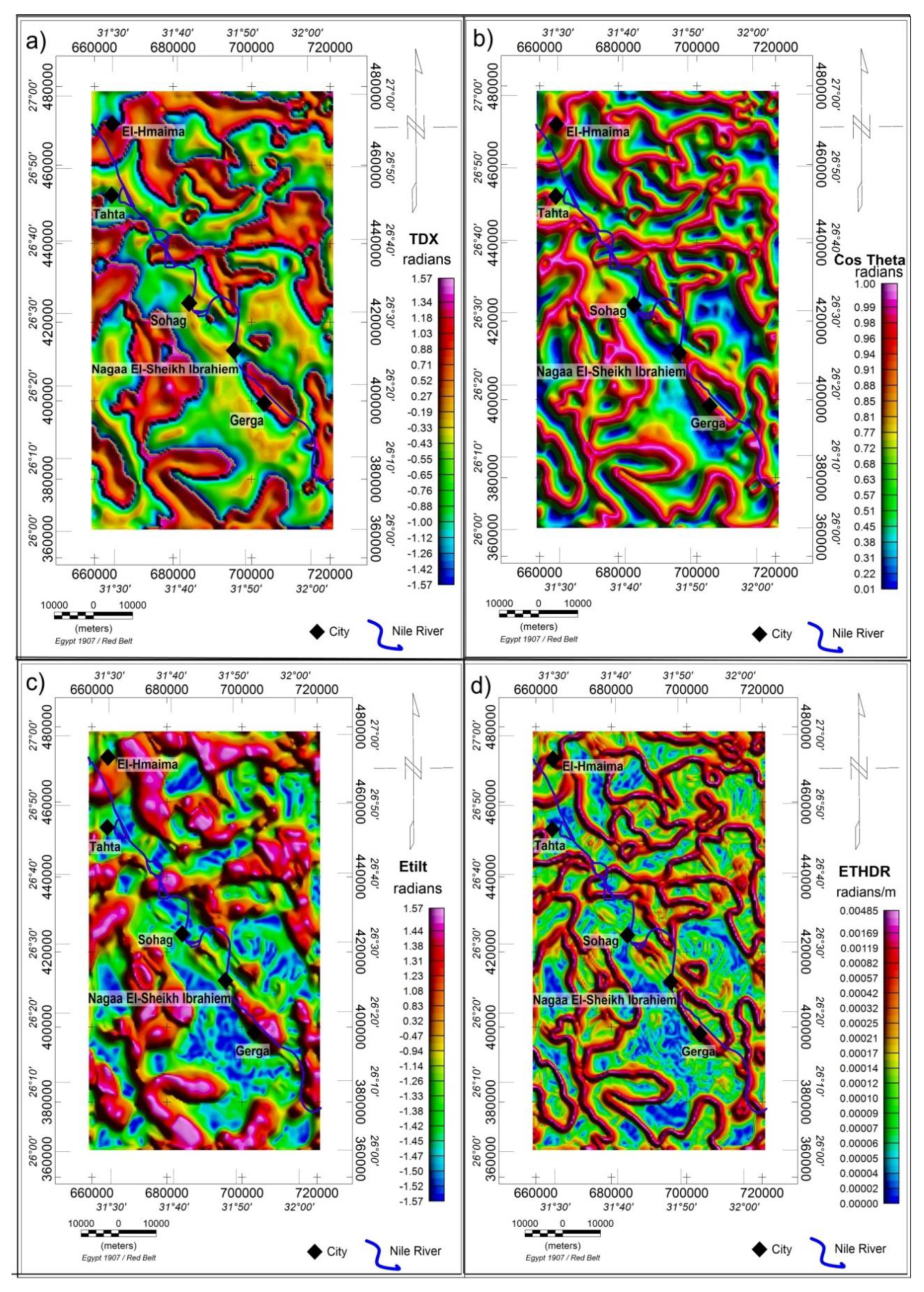
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baranov, V. A new method for interpretation of aeromagnetic maps: Pseudo-gravimetric anomalies. Geophysics 1957, 22, 359–383. [Google Scholar] [CrossRef]
- Arisoy, M.; Dikmen, Ü. Edge detection of magnetic sources using enhanced total horizontal derivative of the Tilt angle. Bull. Earth Sci. Appl. Res. Cent. Hacet. Univ. 2013, 34, 73–82. [Google Scholar]
- Oruç, B. Edge detection and depth estimation using a tilt angle map from gravity gradient data of the Kozaklı-Central Anatolia region, Turkey. Pure Appl. Geophys. 2011, 168, 1769–1780. [Google Scholar] [CrossRef]
- Verduzco, B.; Fairhead, J.D.; Green, C.M.; MacKenzie, C. New insights into magnetic derivatives for structural mapping. Lead. Edge 2004, 23, 116–119. [Google Scholar] [CrossRef]
- Ardestani, V.E.; Motavalli, H. Constraints of analytic signal to determine the depth of gravity anomalies. J. Earth Space Phys. 2007, 33, 77–83. [Google Scholar]
- Ferreira, F.J.F.; de Souza, J.; Bongiolo, A.B.S.; de Castro, L.G. Enhancement of the total horizontal gradient of magnetic anomalies using the tilt angle. Geophysics 2013, 78, J33–J41. [Google Scholar] [CrossRef]
- Evjen, H.M. The place of the vertical gradient in gravitational interpretations. Geophysics 1936, 1, 127–136. [Google Scholar] [CrossRef]
- Thompson, D.T. EULDPH: A technique for making computer assisted depth estimates from magnetic data. Geophysics 1982, 47, 31–37. [Google Scholar] [CrossRef]
- Cordell, L.; Grauch, V.J.S. Mapping basement magnetization zones from aeromagnetic data in the San Juan basin, New Mexico. In The Utility of Regional Gravity and Magnetic Anomaly Maps; Hinzc, W.J., Ed.; Society of Exploration Geophysicists: Tulsa, OK, USA, 1985; pp. 181–197. [Google Scholar] [CrossRef]
- Roest, W.R.; Verhoef, J.; Pilkington, M. Magnetic interpretation using the 3-D analytic signal. Geophysics 1992, 57, 116–125. [Google Scholar] [CrossRef]
- Miller, H.G.; Singh, V. Potential field tilt—A new concept for location of potential field sources. J. Appl. Geophys. 1994, 32, 213–217. [Google Scholar] [CrossRef]
- Fedi, M.; Florio, G. Detection of potential fields source boundaries by enhanced horizontal derivative method. Geophys. Prospect. 2001, 49, 40–58. [Google Scholar] [CrossRef]
- Wijns, C.; Perez, C.; Kowalczyk, P. Theta map: Edge detection in magnetic data. Geophysics 2005, 70, L39–L43. [Google Scholar] [CrossRef]
- Cooper, G.R.J.; Cowan, D.R. Enhancing potential field data using filters based on the local phase. Comput. Geosci. 2006, 32, 1585–1591. [Google Scholar] [CrossRef]
- Phillips, J.D. Processing and Interpretation of Aeromagnetic Data for the Santa Cruz Basin-Patahonia Mountains Area, South-Central Arizona; U.S. Geological Survey Open-File Report 02-98; U.S. Geological Survey: Reston, VA, USA, 2002.
- Oruç, B.; Keskinsezer, A. Structural setting of the northeastern Biga Peninsula (Turkey) from tilt derivatives of gravity gradient tensors and magnitude of horizontal gravity components. Pure Appl. Geophys. 2008, 165, 1913–1927. [Google Scholar] [CrossRef]
- Marson, I.; Klingele, E. Advantages of using the vertical gradient of gravity for 3-D interpretation. Geophysics 1993, 58, 1588–1595. [Google Scholar] [CrossRef]
- Cooper, G.R. Balancing images of potential-field data. Geophysics 2009, 74, L17–L20. [Google Scholar] [CrossRef]
- Ibraheem, I.M.; Gurk, M.; Tougiannidis, N.; Tezkan, B. Subsurface investigation of the Neogene Mygdonian Basin, Greece using magnetic data. Pure Appl. Geophys. 2018, 175, 2955–2973. [Google Scholar] [CrossRef]
- Reid, A.B.; Allsop, J.M.; Granser, H.; Millett, A.J.; Somerton, I.W. Magnetic interpretation in three dimensions using Euler deconvolution. Geophysics 1990, 55, 80–91. [Google Scholar] [CrossRef]
- Zhou, W.; Nan, Z.; Li, J. Self-constrained Euler deconvolution using potential field data of different altitudes. Pure Appl. Geophys. 2016, 173, 2073–2085. [Google Scholar] [CrossRef]
- Ravat, D. Analysis of the Euler method and its applicability in environmental investigations. J. Environ. Eng. Geophys. 1996, 1, 229–238. [Google Scholar] [CrossRef]
- Ibraheem, I.M.; Elawadi, E.A.; El-Qady, G.M. Structural interpretation of aeromagnetic data for the Wadi El Natrun area, northwestern desert, Egypt. J. Afr. Earth Sci. 2018, 139, 14–25. [Google Scholar] [CrossRef]
- Ghazala, H.H.; Ibraheem, I.M.; Haggag, M.; Lamees, M. An integrated approach to evaluate the possibility of urban development around Sohag Governorate, Egypt, using potential field data. Arab. J. Geosci. 2018, 11, 194. [Google Scholar] [CrossRef]
- Said, R. The Geology of Egypt; Elsevier: Amsterdam, The Netherlands, 1962; 377p. [Google Scholar]
- Mahmoud, F.A. Subsurface Geological Conditions, as Deduced from Gravity and Magnetic Data in the Area East of El-Balyana, Sohag, Egypt. Master’s Thesis, Geology Department, Faculty of Science, South Valley University, Sohag, Egypt, 1999. [Google Scholar]
- El Emam, A.E. Geophysical Study around the Epicenter of Earthquake of 1 May 1999, Sohag, Western Desert, Egypt. Master’s Thesis, Mansoura University, Mansoura, Egypt, 2002; 158p. [Google Scholar]
- Conoco. Geologic map of Egypt NG 36 NW Asyut (Scale 1: 500000); General Petroleum Company: Cairo, Egypt, 1987. [Google Scholar]
- Issawi, B.; Francis, M.H.; Youssef, E.A.A.; Osman, R.A. The Phanerozoic geology of Egypt, a geodynamic approach. Egypt. Miner. Resour. Auth. 2009, 81, 192–200. [Google Scholar]
- Said, R. Planktonic foraminifera from the Thebes formation, Luxor, Egypt. Micropaleontology 1960, 6, 277–286. [Google Scholar] [CrossRef]
- Abdel Latif, A.; El Kashouty, M. Groundwater investigation in Awlad Salameh, Southern Sohag, Upper Egypt. Earth Sci. Res. J. 2010, 14, 63–75. [Google Scholar]
- Ganoub El-Wadi Petroleum Holding Company. Geological Report of the Balyana-1 Well; The Egyptian General Petroleum Corporation: Cairo, Egypt, 1994. [Google Scholar]
- El-Shazly, E.M.; Abdel-Hady, M.; El Ghawaby, H.; El Kassas, k.; Khawasik, S.M.; El Shazly, M.M.; Sanad, S. Geologic Interpretation of Land Satellite Images for West Nile Delta Area, Egypt; The Remote Sensing Center, Academy of Scientific Research and Technology: Cairo, Egypt, 1975; p. 38. [Google Scholar]
- El-Shazly, E.M.; Abdel Hady, M.A.; El Kassas, I.A.; Salman, A.B.; El Amin, H.; El Shazly, M.M.; Abdel Megid, A.A. Geology of Kharga-Dakhla Oases Area, Western Desert, from Landsat-1, Satellite images, Nasa Landsat G-27930; Remote Sensing Center, Academy of Scientific Research and Technology: Cairo, Egypt, 1976; p. 64. [Google Scholar]
- Youssef, M.I. Structural pattern of Egypt and its interpretation. AAPG Bull. 1968, 52, 601–614. [Google Scholar]
- Ghazala, H.H.; Ibraheem, I.M.; Lamees, M.; Haggag, M. Structural study using 2D modeling of the potential field data and GIS technique in Sohag Governorate and its surroundings, Upper Egypt. NRIAG J. Astron. Geophys. 2018, 7, 334–346. [Google Scholar] [CrossRef]
- Aero Service Division of the Western Geophysical Company of America. The Total Magnetic Intensity Map of Egypt. Scale of 1: 50,000; Aero Service Division of the Western Geophysical Company of America: San Diego, CA, USA, 1983. [Google Scholar]

| Age | Epoch | Formation | Lithology | Depth (m) |
|---|---|---|---|---|
| Quaternary | Holocene | Nile Valley fill | Pebbly sandstone, siltstone, and shales being fossiliferous with coal fragments. | 893.7 |
| Tertiary | L. Eocene | Esna | Calcareous shale with sandstone, siltstone, and marl. | 1264.9 |
| Cretaceous | Campanian | Duwi | Chalk, silt, and sandstone. | 1330.2 |
| Coniacian | Quseir | Siltstone with coal and sandstone consolidated with clay-stone. | 1520.7 | |
| Taref | Claystone and kaolinitic sandstone with shale and feldspar. | 1640.4 | ||
| Pre-Cambrian | Granitic wash | 1656.3 | ||
| Basement | 1737.1 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibraheem, I.M.; Haggag, M.; Tezkan, B. Edge Detectors as Structural Imaging Tools Using Aeromagnetic Data: A Case Study of Sohag Area, Egypt. Geosciences 2019, 9, 211. https://doi.org/10.3390/geosciences9050211
Ibraheem IM, Haggag M, Tezkan B. Edge Detectors as Structural Imaging Tools Using Aeromagnetic Data: A Case Study of Sohag Area, Egypt. Geosciences. 2019; 9(5):211. https://doi.org/10.3390/geosciences9050211
Chicago/Turabian StyleIbraheem, Ismael M., Menna Haggag, and Bülent Tezkan. 2019. "Edge Detectors as Structural Imaging Tools Using Aeromagnetic Data: A Case Study of Sohag Area, Egypt" Geosciences 9, no. 5: 211. https://doi.org/10.3390/geosciences9050211
APA StyleIbraheem, I. M., Haggag, M., & Tezkan, B. (2019). Edge Detectors as Structural Imaging Tools Using Aeromagnetic Data: A Case Study of Sohag Area, Egypt. Geosciences, 9(5), 211. https://doi.org/10.3390/geosciences9050211






