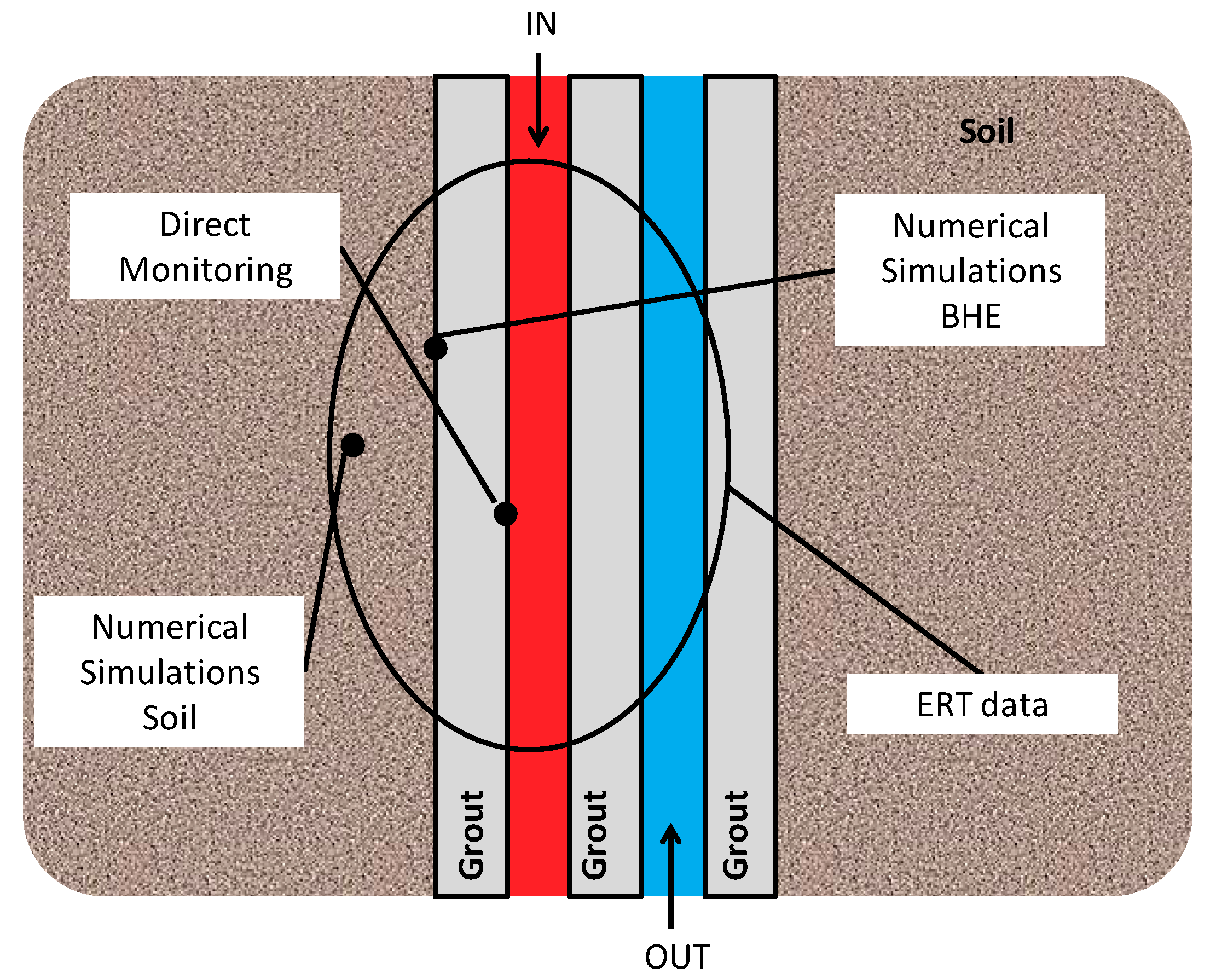
1. Introduction
Underground thermal energy storage is a technology developed in the 1970s (e.g., [
1,
2]), but it is regaining interest since the beginning of the XXI century, with research and demonstration projects being carried out mainly in North-America, Europe and China [
3,
4,
5,
6,
7]. For shallow geothermal applications close-loop systems are commonly used for storing and later retrieving energy from the underground through borehole heat exchangers (BHEs; [
8,
9,
10] and references therein). The assessment of the thermal plume generated by these technologies is of paramount importance to evaluate both the overall system’s performance and its impact on the surrounding environment. The induced temperature change can indeed stimulate trace elements mobility, redox processes and microbial activity variations [
11].
Proper monitoring strategies are therefore crucial for the quantitative evaluation of the thermally affected zone (TAZ) induced by these systems. Conventionally, the TAZ is assumed as the subsurface volume characterized by a variation of at least 1 °C from the undisturbed temperature (e.g., [
12]). Currently, the spatial and temporal control of the underground temperature evolution and the TAZ quantification can be provided through three different approaches: (i) Direct monitoring, with temperature sensors distributed along boreholes (e.g., [
4,
13]) or with fiber optic distributed temperature sensing (DTS; e.g., [
14,
15,
16] and references therein); (ii) numerical modelling of heat transport and thermal propagation, with appropriate software and detailed simulations (e.g., [
17,
18,
19]); and (iii) geophysical surveys, such as electrical resistivity tomography (ERT; e.g., [
20,
21,
22]) and self-potentials (e.g., [
23]).
All of the mentioned approaches have different strengths and limitations. Direct monitoring allows measuring reliable temperature values which are however located in specific subsoil positions and limited in space. Moreover, if temperature sensors are located within the BHEs, the recorded temperatures may be affected by the presence of the heat exchangers and may not reflect the real ground temperatures. Numerical modelling has the advantage of forecasting the impact of geothermal systems with time. Moreover, if reliably calibrated on local temperature measurements, numerical modelling results could allow for spatial imaging of the TAZ over different portions of the subsoil not covered by specific direct temperature measurements. Correct simulations however require precise knowledge of the subsoil’s relevant parameters and of their spatial variability. Information on the thermal conductivity and heat capacity of the bulk material is of primary importance. These parameters depend on several controlling factors (e.g., air and water content, density, porosity, grain size distribution, mineral composition, organic matter content and total dissolved solids in the fluid phase) which need to be properly taken into account. At the same time hydrogeological properties of the medium (e.g., hydraulic conductivity, dispersivity) could play an important role in the field geological setting as well [
24,
25,
26]. Definition of these parameters is not always easily achievable given the number of investigations necessary for a characterization of the subsurface heterogeneity and associated uncertainties. Geophysical investigations have the advantage of exploring larger volumes with respect to direct local temperature monitoring and to take into account the spatial variability of the thermal plume related to the underground conditions. However, geophysical inverse problem suffers from non-uniqueness and usually regularization is necessary for the convergence of the inversion procedure, resulting in smoother than real imaging. It is therefore important to couple all of these techniques in order to improve the global understanding of the subsoil physical variability and to validate the results with multiple monitoring strategies, whether for experimental applications (e.g., [
27,
28,
29]) or for theoretical studies in more complex media (e.g., [
30]).
The present paper aims at comparing and discussing the use of direct monitoring, numerical modelling and time-lapse 3D ERT to image the short-time spatial evolution of the temperature anomaly distribution within an underground unsaturated geological formation subjected to heat injection. The heat source generating the temperature anomaly is a borehole thermal energy storage (BTES) living lab [
31]. Several 3D ERT acquisitions carried out during a single day of operation of the plant were inverted to quantitatively image the time-lapse variation induced by the underground TAZ evolution. A 3D heat propagation numerical simulation, calibrated on the long-time plant behavior and on local temperature measurements of the plant, was used to validate the geophysical interpretation and to discuss strengths and limitations of the different approaches. The results obtained were finally compared with two recent literature works: Giordano et al. [
32], that evaluated the use of apparent and inverted resistivity data for imaging the TAZ of the same case study, but with a 2D acquisition and inversion approach; Lesparre et al. [
29], that carried out a methodology similar to the one presented here (including the use of numerical simulations), but on an open-loop system lying over a saturated heterogeneous alluvial aquifer. With respect to previous literature examples for which similar applications were presented (besides the two above mentioned see also [
33] and following works) the present case study took advantage of a full 3D acquisition and processing of the resistivity data acquired with a surface electrodes disposition, which therefore limits the impact of the geophysical monitoring with respect to more invasive approaches (e.g., borehole ERT).
2. Materials and Methods
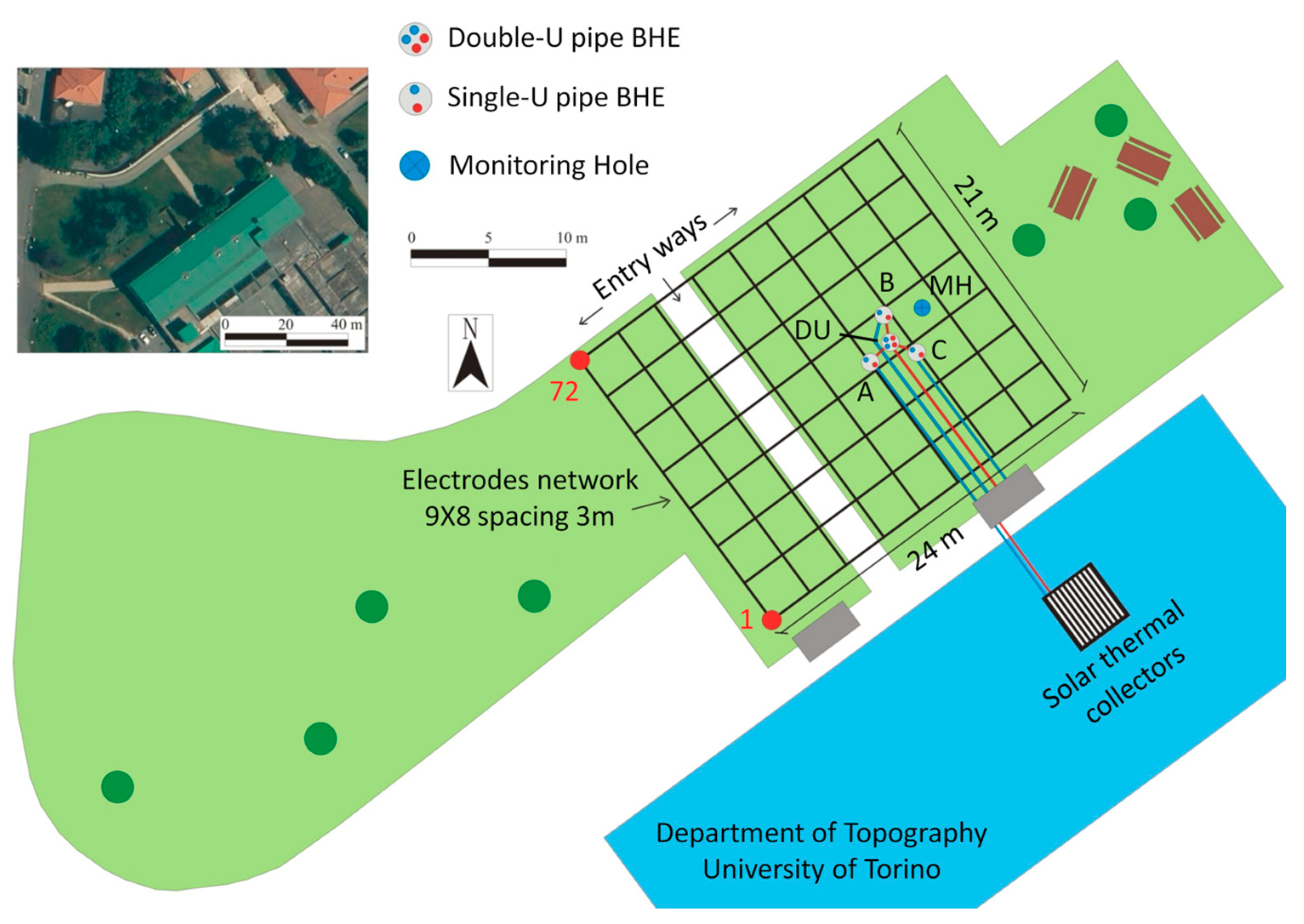
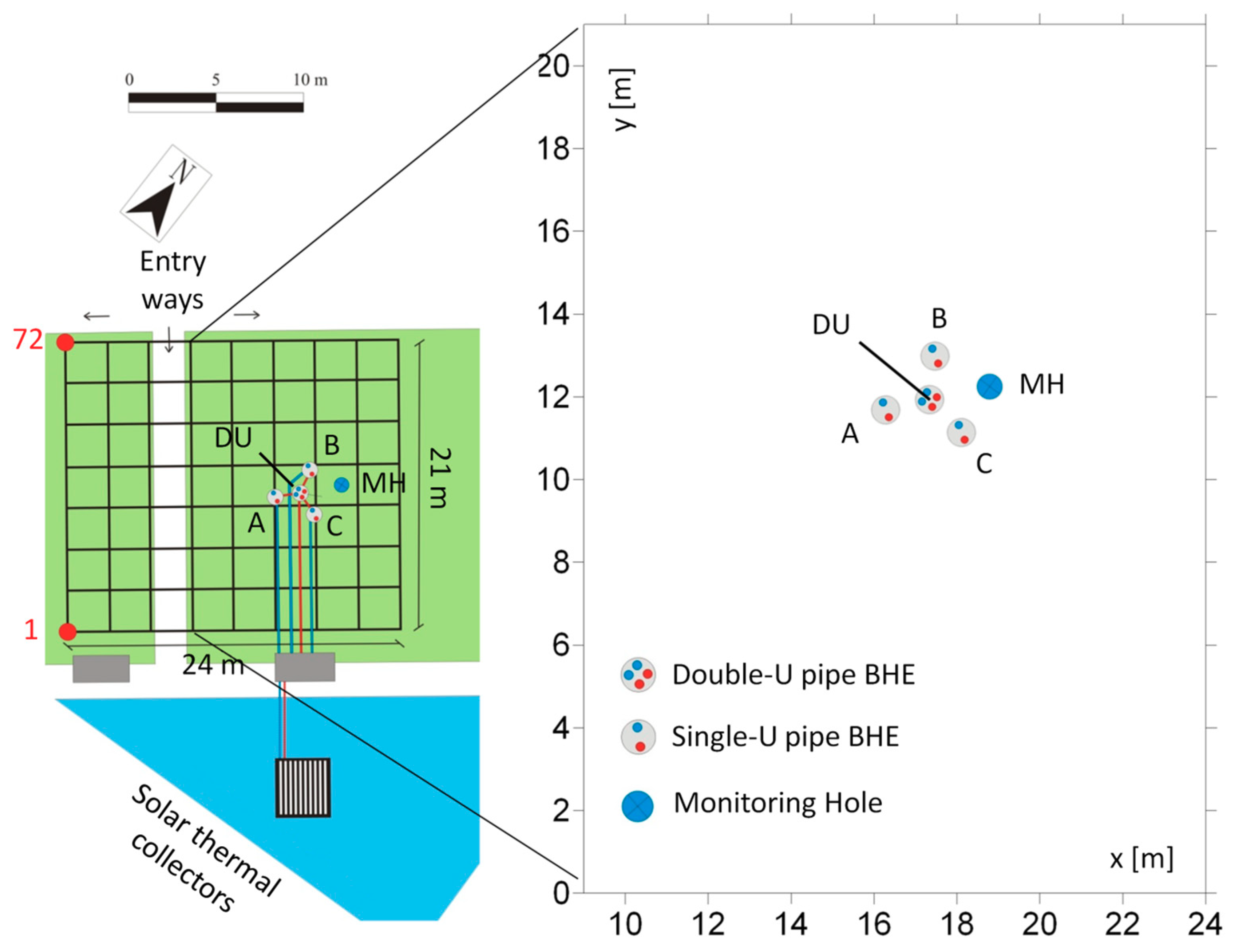
The BTES living lab was built up in Grugliasco (Torino, NW Italy) in 2013 for testing and monitoring the behavior of unsaturated sandy gravels subjected to cycles of charge/discharge of thermal energy. The plant (
Figure 1) is constituted by four 27 m deep BHEs: Three boreholes (
A,
B and
C) are equipped with single-U heat exchangers and placed at the vertexes of a 2 m side triangle; in the center of the triangle, the fourth borehole hosts a double-U heat exchanger (
DU). The top of these four BHEs stand at approximately 1.5 m depth and are covered by filling material to prevent heat dispersion to the atmosphere. At 2 m from the central double-U heat exchanger (
DU), a monitoring hole (
MH) was drilled down to 33 m and equipped with a PVC pipe (screened from 27 to 33 m) to control the fluctuations of the phreatic aquifer (static level at 35 m∙b.g.l.) and monitor the plant behavior.
The four BHEs are coupled to solar panels located on the roof of a nearby Department of Topography building to provide the heat injection. The working mode of the system was decided according to similar operating plants: A core volume benefits from the warmest heat carrier fluid (HCF) and is surrounded by an outer volume fed in cascade by the same fluid at a lower temperature. Therefore, the HCF heated by solar panels in the summertime (April–September) flows in the central double-U heat exchanger (
DU) and then in the external single-U heat exchangers (
A,
B and
C), connected in parallel, before returning back to the solar panels. The system is able to circulate the fluid, or not, according to some temperature constraints. As an example, if the difference between the solar panels and the average ground temperature is higher than 5 °C, the fluid circulation is enabled, and heat is injected into the ground. Else, the circulation is stopped in order to prevent the cooling of the ground. In this way, the plant injects thermal energy only during the day. The system has been operating since April 2014. The results presented in this paper refers to a single injection day during the first working summer (31 July 2014). The wintertime circulation is not described here because considered not important for the purpose of the paper, further detailed information can be found in [
31,
32].
2.1. Direct Temperature Monitoring
The direct temperature monitoring of the plant behavior is allowed by 20 RTD 4-wire Pt100 (measurement range from −50 to 180 °C, accuracy 5%) placed every 5 m down-hole in
A,
B,
DU and
MH boreholes. These direct temperature measurements will offer local reference temperature values to be compared with ERT results. For practical and construction reasons, the temperature sensors in the boreholes were attached to the plastic pipes of the heat exchangers. This can obviously affect the temperature recordings, that could show, during heat injection, temperatures higher than the real ground temperatures given that data are influenced by the HCF [
32]. Data from
MH are instead not disturbed by the presence of the HCF, but its distance from the boreholes makes it difficult to register a significant temperature change in a short-time window, such as the one considered in the present paper. Finally, ten temperature sensors of the same type are placed throughout the whole plant circuit and on the solar panels. These sensors, together with an ultrasonic flowmeter and an energy calculator, complete the monitoring system. All these apparatuses are managed by a data logger which continuously collects the data with a 30-min sampling interval. These collected data were used for the long-time calibration of the numerical model, described in the following section.
2.2. Numerical Simulations
Numerical 3D simulations of the heat propagation within the storage system were performed with the commercial finite element code FeFlow
® [
34]. Performed simulations follow basic state-of-the-art procedures that can be adopted in similar case studies and will offer spatial temperature maps to be compared with ERT results. For more details on the numerical simulations, including governing equations and constitutive laws, please refer to [
34,
35,
36].
A 3D volume of 50 m × 50 m × 50 m was modelled and spatially discretized with a mesh of 373,700 triangular prismatic elements. In the FeFlow environment, BHEs are simulated as one-dimensional elements that vertically connect the nodes along their intersecting edges; the HCF circulates inside the pipes and the heat exchange with the medium is governed by the heat conduction with the surrounding grout and geological underground [
34]. The specific BHE tool implemented in FeFlow
® was adopted to solve the heat transport equation, where the temperature is subject to a set of Dirichlet, Neumann and Cauchy types’ boundary conditions. This tool makes use of the analytical solution proposed by [
37] to solve the heat governing equations within the BHE. This approach, that assumes local steady state conditions and immediate thermal equilibrium between inlet and outlet pipes, was proved to output valuable results when the heat load is constant for times longer than 2–3 h [
35].
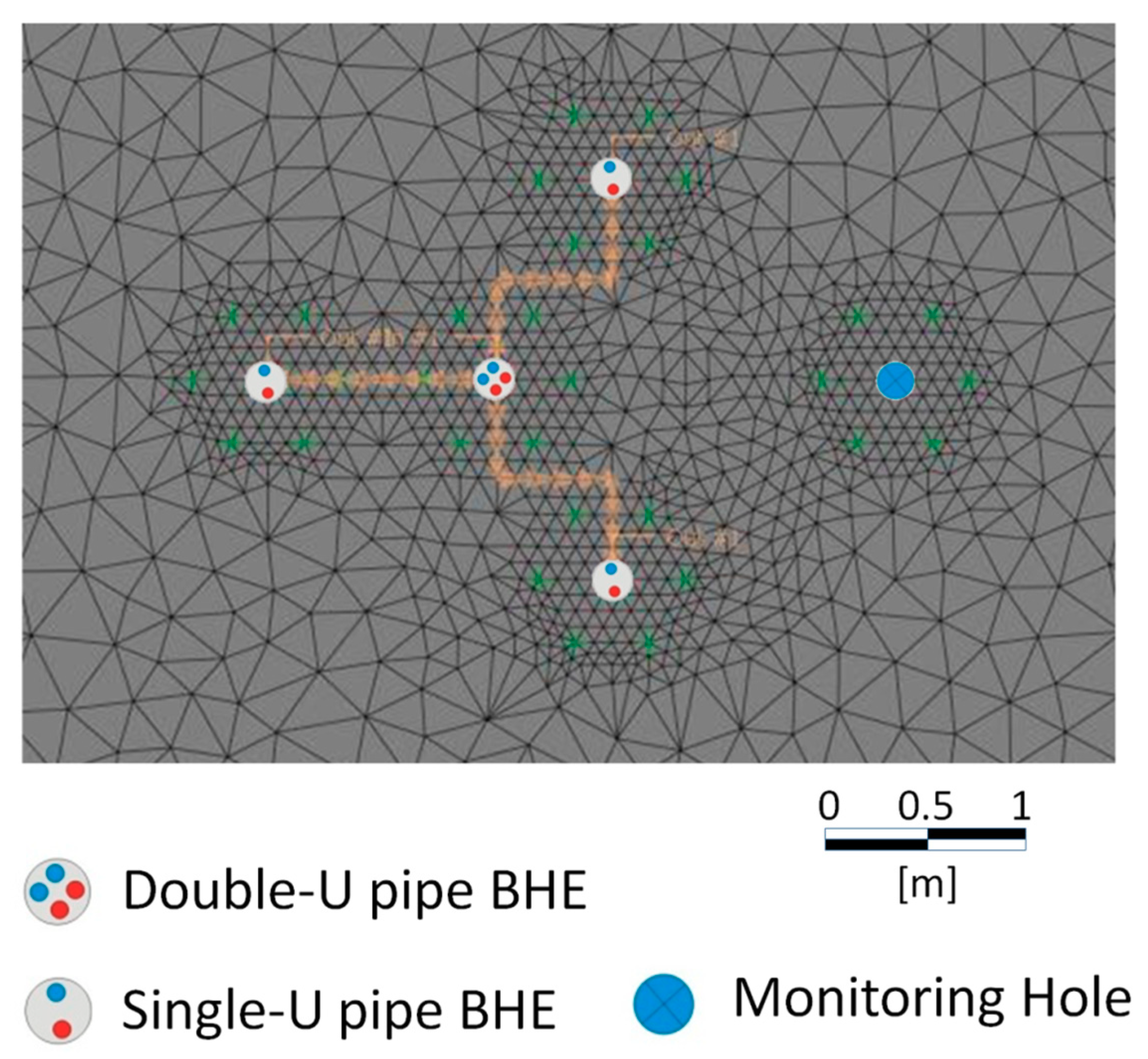
Detailed meshing around BHEs is essential to guarantee the stability and convergence of the simulations. This has been obtained by fixing the position of the nodes around the BHEs in order to allow for a mesh refinement structured in a symmetric shape around them (
Figure 2). An
n value equal to 6 was chosen according to [
35] in order to have an optimal nodal distance of 0.45 m and thus ensure numerical stability and accuracy. Mesh elements’ dimensions around BHEs are of the same order of the BHEs diameter. The dimensions of the elements increase instead further away from the BHEs. The structured mesh was then extended in the vertical direction with 50 layers 1 m thick. The BHEs connection has been simulated consistently with the plant setup (
Figure 2) with the central double-U heat exchanger (
DU) connected directly to solar panels and then the external single-U heat exchangers (
A,
B and
C) connected in parallel.
A constant temperature initial condition, equal to the undisturbed ground (14.2 °C), was assigned to the whole model for the long-term simulations. Hydraulic head equal to zero was assigned as both initial and boundary fluid flow conditions. The hydraulic head remained zero through all the simulations to reflect the water table condition at the site.
Input parameters for the simulations are related to both the plant operation and subsoil properties. In
Table 1 instantaneous values of flow rate, inlet/outlet HCF temperature difference, power and energy transferred to the ground from the monitoring data of 31 July are reported. These data were used as input for the short-term numerical simulations in the day when ERT was performed. Specifically flow rate and inlet temperatures curves were assigned as time series at the BHE elements and simulated via a well function applied to a source term [
35]. Similar data were used for the long-term simulations, that were carried out for the calibration of the subsoil model parameters and to obtain the starting temperature distribution in the investigated day. During simulations an automatic time-step control scheme was adopted for the time discretization to allow the solver to choose the most appropriate time-step depending on the change of the primary variables.
From the analysis of the drilling data related to the construction of the BHEs, and given the general geological setting of the area, the Grugliasco test site can be considered relatively homogeneous from the stratigraphic and hydrogeological point of view [
31]. Therefore, the physical properties of the solid matrix and of the interstitial fluid (
Table 2) were assigned to the entire studied volume, without vertical and/or lateral variations (homogeneity assumption). These physical properties were determined by appropriate measurements on laboratory samples of selected materials coming from a geological context which can be considered analogous to the studied site [
38]. In addition, water content distribution was fixed and considered homogeneous with no relevant temporal variations, given the short time window in which the surveys were executed. Finally, appropriate properties of the grout (TermoPlast grout—Laviosa Chimica Mineraria Spa) were also required for a complete description of the probes. Particularly, the grout thermal conductivity was obtained by laboratory measurements on grout samples (λ ~ 0.45 W m
−1·K
−1, [
38]).
The assumptions performed with respect to these parameters allowed a valid match in the long-term simulations with a reduced discrepancy with monitored plant data, therefore confirming their reliability in the present site. The homogeneity assumption could however reduce the ability of numerical simulations to correctly monitor the plume evolution if local heterogeneities are present around BHEs. This is a common problem that needs to be faced when building an appropriate numerical model for a real test site.
2.3. Electrical Resistivity Tomography
Owing to the limited dimensions of the area around the BHEs field and in the need of trade-off between spatial resolution and satisfactory depth of investigation (DOI), resistivity measurements were performed along a grid constituted by 8 parallel lines of 9 electrodes. This electrodes disposition allows a 3 m inter-electrode spacing on both
x (inline) and
y (offline) directions (see
Figure 1) resulting in a uniform spatial resolution distribution. Other alternative strategies, using a reduced inline interval, would eventually increase the resolution along the lines, but at the same time would either reduce the imaged volume, if the offline spacing was maintained proportional, or drive the resolution in the preferential inline direction. A dipole-dipole sequence was run by a Syscal-Pro georesistivimeter (Iris Instruments) with the shortest possible current injection time (250 ms) in order to record the 561 quadrupoles of the sequence as quick as possible (average total time 25 min), which is crucial given the fast dynamics of the monitored phenomenon. The acquisition sequence adopted was calibrated on similar experiences at the laboratory scale [
27]: Dipole–dipole configuration was used in order to improve data coverage, since the number of electrodes and available space are small. Moreover, dipole–dipole is more prone to evaluate lateral variation in resistivity attended around BHEs. The adopted measuring sequence allowed for satisfactory data coverage around BHEs and a DOI of about 5 m∙b.g.l. The estimated DOI is very shallow, but deep enough to investigate the heat injection in the natural subsoil provided by the borehole field, whose top is at 1.5 m∙b.g.l below the filling material.
Time-lapse measurements processed and discussed in this paper were carried out every 30 min from 09:00 to 17:00. In
Table 1 a schedule of the executed ERT surveys is also reported. Survey 0 was acquired with all the reciprocals (561 times two measurements) in order to quantify the measurement noise, as discussed by [
39]. A 10% threshold was chosen to filter out the values with low signal/noise ratio: A total of 547 measurements were selected for the full 3D inversion of later time steps. A time-lapse noise quantification has not been performed, by repeating reciprocal measurements for every acquisition, due to the requirement of short acquisition times during the following monitoring measurements.
The finite-difference code ERTLab (©Geostudi Astier s.r.l.) was adopted to carry out the resistivity data inversion. The inverted resistivity distribution is estimated upon subdivision of the investigated volume into a number of voxels. For the present case, an average voxel dimension of 0.5 m has been chosen. The resistivity of each voxel is calculated by minimizing the objective function:
where
σi is the estimated data variance,
ρa,i,m and
ρa,i,c are the measured and calculated apparent resistivities. The ill-posedness and non-linearity of the tomographic problem make it difficult to minimize the function in Equation (1). Indeed, apparent resistivities data are affected by random non-gaussian instrumental noise, difficult to model. The current approach is then based on a linearization procedure requiring an initial resistivity model, and on regularization according to the Tikhonov’s strategy [
40]. With this regularization the condition of minimum roughness of the model is used as a stabilizing function [
41]. Throughout the inversion iterations, the effect of non-gaussian noise is also appropriately managed using a robust data weighting algorithm [
42,
43]. With the adoption of the above described inversion strategies the minimizing functional is then transformed in:
where
Wi are the elements of the weighting matrix, based on estimated data variances,
ρi,c and
ρi,mo are the calculated resistivities and the resistivities of an appropriate initial model
mo (eventually null), L
i are the elements of the regularizing matrix, which could account for specific constraints on the local data and, finally, α > 0 is the Lagrange multiplier, also called roughness coefficient or smoothness or damping.
A constrain to an initial resistivity model
mo has been adopted in order to correctly image time-lapse resistivity variations. The adopted initial model to be used as constrain, and as starting model for the inversions, was the one obtained after the inversion of the survey 1 (performed at 10 AM, see
Table 1). The constrain to this initial model was obtained by means of the adoption of a Lagrange multiplier equal to 1 through all the iterations. The inversion is performed using an iterative Gauss-Newton scheme.
The difference in inverted resistivity distribution at each step is therefore obtained by subtracting the resistivity distribution achieved after the inversion of each step to the one of survey 1. This difference is then transformed into temperature, for each voxel of the model, according to Equation (3):
where Δ
ρ (%) is the resistivity difference between a defined step and the zero condition,
Tt and
T0 are temperatures at respective and initial time steps and
m is the fractional change in electrical resistivity (°C
−1). A range of 0.018 ÷ 0.025 °C
−1 has been found by several authors for
m [
33,
44,
45,
46] and it varies according to the type of fluid and sediments.
For the present case, an
m value of 0.021 °C
−1 was assumed after calibration tests at lab scale [
27] and previous geophysical investigations at the field scale [
32]. To obtain temperature differences images it is therefore possible to directly convert the resistivity difference (in percentage) of each voxel. Conversely, when the aim of the analysis is to obtain an absolute temperature value, a reference temperature (
T0) should be assumed, as shown in Equation (3). The reference temperature
T0 could be adopted as homogenous within the whole investigated ground (undisturbed ground temperature of 14.2 °C) if the aim of the investigation is the long term TAZ of the system. Otherwise, in the short term, it could be assumed from the values registered by temperature sensors in the boreholes and in the monitoring hole at the beginning of the day of measurements if a direct comparison with local data is required.
3. Results
In the following, results of direct monitoring, numerical simulations and geophysical investigations are reported and compared. Particular focus is given to evaluate the reliability of ERT data with respect to the other two temperature evolution strategies independently. Due to the limited space available to perform ERT surveys and to the presence of anthropic disturbances (i.e., entry way), known to highly affect electrical signal at the site [
32], the area and depth over which is possible to compare all of the measurements is reduced. Therefore, results are presented and discussed focusing on the zone surrounding the BHEs at the depth of 5 m∙b.g.l. The imaged area is reported in
Figure 3 and starts at 9 m from the first electrode location, after the entry way. The aim of the comparison is twofold: (i) Evaluate the differences between numerical simulations and ERT inversions in representing the TAZ of the system and (ii) evaluate the reliability of all the adopted monitoring strategies at the exact location of the direct temperature measurements in order to establish a quantitative comparison among the different methods.
3.1. Imaging TAZ
In the following, the ERT and numerical simulation temperature evolution strategies are compared at a depth of 5 m∙b.g.l. in terms of TAZ imaging. First the results from the two temperature evolution strategies are reported independently and later they are resumed and compared together with reference also to direct temperature measurements in the MH hole.
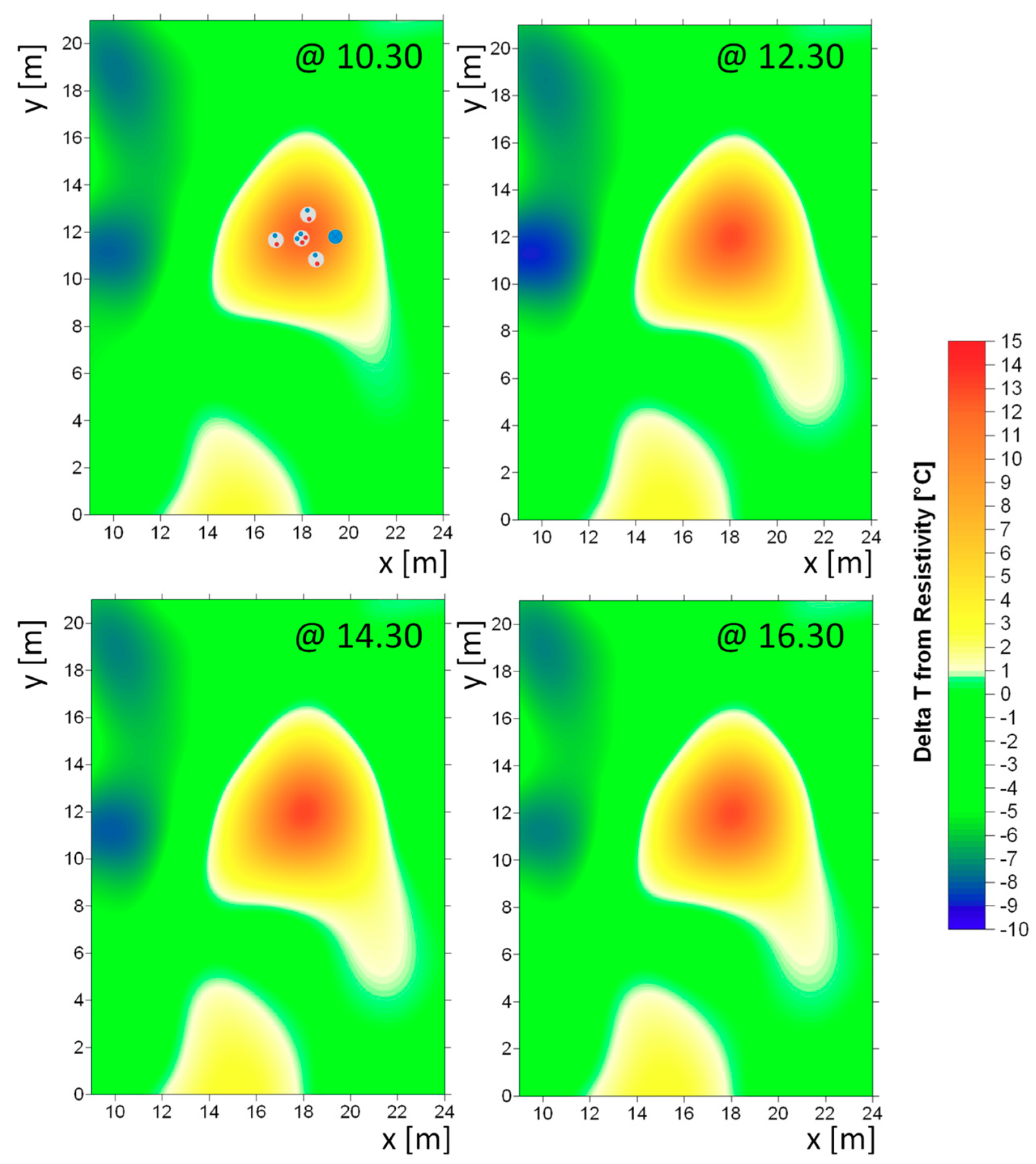
Results of temperature differences obtained from inverted resistivity data (Equation (3)) are reported in
Figure 4 for four different time steps during the monitoring day. From these results it is possible to note that geophysical data are able to locate the thermal anomaly caused by heat injection in the BHEs within the investigated area and define the spatial extension of the TAZ. The area surrounding the BHEs is depicted with an average temperature increase of about 10 °C in its central part, that decreases to about 2 °C at increasing distance from the BHEs. The shape of the TAZ partially reflects the disposition of the BHEs with an apparent elongation of the plume from borehole C in the SE direction. This could reflect local subsurface thermal and hydraulic properties heterogeneities, due to small scale differences in the subsoil or different grouting or soil coupling. The imaged temperature variation remains quite stable during the different time steps, with only localized increases near the BHE locations (see later). The main thermally affected zone caused by heat injection around the BHEs location clearly emerges from other areas in which a resistivity variation is however observed (i.e., in the top left and central bottom portions of the imaged area). The portion near the top left border of the imaged area, with decreasing temperature (increasing resistivity) with time, is known to be affected by the presence of the entry way and underlying water pipes and electric cables [
32]. The portion near the central bottom of the imaged area, with increasing temperature (decreasing resistivity) with time, could possibly be influenced by the pipes carrying the hot fluid to the BHEs. These zones are however also located at the borders of the imaged resistivity volume in reduced data coverage zones so that increased uncertainty is expected in the results.
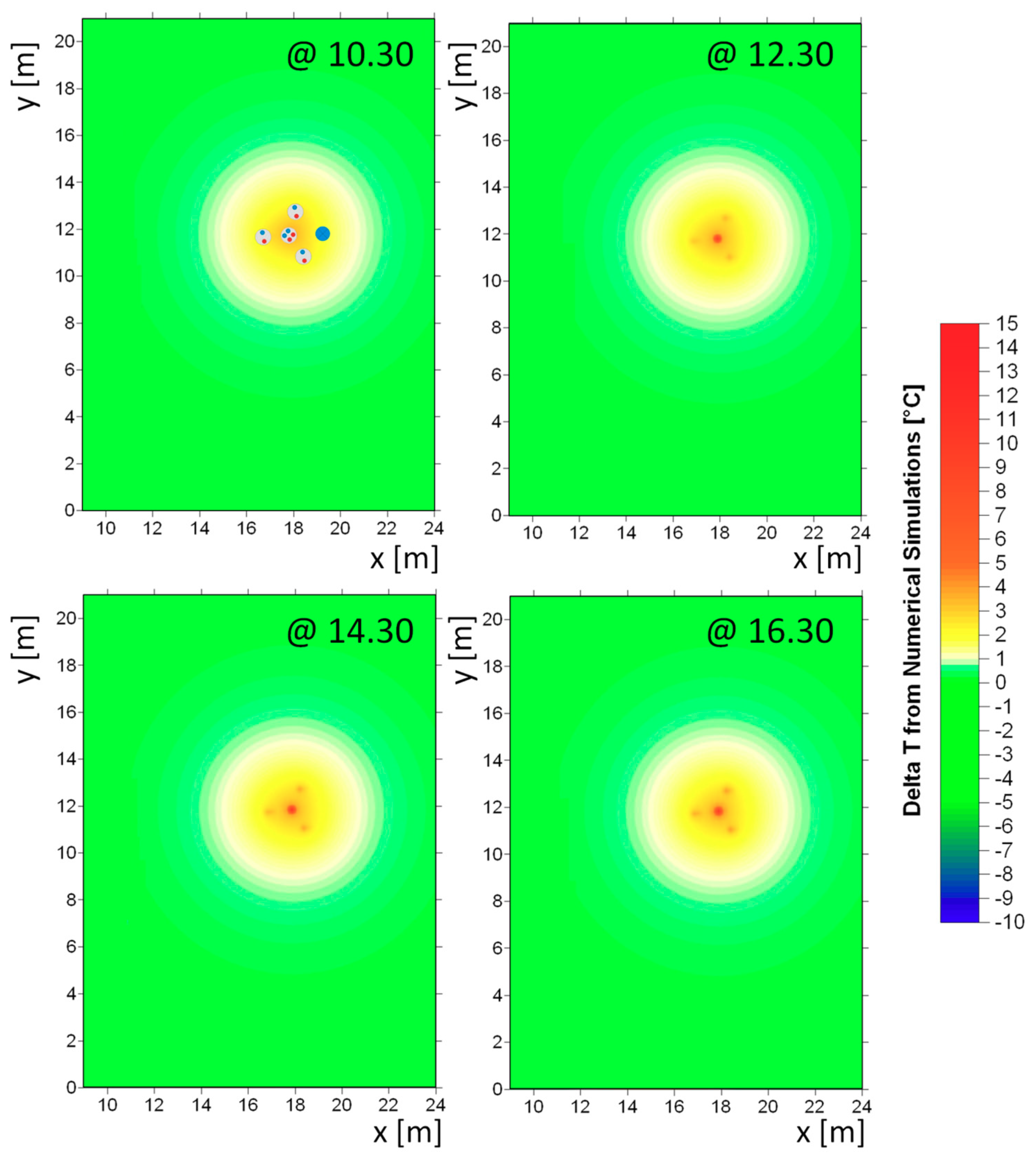
Results of temperature differences obtained from numerical simulations are reported in
Figure 5 for the same time steps of resistivity data during the monitoring day. In order to better represent these data, the temperature scale has been partially adjusted in the positive range. Indeed, numerical simulations report a more localized and less pronounced increase in temperature (around 7–9 °C), that appears strictly located at the positions of the BHEs. Still, the temperature anomaly partially reflects the BHEs disposition even if the same values of temperature differences observed in the ERT data are not obtained with numerical simulations for all the volume inside the TAZ. At an increasing distance from BHEs, the TAZ is observed to be cylindrical and symmetric, due to the homogeneity assumptions related to parameters of the numerical model.
The main difference in the TAZ imaging with the two methodologies can be related to the different procedures involved in their calculation. Particularly, ERT data do not have the necessary resolution, given the spatial distribution of measurements (related to the adopted electrode spacing), to highlight a precise temperature increase at the exact positions of BHEs, but smear out the temperature increase for all the area surrounding the BHEs. This smearing is related to the few and wide space resistivity measurements around the BHEs. Conversely, the numerical simulations are not able to recognize possible temperature differences around the TAZ, due to localized soil heterogeneities given the homogeneity assumption within the model.
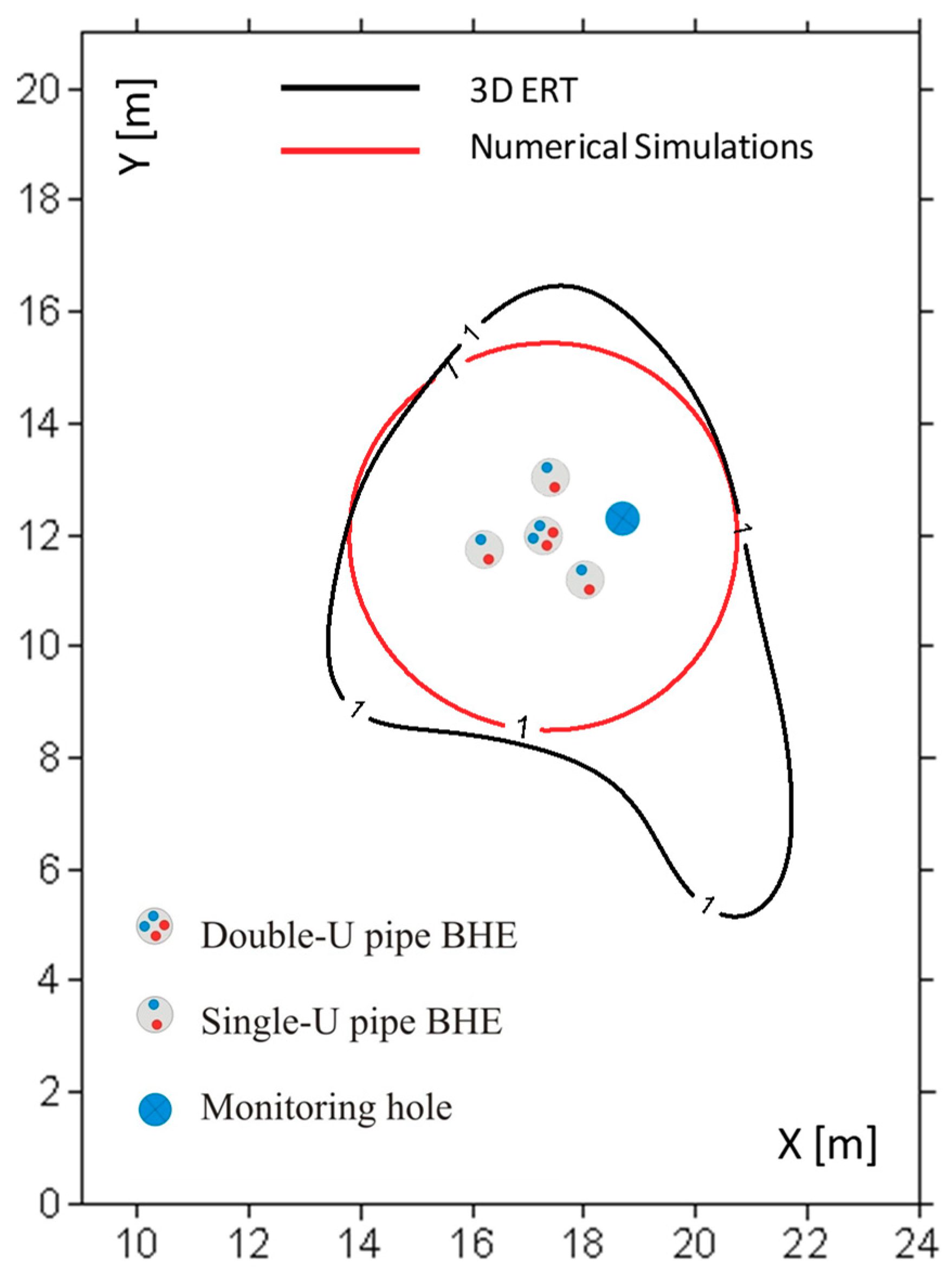
A comparison of the two TAZ (increase of 1 °C temperature from the surrounding) that can be obtained from the above reported maps is depicted in
Figure 6. Besides the above described differences, it can be observed that the similarity of the two results allows for an almost analogous quantification of the TAZ. The area depicted by ERT data is only partially overestimated with respect to numerical simulations. It is moreover important to underline that the TAZ here imaged is also related to global behavior of the charge phase of the plant, that started almost 4 months earlier than our measurements.
In the long term, results at the
MH location could help in understanding the reliability of the different approaches. Particularly, the long-term temperature differences of numerical simulations with direct temperature data recorded in
MH were observed to be around ±0.25 °C [
47], confirming the reliability of numerical simulations in reproducing the underground temperature. From the beginning of the heat injection of the plant (April 2014) MH shows a general increasing temperature trend of about 0.5 °C/month. Data in
Table 3 report a similar increase in temperature for numerical simulations and local temperature measurements, which in this location remains quite reliable, since it is not affected by the presence of the BHE.
3.2. Local Temperature Comparison
In the following the adopted strategies are compared at a depth of 5 m∙b.g.l. at the specific locations of the BHEs. Available direct monitoring data in these locations are used as a reference to discuss the evidence from numerical simulations and ERT derived temperature data. First the results from these two last approaches are reported and compared with evidence from temperature sensors and later all the strategies are resumed and compared together.
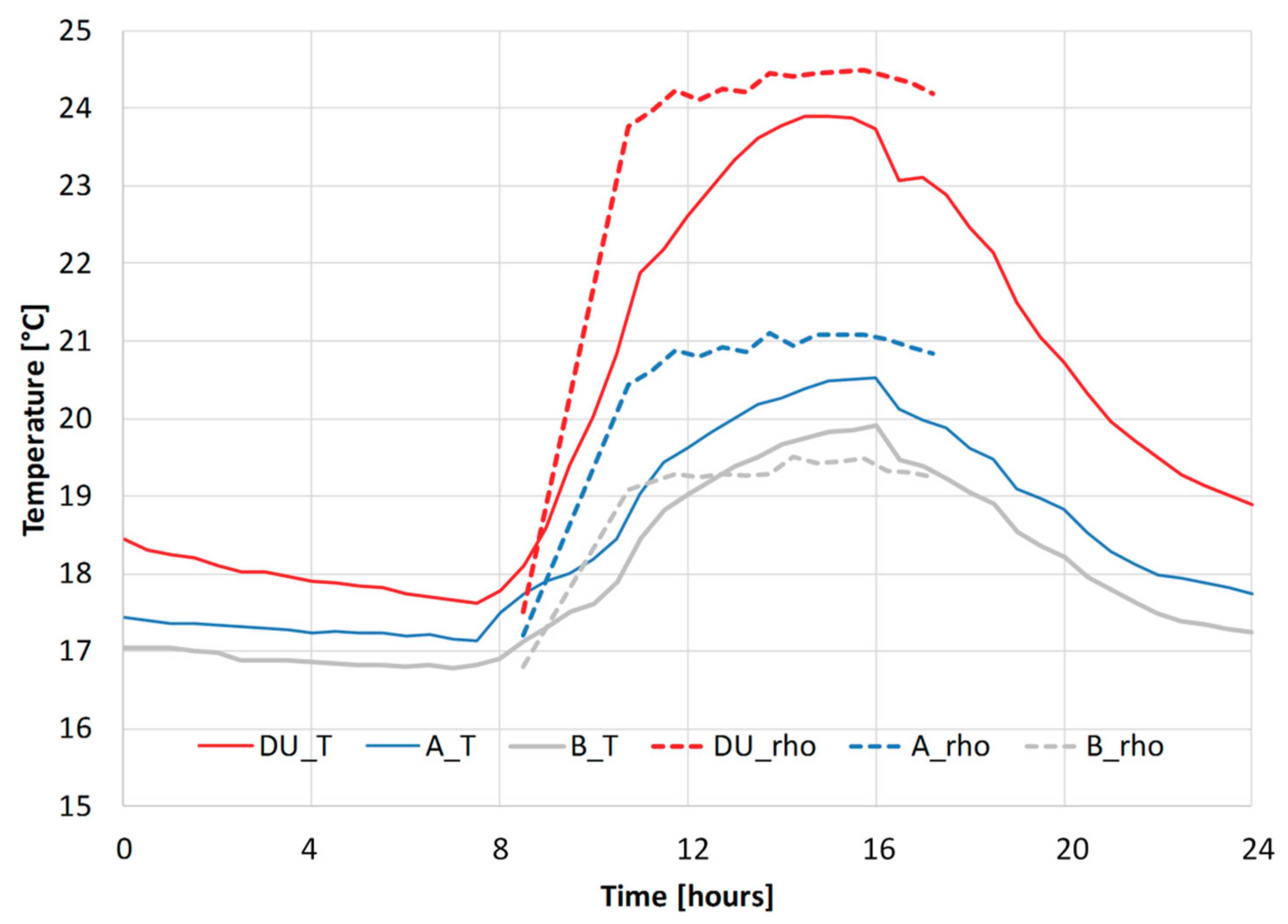
In
Figure 7, a comparison of the temperature values obtained from the interpretation of inverted resistivity data (Equation (3)) and the local direct measurements are reported for three of the BHEs, for the whole monitoring day. It can be observed that resistivity data are able to image the temperature variations near the BHEs, induced by the heat injection within the day, highlighting the difference before and after the beginning of heat injection. Resistivity-derived temperatures are only slightly overestimated for
DU and
A. This effect could be related to the low spatial resolution of resistivity measurements and to the influence of the high temperature HCF circulating within the plant. Coherently with direct observations and with the plant setup, the temperature increase is higher for the central BHE (
DU) than for the external ones (
A and
B). An unexpected difference is also observed in
A and
B. These last, being connected in parallel, should receive the same amount of heat and therefore show a more similar temperature increase within the day. The observed difference, showing a temperature increase higher in
A than in
B, is consistent in both direct measurements and ERT-derived data. This effect could be related to the different performance of the BHEs, due to dissimilar grouting or soil coupling. The fact that ERT data are able to depict the different behavior of the two external BHEs highlights the potentiality of the technique, although with a reduced resolution, to image spatial temperature variations in the underground.
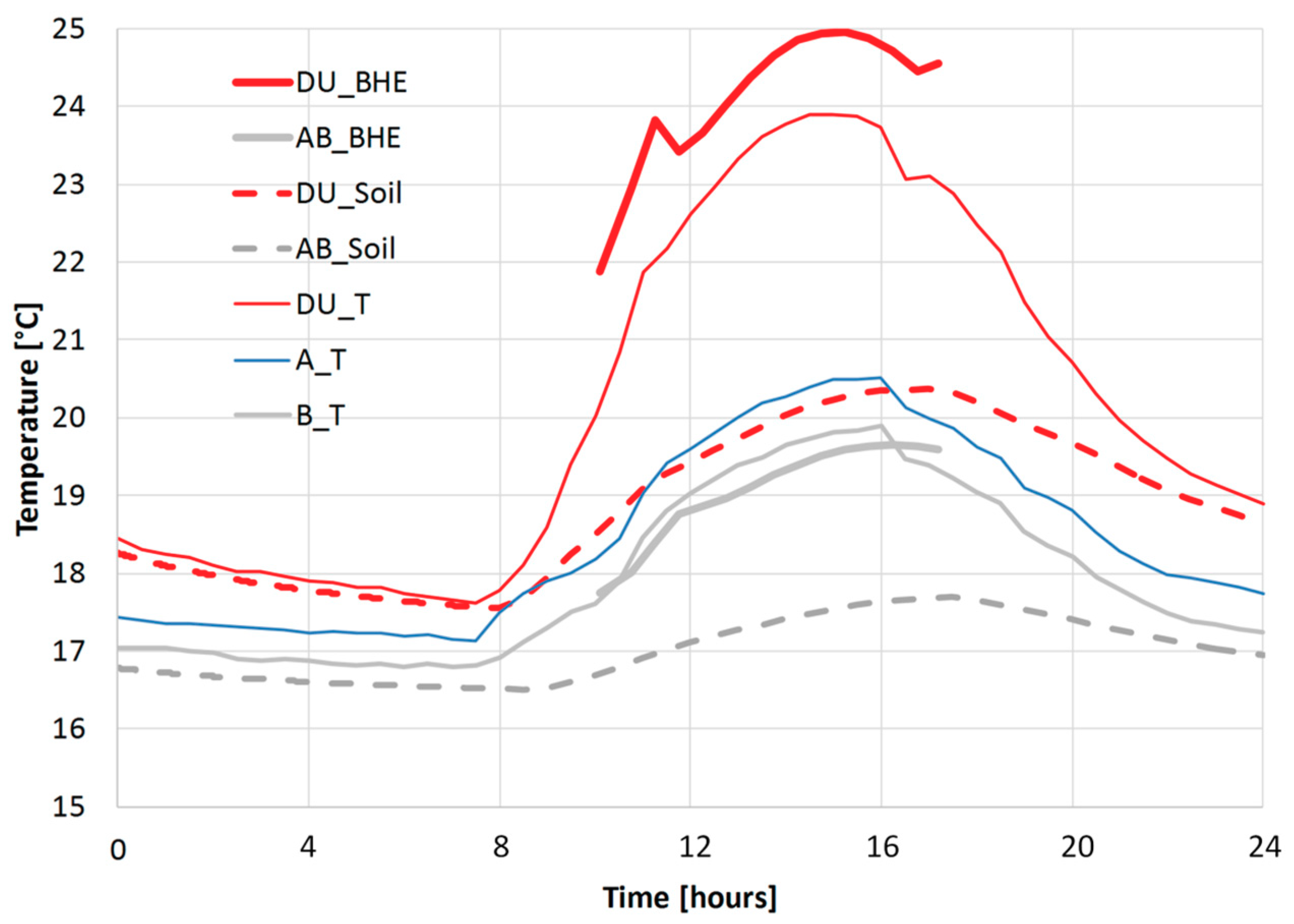
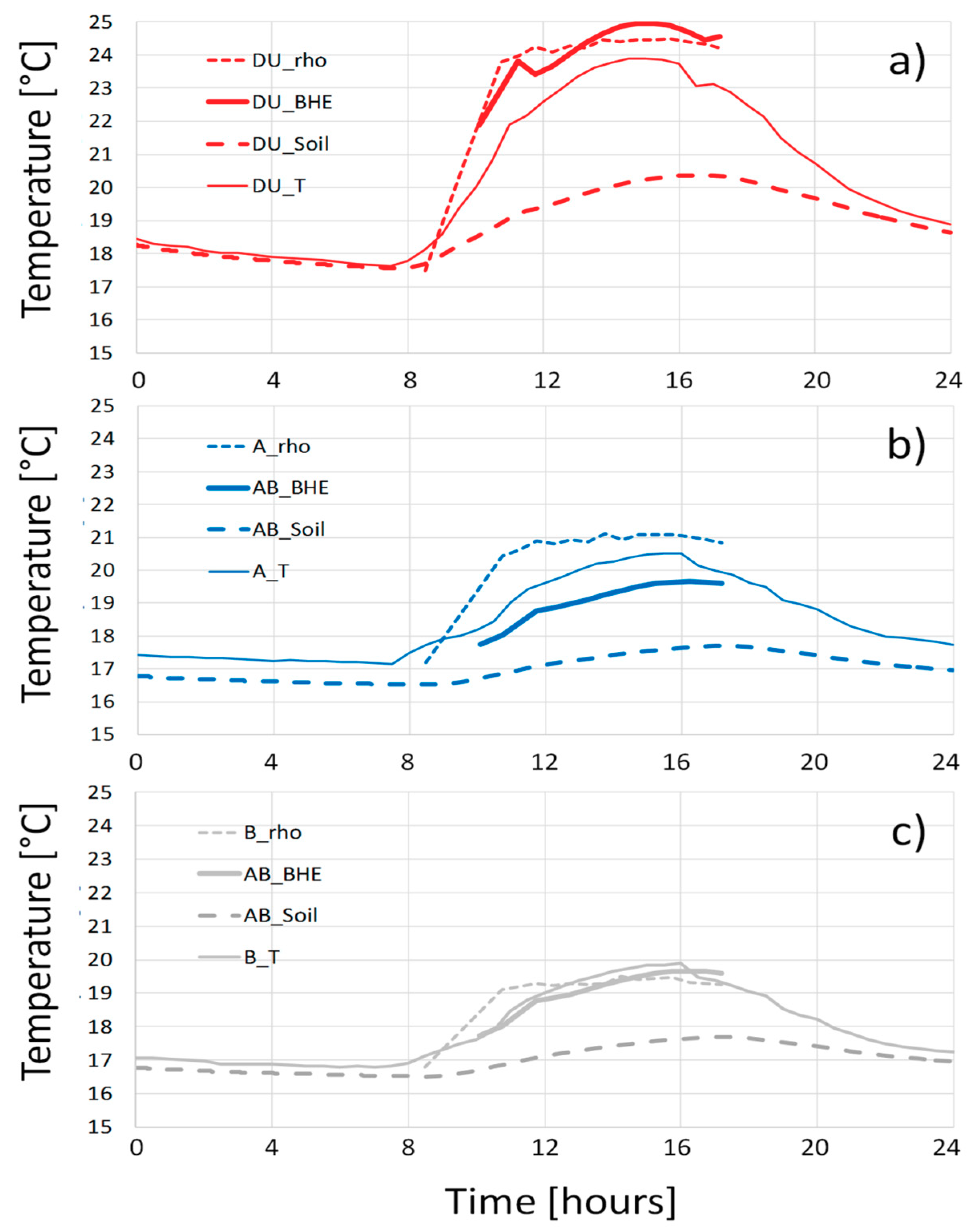
In
Figure 8, a comparison of the temperature values obtained from numerical simulations and the ones from local direct measurements are reported near three of the BHEs, for the whole monitoring day. For numerical simulations, two different temperature values are represented in almost the same BHE location: One within the BHEs (_
BHE in
Figure 8) related to a node in the mesh at the border between the grout and the soil and one outside the BHEs (_
Soil in
Figure 8) related to a node in the mesh at 10 cm from the BHE border (
Figure 9). Given the symmetry of the numerical simulation, only one temperature value common to both
A and
B is reported. From these results, it is possible to highlight that the three different temperature values of
DU (i.e.,
DU _
BHE,
DU_T from direct monitoring and
DU _
Soil) well depict the heat propagation from the HCF to the soil. These same three values also evidence differences in the results related to the different position of the monitoring points (
Figure 9).
Remarkably, during heat injection, the temperature recorded by direct monitoring is slightly lower than
DU_BHE. The two are however both significantly higher than the temperature outside the BHE (
DU_Soil) from numerical simulations. This result, already depicted in the TAZ imaging of
Figure 5, underlines a strong heat dissipation, due to both the borehole and soil thermal resistances. In the time intervals before and after heat injection starts, direct temperature measurements and _
Soil results from numerical simulations directly comparable confirming the reliability of the calibrated numerical model. A similar behavior could also be partially observed for
A and
B data, that record a temperature drop between inside and outside the BHE. However, in this location direct monitoring data in both
A and
B are higher than the one forecasted by numerical simulations (the
B result being more similar) suggesting that numerical simulations could underestimate the performance of the plant.
Finally, in
Figure 10 all the temperature evolution strategies adopted are compared together near three of the BHEs, for the whole monitoring day. It can be observed that ERT data, given their lower spatial resolution, appear to be more influenced by the temperature inside the BHEs (
Figure 9). This, and the reduced spatial data coverage, smears out the temperature increase within a subsoil volume bigger than the one actually affected by high thermal stress, as already evidenced in the TAZ maps (see
Figure 4). However, ERT data are still able to correctly depict the temperature difference among the
DU and
A/
B pipes. This difference is not observed in numerical simulations, due to the homogeneous nature of the model.
4. Discussion
The test site object of this study was already investigated with a 2D ERT setup [
32] which allowed to qualitatively image the TAZ of the system for depths greater than the ones investigated in the present work, even with the use of apparent resistivities only. Nevertheless, resistivity-derived temperature values were not close enough to direct recordings to consider 2D ERT as a valuable quantitative tool for the examined case. On-site anthropic noise (e.g., concrete, electric and water underground services) showed an important negative influence on the results.
At the same time a time lapse ERT approach similar to the one of the above mentioned paper and to the one used in this study was adopted by [
29] for the short-time monitoring of a 6-h heat injection over an open loop system. Lesparre et al. [
29] used 4D ERT acquisitions provided by 6 parallel profiles of 21 electrodes. Adopted electrode spacing (2.5 m) was similar to the one in the present work, whereas the duration of a single acquisition was longer (1.5 h) and a full 3D acquisition was not carried out owing to high-noise cross-line measurements. Results reported in their work underlined qualitatively good imaging of the TAZ for the investigated depths, but again the quantitative correspondence of resistivity-derived temperatures and direct recordings (by means of DTS) was not completely satisfactory. ERT-derived temperature values showed low variability, and were underestimated a few hours after the injection phase and overestimated later [
29].
Therefore, from a quantitative point of view, ERT data in both Giordano et al. [
32] and Lesparre et al. [
29] struggle to correctly match the temperature increase recorded by the direct monitoring (whether temperature sensors, as in [
32], or DTS, as in [
29]). Both works report on a low time-variability of the resistivity measurements, even under a relatively long time and high temperature heat injection. The results reported here showed a partially similar behavior from survey 1 on, but the difference from before and after the beginning of the plant’s circulation was validly described by the adopted constrained inversion and quantitative estimation of the induced temperature was reliably provided. ERT derived temperatures are only partially overestimated with respect to direct temperature measurements, due to the spatial resolution of the surveys and the probable influence of the circulating HCF.
The above reported considerations underline the importance of data acquisition and data inversion strategies for a correct elaboration of ERT time-lapse results. From the acquisition point of view, with respect to the cited literature examples, the adopted full 3D dipole-dipole sequence, including cross-line measurements, allowed a better spatial coverage and resulted to be more prone to evaluate lateral variations of resistivity, as is the case of a radiating thermal plume. Moreover, the presented results benefitted from the short acquisition time of each survey (25 min) and the short monitoring period (8 h), over which it can be reasonably assumed that the resistivity distribution changes were ascribable to the heat injection only. All of these conditions allowed to obtain ERT-derived temperatures closer to the direct recordings with respect to the mentioned works. Nevertheless, given the electrode spacing adopted in the present surveys (3 m), a lower spatial resolution is attained and the smoothness, due to the inversion’s regularization smears out the temperature anomaly throughout the BHE field. With respect to the previously discussed 2D and quasi-3D examples, the 3D setup adopted in this study also provided only a reduced depth of investigation such that it was not possible to image the resistivity variations as a function of depth.
From the data inversion point of view, different time-lapse inversion approaches (full 4D approaches), with a varying degree of sophistication, are available in literature to deal with data similar to the ones acquired in the previous and present works (e.g., [
48,
49,
50,
51]). For these full 4D approaches regularizations introduced in both space and time domains allow for a stabilization of the inversion and for a reduction of inversion artefacts [
49]. Moreover, these approaches usually provide improved sensitivity in regions of resistivity changes [
50] with adopted constraints, estimated on the analysis of field data, proportional to the expected degree of spatial resistivity changes. Such inversion strategies are currently non implemented in the inversion code adopted in the present work, but will be soon realized in further versions of the software (ERTLab ©Geostudi Astier s.r.l.). Applicability of these more sophisticated inversion procedures is however strictly connected with data spatial distribution and resolution. Therefore, in the present case study, given the reduced space available for the surveys and the limited investigation depth, these types of analyses were not adopted. Nevertheless, the described constrained to an initial reference background model inversion approach provided acceptable results given the available data coverage.
The inversion approach adopted by Giordano et al. [
32] was a time-lapse inversion algorithm proposed by [
48]. Conversely, Lesparre et al. [
29] used a traditional Occam’s inversion constrained to an initial reference background model. This last is similar to the one adopted in the present work. The different approaches in all these works underlined the strong influence of the reference resistivity model in the results. This observation leads to the conclusion that the inversion procedure may highly affect the results and, when possible, also the direct use of apparent resistivity data could be useful in the thermal imaging. The use of apparent resistivity data could have the advantage of limit inversion artefacts and data sophistication. The possibility of using apparent resistivity data is however limited by the possible environmental noise, by the space available for survey positioning and adopted electrode spacing. Data presented in [
32], with an electrode spacing (1 m) lower than the one adopted in the present surveys, indeed highlighted good potentiality of apparent resistivity data despite the noisy environment. In the present work, mainly due to the bigger electrode spacing, it was not possible to present accurate enough apparent resistivity maps to be used as an alternative imaging approach.
As far as the numerical simulations are concerned, the numerical model developed by [
29] was built, including more information on the subsoil heterogeneities, due to the major role played by anisotropic hydraulic conductivity on the local convection-driven heat propagation of their case study. Conversely, in the present example, relatively homogeneous underground conditions and conduction-driven heat propagation allowed to set up a simplified model. However, in both cases it turned out that the ERT-derived TAZ extensions overestimated the numerical predictions, with slightly better results in the present work, probably due to the lower complexity of the thermo-hydraulic problem. To better understand differences between the numerical model and ERT derived temperature variations synthetic ERT data from given resistivity distribution under thermal variations could be built, as performed by [
29]. At the Grugliasco site however constraints with respect to the space limitations and limited imaging depths do not allow for in depth investigation of this aspect. Nevertheless, ERT shows higher potentiality with respect to numerical modelling in highlighting local heterogeneities that cannot be taken into account in the numerical simulations when proper hydrogeological a-priori information is not available. Based on ERT results the numerical model could be eventually improved to account for potential heterogeneities evidenced in the thermal plume shape. These data could help to include highlighted hydraulic or thermal subsurface heterogeneities in the numerical model and be relevant for a better depiction of the heat transport.
To sum up, the three discussed studies confirmed ERT data to be a valid tool for underground thermal monitoring. Specific survey’s adjustments (e.g., acquisition time, monitoring period, spatial resolution), as well as inversion procedures and parameters (e.g., constraints, regularization methods) are however critical to provide quantitative estimations comparable to direct monitoring. The obtained results with the adopted surface electrodes disposition, and the constrained to initial model inversion approach, underline the potentiality of full 3D short time ERT as a valuable tool for imaging underground thermal variations and a possible alternative with respect to more invasive borehole ERT surveys (e.g., [
21]). Full 4D inversion approaches could be evaluated as a further development of the work.
5. Conclusions
Time-lapse 3D electrical resistivity surveys were carried out on the BTES living lab in Grugliasco (Torino, Italy) in order to image short-time subsurface temperature variations. Measurements were performed every half hour from 10:00 to 17:00 with a grid of 72 electrodes at 3 m spacing. Different data processing approaches were adopted in order to qualitatively and quantitatively image the TAZ induced by heat injection, being aware of the issues related to a highly man-made and noisy environment. ERT data were discussed and compared to direct temperature monitoring (local temperature sensors) and numerical simulations. The results of the different temperature evolution strategies allowed to underline the strengths and shortcomings of each of them.
The importance of combining different strategies is critical to allow for a comprehensive understanding of the system’s thermally affected zone and of the temperature variations induced in the subsoil. The borehole thermal energy storage living lab examined here presents several problems, such as unfavorable thermo-hydrogeological conditions, limited investigation space and high-level anthropic noise. However, in addition to other recent literature works, this study contributed to highlight the potentiality of 3D ERT acquisition and inversion approach (properly calibrated with local temperature reference values) as a reliable tool for the quantitative estimation of the underground temperature evolution during short-time monitoring periods.
Future activities will encompass the equipment of the MH in Grugliasco with a fiber-optic cable to provide DTS monitoring for better constraining the inversion problem. Smaller electrode spacing together with different inversion procedures will also be adopted to increase the spatial resolution and to push further the quantitative estimation of this non-invasive and cost-effective monitoring tool. Moreover, attempts to better understand the differences between the numerical model and ERT-derived temperature variations will be undertaken with synthetic ERT data simulations and improved numerical modelling to account for heterogeneities highlighted by the ERT and possibly related to hydraulic or thermal subsurface heterogeneities.